The performance of composite schemes and hybrid CC/DFT model in predicting structure, thermodynamic and spectroscopic parameters: the challenge of the conformational equilibrium in glycine.

Abstract

The structures, relative stabilities, and infrared spectra of the six low-energy conformers of glycine have been characterized by a state-of-the-art quantum-mechanical approach allowing the bond distances, conformational enthalpies and vibrational frequencies to be determined well within chemical accuracy. Transition state structures governing interconversion among the different energy minima have also been characterized. In detail, the gas-phase thermodynamic properties (at 15 K and 410 K) of the glycine conformers considered have been obtained with a 1 kJ·mol⁻¹ accuracy, and it has been shown that the employment of DFT geometries usually reduces such accuracy by at most 0.1 kJ·mol⁻¹. As concerns molecular structures, the use of two different composite schemes allowed us to further confirm the suitability of a rather cost-effective approach and provide geometrical parameters with an overall accuracy better than 0.002 Å for distances and 1 degree for angles. Thanks to a hybrid CC/DFT approach, the infrared spectra of all conformers considered and of several deuterated isotopologues have been reproduced (when experimental data were available) or predicted with an accuracy of 10 cm⁻¹. Finally, the joint thermodynamic and spectroscopic investigation allowed us to shed some light on the possible observation of elusive conformers. On the whole, the high accuracy of the computational results allows us to draw a fully consistent interpretation of the available experimental data and to obtain a more complete characterization of the potential energy surface of glycine.

1 Introduction

The simplest amino acid, glycine (H₂NCH₂COOH), is probably the most natural prototypical system for analyzing the intrinsic structural and conformational characteristics of a peptide and protein backbone without the perturbing effect of lateral chains^1–10. This has consequently stimulated an increasing number of experimental^1,11–23 and theoretical studies^24–41, whose outcomes are, however, still not fully conclusive for a number of reasons. Although glycine is known to exist as a zwitterion in condensed phases^31,42–44, in the gas phase the neutral form becomes significantly more stable^42,43. From the experimental point of view, neutral molecules in the gas phase cannot be characterized by the mass spectrometric approaches, which have become the methods of choice for charged species. On the other hand, especially for flexible compounds, spectroscopic analyses in matrices suffer from the perturbing effect of the hosting species, whereas spectroscopy in the gas phase is more difficult^a and prone to interpretative problems. Furthermore, the most stable conformers of glycine have very different dipole-moment components, which strongly complicate an unbiased determination of their relative stabilities. The present situation is that we dispose of the infrared (IR) spectra for three rotamers^b14–16. More recently, Raman studies have pointed out the presence of an additional conformer and have allowed (via variable temperature measurements) an estimation of the relative enthalpies of three rotamers^20,21. However, the thermodynamic characterization is based on the van’t Hoff equation, whose absolute accuracy might be questionable. Lastly, a further less stable conformer and its trideuterated [ND₂,OD] isotopologue have been prepared and characterized in low-temperature matrices^22,23 and their structural and spectroscopic properties have been investigated by means of high-level computational approaches⁴⁰. From the theoretical point of view, the so-called focal point analysis^45–47 (a specific form of extrapolation technique) has provided what is claimed to be an accurate stability order for all the energy minima on the glycine potential energy surface (PES)^30,34. However, the computed enthalpies show some disagreement with experiment that might be ascribed to the employment of the rigid-rotor harmonic-oscillator approximation for a flexible system.

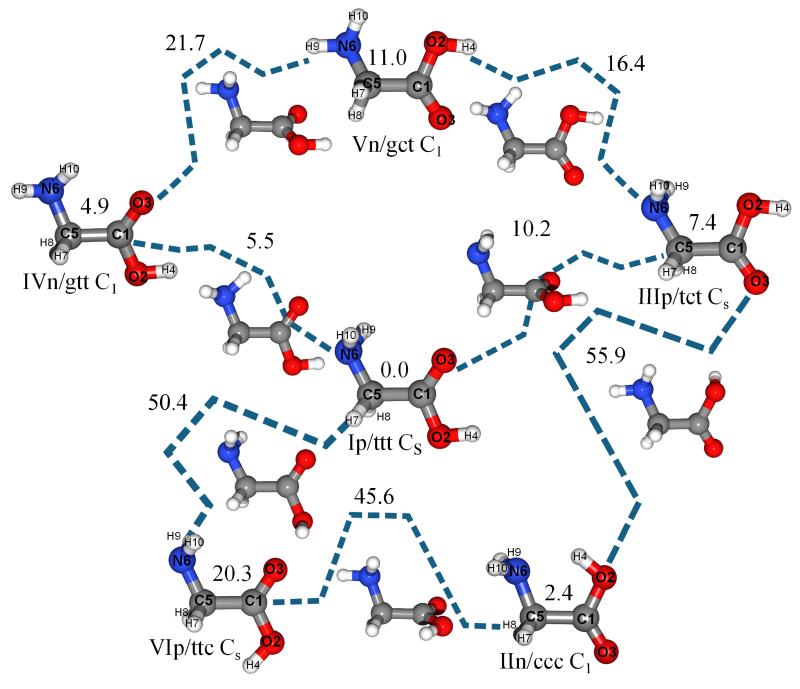
Our previous investigations on uracil and glycine showed that state-of-the-art molecular structures rivalling their experimental counterparts can be obtained also for medium-sized molecules of biological interest using the coupled-cluster (CC) ansatz together with extrapolation to the complete basis set (CBS) limit (by means of second-order Møller-Plesset perturbation theory (MP2)⁴⁸) and inclusion of core-correlation effects.^40,41,49 A similar strategy will be pursued in the present study for the six lowest-in-energy conformers of glycine. Furthermore, a more rigorous (but more expensive) approach employing exclusively CC computations including triple excitations has been exploited for the purpose of validation. This will turn out to be of fundamental importance for the subsequent energetic characterization, as semi-experimental and accurate computed equilibrium geometries are available only for a limited number of conformers^30,40,41. On top of our best-estimated equilibrium geometries, accurate electronic energies will be computed. Unstable conformers can be actually easier to characterize than their more stable counterparts due to longer lifetimes resulting from higher barriers of interconversion to the absolute energy minimum, and/or from less effective tunneling. Since a first analysis of this problem can be based on the evaluation of energy barriers connecting different energy minima, transition state (TS) structures have also been characterized. The situation is more involved for vibrational frequencies (also needed for the computation of zero-point and temperature effects on thermodynamic functions) and, especially, for intensities when the sought accuracy implies going beyond the harmonic oscillator level, thus including anharmonic effects and vibration-rotation couplings. Several studies have demonstrated that electron correlation should be included at a very refined level for harmonic frequencies, while lower computational levels (especially density functional theory (DFT) within the hybrid functional approximation) perform very well for anharmonic terms, provided that the basis sets are carefully chosen^50–58. This led to the introduction of hybrid CC/DFT schemes, which are based on the assumption that the differences between coupled-cluster and DFT anharmonic frequencies are only related to the harmonic terms^50–55. To further improve the description of the harmonic force field, composite schemes, that account for extrapolation to the basis set limit as well as inclusion of core-correlation and diffuse-function corrections, have been successfully applied to the computation of harmonic frequencies^55–57. In recent papers,^40,41,56 such a composite scheme has also been used to evaluate best estimates for IR intensities within the double-harmonic approximation. On the contrary, much less experience is available for IR and, in particular, Raman intensities beyond the harmonic level, but the first general implementation is providing encouraging results^59,60. In summary, we have at our disposal state-of-the-art integrated approaches that allow to obtain very accurate structural, thermodynamic, and spectroscopic results for one of the most important biomolecule building block characterized by the contemporary presence of different nearly iso-energetic conformers. This strategy has already been employed in previous works and is verified in the present investigation once and for all. In detail, we perform an exhaustive structural, energetic and spectroscopic investigation of the conformational PES of glycine by studying its six most stable conformers (namely, Ip/ttt, IIn/ccc, IVn/gtt, IIIp/tct, Vn/gct and VIp/ttc) and the connecting transition states. See Figure 1 for their graphical representation along with atoms and conformers labeling.^c

Fig. 1.

Six low-lying conformers of glycine and corresponding Transition States. Electronic “best/DFT” energies (kJ mol⁻¹): CBS+CV energies computed at the DFT (B3LYP/SNSD) optimized geometry. See text.

2 Methodology and Computational details

Density Functional Theory has been employed for a preliminary investigation of the stable conformers, as well as to compute harmonic and anharmonic force fields. Within the DFT approach, the standard B3LYP functional⁶¹ has been used in conjunction with the SNSD⁶² basis set. All DFT computations have been performed employing a locally modified version of the Gaussian suite of programs for quantum chemistry⁶³.

The MP2⁴⁸ and CC singles and doubles approximation augmented by a perturbative treatment of triple excitations [CCSD(T)]⁶⁴ have been employed in the composite schemes described below. Correlation-consistent basis sets, (aug)-ccp(C)VnZ (n=T,Q,5)^65–67, have been used in conjunction with the aforementioned methods. MP2 and CCSD(T) calculations have been carried out with the quantum-chemical CFOUR program package.⁶⁸

2.1 Conformational analysis

A preliminary investigation of the PES has been carried out at the DFT (B3LYP/SNSD) level in order to characterize the lowest-energy minima and the connecting transition states. Subsequently, the DFT molecular structures of the six low-lying minima have been used as starting points for further accurate investigations by means of state-of-the-art post-Hartree-Fock approaches.

To account simultaneously for basis-set and electronic-correlation effects, equilibrium structures have been determined by making use of composite schemes, in which the various contributions are evaluated separately at the highest possible level and then combined in order to obtain the best theoretical estimates. Two different approaches have actually been employed. In the first scheme the additivity approximation is directly applied to geometrical parameters, while in the second approach the various contributions are added at an energy-gradient level.

The first scheme mainly involves MP2 geometry optimizations. The MP2 method has been used in conjunction with the standard cc-pVnZ basis sets (n=T,Q) as well as a triple-zeta basis set augmented by diffuse functions, aug-cc-pVTZ. In both cases, the frozen core (fc) approximation has been adopted. To account for core-correlation effects, the core-valence correlation-consistent cc-pCVTZ basis set has been used, whereas the CCSD(T) method has been employed together with the cc-pVTZ basis set in order to improve the electronic correlation treatment. All details can be found in Refs.^40,41. In tables, the corresponding best-estimated structures are denoted as “best”.

While in Ref.⁴¹ a more refined procedure was applied only to the conformers of C_s symmetry, because of the reduced computational cost that the higher symmetry implies, in the present work the best estimate of the equilibrium structure determined by exclusively employing CCSD(T) calculations has been extended to all conformers. This permits to provide a significant set of results for verifying the good accuracy obtainable with the first scheme. This approach is more rigorous as it is based on additivity at an energy-gradient level.^69,70 The contributions considered are: the Hartree-Fock self-consistent-field (HF-SCF) energy extrapolated to the basis-set limit, the valence correlation energy at the CCSD(T) level extrapolated to the basis-set limit as well, and the core-correlation correction. The energy gradient used in the geometry optimization is given by

$$\begin{array}{ccc}\hfill \frac{{\mathit{dE}}_{\mathrm{CBS}+\mathrm{CV}}}{\mathit{dx}}=& \frac{{\mathit{dE}}^{\infty }(\mathrm{HF}-\mathrm{SCF})}{\mathit{dx}}+\hfill & \frac{d\Delta E^{\infty }\left(\mathrm{CCSD}\right(\mathrm{T}\left)\right)}{\mathit{dx}}\hfill \\ & +\frac{d\Delta E\left(\mathrm{CV}\right)}{\mathit{dx}},\hfill & \end{array}$$ (1)

where dE^∞(HF–SCF)/dx and dΔE^∞(CCSD(T))/dx are the energy gradients corresponding to the exp(−Cn) extrapolation scheme for HF-SCF⁷¹ and to the n⁻³ extrapolation formula for the CCSD(T) correlation contribution,⁷² respectively. In the expression given above, n=T, Q and 5 (n=D, T and Q for conformers of C₁ symmetry) have been chosen for the HF-SCF extrapolation, while n=T and Q have been used for CCSD(T). Core-correlation effects have been included by adding the corresponding correction, dΔE(CV)/dx, where the core-correlation energy, ΔE(CV), is obtained as difference of all-electron and frozen-core CCSD(T) energies using the core-valence cc-pCVTZ basis set. The corresponding best-estimated structures are denoted as “best-CC”.

In view of establishing accurate energy differences among the conformers as well as accurate energy barriers for their interconversion, single-point energy calculations at the best-estimated equilibrium structure (best-CC, only for minima) and at the B3LYP/SNSD optimized geometries (minima and transition states) have been carried out at the CCSD(T)/CBS+CV level of theory. CBS total energies have been determined by extrapolating the CCSD(T) correlation contribution to the CBS limit by means of the n⁻³ formula⁷²:

$$\Delta E_{\text{corr}}\left(n\right)=\Delta E_{\text{corr}}^{\infty }+{\mathit{An}}^{-3}$$ (2)

and by adding the HF-SCF CBS limit, evaluated by the expression⁷¹

$$E_{\mathrm{SCF}}\left(n\right)=E_{\mathrm{SCF}}^{\infty }+B\mathit{exp}(-Cn).$$ (3)

The cc-pVTZ and cc-pVQZ basis sets have been employed in the former equation, whereas the cc-pVnZ sets, with n=T,Q,5, have been used in the latter. As for geometries, we made use of the additivity approximation to take into account CV effects. The corresponding corrections to the total energies are given as

$$\Delta E_{\mathrm{CV}}=E_{\text{core+val}}-E_{\text{val}},$$ (4)

where E_core+val is the CCSD(T) total energy obtained by correlating all electrons and E_val is the CCSD(T) total energy computed in the frozen-core approximation, both in the cc-pCVTZ basis set.

2.2 Harmonic force field

Best-estimated harmonic force fields for all conformers of glycine have been evaluated by means of a composite scheme. The approach is similar to the first approach employed for evaluating the best-estimated equilibrium structures. At the geometries optimized at various levels of theory, harmonic force fields at the same theory level have been obtained using analytic second derivatives.⁷³ Following the procedure introduced in Ref.⁷⁴, the harmonic frequencies, ω, have been extrapolated to the CBS limit starting from the results obtained at the MP2/cc-pVTZ and MP2/cc-pVQZ levels. The extrapolated correlation contribution has been added to the HF-SCF CBS limit, which is assumed to be reached at the HF/cc-pV5Z level for the conformers of C_s symmetry and estimated by extrapolating to the CBS limit⁷¹ the results at the HF/cc-pVDZ, HF/cc-pVTZ and HF/cc-pVQZ levels for the conformers of C₁ symmetry. The consistency of the results at different levels has been checked for the Ip/ttt conformer: the CBS values extrapolated using the cc-pVDZ, cc-pVTZ and cc-pVQZ basis sets, those extrapolated using the cc-pVTZ, cc-pVQZ and cc-pV5Z sets, and the HF/cc-pV5Z values differ by less than 0.1 cm⁻¹. We also note that harmonic frequencies computed at the HF/cc-pV5Z level show differences with respect to the HF/cc-pVQZ ones largely smaller than 1 cm⁻¹, the largest differences in relative terms being ~0.7%. As for geometries, corrections due to core correlation and effects due to diffuse functions (aug) in the basis set have then been evaluated respectively at the MP2/cc-pCVTZ,

$$\begin{array}{c}\hfill \Delta \omega \left(\mathrm{CV}\right)=\omega (\text{MP2/cc-pCVTZ},\text{all})-\omega (\text{MP2/cc-pCVTZ},\text{fc})\\ \text{and MP2/aug-cc-pVTZ levels},\hfill \\ \hfill \Delta \omega \left(\text{diff}\right)=\omega (\text{MP2/aug-cc-pVTZ},\text{fc})-\omega (\text{MP2/cc-pVTZ},\text{fc})\end{array}$$

. The latter correction has been introduced since diffuse functions are required to properly describe electronegative atoms and also to recover the corresponding limitations affecting the extrapolation procedure when small- to medium-sized basis sets are employed. Higher-order electron-correlation energy contributions, Δω((T)), have been derived by comparing the harmonic frequencies at the MP2 and CCSD(T) levels, both in the cc-pVTZ basis set. The best-estimated harmonic frequencies, ω(best), are then provided by

$$\begin{array}{cc}\hfill \omega \left(\text{best}\right)=& \omega \left(\mathrm{CBS}\right(\mathrm{T},\mathrm{Q}\left)\right)+\Delta \omega \left(\mathrm{CV}\right)+\Delta \omega \left(\text{diff}\right)\hfill \\ & +\Delta \omega \left(\right(\mathrm{T}\left)\right).\hfill \end{array}$$ (5)

An analogous composite scheme has also been used to determine best estimates for the IR intensities, I(best), within the double-harmonic approximation. As extrapolation schemes have not been formulated yet for such a property, Eq. (5) has been rearranged as follows:

$$\begin{array}{cc}\hfill I\left(\text{best}\right)=& I\left(\mathrm{CCSD}\right(\mathrm{T})∕\mathrm{VTZ})+\Delta I\left(\mathrm{CV}\right)\Delta I(\mathrm{QZ}-\mathrm{TZ})\hfill \\ & +\Delta I\left(\text{diff}\right),\hfill \end{array}$$ (6)

where ΔI(QZ–TZ) is the correction due to the “MP2/cc-pVQZ - MP2/cc-pVTZ” difference, and the other contributions are defined in a similar way as for frequencies.

2.3 Anharmonic computations: vibrational energy levels, transition intensities and thermodynamics

The computations of vibrational spectra beyond the double-harmonic approximation and the vibrational contributions to thermodynamic properties have been performed by means of a Hindered-Rotor Anharmonic Oscillator (HRAO) model^58,75,76, within the vibrational second-order perturbation theory (VPT2)^77–82.

The VPT2 approach,^77–82 when applied to a fourth-order representation of the PES, provides a cost-effective route to compute accurate vibrational properties, at least for semi-rigid systems. However, for an efficient implementation to the larger molecular systems, it is necessary to overcome the problem of possible presence of singularities, known as resonances, plaguing the simplest VPT2 model. A standard practice is to remove the resonant terms from the perturbed treatment and then to treat them with a proper reduced-dimensionality variational approach. The first step of this procedure can be referred to as the deperturbed VPT2 (DVPT2) and the second one to the generalized VPT2 (GVPT2). In order to identify the Fermi resonances, the criteria proposed by Martin et al.⁸³ have been used. The GVPT2 model has shown to be reliable to study medium-sized systems, providing results accurate enough to be compared with experiment (see e.g. Refs.^60,84 and references therein). However, it is directly dependent on the reliability of the definition of the near-resonant terms, based on empirical thresholds. Alternatively, a hybrid scheme coupling the degeneracy-corrected second-order perturbation theory (DCPT2) proposed by Kuhler, Truhlar and Isaacson⁸⁵ and the standard VPT2 model, called hybrid DCPT2-VPT2 (HDCPT2), has been proposed by some of the authors⁵⁸. This scheme takes advantage of the reformulation of all potentially resonant terms in a non-resonant expression as done in DCPT2, so that there is no diverging term in the expression of the vibrational energies in the presence of Fermi resonances. Since this transformation can introduce inaccuracies far from resonance, a scaling function is used in HDCPT2 to switch to the better-suited VPT2 expression in this case. HDCPT2 offers a straightforward way to handle near-resonant terms without the need to actually identify them. This makes it a more versatile model than GVPT2 to be used as a black-box procedure, in particular whenever one has to consider a series of force fields for a given system, or a series of structures along a reaction path. It is also well suited to act as a reference to control the reliability of the Martin test in order to verify that there is no singularity present in the GVPT2 calculations.

For the calculation of thermodynamic properties, the simple perturbation theory (SPT) proposed by Truhlar and Isaacson⁸⁶ has been used to compute the partition function at the anharmonic level. In this model, the harmonic approximation of the partition function is used, but the zero-point vibrational energy (ZPVE) and fundamental frequencies are calculated at the VPT2 level. The resonance-free expression of the ZPVE proposed by Schuurman et al.⁸⁷ has been used, and vibrational energies were calculated with the HDCPT2 approach, which provides results on a par with the GVPT2 model⁵⁸.

Finally, to simulate vibrational spectra, the VPT2 formulation of transition properties proposed by some of the authors⁵⁹ has been employed. Similarly to vibrational frequencies, the equations of the transition integrals suffer from the presence of singularities due to Fermi resonances but also 1-1 resonances. For Fermi resonances, the same definition as for the energies, based on the test proposed by Martin et al., is used, while for the 1-1 resonances^39,59,88 the definition proposed in ref.⁵⁹ has been adopted.

The last comment concerns large amplitude motions (here torsions around C–N and C–C bonds). The proper treatment of torsional anharmonicity still represents a challenging aspect toward accurate thermochemical calculations for complex molecules.^76,89–95 Here, we use a generalization to anharmonic force fields of the Hindered-Rotor Harmonic Oscillator (HRHO) model⁷⁶ that automatically identifies internal rotation modes and rotating groups during the normal mode vibrational analysis. This approach employs an effective analytical approximation to the partition function for a one-dimensional hindered internal rotation that reproduces the accurate values with a maximum error of about 2% for a number of reference systems⁷⁶. The one-dimensional rotor treatment is generalized to give useful approximations to multidimensional rotor thermodynamic functions, and in the HRAO model, is further coupled to the simple perturbation theory (SPT) approach to the partition function for the other internal degrees of freedom⁵⁸.

2.4 Hybrid force field

Density functional theory has been employed to compute harmonic as well as anharmonic force fields. Within the DFT approach, the standard B3LYP functional has been used in conjunction with the SNSD basis set. Harmonic force fields have been computed as analytic second derivatives of energy,^96,97 at equilibrium structures optimized using tight convergence criteria, while the cubic (K_ijk) and semi-diagonal quartic (K_iijj and K_iijk) force constants have been obtained by numerical differentiation of the second derivatives of energy with the standard 0.01 Å step.

Recently, hybrid CCSD(T)/DFT schemes, already validated for instance in Refs.^50–55, have been proved to provide accurate results for relatively large systems^56,57, also in cluding the evaluation of accurate ZPVE⁵⁸. In the present study, two slightly different hybrid models have been adopted for frequencies and IR intensities, respectively. The hybrid CCSD(T)/DFT anharmonic force fields have been obtained in a normal-coordinate representation by adding the cubic and semi-diagonal quartic force constants computed at the DFT level to the best-estimated harmonic frequencies within the VPT2 expressions. In view of the fact that the DFT, MP2, and CCSD(T) normal modes are very similar (as expected for most cases), DFT cubic and quartic force constants have been used without any transformation. The hybrid CCSD(T)/DFT anharmonic force fields have then been used to compute spectroscopic parameters and, in particular, anharmonic frequencies, ZPVE and thermodynamic properties. With respect to intensities, anharmonic hybrid CCSD(T)/DFT IR intensities have been obtained by means of an a posteriori scheme. As discussed above, the approximation that the differences between the two levels of theory can be ascribed only to the harmonic part is made. Therefore, our best estimates have been derived by adding the DFT anharmonic corrections, $\Delta I_{\mathit{DFT}}^{\mathit{anh}}$, to our best-estimated harmonic intensities from Eq. (6):

$$I_{\mathit{CC}∕\mathit{DFT}}^{\mathit{anh}}=I^{\mathit{harm}}\left(\text{best}\right)+\Delta I_{\mathit{DFT}}^{\mathit{anh}}.$$ (7)

3 Results and discussion

3.1 Equilibrium structures

The results of the energetic investigation (in terms of energy differences with respect to the Ip/ttt conformer) are summarized in Table 1 and in Figure 1 (which also reports all transition state energies). For all local minima, the electronic energies have been computed by means of the composite scheme described in section 2.1 at the best estimated (best/best) and DFT equilibrium geometries (best/DFT). For transition states, only the best/DFT approach has been considered, except for the TS (IIp/ccc) connecting two equivalent IIn/ccc conformers, whose molecular structure has been investigated in detail. In view of future application to larger systems, it is of great interest to note the reliability of the best/DFT approach. From the comparison of the best/best and best/DFT energies, it is apparent that the differences are usually smaller than 0.1 kJ mol⁻¹, with the only exception of the IIn/ccc conformer, which is particularly challenging because of its flat PES. Although larger discrepancies are expected for the transition states, the values reported in Figure 1 should be considered well within the accuracy required for the following qualitative analysis.

Table 1.

Theoretical^a thermodynamic properties (kJ mol⁻¹) of the glycine conformers.

Conformer	Model	T = 0 K			T = 15 K		T = 410 K
		ΔEele best/DFTb	ΔEele best/bestb	Δ E ZPVE c	ΔH	ΔG	ΔH	ΔG
IIn/ccc	HO	2.45	2.29	3.82	3.82	3.82	2.80	5.41
	HO+HRd	–	–	–	3.85	3.80	2.50	4.57
	SPT(HRAO)d,e	–	–	3.73	3.77	3.72	2.45	4.41
	Exp.f						1.38
IVn/gttg	HO	4.89	4.87	4.81	4.81	4.81	4.59	5.97
	HO+HRd	–	–	–	4.82	4.82	4.68	5.99
	SPT(HRAO)d,e	–	–	4.74	4.75	4.75	4.62	5.78
	Exp.f						4.81
IIIp/tctg	HO	7.42	7.44	7.48	7.59	7.34	7.61	−1.17
	HO+HRd	–	–	–	7.55	7.28	6.59	0.04
	SPT(HRAO)d,e	–	–	7.94	7.90	7.87	6.62	9.72
	Exp.h						5.8
Vn/gct	HO	10.99	10.88	11.22	11.23	11.23	10.87	12.10
	HO+HRd	–	–	–	11.22	11.23	11.21	12.15
	SPT(HRAOd,e)	–	–	11.21	11.21	11.22	11.21	12.02
VIp/ttci	HO	20.34	20.32	19.39	19.89	19.89	20.02	20.34
	HO+HRd	–	–	–	19.80	19.77	20.08	20.24
	SPT(HRAO)d,e	–	–	19.80	19.81	19.80	20.24	20.26
TS IIp/ccc		2.87	2.92

^aConformational energies with respect to the Ip/ttt conformer. All thermodynamic properties have been computed at 1 atm.

^b“best/DFT” means CBS+CV energy computed at the DFT (B3LYP/SNSD) optimized geometry; “best/best” means CBS+CV energy computed at the corresponding optimized geometry.

^cZPVE differences added to the ΔE_ele “best/best”.

^dThe two lowest vibrations have been described by hindered-rotor contributions computed by an automatic procedure⁷⁶.

^eContributions computed by means of the HDCPT2⁵⁸ model using the hybrid CC/DFT force field, in conjunction with simple perturbation theory (SPT)^58,86 (see text for the details).

^fExperimental gas-phase data from Ref.²¹, obtained from the Raman band ratios using the van’t Hoff scheme.

^gRef.⁴¹.

^hExperimental low-temperature matrix data from Ref.¹⁵, obtained based on the integrated intensities of ν(C = O) from the samples evaporated at 358 K and 438 K.

ⁱRef.⁴⁰.

First of all, we note that the stability order pointed out in some previous works^30,34 is confirmed, with the IIn/ccc conformer being the second most stable conformer after Ip/ttt. It is also observed that the energy difference between IIn/ccc and IVn/gtt, which is the third conformer in the stability order, is reduced from about 2 kJ mol⁻¹ to 1 kJ mol⁻¹ once the ZPVE is included. The IIn/ccc conformer does not relax to the most stable Ip/ttt rotamer as the relaxation process proceeds through either IIIp/tct or VIp/ttc and requires barriers of about 50 kJ mol⁻¹ to be overcome in both cases. On the contrary, IVn/gtt can easily relax to the Ip/ttt conformer as it is directly connected to the latter through a low-energy transition state, the barrier height being less than 1 kJ mol⁻¹ with respect to IVn/gtt. Analogously, the IIIp/tct conformer is expected to be able to relax to Ip/ttt, the corresponding transition state lying less than 3 kJ mol⁻¹ above the former. We note that Vn/gct lies rather high in energy (more than 10 kJ mol⁻¹ with respect to Ip/ttt), and is directly connected with IIIp/tct and IVn/gtt through barriers of 5.5 kJ mol⁻¹ and 11 kJ mol⁻¹, respectively. Therefore, its Boltzmann population is rather low (about 2% at 410K), and its possible formation through vibrational pumping can be rather ineffective due to the already difficult detection of IIIp/tct and IVn/gtt themselves. The situation is different for the highest energy conformer considered in this work, VIp/ttc, which lies more than 20 kJ mol⁻¹ above the Ip/ttt global minimum, but is directly connected to the most stable one through a highly energetic transition state. In fact, it has been recently observed that NIR irradiation of the Ip/ttt conformer trapped in low-temperature matrices leads to the laser-induced conformational change toward VIp/ttc²², with the latter showing sufficiently long life-time due to the large barrier (30 kJ mol⁻¹) to be overcome to relax back to Ip/ttt. Moreover, the computed energies of all TS’s are lower than the laser energy employed in the NIR irradiation experiment (about 84 kJ mol⁻¹)²², thus both two-step conformational change pathways, Ip/ttt→IIIp/tct→IIn/ccc and Ip/ttt→VIp/ttc→IIn/ccc, are possible under the experimental conditions, in line with the observed increase of the IIn/ccc conformer population.

In Table 1, the gas-phase thermodynamic properties at 15 K and 410 K of the glycine conformers considered in the present study are also given along with the available experimental data. These two temperatures have been selected as they are those employed in recent IR^22,23 and Raman^20,21 experiments, respectively. We note that the harmonic approximation provides semi-quantitative results for enthalpies and free energies at 15K. At higher temperatures (here 410 K), the entropy of the IIIp/tct rotamer is strongly overestimated, also when torsions are treated by means of the hindered rotor model. Only the full HRAO approach is able to provide a reasonable relative free energy of this conformer. Some experimental estimates^15,21 are available for the relative enthalpies of the IIn/ccc, IIIp/tct, and IVn/gtt rotamers with respect to the Ip/ttt absolute minimum. Our computed values are in remarkable agreement for IVn/gtt (4.6 vs. 4.8 ± 0.3kJ mol⁻¹) and close to the upper bound of the experimental value for IIIp/tct (6.6 vs. 5.8 ± 0.6 kJ mol⁻¹), whereas the situation is less satisfactory for IIn/ccc (2.4 vs. 1.4 ± 0.2 kJ mol⁻¹). However, it must be recalled that the use of the van’t Hoff equation to estimate enthalpy differences from Raman spectra at different temperatures²¹ has a limited accuracy, not to speak about possible perturbing effects of the hosting matrix¹⁵. It is anyway remarkable that the employment of the HRAO model improves the agreement with experiment with respect to the simple harmonic approximation, the difference being non-negligible for IIn/ccc and, especially, for the IIIp/tct rotamer. From our computed data we can derive the Boltzmann population at 410K to be 65%, 18%, 4%, 12%, 2% and 0.2% for Ip/ttt, IIn/ccc, IIIp/tct, IVn/gtt, Vn/gct and VIp/ttc, respectively, while at 15K only the most stable Ip/ttt conformer is populated. On the basis of thermodynamic properties, one might expect that the IVn/gtt conformer should be rather easily detected, however this is not the case^33,41 and this rotamer has been only recently observed in the Raman spectrum of jet-cooled glycine²⁰, while its presence has not been confirmed under low-temperature rare-gas matrix conditions²² and has been only tentatively proposed in standard gas-phase experiments¹⁹. These results can be explained by the low, easy to overcome, barrier for its relaxation toward the Ip/ttt conformer, allowing IVn/gtt to convert during matrix deposition, and by possible tunneling effects, also present in low-temperature matrices. Thus, its detection is clearly more feasible in the non-equilibrium conditions of jet-cooled molecular beams, in particular close to the entrance of the nozzle, fully in line with what has already been observed²⁰. On the contrary, surprisingly high abundance of the IIIp/tct conformer in low temperature matrices (estimated to be about 8% on the basis of the IR intensities in the C=O stretching region¹⁸) can be explained by taking into account that the relaxation of Vn/gct toward IIIp/tct is more probable due to the halved (with respect to the alternative Vn/gct-IVn/gtt pathway) activation energy (about 5.5 kJ mol⁻¹). On the whole, we can conclude that our best-estimated electronic energies in conjunction with the HRAO model lead to a picture fully consistent with the experimental findings.

The best-estimated equilibrium structures of the six low-energy conformers of glycine, as obtained from the first composite scheme (“best”), are collected in Tables 2 and 3, while the results at the MP2 level using different basis sets, the extrapolated CBS structure, as well as the additional corrections (Δr(CV), Δr(diff), Δr(T)) are reported in the supplementary material (Tables S1-S6). For atom labeling, we refer the reader to Figure 1. From Tables S1-S6, it is evident that the corrections due to the extrapolation to the CBS limit, with respect to the MP2/cc-pVQZ level of theory, are of the order of 0.0005–0.003 Å, where the smaller value applies to bonds involving H. The effects due to core correlation are of the same order, with negative corrections ranging from 0.0007 to ~0.003 Å. As expected (see, for example, Refs.^49,98,99), even larger is the effect due to triple excitations, Δr(T), with corrections that can be as large as 0.005-0.006 Å, that generally decrease to 0.001 Å when H is involved in the bond length. On the contrary, inclusion of diffuse functions is less important, the effects being on average smaller than 0.001 Å. As concerns angles, we note that the corrections due to the extrapolation to the CBS limit range from 0.01 to ~0.4 degrees, that can enlarge up to ~1 degree in the case of dihedral angles. Core-correlation effects are rather small, with contributions of the order of 0.01-0.1 degrees (up to 0.2-0.3 in the case of some dihedral angles). The corrections due to diffuse functions and to higher-order correlation energy are larger; in fact, the former is on average about 0.6 degrees, while the later is about 0.3 degrees, but those effects can result in corrections as large as a few degrees for dihedrals.

Table 2.

Equilibrium structures of the Ip/ttt and II/ccc conformers of glycine. Distances in Å, angles in degrees.

Parameters	Ip/ttt				IIn/ccc				IIp/ccc
	besta	best-CCb	$r_e^{\mathrm{SE}}$ b	B3LYP/SNSD	best	best-CC	$r_e^{\mathrm{SE}}$ c	B3LYP/SNSD	best	best-CC	B3LYP/SNSD
C1-O2	1.3486	1.3476	1.34827(31)	1.3556	1.3356	1.3344	1.333(2)	1.3406	1.3348	1.3339	1.3403
C1-O3	1.2025	1.2021	1.20331(62)	1.2078	1.2001	1.1980	1.202(2)	1.2054	1.2004	1.1994	1.2055
O3-C1-O2	123.07	123.05	122.990(31)	122.87	.	.	123.3(2)	123.36	.	.	123.40
O3-C1-C5	.	.	.	125.67	122.61	122.64	.	122.62	122.52	122.43	122.58
O2-H4	0.9651	0.9645	0.9645fix	0.9715	0.9760	0.9751	0.992(2)	0.9856	0.9766	0.9766	0.9858
H4-O2-C1	107.10	106.64	106.64fix	107.20	105.77	105.34	105.2(1)	105.11	105.58	104.96	105.04
C1-C5	1.5141	1.5128	1.51318(47)	1.5253	1.5252	1.5252	1.524(2)	1.5373	1.5260	1.5260	1.5376
C5-C1-O2	111.16	111.35	111.482(41)	111.46	114.39	114.08	114.3(1)	114.01	114.38	114.12	114.01
C5-N6	1.4420	1.4430	1.44245(14)	1.4501	1.4608	1.4603	1.462(2)	1.4710	1.4615	1.4620	1.4713
N6-C5-C1	115.38	115.25	115.285(17)	115.86	111.60	111.36	111.4(2)	111.60	111.78	111.67	111.64
C5-H7	1.0905	1.0903	1.09078(7)	1.0973	1.0891	1.08974	1.084(1)av.	1.0950	1.0887	1.0884	1.0950
C5-H8	1.0905	1.0903	1.09078(7)	1.0973	1.0890	1.08971	1.084(1)av.	1.0952	1.0887	1.0884	1.0950
H7-C5-C1	107.37	107.49	[107.36]	107.55	.	.	.	106.72	.	.	107.05
H7-C5-N6	.	.	.	109.92	110.23	109.82	.	110.99	112.09	112.12	112.07
H8-C5-C1	107.37	107.49	[107.36]	107.55	.	.	.	107.37	.	.	107.05
H8-C5-N6	.	.	.	109.92	113.90	114.42	.	113.13	112.09	112.12	112.07
H7-C5-C1-O3	−123.13	−123.18	[−123.21]	−123.39	.	.	.	62.97	.	.	57.01
H7-C5-N6-C1	.	.	.	122.14	117.85	117.37	.	118.90	119.84	119.90	120.09
H8-C5-C1-O3	123.13	123.18	[123.21]	123.39	.	.	.	−51.10	.	.	−57.01
H8-C5-N6-C1	.	.	.	−122.14	−121.65	−122.37	.	−121.22	−119.84	−119.90	−120.09
N6-H9	1.0109	1.0109	1.01044(10)	1.0170	1.0091	1.0097	1.014(3)av.	1.0147	1.0080	1.0077	1.0143
N6-H10	1.0109	1.0109	1.01044(10)	1.0170	1.0080	1.0083	1.014(3)av.	1.0141	1.0080	1.0077	1.0143
H9-N6-C5	110.55	109.86	[110.10]	110.20	112.06	111.52	.	112.21	112.42	112.09	112.37
H10-N6-C5	110.55	109.86	[110.10]	110.20	112.26	111.87	.	112.38	112.42	112.09	112.37
H9-N6-C5-C1	58.67	57.93	[57.43]	58.11	101.39	97.96	.	109.95	118.87	119.30	119.19
H10-N6-C5-C1	−58.67	−57.93	[−57.43]	−58.11	−136.97	−141.63	.	−128.60	−118.87	−119.30	−119.19
H4-O2-C1-O3	0.0	0.0	0.0	0.0	.	.	.	179.68	.	.	180.0
C5-C1-O3-O2	180.0	180.0	180.0	180.0	.	.	0.12(286)	0.59	.	.	180.0
N6-C5-C1-O3	0.0	0.0	0.0	0.0	−171.93	−169.66	.	−175.61	−180.0	−180.0	180.0
N6-C5-C1-O2	180.0	180.0	180.0	180.0	8.90	11.46	11.2(19)	4.92	0.0	0.0	0.0
H4-O2-C1-C5	180.0	180.0	180.0	180.0	−1.39	−2.01	−2.5(19)	−0.86	0.0	0.0	0.0
θ(CH2 scissor)d	–	–	105.988(10)	105.51	107.17	107.14	106.7(2)	106.67	–	–	–
θ(NH2 scissor)d	–	–	–	105.67	107.91	107.47	107.0(11)	107.62	–	–	–
Δθ(CH2 rock)d	–	–	–	.	4.66	5.89	0.116fix	2.79	–	–	–
Δθ(CH2 twist)d	–	–	–	.	2.68	3.33	0.0642fix	1.49	–	–	–
τ(HNCC av.)d	–	–	–	.	−35.58	−43.67	5.43fix	−18.65	–	–	–
Δθ(CH2 wag)d	–	–	–	.	10.60	10.53	8.0(4)	10.03	–	–	–
Δθ(NH2 rock)d	–	–	–	.	0.20	0.35	8.0(17)	0.17	–	–	–

^aRef.⁴¹.

^bRef.⁴⁰.

^cRef.³⁰.

^dθ(XH₂ scissor) = H-X-H bond angle. Δθ(CH₂ rock) = (H8-C5-N6) + (H8-C5-C1) − (H7-C5-N6) − (H7-C5-C1). Δθ(CH₂ twist) = (H8-C5-N6) − (H8-C5-C1) − (H7-C5-N6) + (H7-C5-C1). τ(HNCC av.) = (H10-N6-C5-C1) − (H9-N6-C5-C1). Δθ(CH₂ wag) = (H8-C5-N6) − (H8-C5-C1) + (H7-C5-N6) − (H7-C5-C1). Δθ(NH₂ wag) = (H10-N6-C5) − (H9-N6-C5).

Table 3.

Equilibrium structures of the IVn/gtt, IIIp/tct, Vn/gtc and VIp/ttc conformers of glycine. Distances in Å, angles in degrees.

Parameters	IVn/gtt			IIIp/tct			Vn/gct			VIp/ttc
	besta	best-CC	B3LYP/SNSD	besta	best-CCa	B3LYP/SNSD	best	best-CC	B3LYP/SNSD	best	best-CC b	B3LYP/SNSD
C1-O2	1.3461	1.3444	1.3531	1.3483	1.3482	1.3560	1.3486	1.3477	1.3552	1.3543	1.3535	1.3617
C1-O3	1.2028	1.2011	1.2082	1.2034	1.2024	1.2083	1.2024	1.2004	1.2075	1.1961	1.1958	1.2016
O3-C1-O2	123.21	123.17	122.99	122.73	122.69	122.56	122.86	122.80	122.71	120.26	120.51	120.14
O2-H4	0.9651	0.9643	0.9713	0.9656	0.9650	0.9717	0.9652	0.9643	0.9712	0.9619	0.9610	0.9681
H4-O2-C1	106.96	106.48	107.01	106.38	105.89	106.50	106.78	106.34	106.91	110.63	110.01	110.70
C1-C5	1.5035	1.5036	1.5133	1.5174	1.5165	1.5282	1.5059	1.5058	1.5161	1.5227	1.5215	1.5345
C5-C1-O2	111.62	111.72	111.80	113.47	113.38	113.51	112.08	111.98	112.40	115.11	115.09	115.48
C5-N6	1.4488	1.4485	1.4568	1.4446	1.4453	1.4524	1.4544	1.4540	1.4619	1.4407	1.4415	1.4488
N6-C5-C1	110.05	109.91	110.67	118.63	118.64	119.42	111.81	111.71	113.02	115.36	115.29	115.82
C5-H7	1.0968	1.0977	1.1049	1.0899	1.0898	1.0966	1.0977	1.0986	1.1062	1.0926	1.0926	1.0995
C5-H8	1.0896	1.0902	1.0966	1.0899	1.0898	1.0966	1.0866	1.0871	1.0930	1.0926	1.0926	1.0995
H7-C5-C1	105.64	105.57	105.54	105.96	106.03	105.94	105.70	105.77	105.39	107.80	107.90	108.01
H8-C5-C1	108.31	108.24	108.42	105.96	106.03	105.94	107.00	106.81	106.67	107.80	107.90	108.01
H7-C5-C1-O3	−106.19	−106.25	−106.12	56.20	56.10	55.82	88.80	90.21	85.90	−122.62	−122.71	−122.87
H8-C5-C1-O3	139.45	139.70	140.27	−56.20	−56.10	−55.82	−25.78	−24.13	−27.53	122.62	122.71	122.87
N6-H9	1.0086	1.0088	1.0148	1.0097	1.0098	1.0161	1.0099	1.0101	1.0162	1.0111	1.0111	1.0172
N6-H10	1.0119	1.0118	1.0175	1.0097	1.0098	1.0161	1.0106	1.0107	1.0164	1.0111	1.0111	1.0172
H9-N6-C5	111.65	110.95	111.01	111.35	110.61	110.96	110.58	109.93	110.01	110.23	109.55	109.90
H10-N6-C5	110.28	109.35	109.82	111.35	110.61	110.96	111.14	110.28	110.80	110.23	109.55	109.90
H9-N6-C5-C1	−155.36	−154.83	−154.57	59.72	58.87	59.08	−178.47	−177.54	−178.54	58.35	57.64	57.85
H10-N6-C5-C1	−34.32	−35.58	−35.06	−59.72	−58.87	−59.08	−58.49	−59.30	−59.99	−58.35	−57.64	−57.85
H4-O2-C1-O3	1.12	0.98	0.98	0.0	0.0	0.0	0.86	1.15	1.14	180.0	180.0	180.0
C5-C1-O3-O2	178.03	177.95	177.98	180.0	180.0	180.0	−176.83	−176.94	−176.67	180.0	180.0	180.0
N6-C5-C1-O3	18.05	18.24	18.54	180.0	180.0	180.0	−146.05	−144.37	−148.14	0.0	0.0	0.0
N6-C5-C1-O2	–	–	−163.28	0.0	0.0	0.0	–	–	34.89	180.0	180.0	180.0
H4-O2-C1-C5	–	–	−177.25	180.0	180.0	180.0	–	–	178.18	0.0	0.0	0.0

^aRef.⁴¹.

^bRef.⁴⁰.

Tables 2 and 3 also report the structural parameters obtained from the second type of composite scheme (“best-CC”; see Eq. (1)). The first comment concerns the extrapolation to the CBS limit at the HF-SCF level, as two different sets of bases have been used for the C₁ (n=D,T,Q) and C_s (n=T,Q,5) conformers (see section 2). For Ip/ttt, it has been verified that the extrapolated structures obtained with the two sets agree well with each other. The “best-CC” approach is well tested and is known to provide highly accurate results (see, for example, Ref.¹⁰⁰ and references therein). Therefore, their comparison with the results from the simpler “best” composite scheme allows us to point out the accuracy of the latter. We note that, apart from very few exceptions, the differences in the bond lengths are well within 0.001 Å, the largest deviation being 0.002 Å. For angles, the deviations are usually smaller than 0.5 degrees and well within 1 degree in almost all cases. The largest discrepancies are observed for dihedral angles, for which deviations larger than 1 degree are noted in a few cases. A special comment is deserved for the IIn/ccc conformer, which is characterized by a flat double-minimum PES, with the minima separated by a low barrier (~2 kJ mol⁻¹). As a consequence, the location of the minimum structure strongly depends on the level of theory and the skeleton dihedral angles are those mostly affected. For these reasons, discrepancies of about 2-4 degrees are observed.

The comparison discussed above confirms the conclusions drawn in Ref.⁴⁹, that is, the less expensive “best” composite scheme can be easily applied to rather large molecules to obtain very accurate geometrical determinations. In view of the positive comparison, noted that the convergence to the CBS limit is smooth and the extent of the CV corrections is similar to what is usually observed, on the basis of the literature on this topic (see, for example, Refs.^{49,69,70,98,100}), the accuracy of the equilibrium geometry obtained with the “best” approach can be conservatively estimated to be about 0.001-0.002 Å for bond distances and about 0.5 degrees for angles. The availability of the semi-experimental equilibrium structure¹⁰¹ for the two most stable conformers, Ip/ttt and IIn/ccc,³⁰ and in particular its revision for the former one (see Refs.^40,41) allows us to further check the accuracy of our computed structure. In fact, in Ref.¹⁰² an accurate investigation drew the conclusion that errors in the determined empirical bond lengths are typically below 0.001 Å for first-row elements, provided that electron correlation is properly included in the calculation of the vibrational corrections. While for Ip/ttt we note a good agreement, i.e., well within the accuracy stated above (for a detailed comparison, the reader is referred to Ref.⁴¹), for the IIn/ccc conformer the comparison needs to be more detailed. For bond lengths, in most cases our computed parameters agree with the semi-experimental distances within 1-2 times the standard errors; the most relevant exception are the N-H and O-H distances which are overestimated by about 0.05 Å and 0.02 Å, respectively, in the semi-experimental structure. For angles, large deviations are observed for all angles involving the NH₂ moiety. These discrepancies and the reduced accuracy of the semi-experimental structure are once again related to the flat double-minimum PES. In fact, the vibrational ground state lies above the transition state. As a consequence, the experimental ground-state rotational constants refer to an averaged structure that essentially it is thought to resemble the IIp/ccc conformer. For this reason, we also investigated the transition state connecting the two IIn/ccc equivalent minima by means of the two composite schemes mentioned above. The corresponding geometrical parameters are collected in Table 2, where they are compared to those of the IIn/ccc conformer. First of all, we note that they are very similar, with negligible differences in most cases. The discrepancies increase when the geometrical parameters related to the torsion of the -NH₂ group are considered; in such cases, they are about 0.001 Å for the N-H distance and a few degrees for angles and dihedrals. Finally, the overestimation of the semi-experimental N-H and O-H bond lengths is confirmed also when they are compared to the corresponding parameters of the TS structure. Therefore, a re-investigation of the semi-experimental equilibrium structure of IIn/ccc is suggested.

3.2 Harmonic frequencies and IR intensities

For the conformers of glycine considered in the present work, the best-estimated harmonic vibrational frequencies, as obtained from the composite scheme described in the methodology section (Eq. 5), are reported in Table 4. To reduce the numbers of tables, the harmonic frequencies computed at the different levels of theory and the various contributions (ω(CBS), Δω(CV), Δω(diff), Δω((T))) are given only in the supplementary material, Tables S7-S12, while Table 5 summarizes the corresponding statistics. From these Tables it is observed that the MP2/cc-pVQZ level of theory already provides a good approximation for the CBS limit, the differences being of the order of 0.5% (i.e., in absolute terms they range from less than 1 cm⁻¹ to about 6 cm⁻¹). Core-correlation corrections are quite small (i.e., from <0.01 to ~8 cm⁻¹, where the larger corrections usually apply to higher frequencies) and mostly positive; in relative terms they are on average of the order of 0.3%. Inclusion of diffuse functions in the basis set generally tends to lower harmonic frequencies (i.e., negative corrections), with changes ranging from negligible (<0.2 cm⁻¹) to large (~25 cm⁻¹) in absolute value terms. With respect to higher-order electron-correlation corrections, for which the inclusion of triples is expected to be the most relevant contribution, the corresponding contributions are generally large, either positive or negative, ranging from <0.1 to 60 cm⁻¹ (i.e. of the order of 0.01–4%). However, the largest contributions are mainly negative, except for the case of ω₃ for IIn/ccc, corresponding to the O-H stretching vibration within the hydrogen bridge, for which inclusion of triples increases the harmonic frequency by 60 cm⁻¹. Special comments are deserved for the IIIp/tct conformer, as it has an imaginary frequency at the SCF level (with all basis sets considered). As a consequence, for this frequency the extrapolation to the CBS limit has been carried out by applying the n⁻³ formula to the entire term, and not only to the correlation contribution (as required).

Table 4.

DFT and best-estimated harmonic frequencies (cm⁻¹).

Mode	Ip/ttta			IIn/ccc			IVn/gttb			IIIp/tctb			Vn/gct			VIp/ttca
	Symm	DFT	best	Symm	DFT	best	Symm	DFT	best	Symm	DFT	best	Symm	DFT	best	Symm	DFT	best
24	A”	64.79	67.35	A	40.21	72.45	A	94.15	95.92	A”	15.89	4.08	A	69.64	70.82	A”	77.79	84.21
23	A”	211.56	200.38	A	245.27	241.62	A	171.79	182.88	A”	246.44	237.78	A	216.03	234.52	A”	202.44	193.28
22	A’	256.66	254.24	A	309.90	314.03	A	279.54	281.68	A’	261.16	262.97	A	283.95	289.17	A’	260.20	257.47
21	A’	463.06	466.62	A	509.36	511.13	A	465.90	469.08	A’	497.87	502.30	A	458.96	455.46	A”	468.16	470.11
20	A”	508.03	507.95	A	548.46	550.53	A	517.43	518.32	A”	513.86	515.21	A	541.38	545.43	A’	462.78	465.36
19	A’	634.56	638.23	A	644.06	643.39	A	624.20	624.85	A’	595.16	597.44	A	596.65	592.51	A”	573.59	567.05
18	A”	654.46	639.24	A	816.82	820.74	A	665.54	655.10	A”	682.63	674.63	A	696.51	693.20	A’	647.30	646.43
17	A’	820.85	826.57	A	864.21	838.35	A	838.90	845.95	A’	798.85	803.91	A	822.71	825.67	A’	830.12	836.48
16	A”	915.63	915.72	A	890.53	884.57	A	841.10	832.07	A”	888.94	884.20	A	838.98	842.10	A”	919.81	921.07
15	A’	920.19	918.72	A	922.09	940.59	A	1018.34	1028.20	A’	906.50	913.21	A	1014.60	1024.19	A’	921.29	919.45
14	A’	1124.46	1137.48	A	1067.82	1087.01	A	1106.93	1119.39	A’	1131.50	1148.60	A	1074.95	1083.08	A’	1120.59	1135.79
13	A’	1162.24	1177.00	A	1164.74	1176.42	A	1149.04	1157.73	A’	1170.32	1182.89	A	1135.79	1148.84	A’	1157.45	1175.39
12	A”	1183.45	1191.68	A	1214.34	1230.41	A	1222.00	1229.98	A”	1187.93	1197.68	A	1227.68	1236.94	A”	1183.70	1193.77
11	A’	1303.20	1313.19	A	1332.03	1335.28	A	1256.06	1268.52	A’	1344.84	1357.08	A	1288.49	1296.28	A’	1284.00	1297.76
10	A”	1382.73	1391.40	A	1352.35	1371.60	A	1324.44	1333.90	A’	1357.76	1370.92	A	1346.01	1359.94	A’	1377.88	1394.05
9	A’	1395.61	1412.92	A	1415.25	1407.05	A	1445.44	1459.56	A”	1381.37	1390.24	A	1423.35	1435.45	A”	1392.07	1402.52
8	A’	1452.92	1469.44	A	1460.56	1479.27	A	1487.40	1502.70	A’	1450.50	1469.73	A	1485.54	1502.08	A’	1458.79	1476.06
7	A’	1672.99	1675.00	A	1658.70	1666.17	A	1637.22	1642.71	A’	1669.95	1674.00	A	1648.75	1654.70	A’	1673.74	1676.27
6	A’	1817.28	1808.01	A	1846.03	1830.63	A	1819.43	1811.28	A’	1811.17	1799.61	A	1821.92	1812.21	A’	1851.00	1839.41
5	A’	3045.20	3061.70	A	3062.43	3071.14	A	2961.01	2999.07	A’	3052.55	3067.68	A	2944.19	2985.87	A’	3017.73	3037.42
4	A”	3080.81	3107.13	A	3108.41	3124.41	A	3063.83	3088.70	A”	3088.40	3114.19	A	3109.77	3128.33	A”	3053.91	3083.35
3	A’	3503.34	3515.73	A	3462.99	3544.72	A	3506.32	3516.29	A’	3512.11	3526.04	A	3507.58	3519.70	A’	3502.99	3515.61
2	A”	3576.77	3592.48	A	3533.31	3539.11	A	3597.76	3612.87	A”	3590.02	3607.59	A	3591.65	3607.48	A”	3575.57	3592.36
1	A’	3739.95	3762.67	A	3614.29	3625.65	A	3745.23	3764.66	A’	3738.98	3757.05	A	3745.90	3764.96	A’	3781.22	3798.64

^aRef.⁴⁰.

^bRef.⁴¹.

Table 5.

Contributions^a to harmonic frequencies (cm⁻¹) for glycine isomers: MIN and MAX stands for signed errors, largest positive (MAX) and largest negative (MIN), MAE stands for Mean Absolute Error.

	Δω(QZ-TZ)	Δω(CBS-QZ)	Δω(CV)	Δω(diff)	Δω((T)
Ip/ttt
MIN	−13.84	−6.56	−0.73	−22.49	−47.22
MAX	8.88	7.45	8.01	6.46	9.44
MAE	2.75	1.76	2.71	5.24	8.59
IIn/ccc
MIN	−10.69	−6.07	−0.93	−24.13	−46.32
MAX	6.91	10.64	7.69	2.07	60.35
MAE	3.69	3.20	2.71	7.26	11.52
IVn/gtt
MIN	−14.82	−8.34	−3.19	−21.67	−44.79
MAX	7.17	13.21	8.41	0.32	14.11
MAE	2.83	2.19	2.86	6.40	9.16
IIIp/tct
MIN	−16.62	−11.91	−1.19	−24.63	−48.08
MAX	9.77	14.18	8.13	2.73	11.64
MAE	3.19	2.78	2.75	6.56	9.49
Vn/gct
MIN	−11.35	−7.79	−1.88	−20.75	−46.01
MAX	7.74	11.35	8.30	2.40	9.70
MAE	2.66	2.02	2.76	5.92	9.10
VIp/ttc
MIN	−12.91	−8.20	−0.67	−24.93	−47.27
MAX	8.42	7.16	7.95	3.35	11.65
MAE	2.77	1.86	2.71	6.26	9.11
All
MAE	2.98	2.30	2.75	6.27	9.50

^aContributions as defined in the text.

Finally, a brief discussion on the accuracy of the best-estimated harmonic frequencies is warranted. On the basis of the approximations made, the corrections included, the estimates for the neglected contributions (which are mainly excitations beyond CCSD(T)), as well as the literature on this topic (see, for example, Refs.^{56,74,103,104}), we expect that the accuracy obtained is of the order of a few wavenumbers: from 3 cm⁻¹ to 15 cm⁻¹, where larger errors affect the larger frequency values and/or challenging vibrational modes. Concerning higher-order effects in the correlation treatment beyond CCSD(T), as discussed in some of our previous papers,^40,41,56 while the effect of the full treatment of triples is expected to be entirely negligible,^103,105 that due to quadruple excitations is predicted to be larger (a decrease of about 0.1% to 0.3%), even if the literature on this topic is very scarce.^{103,104,106,107}

In Table 4, the comparison of the best-estimated and DFT harmonic frequencies is also reported. We note that on average the B3LYP/SNSD level of theory tends to slightly underestimate frequencies with respect to our best results, anyway showing a good agreement. The differences are of the order of 2%, which means average absolute deviations of ~12 cm⁻¹, with the largest discrepancies observed for the lowest torsional mode and the higher frequency values. Concerning previous theoretical investigations of harmonic frequencies, except for our very recent works on the Ip/ttt, IVn/gtt, IIIp/tct and VIp/ttc conformers^40,41, the best determination prior to our study was carried out at the B2PLYP/aug-cc-pVTZ level.³⁹ By comparing the corresponding results with our best-estimated frequencies, we note a good agreement, with the latter being in most cases larger than the B2PLYP ones. The deviations are in fact on average of about 5 cm⁻¹. For both B3LYP and B2PLYP calculations, the largest discrepancy with respect to the best estimates is observed for the O-H stretching frequency of IIn/ccc, for which higher-order correlation effects turned out to be important. B3LYP underestimates ω₃ by about 80 cm⁻¹, in line with what has been observed for other hydrogen-bonded systems¹⁰⁸, while B2PLYP improves the agreement to the best estimates by ~40 cm⁻¹.

As the comparison to experiment is meaningful only once anharmonic corrections are accounted for, we postpone it to the next section.

The different contributions to IR intensities (within the double-harmonic approximation) have been investigated by means of the composite scheme introduced in the methodology section. As for harmonic frequencies, we report only the best-estimated values in Table 6, while for all conformers the various contributions are detailed in the supplementary material (Tables S13-S18) and summarized in Table 7. Unlike harmonic frequencies, intensities show a slow convergence to the CBS limit (see Tables S13-S18); in fact, by comparing the MP2/cc-pVTZ and MP2/cc-pVQZ levels (ΔI(QZ–TZ) corrections) differences in the largest part on the order of 1-2 km/mol are observed, but variations as large as 15-20 km/mol can also appear. As already noted for instance in our previous works,^40,41,56 core-correlation corrections (ΔI(CV)) are small, with the largest contributions being of a few km/mol (4 km/mol at most). By contrast, the effects of diffuse functions (ΔI(diff)) are large, the corresponding corrections being on average of about 5 km/mol, but also as large as 25-35 km/mol. This result is in line with the literature on this topic^84,109–112. Even if CCSD(T)/cc-pVTZ is the reference level of theory in our composite scheme, by comparing results at this level to the MP2/cc-pVTZ ones, we can draw conclusions concerning higher-order correlation-energy contributions. The corresponding effects are on average of about 7 km/mol, which means ~23% in relative terms, with the MP2 level that generally tends to overestimate IR intensities with respect to CCSD(T). A particular case that deserves to be mentioned concerns the Ip/ttt conformer. For the transitions lying at 1138.1 cm⁻¹ (CN stretch + OH bend, best-estimate) and 1176.5 cm⁻¹ (CO stretch + OH bend, best-estimate), at the MP2/cc-pVTZ level the intensities are 223.5 and 60.0 km/mol (252.7 and 47.6 km/mol at the MP2/aug-cc-pVTZ level), respectively, while the CCSD(T)/cc-pVTZ level provides for them very similar intensity values (138.8 and 139.9 km/mol). The experimental IR spectrum¹⁴ clearly shows two strong bands of different intensities, and this is well reproduced by computations at the B2PLYP/aug-cc-pVTZ level³⁹. Starting from the CCSD(T)/cc-pVTZ intensities, increase of the basis set and inclusion of diffuse functions (albeit at the MP2 level) give different contributions to the intensities of these two bands, restoring the agreement with the B2PLYP/aug-cc-pVTZ results and, more importantly, with experiment. In view of the large extent of some contributions and the lack of literature on this topic, it is difficult to assess the accuracy of our best-estimated values. However, it is expected to be similar to that obtained at the CCSD(T) level in conjunction with basis sets of at least aug-cc-pVTZ quality, which already provides quantitatively converged IR intensities¹¹². From Table 6, it is evident that DFT performs reasonably well with respect to our best-estimated values, with discrepancies of the order of 22%. A close inspection of the various contributions involved in our composite scheme (see Table 7) points out that the major source responsible for the differences observed is the effect of triple excitations, as included by the computation at the CCSD(T)/cc-pVTZ level. On the other hand, all MP2 results show a good agreement with those at the B3LYP/SNSD level. However, as far as the accuracy of intensities is concerned, in the next section we limit our discussion at a qualitative level, based on the graphical comparison of spectra.

Table 6.

DFT and best-estimated harmonic IR intensities (km/mol).

Mode	Ip/ttta			IIn/ccc			IVn/gttb			IIIp/tctb			Vn/gct			VIp/ttca
	Symm	DFT	best	Symm	DFT	best	Symm	DFT	best	Symm	DFT	best	Symm	DFT	best	Symm	DFT	best
24	A”	5.05	5.11	A	0.67	2.48	A	4.22	3.21	A”	0.01	0.00	A	2.88	2.30	A”	6.37	6.31
23	A”	43.31	44.31	A	14.38	16.40	A	46.62	47.45	A”	43.61	46.07	A	32.16	30.44	A”	58.18	57.41
22	A’	10.04	10.25	A	18.10	18.99	A	0.31	0.29	A’	2.06	2.38	A	11.30	12.76	A’	26.84	27.03
21	A’	30.05	30.84	A	2.16	2.48	A	13.36	13.05	A’	13.53	14.02	A	6.60	5.73	A”	77.87	84.40
20	A”	29.54	28.84	A	5.56	6.83	A	27.14	29.76	A”	22.44	20.25	A	23.08	27.30	A’	1.49	1.73
19	A’	5.90	5.88	A	5.17	6.57	A	33.52	42.06	A’	47.52	48.79	A	53.08	60.88	A”	14.52	9.60
18	A”	89.82	88.32	A	31.53	53.75	A	74.60	65.37	A”	100.45	98.91	A	83.38	71.76	A’	12.93	13.66
17	A’	75.48	88.48	A	83.11	51.85	A	159.96	137.01	A’	74.63	87.96	A	67.41	20.93	A’	22.63	33.28
16	A”	2.92	1.67	A	84.88	67.71	A	10.16	15.44	A”	139.92	115.48	A	81.51	116.96	A”	1.13	0.75
15	A’	120.24	88.85	A	24.74	58.69	A	4.39	3.84	A’	3.15	1.86	A	10.67	8.66	A’	166.17	139.38
14	A’	190.03	197.53	A	16.64	12.78	A	51.44	53.15	A’	24.13	6.35	A	29.17	37.14	A’	44.14	36.44
13	A’	112.50	106.26	A	2.22	2.10	A	205.23	203.38	A’	233.80	234.87	A	158.11	138.21	A’	3.91	11.05
12	A”	1.34	1.18	A	27.66	20.35	A	56.58	52.68	A”	1.17	1.07	A	76.15	74.63	A”	0.76	0.83
11	A’	13.45	13.94	A	7.62	10.95	A	0.42	2.06	A’	42.41	41.02	A	7.61	6.10	A’	357.17	332.67
10	A”	0.07	0.06	A	8.35	9.39	A	28.07	30.65	A’	17.42	30.16	A	43.40	44.04	A’	23.47	37.29
9	A’	14.44	22.69	A	373.57	369.21	A	23.93	28.52	A”	0.03	0.02	A	32.18	43.95	A”	0.11	0.05
8	A’	15.16	13.78	A	5.89	5.14	A	11.67	12.87	A’	3.13	2.37	A	5.13	4.43	A’	8.19	8.53
7	A’	18.59	17.31	A	31.16	30.03	A	56.86	54.71	A’	26.20	29.17	A	35.21	33.75	A’	20.61	19.98
6	A’	299.88	277.00	A	367.79	332.13	A	291.46	266.88	A’	306.66	287.52	A	332.59	310.43	A’	251.92	230.52
5	A’	16.97	14.71	A	10.71	10.73	A	39.98	31.10	A’	15.32	13.09	A	46.87	34.59	A’	27.99	24.31
4	A”	5.89	4.10	A	4.83	5.43	A	14.18	9.15	A”	4.57	3.19	A	6.41	4.63	A”	9.80	6.58
3	A’	2.17	4.00	A	284.95	230.52	A	5.44	6.24	A’	2.54	4.24	A	1.32	2.40	A’	3.45	5.55
2	A”	5.76	10.88	A	0.26	27.66	A	12.94	18.35	A”	5.96	11.28	A	6.37	12.31	A”	7.34	12.55
1	A’	58.41	70.35	A	16.53	15.94	A	70.46	76.90	A’	66.79	73.31	A	68.80	76.31	A’	44.19	53.80

^aRef.⁴⁰.

^bRef.⁴¹.

Table 7.

Contributions^a to harmonic intensities (km/mol) for glycine isomers: MIN and MAX stands for signed errors, largest positive (MAX) and largest negative (MIN), MAE stands for Mean Absolute Error.

	ΔI(QZ-TZ)	ΔI(CV)	ΔI(diff)	ΔI((T))
Ip/ttt
MIN	−16.77	−8.16	−29.10	−84.67
MAX	25.90	8.55	29.19	79.91
MAE	2.98	0.89	3.16	5.28
IIn/ccc
MIN	−12.78	−2.75	−21.85	−70.57
MAX	19.14	4.65	35.35	26.24
MAE	2.35	0.62	3.91	5.93
IVn/gtt
MIN	−30.08	−4.54	−42.06	−33.83
MAX	33.65	9.56	29.07	29.81
MAE	3.58	0.91	4.61	5.37
IIIp/tct
MIN	−15.57	−2.25	−27.22	−64.37
MAX	14.98	4.70	26.95	62.26
MAE	2.57	0.63	4.04	4.47
Vn/gct
MIN	−17.61	−8.34	−26.42	−20.11
MAX	16.53	11.51	29.22	21.27
MAE	2.70	0.85	3.87	4.07
VIp/ttc
MIN	−15.55	−8.30	−25.11	−27.32
MAX	19.95	8.07	23.67	18.81
MAE	2.94	0.83	3.80	3.95
All
MAE	2.85	0.79	3.90	4.85

^aContributions as defined in the text.

3.3 IR spectra

Anharmonic vibrational frequencies and IR intensities have been obtained as explained in the methodology section for the six low-lying glycine conformers, considering the main isotopic species (d₀) and its bi-[CD₂](d₂), tri-[ND₂,OD](d₃) and penta-[CD₂,ND₂,OD](d₅) deuterated isotopologues. The best-estimated anharmonic vibrational frequencies and IR intensities for the main isotopic species are listed in Table 8 along with the available experimental data, while the simulated IR spectra of d₀ and d₃ in selected frequency regions are presented in Figures 2, and 3, respectively. The detailed computational results for the six conformers, for main and deuterated species, namely, the best-estimated vibrational frequencies for all fundamental bands, overtones (2ν_i) and combination bands (ν_i+ν_j) along with their best-estimated IR intensities are collected in the ESI. The accuracy and robustness of the CC/DFT hybrid approach have been validated in a number of recent papers including both small systems^50–55,58 and biomolecule building blocks^40,41,56,57. Although DFT-only approaches are usually quite adequate, the increased cost of CCSD(T) harmonic frequencies (when feasible) remains advisable not only in view of a general improvement in the accuracy, but also for the strong reduction of the outliers with respect to experimental frequencies. On the other hand, the larger errors inevitably connected to the use of lower computational levels (e.g., MP2 or, better, DFT) can be tolerated for the more expensive anharmonic corrections due to their smaller contribution (well below 10% even for XH stretchings). The accuracy of our theoretical estimates is further confirmed by the comparison with experiment for the conformers Ip/ttt, IIn/ccc and IIIp/tct, for which several IR transitions have been detected and unequivocally assigned. Most of the experimental results reported in Table 8 have been measured in low-temperature matrices, but the results obtained in different rare-gas low-temperature environments (both matrices and nanodroplets)^{14–16,22,23} and in the gas phase^19,20 show that matrix effects are not significant for most of the observed transitions and are clearly noted only for the higher frequency modes. Thus, anharmonic best estimates can be directly compared with the experimental IR spectra recorded in low-temperature matrices^14,15,22,23, except for the OH stretching vibrations of Ip/ttt, IIn/ccc and IIIp/tct, for which unperturbed frequencies have been measured in helium nanodroplets¹⁶. For the ν_OH frequency of the other conformers, we take into account the matrix-induced red shift by applying a correction of about 20-30 cm⁻¹. In all cases, experimental data measured in argon matrices are considered^14,23, with the most recent results reported in Table 8. For what concerns the experimental transitions reported in Refs.^14,19 which are not assigned or only tentatively assigned, the best matching frequencies of IVn/gtt are compared. Moreover, experimental data for VIp/ttc are also included for comparison purposes: once again the agreement between the two set of data is remarkable. For the most stable Ip/ttt conformer, experimental data for almost all (23 over 24) fundamental vibrational transitions are available, with the theoretical predictions showing a mean absolute error (MAE) of 8 cm⁻¹ and all values well within 20 cm⁻¹. On the whole, all conformers show MAE below 10 cm⁻¹, and only a few frequencies deviate from experiment by more than 20 cm⁻¹. We also note that for strongly anharmonic modes, improved results can be obtained by hybrid computations with anharmonic corrections at the B2PLYP/aug-cc-pVTZ level. For the OH stretching of IIn/ccc involved in the hydrogen bridge, CC/B2PLYP halves the deviation from experiment with respect to CC/B3LYP (20 cm⁻¹ and 42 cm⁻¹, respectively), albeit at largely increased computational cost.

Table 8.

Best-estimated anharmonic frequencies (cm⁻¹) and IR intensities (km/mol) of the Ip/ttt, IIn/ccc, IIIp/tct, IVn/gtt, Vn/gct and VIp/ttc conformers of glycine (main isotopologue). Selected experimental data are reported for comparison.

	Ip/ttt				IIn/ccc				IIIp/tct				IVn/gtt				Vn/gct		VIp/ttc
Modela	Exp.	Ref.	Calc.	Icalc	Exp.	Ref.	Calc.	Icalc	Exp.	Ref.	Calc.	Icalc	Exp.b	Ref.	Calc.	Icalc	Calc.	Icalc	Exp.c	Calc.d	Icalcd
1	3585	16	3575	58.6	3447	23	3454	8.8	3579.3	16	3576	63.7			3579	65.5	3582	64.9	3606	3611	44.5
2	3410	14,23	3418	8.2	3381	23	3384	357.2	3430	23	3434	6.0			3441	15.0	3438	10.1	3410	3416	9.4
3	3359	23	3367	3	3275	16	3294e	215.2			3391	3.6			3361	6.9	3367	2.4		3367	4.3
4	2969	15	2961	5.6	2968	23	2976	6.9	2968	23	2967	7.5	2944	14	2956	12.1	2990	7.1		2937	9.5
5	2943	23	2947	14.2	2941	23	2956	11.8			2953	10.0	2868	19	2866	32.1	2845	33.1		2931	25.4
6	1779	14	1774	174.2	1790	14,23	1793	198	1767	14,23	1770	217.0	1773	14	1779	204.4	1779	277.5	1805	1803	100.2
7	1608	23	1612	17.3	1622	14,23	1599	15.2	1624	23	1637	16.9			1618	27.7	1644	29.1		1628	19.9
8	1429	14,23	1435	8.1			1432	4.8			1432	0.7			1455	8.5	1460	2.0		1436	7.7
9	1405	23	1387	15.2	1390	14,23	1364	194.7			1351	0.2	1427	14	1413	20.3	1400	25.0		1366	0.1
10	1340	15	1353	0			1325	15.4	1352	23	1343	34.4			1308	26.0	1307	13.0		1378	33.1
11	1297	23	1286	18.2			1312	8.7	1325	23	1336	30.1			1231	6.4	1259	5.1	1257	1260	217.3
12	1166	23	1164	0.4	1189	23	1182	18.8	1177	23	1172	0.1			1197	15.7	1191	34.5		1166	0.4
13	1136	14,23	1144	67.5			1158	2.3	1147	14	1147	155.6	1130	14	1122	185.0	1118	107.1		1148	10.8
14	1101	14,23	1103	193.1	1059	23	1061	13.2	1101	23	1119	43.6	1099	14	1098	66.3	1062	38.1	1109	1108	42.1
15	907	14,23	907	2.1	911	14	896	38.5	903	23	902	0.5			997	0.5	987	0.6		912	1.6
16	883	14,23	863	59.2	867	14,23	851	67	852	14,23	832	54.2	809	14	812	35.7	806	46.1	884	864	97.9
17	801	14,23	802	118.3	808	23	785	82.6	777	14,23	779	100.7	785	14	782	118.1	788	223.1		814	52.7
18	619	14,23	603	74.5	786	14,23	784	45.8	648	14,23	646	97.3			620	33.5	671	52.5		632	12.3
19	615	23	633	4.2			638	5.6	594	23	596	46.2	617	14	617	55.4	577	56.0		547	5.7
20	500	14	494	34.5			543	6.6			509	10.6	498	14	502	36.4	535	28.5		467	1.6
21	458	20	461	28.7			506	1.9			499	11.1			467	14.1	453	6.8		439	88.7
22	250	20	255	9.8	303	20	304	19.5			269	1.1	275	20	278	0.6	283	7.7		256	24.8
23	204	20	203	41.8			232	13			246	20.2	171	20	156	33.1	238	30.4		193	53.9
MINf			−20				−26				−20				−15					−20
MAXf			18				20				18				12					6
MAEf			7.8				7.4				4.1				3.1					1.6

^aNormal modes are reported in decreasing wavenumber order.

^bFor Ref.¹⁴, experimental transitions not assigned to Ip/ttt, IIn/ccc or IIIp/tct are reported.

^cRef.²³.

^dRef.⁴⁰.

^eanharmonic correction computed at the B2PLYP/aug-cc-pVTZ level (CC/B2PLYP model).

^fMIN and MAX stands for signed errors, largest positive (MAX) and largest negative (MIN). MAE stands for Mean Absolute Error.

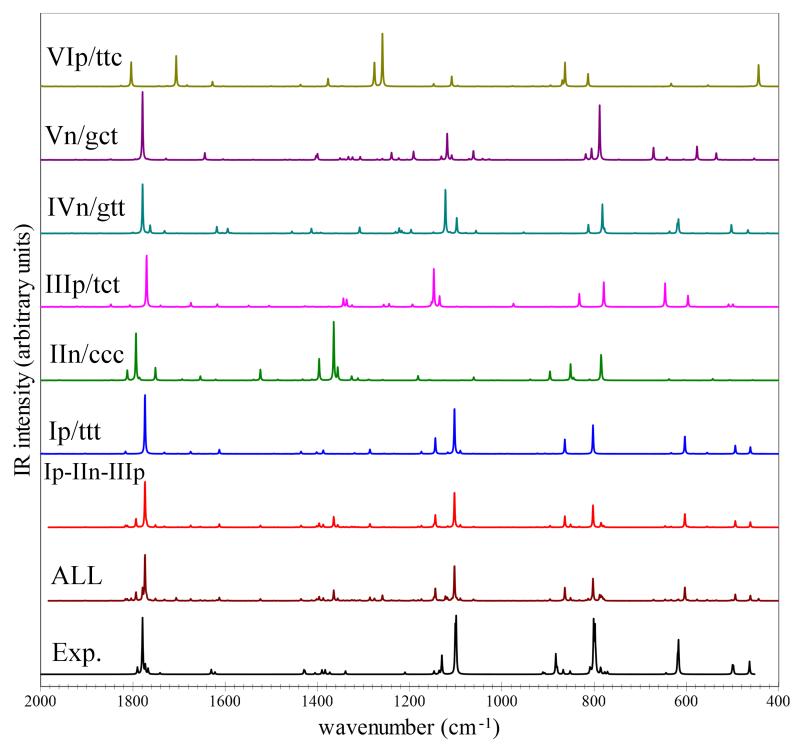
Fig. 2.

Best-estimated MI-IR spectra in the (2000-400 cm⁻¹) frequency region, for the main glycine isotopologue. Simulated theoretical spectra: single contributions from Ip/ttt, IIn/ccc, IIIp/tct, IVn/gtt, Vn/gct and VIp/ttc, the sum of the Ip/ttt, IIn/ccc and IIIp/tct (Ip-IIn-IIIp) contributions weighted for relative abundances (as computed in this work (T=410 K), also assuming the conformational cooling IVn/gtt→Ip/ttt and Vn/gct→IIIp/tct), and the Ip-IIn-IIIp sum complemented by minor contributions (1%) from the IVn/gtt, Vn/gct and VIp/tcc (ALL). Experimental IR spectra recorded in low-temperature Ar Matrix generated using the data of Table 5 of Ref.¹⁴. IR spectra line-shapes (both theoretical end experimental) have been convoluted with Lorentzian functions with a half-width at half-maximum (HWHM) of 1 cm⁻¹.

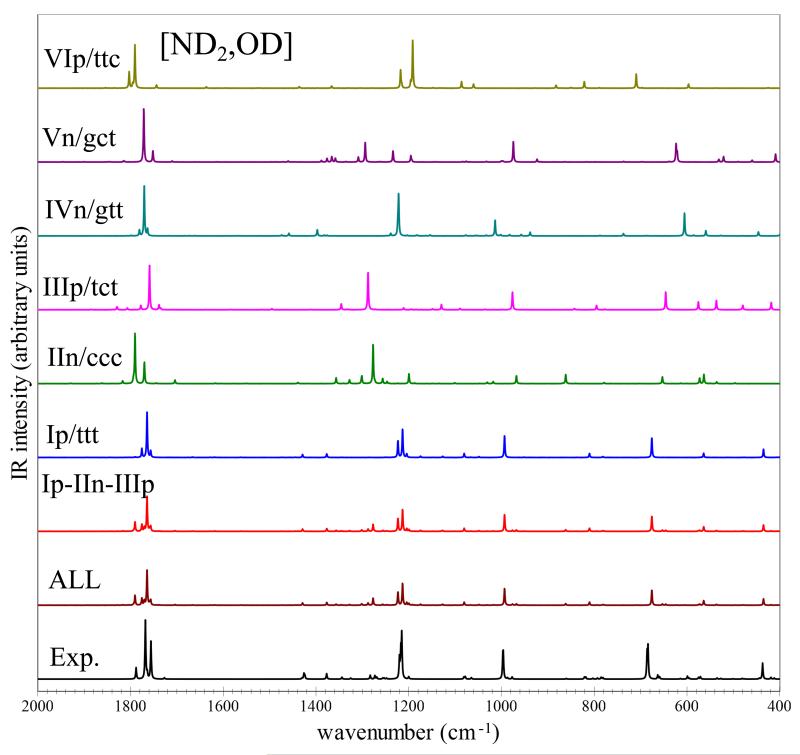
Fig. 3.

Best-estimated MI-IR spectra in the (2000-400 cm⁻¹) frequency region for the d₃-glycine isotopologue [ND₂,OD]. Simulated theoretical spectra: single contributions from Ip/ttt, IIn/ccc, IIIp/tct, IVn/gtt, Vn/gct and VIp/ttc conformers, the sum of the Ip/ttt, IIn/ccc and IIIp/tct (Ip-IIn-IIIp) contributions weighted for relative abundances (as computed in this work (T=410 K), also assuming the conformational cooling IVn/gtt→Ip/ttt and Vn/gct→IIIp/tct), and the Ip-IIn-IIIp sum complemented by minor contributions (1%) from the IVn/gtt, Vn/gct and VIp/ttc (ALL). Experimental IR spectra recorded in low-temperature Ar Matrix generated using the data of Table 7 of Ref.¹⁴. IR spectra line-shapes (both theoretical end experimental) have been convoluted with Lorentzian functions with a HWHM of 1 cm⁻¹.

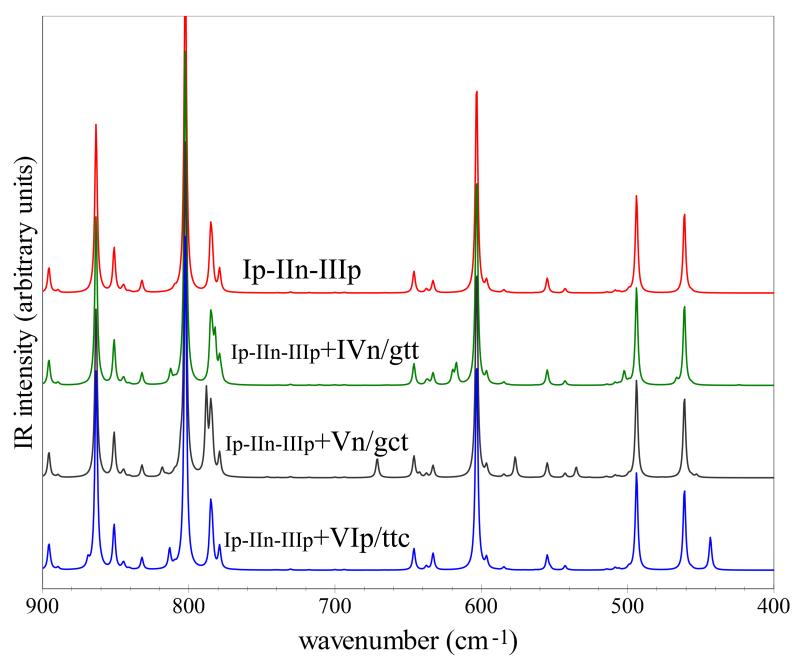
The theoretical model applied in this work allows the direct comparison between simulated and experimental IR spectra, including also weak transitions from overtones and combination bands. Figures 2 and 3 compare the main features of the low-temperature Ar-Matrix MI-IR spectra of d₀- and d₃-glycine, reported in Ref.¹⁴ with theoretical predictions. The overall spectrum has been obtained as a sum of three conformers, Ip/ttt, IIn/ccc and IIIp/tct, with each contribution weighted according to the relative Boltzmann population at 410 K. Moreover, the abundances of Ip/ttt and IIIp/tct have been increased in order to account for the IVn/gtt and Vn/gct conformational cooling (IVn/gtt→Ip/ttt and Vn/gct→IIIp/tct), thus leading to relative contributions to the spectra of 77%, 18% and 6% for Ip/ttt, IIn/ccc and IIIp/tct, respectively. Figures 2 and 3 demonstrate that the corresponding simulated spectra (Ip/ttt-IIn/ccc-IIIp/tct) match well the intensity pattern of their experimental counterparts. It is also evident that some additional weak features are present when possible minor contributions (1%) from the IVn/gtt, Vn/gct and VIp/ttc conformers are considered. However, for a more detailed analysis of experimental data, in view of searching for other glycine conformers, a full list of the observed experimental transitions would be necessary, while Ref.¹⁴ (and all other experimental works) reports only some of them. Thus, to help further experimental investigations (either re-investigation of already available spectra or new measurements), a full list of best-estimated vibrational frequencies and IR intensities is reported in the ESI, which allows to simulate spectra for any kind of experimental conditions and several isotopologues. As an example, Figures 2 and 3 also depict the single contributions from each conformer. Instead, Figure 4 shows a detailed comparison for the 900-400 cm⁻¹ region of the Ip/ttt-IIn/ccc-IIIp/tct combined spectrum from Figure 2 with simulated spectra which also account for the additional contributions from IVn/gtt, Vn/gct, and VIp/ttc (10%). It is apparent that detailed spectral features can be distinguished in the simulated spectra, thus clearly facilitating the analysis of experimental data. In our opinion the results presented in this work point out the advantages arising from the direct comparison between simulated and experimental spectra and the high accuracy of the theoretical models here applied.

Fig. 4.

Computed IR spectra in the 900-400 cm⁻¹ energy range: the theoretical spectrum Ip-IIn-IIIp from Figure 2 and the simulations also including a 10% contribution from IVn/gtt (Ip-IIn-IIIp+IVn/gtt), Vn (Ip-IIn-IIIp+Vn/gct) and VIp (Ip-IIn-IIIp+VIp/ttc). IR spectra line-shapes have been convoluted with Lorentzian functions with a HWHM of 1 cm⁻¹.

4 Conclusions

In conclusion, state-of-the-art quantum-chemical computations allowed us to complement the limited experimental data available for several glycine conformers, thus leading to a complete structural, thermodynamic, and spectroscopic characterization of the whole potential energy surface governed by soft degrees of freedom with an accuracy rivalling the best experimental determinations for the most stable conformers. In particular, the approach employed is expected to provide structural, thermodynamic and spectroscopic properties with accuracies largely sufficient for validation and/or integration of the most sophisticated experimental data. From a more general point of view, this and related works are paving the route toward integrated experimental and computational tools that allow the characterization of medium-sized molecular systems of current interest in several fields of chemistry with an accuracy reached so far only for very small rigid systems.