Modulation of a Single Neuron Has State-Dependent Actions on Circuit Dynamics

We use computational models to examine the circumstances under which modulation of a single neuron can alter the dynamics of an entire circuit. We show that under some circumstances, the circuit's behavior is robust to the neuromodulation of a single hub neuron, while under other circumstances the same neuromodulatory action of a single neuron can produce a large variety of circuit outcomes.

Abstract

Cover Figure.

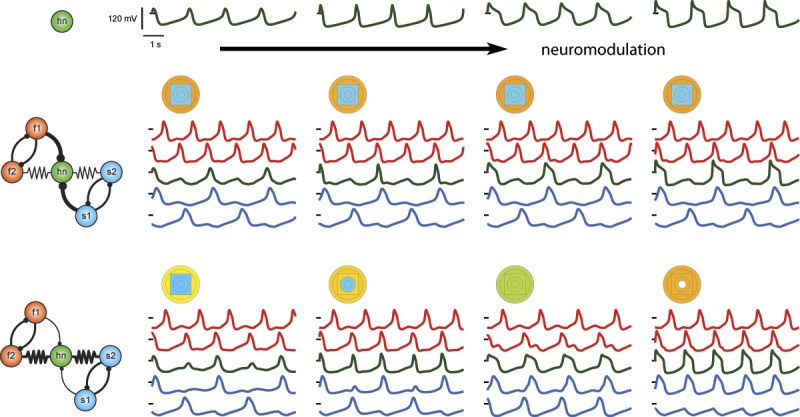
Neuromodulation of a single neuron in a circuit can either have little to no effect on the output of the circuit, or it can change the pattern of activity within that circuit. This is dependent on the synaptic parameters given the same circuit architecture, thus illustrating the insufficiency of the connectome alone for determining circuit behavior.

When does neuromodulation of a single neuron influence the output of the entire network? We constructed a five-cell circuit in which a neuron is at the center of the circuit and the remaining neurons form two distinct oscillatory subnetworks. All neurons were modeled as modified Morris−Lecar models with a hyperpolarization-activated conductance (ḡ_h) in addition to calcium (ḡ_Ca), potassium (ḡ_K), and leak conductances. We determined the effects of varying ḡ_Ca, ḡ_K, and ḡ_h on the frequency, amplitude, and duty cycle of a single neuron oscillator. The frequency of the single neuron was highest when the ḡ_K and ḡ_h conductances were high and ḡ_Ca was moderate whereas, in the traditional Morris−Lecar model, the highest frequencies occur when both ḡ_K and ḡ_Ca are high.

We randomly sampled parameter space to find 143 hub oscillators with nearly identical frequencies but with disparate maximal conductance, duty cycles, and burst amplitudes, and then embedded each of these hub neurons into networks with different sets of synaptic parameters. For one set of network parameters, circuit behavior was virtually identical regardless of the underlying conductances of the hub neuron. For a different set of network parameters, circuit behavior varied with the maximal conductances of the hub neuron. This demonstrates that neuromodulation of a single target neuron may dramatically alter the performance of an entire network when the network is in one state, but have almost no effect when the circuit is in a different state.

Significance Statement

We use computational models to examine the circumstances under which modulation of a single neuron can alter the dynamics of an entire circuit. We show that under some circumstances, the circuit's behavior is robust to the neuromodulation of a single hub neuron, while under other circumstances the same neuromodulatory action of a single neuron can produce a large variety of circuit outcomes.

Introduction

Neuromodulators change the excitability of individual neurons and can also alter the strengths of synapses by acting on one or more of the voltage-dependent conductances of network neurons (Levitan, 1978, 1988; Marder and Bucher, 2007; Stein, 2009; Harris-Warrick, 2011; Johnson et al., 2011; Marder, 2012; Marder et al., 2014; Nadim and Bucher, 2014). In so doing, neuromodulators can modify circuit dynamics (Morgan et al., 2000; Blitz and Nusbaum, 2012; Diehl et al., 2013). In some cases, the same neuromodulator may act on many network neurons simultaneously (Harris-Warrick et al., 1998; Swensen and Marder, 2001; Harris-Warrick and Johnson, 2010; Harris-Warrick, 2011), or a neuromodulator may target one or a few neurons in a network (Nadim and Bucher, 2014).

To what extent is modulation of a single neuron in an interconnected network likely to alter the activity of many or all neurons of the network, and how might this depend on the properties of the modulated neuron and other parameters in the network? Under some conditions, changes in the intrinsic properties of a single neuron might be subordinate to the network inputs it receives, while under other conditions, changes in the intrinsic properties of a single neuron may have more of an influence on its output as well as the output produced by other network neurons.

To address these questions, we look at the effects of neuromodulation of a single hub neuron at the center of a five-cell coupled-oscillator network. This network is loosely motivated by the core connectivity within the crustacean stomatogastric ganglion, and consists of two reciprocally inhibitory half-center oscillators, with different intrinsic frequencies, connected via electrical synapses through an intrinsically oscillatory hub neuron (Gutierrez and Marder, 2013; Gutierrez et al. 2013). This five-cell circuit can show a variety of different patterns of coordination among the neurons as a function of the chemical and electrical synapses. We investigated the effects of neuromodulation of the hub neuron on the patterns of activity produced in the five-cell network. The neurons used in this study are Morris−Lecar model neurons with an added h-conductance (LoFaro et al. 1994). As a first step in understanding the role of modulation of the hub neuron, we characterize the behavior of this model neuron as a function of its maximal conductances.

This raises a series of timely questions about the circumstances under which having the connectivity diagram or “connectome” is, as a first approximation, sufficient to determine circuit dynamics.

Materials and Methods

Morris−Lecar model neuron with h-conductance

Neurons were modeled as Morris−Lecar (Morris and Lecar, 1981; LoFaro et al., 1994), single-compartment neurons with the addition of a hyperpolarization-activated conductance (h-conductance), as in Gutierrez et al. (2013). Each cell’s membrane voltage, V_m, was computed by solving the equation:

$$C_m\frac{{dV}_m}{dt}=-\left[I_{leak}+I_{ca}+I_K+I_h+I_{elec}+I_{syn}\right]$$

C_m is the membrane capacitance and is equal to 1 nF for all neurons. Reversal potentials for the various currents are V_leak = −40 mV, V_ca = 100 mV, V_k = −80 mV, V_h = −20 mV, V_syn = −75 mV. The hyperpolarization-activated current is based on equations and parameters that were modified from Turrigiano et al. (1995). The remaining ionic currents are based on equations modified from Skinner et al. (1993). Ionic conductances ḡ_Ca and ḡ_K were sampled from a 5 to 75 nS range in 5 nS intervals. The h-conductance was sampled from a 0 to 75 nS range in 5 nS intervals. ḡ_leak was set to 0.1, 1, or 10 nS.

$$I_{leak}={\overline{g}}_{leak}\left(V_m-V_{\mathit{leak}}\right)$$

I_ca = ḡ_caM_∞(V_m − V_ca), $M_{\mathrm{\infty }}=0.5\left(1+tanh\left(\frac{V_m-v_1}{v_2}\right)\right)$, where v₁ = 0 mV and v₂ = 20 mV.

I_K = ḡ_KN(V_m − V _K), $\frac{dN}{dt}={\lambda }_N\left(N_{\mathrm{\infty }}-N\right)$, $N_{\mathrm{\infty }}=0.5\left(1+tanh\left(\frac{V_m-v_3}{v_4}\right)\right)$, ${\lambda }_N={\phi }_{N}cosh\left(\frac{V_m-v_3}{2v_4}\right)$, where v₃ = 0 mV and v₄ = 15 mV.

I_h = ḡ_hH(V_m − V_h), $\frac{dH}{dt}=\frac{\left(H_{\mathrm{\infty }}-H\right)}{{\tau }_h}$, $H_{\mathrm{\infty }}=\frac{1}{(1+exp\left(\frac{V_m+v_5}{v_6}\right))}$, ${\tau }_h=272-\left(\frac{-1499}{(1+exp\left(\frac{{-V}_m+v_7}{v_8}\right))}\right)$, where v₅ = 78.3 mV, v₆ = 10.5 mV, v₇ = −42.2 mV, v₈ = 87.3 mV.

M_∞, N_∞, and H_∞ are steady-state gating variables for the calcium, potassium, and hyperpolarization-activated currents, respectively. N and H are time-dependent gating variables for the potassium and hyperpolarization-activated currents, respectively. The gating variable, N, is modified by λ_N, a hyperbolic, U-shaped curve whose nadir height and eccentricity are determined by φ_N, which equals 0.002 ms⁻¹. The variable τ_h is the voltage-dependent recovery time constant. It controls the rate of change of H so that H changes less steeply for more depolarized voltages.

A database of 3600 neurons was constructed and oscillation frequencies were measured. Individual neuron simulations were done with MATLAB’s variable time step ode45 integrator with the maximum time step capped at 50 ms. Simulations for each conductance combination were 330 s long with the first 30 s discarded.

Hub neuron candidate selection

From the database of 3600 model neurons, we selected candidate hub neurons (hn) with frequencies of 0.5717 ± 0.15 Hz. This frequency was chosen because it is intermediate between the fast and slow half-center oscillation frequencies in the circuit (described below). These coarse tolerance candidates were then used to seed a finer tolerance hub neuron candidate search. For each coarse tolerance candidate, a cloud of 40 random points within a range of ±10 nS of each of their ionic conductances was generated and tested for hub neuron candidacy based on oscillation frequency. Negative conductance values were excluded. The resulting set of 190 fine tolerance hub neuron candidates had an oscillation frequency of 0.5717 ± 0.01 Hz. One hn candidate in any pair that was separated by a Euclidean distance of 2 nS or less was eliminated, leaving 143 hn candidates that were used for the remaining analysis.

Quantification of individual neuron properties

The intrinsic properties of the hub neuron candidates were analyzed using our MATLAB code. Duty cycle is defined as the proportion of cycle time that the neuron is above threshold, i.e., the time the oscillator spends at voltages larger than 0 mV divided by the period (0 mV; Fig. 1A, magenta arrow). Here, this quantity was computed as the mean duty cycle of the complete cycles taking place over the last 300 s of the simulation. The peak and trough voltages are the most positive and most negative voltages in the wave form, respectively (Fig. 1A, cyan and blue lines and arrows). The peak voltage quantity subsequently refers to the mean of the suprathreshold peak voltages over the last 300 s of simulation time. The trough voltage for each neuron is the mean voltage of the subthreshold troughs over the last 300 s of the simulation.

Figure 1.

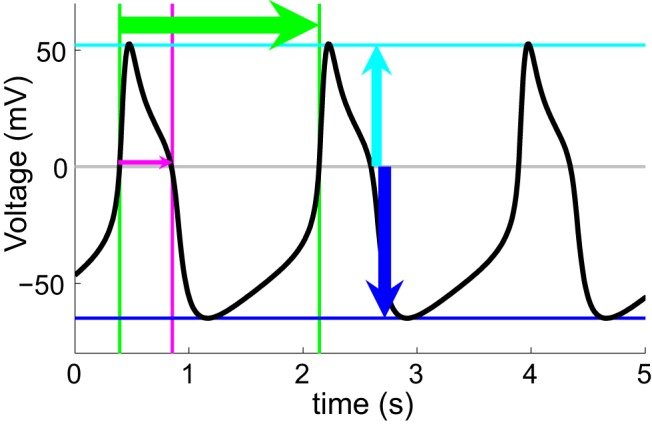
Morris−Lecar model neuron with h-conductance. Voltage wave form example of an oscillating model neuron is shown. In this study, we quantify oscillation frequency (period illustrated by green lines and arrow), duty cycle (magenta), peak voltage (cyan), and baseline voltage (blue).

Correlations between the various quantities were computed using MATLAB’s built-in corrcoef function for obtaining Pearson correlation coefficients and p-values. All correlations were calculated using the entire set of 143 hub neuron candidates. Phase response curves (PRCs) (Gutkin et al., 2001, 2005; Ly et al., 2011) were simulated by giving a 50 ms current pulse of ± 50 nA during various phases of the neuron’s cycle and calculating the change in the period due to the current pulse.

Circuit simulations

The hn candidates were individually placed into the hub position of the five-cell network as described in Gutierrez et al. (2013). Simulations were done with MATLAB’s variable time step ode45 integrator. All network simulations were 655 s long with the first 55 s discarded. Circuit neuron frequencies were calculated from the inverse of the mean interspike intervals over the last 600 s of the simulation.

All synapses were modeled as instantaneous. The electrical conductance, ḡ_el, determined the strength of the electrical synapses.

$$I_{elec}={\overline{g}}_{el}\left(V_m^{post}-V_m^{pre}\right)$$

Chemical inhibitory synapses were modeled by equations modified from Prinz et al. (2004). S_∞ is the steady-state synaptic current-gating variable and was modeled after the graded synaptic transmission seen in crustacean stomatogastric neurons (Manor et al. 1997). We used inhibitory synaptic conductance strengths (ḡ_synHC and ḡ_syn1) ranging from 0 nS to 10 nS. Each of the two synapses that form a half-center coupling have the conductance value denoted by ḡ_synHC.

$I_{syn}={\overline{g}}_{syn}\mathrm{ }{S}_{\mathrm{\infty }}^{pre}\left(V_m^{post}-V_{syn}\right)$, $S_{\mathrm{\infty }}=\frac{1}{(1+exp\left(\frac{v_{th}-V_m}{v_{\beta }}\right))}$ where v_β = 5 mV and v_th = −25 mV.

All model neurons in this study are endogenous oscillators and the maximal conductances for the different neurons were chosen to achieve the intrinsic oscillation frequencies required. Conductances for the neurons in the five-cell circuit were as follows [fast; f1,f2: ḡ_Ca = 1.9 × 10⁻² μS, ḡ_K = 3.9 × 10⁻² μS, ḡ_h = 2.5 × 10⁻² μS; hub neuron (default parameters); hn: ḡ_Ca = 1.7 × 10⁻² μS, ḡ_K = 1.9 × 10⁻² μS, ḡ_h = 8.0 × 10⁻³ μS; slow; s1,s2: ḡ_Ca = 8.5 × 10⁻³ μS, ḡ_K = 1.5 × 10⁻² μS, ḡ_h = 1.0 × 10⁻² μS; all ḡ_leak = 1 × 10⁻⁴ μS].

Circuit behavior definitions and tolerances

Circuit output was quantified using our MATLAB code to determine synchrony among the different neurons within the five-cell circuit. Neurons oscillating within 0.05 Hz of each other were deemed synchronous. The output pattern of the circuit is classified by which neurons are synchronously active.

Results

Neuron database

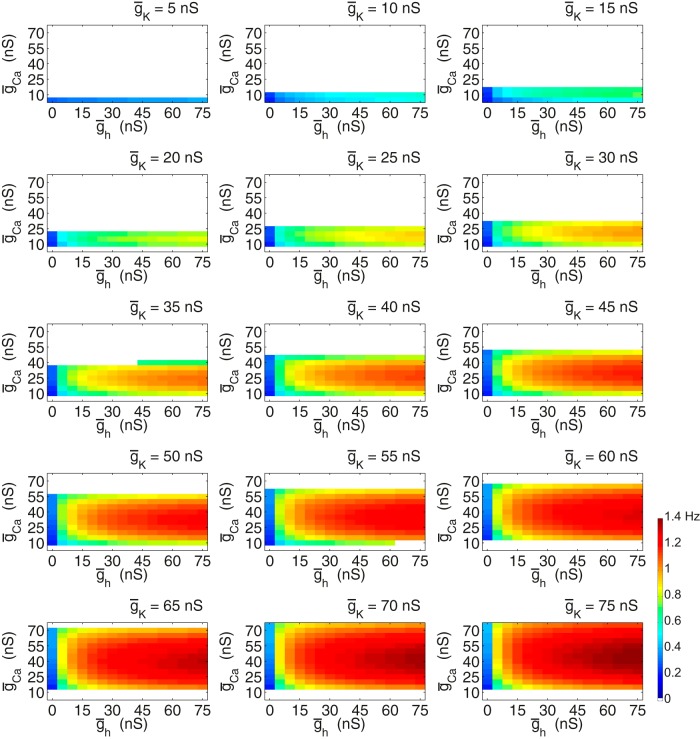
A database of Morris−Lecar neurons modified by a hyperpolarization-activated current was created (Fig. 2). A coarse sampling of the three-dimensional conductance space formed by the potassium, calcium, and h-conductances yielded many intrinsically oscillating neurons. In Figure 2, we show two-dimensional plots of the effects of altering ḡ_Ca and ḡ_h on oscillation frequency for each of 15 values of ḡ_K. The regions of white space indicate sets of parameters at which the neuron is not oscillatory. As ḡ_K is increased, oscillatory behavior becomes increasingly predominant. Note that at each value of ḡ_K and ḡ_Ca, increasing ḡ_h increases the oscillation frequency. In contrast, increasing ḡ_Ca produces a rotated “U” in oscillator frequency, with the highest frequencies seen at the middle range of ḡ_Ca. Consequently, at each value of ḡ_h and ḡ_K, it is likely that there are two or more models (with different ḡ_Ca values) that produce similar frequency oscillations.

Figure 2.

Morris−Lecar neuron with h-conductance database frequencies. This series of panels show the oscillation frequencies of the individual neurons in the database with intrinsic ionic conductances corresponding to the titles and axes. Neuron potassium conductance increases from the top left to bottom right panels. Maximal calcium conductance is on the y-axis and maximal h-conductance is on the x-axis. The color bar in the bottom right corner conveys the frequency color coding that applies for all plots in this figure. White spaces indicate neurons that are silent, non-oscillatory, or do not cross threshold. All neurons have a ḡ_leak of 0.1 nS.

We took two neurons with intrinsic frequencies within 1.5% of each other (0.0083 Hz difference) from among model neurons with a maximal potassium conductance of 40 nS. In Figure 3A, these are shown with dashed outlines at the two sets of parameters that give rise to these neurons. The voltage traces (Fig. 3B) reveal that, although these two neurons have similar frequencies, they have very different peak voltages, amplitudes, and duty cycles. Figure 3C shows the duty cycles for all of the model neurons with ḡ_K = 40 nS and indicates that duty cycle in the isolated neurons increases steadily as ḡ_Ca increases. This increase in duty cycle effectively explains the rotated U shape of the frequencies seen in Figure 3A, because as the plateau phase of the oscillator increases, eventually the oscillator period must extend because the interburst interval has to be long enough to allow the next burst to occur (Skinner et al., 1993, 1994).

Figure 3.

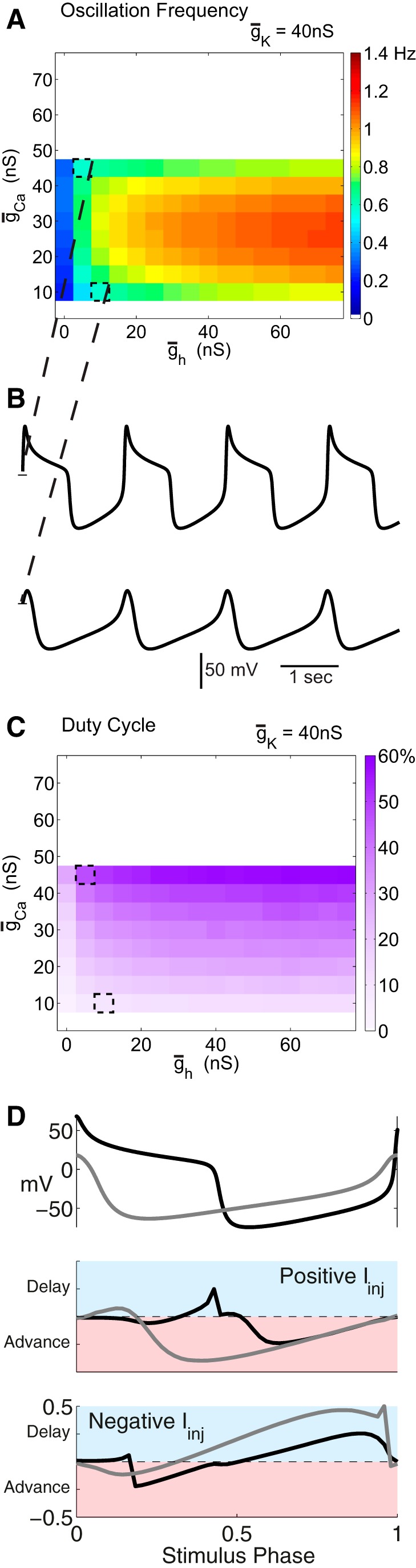
Comparison of two database neurons. A, A selected panel from the neuron database is displayed in which K⁺ conductance is 40 nS. Two neurons in this plane have frequencies very close to each other despite their disparate ionic conductances [ḡ_h = 5 nS, ḡ_Ca = 45 nS, 0.5705 Hz; ḡ_h= 10 nS, ḡ_Ca = 10 nS, 0.5787 Hz]. B, These two neurons differ in their wave form profile, however, as shown in the traces. C, A plot of duty cycles illustrates how much these two neurons differ in that respect. Duty cycle is depicted as the percentage of the cycle in which the neuron is above threshold. D, Phase response curves. One full period is plotted (top) for each of the two neurons highlighted above. The neuron with the higher maximal calcium conductance is in black and the lower calcium neuron is shown in gray. PRCs in response to positive current pulses of 50 nA (middle) and PRCs in response to negative current pulses of −50 nA (bottom) are shown.

The phase response curves (PRCs) of these two neurons further illustrate their differences (Fig. 3D). When positive pulses are delivered at various points in their phases, the neuron with the lower calcium conductance shows a phase advance over most of the cycle. In contrast, the PRC of the higher calcium conductance neuron shows more modest advances late in the cycle. The differences in these PRCs are associated with the length of the action potential depolarization (see voltage traces). When negative pulses are delivered, both neurons are delayed late in the cycle, with advances seen early in the cycle. Again, this makes sense as the transition between the advance and delay is determined, in part, by the duration of the action potential. A negative current pulse during the plateau terminates the spike early, thus permitting the next spike to occur sooner than without the negative current pulse.

Competing oscillators circuit model

We next wanted to look at the consequences of altering the intrinsic properties of an individual neuron on a circuit’s performance. For this purpose, we made use of a circuit model of intrinsic oscillators that compete for the recruitment of a hub neuron (hn; Fig. 4A) (Gutierrez et al., 2013). The competing components of the circuit are two sets of mutually inhibitory half-center oscillators, one fast and one slow set. f1 and f2 are identical, intrinsically fast, oscillating neurons whose mutually inhibiting synapses have conductance strength ḡ_synHC. Likewise for s1 and s2, which are intrinsically slow oscillators. The hn is electrically coupled (ḡ_el) to one neuron in each half-center pair and it receives an inhibitory synapse (ḡ_syn1) from the other neuron in each half-center pair. Without ḡ_el and ḡ_syn1, hn oscillates at a frequency that is directly between that of the fast and slow half-center frequencies. The frequencies of all of the neurons in the circuit can be displayed at once using a set of colored concentric circles and squares, as illustrated in the top right of Figure 4A and above the traces in Figures 4, B and C.

Figure 4.

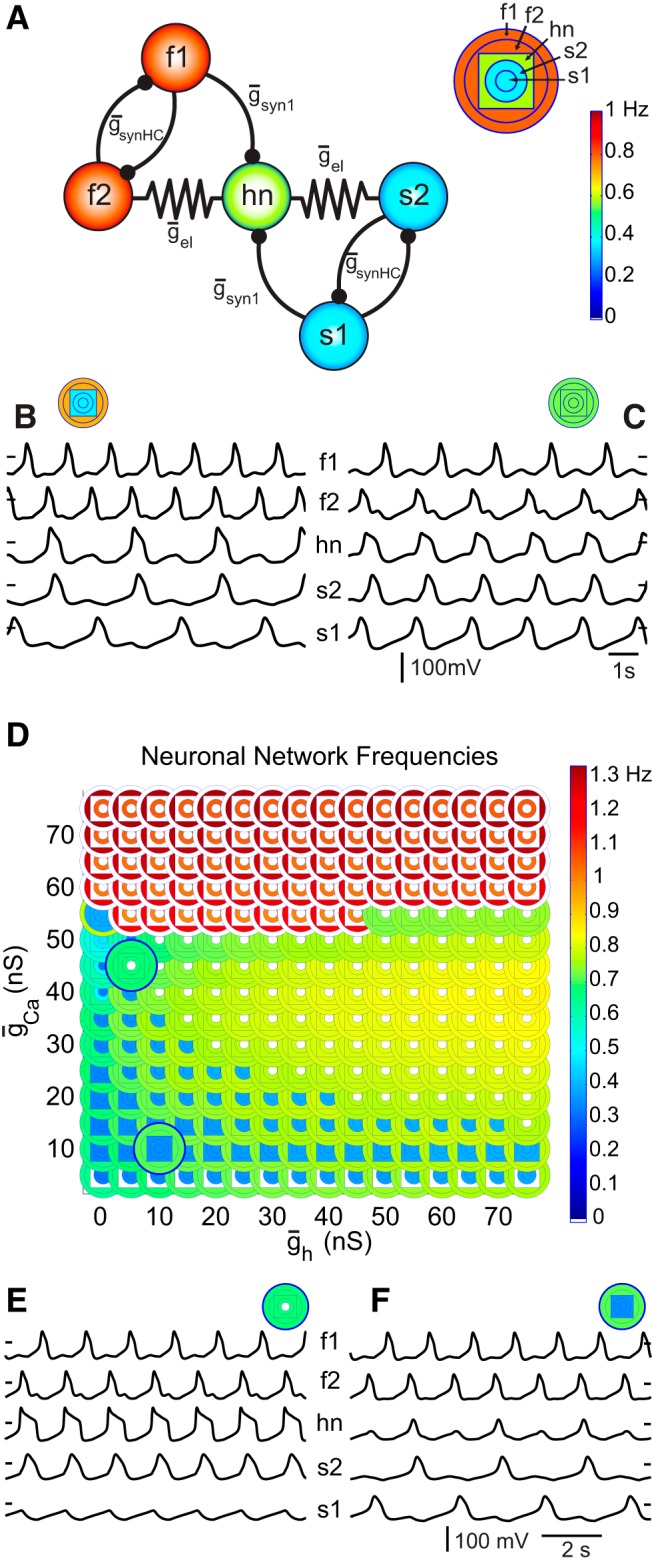
Model circuit. A, The model circuit in this study contains five model neurons with distinct intrinsic properties. The f1 and f2 neurons are the intrinsically fast oscillating neurons in the circuit while the s1 and s2 neurons are intrinsically slowly oscillating. The hn’s intrinsic frequency is intermediate of the fast and slow half-center frequencies. The key above and to the right of the circuit introduces a parameterscape point. The series of concentric shapes relay the frequencies of the neurons in the circuit with s1 represented by the innermost circle, f1 represented by the outermost circle, and hn represented by the square between the circles for f2 and s2. The colors of these shapes convey the neuron’s oscillation frequency according to the color bar heat map. This particular point (above circuit, right) conveys the frequencies of the five neurons when hn is not electrically coupled nor synaptically inhibited by the other neurons in the circuit. B, When the electrical coupling conductance (ḡ_el) is 2 nS and the synaptic inhibition to hn (ḡ_syn1) is 6 nS, the circuit exhibits a behavior in which hn oscillates in time with the slow oscillators as illustrated by the traces and the parameterscape point (ḡ_synHC is 5 nS). C, When ḡ_el is 6 nS and ḡ_syn1 is 2 nS, the circuit exhibits a behavior in which all of the neurons oscillate at the same frequency. D, The neurons from Figure 3A are inserted into the five-cell circuit as the hub neuron. This parameterscape illustrates the circuit behavior that results from having any of these model neurons take their place as the hub neuron. The concentric shapes indicate the frequencies of the circuit neurons according to the key (A). The two parameterscape points that are popped-out correspond to the two dashed boxes Figure 3A. Circuit synaptic parameters for all points in the parameterscape are as follows; ḡ_syn1 = 3 nS, ḡ_synHC = 5 nS, ḡ_el = 3 nS. E, F, Voltages traces display the circuit activity at the two highlighted points.

The circuit produces a number of different output patterns depending on the synaptic conductances chosen. For example, in Figure 4B, the fast half-center pair is oscillating at a high frequency (top traces and the two outer orange circles depicting the f1 and f2 frequencies) relative to the slow half-center pair (bottom traces and the inner blue circles depicting the s1 and s2 frequencies). In this instance, the electrical coupling is low while the synaptic inhibition onto hn is high and hn oscillates at the frequency of the slow oscillators (Fig. 4B; middle trace and blue square nested between orange circles and blue circles). In Figure 4C, the electrical coupling is high while synaptic inhibition to hn is low and all neurons in the circuit oscillate at the same frequency (as shown in the traces and the five green concentric shapes above them). Previous work using this circuit (Gutierrez et al., 2013) demonstrated that modulation of inhibitory and electrical synaptic conductances can alter circuit behavior, as shown in this example. In contrast, the present study explores the modulation of ionic conductances in the hn and the subsequent effect on circuit output.

Hub neuron intrinsic conductances shape circuit behavior

Using the five-cell circuit model, we studied the effect on circuit output when synaptic conductances remain constant and only the ionic conductances of the hn are changed. In Figure 4D, we observe the circuit output as a function of two of the hn ionic conductances; ḡ_Ca and ḡ_h. Essentially, each of the database neurons from Figure 3A is inserted into the circuit in the hn position. At each point of this “parameterscape” (Gutierrez et al., 2013), the behavior of the full circuit is indicated as a set of nested, color-coded circles and squares that are colored according to the frequency exhibited by each circuit neuron (Fig. 4D). Note that some neurons that were not oscillatory in isolation do oscillate when placed into the circuit as the hn. This is the case for neurons with a ḡ_Ca value of 50 nS and a few neurons with a ḡ_Ca of 55 nS. More importantly, Figure 4D shows that when the two neurons indicated in the boxes in Figure 3A are placed in the network as the hn with all other circuit parameters being identical, the circuit outputs are entirely different despite the two neurons having almost identical frequencies when in isolation. In one case (the hn with high ḡ_Ca), four of the neurons oscillate at a moderate frequency and s1 is silent (Fig. 4E). In the other case (the hn with low ḡ_Ca), all five neurons are oscillatory, but f1 and f2 oscillate at a moderate frequency, while the other three neurons oscillate together at a low frequency (Fig. 4F).

The differences between the waveforms for the two neurons shown in Figure 3B suggest an explanation for the different circuit behaviors that are produced in Figure 4, D−F. When the hn has a long duration, large amplitude oscillation, the electrical coupling is sufficient to synchronize the f2, hn, and s2 neurons, and the f1/f2 half-center maintains its alternation. The s1 neuron doesn’t have enough h-conductance to rebound from the relatively rapid s2 inhibitions it receives, and thus it falls silent. In the second case (low hn ḡ_Ca levels), the electrical coupling synchronizes the bursts in f2, hn, and s2, but the inhibition from s1 (which alternates with s2) is strong enough to suppress the hn whose oscillations barely cross threshold. Therefore it only fires every other fast cycle, thus joining the slow oscillatory regime.

Intrinsic properties of hub neuron candidates with same frequency

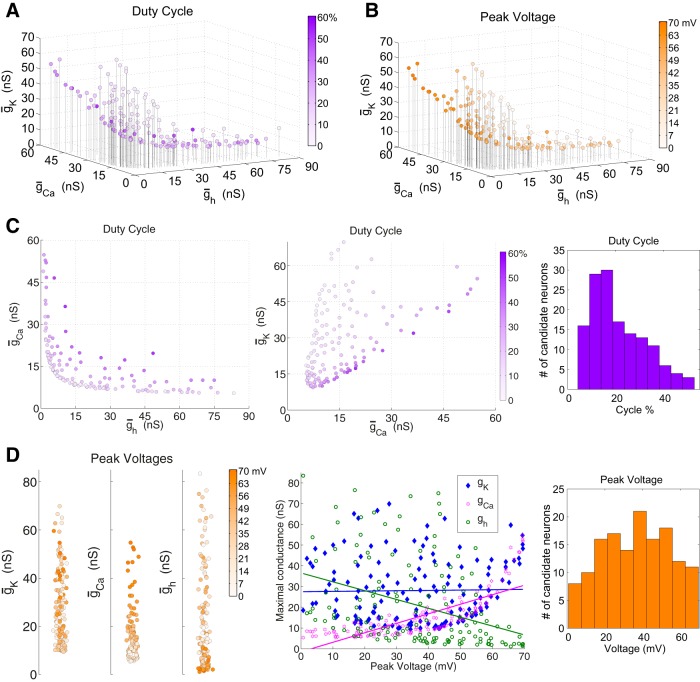
We created a population of model neurons with vastly ranging conductances and similar frequencies to examine the effects of modulation of the intrinsic properties of these centralized neurons on circuit output. Therefore, we generated 143 hub neuron candidates with frequencies of 0.5717 ± 0.01 Hz. Figure 5 shows their properties.

Figure 5.

hn candidates and intrinsic properties. The hn candidates all have isolated frequencies within the range of 0.5717 ± 0.01 Hz. The set of 143 individual neurons spans ionic conductance space in a V-formation. A, hn candidate duty cycles spanned the range of 4.27% to 52.7%. B, The peak voltages are the mean supra-threshold oscillation peak voltages and these ranged from 0.7132 to 69.5211 mV. C, The first two panels are two-dimensional plots of duty cycles containing the same data as A. A histogram for hn candidate duty cycles (right); mean duty cycle is 21.33%, standard deviation 11.24. D, One-dimensional plots for peak voltages as function of individual hn conductances (left) make the correlations in B more apparent. These are further summarized in the middle plot showing the relationships between the three conductances and the peak voltages of the hn candidates with regression lines. Right, Histogram for hn candidate peak voltages; mean of peak voltages is 36.2955 mV, standard deviation 17.8493 mV.

The resulting 143 hn candidates span ionic conductance space in an L-shape that hugs the ḡ_Ca and ḡ_h axes, indicating that the two inward currents compensate for each other to some degree (Fig. 5). Indeed, the three conductances are all significantly correlated with each other (p < 0.05). As one might expect, there is a positive correlation between the Ca²⁺ and K⁺ conductances (r = 0.48). However, the h-conductance is negatively correlated with the Ca²⁺ and K⁺ conductances (r = −0.68 and −0.53, respectively).

The duty cycles in this group of hn candidates spanned a broad range (Fig. 5A,C). The hn candidates along the inner rim of the L-formation tend to have longer duty cycles than the candidates outside of the elbow. The Ca²⁺ and h-conductances are positively correlated with duty cycle but only the Ca²⁺ conductance is significant (r = 0.46, p < 0.001; r = 0.14, p = 0.085). The K⁺ conductance is negatively and significantly correlated with duty cycle (r = −0.40, p < 0.001).

The voltage excursions of the candidate neurons’ oscillations also vary considerably. The maximum voltages of the oscillation peaks are as high as +70 mV for some neurons, but barely cross threshold in others (Fig. 5B,D). Voltage minima (not shown) are less variable, with a mean of −61.9 mV and a standard deviation of 8.0 mV. All conductances are significantly correlated with baseline voltages as well as the full voltage range. The correlation between peak voltage and either Ca²⁺ or h-conductance is highly significant (p < 0.001), but there is no significant correlation between K⁺ conductance and peak voltage (p = 0.82). Ca²⁺ conductance is positively correlated with peak voltage (r = 0.78), whereas h-conductance is negatively correlated with it (r = −0.37) (Fig. 5D, left and middle). The relationship between Ca²⁺ conductance and peak voltage can be seen in the distribution of peak voltage values in the conductance space as candidate hub neurons with higher Ca²⁺ conductances also tend to have higher peak voltages (Fig. 5B and D, left). Likewise, the negative correlation between h-conductance and peak voltage is seen in the decreasing peak voltages for increasing h-conductance.

Impact of the hub neuron’s intrinsic conductances on circuit output

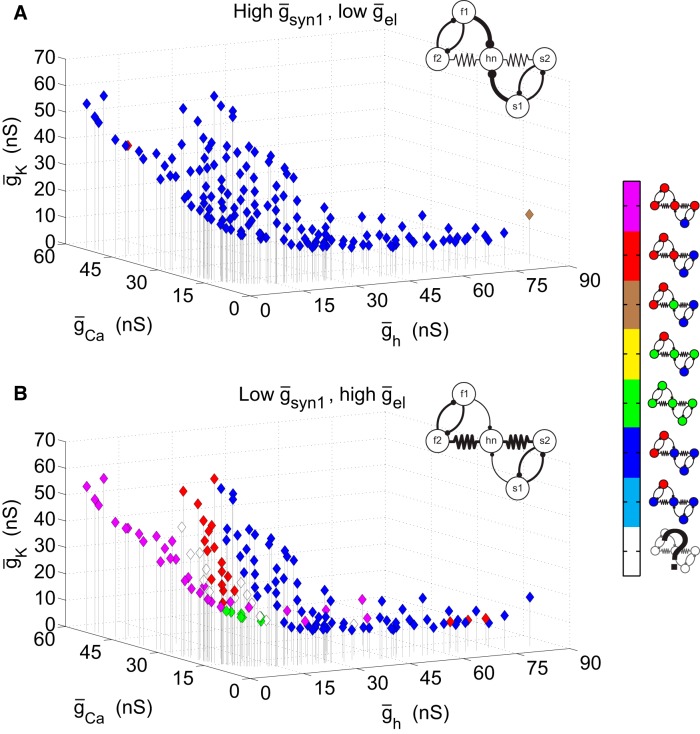
We next embedded each of the 143 candidate hn neurons (from Fig. 5) into two different versions of the five-cell circuit, one with a high value for ḡ_syn1 and low ḡ_el, and vice versa for the other. This allowed us to determine how each of a large set of neurons with the same frequency in isolation influences circuit output. By studying two sets of synaptic circuit parameters, we were also able to observe the extent of the synaptic parameters’ influence on the circuit output. For the sake of tractability, the maximal ionic conductances of the intrinsically slow and fast oscillator neurons remained unchanged.

In Figure 6, the resulting circuit output is shown for the two different circuit configurations. With high ḡ_syn1 and low ḡ_el (Fig. 6A), almost all of the hn candidate-containing circuits produced qualitatively similar behavior. This behavior is characterized by hn being active with the slow half-center oscillators while the fast half-centers oscillate at their own frequency (output pattern indicated in the legend by dark blue color). Although the network pattern is largely the same for this synaptic configuration, these networks do not necessarily have identical frequencies. The networks with higher overall frequencies generally had hns with lower Ca²⁺ and K⁺ conductances and higher h-conductances (data not shown). With the synaptic conductance values inverted so that ḡ_syn1 is low and ḡ_el is high, a number of qualitatively different circuit behaviors are seen for the different hn neurons (Fig. 6B). Several of them produce the behavior represented by dark blue in which hn is active with the slow oscillators, especially when hn has a relatively high h-conductance. Unlike in Figure 6A, Figure 6B displays a variety of other circuit output patterns. Clustered around low values of ḡ_h are circuits in which hn joins the fast oscillators (represented by red). Also for low values of ḡ_h but spanning the range of ḡ_Ca, there are circuits in which all but the s1 neuron are part of the fast oscillator (purple). There are also a few circuits in which all five neurons are active at the same frequency (green). These tend to have low values of all three ionic conductances. Finally, there are circuits (white diamonds) that were sufficiently irregular to defy simple classification. Such circuits tend to lie at the boundaries between clusters of circuits with classifiable behavior.

Figure 6.

Circuit behavior with different hub neurons. Each diamond represents a circuit that contains an hn candidate with intrinsic conductances at that particular point in ionic conductance space. The circuit behavior that results is encoded according to the color key on the right. A, ḡ_syn1 = 6 nS, ḡ_el = 2 nS; most of the hn candidate-containing circuits with these synaptic parameters display a behavior in which hn is active with the slow oscillators while the fast oscillators are active at their own frequency. B, ḡ_syn1 = 2 nS, ḡ_el = 6 nS; with these synaptic parameters, there is much more variability among the output from hn candidate-containing circuits. ḡ_synHC is 5 nS for both panels.

For the synaptic configuration with low electrical coupling and high synaptic coupling in Figure 6A, it is not simply a matter of having sufficiently weak electrical coupling to allow the networks to be in an inhibition-dominated regime because with still lower electrical coupling (ḡ_el = 0.5 nS), the candidate circuits produce a variety of network patterns. This is an effect of the electrical coupling being too weak to produce integer coupling among the distinct rhythms in the circuit (Gutierrez et al., 2013). Nor is the configuration in Figure 6A dependent on a precisely tuned value of the electrical coupling. This same effect is observed with electrical coupling up to 4 nS (with all other parameters kept the same) as well as with a number of different circuit configurations. Therefore, these particular examples in Figure 6 contrast two qualitatively different regimes. In one regime, modulation of the hub neuron results in significant alteration of the circuit patterns. In contrast, in the other regime, modulation of the hub neuron produces only modest circuit changes, which ultimately do not lead to a change in the qualitative behavior of the network.

Discussion

All nervous systems are modulated, both by hormones and local modulatory inputs (Marder, 2012). Neuromodulatory substances such as amines and neuropeptides can modify one or more voltage-dependent conductances (Levitan, 1988; Nicoll, 1988; McCormick, 1989), can act directly on signal transduction pathways (Levitan and Levitan, 1988; Clark et al., 2008; Zhang et al., 2010; Shinkai et al., 2011), and can result in changes in synaptic transmission (Kandel and Schwartz, 1982; Thirumalai et al., 2006; Nadim and Bucher, 2014).

In the stomatogastric ganglion, one of the most intensively studied small circuits, every neuron and every synapse is subject to neuromodulation by one or more substances (Marder and Bucher, 2007; Stein, 2009; Harris-Warrick, 2011; Johnson et al., 2011; Marder et al., 2014; Nadim and Bucher, 2014). Additionally, some neuromodulatory actions are contingent on the presence of other modulators, or recent history of neuromodulation, often with significant behavioral consequences (Dickinson et al., 1997; Nadim et al., 2008; Chalasani et al., 2010; Wu et al., 2010; Rodgers et al., 2011a, 2011b; Jang et al., 2012; Kwiatkowski et al., 2013; Krenz et al., 2014; Nadim and Bucher, 2014). In principle, the action of any given neuromodulator on a circuit can be restricted to a few circuit elements, or can be more widespread. How a given neuromodulator reconfigures a specific circuit depends on which neurons are direct targets of the modulator (Swensen and Marder, 2001), and secondarily on how the affected or modulated neuron interacts with other circuit components (Nadim and Bucher, 2014). In this paper, we restrict ourselves to “modulation” of a single neuron, and determine its influence, or lack thereof, on an entire circuit. Perhaps remarkably, there is a richness of behaviors to be seen when only one neuron is modulated. But, in principle, one could investigate the consequences of modulating multiple targets in different circuit configurations.

Our results are in line with previous results that have shown that the synchronization properties of a network can change when the properties of a single neuron are varied but its frequency in isolation is maintained (Ermentrout et al., 2001). In this study, we used parameter sweeps of the three active conductances in the hub neuron to model the changes in intrinsic membrane properties that could occur during neuromodulation or homeostasis. Of course, biological neurons often have many more conductances, any and all of which are likely to be subject to modulation. We chose to use a relatively simple model rather than one with many more conductances because the three conductances that we modeled capture the basic dynamics seen in most neurons and they each have distinct functions. Thus, the relative simplicity of the model used here gives results that are more directly visible and visualizable than is often the case with more complex models. Conversely, we chose a conductance-based model over a more simple phase-oscillator model so as to relate our results to the actions of specific currents (i.e., depolarizing, hyperpolarizing, or hyperpolarization-activated depolarization). Although we have chosen to highlight a few specific cases in this very general model, our findings address the possible consequences of targeted modulation for oscillatory circuits with electrical and inhibitory chemical synapses—such as those one might find in any invertebrate or vertebrate nervous system.

Characterization of the properties of the Morris−Lecar model with h-conductance

Altering the conductances of the three currents in the hub neuron model produces substantial changes in the frequency, wave form, duty cycle, and the amplitudes of the voltage excursions of this model neuron. Increasing the Ca²⁺ conductance produces monotonic increases in duty cycle (Fig. 3), which accounts for the U-shaped effect of increasing the Ca²⁺ conductance on frequency. This occurs because the oscillator continuously broadens, which eventually forces it to decrease in frequency. This is similar to behavior in the unmodified Morris−Lecar (Skinner et al., 1993, 1994), and demonstrates that even very simple model neurons can show quite different behaviors as a function of parameter choices. Of course, this model does not generate fast action potentials, but rather slower oscillations, on which action potentials could ride if they had also been modeled. Given the increased use of methods that monitor Ca²⁺ dynamics as a proxy for voltage in many invertebrate and vertebrate preparations, the fact that an increase in frequency could occur as a function of either increasing or decreasing calcium conductance is important to know for the potential interpretation of either genetic or pharmacological manipulations of currents.

Other studies have used conventional Morris−Lecar models (Wang and Rinzel, 1992; Skinner et al., 1993, 1994; Rinzel and Ermentrout, 1998; Tsumoto et al., 2006; Zhang et al., 2009). The Morris−Lecar with h-current (LoFaro et al., 1994) has useful features that make it a valuable tool for studying neuron and circuit dynamics. It is simple, yet captures more physiological detail than the conventional Morris−Lecar model. The h-current expands the voltage range and produces more realistic responses to inhibition, especially when the modeled system itself has an h-current. Therefore, for circuits with inhibition, it may be preferable to other reduced models. Additionally, the modified Morris−Lecar, as well as the conventional Morris−Lecar—or any other conductance based oscillator—allows one to attribute neuronal and network dynamics to physiologically based currents.

Global versus local changes

One of the big challenges in understanding how neuromodulators change the output of neuronal circuits is determining which changes in circuit performance arise from the direct actions of a modulator on individual target neurons, without appreciably changing the behavior of the other circuit elements, and which emerge as a consequence of the modulated neuron(s) interacting with other circuit components, thus indirectly altering the activity of many neurons that are themselves not direct targets of the modulator. Figure 6 highlights two extreme cases. In Figure 6A, modulation of the hub neuron will produce local changes, that is, the modulated neuron’s intrinsic properties will be altered, and while other neurons in the network may also change their behaviors somewhat because of the electrical coupling, the overall structure of the circuit output is preserved. In contrast, in Figure 6B, changes in only the hub neuron produce global changes, and the coordination patterns among all of the circuit neurons are substantially altered, merely by changing the properties of a single neuron.

Importantly, the two cases have identical connectomes—the synaptic architecture is the same. The intrinsic properties of the neurons are identical in the two cases, and they differ only in the strengths of the chemical and electrical synapses. This work shows that under some sets of circumstances, even modest modulation of one current in one neuron can create a number of different circuit output patterns (Fig. 6B). For example, increasing ḡ_Ca can transition the circuit through three different output patterns. Starting at a point in the elbow of the group where calcium and potassium conductances are low, and increasing those conductance together, as might happen with homeostasis, leads to different output patterns. The circuit would go from a pattern in which the hub neuron is oscillating in time with the slow oscillators, to a pattern in which the hub neuron would switch to oscillating with the fast rhythm, and finally switching to a pattern in which the electrically coupled slow oscillator is recruited into the fast rhythm.

Implications for evaluating connectomes

It is now widely appreciated that the connectome, while necessary to understand circuit dynamics, is not sufficient (Brezina, 2010; Bargmann, 2012; Bargmann and Marder, 2013), partially because of neuromodulation, and partially as a simple function of the necessity of knowing the intrinsic properties of neurons and the synaptic strengths in the circuit. That said, the ambiguities inherent in the connectome are even more considerable when electrical synapses are part of the circuit, as current can flow bi-directionally between neurons and produce changes in circuit output that are difficult to predict, with or without rectification of the electrical synapses (Kopell et al., 1998; Soto-Trevino et al., 2005; Gutierrez and Marder, 2013; Gutierrez et al., 2013).

It is interesting that the limitations of the connectome itself for predicting circuit output also depend on the circuit parameters. In Figure 6B, we see that altering the intrinsic properties of the hub neuron can drastically alter the circuit’s behavior. Nonetheless, in other parameter regimes, the circuit is robust to the changes in the intrinsic properties of the hub neuron. In these conditions, an anatomic wiring diagram or “connectome” would adequately describe the circuit’s function (Plaza et al., 2014). In other words, a modulatory environment that sets circuit parameters can produce a mode switch from one in which the circuit is insensitive to parameter changes (e.g., well characterized by its connectome), and another in which the entire modulatory environment must be specified, and the connectome sets the stage on which the modulators act to configure the circuit’s output. It is now widely appreciated that an anatomic connectome is not necessarily sufficient for understanding how a circuit will work (Bargmann, 2012), but this study shows that the sufficiency of the connectome for elucidating circuit function is in itself under neuromodulatory control.

Synthesis

The decision was a result of the Reviewing Editor Leonard Maler, University of Ottawa and the peer reviewers coming together and discussing their recommendations until a consensus was reached. A fact-based synthesis statement explaining their decision and outlining what is needed to prepare a revision is listed below. The following reviewer agreed to reveal his identity: Jorge Golowasch

Synthesis:

The reviewers had very different perspectives on this manuscript. From the standpoint of a theoretician the work presented does not offer any novel insights. Analysis of the neuronal dynamics has shown, as per the citations in this review, that as a conductance is varied, the firing rate of a model neuron may remain constant while the network synchronization properties vary.

However, the reviewers also agreed that this manuscript provides a very clear demonstration of how a simple “connectome” analysis may completely fail to characterize network dynamics when the intrinsic conductances of even a single cell in the network is modulated.

I therefore ask the authors to revise the manuscript according to the critiques provided by the reviewers. Notably, a connection should be made to the dynamical system study of Ermentrout et al so that it is clear that the author's results would, in fact, be anticipated based on previous theoretical work. There should also be detailed answers provided to the questions raised by the reviewers with respect to dynamics, as well as making the minor changes requested by the reviewers.

These changes should result in a manuscript that clearly identifies, in one concrete simple model system, how the “dynamics in circuits depend on both the cellular dynamics and circuit structure”.

Reviews:

Reviewer #1: The study presents a numerical analysis of a simplified circuit, inspired in part by the stomatogastric ganglion, yet contains sufficiently general properties to be applicable elsewhere. The authors investigate how intrinsic and circuit properties combine to define functional invariants in overall response. The main finding involves identifying a neuromodulatory path that fixes the output firing rate of a neuron when it is isolation. However, when this neuron is imbedded into a circuit (as a hub neuron), the coupling of the circuit may (or may not) allow the circuit dynamics to inherit the invariance along the modulatory path. The paper is well written, builds on previous work, and the figures do a nice job at explaining the main story. However, I question the overall novelty of the work. Up until Fig. 6 (the last figure), nothing in the paper was surprising. It is well known that a parameter path where firing rate is invariant does not guarantee invariance in other output statistics (Fig. 3B and Fig. 5). Indeed, the phase resetting curve of a neuron may be radically different despite the period of the limit cycle being the same. As an example, see Fig. 5 of Ermentrout, Pascal, and Gutkin, Neural Computation, 13, 2001 as M-current conductance is varied. Here, the overall synchronization properties of the circuit change as one moves along a parameter path that would keep the isolated cell's firing rate fixed. Thus, for this reason I feel that the results of Figures 1,2,3 and 5 offer nothing new to the community. That leaves Figures 4 and 6. Figure 4 describes a ‘parameterscape’ study of their Morris-Lecar circuit for cellular parameters, as opposed to synaptic coupling as was done in their 2013 Neuron paper. This is simply descriptive, and while the results are new, the authors do not give clear intuition for the result. Finally, Figure 6 shows that if the feedforward synaptic strength to the hub is large and the electrical coupling between the hub and the circuit is small, then as the hub neuron is modulated along the firing rate invariant path, the locking of the hub to the rest of the circuit is also invariant. However, the converse is not true, i.e when the synaptic coupling is weak and the electrical is strong, locking invariance does not follow from firing rate invariance. This is not immediately obvious, however this result is only given a single paragraph at the end of the paper, and the authors do not explore this effect further. Many questions are left unanswered. Two that come to mind are: 1. Is an electrical coupling of 2nS sufficiently weak so that the entire circuit is feedforward in the first case? If so, then is Fig. 6A somewhat expected. 2. While, the first invariant is really a strict quantitative invariance (neuron is firing at 0.5717 /pm 0.01 Hz), the network invariant in Figure 6 is merely the qualitative invariant of what locking relationships exist. As the neuromodulatory path is explored in the circuit, doe the firing rates of the neurons that are locked change? Basically, just because in Figure 6A all of the points are blue does not mean that there is a strict invariance of network dynamics (like the period of the oscillatory dynamics). In the end the authors are using the renewed interest in the ‘connectome’ as a straw-man for revisiting an idea that has been know for a long time: dynamics in circuits depend on both the cellular dynamics and circuit structure of the network. Unfortunately, the specifics are case by case dependent, and the authors analyze one such case.

Reviewer #2: This is an elegant study that illustrates how the intrinsic properties of members of a network, even single members of the network, will determine the output of the entire network, a phenomenon widely observed in networks subject to neuromodulation. I have no major concerns. Minor details p. 14, last paragraph. I just don't see the V shape in the figure (“V formation” in legend of Fig. 5). If anything, if what you mean is that the point that produce network oscillations hug the axes, I would call than an L shape distribution, but I am not sure if that is what you mean. Please clarify this. p. 15, 3rd line from the end. Remove “calcium” or “Ca2+”. Also, in this paragraph you indicate that there is no correlation of g_K and V+peakm which is not very obvious to me from the figure. I see that both V_peak and DC a positive correlation with g_K. Perhaps showing a projection of the g_Ca-g_h plane to more clearly show their relationship to V_peak and DC would be useful in Fig. 5 p. 16, last line of first paragraph. This sentence is somewhat confusing. I would suggest “For the sake of tractability, the frequency of the slow and fast oscillator neurons were left unchanged”. Figure 6A. There is a brown and a red diamond in the midst of all the blue ones. What's the story with them? Also, the labels should say g_syn1 rather than g_synA for consistency with the rest of the paper. Generally, the figures all show maximal conductances without the bar over the g, while the text shows the bar.

Author Response Letter:

Reviews:

Reviewer #1: The study presents a numerical analysis of a simplified circuit, inspired in part by the stomatogastric ganglion, yet contains sufficiently general properties to be applicable elsewhere. The authors investigate how intrinsic and circuit properties combine to define functional invariants in overall response. The main finding involves identifying a neuromodulatory path that fixes the output firing rate of a neuron when it is isolation. However, when this neuron is imbedded into a circuit (as a hub neuron), the coupling of the circuit may (or may not) allow the circuit dynamics to inherit the invariance along the modulatory path. The paper is well written, builds on previous work, and the figures do a nice job at explaining the main story. However, I question the overall novelty of the work. Up until Fig. 6 (the last figure), nothing in the paper was surprising. It is well known that a parameter path where firing rate is invariant does not guarantee invariance in other output statistics (Fig. 3B and Fig. 5). Indeed, the phase resetting curve of a neuron may be radically different despite the period of the limit cycle being the same. As an example, see Fig. 5 of Ermentrout, Pascal, and Gutkin, Neural Computation, 13, 2001 as M-current conductance is varied. Here, the overall synchronization properties of the circuit change as one moves along a parameter path that would keep the isolated cell's firing rate fixed. Thus, for this reason I feel that the results of Figures 1,2,3 and 5 offer nothing new to the community.

We understand the reviewer's point, but our goal in this paper is not to provide new and illuminating mathematics for the computational community, but to use these numerical studies to highlight fundamental issues relevant to experimental neuroscientists who are sadly unable or unlikely to read the mathematical literature. For example, the simple fact that increasing a current can first increase and then decrease the frequency of an oscillator is not appreciated by most experimentalists. Moreover, while the study of the effects of parameters on the properties of the Morris-Lecar plus h current model does not break new mathematical ground, the basic properties of this model have not been carefully documented before, and are of interest. We are pleased that the reviewer found the figures and text relatively clear and straightforward, because they are meant for a general target audience.

We thank the reviewer for prompting us to look at the PRCs for these models. We include a panel in Figure 3 comparing the PRCs of the two neurons we show there. Again, it is not surprising, but illustrates why the two neurons will respond differently to inputs in the earlier part of their cycles.

That leaves Figures 4 and 6. Figure 4 describes a ‘parameterscape’ study of their Morris-Lecar circuit for cellular parameters, as opposed to synaptic coupling as was done in their 2013 Neuron paper. This is simply descriptive, and while the results are new, the authors do not give clear intuition for the result.

Figure 4D is intended to introduce the reader to the 5-cell circuit and to provide the groundwork for the results that follow by showing that two neurons that have the same frequency in isolation but different conductances can have very different effects on the network output pattern even if all other things are the equal. In the first full paragraph of p.14, we focused on the intuition for that particular result rather than attempt to analyze the entire parameterscape shown.

Finally, Figure 6 shows that if the feedforward synaptic strength to the hub is large and the electrical coupling between the hub and the circuit is small, then as the hub neuron is modulated along the firing rate invariant path, the locking of the hub to the rest of the circuit is also invariant. However, the converse is not true, i.e when the synaptic coupling is weak and the electrical is strong, locking invariance does not follow from firing rate invariance. This is not immediately obvious, however this result is only given a single paragraph at the end of the paper, and the authors do not explore this effect further. Many questions are left unanswered. Two that come to mind are: 1. Is an electrical coupling of 2nS sufficiently weak so that the entire circuit is feedforward in the first case? If so, then is Fig. 6A somewhat expected.

When gel is very weak (gel=0.5, gsyn1=6, gsynHC=5), the candidate networks produce a variety of output patterns, for reasons that are dealt with in the discussion of the “tongue” in Gutierrez et al. 2013. If gel is increased to 3.5nS, the network behavior is basically the same as when gel=2nS. When gel is further increased to 4.5nS, multiple network patterns begin to share the stage with the one originally observed.

However, when gel=2nS but gsyn1 is much lower (1nS), the candidates produce 2 or 3 main output patterns, which is 1 or 2 more than if the feedforward connections were much higher.

We have added a paragraph at the end of the results on p.17 stating that it's not simply a matter of imposing a weak electrical coupling that puts the network in a feedforword, inhibition dominated regime, since a much lower electrical coupling can actually allow multiple network patterns to emerge among the candidate circuits.

2. While, the first invariant is really a strict quantitative invariance (neuron is firing at 0.5717 /pm 0.01 Hz), the network invariant in Figure 6 is merely the qualitative invariant of what locking relationships exist. As the neuromodulatory path is explored in the circuit, doe the firing rates of the neurons that are locked change? Basically, just because in Figure 6A all of the points are blue does not mean that there is a strict invariance of network dynamics (like the period of the oscillatory dynamics).

Figure 6 only describes the locking relationships and not the frequencies. We do find that the oscillatory periods vary in Figure 6A and thus the network behaviour is not strictly invariant, only the overall oscillatory pattern is. We feel that extensive discussion of the variable frequencies would detract from the novel part of our finding which relates to the effect of neuromodulation on the network locking patterns. However, we have added a sentence on p.16 stating that although the network patterns and locking relationships are invariant, the exact frequencies do vary.

In the end the authors are using the renewed interest in the ‘connectome’ as a straw-man for revisiting an idea that has been know for a long time: dynamics in circuits depend on both the cellular dynamics and circuit structure of the network. Unfortunately, the specifics are case by case dependent, and the authors analyze one such case.

It's true that we frame this story as a cautionary tale of the connectome. And it's true that the specifics are case by case dependent – we don't wish to claim otherwise. Of course, every circuit is different. Our goal here is to give experimentalists who are using genetic, optogenetic and pharmacological tools to manipulate cells and circuits the intuition that not all manipulations will give easy and predictable results, and that non-intuitive results are not necessarily wrong or unreasonable.

Consequently, we fleshed out some of these ideas in an amplified section of the Discussion.

Reviewer #2: This is an elegant study that illustrates how the intrinsic properties of members of a network, even single members of the network, will determine the output of the entire network, a phenomenon widely observed in networks subject to neuromodulation. I have no major concerns.

Minor details p. 14, last paragraph. I just don't see the V shape in the figure (“V formation” in legend of Fig. 5). If anything, if what you mean is that the point that produce network oscillations hug the axes, I would call than an L shape distribution, but I am not sure if that is what you mean. Please clarify this.

We've adjusted the wording to make this clearer.

p. 15, 3rd line from the end. Remove “calcium” or “Ca2+”.

Done.

Also, in this paragraph you indicate that there is no correlation of g_K and V+peakm which is not very obvious to me from the figure. I see that both V_peak and DC a positive correlation with g_K. Perhaps showing a projection of the g_Ca-g_h plane to more clearly show their relationship to V_peak and DC would be useful in Fig. 5

We have added panels to Figure 5 to make these relationships more easy to understand.

p. 16, last line of first paragraph. This sentence is somewhat confusing. I would suggest “For the sake of tractability, the frequency of the slow and fast oscillator neurons were left unchanged”.

What we mean to say is that we don't vary the ionic conductances of the intrinsically fast and slow oscillators, only the ionic conductances of the hub neuron. The wording has been changed to make this clearer.

Figure 6A. There is a brown and a red diamond in the midst of all the blue ones. What's the story with them?

We chose not to bring the focus to these two data points because as a whole, the points in this figure are by and large blue and that was the main point we wished to make with this figure.

Also, the labels should say g_syn1 rather than g_synA for consistency with the rest of the paper. Generally, the figures all show maximal conductances without the bar over the g, while the text shows the bar.

Thank you for bringing our attention to those errors. We have made the necessary changes to remain consistent with our labeling.