A Structural Theory of Pitch

Melodies are composed of sounds that can be ordered on a musical scale. “Pitch” is the perceptual dimension on that scale.

Abstract

Musical notes can be ordered from low to high along a perceptual dimension called “pitch”. A characteristic property of these sounds is their periodic waveform, and periodicity generally correlates with pitch. Thus, pitch is often described as the perceptual correlate of the periodicity of the sound’s waveform. However, the existence and salience of pitch also depends in a complex way on other factors, in particular harmonic content. For example, periodic sounds made of high-order harmonics tend to have a weaker pitch than those made of low-order harmonics. Here we examine the theoretical proposition that pitch is the perceptual correlate of the regularity structure of the vibration pattern of the basilar membrane, across place and time—a generalization of the traditional view on pitch. While this proposition also attributes pitch to periodic sounds, we show that it predicts differences between resolved and unresolved harmonic complexes and a complex domain of existence of pitch, in agreement with psychophysical experiments. We also present a possible neural mechanism for pitch estimation based on coincidence detection, which does not require long delays, in contrast with standard temporal models of pitch.

Significance Statement

Melodies are composed of sounds that can be ordered on a musical scale. “Pitch” is the perceptual dimension on that scale. To a large extent, the periodicity of the sound’s waveform can be mapped to pitch. However, the existence and strength of pitch also depends on the harmonic content sounds, i.e., their timbre, which does not fit with this simple view. We propose to explain these observations by the fact that the input to the auditory system is the spatiotemporal vibration of the basilar membrane in the cochlea, rather than the acoustic waveform. We show that defining pitch as the regularity structure of that vibration can explain some aspects of the complexity of pitch perception.

Introduction

A musical note played by a piano or a trumpet has a perceptual attribute called “pitch”, which can be low or high. The same key played on different instruments produces sounds with different spectral content but identical pitch. To a large extent, pitch can be mapped to the periodicity, or repetition rate (f0), of the acoustic waveform (Oxenham, 2012). For this reason, theories of pitch perception have focused on how the auditory system extracts periodicity. In the cochlea, the mechanical response of the basilar membrane (BM) to sounds has both a spatial and a temporal dimension. The BM vibrates in response to tones, following the frequency of the tone. The place of maximal vibration along the BM also changes gradually with tone frequency, from the base (high frequency) to the apex (low frequency). Accordingly, there are two broad types of theories of pitch, emphasizing either time or place (de Cheveigné, 2010).

Place theories (or pattern recognition theories) propose that the spatial pattern of BM vibration is compared to internal templates, consisting of harmonic series of fundamental frequencies (Terhardt, 1974). Pitch is then estimated from the fundamental frequency of the best-matching template. This mechanism requires that harmonics of the sound produce clear peaks in the spatial pattern of BM vibration, i.e., that harmonics are “resolved” by the cochlea, but this is typically not the case for high-order harmonics because the bandwidth of cochlear filters increases with center frequency. In contrast, tone complexes with only unresolved harmonics can elicit a pitch (Ritsma, 1962; Oxenham et al., 2011). In addition, the firing rate of auditory nerve fibers, as well as most neurons in the cochlear nucleus, saturates at high levels, but pitch perception does not degrade at high levels (Cedolin and Delgutte, 2005).

Temporal theories propose that periodicity is estimated from the temporal waveform in each auditory channel (cochlear place), and estimates are then combined across channels (Licklider, 1951; Meddis and O’Mard, 1997; de Cheveigné, 2010). Sound periodicity is indeed accurately reflected in the patterns of spikes produced by auditory nerve fibers (Cariani and Delgutte, 1996a, 1996b; Cedolin and Delgutte, 2005). Resolvability plays little role in these theories, but pitch based on resolved harmonics is more salient and easier to discriminate than pitch based on unresolved harmonics (Houtsma and Smurzynski, 1990; Carlyon and Shackleton, 1994; Carlyon, 1998; Bernstein and Oxenham, 2003). Finally, detecting the periodicity of a waveform with repetition rate f0 = 30 Hz [the lower limit of pitch (Pressnitzer et al., 2001)] would require delays of about 30 ms, of which there is no clear physiological evidence.

In addition, the domain of existence of pitch is complex, which neither type of theory explains: the existence of pitch depends not only on f0 but also on resolvability of harmonics and spectral content (Pressnitzer et al., 2001; Oxenham et al., 2004b, 2011). For example, high-frequency complex tones (>4 kHz) with f0 = 120 Hz do not have a clear pitch while a pure tone with the same f0 does (Oxenham et al., 2004b); but high-frequency complex tones with f0 > 400 Hz do have a clear pitch (Oxenham et al., 2011). Finally, while pitch is generally independent of sound intensity [contradicting place theories (Micheyl and Oxenham, 2007)], a few studies suggest a small but significant intensity dependence of pitch for low-frequency pure tones (Morgan et al., 1951; Verschuure and Van Meeteren, 1975; Burns, 1982) (contradicting temporal theories).

Here we propose to address these issues by reexamining the postulate that pitch is the perceptual correlate of the periodicity of the acoustic waveform. Starting from the observation that the input to the auditory system is not the acoustic waveform but the vibration pattern of the BM, we propose instead that pitch is the perceptual correlate of the regularity structure of the BM vibration pattern, across place and time. While this proposition also attributes pitch to periodic sounds, we show that it predicts differences between resolved and unresolved harmonic complexes and a complex domain of existence of pitch. We also present a possible neural mechanism for pitch estimation based on coincidence detection, which does not require long delays.

Materials and Methods

Auditory filters

Auditory filters were modeled as gammatone filters (Slaney, 1993; Fontaine et al., 2011), which approximate reverse correlation filters of cat auditory nerve fibers (de Boer and de Jongh, 1978; Carney and Yin, 1988) and have been matched to psychophysical measurements in humans (Glasberg and Moore, 1990). Their impulse response defined by: H(t) = t^{n −1} e ^{-t /τ} cos(2π · CF · t), where CF is the characteristic frequency, n is the order, and the bandwidth is set by τ = (2π · 1.019 · (24.7 + 0.108 · CF))⁻¹. Filters were spaced uniformly in equivalent rectangular bandwidth scale (Glasberg and Moore, 1990) with CF between 100 and 8000 Hz.

Neural model of pitch estimation

The neural model of pitch estimation includes two layers: the input layer (putatively cochlear nucleus) and coincidence detector neurons.

Input layer

Each neuron receives the output x(t) of a gammatone filter, after half-wave rectification and compression with a power law with exponent γ = 0.3 (Stevens, 1971; Zwislocki, 1973): y(t) = κ([x(t)⁺]^γ) (varying the exponent between 0.2 and 0.5 did not affect the results).

We tested different spiking neuron models (Fig. 4), defined by a membrane equation of the following form:

$$C\frac{dV}{dt}=g_L\left(E_L-V\right)+y\left(t\right)+\sigma \xi \left(t\right)+I\left(V\right),$$ (1)

where V is the membrane potential, g_L(E_L − V) represent the nonspecific leak current, σ is the noise level, C is the membrane capacitance and I(V) represents currents from voltage-gated channels.

Figure 4.

Neural network model of pitch estimation using within- and cross-channel structure. A, Spectrogram of a trumpet sound showing the first two harmonics. Two neurons with CF around the first harmonic and input delay δ receive the same signal (red and blue rectangles and input signals below). As a result, the two neurons fire synchronously for all three neuron models used: biophysical model of chopper and octopus cells, and leaky integrate-and-fire model (voltage traces). B, Spectrogram of a rolling sea wave sound, which shows no regularity structure. In particular, the two neurons do not receive the same signals (input, shaded area: difference between the two signals) and thus do not fire synchronously. C, Spectrogram of a harpsichord sound with unresolved harmonics in high frequency. The inset shows the periodicity of the envelope. Two neurons fire synchronously if they receive inputs from the same place delayed by δ = 1/f0. D, In the same high-frequency region, the inharmonic sound of a sea wave does not produce within-channel structure and therefore the two neurons do not fire synchronously. E, Synaptic connections for a pitch-selective group tuned to f0 = 220 Hz. Harmonics are shown on the left (red comb) superimposed on auditory filters. Resolved harmonics (bottom) produce regularity structure both across and within channels: color saturation represents the amplitude of the filter output while hue represents its phase for different delays (horizontal axis) and characteristic frequencies (vertical axis). Neurons with the same color fire synchronously and project to a common neuron. Unresolved harmonics (top) produce regularity structure within channels only. Here two identical colors correspond to two identical input signals only when the neurons have identical CF (same row). F, Same as E for f0 = 261 Hz, producing a different regularity structure, corresponding to a different synchrony pattern in input neurons. Synchronous neurons project to another group of neurons, selective for this pitch.

The chopper cell model (T-multipolar) is based on Rothman and Manis’s (2003a) model, with maximal conductances g_Na = 1000 nS, g_KHT = 150 nS, and g_h = 0.5 nS. Octopus cells are also based on the same model but include a low-threshold potassium channel (KLT) and model of I_htaken from Khurana et al. (2011), with g_Na = 1000 nS, g_KHT = 150 nS, g_KLT = 600 nS, and g_h = 40nS. These two models were used only in Figure 4.

We also used a leaky integrate-and-fire model, a phenomenological model with good predictive value for a broad class of neurons (Jolivet et al., 2004; Gerstner and Naud, 2009). The membrane time constant was τ = g_L/C = 1.5 ms. The model spikes when V(t) reaches the threshold θ = −40 mV, and V(t) is then reset to V_r = −60 mV and clamped at this value for a refractory time of τ_r = 1 ms. This model was used in all simulations, unless otherwise specified.

Coincidence detectors

The second layer consists of coincidence detectors, which are modeled as integrate-and-fire models (as above) with an adaptive threshold governed by the following equation (Platkiewicz and Brette, 2010, 2011; Fontaine et al., 2014):

$${\tau }_{\theta }\frac{d\theta }{dt}={\theta }_0-\theta +V-E_L,$$ (2)

where θ₀ = −40mV is the value of threshold at rest and τ_θ = 5 ms (note that half-wave rectification can be discarded here because V is always above E_L, as there are only excitatory synapses). This equation ensures that the neuron is always in a fluctuation-driven regime where it is sensitive to coincidences (Platkiewicz and Brette, 2011). The response of the coincidence detectors was only considered after 30 ms following note onset.

Synaptic connections

For each possible f0, we build a group of coincidence detectors whose inputs are synchronous when a sound of period 1/f0 is presented. For any sound, the synchrony partition is defined as the set of groups of input neurons that fire in synchrony for that particular sound (Brette, 2012) (synchrony is within group, not across groups). One coincidence detector neuron is assigned to each group (synaptic connections from each input neuron to the coincidence detector), so that the synchrony partition corresponds to a set of coincidence detector neurons.

To build a group of coincidence detector neurons tuned to periodic sounds with fundamental frequency f0, we consider the synchrony partition of the complex tone made of all harmonics of f0, i.e., tones of frequency k · f0. For each harmonic, we select all pairs of channels in our filter bank that satisfy the following properties (Fig. 2D): (1) the gain at k · f0 is greater than a threshold G_min = 0.25 (Fig. 2D, dashed line), (2) the two gains at k · f0 are within ε = 0.02 of each other, and (3) the gain at neighboring harmonics (order k − 1 and k + 1) is lower than the threshold G_min (resolvability criterion). For each selected pair of channels, we connect the corresponding input neurons to a single coincidence detector neuron. The connection from the neuron with higher CF has an axonal delay δ = Δφ/kf₀, where Δφ is the phase difference between the two filters at k · f0 [which is known analytically for a gammatone (Zhang et al., 2001)]. In addition, for each channel, multiple neurons receiving inputs from the same filter project to a single coincidence detector neuron with axonal delays δ = k/f₀ (as in Licklider’s model), where k in the integer varying between 1 and a value determined by the maximum delay δ_max.

Figure 2.

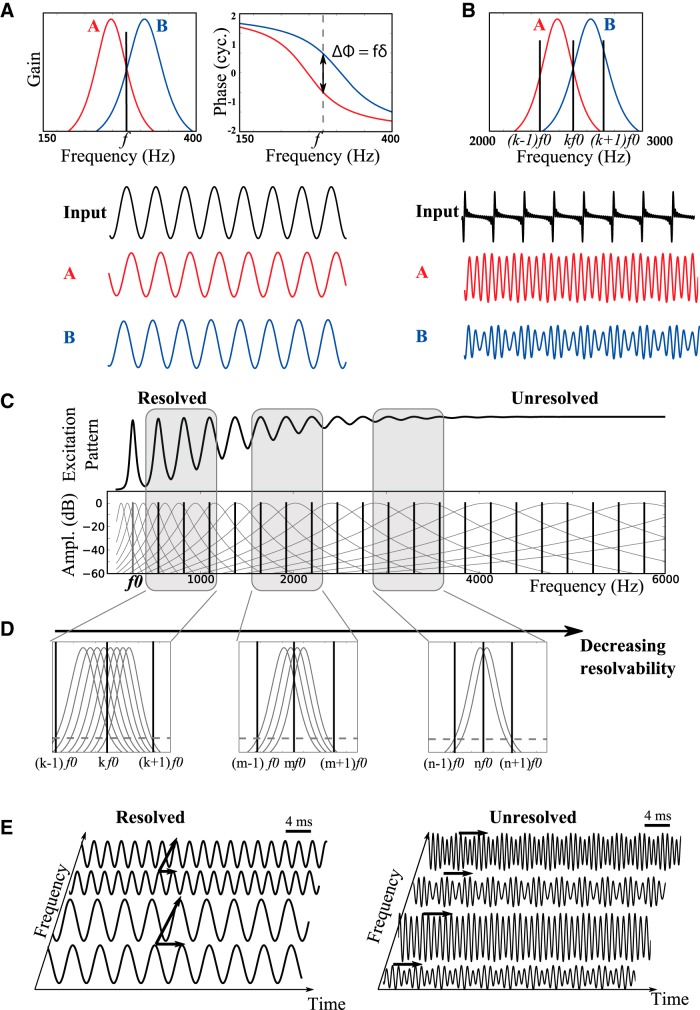
Harmonic resolvability and cross-channel structure. A, Amplitude and phase spectrum of two gammatone filters. Only a pure tone of frequency f (“Input” waveform) is attenuated in the same way by the two filters (red and blue waveforms: filter outputs). At that frequency, the delay between the outputs of the two filters is δ = Δφ/f. B, If several harmonic components fall within the bandwidths of the two filters, then the outputs of the two filters differ (no cross-channel similarity). C, Excitation pattern produced on the cochlea by a harmonic complex. Top, Amplitude versus center frequency of gammatone filters. Bottom, Spectrum of harmonic complex and of gammatone filters. Harmonic components are resolved when they can be separated on the cochlear activation pattern. Higher-frequency components are unresolved because cochlear filters are broader. D, Resolved components produce cross-channel similarity between many pairs of filters (as in A). Unresolved components produce little cross-channel structure (as in B). E, Thus, the vibration pattern produced by resolved components displays both within-channel and cross-channel structure (left), while unresolved components only produce within-channel structure (right).

Sounds

Musical instruments

To test the neural model in a pitch-recognition task, we used recordings of musical instruments and vowels from the RWC Music Database (Musical Instrument Sound), including 762 notes between A2 and A4, 41 instruments (587 notes), and five sung vowels (175 notes). Notes were gated by a 10 ms cosine ramp and truncated after 500 ms.

Environmental noises

We also used a set of 63 environmental sounds containing stationary noises including: airplanes, thunderstorm, rain, water bubbles, sea waves, fire, and street sounds (recordings obtained from www.freesound.org). We selected 500 ms segments from these sounds, gated by a 10 ms cosine ramp.

Analytical description of the auditory nerve phase response

To analyze the discriminability of cross-channel structure (Fig. 6E,F), we fitted an analytical formula to the phase φ(L, f, CF) of auditory nerve responses recorded at different levels L and tone frequencies f in fibers with different CF, using a data set from Palmer and Shackleton (2009), similarly to Carlyon et al. (2012). For each level, we fitted a function corresponding to the phase response of a gammatone filter bank:

$$\varphi \left(L,f,\mathrm{C}\mathrm{F}\right)=\mathrm{ }f\psi \left(L,CF\right)+n\arctan \left(2\pi \tau \left(\mathrm{C}\mathrm{F},L\right)\left(f-\mathrm{C}\mathrm{F}\right)\right)$$

where ψ(L, CF) is the initial delay of the travelling wave [a parameterized function of CF (Zhang et al., 2001, their Eq. 3)], in the order of the gammatone filter and τ(CF, L) = α(L)CF^{β(L )} is inversely related to the bandwidth of the filter.

Figure 6.

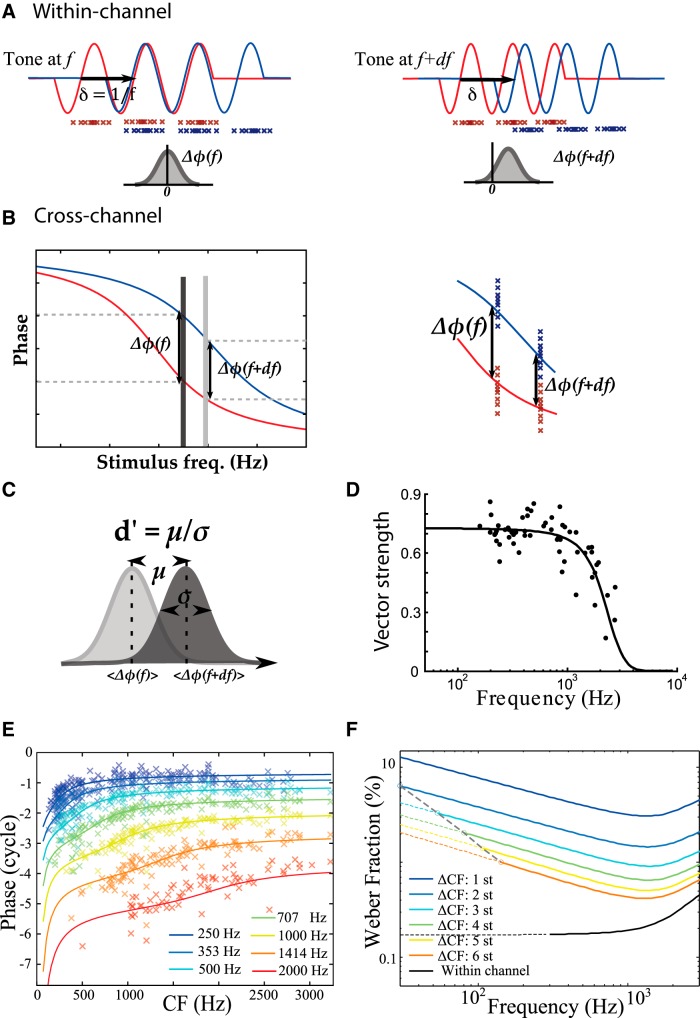
Pitch discriminability. A, Two neurons tuned to the same frequency (within-channel) but with delay mismatch δ = 1/f produce phase-locked spikes (red and blue crosses) in response to a tone (sine waves). When the tone frequency is f (left), the two input signals match and the difference of phases of spikes ΔΦ(f) between the two neurons is distributed around 0 (shaded curve). When the tone frequency is f + df (right), the two signals are slightly mismatched and the distribution of ΔΦ(f) is not centered on 0. B, Two neurons tuned to different frequencies (cross-channel) respond at different mean phases to tones (red and blue curves). C, The discriminability index d' is defined as the distance µ between the centers of be two phase difference distributions (ΔΦ(f) and ΔΦ(f + df)) relative to their standard deviation σ. D, The standard deviation of the phase distribution is related to the precision of phase locking, measured by the vector strength (dots: vector strength vs characteristic frequency for guinea pig auditory fibers; solid curve: fit). E, Mean phase of spikes produced by auditory nerve fibers of guinea pigs for different tone frequencies (data from Palmer and Shackleton, 2009), as a function of CF (crosses) with fits (solid lines). F, Weber fraction (Δf/f, where Δf is the just noticeable difference in frequency) as a function of tone frequency for cross-channel structure (colored curves) and within-channel structure (black curve). Color represent different frequency spacings between the two channels (1 − 6 semitones). Dotted lines represent the limitations implied by a maximal delay δ_max = 5 ms.

We also tested another function: φ(L, f, CF) = α(L, f) + β(L, f) arctan(CF/γ(L, f)) as in Carlyon et al. (2012), where α, β and γ were second-order polynomial functions of L and f. The fits gave similar results.

Discriminability of cross-channel and within-channel structure

We used signal detection theory (Green and Swets, 1966) to estimate the discriminability of tone frequency based on regularity structure, using only phase information (to simplify). We consider two places on the cochlea tuned to frequencies f_A and f_B. A tone of frequency f is detected when the two waveforms at places A and B are in phase after a delay d is introduced in channel B: φ(f_B, f) + fd = φ(f_A, f) + n, where n is an integer (phases are expressed in cycles). Note that n is related to related to the maximum delay δ _max (when f < 1/δ _max, there is at most one possible value for n).

We note Δφ_AB(f) = φ(f_B, f) − φ(f_A, f) the phase difference between the two places (before the delay is introduced), so that the equation reads:

$$\mathrm{\Delta }{\mathrm{\varphi }}_{AB}\left(f\right)+f\mathrm{\delta }=n$$ (3)

That is, the phase difference after the delay is introduced is 0 cycle. When a tone of frequency f + df is presented, the phase difference after the delay is introduced is $\mathrm{\Delta }{\varphi }_{AB}\left(f+df\right)+\left(f+df\right)\delta =\mathrm{\Delta }{\varphi }_{AB}\left(f\right)+f\delta +\left(\mathrm{\Delta }{\varphi }_{AB}^{\text{'}}\left(f\right)+\delta \right)·df=n+\left(\mathrm{\Delta }{\varphi }_{AB}^{\text{'}}\left(f\right)+\delta \right)·df$. Thus, a frequency shift of df induces a phase shift of $\left(\mathrm{\Delta }{\varphi }_{AB}^{\text{'}}\left(f\right)+\delta \right)·df$ between the two channels, after introduction of the delay.

We consider that neurons corresponding to channels A and B fire spikes in a phase-locked manner with precision σ (standard deviation of spike phase). Then the discriminability index d′ is the mean phase shift divided by the precision:

$$d^{\mathrm{\text{'}}}=\frac{\left(\mathrm{\Delta }{\varphi }_{AB}^{\mathrm{\text{'}}}\left(f\right)+\delta \right).df}{\sigma }$$

The just-noticeable difference (JND) for 75% correct discrimination is then:

$$\mathrm{J}\mathrm{N}\mathrm{D}=1.35\frac{\sigma }{\mathrm{\Delta }{\varphi }_{AB}^{\mathrm{\text{'}}}\left(f\right)+\delta }$$

The Weber fraction is JND/f. For two identical channels (within-channel structure), δ =1/f and the formula simplifies to:

$$\mathrm{J}\mathrm{N}{\mathrm{D}}_{75\%}=1.35\sigma f$$

For distinct channels (cross-channel structure), d is determined by Equation 3, and the formula reads:

$$\mathrm{J}\mathrm{N}{\mathrm{D}}_{75\%}=1.35\frac{\sigma f}{(f·\mathrm{\Delta }{\varphi }^{\mathrm{\text{'}}}\left(f\right)+n-\mathrm{\Delta }{\varphi }_{AB}\left(f\right))}$$

Finally, we relate phase precision with vector strength VS using the following formula, based on the assumption that phases are distributed following a wrapped-normal distribution:

$$\sigma =\sqrt{-\ln \left({\mathrm{V}\mathrm{S}}^2\right)}/2\pi$$

Results

The proposition

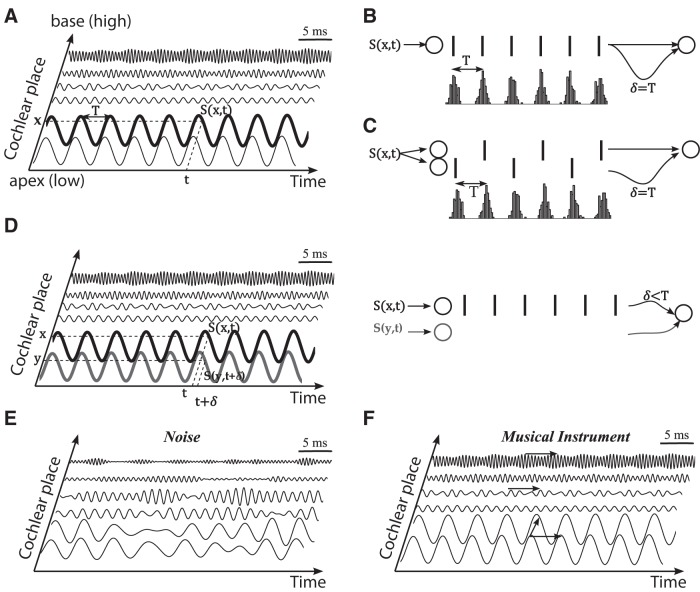
In the cochlea, the BM vibrates in response to sounds. We denote the displacement of the BM at time t and place x by S(x,t). This displacement is represented in Figure 1A as the output of a gammatone filterbank with bandwidth based on psychophysical measurements (see Materials and Methods, above). Each auditory nerve fiber transduces the temporal vibration S(x,t) at a specific place into a spike train. In Licklider's delay line model [the classical temporal model (Licklider, 1951)], the periodicity of the mechanical vibration is detected by a coincidence detector neuron receiving synaptic inputs from a single cochlear place x. It fires when it receives coincidences between a spike train produced by a fiber originating from that place and the same spike train delayed by a fixed amount δ (Fig. 1B). Conceptually, this neuron detects the identity S(x,t + δ) = S(x,t) for all t, that is, the fact that S(x,.) is periodic with period T = δ. This mechanism must be slightly amended to account for the refractory period of fibers, which sets a lower limit to the period that can be detected. This issue can be addressed by postulating that the neuron receives inputs from two different fibers originating from the same place (Fig. 1C).

Figure 1.

Regularity structure of the BM vibration pattern. A, Vibration of the basilar membrane produced by a periodic sound S(x,t) (clarinet musical note), at places x tuned to different frequencies (modeled by band-pass filters). B, The vibration at one place is transformed into spikes produced by an auditory nerve fiber (bottom, poststimulus time histogram of spikes). In Licklider’s model, the fiber projects to a coincidence detector neuron through two axons with conduction delays differing by δ. The neuron fires maximally when the signal’s periodicity T equals δ. C, If the signal’s period T is smaller than the neuron’s refractory time, then the neuron must detect coincidences between spikes coming from different fibers. D, If the fibers originate from slightly different places x and y on the cochlea, then the neuron responds to similarities between BM vibrations at different places. E, Vibration pattern of the BM produced by a nonperiodic sound (noise): there is no regularity structure across place and time. F, Vibration pattern produced by a musical note: there are signal similarities across time (horizontal arrows) and place (oblique arrow).

We now consider the possibility that these two fibers may originate from slightly different cochlear places x and y. In this case, the neuron detects the identity S(y,t + δ) = S(x,t), that is, similarity of sensory signals across both place and time (Fig. 1D). We note in this example (a harmonic sound) that the delay δ may now be different from the period T of the vibration. Compared to the detection of periodicity, this does not require any additional anatomical or physiological assumption. Thus, we propose to examine the proposition that pitch is the perceptual correlate of the regularity structure of the BM vibration pattern, across both time and place, defined as the set of identities of the form S(x,t) = S(y,t + δ) for all t. A few previous models of pitch also use cross-channel comparisons (Loeb et al., 1983; Shamma, 1985; Carney et al., 2002), and we will relate them to our theory in the discussion.

To illustrate our proposition, Figure 1, E and F, shows the cochleograms obtained by filtering two sounds with a gammatone filterbank. A noise-like sea wave (Fig. 1E) produces no regularity structure in the cochleogram; that is, there are no identities S(x,t) = S(y,t + δ) in the signals. A clarinet note, in contrast, produces a rich regularity structure (Fig. 1F). Because this is a periodic sound, the BM vibrates at the sound’s period T at all places (or more generally T/k, where k is an integer), as shown by horizontal arrows: S(x,t + T) = S(x,t) for all t and x. We call this set of identities the within-channel structure. More interestingly, we also observe identities across places, as shown by oblique arrows: S(x,t) = S(y,t + δ) for all t. These occur for specific pairs of places x and y, which tend to be in low-frequency regions. We note that the time shift δ is different from the sound’s period T. We call this set of identities the cross-channel structure.

Resolvability and regularity structure

We now examine the type of regularity structure produced by sounds. First, if the sound is periodic, then the BM vibrates at the sound’s period T at all places, provided there is energy at the corresponding frequency. That is, S(x,t + T) = S(x,t) for all x and t. Conversely, the identity S(x,t + T) = S(x,t) means that the BM vibrates periodically, which can only occur if the sound itself is periodic, at least within the bandwidth of the cochlear filter at place x. Thus, within-channel structure is simply the periodicity structure at each cochlear place.

Cross-channel structure is less trivial. What kind of sound produces the same vibration (possibly delayed) at different places of the cochlea? To simplify the argument, we consider that cochlear filters are linear (we come back to this point in the Discussion, below), and we examine the identity S(x,t) = S(y,t + δ) in the frequency domain. If the two signals at places x and y match, then all their frequency components must match, both in phase and amplitude. But these two signals originate from the same sound, filtered in two different ways. Figure 2A shows the gain (left) and phase (right) of the two filters A and B as a function of frequency. The only way that a frequency component is filtered in the same way by the two filters is that the gains are identical at that frequency, which happens in this case at a single frequency f (illustrated on Fig. 2a, bottom). Additionally, the phases of the two filters must match at frequency f, taking into account the delay δ. That is, the phase difference Δφ must equal f · δ (modulo 1 cycle).

In summary, the only type of sound that produces cross-channel structure is a sound with a single frequency component within the bandwidth of the two considered cochlear filters. This is a notion of resolvability, and we will say that the frequency component is resolved with respect to the pair of filters. Figure 2B illustrates what happens when a periodic sound with unresolved harmonics is passed through the two filters. Here the output of filter A is a combination of harmonics k and k − 1, while that of filter B is a combination of harmonics k and k + 1. Therefore, the two resulting signals are different (Fig. 2B, bottom): there is no cross-channel structure.

Thus, the amount of cross-channel structure produced by a harmonic sound depends on the resolvability on its frequency components. Figure 2C shows the amplitude spectrum of a periodic sound with all harmonics k · f0 (bottom). Because harmonics are linearly spaced but cochlear filter bandwidth increases with frequency (filter amplitude in gray), the excitation pattern of the BM as a function of center frequency (top) shows distinct peaks for low-order harmonics (which are thus considered “resolved”) but not for high-order harmonics (unresolved). More precisely, low-order harmonics are resolved for many pairs of cochlear filters, meaning that they produce cross-channel structure for many filter pairs (Fig. 2D, left); high-order harmonics produce little or no cross-channel structure (Fig. 2D, right). The amount of cross-channel structure is directly determined by the spacing between frequency components (f0) relative to the cochlear filter bandwidth. With the approximation that filter bandwidth is proportional to center frequency (k · f0 if centered at the kth harmonic), this means that the amount of cross-channel structure is determined by the harmonic number k. Therefore, there is a direct relationship between resolvability defined in a conventional sense and the amount of cross-channel structure produced by the sound.

Figure 2E illustrates this point with a resolved harmonic complex consisting of resolved components (left) and an unresolved harmonic complex (right). Both sounds produce within-channel structure (horizontal arrows), but the resolved complex additionally produces cross-channel structure. Thus, the structural theory attributes a pitch to all periodic sounds, but the amount of regularity structure, and therefore of information about f0, depends on resolvability. It follows in particular that discrimination of f0 based on regularity structure should be more precise for resolved than unresolved sounds (Houtsma and Smurzynski, 1990; Carlyon and Shackleton, 1994; Carlyon, 1998; Bernstein and Oxenham, 2003), since there is more information (the exact quantitative assessment would depend on the specific estimator chosen).

The domain of existence of pitch

From the definitions above, the set of sounds that produce regularity structure is exactly the set of periodic sounds. However, perceptually, not all periodic sounds have a melodic pitch. In particular, pitch only exists for f0 between 30 Hz (Pressnitzer et al., 2001) and 5 kHz (Semal and Demany, 1990). Within this range, periodic sounds may or may not have a clear pitch, depending on their harmonic content. In the structural theory, the domain of existence of pitch is restricted when we impose constraints on the comparisons between signals (cross- or within-channel) that the auditory system can do. Two physiological constraints seem unavoidable: (1) there is a maximum time shift δ_max (possibly corresponding to a maximum neural conduction delay) and (2) temporal precision is limited (possibly corresponding to phase locking precision). We may also consider that there is a maximum distance along the BM across which signals can be compared, but it will not play a role in the discussion below. The temporal precision sets an upper limit to pitch, exactly in the same way as in standard temporal theories. Thus, we shall restrict our analysis to the constraint of a maximum delay δ_max. We consider the simplest possible assumption, which is a constant maximal delay δ_max, independent of frequency.

We start by analyzing the domain of existence of within-channel structure (Fig. 3A). Since this is just the periodicity structure, its domain of existence is the same as in standard temporal theories of pitch. When the sound’s period exceeds the maximum delay δ_max, periodicity cannot be detected anymore. Therefore, the lower limit (minimum f0) is the inverse of the maximum delay: f0 = 1/δ_max.

Figure 3.

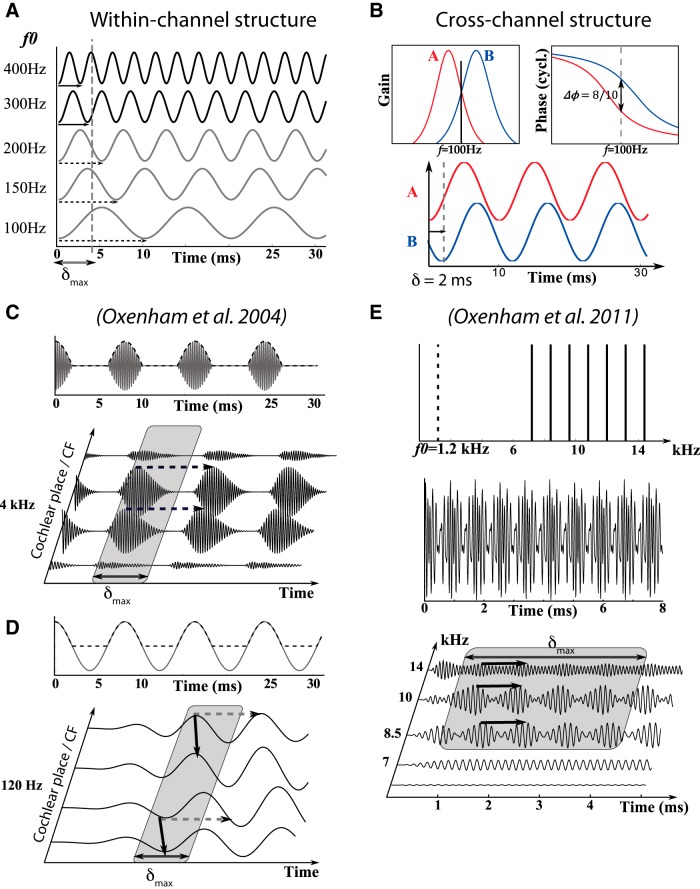
Domain of existence of pitch. A, Within-channel structure produced by a periodic sound can be decoded if the sound’s period is smaller than the maximal neural delay δ_max. When δ_max = 4 ms, it occurs for sounds of fundamental frequency greater than 250 Hz. B, A pure tone or resolved harmonic produces cross-channel structure with arbitrarily small delays between channels, corresponding to the phase difference between the two filters at the sound’s frequency: here a 100 Hz tone produces two identical waveforms delayed by δ = 2 ms, while the sound’s period is 10 ms. C, A transposed tone with a high-frequency carrier (>4 kHz) modulated by a low-frequency envelope (<320 Hz) elicits a very weak pitch (Oxenham et al., 2004a) (top: f0 = 120 Hz). Such sounds produce only within-channel structure because they only have high-frequency content (middle). The structural theory of pitch predicts an absence of pitch when the envelope’s periodicity is larger than δ_max, which is consistent with psychophysics if δ_max< 3 ms. D, A pure tone with the same fundamental frequency (f0 = 120 Hz) produces cross-channel structure with short delays. The structural theory of pitch predicts the existence of pitch in this case, consistently with psychophysical results (Oxenham et al., 2004a). E, Complex tones with f0 between 400 Hz and 2 kHz and all harmonics above 5 kHz elicit a pitch (Oxenham et al., 2011) (top, spectrum of a complex tone; middle, temporal waveform). Such tones produce only within-channel structure in high frequency (bottom), and the structural theory of pitch predicts the existence of pitch if the sound’s period is smaller than δ_max, which is consistent with psychophysics if δ_max > 2.5 ms.

A different limit is found for cross-channel structure, because the delay δ between signals across channels is not the same as the sound’s period (Fig. 1F). In fact, this delay can be arbitrary small, if the two places are close enough on the BM. Figure 3B shows an example of a 100 Hz pure tone passed through two filters, A and B. The gains of the two filters are the same at 100 Hz and there is a phase difference of 8/10 cycle, which is equivalent to −2/10 cycle. As a result, the output of the two filters is a pair of tones with identical amplitude and delay δ = 2 ms (2/10 of 10 ms), much smaller than the sound’s period. This delay would be even smaller if the center frequencies of the two filters were closer. Thus, the lower limit of cross-channel structure is not set by the maximum delay δ_max. Instead, it is set by the center frequencies of the filters. Indeed the frequency of the tone (or resolved harmonic) must lie between the two center frequencies of the filters, and therefore the lowest such frequency corresponds to the lowest center frequency of cochlear filters. This minimum frequency is not known in humans, but the lower limit of the hearing range is about 20 Hz, which suggests a lower limit of cross-channel structure slightly above 20 Hz. This is consistent with psychophysical measurements of the lower limit of pitch, around 30 Hz for tones (Pressnitzer et al., 2001).

Therefore, the structural theory of pitch predicts different lower limits of pitch depending on whether the sound contains resolved harmonics or not. When it does, the lower limit is determined by cross-channel structure, and thus by the lowest center frequency of cochlear filters, on the order of a few tens of Hertz. When it does not, the lower limit of pitch is determined by within-channel structure, and is thus 1/δ_max. We now compare these theoretical predictions with two recent psychophysical studies. In Oxenham et al. (2004a), transposed stimuli were created by modulating a high-frequency carrier (>4 kHz) with the temporal envelope of a half-wave rectified low frequency tone (<320 Hz) (Fig. 3C, top). Human subjects displayed poor pitch perception for these stimuli, even though the repetition rate f0 was in the range of pitch perception for pure tones. This finding poses a challenge for temporal theories, but is consistent with the structural theory, as is illustrated in Figure 3C. Indeed, these transposed tones do not contain resolved harmonics, and therefore only produce within-channel structure (Fig. 3C, horizontal arrows). As described above, the lower limit of pitch is 1/δ_max in this case. If this maximal delay is δ_max < 3 ms, then transposed tones do not produce a pitch when the frequency of the tone is lower than 330 Hz. However, for pure tones, the lower limit of pitch is much lower than 330 Hz because of the presence of cross-channel structure (Fig. 3D, oblique arrows). In Oxenham et al. (2011), it was shown that complex tones with f0 between 400 Hz and 2 kHz and all harmonics above 5 kHz elicit a pitch. In the structural theory, all periodic sounds with f0 > 1/δ_max produce a pitch, irrespective of their harmonic content. This is shown in Figure 3E, which shows the cochlear filter responses to a complex tone with f0 = 1.2 kHz and all harmonics above 5 kHz. Therefore, this psychophysical study is consistent with the structural theory if δ_max > 2.5 ms. In summary, both psychophysical studies are consistent with the structural theory if δ_max is on the order of 3 ms.

A possible neural mechanism

We now propose a possible neural mechanism to estimate f0 based on the vibration structure of the BM. Since the theory is based on similarity between signals, the same mechanism as for temporal models can be suggested. A straightforward generalization of Licklider's model (Licklider, 1951) is illustrated in Figure 1D: a neuron receives inputs from two presynaptic neurons (X and Y), which encode the BM vibration at two cochlear locations x and y in precisely timed spike trains, and there is a mismatch δ in their conduction delays. We assume that the postsynaptic neuron responds preferentially when it receives coincident input spikes. Indeed, neurons are highly sensitive to coincidences in their inputs, under broad conditions (Rossant et al., 2011). By acting as a coincidence detector, the postsynaptic neuron signals a particular identity S(y, t + δ) = S(x, t).

Anatomically, neurons X and Y could be auditory nerve fibers and the postsynaptic neuron could be in the cochlear nucleus. Alternatively, neurons X and Y could be primary-like neurons in the cochlear nucleus, for example spherical bushy cells, and the postsynaptic neuron could be in the inferior colliculus or in the medial superior olive. Indeed, as demonstrated in Figure 4, A and B, the synchrony between two neurons depends on the similarity between the signals they encode, rather than on their specific cellular properties. Figure 4A shows the cochleogram of a trumpet note with f0 = 277 Hz (top). The red and blue boxes highlight the BM vibration at characteristic frequencies 247 Hz and 307 Hz, around the first harmonic. This harmonic produces cross-channel similarity with delay δ, as seen on the red and blue signals in the bottom half of Figure 4, A and B (grey shading is the mismatch). As a result, neurons that encode these two signals into spike trains fire in synchrony, as is shown below for three different models: a biophysical model of a type Ic chopper neuron (Rothman and Manis, 2003b), a type II model of an octopus cell, and a leaky integrate-and-fire model. In contrast, when an inharmonic sound is presented, such as a rolling sea wave (Fig. 4B), the inputs do not match and neural responses are not synchronous, for any of the three models.

The same mechanism applies for within-channel structure. In Figure 4C, we consider two high-frequency neurons with the same characteristic frequency CF = 2700 Hz but a delay mismatch δ = 4.5 ms. When a periodic sound with repetition rate 220 Hz is presented (here a harpsichord note), their input signals match, which results in synchronous discharges. We note that not all output spikes are coincident. This occurs because the neurons discharge in more complex spiking patterns (Laudanski et al., 2010) and do not fire one spike per cycle: they may miss a cycle or fire several times in one cycle. Nevertheless, coincidences of output spikes occur much less often with an inharmonic sound (Fig. 4D). This mechanism is analog to Licklider’s model (Licklider, 1951), in which each neuron signals a particular identity S(x, t + δ) = S(x, t). Thus, the neural mechanism we describe is simply an extension of Licklider’s model to cross-channel similarity.

As a proof of concept, we now build a simple neural model that estimates f0 by detecting regularity structure. For each f0 between notes A2 and A4 (110 − 440 Hz), we build a group of coincidence detector neurons, one for each similarity identity S(y, t + δ) = S(x, t) that is present for sounds with that particular f0. To this aim, we examine the BM response (modeled as gammatone filters) to a complex tone with all harmonics n · f0 (Fig. 4E, red comb on the left). In Figure 4, E and F, we represent the BM response using color disks arranged as a function of cochlear location (vertical axis) and delay (horizontal axis): color saturation represents the amplitude of the filter output while hue represents its phase. For low-order harmonics (resolved, bottom), the BM vibrates as a sine wave and therefore disks with the same color correspond to identical signals, and thus to encoding neurons firing in synchrony. For high-order harmonics (unresolved, top), the BM vibrates in a more complex way and there only identically colored disks within the same channel correspond to identical signals. We then set synaptic connections from neurons encoding the same BM signal to a specific coincidence detector neuron (all modeled as integrate-and-fire neurons). Thus, we obtain a group of neurons that fire preferentially when the identities S(y, t + δ) = S(x, t) corresponding to a particular f0 occur (note that we have omitted a number of possible identities for simplicity, e.g., cross-channel identities occurring with high-frequency pure tones). In this way, the mean firing rate of the group of neurons is tuned to f0.

We iterate this construction for every f0 between A2 and A4 (by semitone steps). As illustrated in Fig. 4F, a different f0 produces a different regularity structure (colored disks) from which we build a different set of synaptic connections to the pitch-tuned group of coincidence neurons (one group per f0). To estimate f0, we then simply look for the pitch-tuned group with the highest mean firing rate.

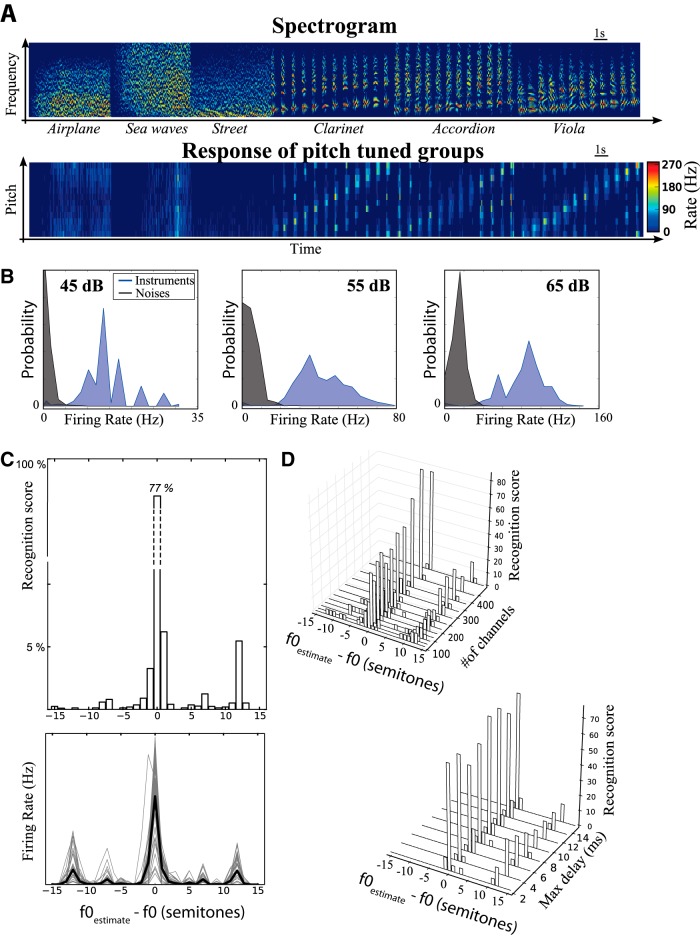
We presented two types of natural sounds to this model (spectrograms shown in Fig. 5A, top): inharmonic sounds (e.g., an airplane, a sea wave, and street noise) and harmonic sounds (e.g., clarinet, accordion, and viola) with f0 between A2 and G4. For each sound, we measure the average firing rate of all pitch-tuned neuron groups (Fig. 5a, bottom). Inharmonic sounds generally produce little activation of these neurons, whereas harmonic sounds activate specific groups of neurons (with some octave confusions, see below). In Figure 5A, musical notes were played in chromatic sequence, which appears in the response of pitch-tuned groups. Figure 5B shows the distribution of group firing rates, measured in the entire neuron model, for inharmonic (grey) and harmonic sounds (blue), at three different sound levels. Although an increase in sound level produces an overall increase in population firing rate, there is little overlap between the rate distributions for harmonic and inharmonic sounds.

Figure 5.

Pitch recognition by a neural network model based on the structural theory. A, Top, Spectrogram of a sequence of sounds, which are either either environmental noises (inharmonic) or musical notes of the chromatic scale (A3-A4) played by different instruments. Bottom, Firing rate of all pitch-specific neural groups responding to these sounds (vertical axis: preferred pitch, A3−A4). B, Distribution of firing rates of pitch-specific groups for instruments played at the preferred pitch (blue) and for noises (grey) for three different sound levels. C, Top, Pitch recognition scores of the model (horizontal axis: error in semitones) on a set of 762 notes between A2 and A4, including 41 instruments (587 notes) and five sung vowels (175 notes). Bottom, Firing rate of all pitch-specific groups as a function of the difference between presented f0 and preferred f0, for all sounds (solid black: average). Peaks appear at octaves (12 semitones) and perfect fifths (7 semitones). D, Impact of the number of frequency channels (top) and maximal delay δ_max (bottom) on recognition performance.

From the activity of these neurons, we estimate the pitch of a presented harmonic sound as the pitch associated to the maximally activated group of neurons. This estimation was correct in 77% of cases, and was within one semitone of the actual pitch in 88% of cases (Fig. 5C, top). Most errors greater than one semitone correspond to octaves or fifths (octaves: 5.5%, fifth: <2%), which also shows in the distribution of firing rate of pitch-tuned groups (Fig. 5C, bottom). This performance was obtained with 400 frequency channels spanning 50 Hz to 8 kHz, and it degrades if the number of channels is reduced (e.g., 35% score for N = 100; Fig. 5D, top), because the model relies on comparisons between neighboring channels. We then tested how performance was affected by constraints on the maximum delay (Fig. 5D, bottom). We found no difference in performance when maximum delay δ_max was varied between 2 and 15 ms. The highest f0 in our sound database was 440 Hz (A4), which corresponds to a period greater than 2 ms. Therefore, with δ_max = 2 ms, the model reached the same level of performance with only cross-channel comparisons.

Pitch discriminability

Finally, we examine the discriminability of pure tones based on regularity structure. To simplify, we ignore amplitude differences and focus on phase differences between channels. We start with within-channel structure and consider two neurons (e.g., auditory nerve fibers) encoding BM vibration from the same place x (i.e., same characteristic frequency) into phase-locked spike trains, with a delay mismatch δ = 1/f (Fig. 6A). These two neurons fire in synchrony when a pure tone of frequency f is presented. More precisely, given that there is some stochasticity in neural firing, the two neurons produce spikes with the same mean phase relative to the tone, so the difference of phases of spikes ΔΦ(f) is distributed around 0 (Fig. 6A, left). When a tone of frequency f + df is presented, ΔΦ(f) shifts by an amount of δ · df = df/f (Fig. 6A, right).

The same analysis applies for cross-channel structure, where the two neurons encode BM vibration at two different places, A and B (different CFs; Fig. 6B). Here the delay δ is related to the mismatch in phase response at the places at tone frequency f. When a tone of frequency f + df is presented, ΔΦ(f) shifts because of both the delay and the relative change in response phase at the two places on the BM (see Materials and Methods).

Thus, discriminating between tones of nearby frequencies corresponds to discriminating between two circular random variables ΔΦ(f) and ΔΦ(f + df) with different means, which can be analyzed with signal detection theory (Green and Swets, 1966). Specifically, the discriminability index d′ is the mean phase shift µ divided by the precision σ (standard deviation of phase) (Fig. 6C). The precision of phase locking is often measured by the vector strength (VS), which is relatively independent of frequency below a critical frequency above which it decays rapidly to 0 (Fig. 6D, guinea pig auditory nerve). We estimate the standard deviation σ from VS assuming a wrapped normal distribution (see Materials and Methods). To estimate µ, we used spike trains recorded in guinea pig auditory nerve fibers with different CFs in response to tones with various frequencies (Palmer and Shackleton, 2009) and estimated the average spike phase as function of both CF and tone frequency (see Materials and Methods) (Fig. 6E).

We used these estimates to calculate the just-noticeable difference (JND) for 75% correct discrimination, which is the frequency change df producing a discriminability index d′ = 1.35. Figure 6F shows the JND relative to tone frequency (JND(f)/f), called the Weber fraction, as a function of tone frequency, for within-channel structure (black), and for cross-channel structure (colors), for pairs of channels varying by their spacing in CF (1 − 6 semitones). For both types of structure, the Weber fraction increases in high frequency because of the loss of phase locking (VS goes to 0). The two types differ in the low-frequency end: while the Weber fraction is independent of frequency for within-channel structure, it tends to increase with lower frequency for cross-channel structure. We also note that discriminability is better for widely spaced channels (orange) than for neighboring channels (blue), but the former require larger delays.

Discussion

We have proposed that pitch is the perceptual correlate of the regularity structure of the BM vibration pattern, defined as the set of identities of the form S(x,t) = S(y,t + δ) for all t, where S(x,t) is the displacement of the BM at time t and place x. The regularity structure generalizes the notion of periodicity. This proposition assigns a pitch to periodic sounds and therefore has many similarities with the standard view that pitch is the perceptual correlate of the periodicity of the acoustic waveform. However, it also predicts that resolved harmonic complexes elicit a stronger pitch than unresolved harmonic complexes (richer structure), and it predicts a complex region of existence of pitch that depends on harmonic content. In particular, it predicts that high frequency complex tones only elicit a clear pitch if f0 is high, in agreement with previous experiments (Oxenham et al., 2004b, 2011). Finally, it does not rely on the existence of long conduction delays in the auditory system.

Previous studies have proposed mechanisms to extract the fundamental frequency of either resolved or unresolved harmonic complexes (for detailed discussion, see Related theories of pitch, below). Some share common ideas with our proposition: for example, classical temporal models address the extraction of within-channel periodicity (S(x,t) = S(x,t + T)) (de Cheveigné, 2010), which does not distinguish between resolved and unresolved components; other authors have proposed that the frequency of resolved components can be estimated with cross-channel comparisons or operations (Loeb et al., 1983; Shamma, 1985; Carney et al., 2002). These ideas are also present in our proposition. However, instead of proposing a particular mechanism to extract f0, we propose that pitch is not the correlate of the periodicity of the sound waveform but of the regularity structure of the BM vibration pattern (with a limited temporal window). The main implications for pitch perception (as shown in Fig. 3) are to a large extent independent of the particular mechanism that extracts that structure. In particular, this single proposition implies that resolved and unresolved harmonic complexes have different perceptual properties.

Neural mechanism

A separate issue is the physiological implementation of this theory, that is, how pitch defined according to the regularity structure of the BM vibration pattern might be estimated by the auditory system. There are different ways in which the auditory system might extract that information. It may also be the case that pitch is not conveyed by the increased firing of pitch-tuned neurons but by temporal relationships in their firing (Cariani, 2001). Here we have simply made a suggestion of a possible mechanism that makes minimal physiological assumptions. But we stress that our core proposition does not rely on a particular mechanism, but on the regularity structure of the BM vibration. The most straightforward implementation is a generalization of Licklider’s delay line model (Licklider, 1951), in which a pitch-selective neuron detects coincidences between two inputs with different axonal conduction delays. In the original model, the two inputs originate from the same place in the cochlea. An implementation of the structural theory is obtained simply by allowing the two inputs to originate from slightly different places. If a neural circuit resembling Licklider’s model indeed exists in the auditory brainstem, then it is plausible that inputs to these coincidence detector neurons are not exactly identical. Because our proposition relies on the temporal fine structure of sounds, the matching mechanism between the outputs of two channels (whether it is based on coincidence detection or not) should occur early in the auditory periphery. Input neurons could be auditory nerve fibers and the coincidence detector neuron could be in the cochlear nucleus. Alternatively, input neurons could be primary-like neurons in the cochlear nucleus, for example spherical bushy cells, and the coincidence detector neuron could be in the inferior colliculus or in the medial superior olive (MSO). The latter possibility has some appeal because neurons in the MSO are thought to receive few synaptic inputs (Couchman et al., 2010) and are known to act as coincidence detectors (Yin and Chan, 1990), although possibly not monaurally (Agmon-Snir et al., 1998), and there are cases of binaural pitch for sounds that have no monaural structure. In the inferior colliculus, there is some physiological evidence of tuning to pitch (Langner, 1992). Specifically, in a number of mammalian species, IC neurons are tuned in their firing rate to the modulation frequency of amplitude-modulated tones, up to about 1000 Hz, independently of their characteristic frequency, although the best modulating frequency may depend on carrier frequency. There is also some evidence of a topographic organization of periodicity tuning, orthogonal to the tonotopical organization.

As a proof of principle, we have shown with a spiking neural model that such a mechanism can indeed estimate the pitch of harmonic sounds, even with short conduction delays. Standard temporal models of pitch have been criticized because they require long delays for low f0, up to 30 ms for the lowest pitch (Pressnitzer et al., 2001). There is no experimental evidence of such long axonal delays in the auditory brainstem. In a recent anatomical study of axons of spherical bushy cells in cats (cochlear nucleus projections to the MSO), the range of axonal delays was estimated to be just a few hundred microseconds (Karino et al., 2011), far from the required 30 ms (although these were anatomical estimates, not functional measurements). This range could be larger in humans, as axons are presumably longer, but it could also be similar if axonal diameter scales in the same way (since conduction speed is approximately proportional to diameter in myelinated axons (Rushton, 1951)). In either case, the range of axonal delays is unlikely to be much greater than a few milliseconds. Another possibility is to consider dendritic propagation delays or intrinsic delays induced by ionic channels. These could contribute additional delays, but the duration of postsynaptic potentials measured at the soma of auditory brainstem neurons tends to be short (Trussell, 199 7, 1999), which makes this scenario rather implausible for large delays. We have shown that the structural theory is compatible with psychophysical results when the delays are limited to a few milliseconds, and the neural mechanism based on coincidence detection remains functional even for low f0.

Related theories of pitch

Two previous propositions are directly related to the structural theory. Loeb et al. (1983) proposed that the frequency of a pure tone can be estimated by comparing signals across the BM: the distance that separates places that vibrate in phase is indeed related to the tone’s frequency. This is a special case of the structural theory, when the maximal delay is 0 ms (i.e., identities of the form S(x,t) = S(y,t) for all t). However, this proposition restricts pitch to resolved harmonic complexes only, and in fact to complexes made of widely separated tones.

The phase opponency model (Carney et al., 2002) is a similar proposition, in which a tone of a particular frequency is detected when signals at two different places on the BM are out of phase. This corresponds to detecting identities of the form S(x,t) = −S(y,t) for all t. This model suffers from the same problem as Loeb’s model, that is, it applies to a limited subset of pitch-evoking sounds.

We may also consider a variation of the structural theory, in which amplitude is discarded (as we did when analyzing frequency discrimination). This variation corresponds to considering identities of the form S(x,y) = a · S(y,t + δ) for all t. This variation has the same qualitative properties as the original formulation, and is physiologically motivated by the observation that low threshold AN fibers saturate quickly when intensity is increased (Sachs and Abbas, 1974).

Place theories of pitch are based on the comparison of internal templates with the spatial pattern of BM vibration encoded in the firing of auditory nerve fibers. A weakness of these theories is that the firing rate of auditory nerve fibers as well as of most neurons in the cochlear nucleus saturate at high levels (Sachs and Young, 1979; Cedolin and Delgutte, 2005). To address this problem, it has been proposed that the spatial profile is first sharpened by lateral inhibition, prior to template matching (Shamma, 1985). This preprocessing step enhances the responses at places where the phase changes rapidly, which occurs where the BM is tuned to the sound’s frequency. A recent analysis of cat auditory nerve responses has shown that such preprocessing produces spatial profiles from which f0 can indeed be extracted even at high levels (Cedolin and Delgutte, 2010), although a more recent analysis (in guinea pigs and with different methods) suggested that the estimated f0 is very sensitive to level (Carlyon et al., 2012). Because this preprocessing step relies on temporal cues, template-based models of pitch using this stage as input are often described as spatiotemporal models (Cedolin and Delgutte, 2010). However, these are very different from the structural theory we have presented, as they are in fact models based on matching spatial templates where temporal information is discarded, only with an input that is obtained from a spatiotemporal transformation of the auditory nerve response. In contrast, matching in the structural theory as well as in the two related models mentioned above and in standard temporal models is performed on the entire temporal signals.

Unlike the structural theory, none of these three models addresses the pitch of unresolved harmonic complexes.

The nature of pitch in theories of pitch

In standard temporal theories of pitch, pitch is the perceptual correlate of the periodicity of the acoustical waveform. Independently of how the periodicity is physiologically extracted, this proposition implies, for example, that periodic sounds have a pitch, nonperiodic sounds do not have pitch, and pitch saliency is related to how close to periodic a sound is. It also implies that two sounds with the same periodicity are similar, and that two sounds with fundamental frequencies differing by an octave are similar, in the sense that they have a periodicity in common. Thus, this characterization of pitch entails a particular region of existence of pitch (what sounds produce pitch) and a particular topology of pitch (how pitch-evoking sounds relate to each other). These two aspects do not rely on learning, in the sense that they do not depend on the specific sounds the auditory system is exposed to. Instead, they derive from the existence of a general mechanism that identifies periodicity.

In a similar way, the structural theory of pitch defines pitch as the perceptual correlate of the regularity structure of the BM vibration pattern. It also entails an existence region of pitch, which is more complex than in temporal theories, and a particular topology of pitch, which is similar to that implied by temporal theories (but see below for the effect of level on pitch). In the same way, these two aspects do not rely on learning.

In standard place theories of pitch based on templates, what characterizes pitch-evoking sounds is that they are similar to some internal template (Terhardt, 1974). Thus, pitch is the perceptual correlate of a particular category of sounds, which is formed by previous exposure to pitch-evoking sounds. There is an obvious problem of circularity in this characterization, which means that in addition to exposure to the sounds, these sounds must be labeled as having or not having a pitch. That is, pitch is characterized independently of the sounds themselves. An example would be that vocalizations are those special sounds that are considered as producing pitch. Accordingly, a more rigorous characterization of pitch in place theories is the following: pitch is the perceptual correlate of spectral similarity to vocalizations (or any other externally defined category of sounds).

This characterization is problematic for several reasons. First, it defines an existence region of pitch but not a topology of pitch, unless the spatial activation profiles produced by sounds with the same pitch are similar. This issue might be addressed to some extent by spatial sharpening, as previously mentioned (Shamma, 1985), although there is no indication that such an operation occurs in the auditory system. A second problem is that not all pitch-evoking sounds are spectrally similar to vocalizations, for example low-frequency pure tones. Finally, infants have a sense of musical pitch (Montgomery and Clarkson, 1997). The latter two issues have been addressed in a model in which harmonic templates are learned from inharmonic sounds (Shamma and Klein, 2000). Indeed auditory nerve fibers with harmonically related CFs are expected to fire with some degree of correlation in response to noise, because of nonlinearities in their response. Thus, a Hebbian mechanism could form harmonic templates by selecting temporally correlated fibers. In this scheme, pitch is then the perceptual correlate of the similarity between the places of activation on the BM and places that are generally expected to be correlated.

In addition to the fact that this only addresses the pitch of unresolved harmonic complexes, this proposition is somehow paradoxical. On one hand, the formation of internal templates critically relies on the temporal fine structure of the sounds, and fine correlations between channels. Indeed in Hebbian models, the learning signal is the correlation between input and output (presynaptic and postsynaptic neurons), and therefore it requires that the output firing is sensitive to input correlations. On the other hand, pitch estimation by template matching assumes that this temporal fine structure is then entirely discarded: only average spectrum is considered, and correlations between channels (relative phases of harmonics in a complex tone) are assumed to have no effect on pitch. To reconcile the two aspects of the model requires either that the neurons are initially sensitive to input correlations and become insensitive to them after a critical period (after learning), or that learning is based on input correlations but not through a Hebbian mechanism (i.e., not involving input−ouput correlations).

Experimental predictions

We can formulate two types of predictions, for psychophysical experiments and for physiological experiments. The strongest psychophysical prediction concerns the effect of level on pitch. The phase of the BM response to tones depends on level (Robles and Ruggero, 2001), because of nonlinear effects. Consequently, cross-channel structure should depend on level. However, within-channel structure should not depend on level because such nonlinearities have no effect on periodicity. If we assume that sounds are matched in pitch when they produce some common regularity structure on the BM, then a pitch-matching experiment between sounds with different levels should reveal an effect of level on the pitch of sounds that produce cross-channel structure but not within-channel structure. According to our analysis, these are pure tones of low frequency, i.e., with period larger than the maximum delay. The few studies on such effects support this prediction (Morgan et al., 1951; Verschuure and Van Meeteren, 1975; Burns, 1982), but a more exhaustive and controlled study would be required.

Predictions for physiological experiments can be made for specific hypotheses about the neural mechanism. For example, low-frequency spherical bushy cells are primary-like neurons of the cochlear nucleus with strong phase-locking properties (Joris et al., 1994; Fontaine et al., 2013) (possibly stronger than the auditory nerve), and their pattern of synchrony in response to sounds could then reflect the regularity structure of the BM vibration. The prediction is then that the synchrony receptive field of two such cells, defined as the set of sounds that produce synchronous responses in the two cells (Brette, 2012), should consist of pitch-evoking sounds—in fact, of a pure tone of specific frequency. Ideally, such recordings should be done simultaneously, because shared variability (e.g., due to local synaptic connections or shared modulatory input) affects phase locking and reproducibility but not synchrony (Brette, 2012).

Synthesis

The decision was a result of the Reviewing Editor Tatyana Sharpee and the peer reviewers coming together and discussing their recommendations until a consensus was reached. A fact-based synthesis statement explaining their decision and outlining what is needed to prepare a revision is listed below. The following reviewers agreed to reveal their identity: Shihab Shamma and Charles F. Stevens

Both reviewers suggested additional discussion points to include in the manuscript. Further, to the extent possible, please emphasize how the existing ideas when considered together give rise to new theory.

Reviewer 1:

This paper proposes a “structural theory” of pitch perception (or computations) which essentially combines features of all the myriad algorithms previously proposed for pitch extraction. The paper is well-written and quite comprehensive, well-referenced, and mentioned models are (for the most part) carefully described and evaluated.

This paper however feels more of a good review rather than an original contribution. As the author discusses, it combines many ideas already described either separately or in combination (such as the dual theory of pitch perception of Carlyon). The combined model s/he proposes therefore overcomes some of the challenges that in the first place motivated the development of the variety of pitch extraction algorithms mentioned in the paper

For the most part, the author cites in the final Discussion previous work and accurately sums up the deficiencies of each study. The glaring exceptions are a matter of taste and not really science. For example, the neural substrates that exploit temporal fine-structure (TFS) to extract pitch information remain uncertain whether they are the delays (cross or within channels) favored by the author and the temporal theories, or the cross-channel comparisons used in Lateral inhibition and phase-opponency models.

Furthermore, once the pitch is extracted from he TFS by these algorithms, it is then disposed off and not used again. This is for some reason acceptable for the author, but not when the TFS is used and disposed off to form the harmonic templates! Once again, this is just a matter of taste.

In summary, this is a good review paper, but not really an original theory. It is an amalgam of many ideas already found in the literature and are well-cited and discussed in this paper.

Reviewer 2

This is a nice theory for an important phenomenon (pitch). The neurobiological data indicate that pitch/periodicity representation occurs in the inferior colliculicus, so that further work by these authors might wish to include these observations in their speculations about neurobiological mechanisms.

Author Response

Dear editor and reviewers,

Thank you for your comments on our manuscript. The suggested changes concerned the discussion and the relation of our proposition with existing ideas in the field. We have done our best to address your remarks and we hope you will be satisfied with this revision (we have highlighted changes in red).

We are looking forward to reading your comments on this revised version.

Best regards.

Detailed response

Reviewer 1

This paper proposes a “structural theory” of pitch perception (or computations) which essentially combines features of all the myriad algorithms previously proposed for pitch extraction. The paper is well-written and quite comprehensive, well-referenced, and mentioned models are (for the most part) carefully described and evaluated.

This paper however feels more of a good review rather than an original contribution. As the author discusses, it combines many ideas already described either separately or in combination (such as the dual theory of pitch perception of Carlyon). The combined model s/he proposes therefore overcomes some of the challenges that in the first place motivated the development of the variety of pitch extraction algorithms mentioned in the paper.

For the most part, the author cites in the final Discussion previous work and accurately sums up the deficiencies of each study. The glaring exceptions are a matter of taste and not really science. For example, the neural substrates that exploit temporal fine-structure (TFS) to extract pitch information remain uncertain whether they are the delays (cross or within channels) favored by the author and the temporal theories, or the cross-channel comparisons used in Lateral inhibition and phaseopponency models.

Furthermore, once the pitch is extracted from he TFS by these algorithms, it is then disposed off and not used again. This is for some reason acceptable for the author, but not when the TFS is used and disposed off to form the harmonic templates! Once again, this is just a matter of taste.

In summary, this is a good review paper, but not really an original theory. It is an amalgam of many ideas already found in the literature and are well-cited and discussed in this paper.

Thank you for your remarks. We agree that there are common ideas in our proposition with previous ideas in the field, which we acknowledge in the discussion. We tried to explain how it differs from previous ideas (Discussion, “Related theories of pitch”, where we emphasized that “Unlike the structural theory, none of these three models addresses the pitch of unresolved harmonic complexes.”) but it seems that we have not completely managed to do it clearly enough.

First, we want to emphasize that our core proposition is not about the mechanism (or “computation”) that extracts pitch. Most previous studies have proposed mechanisms to extract the fundamental frequency (f0) of periodic sounds. Our proposition is not a new mechanism. It is the idea that pitch is not actually the correlate of periodicity, but of the regularity structure of cochlear vibration over a restricted temporal window. Instead of being defined by a single identity on the sound waveform (S(t)=S(t+T)), it is defined a set of identities (Si(t)=Sj(t+T)). It is important to emphasize that this is a single proposition from which it follows that resolved and unresolved complexes have different properties (in contrast with dual mechanism models).

Then one might imagine different ways that the nervous system might detect these identities. We have suggested a possible one (coincidence detection between excitatory neurons), but the core proposition does not rely on a particular mechanism. We might also imagine that the structure is not converted into the firing of specific neurons at all (as proposed by Peter Cariani for instance). Our proposed mechanism is simply a suggestion, which is intended to show as a proof of concept that it is indeed possible and not particulary complicated for the auditory system to extract the relevant information, and does not require long delays. The core proposition is about the pattern of cochlear vibration, and the relation to psychophysics (esp. Fig. 3) is explained in these terms in the manuscript, independently of the “decoding” mechanism.

Regarding the remark on discarding TFS in the formation of harmonic templates, we might not have been clear in our text. In the harmonic template idea, TFS must be present in the inputs to form the templates, since it is based on input correlations. In Hebbian models, this requires that output firing is sensitive to input correlations (because the plasticity signal is correlations between pre- and postsynaptic neuron). But that requirement is exactly opposite to the requirement that the neuron should be insensitive to the TFS of its inputs in the normal operation of the model (otherwise firing would depend on relative phases of resolved components). We do not mean that it is impossible, but it means that learning must be based on something else than Hebbian mechanisms, or alternatively that input correlation sensitivity is lost after learning.

We tried to clarify the text (discussion) in this revised version.

Reviewer 2

This is a nice theory for an important phenomenon (pitch). The neurobiological data indicate that pitch/periodicity representation occurs in the inferior colliculicus, so that further work by these authors might wish to include these observations in their speculations about neurobiological mechanisms.

Thank you. In this revised text, we added some references to physiological work on the inferior colliculus (in “Neural mechanism”).