Modulation of Phenol Oxidation in Cofacial Dyads

Abstract

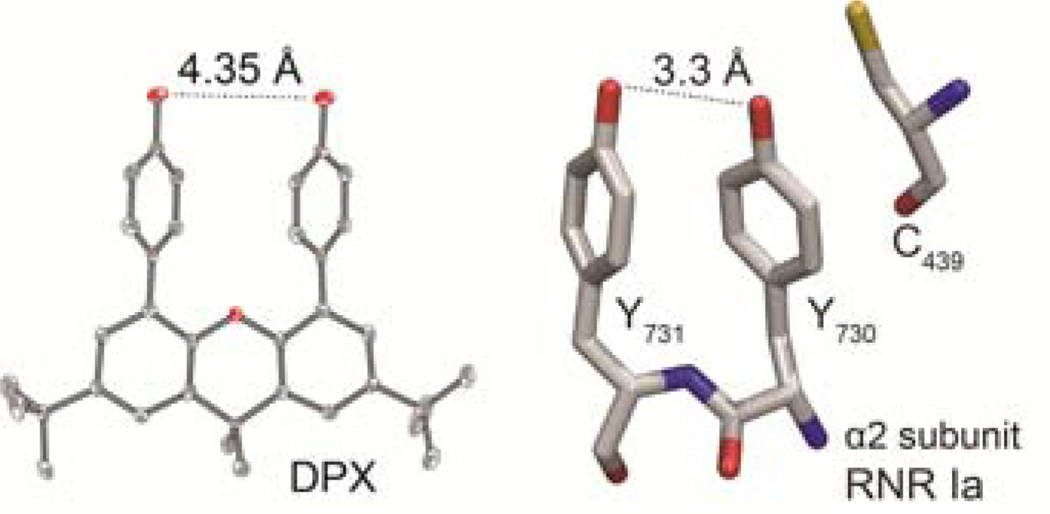
The presentation of two phenols on a xanthene backbone is akin to the tyrosine dyad (Y₇₃₀ and Y₇₃₁) of ribonucleotide reductase. X-ray crystallography reveals that the two phenol moieties are cofacially disposed at 4.35 Å. Cyclic voltammetry (CV) reveals that phenol oxidation is modulated within the dyad, which exhibits a splitting of one-electron waves with the second oxidation of the phenol dyad occurring at larger positive potential than that of a typical phenol. In contrast, a single phenol appended to a xanthene exhibits a two-electron (ECE) process, consistent with reported oxidation pathways of phenols in acetonitrile. The perturbation of the phenol potential by stacking is reminiscent of a similar effect for guanines stacked within DNA base pairs.

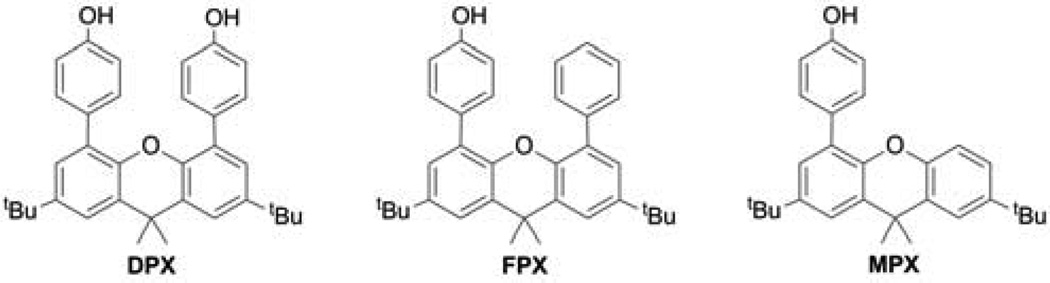
Amino acid radicals play an essential role in the biochemistry of metabolism and catalysis.¹ In physiological conditions, the generation and transport of amino acid radicals requires the coupling of a proton and an electron. The prominence of proton-coupled electron transfer (PCET) is arguably nowhere better exemplified than in E. coli class Ia ribonucleotide reductase (RNR), which catalyzes the reduction of nucleoside diphosphates to deoxynucleoside diphosphates.^2–4 RNR function relies on reversibly transferring a radical over a ~35 Å pathway between the amino acid, Y₁₂₂ in β2 and C₄₃₉ in α2 of E. coli class Ia RNR. The proposed pathway, for both forward and backward transfer, is β-Y₁₂₂ ⇄ β-Y₃₅₆ ⇄ α-Y₇₃₁ ⇄ α-Y₇₃₀ ⇄ α-C₄₃₉.^1–3 Radical injection from β-Y₃₅₆ into Y₇₃₁ of the α2 subunit is facilitated by the presence of adjacent Y₇₃₀ (Figure 1).^5,6 This result suggests that the dyad of two tyrosines does not simply provide two sequential radical pathway steps but that there is a collective property of two tyrosines, Y₇₃₀ and Y₇₃₁. Whereas the oxidation kinetics of phenol, a redox active residue of tyrosine, have been thoroughly studied by photochemical, electrochemical, and radiochemical methods in the context of PCET,^7–13 the redox chemistry of π-stacked, cofacially-aligned phenol dyads is unknown. In much the same way that the potential of guanines is perturbed by the presence of a neighboring guanine in DNA,^14,15 we wondered whether the potential of tyrosine is affected by the presence of a neighboring tyrosine. To address this issue, we have prepared the models shown in Scheme 1. Two phenols may be cofacially positioned at a fixed distance from a 2,7-di-tertbutyl-4,5-di(4-hydroxyphenyl)-9,9-dimethylxanthene backbone (DPX). We have also developed control model systems FPX and MPX (Scheme 1) to allow the π-interaction between neighboring phenol units to be assessed. Electrochemical studies together with computational results establish that the phenol oxidation potential is perturbed within dyad DPX as compared to FPX and MPX. The perturbation in the redox potential has significant implications to the PCET pathway of RNR.

Figure 1.

(left) X-ray crystal structure of diphenol xanthene: oxygen (red) carbon (grey) hydrogen omitted for clarity. (right) RNR α2 Y₇₃₁ and Y₇₃₀ from protein crystal structure 4R1R.

Scheme 1.

Stacked phenol and control systems for modeling the tyrosine dyad in RNR

The syntheses and characterization of DPX, FPX and MPX are presented in the Supporting Information. X-ray crystallography shows that two phenols are cofacially arranged as are Y₇₃₁ and Y₇₃₀ in RNR.¹⁶ The O…O distance between phenols is 4.35 Å and the centroid distance is 4.41 Å.

The CVs of the mono-phenol systems FPX and MPX in acetonitrile show a single peak (peak IV and peak V, respectively, in Figure 2). Using the xanthene backbone peak as an internal one-electron redox reference, both MPX and FPX show that the total charge passed during phenol oxidation corresponds to two-electron processes. This peak amplitude is consistent with the well-established two-electron ECE mechanism of phenol oxidation in CH₃CN:^17,18 The first oxidation yields a phenol radical cation (F₁), which has a pK_a ~ –5 in acetonitrile, some ~20 pK_a units more acidic than the starting phenol. F₁ deprotonates to a neutral phenol radical F₂,⁷ which is oxidized to phenoxium (F₃) at a lower anodic potential than the initial oxidation, thus resulting a single peak for the total twoelectron process. A wave centered at 1.12 V is consistent with the one-electron chemically reversible oxidation of the xanthene backbone; this oxidation does not interfere the phenol oxidation as shown by electrochemical analysis of various substituted xanthenes with phenyl analogues (Figure S3).

(1)

Figure 2.

Cyclic voltammograms of DPX (green), FPX (blue), and MPX (red). All CVs were taken in 500 µM analyte, 0.1 M TBAPF₆ electrolyte in dry acetonitrile with a Pt working electrode and referenced to Fc⁺/Fc. The peak potentials of peaks I, II, III, IV, and V are 0.88 V, 0.98 V, 1.29 V, 0.92 V, and 0.89 V, respectively.

In contrast to the single two-electron ECE wave for phenol oxidation in MPX (and FPX), the CV of DPX shows two oxidation peaks at 0.88 V and 0.98 V (peaks I and II in Figure 2, respectively), with the xanthene oxidation peak centered at 1.23 V. The total charge associated with the two waves corresponds to a two-electron process, as references to the one-electron xanthene wave. That two waves are separated in DPX indicates that the oxidation process of stacked phenols is perturbed in the dyad structure. We note that the peak potentials and ratio of peak amplitudes are invariant over a concentration range of 0.1–5 mM (Figure S5), confirming that the CV characteristics are not a result of an intermolecular interaction. CV features I and II exhibit a peak potential dependence on scan rate of ~60 mV/decade (Figure 3a), suggesting the coupling of a chemical step with each electron transfer step.¹⁷ A computational analysis of related systems^19,20 suggests that the modulation of phenol oxidation, such as DPX, can originate from the hydrogen bonding. Consistent with this contention is the disparate behavior of DPX and FPX despite similar π-aromatic electronic environments.

Figure 3.

Scan rate dependence of DPX: (a) peak I and peak II amplitudes at 0.1 V/s (left, green), 1 V/s (middle, dark green), 10 V/s (right, emerald); (b) the change in DPX’s peak I and II with TBAOH titration of 0 (green), 0.5 (violet), 1.0 (blue), 2.0 equiv (orange).

To investigate the effect of intramolecular hydrogen bonding on the redox properties of the dyad, cyclic voltammetry was performed on DPX and MPX with titration of tetrabutylammonium hydroxide, TBAOH.¹³ Base addition to MPX (Figure S8) results in a wave corresponding to phenolate oxidation at lower potentials (−0.3 ~ 0.6 V). For DPX, base addition affected peak I whereas peak II was largely unperturbed; these results suggest that peak II is a one-electron oxidation process largely independent of a proton (Figure 3b) whereas peak I is more intimately related to the proton. Consistent with this contention, peak I shifts to –0.25 V with the addition of base, in accordance with the shift in potential resulting for the one-electron oxidation of phenolate to phenoxy radical (Figure S7).¹⁸ The first one-electron oxidation of DPX in base is described by D₅ to D₂ in Scheme 2. In base, phenol D₀ is deprotonated to phenolate D₅, which is the species that is oxidized by one-electron to produce phenoxy radical D₂. Given peak II is proton independent (base < 2 equiv), the subsequent oxidation of D₂ proceeds from phenolate. In the absence of base, D₂ is produced by the direct one-electron oxidation (peak I in Figure 2) of D₀ to produce phenol radical cation species (D₁ in Scheme 2) followed by fast deprotonation to yield phenol radical (D₂).^{7, 21} A scan rate dependent shift of the peak I potential indicates involvement of a chemical step, which is consistent with deprotonation accompanying the conversion of D₀ to D₂. Further oxidation of D₂ may follow two paths, indicated by Path A and B. In Path A, the two-electron oxidation process results in one phenoxium and an intact phenol unit (D₃) and in Path B, D₄ is produced. Computation shows that biradical D₄ (triplet) is considerably more stable than D₃ (vide infra). Spectroelectochemistry shows that this product is unstable, and it cannot be isolated. Because the standard potential of the second oxidation step (from D₂ to D₄) is greater than that of the first oxidation step (from D₁ to D₂), the phenol oxidation peaks are separated. The separation of ~100 mV occurs about the potential that is observed for the single wave oxidation of FPX. Note that the overall ECE mechanism is similar for both DPX and FPX. However, the presence of the hydrogen bonding from the second phenol in DPX stabilizes the first oxidation with respect to the ensuing oxidation, thus resulting in a split peak in the CV.

Scheme 2.

The postulated oxidation pathways of DPX

Computational methods were employed to further analyze the mechanistic pathways of Scheme 2. Density functional theory (DFT) calculations were performed with Gaussian 09 where all structures were optimized in the gas phase at the B3LYP/6-311+G(d,p) level of theory with Grimme’s D3 dispersion correction²² and verified by the absence of imaginary vibrational frequencies as local minima. Solvation free energies in acetonitrile were computed by the SMD polarizable continuum model,²³ which includes corrections for non-electrostatic interactions. From these gas-phase free energies, solution-phase reaction free energies were calculated for each step of the mechanism using the Born-Haber cycle.²⁴ The free energies were converted to reduction potentials^24–27 or pK_as^27–31 by using appropriate reference reactions to account for systematic error in the computations, primarily stemming from the calculation of solvation and thermal energies as well as functional and basis set limitations. For the phenol systems, oxidation of the xanthene backbone (reversible peak III in Figure 2) served as an internal reference between calculated and experimental reduction potentials, while the isodesmic reaction between the phenol systems and 4-tert-butylphenol was employed for improving the accuracy of calculated pK_as.

The calculated electronics and energetics of the phenol systems (Figure 4 for DPX, Figures S9 and S10 for FPX and MPX, respectively) are consistent with their proposed mechanistic pathways (Scheme 2). First, the calculated reduction potentials for all three model systems agree with an ECE mechanism. The first oxidation facilitates the deprotonation of a phenol unit, where the calculated first pK_as decreases by 13–20 units to pK_as = ~7 in acetonitrile, which establishes a minor equilibrium of singly deprotonated phenol systems. This then enables the second oxidation to occur at similar potentials as the first oxidation, which is consistent with the integration of the first oxidation wave to a two-electron process in the CVs of the model systems (peaks I/II, IV, and V in Figure 2). In particular, DFT calculates a larger first and second reduction potential difference for DPX of ~60 mV compared to that of FPX and MPX (of 10–20 mV gap), which explains why DPX exhibits split peaks (I and II in Figure 2) in CVs whereas FPX and MPX only display a single peak (IV and V in Figure 2) as the second oxidation closely overlaps with the first oxidation. In contrast, calculations show that without the intermediate deprotonation step, the second oxidation of the phenols occurs ~500–700 mV to higher anodic potential, which supports the assignment that the second oxidation is the subsequent oxidation of deprotonated product. Similarly, when the phenol are deprotonated prior to any oxidations (by the addition of base), the calculations predict a drastic ~900–1200 mV cathodic shift of the first reduction potential that is observed in the CVs of base-titrated phenol systems (Figure S7 and S8), where the first oxidation now occurs from −0.25 to −0.30 V vs. Fc⁺/Fc. Direct comparison of calculated to experimental reduction potentials is discouraged because DFT reports reversible potentials while CVs show only peak potentials for oxidation of the phenol systems—the experimental reversible reduction potentials are unknown. Notwithstanding, the PCET effects of oxidations and deprotonations on the phenol systems are readily reproduced by computation.

Figure 4.

Calculated reduction potentials and pK_as for DPX. Bolded labels correspond to DPX states defined in Scheme 2. Molecular orbitals depict the HOMO for singlet (S = 0) states and the “spin density” SOMO for doublet and triplet states (S = 1/2 and 1, respectively). In addition, the “spin density” SOMO is shown for the D₄ state of DPX and is predicted to be a “broken symmetry” singlet. The triplet ground state of D₄ is more stable than the singlet. Explicit spin density plots for the second oxidation from D₂ is shown in Figure S9.

Analysis of calculated molecular orbitals and spin densities provides a qualitative view of the electronic interaction occurring in the phenol model systems, and in particular, suggests that the second oxidation of DPX is distributed on the adjacent phenol moiety (Path B in Scheme 2). In all phenol systems, visualization of the spin density via the corresponding singly occupied molecular orbital (SOMO) shows that the first oxidation results in a radical cation that is distributed on a single phenol with minor extension of spin to the xanthene backbone (e.g., see the D₁ state for DPX in Figure 4). Upon deprotonation, the radical cation becomes primarily localized on the single phenol unit, which is consistent with Scheme 2 (i.e., D₂ and F₂ in Scheme 2 and Equation 1, respectively). The second oxidation after deprotonation favors the singlet (phenoxium cation) over the triplet (biradical) state by ~4–6 kcal/mol. For FPX and MPX, the spin density of this singlet state was zero, demonstrating that the second oxidation removes an electron from the same phenol unit that had initially undergone the first oxidation and deprotonation (e.g., F₃ in Equation 1). Conversely, for DPX, the same singly-deprotonated, doubly-oxidized singlet state exhibited significant spin density of opposing character on each of the phenol units (triplet biradical D₄ in Figure 4 and Scheme 2, and Figure S9), signifying the presence of “broken symmetry” where the α and β spins of the highest occupied molecular orbital (HOMO) are localized as antiferromagnetically-coupled radical cations on each of the phenol units, respectively.^32,33 Thus, a formal singlet spin state is preserved while retaining local diradical character. These calculations suggest that the biradical is stabilized by the coupling of phenol rings (via hydrogen bonding) and thus Path B in Scheme 2 describes the second oxidation of DPX.

In summary, we have shown that oxidation of a phenol moiety is perturbed when it resides within a cofacial dyad. The stacked phenol units of DPX display a cooperative ECE oxidation mechanism that is unique from that of mono-phenol analogues (FPX and MPX). Unlike the ECE mechanism of FPX and MPX in acetonitrile, DPX showed two one-electron oxidations. The presence of broken symmetry in DPX, but not in FPX and MPX, indicates the importance of the hydroxide group on the adjacent phenol, which aids in electronically modifying electron density (and by extension, the radical) within the dyad and also assists in coupling the two units via hydrogen bonding site. Consequently, the strong coupling of phenols in DPX results in each phenol not behaving as independent redox units but rather as a cooperative redox entity where removal of a second electron from the system occurs at a higher anodic potential than that of the first oxidation. These results have implications to the radical transport pathway in RNR. Comparison of DPX to FPX shows that the potential of phenol is perturbed by ~50 mV, (peak potential difference between the first oxidation of DPX and FPX). We note that the entire redox ramp for radical transport in RNR—from Y356 to Y731—is estimated to be ~100 mV uphill.³⁴ Thus the perturbation of the oxidation of the phenol moiety within the dyad would represent significant tuning of the redox potential within the radical transport pathway of RNR. Both statistical and computational analyses suggest that pairs of aromatic amino acids with a centroid distance range of 3.4 – 7 Å, like that of the Y₇₃₀ and Y₇₃₁ dyad, are likely to play crucial functions in substrate recognition, structure, and catalysis in proteins.^35,36 Various aspects of through-space π-interaction have been investigated for their effects on charge transfer, pK_a and energy transfer.^37–39 We now show that the redox properties of the phenol moiety of tyrosine will be affected by cofacial disposition within a dyad, thus highlighting the fidelity of the RNR radical transport pathway. Further investigation on the energetics and mechanism of DPX oxidation in terms of hydrogen bonding and π–interaction will afford greater insight into how these non-covalent interactions are being used in enzyme systems like RNR.