BCG Artifact Removal for Reconstructing Full-scalp EEG inside the MR Scanner

Abstract

In simultaneous EEG/fMRI acquisition, the ballistocardiogram (BCG) artifact presents a major challenge for meaningful EEG signal interpretation and needs to be removed. This is very difficult, especially in continuous studies where BCG cannot be removed with averaging. In this study, we take advantage of a high-density EEG-cap and propose an integrated learning and inference approach to estimate the BCG contribution to the overall noisy recording. In particular, we present a special-designed experiment to enable a near-optimal subset selection scheme to identify a small set (20 out of 256 channels), and argue that in real-recording, BCG artifact signal from all channels can be estimated from this set. We call this new approach “Direct Recording Temporal Spatial Encoding” (DRTSE) to reflect these properties. In a preliminary evaluation, the DRTSE is combined with a direct subtraction and an optimization scheme to reconstruct the EEG signal. The performance was compared against the benchmark Optimal Basis Set (OBS) method. In the challenging nonevent-related EEG studies, the DRTSE method, with the optimization-based approach, yields an EEG reconstruction that reduces the normalized RMSE by approximately 13 folds, compared to OBS.

I. Introduction

Simultaneous acquisition of electroencephalography (EEG) and functional magnetic resonance imaging (fMRI) provides complementary yet functionally linked information about underlying brain activity with different temporal and spatial resolutions. However ballistocardiogram (BCG) artifacts appearing in the EEG data recorded inside the MR scanner still present daunting obstacles, especially when examining continuous (non-event-related) brain activity under high field strength, where the effect of BCG cannot be alleviated by averaging among a large number of event-triggered segments. Suggested to be related to cardiac pulsation and breathing, the BCG artifacts exhibit variation in both time and space, with a magnitude ten times that of normal brain signals when imaging at moderate to high magnetic field strengths. As the most widely used method for BCG removal, the Optimal Basis Sets method (OBS) [1], suppresses the BCG artifacts through channel-wise principal component analysis (PCA). The first few (default 3) principal components then are regressed out of the original data on a heartbeat-by-heartbeat basis.

The recent development of MR-compatible EEG hardware with denser channels provides an opportunity to acquire BCG-only signal from some channels by insulating them from the scalp, and use such knowledge to help denoise EEG for other channels [2]. Because the BCG artifact is related to the movement of conductive liquid, e.g., surface blood flow or movement of electrodes from breathing or pulsation of blood vessels, we expect adjacent channels to share similar BCG behaviors. Based on this first principle, we proposed previously [4] to surround each channel with a neighborhood of insulated channels in which the BCG artifacts are observable to ensure access to at least one proper prior. This approach, though it performs well, has two limitations: (1) one needs to determine which channel to examine, and to tailor the neighborhood insulation accordingly; and (2) the large number of insulated channels compromises the improved spatial resolution from of a dense EEG net. For the purpose of exploring brain activity patterns, in contrast to local probing, a sparse and stable insulation pattern is highly desirable.

To this end, we consider two seemingly conflicting aims: to (1) minimize the number of insulated channels, and (2) to denoise the EEG signals in the remaining channels with high accuracy. In an optimization framework, we jointly seek to insulate an optimal subset of a small cardinality, and learn an inference model to estimate the BCG components for the other channels based on the insulated readings. We propose a greedy scheme based on orthogonal matching pursuit and report its performance in comparison with both the benchmark OBS method and two alternative ad hoc insulation schemes.

II. Method

A. Generative model for contaminated EEG data

It is reasonable to assume that the BCG artifacts and the normal brain EEG signals are generated from independent sources. The voltage recording at each EEG channel can be considered as the linear superposition of these two components, subject to noise contamination

$$\mathbf{Y}={\mathbf{X}}_{bcg}+{\mathbf{X}}_{eeg}+\text{noise}.$$ (1)

B. Experimental setup

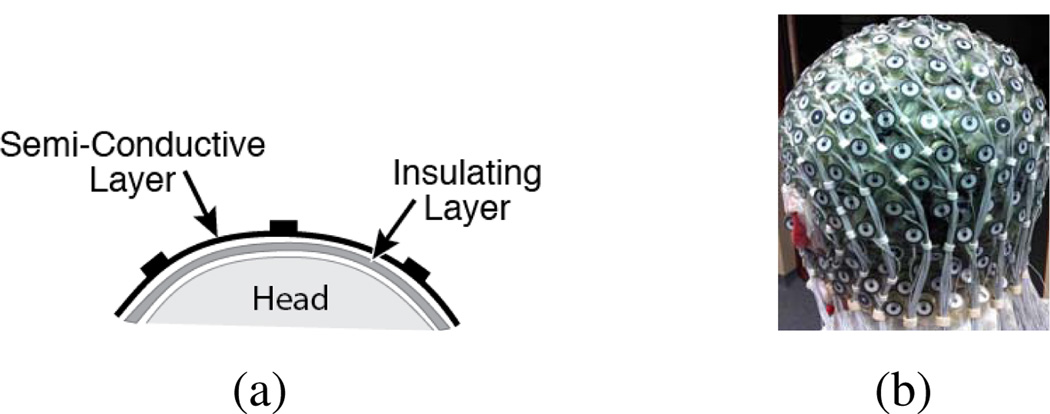
We acquire signals (256-channel, Electrical Geodesic Inc. GES300MR) sampled at 250 Hz from both inside and outside the scanner (Siemens Trio MRI). To obtain a BCG-only recording at a specific channel location, we insert two additional layer between the scalp and the EEG net, as illustrated in Fig. 1. The first one, a plastic insulating layer in contact with the scalp, blocks any brain signals; the second, a semi-conductive layer in contact with the electrodes, permits collection of any signals not arising from the brain. When the MRI gradients are not operating, we collect BCG artifacts (with potential electronic noise) from those insulated EEG electrodes inside the scanner.

Figure 1.

Experimental Setup: (a) Two-layer configuration for acquiring BCG artifacts; (b) Inserted two layers between the scalp and the EEG electrodes.

C. General inference logic and work flow

We speculate that the correlation among the BCG signals are approximately consistent, even though the signal traces themselves are temporally nonstationary. Consider a subset of the channels, represented by INS for “insulated”, and the complementary by NINS = SCLP \ INS. Then,

$${\mathbf{X}}_{bcg}[NINS,:]\approx {\mathbf{W}}^{|NINS|\times |INS|}{\mathbf{X}}_{bcg}[INS,:],$$ (2)

where the first and second dimension of data indicates space (channel indexing) and time respectively.

We propose a two-step procedure. In a model-building stage, all channels are insulated for the purpose of understanding the correlation relationship - the subset INS is selected and the inference weights W in Eq. 2 is estimated. In the acquisition stage, the channels in the subset INS remain insulated, while the remainder of the channels measure normal recording of the brain signal; their BCG components which are estimated via Eq. 2 with the weights from the model-building stage.

D. Channel selection

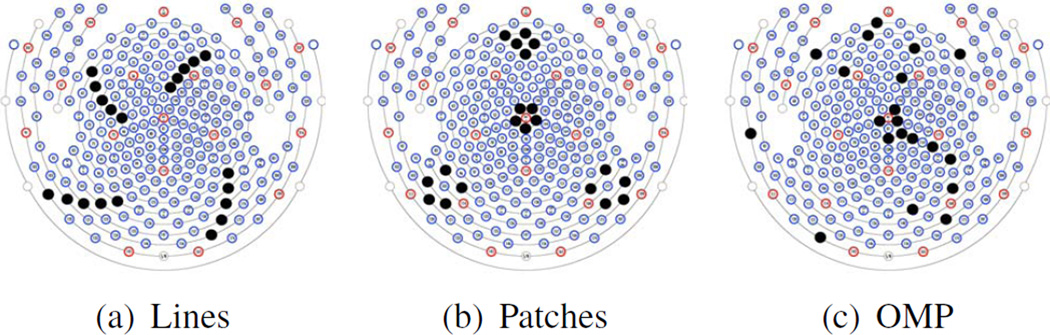
To preserve the benefit of high-density EEG recordings, we wish to minimize the number of channels used for BCG estimation; here we choose a “budget” of insulating |INS| = 20 out of the |SCLP| = 256 channels by cross-validation. We devised two ad hoc patterns: a “lines” pattern containing 4 groups of 5 channels arranged in a line, as shown in Fig. 2(a); and a “patches” pattern containing 4 groups of 5 channels arranged in a circle, as shown in Fig. 2(b).

Figure 2.

Three patterns for insulating channel (solid black dots) selection: (a) the “lines’ pattern, (b) the “patches” pattern, and (c) a pattern determined by OMP.

As an alternative, we can choose the subset with the best inference performance by solving the minimization-minimization problem

$$\underset{INS}{\text{min}}\{\underset{\mathbf{W}(INS)}{\text{min}}\Vert {\mathbf{X}}_{bcg}[NINS,:]-\mathbf{W}{\mathbf{X}}_{bcg}[INS,:]\Vert \},$$ (3)

where we use W (INS) to indicate explicitly the dependence of the optimal W on the set INS. Note that the inner problem of solving for W given INS is easy, but the outer set selection problem is NP-hard. We note also that by introducing an identity map on the insulated portion W̃ = [I;W], Eq. 3 can be converted to

$$\underset{INS}{\text{min}}\{\underset{\mathbf{W}}{\text{min}}\Vert {\mathbf{X}}_{bcg}[SCLP,:]-\mathbf{W̃}{\mathbf{X}}_{bcg}[INS,:]\Vert \},$$ (4)

which has a regression goal independent of the insulation set INS.

For practical purposes, we adopt a greedy Orthogonal Matching Pursuit (OMP) approach [3] as follows.

1. Equalize X = X_bcg[SCLP, :] so that it has unit ℓ₂-norm for each row (channel).

2. Initialize k ← 0; INS^(k) ← ∅;W^(k) ← 0;

   $${\mathbf{R}}^{(k)}\leftarrow {\mathbf{X}}_{bcg}[SCLP,:];k\leftarrow k+1.$$

   Where R^(k) is the residual signal that is not yet explained by regressing on the selected set INS(k).
3. Increment the selected subset : At step k (k ≥ 1), (k − 1) channels have been selected from previous steps, and the weight matrix W^(k−1) is of dimension SCLP × (k − 1). A channel i is added to the INST set if it explains the residual best

   $$i=\text{agr}\underset{i}{\text{max}}\sum _{j=1}^{|SCLP|}{\langle {\mathbf{R}}^{(k-1)}[j,:],\mathbf{X}[i,:]\rangle }^2.$$
   Upon this selection, everything is updated:

   $$IN{S}^{(k)}\leftarrow IN{S}^{(k-1)}\cup \{i\};{\mathbf{W}}^{(k)}=\text{agr}\underset{\mathbf{W}}{\text{min}}\Vert {\mathbf{X}}_{bcg}[SCLP,:]-\mathbf{W}{\mathbf{X}}_{bcg}[IN{S}^{(k)},:]\Vert ;{\mathbf{R}}^{(k)}={\mathbf{X}}_{bcg}[SCLP,:]-{\mathbf{W}}^{(k)}{\mathbf{X}}_{bcg}[IN{S}^{(k)},:];k\leftarrow k+1.$$

   Continue until |INS| reaches budgeted size.

4. Store the final selected set INS = INS^(k) and the inference matrix W = W^(k).

E. Reconstruction of BCG and EEG

We report two methods for reconstruction: a direct subtraction approach and an optimization-based approach.

1) Direct subtraction

When noise contamination in Eq. 1 is low, one may obtain directly an estimate of X_eeg by removing the estimated BCG component from the recorded superposition Y:

$${\mathbf{X̂}}_{eeg}=\mathbf{Y}-{\mathbf{X̂}}_{bcg}.$$

2) Optimization-based reconstruction

Recently we have developed an optimization-based [4] scheme for temporally concatenated segments to incorporate the EEG basis learned from the out-of-scanner experiment and the group sparse structure of the EEG coefficients. At the heart of this approach is the estimation of the coefficient C_eeg for the learned basis B_{e_prior} by minimizing

$$\mathrm{\Phi }({\mathbf{C}}_{eeg})={\Vert {\mathbf{C}}_{eeg}\Vert }_{1,2}+\frac{1}{2}\mu {\Vert {\mathbf{Y}}_{eeg}-{\mathbf{B}}_{e\_\mathit{\text{prior}}}{\mathbf{C}}_{eeg}\Vert }_F^2,$$ (5)

where Y_eeg is noisy observation of the EEG component after subtracting the estimated BCG from the contaminated data. The scalar parameter μ balances the contribution from each energy term. Subsequently, the temporally concatenated EEG component is recovered with multiplying the learned basis with the estimated EEG coefficients.

III. Results

We report the estimation performance regarding either the BCG reconstruction and the ultimate EEG recovery with channel-wise normalized root mean squared error nRMSE_i = ‖X. − X̂.‖₂/|X.‖₂, and a spatial collective average over a domain Ω with ave $nRMSE=\frac{1}{|\mathrm{\Omega }|}{\sum }_{i\in \mathrm{\Omega }}nRMS{E}_i$. The former will be displayed with tomographic maps for visualization.

A. Impact of model building length

For practical purposes, we desire the model building stage to be short. We first assess the impact of the model building length on the estimation accuracy. For a total of 13 minutes of full scalp BCG-only reading, we use the first few minutes for model building, and the remainder to evaluate the estimation accuracy on the full BCG recovery. Table I reports the BCG estimation performance as function of the duration of model building. It can be observed that (1) the OMP approach offers better estimation of BCG than the other two ad hoc patterns; and (2) the duration of model building sample has an identifiable but small impact on the estimation performance. This suggests the feasibility of a short model building duration, desirable for both efficiency and fast adaptation.

Table I.

BCG estimation error for different channel selection methods, as a function of the model building duration.

B. Consistency of the inference relationship

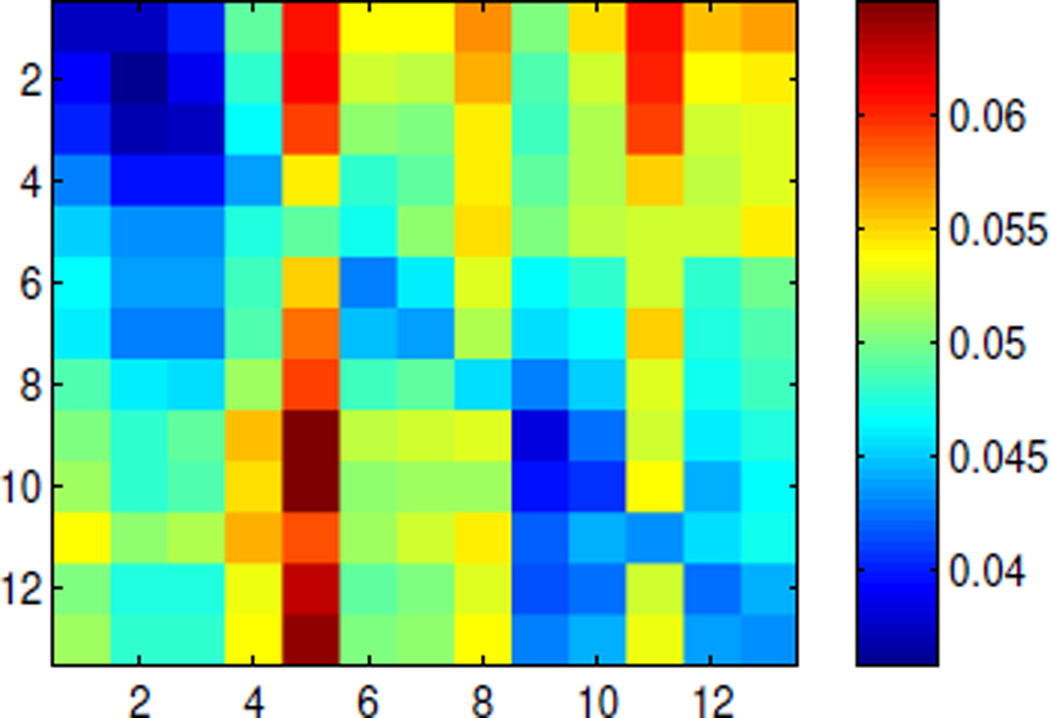
Note that because BCG signals is temporally nonstationary, our method relies on the consistency of the spatial inference relation instead. We validate this presumption by dividing the 13-minute full-scalp BCG signal into 13 segments of one minute each, and formulating the inference performance Fig. 3 whose (i, j)th entry contains the ave nRMSE for segment i based on the model built on segment j. The errors are uniformly bounded above by 10%, indicating general stability of the inference relationship. On the other hand, the (sub)diagonal structure suggests mild nonstatioinarity.

Figure 3.

Spatial ave nRMSE exhibits (sub)diagonal structure for model built on one segment and applied to another segment.

C. Performance evaluation on EEG signal reconstruction

To address the ultimate goal of reconstructing the EEG signal, we simulated the contaminated data based on Eq. 1 with EEG data acquired outside the scanner and BCG component from full-scalp insulation setting at a different time session within the imager. This provides us with access to ground-truth that is absent from normal acquisitions for calculating nRMSE. We compare the performance among the following three methods.

• OBS: EEGLab standard implementation is used with with 3 principal components.

• Inference + Direct Subtraction: the estimated BCG signals are subtracted from the contaminated EEG recordings to yield the reconstructed EEG signals.

• Inference + Optimization: the estimated BCG signals are subtracted from the contaminated data to generate (Y_eeg = Y − X̂_bcg) in Eq. 5.

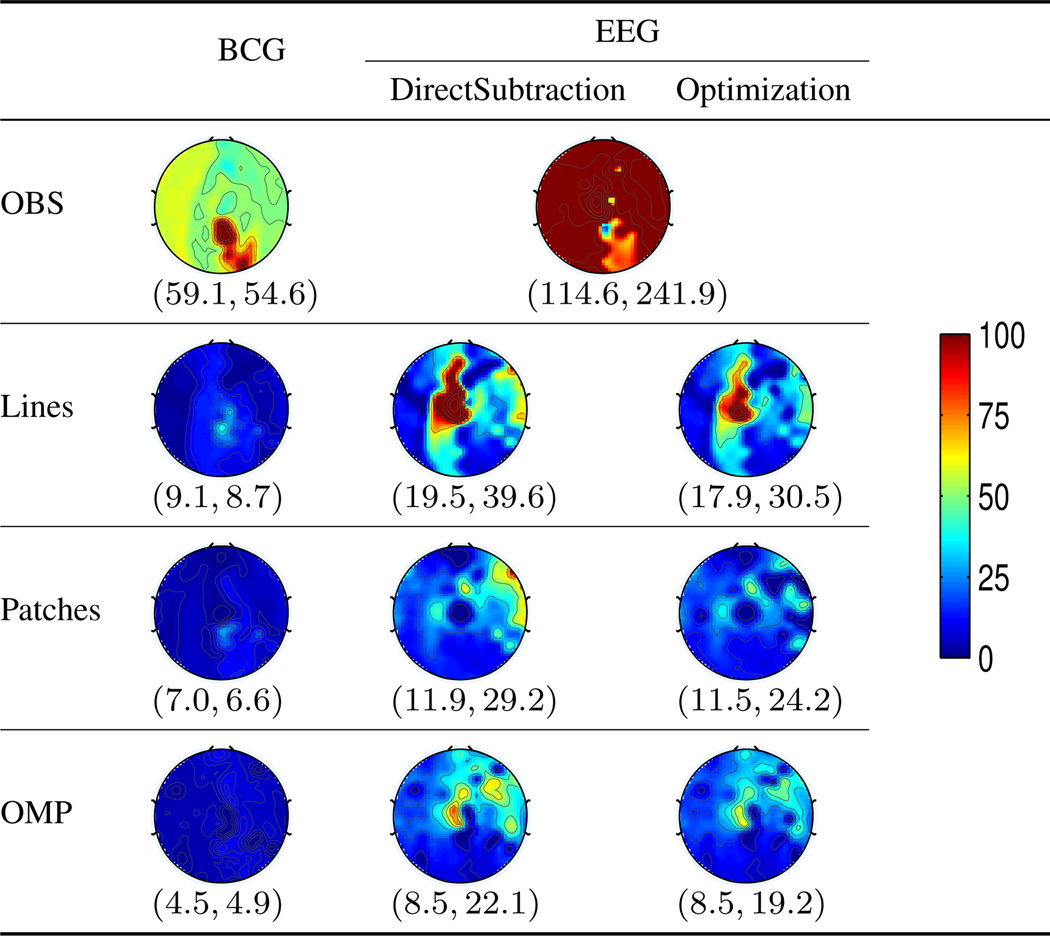
For inference based approaches, the performance corresponding to the ad hoc “lines”, “patches” and the proposed OMP pattern is compared. Table II reports the spatial distribution and the average nRMSE for full-scalp and the occipital region where the EEG signal is of primary interest during rest state under continuous acquisition. The OMP approach combined with the optimization based reconstruction offers roughly 13 folds improvement from the OBS approach, reducing the ave nRMSE from 241.9% to 19.2% and from 114.6% to 8.5% in full scalp and the occipital region respectively.

Table II.

Tomographic maps of nRMSE (in percentage). The spatially collective ave nRMSE pair correspond to Ω = occipital and Ω = whole scalp respectively.

IV. Discussions and Conclusions

We have developed an experimental platform, and a signal processing module, to reconstruct a BCG artifact map for the whole scalp, based on a small subset of insulated EEG channels.

The inference relationship is generally consistent, but degrades mildly as the model construction and the application are further apart. Fortunately, the OMP-based approach yields good estimate quickly (1 min), enabling fast adaptation of the inference map when necessary.

Compared to the conventional OBS method, even the ad hoc insulating patterns with direct subtraction provides notable improvement of about 6̃8 folds, demonstrating the value of informative priors obtained from the insulated subset. The OMP approach combined with the optimization-based reconstruction method reduces the error further by another fold.

Combined, these methods can do much to mitigate the serious artifacts that appear otherwise in combined EEG/fMRI recordings. The practical advantage of doing so may be very large and fills the void in BCG artifact removal in continuous recordings, necessary to study the tantalizing relationships between BOLD signal and brain EEG rhythms, as well as important disease entities such as epilepsy, where there is little opportunity to average EEG events.