Tracer-based estimates of protein flux in cases of incomplete product renewal: evidence and implications of heterogeneity in collagen turnover

Abstract

The synthesis of various molecules can be estimated by measuring the incorporation of a labeled precursor into a product of interest. Unfortunately, a central problem in many studies has been an inability to estimate the intracellular dilution of the precursor and therein correctly calculate the synthesis of the product; it is generally assumed that measuring the true product labeling is straightforward. We initiated a study to examine liver collagen synthesis and identified an apparent problem with assumptions regarding measurements of the product labeling. Since it is well known that collagen production is relatively slow, we relied on the use of [²H]H₂O labeling (analogous to a primed infusion) and sampled animals over the course of 16 days. Although the water labeling (the precursor) remained stable and we observed the incorporation of labeled amino acids into collagen, the asymptotic protein labeling was considerably lower than what would be expected based on the precursor labeling. Although this observation is not necessarily surprising (i.e., one might expect that a substantial fraction of the collagen pool would appear “inert” or turn over at a very slow rate), its implications are of interest in certain areas. Herein, we discuss a novel situation in which tracers are used to quantify rates of flux under conditions where a product may not undergo complete replacement. We demonstrate how heterogeneity in the product pool can lead one to the wrong conclusions regarding estimates of flux, and we outline an approach that may help to minimize errors surrounding data interpretation.

The Logic Surrounding the Use of Primed Infusions and the Reliance on Precursor/Product Labeling Ratios

numerous discussions have considered concepts surrounding the use of primed infusions for quantifying the synthesis of a product (19, 20). Briefly, in a perfect experiment, the precursor labeling will be described by a square wave, and the product labeling, in the simplest case, will be described by a single exponential. Under these conditions there are two generally accepted approaches for calculating the fractional synthetic rate (FSR) of the product (4). First, if an experiment is run over a relatively short time course, one can compare the initial (pseudolinear) change in the product labeling with the steady-state precursor labeling according the equation

$$\text{FSR}=\text{change in product labeling}/\text{precursor labeling}$$ (Eq.1)

The problem with this approach has been in identifying the true precursor labeling. For example, although a labeled amino acid can be infused directly into the systemic circulation, it typically undergoes substantial intracellular dilution via local protein breakdown; estimates of the FSR will be in error if one does not account for the dilution. A second approach for estimating the FSR is to model the temporal labeling profile of the product, i.e., determine the time it takes to approach steady-state labeling according to the equation

$${\text{product labeling}}_{timet}=\text{final labeling}\times \left(1-e^{-\text{FSR}\times timet}\right)$$ (Eq.2)

where “time t” is the time after exposure to a constant administration of a tracer and “final labeling” represents the asymptotic labeling of the product.

A general assumption that is made when using Eq. 2 is that the steady-state labeling of the product reflects the degree of intracellular labeling of the precursor (19, 20). If true, it is then possible to infer the dilution by comparing the labeling in a plasma amino acid with that of the steady-state labeling in the product protein. This logic has been clearly demonstrated, and extensively relied upon, in studies of apoprotein flux (11). For example, VLDL-apolipoprotein B (apoB) will approach steady-state labeling within several hours during a primed infusion of a labeled amino acid; however, the data clearly show a sizeable difference (i.e., 30–40%) between the labeling of a plasma amino acid and that bound in VLDL-apoB (11). In contrast, the labeling of LDL-apoB follows a slower (pseudolinear) temporal profile over the same period; consequently, investigators typically estimate LDL-apoB synthesis by assuming that the true precursor labeling is that of VLDL-apoB (11).

It is important to recognize a major underlying assumption with the logic that has been outlined to this point, namely that product molecules will experience complete turnover. For example, if one observes that the steady-state labeling of a protein is less than that of the extracellular precursor amino acid, it is not immediately possible to know whether this is related to intracellular dilution of the amino acid and/or heterogeneity of the product. A common view in the literature is that products undergo complete renewal; therefore, extra- to intracellular precursor-labeling gradients almost exclusively drive the apparent differences in precursor/product labeling ratios (19, 20). Although we agree that this assumption is valid in many instances, an alternative explanation is that some fraction of the product molecules may not be subject to renewal; this alternative view can have serious implications with regard to the data interpretation. Herein, we discuss an example surrounding studies of collagen synthesis. Given the underlying biology, one would expect that some pools of collagen appear “inert” and/or have a negligible turnover (1). For example, a stable extracellular protein matrix is central to ensure normal organ structure and function. Therefore, once in place, it seems reasonable that this network would remain largely inactive (15).

Identification and Measurement of the True Precursor Labeling: A Potential Advantage of Using Labeled Water Vs. Prelabeled Amino Acids

The use of [²H]H₂O or [¹⁸O]H₂O can circumvent some of the problems noted above (16, 21). Namely, since it is expected that water rapidly and completely mixes between extra- and intracellular pools, one assumes negligible precursor-labeling gradients (8). Therefore, if intracellular metabolism rapidly generates ²H- or ¹⁸O-labeled amino acids, one can infer the true precursor labeling by measuring the ²H or ¹⁸O labeling of plasma water and applying an exchange factor to account for the number of labeled ²H or ¹⁸O atoms per amino acid (8, 16, 21). In addition, [²H]H₂O or [¹⁸O]H₂O avoids the use of extensive surgical manipulations for tracer administration; a primed infusion can be accomplished via an intraperitoneal bolus, followed by the addition of ²H- or ¹⁸O-water to the drinking water.

A caveat in studies that rely on [²H]H₂O centers on the rate at which amino acids become labeled. It is well known that one will observe a dilution between ²H labeling in drinking water and body water; this is related to digestion and respiration (9). In addition, free amino acids will reach different degrees of ²H labeling in terms of both time and magnitude (6, 8, 16). In our experience, the equilibration of ²H labeling is rapid enough to permit studies of protein kinetics even when they are characterized by relatively short half-lives (21).

It is important to note that other tracers could also be used in the scenario described here, with the caveat that it would be necessary to continuously administer a prelabeled amino acid for a prolonged period to approximate steady-state labeling in the product of interest and that one would need to obtain some estimate of the extra- to intracellular dilution. The enrichment of 1) a keto-acid equivalent (e.g., [¹³C]ketoisocaproate is a surrogate for [¹³C]leucine), 2) a conjugated metabolite (e.g., [¹³C]hippurate is a surrogate for hepatic [¹³C]glycine), 3) fast-turning over protein labeling (e.g., VLDL-apoB is a surrogate for LDL-apoB), and/or 4) t-RNA-bound amino acids has been used for such purposes (19, 20). A key advantage in studies that utilize labeled water centers on the duration of the experiment. For example, it is possible to easily maintain a steady-state labeling of body water for a prolonged period of time. This is helpful in cases where the product labeling may be relatively slow, and investigators can simply extend the experimental time to improve the analytical window.

Studies on Liver Collagen Synthesis: Experimental Evidence Suggesting Incomplete Product Turnover

We initiated a study aimed at determining liver collagen synthesis in mice. To maintain a stable enrichment of body water, for 16 days mice were given a bolus of ²H-labeled water (20 μl of 99% [²H]H₂O/g body wt) and then allowed free access to food and 5% ²H-labeled drinking water. A primary objective of this pilot experiment was to examine how the timing of sample collection would affect the analytical measurements. For example, since we expected that the FSR of collagen would be relatively slow, we collected samples at various times over 16 days (n = 3 mice/point) to examine the magnitude of labeling.

The collagen extract was prepared as described previously (5). Briefly, frozen liver (∼20 mg) was homogenized in 450 μl of 100 mM NaOH. After centrifugation at 7,000 g for 10 min, the supernatant was removed and the pellet briefly vortexed in 500 μl of H₂O. The pellet was dissolved in 5 μl of SDS-PAGE buffer and 4 M urea, and samples were then boiled for 5 min, after which the dissolved material was separated by 7.5% SDS-PAGE. The corresponding collagen band was cut and digested overnight (in-gel) using trypsin. The supernatant of the digest was dried and reconstituted with 40 μl of 0.1% formic acid in water. The resulting sample (3 μl) was analyzed by an Orbitrap Velos mass spectrometer coupled with an EasySpray interface. For protein identification, the instrument was operated using a data-dependent top 15 experiment with 60K resolution for the full scans. For isotope enrichment measurement of the parent peptides, the instrument was set as full scan only with 60K resolution.

As a control, we analyzed the labeling of circulating albumin; 4 μl of plasma was digested using a previously published protocol (10). The digests were then analyzed using the same liquid chromatography (LC)-mass spectrometry (MS) methodology as those described above for collagen analysis.

The ²H labeling of plasma water was determined using GC-q-MS (17). Briefly, ²H present in water was exchanged with hydrogen bound to acetone by incubating 10 μl of plasma or known standards in a 2-ml glass screw-top GC vial at room temperature for 4 h with 2 μl of 10 N NaOH (Fisher Scientific) and 5 μl of acetone (Sigma-Aldrich). The instrument is programmed to inject 5 μl of headspace gas from the GC vial in a splitless mode using an isothermal run (Agilent 5973 MS coupled to a 6890 GC oven fitted with an Agilent DB-5MS column), and the mass spectrometer is operated in selected ion monitoring (electron impact ionization, m/z 58 and 59, 10 ms of dwell time per ion).

Theoretical spectra were estimated using freely available software that was developed by Dr. R.G. Sadygov (https://ispace.utmb.edu/users/rgsadygo/Proteomics/DeuterimiumEnrichment) (8). Briefly, the program simulated the asymptotic isotope distribution of a product molecule based on body water enrichment and the maximum number of metabolically exchangeable H atoms. The setting of those exchange constants was based on direct observations of the ²H labeling of free amino acids. Note that the complexity of some spectra can present a challenge when trying to determine a true enrichment; therefore, the peptide data are shown here as the M1/M0 labeling ratio.

Validating a Central Assumption Regarding the Use of [²H]H₂O to Study Protein Synthesis: Evidence in Support of a Collagen Heterogeneity

A prerequisite surrounding the use of [²H]H₂O in studies of protein synthesis is the expectation of rapid equilibration between the ²H labeling of water and free amino acids (Fig. 1A); otherwise the ²H labeling of protein-bound amino acids may be artificially low and lead one to an erroneous conclusion regarding protein synthesis. We believe that the majority of free amino acids will approach a sufficient equilibrium within a few hours or less (6, 8, 16); therefore, the seemingly low level of steady-state ²H labeling of liver collagen (Fig. 1, B and C) reflects a sizeable heterogeneity of the collagen pool and not a limitation of the tracer method. We briefly comment on some of the key data that support the notion of rapid equilibration of ²H labeling in free amino acids to put the current observations regarding ²H labeling of collagen in better context.

Fig. 1.

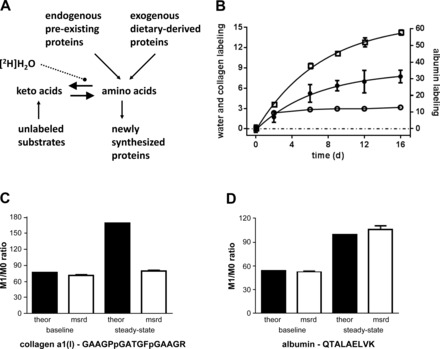
Temporal enrichment of plasma water, liver collagen, and circulating albumin in control mice. A: hypothesis on which the [²H]H₂O method is based; one expects the equilibration of ²H labeling during transamination to be faster than the rate of new protein synthesis. B: steady-state labeling of body water (○) was achieved via a “primed infusion” (i.e., an intraperitoneal bolus followed by addition of tracer to the drinking water). There was an exponential increase in the enrichment of collagen α1(I) GAAGPpGATGFpGAAGR (●) and albumin QTALAELVK (□). Using Eq. 2, the fractional synthetic rate (FSR) of collagen and albumin was 0.149 ± 0.04 and 0.139 ± 0.02 pools/day, respectively. Note that the labeling data are shown as the [M1/M0_D2O-treated − M1/M0_baseline] × 100; these represent means ± SE (n = 3 mice/time point). C and D: theoretical (theor) and measured (msrd) M1/M0 ratios (collagen and albumin, respectively) that are expected at baseline and after exposure to 2.75% ²H labeling in water and allow for steady-state (asymptotic) labeling in the case of theoretical spectra and that which is measured in the current study after 16 days of labeling. Data for measured samples are shown as means ± SE; n = 3 mice/time point, determined using samples collected after 0 or 16 days of exposure to [²H]H₂O.

Nearly 15 years ago, when we began to (re)invent the use of [²H]H₂O for studying protein kinetics (14), we recognized that rates of protein synthesis could not be interpreted if the ²H labeling of amino acids approached the rate of protein synthesis. We expected that problems could arise during in vivo studies, i.e., open systems, since there is continuous influx of unlabeled precursors. Namely, the model of hydrogen kinetics that was reported by Ballou and Thompson (1) clearly outlined the problem, but the studies did not address the potential magnitude of the flux rates. Therefore, we directed attention toward understanding whether the ²H labeling of free amino acids could be altered by sudden pertubations. We used the [³H]H₂O data reported by Commerford et al. (3) as a guide of the anticipated asymptotic labeling, since one expects that exposure to [³H]H₂O from conception to 3 mo of age would likely represent the best test of whether all amino acids can be labeled and to what degree relative to body water.

To examine the limits of the [²H]H₂O method, we quantified the ²H labeling of circulating amino acids under conditions where the entry of cold sources could be varied. For example, we contrasted studies in fed vs. fasted conditions, the hypothesis being that the rapid entry of cold substrates (either amino acids and/or other carbon sources that could generate amino acids) would provide a sizeable perturbation and therein challenge the method (6, 8, 16). Surprisingly, our data regarding the total ²H labeling of many amino acids was in close agreement with those reported by Commerford et al. (3). In parallel studies, the equilibration of ²H labeling was tested using an orthogonal approach via studies involving [¹⁸O]H₂O (1a, 16, 21). Note that the mechanism(s) by which [¹⁸O]H₂O generates ¹⁸O-labeled proteins shares some overlap with the mechanism(s) by which [²H]H₂O will be incorporated (21); however, [¹⁸O]H₂O would be expected to label amino acids as fast (if not faster than) [²H]H₂O. In our experience, we found similar rates of protein synthesis using either water tracer, especially when looking at proteins with relatively short half-lives {a setting that was expected to draw out the largest effect(s) if there were any delays in [²H]H₂O equilibration with amino acids} (16, 21). In total, 1) the direct observation of amino acid equilibration, 2) the comparison of estimates of protein synthesis using ²H- vs ¹⁸O-labeled water, and 3) the ability to quantify the synthesis of proteins with very short half-lives were all supportive of the central hypothesis surrounding “rapid and stable” ²H labeling of free amino acids. These data imply that one can use [²H]H₂O to estimate rates of protein synthesis.

Although we have not observed any major limitations in the equilibration of ²H labeling, we recognize other data that present modest discrepancies with our views. For example, Kombu et al. (9) reported a slower labeling of glutathione when contrasting samples that were collected 2 vs. 31 days after [²H]H₂O administration; it is worth taking a closer look at the reported numbers. Briefly, the ²H labeling of liver glutathione approached 9.4 vs. 14.1% at 2 vs. 31 days, respectively. Although this suggested a slower equilibration between [²H]H₂O and free amino acids, the ²H labeling of liver ophthalmate (i.e., glutamyl-aminobutyryl-glycine, an analog of glutathione where cysteine is replaced by aminobutyrate) showed virtually identical enrichment at 2 vs. 31 days, i.e., 13.5 vs. 13.3%, respectively. This is somewhat striking since Kombu et al. (9) provide a lengthy discussion surrounding the potential impact of the large glutamate/glutamine pool on the equilibration of ²H with the amino acids used in glutathione synthesis, and yet the structural difference between glutathione and ophthalamate is not glutamate. Furthermore, the ²H labeling of body water (Supplemental Figure 3 in Ref. 9) was enriched to ∼2.0% over the initial 2 days and then to ∼2.5% for the remainder of the study. This slight but substantial jump in “steady-state” water labeling (∼1.3 times) does not seem to be accounted for in their model of protein synthesis, but it will lead directly to an apparent difference when calculating the FSR and inferring the asymptotic labeling of amino acids/protein products over the 2- vs. 31-day interval (which was ∼1.5 times using the respective times) (9). Although we believe that additional studies in this area are always of value, it appears that the majority of free amino acids will likely equilibrate relatively fast. Our comments are not meant to discredit the studies done by Kombu et al. (9); our remarks reflect the nuances surrounding the interpretation. We believe that our data are more closely aligned than the nature of the comments in their discussion.

In the current study, we were able to maintain a reasonably stable steady-state labeling of plasma water (Fig. 1B). Despite the fact that we observed the incorporation of ²H-labeled amino acids into collagen α1-I and that the collagen labeling profile tended to approach an asymptotic value, we observed a somewhat minor change in the M1/M0 labeling ratio (Fig. 1, B and C). For example, given the amino acid sequence and the fact that body water was enriched to ∼2.75%, we would have expected the steady-state labeling of the collagen to be severalfold higher than the observed value if the entire protein pool turned over (Fig. 1C). Although we did not measure the equilibration between ²H labeling of body water and free amino acids herein (2, 6), we measured the change in ²H labeling of circulating albumin. Consistent with previous efforts (8, 16) and the underlying theory that is outlined above, we observed a substantial increase in the ²H labeling of albumin (Fig. 1, B and D). These observations support the hypothesis that there is a reasonably rapid equilibration between ²H labeling of body water and free amino acids; otherwise, albumin (a liver-derived protein) would not have been so heavily labeled.

Since slow amino acid equilibration is probably not a major contributing factor to the collagen labeling, we concluded that the striking contrast between the ²H labeling of collagen and albumin is related to an incomplete turnover of collagen. Our observation (Fig. 1, B–D) is in close agreement with data in the literature. For example, Ballou and Thompson (1) studied collagen kinetics (using [³H]H₂O) over the course of ∼1 yr. They found that nearly 75% of the collagen pool has a half-life of ∼1,000 days and that the remainder has a half-life of ∼15 days. Those observations are consistent with the data reported by Gardner et al. (5); i.e., they showed that the ²H labeling of liver collagen approached a steady-state within ∼21 days. As discussed by Ballou and Thompson (1), and in agreement with our observations (Fig. 1), Gardner et al. found that ∼35% of the collagen was replaced (5).

In total, these observations are not necessarily surprising since one might expect that a substantial fraction of the collagen could appear as “metabolically inert” (or at least undergo very slow renewal) (7, 12, 13). For example, collagen is a major structural protein that provides extracellular matrix support (15). Although this is certainly important in areas of biology surrounding wound healing and tissue regeneration, the implications of collagen heterogeneity in cases where one aims to estimate the kinetics were not discussed by Ballou and Thompson (1) or Gardner et al. (5). Consequently, we are back to the central question: How does one estimate FSR in cases where a product may experience incomplete turnover and/or what errors can one encounter with regard to the interpretation? We now discuss the implications of this observation in the context of these types of tracer studies.

Implications of Incomplete Product (e.g., Protein) Turnover

When an investigator considers an experimental plan to study the kinetics of a slowly turning-over product, e.g., collagen, one may almost immediately consider estimating the FSR by measuring the initial rate of change in labeling (Eq. 1). Namely, provided that one knew the true precursor labeling, it seems reasonable to apply a logic that has been used in numerous other studies, e.g., when studying LDL-apoB (11). Presumably, such an approach would minimize resources, including the time that is required to examine tracer kinetics. However, what are the implications if the product does not undergo complete renewal, such as in studies of collagen kinetics?

Figure 2 considers a simple example of this problem that should facilitate the remaining discussion. Again, assuming a single-compartment model, one can infer the FSR by modeling the temporal change in product labeling (4, 20). In the control scenario (Fig. 2B), we have assumed that 50% of the product is “inert” (or at least it is very slow to turn over, and therefore, it is considered to be “inactive”) and that the remaining 50% of the product is turning over at a FSR of ∼10%/day (and it is considered to be “active”). In Fig. 2C (○), it is demonstrated that the protein labeling will approach an asymptotic value and that it will be enriched to ∼50% at steady state (note that we have assumed that the precursor is 100% labeled to better visualize the problem being considered). If we collect data as described here for a period of 16 days, and we fit those measurements to a single exponential curve (e.g., using GraphPad), we indeed conclude that the FSR is ∼10%/day (control group; Fig. 2D, black bars). However, if we collect data for only 2 days and assume that the precursor is labeled to 100%, we conclude that the FSR is ∼4.5%/day (control group; Fig. 2D, hatched bars). This value is about half of the true value since we now dilute the product labeling via the total pool that is present, of which 50% is considered inactive in the context of the model. If we then estimated the apparent absolute production rate (e.g., the grams of protein made per day), we would reach nearly the same conclusions regardless of the fact that the FSR is dramatically different using the various approaches (control group; Fig. 2E). For example, the absolute production rate equals the FSR multiplied by the pool size. In the case where we model the data for 16 days, we conclude that the FSR is ∼10%/day, but we have determined that only ∼50% of the total product is actively being renewed; therefore, we would conclude that ∼5 g/day protein is being made. In the case where we sample only for 2 days, we conclude that ∼4.5% of the product molecules were made, yet we are not aware that only ∼50% of the product is active. Nevertheless, we would reach a similar conclusion since we would multiply the lower FSR (Fig. 2D) by the total pool size (Fig. 2B).

Fig. 2.

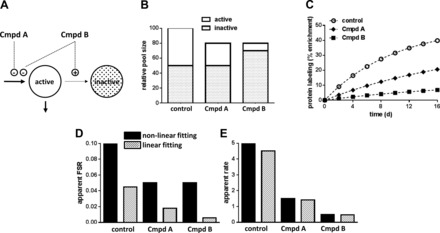
Estimating protein synthesis when there is incomplete product renewal. A: hypothetical model containing active and inactive pools of a product molecule. Under “control” conditions the conversion of active to inactive is negligible; therefore, this system reflects a pseudo-single-compartment model. Compounds (Cmpd) A and B both inhibit the production of active molecules; however, Cmpd B also stimulates the conversion of molecules in the active pool to the inactive pool. B: different scenarios involving changes to the total pool size and redistribution of the active and inactive pools. C: temporal changes in the labeling of total protein in various pools; simulations assumed that the FSR in the active pool was 0.10 in the control group and 0.05 in either the Cmpd A- or Cmpd B-treated group. D: apparent FSR that is obtained when data are fit using a nonlinear method (i.e., a single exponential plot through all the data points for a given curve in C; Eq. 2) or a linear fit (i.e., only using the samples collected up to day 2 and assuming that the precursor labeling was 100%; Eq. 1). E: apparent absolute rate of synthesis; i.e., multiply data in B and D.

This point now becomes convoluted if we consider the impact of various scenarios that could modulate the production of active molecules (compound A; Fig. 2A) or affect the production of active molecules and the conversion of active to inactive molecules (compound B; Fig. 2A). Let us assume that an intervention aims to reduce the amount of the product; for example, we administer two potentially novel therapeutics (e.g., compounds A and B) over a period of time, and we observe that each appears to have a beneficial effect in terms of reducing the total product mass (Fig. 2B). We then conduct a tracer study to examine the kinetics that are associated with the respective changes in mass (Fig. 2C). However, let us assume that all changes in product mass are not equal in terms of efficacy. It could be that we are really interested in reducing the product pool while avoiding any increase in the inactive fraction; namely, we are looking to specifically reduce the amount of active product. In the case of collagen, this could be analogous to reducing the production of soluble protein while we minimize any accumulation of insoluble extracellular matrix protein.

The simulations reflect potentially “good” or “bad” outcomes in which compound A or B, respectively, is given. As shown, the total product pool has decreased in both conditions; however, in the case of a good outcome the change is only in the amount of active product, whereas in the case of a bad outcome the change also reflects a conversion of active product to inactive product (Fig. 2B). Now let us apply the same logic noted above, i.e., contrast our conclusions regarding the physiology if we rely on curve fitting (Eq. 2) vs. a seemingly straightforward “initial slope” method (Eq. 1) for estimating flux. Our example of the “control” scenario shows that the two mathematical approaches are generally equivalent. In the scenarios surrounding compounds A and B, we have simulated conditions in which the FSR of the active product pool is ∼5%. When using a nonlinear fitting method on the data collected over 16 days, we obtain the expected FSR values in each case (Fig. 2, C and D). Estimates of the asymptotic product labeling (Fig. 2C) would reflect the true picture; in the case of the good outcome (compound A) the simulation suggests that ∼37.5% of the product should be labeled (i.e., 30 active/80 total molecules), whereas in the case of the bad outcome (compound B) ∼12.5% of the product should be labeled (i.e., 10 active/80 total molecules) (Fig. 2B). From these data we could immediately infer the distinct differences in the apparent outcomes for the respective compounds. For example, in each scenario we have a reduced amount of product, and therefore, it would appear that we reached our goal with both compounds. However, inspection of the tracer data suggests two different outcomes. In one case we have a truly good outcome, i.e., compound A reduced the production of the active product alone, whereas in the other case we have a bad outcome, i.e., compound B actually promoted the formation of the inactive product. In this scenario, the use of temporal labeling profiles appears to aid in differentiating the outcomes.

If we had considered the model problem outlined above but we chose to use only a limited data set (e.g., the pseudolinear change in product labeling over the initial 2 days; Eq. 1), we could end up in a situation where we believe the wrong answer. For example, using labeling data collected for only the initial 2 days, we would conclude that both therapies reduced the production of the product molecules, and therefore, we might feel confident in the potential merit of the two compounds. However, we might be inclined to advance our efforts on compound B since, compared with compound A, it appeared to have a greater impact on the FSR (Fig. 2D) and the apparent absolute production rate (Fig. 2E). This would be somewhat unfortunate since the simulation clearly shows that compound B had a dramatic effect on promoting the conversion of active product into inert product, i.e., the therapeutic outcome we might have been trying to avoid.

Summary

The application of precursor/product labeling ratios in studies of metabolic flux have typically been plagued by concerns regarding the true precursor labeling. Fortunately, various strategies have been proposed to address this problem, therein giving investigators greater confidence regarding the interpretation of tracer data. An assumption in these studies is that the product undergoes complete turnover. Although this assumption is valid in many circumstances, this assumption could have major implications in studies of very slowly turning over products (e.g., collagen, muscle glycogen, and DNA). We have outlined a conceptual framework that is supported by experimental data (obtained from an in vivo experiment and derived via simulations), which attempts to address part of this problem.

Based on the example discussed herein, we hypothesized that one can reliably estimate the production of molecules that are subject to incomplete renewal (e.g., collagen) by measuring the temporal change in enrichment. For example, knowledge of the true precursor labeling (as appears to be the case in studies that rely on labeled water) allows one to utilize the asymptotic labeling of the product molecules to infer the partitioning between active and inactive (or less active) product pools. Presumably, this logic can be used to more completely interrogate problems surrounding metabolic flux in selected scenarios. We recognize that it is not practical to run long-term studies with numerous sampling points. Perhaps it is possible to adapt the use of a “three-point” method in some scenarios. For example, the initial slope using two data points gets measured and compared with a third data point using a sample that is collected much later when one expects the product labeling to have reached a steady state. Although this type of logic can, in theory, be useful for solving the problem described herein and would circumvent the need for time course studies, this has the obvious problem that one might need to determine when such a steady state is actually expected in the product labeling. Consequently, one would likely need various pilot studies to develop confidence in determining when to collect the third (or asymptotic) point. We hope that our discussion of this observation, albeit in a simple form, will stimulate a deeper examination in future studies.

GRANTS

T. Kasumov and R. G. Sadygov are supported by National Institutes of Health Grant 1-R01-GM-112044-01A1.

DISCLOSURES

H. Zhou, Sheng-Ping Wang, K. Herath, S. F. Previs, and D. E. Kelley are employed by Merck and own stock or stock options.

AUTHOR CONTRIBUTIONS

H.Z., S.-P.W., K.H., T.K., R.S., and S.F.P. performed experiments; H.Z., S.-P.W., K.H., and S.F.P. analyzed data; H.Z., K.H., and S.F.P. prepared figures; H.Z., S.-P.W., K.H., S.F.P., and D.E.K. drafted manuscript; H.Z., S.-P.W., K.H., T.K., R.S., S.F.P., and D.E.K. approved final version of manuscript; T.K., R.S., S.F.P., H.Z., and D.E.K. interpreted results of experiments; S.F.P. conception and design of research; S.F.P. and D.E.K. edited and revised manuscript.