Summary
Navigation is usually thought of relative to landmarks, but neural signals representing space also use information generated by an animal’s movements. These signals include grid cells, which fire at multiple locations forming a repeating grid pattern. Grid cell generation depends upon theta rhythm, a 6-10 Hz EEG oscillation that is modulated by the animals’ movement velocity. We passively moved rats in a clear cart to eliminate motor related self-movement cues that drive moment-to-moment changes in theta rhythmicity. We found that passive movement maintained theta power and frequency at levels equivalent to low active movement velocity, spared overall HD cell characteristics, and abolished velocity modulation of theta rhythmicity and grid cell firing patterns. These results indicate that self-movement motor cues are necessary for generating grid-specific firing patterns, possibly by driving velocity modulation of theta rhythmicity. Velocity modulation of theta may be used as a speed signal to generate the repeating pattern of grid cells.
Keywords: Grid cell, Passive transport, Head direction cell, Theta rhythm, Self-movement cues
Introduction
Animals must maintain knowledge of their spatial location and orientation within their environment to navigate accurately. The rodent brain contains spatially-tuned neurons that are interconnected to form a spatial processing circuit spanning brainstem to cortex. In the medial entorhinal cortex (MEC) and parasubiculum, grid cells fire as a function of the animal’s location, exhibiting multiple, evenly spaced firing fields that form a triangular grid pattern across the entire environment [1, 2, 3]. These neurons are largely driven by self-motion cues and are thought to function as a path integrator, continually updating neural representations of the animal’s location as it performs linear and angular movements [4]. Both attractor and oscillatory interference models provide contrasting explanations of the generation of grid cell activity, but share a common requirement that the MEC receives input conveying information about direction and speed [4, 5, 6, 7]. Head direction (HD) cells fire as a function of the animal’s directional orientation, are generated from self-movement cues from the vestibular system, and some contain conjunctive characteristics with grid-specific firing in the MEC [8, 9]. These cells provide the directional signal for grid cell generation, as lesions or inactivation of the HD network abolishes grid and HD cell activity in the MEC [10]. Theta rhythmicity is a 6-10 Hz oscillation observed in the local field potential (LFP) of the MEC that is modulated by an animal’s movement velocity [11, 12]. Inactivation of the medial septal area abolished theta rhythmicity and grid cell activity, but spared HD cell firing [13, 14]. While this finding demonstrates a necessary role for the medial septal area, and likely its theta rhythmicity inputs, it does not reveal the nature of the information it conveys.
There are two components to theta that may be important for the generation of grid-like activity: the rhythmic pattern of activity and the strength of the rhythm, which is measured by frequency and power, respectively [6, 7]. The ongoing theta rhythm may interact with individual subthreshold membrane oscillations in the MEC. This resulting interaction could be sufficient for the generation of grid-like activity and account for the relationship between grid cell spacing and theta frequency gradient observed across the MEC [15]. Theta rhythmicity is not a constant signal, but instead the power and frequency change with the animal’s movement velocity, which is largely driven by self-movement motor cues of proprioception and motor efference [16]. To investigate the role of these two theta components, we compared grid cell activity in rats under two movement conditions: active versus passive movement. In the passive condition rats were passively moved throughout an environment while in a clear plastic cart. This manipulation has been shown to leave theta activity intact in the hippocampus while decoupling it from the rat’s movement velocity [16], allowing us to dissociate which component of theta may be necessary for grid-like firing patterns. If velocity modulation of theta rhythmicity is critical, then passive transport should completely disrupt grid-like firing; however, if rhythmicity is sufficient, then grid-like firing should be spared.
Results
Passive transport disrupts grid cells
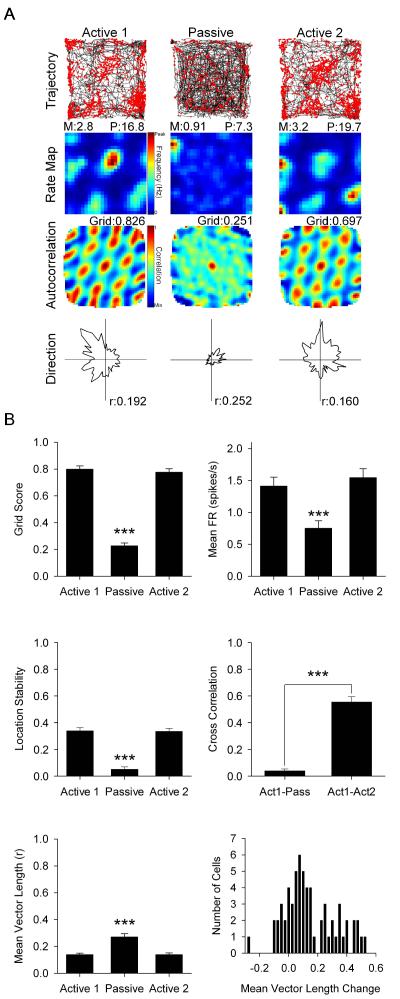
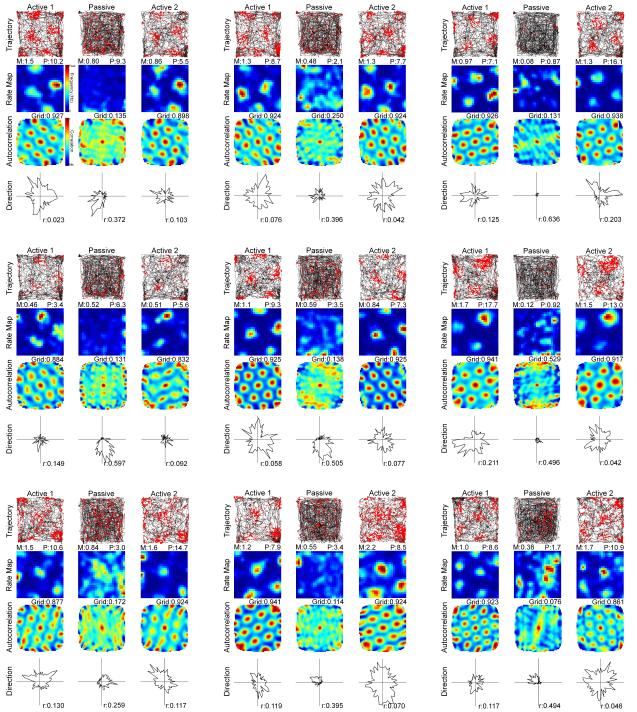
Active sessions were recorded when rats foraged for food pellets in a square environment with a prominent white cue along one wall. During passive sessions rats were placed in a clear plastic cart on wheels (Fig. S1A) and recorded for 20 min of passive movement at speeds which mimicked the speeds experienced in the active sessions. Passive transport significantly decreased grid scores of grid cells (n = 63 cells; Active 1 mean ± standard error: 0.800 ± 0.024; Passive: 0.228 ± 0.020; Active 2: 0.777 ± 0.026; F(2,124) = 237.298, p < 0.001; see Fig. 1A and Fig. 2 for representative cells). Post-hoc analysis showed that grid scores during passive sessions were significantly reduced relative to active sessions (p < 0.001), which were not different from each other (p = 1.0; Fig. 1B top left). Passive transport significantly decreased grid cell mean firing rate (Active 1: 1.414 ± 0.139; Passive: 0.753 ± 0.117; Active 2: 1.546 ± 0.141; F(1.813,112.403) = 31.460, p < 0.001). Post-hoc analysis showed that passive mean firing rates were significantly reduced relative to active sessions (p < 0.001), which were not different from each other (p = 0.428; Fig. 1B top right). Passive transport significantly decreased grid cell location stability (Active 1: 0.339 ± 0.025; Passive: 0.051 ± 0.018; Active 2: 0.335 ± 0.023; F(1.794,111.202) = 69.694, p < 0.001). Post-hoc analysis showed that passive location stability was significantly reduced relative to active sessions (p < 0.001), which were not different from each other (p = 1.0; Fig. 1B middle left). The cross correlation of smoothed rate maps was significantly reduced when comparing active and passive sessions (Act1-Pass) versus active only (Act1-Act2) sessions (Act1-Pass: 0.039 ± 0.014; Act1-Act2: 0.555 ± 0.040; t(62) = −12.490, p < 0.001; Fig. 1B middle right). Inspection of grid cell smoothed rate maps and rate map autocorrelograms across sessions showed a consistent effect of passive movement on all grid cells independent of grid node size and spacing, suggesting that grid cells were impaired independent of the functional module they were recorded from.
Fig. 1.
(A) Representative grid cell response to Active 1 (left column), Passive (middle column), and Active 2 (right column) sessions. Row 1: rat path and individual spikes (red dots). Row 2: smoothed firing rate map. Row 3: autocorrelation map. Row 4: polar plot of firing rate by direction. M = mean firing rate in spikes/s, P = peak firing rate in spikes/s, Grid = grid score, r = mean vector length. (B) Data for grid score (top left), mean firing rate (top right), within-session location stability (middle left), smoothed rate map cross correlation (middle right), mean vector length (bottom left), and a histogram showing the change in mean vector length between Active 1 and Passive sessions (bottom right). Data are represented as mean ± SEM. Asterisks indicate difference from Active 1 and Active 2. *** = p < 0.001. See also Fig. S4 and S5.
Fig. 2.
Representative grid cell responses to Active 1, Passive, and Active 2 sessions as in Fig. 1.
Interestingly, grid cell mean vector length, a measure of directionality, was significantly increased during passive transport (Active 1: 0.139 ± 0.011; Passive: 0.271 ± 0.023; Active 2: 0.139 ± 0.013; F(1.395,86.507) = 29.160, p < 0.001; Fig. 1B bottom left). Post-hoc analysis showed that passive mean vector length was significantly increased relative to active sessions (p < 0.001), which were not different from each other (p = 1.0). Of all grid cells, 78% increased their directionality by a mean of 0.191 and 22% deceased their directionality by a mean of −0.072 (Fig. 1B bottom right). Importantly, these cells were non-conjunctive for grid × HD during active movement as their scores did not pass the 95th percentile criteria for mean vector length and directional stability. Additionally, non-conjunctive grid cells that had an initial low mean vector length (< 0.100) were observed to have a significant increase in mean vector length during the passive session (n = 25 cells; Active 1: 0.066 ± 0.005; Passive: 0.206 ± 0.029; Active 2: 0.101 ± 0.014; F(1.390,33.370) = 14.879, p < 0.001), illustrating that increased mean vector length was found in cells with no directional representation during active movement. Additionally, of the 63 grid cells, only 6 cells exhibited an increase in mean vector length and directional stability that surpassed the 95th percentile criteria to be considered directionally tuned. These results indicate that passive transport selectively disrupts grid characteristics. As discussed below, HD characteristics were spared resulting in directional inputs providing proportionally more drive to grid cell firing and elevating grid cell mean vector length.
Passive transport spares HD cells
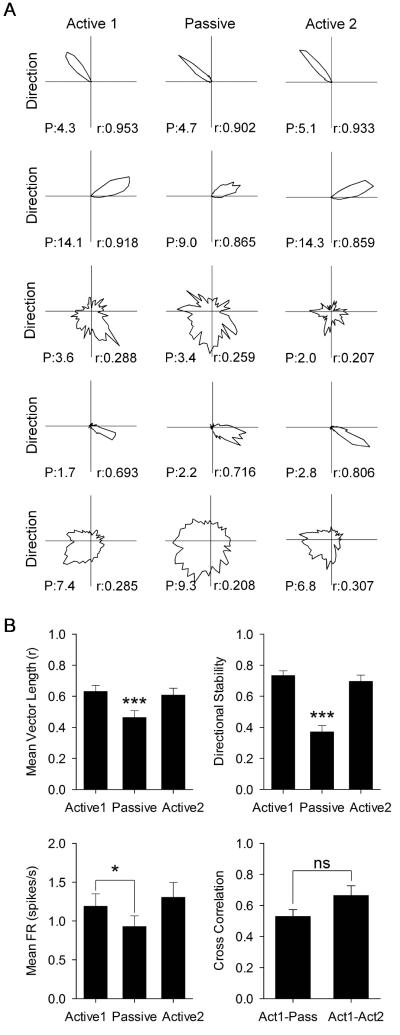
The parahippocampal cortex contains cells with directional tuning [17]; however, many of them had a wide tuning width, low firing rate, and low directional stability. A cell was classified as an HD cell if it passed the 95th percentile of a shuffled distribution for mean vector length (0.211) and directional stability (0.375), which is the mean cross-correlation across the recording session (see Methods). Although passive transport significantly decreased HD cell mean vector length (n = 40 cells; Active 1: 0.631 ± 0.039; Passive: 0.462 ± 0.044; Active 2: 0.608 ± 0.045; F(2,78) = 27.015, p < 0.001; see Fig. 3A for representative cells), cells remained above the criteria to be classified as directional. Post-hoc analysis showed that the passive mean vector length was significantly reduced relative to active sessions (p < 0.001), which were not different from each other (p = 0.869; Fig. 3B top left). Passive transport significantly decreased HD cell directional stability (Active 1: 0.734 ± 0.030; Passive: 0.371 ± 0.040; Active 2: 0.696 ± 0.041; F(1.484,57.863) = 52.690, p < 0.001; Fig. 3B top right). Post-hoc analysis showed that passive directional stability was significantly reduced relative to active sessions (p < 0.001), which were not different from each other (p = 0.591). There are two types of HD cells, “classic” HD cells with a high mean vector length and narrow firing range (<100°) (Fig. 3A cells 1,2, and 4), and “directionally-modulated” cells with a low mean vector length and wide firing range (>100°) (Fig. 3A cells 3 and 5). All cells that remained above the criteria to be considered directional were classic HD cells (19 of 40 cells) and all directionally-modulated cells fell below the criteria to be considered directional during the passive condition. Passive transport significantly decreased HD cell mean firing rate (Active 1: 1.189 ± 0.160; Passive: 0.927 ± 0.139; Active 2: 1.304 ± 0.193; F(1.320,51.477) = 5.545, p = 0.015). Post-hoc analysis showed that the passive mean firing rate was significantly reduced relative to Active 1 (p = 0.043) but not Active 2 (p = 0.051), and active sessions were not different from each other (p = 0.532; Fig. 3B bottom left). The cross correlation of directional firing was significantly reduced when comparing active and passive sessions versus active only sessions (Act1-Pass: 0.529 ± 0.045; Act1-Act2: 0.665 ± 0.062; t(39) = −1.882, p = 0.067; Fig. 3B bottom right). These results indicate that passive transport significantly degraded HD cell characteristics, but did not abolish direction-specific firing. This disruption is likely due to conflicts between vestibular and motor-related self-movement information in the HD circuit, and possibly landmark control if visual acuity was impaired in the cart, although this latter possibility is unlikely because of the transparency of the cart walls.
Fig. 3.
(A) Representative HD cell responses to Active 1, Passive, and Active 2 sessions. Columns are the same as in Fig. 1. Each row is a different cell’s polar plot of firing rate by direction. r = mean vector length. P = peak firing rate in spikes/s. (B) Data for mean vector length (top left), within-session directional stability (top right), mean firing rate (bottom left), and directional firing cross correlation (bottom right). Data are represented as mean ± SEM. Asterisks indicate difference from Active 1 and Active 2 unless otherwise indicated. * = p < 0.05; *** = p < 0.001.
Grid and HD signals are dissociated in conjunctive cells
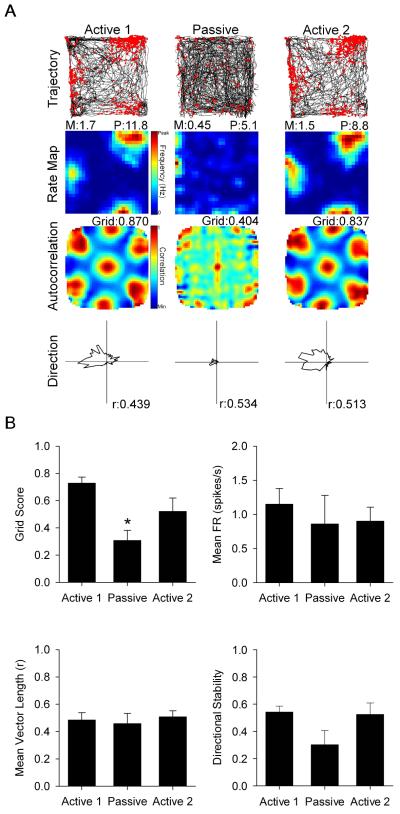
A small sample of conjunctive grid × HD cells were also recorded and demonstrated a similar pattern of results as described above. Thus, passive transport significantly decreased conjunctive cell grid scores (n = 7 cells; Active 1: 0.728 ± 0.044; Passive: 0.309 ± 0.073; Active 2: 0.521 ± 0.099; F(2,12) = 11.776, p = 0.001; see Fig. 4A for a representative cell). Post-hoc analysis showed that passive grid scores were significantly reduced relative to active sessions (p < 0.05), which were not different from each other (p = 0.316; Fig. 4B top left). Passive transport did not influence: 1) conjunctive cell mean firing rate (Active 1: 1.631 ± 0.457; Passive: 1.276 ± 0.688; Active 2: 1.493 ± 0.524; F(1.061,6.366) = 0.198, p = 0.686; Fig. 4B top right), 2) conjunctive cell mean vector length (Active 1: 0.485 ± 0.053; Passive: 0.459 ± 0.074; Active 2: 0.508 ± 0.044; F(2,12) = 0.584, p = 0.573; Fig. 4B bottom left), or 3) conjunctive cell directional stability (Active 1: 0.542 ± 0.044; Passive: 0.303 ± 0.105; Active 2: 0.524 ± 0.084; F(2,12) = 3.724, p = 0.055; Fig. 4B bottom right), although it did approach significance on this last measure. These results indicate that conjunctive grid × HD cell characteristics are influenced in a very similar manner as grid and HD cells.
Fig. 4.
(A) Representative conjunctive grid × HD cell response to Active 1, Passive, and Active 2 sessions. Rows, columns, and abbreviations are the same from Fig. 1. (B) Data for grid score (top left), mean firing rate (top right), mean vector length (bottom left), and within-session directional stability (bottom right). Data are represented as mean ± SEM. Asterisks indicate difference from Active 1 and Active 2. * = p < 0.05.
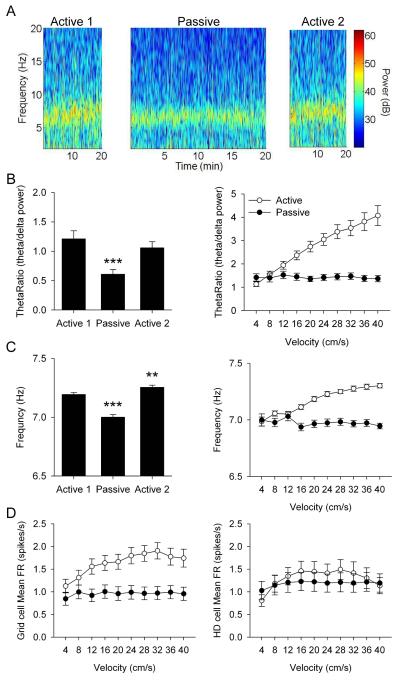
Passive transport degrades theta rhythmicity
Theta rhythmicity in the following analyses ranged from 6 to 10 Hz bands of the LFP, but in separate analyses we also analyzed a 5 to 10 Hz range in case passive transport depressed theta below 6 Hz. However, we found the same results for the 5-10 Hz range as the results presented below for the 6-10 Hz range. Passive transport significantly decreased our measure of theta power - the theta ratio (theta/delta power) in the LFP (n = 33 sessions; Active 1: 1.211 ± 0.135; Passive: 0.610 ± 0.076; Active 2: 1.058 ± 0.104; F(1.458,46.668) = 13.656, p < 0.001; Fig. 5A). Post-hoc analysis showed that the passive theta ratio was significantly reduced relative to active sessions (p < 0.001), which were not different from each other (p = 0.355; Fig. 5B left). Passive transport significantly decreased theta frequency (n = 33 sessions; Active 1: 7.194 ± 0.016; Passive: 7.001 ± 0.023; Active 2: 7.255 ± 0.018; F(2,64) = 73.008, p < 0.001; Fig. 5A). Post-hoc analysis showed that the passive theta frequency was significantly reduced relative to active sessions (p < 0.001), and Active 2 was significantly higher than Active 1 (p = 0.004; Fig. 5C left). Importantly, although theta power and frequency were reduced during passive transport, they were still significantly present in the LFP indicating that theta was not abolished and may still be sufficiently rhythmic to drive grid cell activity. In addition, based on each cell’s spike autocorrelogram the rhythmic activity of grid cell firing was not disrupted during the passive sessions (Fig. S3).
Fig. 5.
(A) Local field potential displaying theta rhythmicity from Active 1 (left), Passive (middle), and Active 2 (right) sessions. (B) Data for theta ratio across sessions (left) and as a function of linear velocity (right). (C) Data for frequency across sessions (left) and as a function of linear velocity (right). (D) Data for mean firing rate of grid cell (left) and HD cell (right) activity as a function of linear velocity. Data are represented as mean ± SEM. Asterisks indicate difference from Active 1 and Active 2. ** = p < 0.01, *** = p < 0.001.
Passive transport disrupts velocity modulation
Previous reports have shown that passive transport does not reduce overall theta rhythmicity, but eliminates linear velocity modulation of theta, resulting in static theta rhythm that does not increase with linear velocity [16]. Because of this previous observation, we investigated the influence of linear velocity on the spatial signals within the parahippocampal cortex. Passive transport eliminated linear velocity modulation of theta power. There were significant main effects of session (F(1,31) = 39.082, p < 0.001), velocity (F(2.289,70.949) = 44.831, p < 0.001), and interaction of session × velocity (F(1.979,61.363) = 40.547, p < 0.001; Fig. 5B right). For post-hoc analysis we analyzed each session using a within-subjects ANOVA to determine linear velocity modulation. Theta ratio was significantly modulated by linear velocity during active movement (F(1.650,52.801) = 55.582, p < 0.001), with a significant linear trend indicating increasing rhythmic power with increasing linear velocity (F(1,32) = 71.649, p < 0.001). Theta ratio was not influenced by linear velocity during passive movement (F(4.381,135.822) = 0.637, p = 0.651).
Passive transport eliminated linear velocity modulation of theta frequency. There were significant main effects for session (F(1,30) = 60.676, p < 0.001), velocity (F(3.101,93.033) = 8.585, p < 0.001), and interaction of session × velocity (F(4.656,139.667) = 17.710, p < 0.001; Fig. 5C right). Theta frequency was significantly modulated by linear velocity during active movement (F(2.710,86.727) = 34.098, p < 0.001), with a significant linear relationship indicating increasing frequency with increasing linear velocity (F(1,32) = 87.575, p < 0.001). Theta frequency was not influenced by linear velocity during passive movement (F(4.350,130.510) = 1.002, p = 0.413). Passive transport eliminated linear velocity modulation of grid cell mean firing rates. There were significant main effects of session (F(1,62) = 21.019, p < 0.001), velocity (F(4.208,260.913) = 10.889, p < 0.001), and interaction of session × velocity (F(4.886,302.910) = 7.230, p < 0.001; Fig. 5D left). Grid cell mean firing rates were significantly modulated by linear velocity during active movement (F(4.491,278.453) = 11.983, p < 0.001) with a significant linear trend indicating increasing firing rate with increasing linear velocity (F(1,62) = 24.123, p < 0.001). In contrast, grid cell mean firing rates were not influenced by linear velocity during passive movement (F(3.211,199.104) = 1.237, p = 0.298). In addition, passive transport did not influence linear velocity modulation of HD cell mean firing rates. There was a significant main effect of velocity (F(3.702,140.684) = 5.042, p = 0.001), but no main effect of session (F(1,38) = 0.579, p = 0.451) or interaction of session × velocity (F(4.117,156.441) = 2.067, p = 0.086; Fig. 5D right). Linear velocity modulation of HD cell mean firing rates was non-linear (F(1,38) = 2.684, p = 0.110). Passive transport spared HD cell linear velocity modulation while eliminating grid cell and theta rhythm linear velocity modulation. Importantly, passive transport did not depress theta rhythm, but rather failed to increase theta rhythm during increasing linear velocity as occurs during self-movement. Throughout passive sessions theta rhythm was maintained at levels comparable to those observed at low linear velocity during active sessions. Therefore, it is not the overall reduction of theta rhythm during passive sessions, but rather the loss of linear velocity modulation of theta rhythm that coincided with the loss of grid cell firing patterns.
Passive transport leads to an increased movement profile
Passive sessions had increased movement profiles relative to active sessions, meaning the rats traveled a longer distance, and had higher mean linear and angular head velocities (AHV). The passive cart was moved in an attempt to reproduce actual movement velocities of the rat. However, the cart was moved continuously as rats remained stationary while the cart was in motion. This procedure helped to ensure that movement of the cart was aligned with the orientation of the rat. To determine whether this different movement profile was affecting grid cell measures, movements during the passive session were reduced by 1) truncating the passive session to equivocate distance traveled, 2) eliminating episodes of linear velocity that were above a threshold to equivocate mean linear velocity, or 3) eliminating episodes of AHV above a threshold to equivocate mean AHV. Reduction of movement profiles during passive sessions failed to improve spatial tuning in grid or HD cells during passive transport relative to active sessions (see supplemental results and Fig. S2).
Discussion
The current study found that passive transport resulted in a significant disruption in the grid-like firing pattern of grid cells, a decrease in overall theta rhythmicity (frequency and power), and sparing of HD cell firing characteristics. Passive transport also resulted in significant disruption of linear velocity modulation of theta frequency, theta power, and grid cell mean firing rates, but spared linear velocity modulation of HD cell mean firing rates. These results indicate that self-movement motor cues generated during active movement are necessary for grid cell activity and linear velocity modulation of signals within the parahippocampal cortex, and rhythmic activity alone is insufficient for generating grid cell firing patterns.
Self-movement cues are critically involved in the generation of many spatially-tuned signals in the brain and the current study provides further evidence of their importance in spatial cognition. During passive transport vestibular and optic flow cues were spared but proprioceptive and motor efference cues became decoupled from the rat’s movement and position within the environment. Vestibular inputs are necessary for generating the HD signal as manipulations that interfere with the vestibular system disrupt direction-specific firing across the HD circuit [18, 19, 20]. Except for the maintenance of a stable preferred firing direction when entering a novel environment [21], other HD cell characteristics, such as mean vector length, tuning width, and firing rate, are largely unaffected by passive transport [22, 23]. Although we found a significant decrease in HD characteristics during passive transport, HD cells maintained significant directionality indicating that vestibular inputs were spared. Passive sessions were 20 min in length with near continuous movement, resulting in a much longer duration and total distance traveled than in previous studies, which may produce more error in the cell’s preferred firing direction. Additionally, rats were not restrained during passive transport in the cart, allowing for the ability to make small movements, most of which consist of turning with little or no linear displacement. These movements produce conflict between self-movement cues that could degrade the HD signal.
Inactivation of the vestibular system has also been shown to influence linear velocity modulation of theta power in the MEC [24]. In this study, vestibular inactivation reduced linear velocity modulation of theta power in parallel with reduced movement velocity. Theta power and frequency are modulated by linear velocity in the MEC [11, 12]. Therefore, the reduction in linear velocity-modulated theta power observed may in part be attributed to reduced movement velocity during recording sessions rather than entirely a result of reduced vestibular modulation. It is likely that vestibular information has some influence or modulatory effect upon theta power; however, the current study indicates that linear velocity modulation of theta power is highly dependent upon motor related self-movement cues. Passive transport produces a similar result upon theta power in the hippocampus [16]. However, a notable difference was that although passive transport significantly reduced the linear velocity modulation of theta power, a weak relationship still persisted. In contrast, we found that passive transport abolished the linear velocity modulation of theta power in the parahippocampal cortex. There are two possible explanations for this difference. First, our experiments used near continuous movements and moved in all linear and angular directions covering the entire environment (see Fig. S2), whereas Terrazas et al., [16] used stereotyped movements restricted to a circular track. This difference would allow for highly predictable location by the animal, which could be easily identified with visual cues. Stereotyped movement predictability may have allowed for compensation from other spatial cues after the loss of self-movement motor cues, whereas our methods may not have been permissive of this compensation. Second, the hippocampus and MEC play different roles in spatial processing [25], and it is possible they process self-movement cues differently, resulting in the MEC being more reliant upon motor related self-movement cues than the hippocampus. This interpretation is plausible given the recent discovery of speed cells within the MEC [26].
Theta rhythmicity conveys necessary information for generating the grid-like firing pattern of grid cells. The medial septal area is a structure that projects to and drives MEC theta rhythmicity [27] and inactivation abolishes grid cell firing patterns [13, 14]. These studies reported that even a 50% reduction in theta power was sufficient to disrupt grid cell activity. When we assessed theta power across the entire passive session we found an overall 50% decrease in theta power; however, when we divided the passive session into groups of varying movement velocity, theta power was never decreased below low velocity levels observed during active sessions. Instead, passive transport resulted in theta power maintaining a consistent level across the session independent of the movement velocity of the rat. Therefore, passive transport did not depress theta power, but failed to allow power to increase with the movement velocity of the rat, as it does during active movement. It is unlikely that the “reduction” of overall theta power during passive movement abolished grid cell activity, but instead it was the result of the selective loss of theta rhythmicity modulation by movement velocity, which is also known to impair performance on a spatial alternation task [28]. Our results provide evidence that self-movement motor cues are necessary for modulating theta rhythmicity within the parahippocampal cortex, but they do not indicate the sources of this information. Velocity information may be conveyed by medial septal theta activity directly [27]. Alternatively, the parietal cortex, whose activity has been associated with self-motion and movement speeds [29, 30], may be responsible for the theta velocity modulation in the parahippocampal cortex.
It is possible that our results are caused by a change in reference frame. Grid cells have been shown to change their response within the same environment when significant changes are made to the layout [31]. Grid cells may no longer be using the large square environment as their reference frame but instead were using the cart, which is smaller than many grid cell firing fields. However, this possibility is unlikely because 1) HD cells maintain their orientation relative to the larger environment, 2) grid cell generation is dependent upon HD cells [10], and 3) grid cells and HD cells responded in coherence during environmental manipulations [32]. If grid cells adopted the cart as a reference frame then this would result in a dissociation of reference frames across spatially-tuned cells, because HD cells maintained their reference frame to the larger environment. These observations suggest that HD and grid cells maintained the same reference frame in the passive condition [however see 33]. If a grid cell was representing location relative to inside the cart and the cart is smaller than the size of many grid cell firing fields, then the rat would be restricted from entering or leaving a firing field while in the cart. This occurrence would result in a grid cell always being active if the firing field was present in the cart, or always being inactive if the firing field was not present in the cart. We found that grid cell mean firing rates decreased by about 50% and firing was randomly dispersed throughout the square environment, indicating that no cell was permanently on or off while the rat was in the cart. Finally, the rat’s inability to make contact with the wall of the environment, which could serve as the reference frame, may cause a disruption in the rat’s ability to locate itself within the environment. The inability to contact the wall could disrupt border cell activity, which is involved in correcting the accumulation of error in grid cell firing over time [34]. If disrupted border cell activity was the cause of impaired grid cell firing patterns, then we should see an accumulation of error over time in grid patterns during passive sessions. When the activity of each grid cell was plotted for the first minute of passive sessions, grid cells did not fire relative to the location of grid nodes exhibited during active sessions. Grid cells sometimes had firing outside of grid node locations, and at other times lacked firing inside grid node locations, demonstrating random firing throughout the environment. Therefore, grid cell activity did not degrade over time due to an accumulation of error from loss of border cell activity, but was abolished from the beginning of the passive session.
It is also possible that grid cell activity was disrupted because the rats had no motivation to encode their spatial orientation during the passive sessions. However, it is unlikely that rats disengaged from spatial encoding during the passive sessions because HD cells maintained their spatial representation and theta rhythmicity was still present. Hippocampal place cells have also been shown to maintain spatial coding during passive transport, although their spatial representation may be distorted or remapped [16]. Grid cell activity is dependent upon HD cell input [10], medial septal area theta input [13, 14], and hippocampal input [35]. During passive transport grid cells continue to receive all of these spatially-tuned inputs that drive grid cell firing. There was an observed decrease in grid cell mean firing rates, but they were only decreased by about 50% relative to active sessions. The most likely explanation for the loss of grid cell firing patterns during the passive session is that the spatial signals driving grid cells are no longer in conjunction with one another. The disconnection occurs because the HD signal is spared, but the theta rhythm, although present, is no longer modulated by velocity. The absence of this modulation results in a change in the nature of information that the theta rhythm is conveying. The theta rhythm is no longer accurately representing the linear velocity/displacement of the rat, whereas HD cells are still accurately representing angular displacement. This disconnection of linear movement from angular displacement leads to a disruption in the representation of distance traveled within two-dimensions, which is the information that grid cells are presumably encoding.
In conclusion, grid cell activity is dependent upon self-movement motor cues, which also modulate theta power in a velocity dependent manner. Passive movement selectively disrupts velocity modulation while maintaining theta rhythmicity observed at low movement velocity. This manipulation selectively disrupts grid cells while sparing HD cells. These results provide further evidence of the importance of self-movement cues in the generation of all spatially-tuned cells in the brain and their foundation in spatial processing.
Experimental Procedures
Subjects were five female Long-Evans rats. All procedures were performed in compliance with institutional standards. Rats were implanted with a microdrive with four tetrodes in the medial entorhinal cortex (MEC). Rats were trained to forage for food in a square box with a white cue attached to one wall. Initial 20 min recording sessions were done to identify grid cells (Active 1). Then rats were placed in a clear cart (see Fig. S1A) and pushed for a 20 min recording session to parallel active conditions (Passive). We attempted to move the cart in the direction of the rat’s orientation. If the rat turned in the cart it was stopped momentarily and movement was continued in the direction of the rat’s orientation. Rats were recorded again under active movement (Active 2). Electrodes were advanced at the end of each testing day. Rats experienced the passive manipulation across multiple days. There was no experience dependent effect of passive manipulation on grid cells. During the passive session, rats typically remained stationary while the cart was in motion and explored when it was stationary resulting in the cart being moved in a near continuous manner to reduce self-movement of the rat. At the end of the experiment all rats were sacrificed, and their brains were removed to determine recording location within the parahippocampal cortex (see Fig. S1B).
Spike sorting was conducted using SpikeSort3D. Cell activity was analyzed using custom Matlab scripts to determine position and head direction characteristics. All measures were analyzed using repeated measures ANOVAs and Bonferroni post-hoc comparisons or paired-sample t-tests. The Greenhouse-Geisser correction was used when sphericity was violated. Rat’s location and orientation was tracked by an overhead camera at 60 Hz using two LEDs mounted on the headstage. Location was determined by sorting the environment into 5 × 5 cm bins and smoothing using a Gaussian function for the surrounding 5 × 5 bins. Grid cell mean firing rate was computed from the smoothed rate maps by dividing the number of spikes by the amount of time per bin. Spatial autocorrelation maps were computed from the smoothed rate maps by correlating the smoothed rate map with a copy of itself shifted to all possible combinations of x-y offsets. Grid cells were visually identified. Grid cell grid score was computed from the autocorrelation maps by correlating the autocorrelation map with itself rotated in 6° increments from 0 to 180° and subsequently fitting a sinusoid to the series of correlations. For these rotations a circular sample of the autocorrelation map was used with the central peak removed and a moving radius for the outer diameter of the circular sample. Location stability was determined by dividing the session in half and correlating the smoothed rate maps for each half. Direction was determined by sorting the environment into sixty 6° bins. Head direction cell mean firing rate was computed by dividing the number of spikes by the amount of time in each bin. Mean vector length was computed to determine the directionality of cell firing. Directional stability was computed as the mean cross-correlation between the directional bins across four quarters of the session. Cells were classified as head direction if the mean vector length (> 0.211) and directional stability (> 0.375) scores exceeded the 95th percentile of shuffled neural data.
Theta frequency and power from the local field potential were computed using the Matlab function spectrogram, which conducts a Fourier transform using a Hanning window with a resolution of 1 Hz (i.e., 1 sec temporal window) between bands of 0 to 20 Hz in 0.25 Hz steps. Theta frequency was the band with the maximum power between 6-10 Hz, and maximum frequencies outside of this range were excluded. Theta power was measured using a theta ratio of instantaneous theta power (6-10 Hz) divided by mean delta power (2-4 Hz) across the session. The theta ratio was used to adjust for variations in local field potential power [13, 16].
To measure the linear velocity modulation of cell mean firing rates, theta frequency, and theta power, we calculated the instantaneous linear velocity by measuring the x and y displacement between successive video samples. Then we measured mean linear velocity over a 5 sec window, sliding 1 sec at a time from the beginning to the end of a session. For cell mean firing rates, we summed the spikes per 5 sec window and calculated the firing rate for that window. For theta frequency and power, we generated a power spectrogram per 5 sec window and calculated theta frequency and power for that window. Finally, we measured the firing rate and theta frequency and power for all windows and calculated the overall mean for all windows in each bin.
A detailed description of all experimental procedures can be found in the supplemental experimental procedures.
Supplementary Material
Acknowledgements
The authors would like to thank Jennifer Marcroft for technical support and Jeremy Barry for feedback on data analysis. This research was supported through the National Institute of Health grant NS053907 (J.S.T.)
Footnotes
Author Contributions
S.S.W. and J.S.T. designed the experiments. S.S.W. collected the data. S.S.W., M.L.M., and B.J.C. analyzed the data. All authors contributed to writing the manuscript.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Fyhn M, Molden S, Witter MP, Moser EI, Moser MB. Spatial representation in the entorhinal cortex. Science. 2004;305:1258–1264. doi: 10.1126/science.1099901. [DOI] [PubMed] [Google Scholar]
- 2.Hafting T, Fyhn M, Modlen S, Moser MB, Moser EI. Microstructure of a spatial map in the entorhinal cortex. Nature. 2005;436:801–806. doi: 10.1038/nature03721. [DOI] [PubMed] [Google Scholar]
- 3.Boccara CN, Sargolini F, Thoresen VH, Solstad T, Witter MP, Moser EI, Moser MB. Grid cells in pre- and parasubiculum. Nature Neurosci. 2010;13:987–994. doi: 10.1038/nn.2602. [DOI] [PubMed] [Google Scholar]
- 4.McNaughton BL, Battaglia FP, Jensen O, Moser EI, Moser MB. Path integration and the neural basis of the ‘cognitive map’. Nat. Rev. Neurosci. 2006;7:663–678. doi: 10.1038/nrn1932. [DOI] [PubMed] [Google Scholar]
- 5.Moser EI, Kropff E, Moser MB. Place cells, grid cells, and the brain’s spatial representation system. Annu. Rev. Neurosci. 2008;31:69–89. doi: 10.1146/annurev.neuro.31.061307.090723. [DOI] [PubMed] [Google Scholar]
- 6.Hasselmo ME, Giocomo LM, Zilli EA. Grid cell firing may arise from interference of theta frequency membrane potential oscillations in single neurons. Hippocampus. 2007;17:1252–1271. doi: 10.1002/hipo.20374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Burgess N, Barry C, O’Keefe J. An oscillatory interference model of grid cell firing. Hippocampus. 2007;17:801–812. doi: 10.1002/hipo.20327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Sargolini F, Fyhn M, Hafting T, McNaughton BL, Witter MP, Moser MB, Moser EI. Conjunctive representation of position, direction, and velocity in the entorhinal cortex. Science. 2006;312:758–762. doi: 10.1126/science.1125572. [DOI] [PubMed] [Google Scholar]
- 9.Taube JS. The head direction signal: origins and sensory-motor integration. Annu. Rev. Neurosci. 2007;30:181–207. doi: 10.1146/annurev.neuro.29.051605.112854. [DOI] [PubMed] [Google Scholar]
- 10.Winter SS, Clark BJ, Taube JS. Disruption of the head direction cell network impairs the parahippocampal grid cell signal. Science. 2015;347:870–874. doi: 10.1126/science.1259591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Jeewajee A, Barry C, O’Keefe J, Burgess N. Grid cells and theta as oscillatory interference: electrophysiological data from freely moving rats. Hippocampus. 2008;18:1175–1185. doi: 10.1002/hipo.20510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Newman EL, Gillet SN, Climer JR, Hasselmo ME. Cholinergic blockade reduces theta-gamma phase amplitude coupling and speed modulation of theta frequency consistent with behavioral effects on encoding. J. Neurosci. 2013;33:19635–19646. doi: 10.1523/JNEUROSCI.2586-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Brandon MP, Bogaard AR, Libby CP, Connerney MA, Gupta K, Hasselmo ME. Reduction of theta rhythm dissociates grid cell spatial periodicity from directional tuning. Science. 2011;332:595–599. doi: 10.1126/science.1201652. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Koenig J, Linder AN, Leutgeb JK, Leutgeb S. The spatial periodicity of grid cells is not sustained during reduced theta oscillations. Science. 2011;332:592–595. doi: 10.1126/science.1201685. [DOI] [PubMed] [Google Scholar]
- 15.Giocomo LM, Zilli EA, Fransen E, Hasselmo ME. Temporal frequency of subthreshold oscillations scales with entorhinal grid cell field spacing. Science. 2007;315:1719–1722. doi: 10.1126/science.1139207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Terrazas A, Krause M, Lipa P, Gothard KM, Barnes CA, McNaughton BL. Self-motion and the hippocampal spatial metric. J. Neurosci. 2005;25:8085–8096. doi: 10.1523/JNEUROSCI.0693-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Burgalossi A, Herfst L, von Heimendahl M, Forste H, Haskic K, Schmidt M, Brecht M. Microcircuits of functionally identified neurons in the rat medial entorhinal cortex. Neuron. 2011;70:773–786. doi: 10.1016/j.neuron.2011.04.003. [DOI] [PubMed] [Google Scholar]
- 18.Stackman RW, Taube JS. Firing properties of head direction cells in the rat anterior thalamic nucleus: dependence on vestibular input. J. Neurosci. 1997;17:4349–4358. doi: 10.1523/JNEUROSCI.17-11-04349.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Stackman RW, Clark AS, Taube JS. Hippocampal spatial representations require vestibular input. Hippocampus. 2002;12:291–303. doi: 10.1002/hipo.1112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Muir GM, Brown JE, Carey JP, Hirvonen TP, Della Santina CC, Minor LB, Taube JS. Disruption of the head direction cell signal after occlusion of the semicircular canals in the freely moving chinchilla. J. Neurosci. 2009;29:14521–14533. doi: 10.1523/JNEUROSCI.3450-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Stackman RW, Golob EJ, Bassett JP, Taube JS. Passive transport disrupts directional path integration by rat head direction cells. J. Neurophysiol. 2003;90:2862–2874. doi: 10.1152/jn.00346.2003. [DOI] [PubMed] [Google Scholar]
- 22.Bassett JP, Zugaro MB, Muir GM, Golob EJ, Muller RU, Taube JS. Passive movements of the head do not abolish anticipatory firing properties of head direction cells. J. Neurophysiol. 2005;93:1304–1316. doi: 10.1152/jn.00490.2004. [DOI] [PubMed] [Google Scholar]
- 23.Yoder RM, Clark BJ, Brown JE, Lamia MV, Valerio S, Shinder ME, Taube JS. Both visual and idiothetic cues contribute to head direction cell stability during navigation along complex routes. J. Neurophysiol. 2011;105:2989–3001. doi: 10.1152/jn.01041.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Jacob PY, Poucet B, Liberge M, Save E, Sargolini F. Vestibular control of entorhinal cortex activity in spatial navigation. Front. Integr. Neurosci. 2014;8:1–9. doi: 10.3389/fnint.2014.00038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Winter SS, Koppen JR, Ebert TBN, Wallace DG. Limbic system structures differentially contribute to exploratory trip organization of the rat. Hippocampus. 2013;23:139–152. doi: 10.1002/hipo.22075. [DOI] [PubMed] [Google Scholar]
- 26.Kropff E, Carmichael JE, Moser MB, Moser EI. Speed cells in the medial entorhinal cortex. Nature. 2015;523:419–424. doi: 10.1038/nature14622. [DOI] [PubMed] [Google Scholar]
- 27.Jeffery KJ, Donnett JG, O’Keefe J. Medial septal control of theta-correlated unit firing in the entorhinal cortex of awake rats. Neuroreport. 1995;6:2166–2170. doi: 10.1097/00001756-199511000-00017. [DOI] [PubMed] [Google Scholar]
- 28.Richard GR, Titiz A, Tyler A, Holmes GL, Scott RC, Lenck-Santini PP. Speed modulation of hippocampal theta frequency correlates with spatial memory performance. Hippocampus. 2013;23:1269–1279. doi: 10.1002/hipo.22164. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Whitlock JR, Pfuhl G, Dagslott N, Moser MB, Moser EI. Functional split between parietal and entorhinal cortices in the rat. Neuron. 2012;73:789–802. doi: 10.1016/j.neuron.2011.12.028. [DOI] [PubMed] [Google Scholar]
- 30.Wilber AA, Clark BJ, Forster TC, Tatsuno M, McNaughton BL. Interaction of egocentric and world-centered reference frames in the rat posterior parietal cortex. J. Neurosci. 2014;34:5434–5446. doi: 10.1523/JNEUROSCI.0511-14.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Derdikman D, Whitlock JR, Tsao A, Fyhn M, Hafting T, Moser MB, Moser EI. Fragmentation of grid cell maps in a multicompartment environment. Nature Neurosci. 2009;12:1325–1332. doi: 10.1038/nn.2396. [DOI] [PubMed] [Google Scholar]
- 32.Solstad T, Boccara CN, Kropff E, Moser MB, Moser EI. Representation of geometric borders in the entorhinal cortex. Science. 2008;322:1865–1868. doi: 10.1126/science.1166466. [DOI] [PubMed] [Google Scholar]
- 33.Whitlock JR, Derdikman D. Head direction maps remain stable despite grid map fragmentation. Front. Neural Circuits. 2012;6:1–10. doi: 10.3389/fncir.2012.00009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Hardcastle K, Ganguli S, Giocomo LM. Environmental boundaries as an error correction mechanism for grid cells. Neuron. 2015;86:827–839. doi: 10.1016/j.neuron.2015.03.039. [DOI] [PubMed] [Google Scholar]
- 35.Bonnevie T, Dunn B, Fyhn M, Hafting T, Derdikman D, Kubie JL, Roudi Y, Moser EI, Moser MB. Grid cells require excitatory drive from the hippocampus. Nat Neurosci. 2013;16:309–317. doi: 10.1038/nn.3311. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.