Optimization of Multi-Stage Dynamic Treatment Regimes Utilizing Accumulated Data

Abstract

In medical therapies involving multiple stages, a physician’s choice of a subject’s treatment at each stage depends on the subject’s history of previous treatments and outcomes. The sequence of decisions is known as a dynamic treatment regime, or treatment policy. We consider dynamic treatment regimes in settings where each subject’s final outcome can be defined as the sum of longitudinally observed values, each corresponding to a stage of the regime. Q-learning, which is a backward induction method, is used to first optimize the last stage treatment, then sequentially optimize each previous stage treatment until the first stage treatment is optimized. During this process, model-based expectations of outcomes of late stages are used in the optimization of earlier stages. When the outcome models are misspecified, bias can accumulate from stage to stage and become severe, especially when the number of treatment stages is large. We demonstrate that a modification of standard Q-learning can help reduce the accumulated bias. We provide a computational algorithm, estimators, and closed-form variance formulas. Simulation studies show that the modified Q-learning method has a higher probability of identifying the optimal treatment regime even in settings with mis-specified models for outcomes. It is applied to identify optimal treatment regimes in a study for advanced prostate cancer, and to estimate and compare the final mean rewards of all the possible discrete two-stage treatment sequences.

1. Introduction

A dynamic treatment regime is a mathematical formalism for what physicians do routinely when making therapeutic decisions sequentially. The physician chooses a first treatment using diagnostic information, administers it, and observes the patient’s response. A second decision is based on the diagnostic information, first treatment, and newly observed response. This process may be continued, using the patient’s history up to the current stage for each decision, until either a satisfactory outcome is achieved or no further treatment is considered acceptable. The dynamic treatment regime is the sequence of decision rules embedded in the sequence of alternating observations and treatments.

Methods for evaluating dynamic treatment regimes have been used increasingly for patients undergoing long-term care involving multi-stage therapies. It is challenging to identify optimal decision rules in such multi-stage treatment settings because of the complicated relationships between the alternating sequences of observed outcomes and treatments. The decision at each treatment stage depends on all observed historical data, and influences all future outcomes and treatments. In turn, outcomes at each stage are affected by all previous treatments, and influence all future treatment decisions. It is well-known that simply optimizing the immediate outcome of each stage, which is called a myopic or greedy optimization, may not achieve the best final outcome. Simulation studies in Section 3 demonstrate this point.

Despite these complications, many approaches have been proposed to identify, estimate, or optimize dynamic treatment regimes based on observational data. Most methods have their origins in the seminal papers by Robins and colleagues [1, 2, 3, 4, 5] and Murphy [6], including inverse probability of treatment weighting (IPTW) and g-estimation for structural nested models. Many variants of IPTW and g-estimation have been proposed [7, 8, 9, 10, 11, 12, 13, 14, 15, 16]. They show the importance, when evaluating causal treatment effects, of correcting for bias introduced by physicians’ adaptive treatment decisions based on each patient’s current health status. Recent applications include estimation of survival for dynamic treatment regimes in a sequentially randomized prostate cancer trial [17], and in a partially randomized trial of chemotherapy for acute leukemia [18]. Clinical trial designs that compare multi-stage treatment strategies by adaptively re-randomizing patients have been proposed [19, 20, 21, 22].

We address the multi-stage decision making problem in settings where the final outcome to be optimized can be expressed as the sum of values observed at each stage. An important application is that where survival time is the final outcome and the cumulative value at each stage is the patient’s current survival time. Another application is a study where the cumulative outcome is the amount of time that the patient’s health index was within a specific target range. In such situations, a natural approach is to assume a conditional model for the outcome of each stage. However, due to the dependence of each outcome on previous treatments and outcomes, this approach may lead to a very complex model for the final outcome, which in turn makes global optimization of the treatment sequence difficult or intractable.

An alternative approach, called Q-learning [23, 24, 25, 26, 27, 28, 29, 30], is to use backward induction [31] to first optimize the last stage treatment, then sequentially optimize the treatment in each previous stage. At each stage, a model is assumed for the cumulative rewards from this stage onward, with all the future stages already optimized. This approach is well-suited for global optimization, but depends on the correct specification of reward models at all stages. At the optimization at each stage, misspecified models cause bias, and a severe problem is that bias is carried forward from each stage to the optimization of the previous stage. Consequently, even small bias at each stage may produce a large cumulative bias for the optimization of the entire regime.

In this article, we show that a slight modification of standard Q-learning can reduce cumulative bias. At each stage, when computing the rewards from those “already-optimized” future stage, standard Q-learning uses the maximum of model-based values. The modified Q-learning uses the actual observed rewards plus estimated loss due to suboptimal actions. If the optimal actions were actually taken for all future stages, then the estimated loss is zero, and the actual observed rewards are used. Consequently, comparing with standard Q-learning, the modified Q-learning is more likely to use the originally observed rewards instead of model-based ones, thus it is more robust to model misspecification, and less likely to carry the bias from stage to stage during the backward reduction. This is demonstrated by simulation studies in Section 3.

When applying the modified Q-learning to a prostate cancer study in Section 4, we provide a by-product that is convenient for the practical use of both standard and modified Q-learning. In many situations where the treatment options are discrete, it is often of interest to estimate the mean rewards of all the treatment sequences. However, Q-learning does not require fully specified reward functions for all possible treatment strategies. This helps achieving simplicity. On the other hand, it fails to provide all the estimates of interest in the above situation. Therefore, this seems to be a shortcoming of Q-learning. Nevertheless, in Section 4.3, we provide a trick to use Q-learning (standard or modified) to estimate the mean rewards for all possible multi-stage (discrete) treatment sequences, and make inference about the reward differences between any two treatment sequences. This technique of Q-learning application is useful in practice, but has not appeared in the literature, to the best of our knowledge.

The article is organized as follows. The modified Q-learning method and its properties are described in Section 2. Its performance for identifying optimal treatment regimes in settings with misspecified reward models is evaluated by simulation in Section 3. We apply the method in Section 4 to analyze data from a prostate cancer trial. A summary and discussion of the modified Q-learning method are presented in Section 5. Mathematical details are provided in Appendices.

2. Backward Induction For Sequential Treatment Optimization

We use the framework of potential (counterfactual) outcomes of all possible treatment options for each individual, and make the usual assumptions [32] that (i) an individual’s potential outcome under the treatment actually received is the observed outcome (consistency), (ii) given the history at each stage, the treatment decision is independent of the potential outcomes (sequential randomization or no unmeasured confounders), and (iii) all treatment strategies being considered have a positive probability of being observed (positivity). To identify the optimal action at each stage of backward induction, the estimated reward is computed for each possible action assuming that the actions at all future stages will be optimal. This is done by fitting a parametric model for the counterfactual future reward as a function of actions and current history. The final cumulative reward is the estimate of what the patient’s total reward would be if all actions were optimal. In the sequel, we will use the terms ’payoff’ and ’reward’ interchangeably to mean the same thing.

2.1. Notation and Method

For each subject i = 1,⋯, n and stage s = 1,⋯, K, where n denotes the sample size, and K denotes the total number of multiple stages, let Z_i,s denote the time-dependent covariates measured at the beginning of s-th stage, A_i,s the treatment or action, and Y_i,s the observed outcome. Without loss of generality, we assume that larger values of Y_i,s are preferable. We denote the corresponding vectors of these variables through s stages by Z̄_i,s = (Z_i,1,⋯, Z_i,s), Ā_i,s = (A_i,1,⋯, A_i,s), and Ȳ_i,s = (Y_i,1,⋯, Y_i,s). At stage 1, the subject’s history is simply H̄_i,1 = Z_i,1. For each subsequent stage s ≥ 2 the history is H̄_i,s = (Z̄_i,s, Ā_i,s−1, Ȳ_i,s−1). We denote the optimal action at stage s by $A_{i,s}^{\mathit{\text{opt}}}$ and the associated counterfactual outcome that would occur if this optimal action were taken by $Y_{i,s}^{*}$ For all s < K, we define the counterfactual cumulative outcome for stages s through K under (A_i,s, $A_{i,s+1}^{\mathit{\text{opt}}},\cdots ,A_{i,K}^{\mathit{\text{opt}}}$) as follows:

$$Q_{i,s}^M={}_{\mathit{\text{def}}}{Y}_{i,s}+\sum _{r=s+1}^K{Y}_{i,r}^{*},$$ (1)

where each $A_{i,j}^{\mathit{\text{opt}}}$ is conditional on all the historic information observed prior to stage j, including previous treatments and responses. For simplicity, we have suppressed conditional notation. In words, this equation says that

$$[\text{Current}+\text{FuturePayoff}]=[\text{Observed Stage s Outcome}]+[\text{Best Possible Future Outcomes After Stage s}]$$

That is, $Q_{i,s}^M$ is the future payoff, starting at stage s, if all actions from s + 1 to K are optimized, but the actual (possibly suboptimal) action A_i,s is taken at stage s. For the final stage, because there are no future actions to optimize, we define $Q_{i,K}^M=Y_{i,K}$. In our notation $Q_{i,s}^M’s$ are random variables, rather than mean functions as denoted by other authors.

We next define Δ_i,s to be the total future loss from stages s to K if action A_i,s is taken instead of $A_{i,s}^{\mathit{\text{opt}}}$ while all actions from stage s + 1 to K are optimal. Thus, if $A_{i,s}=A_{i,s}^{\mathit{\text{opt}}}$ then Δ_i,s = 0, whereas if A_i,s is not optimal then Δ_i,s > 0. This Δ_i,s is essentially Murphy’s regret function [6]. Robins defined a similar blip function by comparison with a “zero" treatment instead of the optimal one [5]. We use the counterfactual in (1) and loss Δ_i,s to define the cumulative future reward to patient i, from stages s to stage K, for taking the optimal action from stage s onward as

$$R_{i,s}={}_{\mathit{\text{def}}}{Q}_{i,s}^M+{\mathrm{\Delta }}_{i,s}I(A_{i,s}\ne A_{i,s}^{\mathit{\text{opt}}})=Y_{i,s}+\sum _{r=s+1}^K{Y}_{i,r}^{*}+{\mathrm{\Delta }}_{i,s}I(A_{i,s}\ne A_{i,s}^{\mathit{\text{opt}}}).$$ (2)

The basic idea is that the reward R_i,s is obtained from $Q_{i,s}^M$ by adding back the future loss due to taking a suboptimal action at stage s. For example, if Y_i,s is the increment in survival time for stage s, then R_i,s is the sum of the stagewise survival times from stage s onward associated with all current and future actions being optimal, given the past treatment and response history.

Given the above structure for the future reward R_i,s at each stage s, the counterfactual cumulative outcome in equation (1) can be written in the more compact form

$$Q_{i,s}^M=Y_{i,s}+R_{i,s+1},\text{for}s<K.$$ (3)

If all optimal actions and Δ_i,s’s were known, one could simply work backward and compute R_i,s for each s = K, K − 1,⋯, 1, and thus obtain the final payoff R_i,1. To derive $A_{i,K}^{\mathit{\text{opt}}},\cdots ,A_{i,1}^{\mathit{\text{opt}}}$ in the steps of the backward induction, we will exploit the decomposition given by equations (1) – (3) by assuming an additive parametric regression model for $Q_{i,s}^M$ as a function of A_i,s and the most recent history ${\overline{H}}_{i,s}^M={(Z_{i,s-1},Z_{i,s},Y_{i,s-1},A_{i,s-1})}^T$. We formulate the regression model in terms of ${\overline{H}}_{i,s}^M$ rather than the complete history H̄_i,s, to control the number of parameters so that the method may be applied feasibly. This requires us to make a Markovian assumption. The fitted model will provide estimates of the Δ_i,s’s and thus identify the $A_{i,s}^{\mathit{\text{opt}}}$ values and thus the optimal payoffs.

Appendices A provides details of the parametric regression model that we assume for $Q_{i,s}^M$. In particular, Appendix D provides an illustration for a special case of three treatment stages with three treatment options each stage. An important aspect of our approach is that we assume a regression model for $Q_{i,s}^M$ rather than assuming simple models for Y_s, 1 ≤ s ≤ K, which could result in a model for $Y={\sum }_{s=1}^K{Y}_s$ that may be too complicated for optimization.

2.2. Backward Induction

Our method requires the the cumulative causal effect of treatment j versus l at stage s, which we define formally, for j > l, as

$$D_{i,s}(j,l)=Q_{i,s}^M(A_{i,s}=j,{\overline{H}}_{i,s}^M)-Q_{i,s}^M(A_{i,s}=l,{\overline{H}}_{i,s}^M)$$

In words, this cumulative causal effect is

$$[\text{Current}+\text{Future Payoff for Action}j\text{at Stage}s]-[\text{Current}+\text{Future Payoff for Action}l\text{at Stage}s].$$

Substituting the parameter estimates obtained from the fitted regression model, given in Appendix A, gives the estimated cumulative payoff, ${\hat{Q}}_{i,s}^M$, estimated causal effects, D̂_i,s(j, l), and estimated cumulative future rewards R̂_i,s. The backward induction is carried out as follows:

• Step 1. Start with s = K and set $Q_{i,K}^M=Y_{i,K}$.

• Step 2. For the current step s,

  • Step 2.1 Fit the regression model (15) for $Q_{i,s}^M$ to obtain (β̂_s, ${\hat{\psi }}_s^{(2)},\cdots ,{\hat{\psi }}_s^{(J_s)}$) and thus ${\hat{Q}}_{i,s}^M$.
  • Step 2.2 Use the estimated causal effects D̂_i,s(j, l) given by (16) to identify the estimated optimal action ${Â}_{i,s}^{\mathit{\text{opt}}}={\text{argmax}}_{1\le j\le J_s}\{{\text{max}}_{l\ne j}{\hat{D}}_{i,s}(j,l)\}$.
  • Step 2.3 Define the estimated future loss due to taking action A_i,s to be ${\hat{\mathrm{\Delta }}}_{i,s}={}_{\mathit{\text{def}}}{Y}_{i,s}{}_{\mathit{\text{def}}}{Y}_{i,s}{}_{\mathit{\text{def}}}{Y}_{i,s}({Â}_{i,s}^{\mathit{\text{opt}}})-{\hat{Q}}_{i,s}^M(A_{i,s})$. Step 2.4 By(2), Step 2.3 gives the estimate ${\hat{R}}_{i,s}={}_{\mathit{\text{def}}}{Q}_{i,s}^M+{\hat{\mathrm{\Delta }}}_{i,s}I(A_{i,s}\ne {Â}_{i,s}^{\mathit{\text{opt}}})$.

• Step 3. If s > 1, decrement s → s − 1. By (3), set $Q_{i,s}^M=Y_{i,s}+{\hat{R}}_{i,s+1}$, and go to Step 2.1 If s = 1, stop.

At the end of these steps, ${Â}_{i,1}^{\mathit{\text{opt}}},\cdots ,{Â}_{i,K}^{\mathit{\text{opt}}}$, the optimal treatments for all subjects at all stages, have been identified, and R̂_i,1 is the estimated total payoff from taking these estimated optimal actions. With this algorithm, the optimization is global rather than myopic or local.

Asymptotic properties of the estimators are given in Appendix B. The “Sandwich” formula [33] is used to account for the extra variation due to plugging in an estimator from a late treatment stage into the regression models for an early stage.

2.3. Comparison with Standard Q-learning

The method described above is a robust modification of standard Q-learning [23, 28]. For all treatment stages except the last, to estimate counterfactual outcomes under optimal actions, standard Q-learning uses predicted values from previously fitted linear models plus estimated loss due to suboptimal actions. In contrast, our modified Q-learning method uses the values actually observed plus the estimated loss. Let $Q_{i,s}^{\mathit{\text{std}}}$ denote the standard Q-learning method’s objective function, that plays the role of our function $Q_{i,s}^M$. For the first step of the backward induction used in our method, $Q_{i,K}^{\mathit{\text{std}}}=Q_{i,K}^M$.

Standard Q-learning does backward induction using the same steps as our backward induction algorithm through Step 2.3, but it uses the estimated stage K reward

$${\hat{R}}_{i,K}^{\mathit{\text{std}}}={}_{\mathit{\text{def}}}{\hat{Q}}_{i,K}^{\mathit{\text{std}}}+{\hat{\mathrm{\Delta }}}_{i,K}I(A_{i,K}\ne {Â}_{i,K}^{\mathit{\text{opt}}}).$$

In contrast, our estimated stage K reward is

$${\hat{R}}_{i,K}={}_{\mathit{\text{def}}}{Q}_{i,K}^M+{\hat{\mathrm{\Delta }}}_{i,K}I(A_{i,K}\ne {Â}_{i,K}^{\mathit{\text{opt}}}).$$

The difference is that standard Q-learning uses predicted values ${\hat{Q}}_{i,K}^{\mathit{\text{std}}}$, while our modified Q-learning method uses the observed values $Q_{i,K}^M$. This difference is carried to the next stage, s = K − 1, through the formulations of ${\hat{Q}}_{i,K-1}^{\mathit{\text{std}}}=Y_{K-1}+{\hat{R}}_{i,K}^{\mathit{\text{std}}}$ and $Q_{i,K-1}^M=Y_{K-1}+{\hat{R}}_{i,K}$. Similar differences are accumulated during the iteration of this process in the backward induction steps from s = K − 1 to s = 1.

The modified Q-learning method has the following advantages. First, $Q_{i,s}^M$ uses observed outcomes whenever possible for any s ≤ K, whereas $Q_{i,s}^{\mathit{\text{std}}}$ uses model-based expectations for any s < K. Retaining the original outcomes helps the modified Q-learning rely less on the specification of the models used in (15), and thus improves robustness. This is shown by our simulation study in the next section when the model (15) is misspecified, for example, when some relevant covariates are not included in the data set. The simulations show that $Q_{i,s}^M$ has a more robust performance than $Q_{i,s}^{\mathit{\text{std}}}$.

The second advantage of the modified Q-learning method follows from the fact that definition (3) ensures $Q_{i,s}^M\ge {\sum }_{r=s}^K{Y}_{i,r}$. This means that the predicted reward under optimal treatment regimes for stage s + 1 onward is always at least the observed reward under the actual regimes, which may be suboptimal. This is a desirable property that does not always hold for standard Q-learning because, in practice, one may observe $Q_{i,s}^{\mathit{\text{std}}}<{\sum }_{j=s}^K{Y}_i$ for some s < K. This happens simply because, for some subjects, the predicted rewards under optimal treatment regimes for stage s + 1 onward are less than their observed actual reward. Furthermore, for s < K, if a patient has received the optimal treatment regimes for stage s + 1 onward, then with the modified Q-learning, because Δ_i,r = 0 for all r ≥ s + 1, the potential outcome under the treatment sequence {A_is, $A_{i,s+1}^{\mathit{\text{opt}}},\cdots ,A_{i,K}^{\mathit{\text{opt}}}$} for this patient, is $Q_{i,s}^M={\sum }_{r=s}^K{Y}_{i,r}$, the observed reward from stage s onward. This is in agreement with the “consistency assumption”. This assumption, stated at the beginning of Section 2, requires that the assumed counterfactual outcomes under the actual observed actions must be equal to the observed outcomes. It is a very natural assumption and commonly required in causal inference [34]. In contrast, with standard Q-learning, $Q_{i,s}^{\mathit{\text{std}}}$ may not equal ${\sum }_{r=s}^K{Y}_{i,r}$, even if a patient receives the optimal treatment regimes for stage s + 1 onward. That is, as an estimate of the counterfactual outcome, $Q_{i,s}^{\mathit{\text{std}}}$ may violate the consistency assumption on individual basis, although it satisfies this assumption in expectation when the reward models are correctly specified. We will compare the performance of standard and modified Q-learning in the next section by simulation.

3. Simulation Studies

The correct specification of reward models is very important for Q-learning [32]. In this section, we use simulations to show that, in some scenarios when the reward models are misspecified, the modified Q-learning out-performs standard Q-learning. For simplicity, we evaluate two-stage treatment sequences. Sample sizes 50, 100, 200 and 400 are considered. We use three scenarios, each simulation scenario is replicated 1,000 times.

3.1. Scenario I

In Scenario I, we assume an unobserved variable V ~ Normal(0, 2²). For the first treatment stage, we generate covariate Z₁ ~ Normal(0, 1), treatment A₁ ~ Bernoulli(0.5), and outcome Y₁ = Z₁(A₁ − 0.5) + V + ε₁, with ε₁ ~ Normal(0, 1). The second stage treatment A₂ ~ Bernoulli(0.5), and outcome Y₂ = −2Z₁(A₁ − 0.5) + (A₁ − 0.5)(A₂ − 0.5) − V + ε₂, with ε₂ ~ Normal(0, 1). The final cumulative outcome is Y = Y₁ + Y₂. With the observed data of (Z₁, A₁, Y₁, A₂, Y₂) for all subjects, the goal is to find the optimal two-stage treatment regimes that maximizes Y.

In the simulation, both treatments A₁ and A₂ are randomized. The optimal stage-2 treatment is $A_2^{\mathit{\text{opt}}}=I(A_1=1)$. Then the reward for stage 2 under $A_2^{\mathit{\text{opt}}}$ is R₂ = −2Z₁(A₁ − 0.5) + 0.25 − V + ε₂. Recalling that $Q_2^M=Y_2$, and $Q_1^M=Y_1+R_2=-Z_1(A_1-0.5)+0.25+{\epsilon }_1+{\epsilon }_2$. We assume the following model to optimize A₁.

$$Q_1^M={\beta }_{10}+{\beta }_{11}{Z}_1+A_1({\psi }_{10}+{\psi }_{11}{Z}_1)+e_1,$$ (4)

The true values for the above parameters are β₁ = (β₁₀, β₁₁)^T = (0.25, 0.5)^T and ψ₁ = (ψ₁₀, ψ₁₁)^T = (0, − 1)^T. The optimal stage-1 treatment is $A_1^{\mathit{\text{opt}}}=I(Z_1<0)$. If we use a myopic strategy to optimize A₁ by maximizing Y₁ = Z₁(A₁ − 0.5) + V + ε₁, we will get a wrong solution $A_1^{\mathit{\text{opt}}}=I(Z_1\ge 0)$.

To apply the modified Q-learning, we first fit the following model,

$$Q_2^M=Y_2={\beta }_{20}+{\beta }_{21}{Z}_1+{\beta }_{22}{A}_1+{\beta }_{23}{Y}_1+A_2({\psi }_{20}+{\psi }_{21}{Z}_1+{\psi }_{22}{A}_1+{\psi }_{23}{Y}_1)+e_2.$$ (5)

From the data generation mechanism, it can be derived that the true values for the above parameters are β₂ = (β₂₀, β₂₁, β₂₂, β₂₃)^T = (0.25, 0,−0.5,−0.857)^T, and ψ₂ = (ψ₂₀, ψ₂₁, ψ₂₂, ψ₂₃)^T = (−0.5, 0, 1, 0)^T. The coefficient β₂₃ = −0.857 is the effect of V on Y₂ through Y₁, namely ${\beta }_{23}=E(Y_1{Y}_2)/E(Y_1^2)$. Details about the above derivation is provided in Appendix C. After fitting the above model to obtain β̂₂ and ψ̂₂, the estimated optimal stage-2 treatment is

$${Â}_2^{\mathit{\text{opt}}}=I({\hat{\psi }}_{20}+{\hat{\psi }}_{21}{Z}_1+{\hat{\psi }}_{22}{A}_1+{\hat{\psi }}_{23}{Y}_1>0).$$ (6)

Then let

$${\hat{R}}_2=Y_2+I(A_2\ne {Â}_2^{\mathit{\text{opt}}})|{\hat{\psi }}_{20}+{\hat{\psi }}_{21}{Z}_1+{\hat{\psi }}_{22}{A}_1+{\hat{\psi }}_{23}{Y}_1|,$$

$$Q_1^M=Y_1+{\hat{R}}_2,$$ (7)

with |·| denotes absolute value. We use the outcome $Q_1^M$ to fit the model in (4). After estimators β̂₁ and ψ̂₁ are obtained, the estimated optimal stage-1 treatment is

$${Â}_1^{\mathit{\text{opt}}}=I({\hat{\psi }}_{10}+{\hat{\psi }}_{11}{Z}_1>0).$$ (8)

The simulation results for samples of size 200 are given Table 1 and Table 2 (each first panel from the left, Scenario I). In general, the bias is small, and the empirical and asymptotic standard errors (SE and ASE) match well, with coverage probabilities of the 95% confidence intervals all close to nominal. The modified Q-learning correctly identified the optimal stage-1 and stage-2 treatments 91.1% and 88.4% of the time, respectively. Parameter estimations for other sample sizes (n=50, 100, or 400) are also performed well by the modified Q-learning (results not shown).

Table 1.

Parameter estimates for treatment stage 1

		Modified Q-Learning				Standard Q-Learning				g-estimation*				Regret Minimization*
	True	Est	SE	ASE	CP	Est	SE	ASE	CP	Est	SE	ASE	CP	Est	SE	ASE	CP
Scenario I: Pr(A1 = 1) = Pr(A2 = 1) = 0.5
β10	0.25	0.282	0.180	0.243	0.988	0.281	0.192	0.202	0.952
β11	0.5	0.489	0.171	0.200	0.980	−0.068	0.157	0.147	0.039
ψ10	0	−0.008	0.270	0.341	0.988	−0.004	0.281	0.282	0.953	−0.009	0.269	0.256	0.947	0.009	0.264	0.256	0.928
ψ11	−1	−0.969	0.264	0.263	0.933	0.139	0.178	0.178	0.000	−0.980	0.263	0.249	0.926	−1.012	0.274	0.258	0.922
Scenario II: logit{Pr(A1 = 1)} = Z1, logit{Pr(A2 = 1)} = 0.3Y1
β10	0.25	0.274	0.199	0.263	0.989	0.044	0.205	0.217	0.851
β11	0.5	0.483	0.193	0.217	0.970	−0.072	0.177	0.159	0.074
ψ10	0	0.008	0.274	0.369	0.993	0.009	0.291	0.304	0.942	0.008	0.275	0.276	0.945	0.021	0.293	0.282	0.934
ψ11	−1	−0.963	0.288	0.287	0.938	0.147	0.202	0.194	0.000	−0.990	0.329	0.315	0.926	−1.051	0.346	0.347	0.948
Scenario III: logit{Pr(A1 = 1)} = Z1 + V, logit}Pr(A2 = 1)} = 0.3Y1 + V
β10	0.25	0.419	0.194	0.378	0.996	0.289	0.192	0.348	0.999
β11	0.5	0.556	0.177	0.229	0.977	0.098	0.168	0.179	0.393
ψ10	0	−0.086	0.253	0.474	0.998	−0.087	0.256	0.429	0.995	−0.056	0.270	0.274	0.945	−0.038	0.284	0.301	0.949
ψ11	−1	−0.982	0.261	0.281	0.950	−0.066	0.206	0.196	0.002	−0.991	0.264	0.284	0.959	−1.016	0.287	0.339	0.96

^*g-estimation and regret minimization specify treatment selection probabilities (not shown), but do not need β₁₀ or β₁₁;

Est, mean of estimates; SE, empirical standard error;

ASE, average of standard error estimates; ASE for g-estimation and regret minimization obtained by 200 bootstrap samples.

CP, coverage probability of 95% confidence interval.

Table 2.

Parameter estimates for treatment stage 2

		Standard or modified Q-Learning*				g-estimation**				Regret Minimization**
	True	Est	SE	ASE	CP	Est	SE	ASE	CP	Est	SE	ASE	CP
Scenario I: Pr(A1 = 1) = Pr(A2 = 1) = 0.5
β20	0.25	0.255	0.207	0.210	0.949
β21	0	0.002	0.170	0.149	0.907
β22	−0.5	−0.495	0.298	0.297	0.947
β23	−0.857	−0.858	0.063	0.065	0.960
ψ20	−0.5	−0.510	0.294	0.297	0.952	−0.510	0.284	0.289	0.952	−0.509	0.282	0.292	0.947
ψ21	0	−0.003	0.240	0.212	0.919	−0.004	0.229	0.227	0.946	−0.014	0.214	0.219	0.955
ψ22	1	0.997	0.413	0.420	0.949	0.997	0.378	0.396	0.959	1.027	0.410	0.420	0.948
ψ23	0	0.004	0.091	0.093	0.952	0.004	0.091	0.094	0.950	−0.002	0.100	0.097	0.932
Scenario II: Scenario II: logit{Pr(A1 = 1)} = Z1, logit{Pr(A2 = 1)} = 0.3Y1
β20	0.25	0.019	0.217	0.220	0.823
β21	0	0.006	0.194	0.165	0.904
β22	−0.5	−0.501	0.321	0.319	0.942
β23	−0.857	−0.842	0.070	0.069	0.939
ψ20	−0.5	−0.517	0.309	0.316	0.965	−0.514	0.310	0.318	0.955	−0.476	0.325	0.324	0.944
ψ21	0	−0.008	0.268	0.230	0.906	−0.004	0.269	0.258	0.933	−0.002	0.266	0.271	0.960
ψ22	1	1.023	0.455	0.456	0.943	1.019	0.453	0.464	0.945	0.996	0.488	0.488	0.938
ψ23	0	−0.005	0.097	0.096	0.954	−0.005	0.107	0.107	0.949	0.001	0.114	0.119	0.957
Scenario III: Scenario III: logit{Pr(A1 = 1)} = Z1 + V, logit{Pr(A2 = 1)} = 0.3Y1 + V
β20	0.25	0.639	0.233	0.235	0.617
β21	0	0.343	0.182	0.157	0.422
β22	−0.5	−1.31	0.394	0.364	0.391
β23	−0.857	−0.724	0.0871	0.0873	0.669
ψ20	−0.5	−1.32	0.401	0.363	0.407	−0.965	0.409	0.399	0.774	−1.089	0.393	0.392	0.667
ψ21	0	−0.539	0.245	0.218	0.315	−0.020	0.327	0.314	0.934	0.046	0.316	0.353	0.966
ψ22	1	1.725	0.548	0.503	0.697	1.020	0.591	0.579	0.932	0.969	0.606	0.625	0.953
ψ23	0	−0.010	0.124	0.123	0.948	−0.005	0.202	0.206	0.953	−0.009	0.222	0.238	0.950

^*Standard and modified Q-Learning methods use the same estimating equations and give the same results for the last treatment stage;

^**g-estimation and regret minimization specify treatment selection probabilities (not shown), but do not need β’s;

Est, mean of estimates; SE, empirical standard error;

ASE, average of standard error estimates; ASE for g-estimation and regret minimization obtained by 200 bootstrap samples.

CP, coverage probability of 95% confidence interval.

We apply standard Q-learning to the same data sets. Both standard and modified Q-learning fit the same regression models (5) for treatment stage 2. Naturally, they obtain exactly the same results for stage 2 (see Table 2), but differ for the stage-1 estimates (Table 1). As shown in equation (7), the outcome used by the modified Q-learning is the actually observed values Y₂ plus the estimated loss due to suboptimal stage-2 actions. In contrast, the outcome used by standard Q-learning for stage 1 is the predicted value Ŷ₂ from stage 2 plus the same estimated loss, as follows.

$${\hat{R}}_2^{\mathit{\text{std}}}={Ŷ}_2+I(A_2\ne {Â}_2^{\mathit{\text{opt}}})|{\hat{\psi }}_{20}+{\hat{\psi }}_{21}{Z}_1+{\hat{\psi }}_{22}{A}_1+{\hat{\psi }}_{23}{Y}_1|,$$

$$Q_1^{\mathit{\text{std}}}=Y_1+{\hat{R}}_2^{\mathit{\text{std}}}.$$ (9)

Using $Q_1^{\mathit{\text{std}}}$ to replace $Q_1^M$ in (4), the same linear regression model in (4) is fit to identify the optimal stage-1 treatments. Note that $Q_1^M$ carries this information from V by using the original data Y₂, but $Q_1^{\mathit{\text{std}}}$ discards this information by using the model based value Ŷ₂. Due to this difference, the two methods obtain different stage-1 estimates (see Table 1). Standard Q-learning gives biased estimates for β₁₁ and ψ₁₁. Consequently, the probability that it correctly identifies the optimal stage-1 treatments is only 38.2%, much lower than that achieved by the modified Q-learning (91.1%). In summary, standard Q-learning uses model based values in the construction of counterfactual outcomes, and is prone to bias introduced by model mis-specification. As the number of treatment stages increases, the model-based values will be used more times during the backward induction, and this bias problem will become more severe. In contrast, the modified Q-learning achieves robustness against model mis-specification by using the original data instead of model-based values whenever possible.

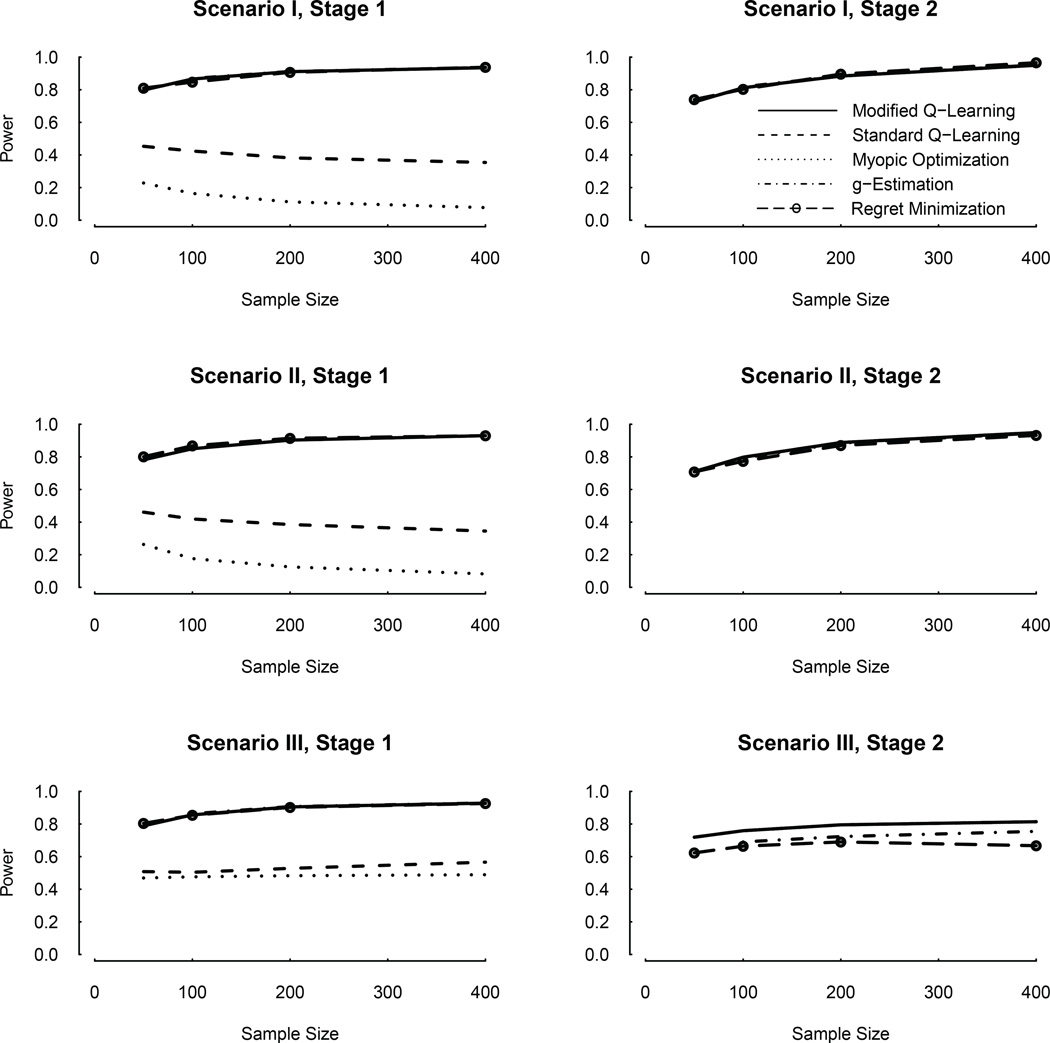
Since the main goal of Q-learning is to correctly identify optimal treatments, we conducted additional simulations for a range of sample sizes and compared performance of modified Q-learning with standard Q-learning. We also compared their performances with the myopic strategy that uses Y₁ to optimize A₁ and Y₂ to optimize A₂. Figure 1 shows these probabilities under a range of sample sizes. The modified Q-learning has larger probabilities than standard Q-learning to correctly identify the optimal stage-1 treatments. Both the modified and standard Q-learning have much better performances than the myopic strategy.

Figure 1.

Comparisons between the modified and standard Q-learning, myopic optimization, g-estimation and regret minimization: probability (power) of correctly identifying the optimal stage-1 and stage-2 treatments in Scenarios I, II, and III. Note: For stage-1, in all Scenarios, the power curves for the modified Q-learning, g-estimation and regret minimization almost overlap with each other. For stage-2, in all Scenarios, the power curves for the modified and standard Q-learning and myopic optimization overlap with each other, so that only the solid curve (modified Q-learning) is visible; they almost overlap with those for g-estimation and regret minimization in Scenarios I and II, and are higher than those for g-estimation and regret minimization in Scenarios III.

It is also interesting to note that, in this setting with misspecified reward models, the optimal treatment selection power of the modified Q-learning increases with sample size, but this is not true for either standard Q-learning or myopic optimization. This shows that in situations of model mis-specification, a large sample size cannot remedy a non-robust or incorrectly designed optimization algorithm, and may even make things worse. Specifically in this simulation setting, since there are only two treatment options at each stage, a pure random selection of any one of them has a probability of 50% of being correct. The less than 50% power of standard Q-learning and myopic optimization shown in Figure 1 reveal that they are severely biased in such a situation with misspecified reward models. It also explains why their empirical power levels decrease with sample size. This is because their true power levels are less than 50% as n → ∞, and equal to 50% as n → 0 (equivalent to a pure random selection).

3.2. Scenarios II & III, and other optimization methods

Treatments in the above Scenario I are randomized. We also consider other treatment selection models. In Scenario II, treatment assignment probabilities depend on observed covariates and outcomes, namely, A₁ ~ Bernoulli(Z₁), A₂ ~ Bernoulli(0.3Y₁). In Scenario III, treatment assignments further depend on the unobserved variable V, as below, A₁ ~ Bernoulli(Z₁ + V), A₂ ~ Bernoulli(0.3Y₁ + V). All the other data generation mechanisms remain the same as in Scenario I. The same data analyses shown in the previous subsection for Scenario I by standard and modified Q-learning, and by the myopic optimization method, are also conducted for Scenarios II & III.

As suggested by a reviewer, we also compare the proposed estimator to the estimators by Murphy [6] and Robins [5]. Moodie et al [25] provided a nice description of these estimators together with R functions for implementing them, which are used below with combination of her and our notations.

In our setting of data generation, the g-estimator (Robins, 2004) starts with the following estimation functions. Denote by 𝔥_j the observed history prior to A_j, j = 1, 2. Let γ₁(𝔥₁, a₁; ψ) = a₁(ψ₁₀ + ψ₁₁z₁) and γ₂(𝔥₂, a₂; ψ) = a₂(ψ₂₀ + ψ₂₁z₁ + ψ₂₂a₁ + ψ₂₃y₁) be the blip functions (Robins, 2004) defining the expected differences in outcome, respectively, between treatments A₁ = a₁ and A₁ = 0, and between A₂ = a₂ and A₂ = 0. Consequently, this would identify the optimal stage 2 treatment as $d_2^{\mathit{\text{opt}}}({𝔥}_2)=I({\psi }_{20}+{\psi }_{21}{z}_1+{\psi }_{22}{a}_1+{\psi }_{23}{y}_1>0)$, and $d_1^{\mathit{\text{opt}}}({𝔥}_1)=I({\psi }_{10}+{\psi }_{11}{z}_1>0)$. By the data generation described earlier, we have ψ₁ = (ψ₁₀, ψ₁₁)^T = (0, −1)^T and ψ₂ = (ψ₂₀, ψ₂₁, psi₂₂, ψ₂₃)^T = (−0.5, 0, 1, 0)^T. Denote S₁(a₁) = a₁(1, z₁)^T and S₂(a₂) = a₂(1, z₁, a₁, y₁)^T. Define

$$H_{\mathit{\text{mod}},2}(\psi )=Y-{\gamma }_2({𝔥}_2,a_2;\psi )$$ (10)

$$H_{\mathit{\text{mod}},1}(\psi )=Y-{\gamma }_1({𝔥}_1,a_1;\psi )+\{{\gamma }_2({𝔥}_2,d_2^{\mathit{\text{opt}}};\psi )-{\gamma }_2({𝔥}_2,a_2;\psi )\}$$ (11)

Also assume treatment selection models as below,

$$\mathit{\text{logit}}\{\text{Pr}(A_1=1|Z_1)\}={\alpha }_{10}+{\alpha }_{11}{Z}_1,$$

$$\mathit{\text{logit}}\{\text{Pr}(A_2=1|Z_1,A_1,Y_1)\}={\alpha }_{20}+{\alpha }_{21}{Z}_1+{\alpha }_{22}{A}_1+{\alpha }_{23}{Y}_1,$$

The resulting estimator α̂ from above is used in the estimating equation below to estimate ψ and then find out the optimal treatment regimes,

$$U_j^{†}(\psi ,s,\hat{\alpha })=[H_{\mathit{\text{mod}},j}(\psi )-E\{H_{\mathit{\text{mod}},j}(\psi )|{𝔥}_j\}]\times [S_j(a_j)-E\{S_j(A_j)|{𝔥}_j\}],\hspace{1em}j=1,2.$$ (12)

Murphy(2003) defined a regret function as the loss due to taking a sub-optimal action. In notation above, the regret functions for the two stages can be written as μ_j(𝔥_j, a_j) = max_a{γ_j(𝔥_j, a) − γ_j(𝔥_j, a_j)} (Moodie et al, 2007). If an optimal action is taken, i.e., $a_j=d_j^{\mathit{\text{opt}}}({𝔥}_j)$, then the regret is zero, namely, μ_j(𝔥_j, a_j) = 0. The true regret functions are μ₁(𝔥₁, a₁) = |z₁|I{a₁ ≠ I(z₁ < 0)} and μ₂(𝔥₂, a₂) = |a₁ − 0.5|I(a₂ ≠ a₁). Using the methods proposed by Murphy (2003) and also adopted by Moodie et al (2007), logistic functions as below are used to approximate the above piece-wise linear functions,

$${\mu }_1^{*}(z_1,a_1)=({\psi }_{10}+{\psi }_{11}{z}_1)\{\frac{\text{exp}\{30({\psi }_{10}+{\psi }_{11}{z}_1)\}}{1+\text{exp}\{30({\psi }_{10}+{\psi }_{11}{z}_1)\}}-a_1\}$$ (13)

$${\mu }_2^{*}(z_1,a_1,y_1,a_2)=({\psi }_{20}+{\psi }_{21}{z}_1+{\psi }_{22}{a}_1+{\psi }_{23}{y}_1)\{\frac{\text{exp}\{30({\psi }_{20}+{\psi }_{21}{z}_1+{\psi }_{22}{a}_1+{\psi }_{23}{y}_1)\}}{1+\text{exp}\{30({\psi }_{20}+{\psi }_{21}{z}_1+{\psi }_{22}{a}_1+{\psi }_{23}{y}_1)\}}-a_2\}.$$ (14)

The true values of the above ψ’s are the same as that for the g-estimation.

For all the methods, the parameter estimates and their empirical and asymptotic standard errors are reported in Tables 1 and 2. The standard and modified Q-learning, and the myopic optimization use more parameters for their outcome models (both β’s and ψ’s), whereas the g-estimation and regret minimization use less parameters for their outcome models (only the ψ’s). However, they use logistic regression models for treatment selection, for which the estimated parameters are not reported. Similarly as Moodie et al (2007), the bootstrap method (200 randomly-drawn samples from the original data with replacement) are used to compute the asymptotic standard errors for the g-estimation and regret minimization. In the above Tables, standard Q-learning estimators show substantial bias for the stage-1 parameters β₁₁ and ψ₁₁ in all the three Scenarios. The modified Q-learning, g-estimation and regret minimization have only very small bias in Scenarios I and II, but some bias in Scenario III, in which both the outcome and treatment assignment models are mis-specified.

The power levels for all the methods to correctly identify the optimal treatments are depicted in Figure 1. For stage-1, in all three Scenarios, the modified Q-learning, g-estimation and regret minimization perform almost the same, whereas the myopic optimization and standard Q-learning have poor performance. For stage 2, the standard and modified Q-learning, and the myopic optimization have the same performance. Comparing with them, the g-estimation and regret minimization have slightly lower power levels in Scenario III, but the same power levels in Scenario I and II. In this Figure, the case of n = 50 for g-estimation is not shown because it involves singular matrices and other computation issues.

4. Application To A prostate Cancer Study

We applied the modified Q-learning to analyse data from a clinical trial of advanced prostate cancer conducted at MD Anderson Cancer Center from 1998 to 2006 to evaluate multi-stage therapeutic strategies [17, 19]. One hundred and fifty patients with advanced prostate cancer were randomized at enrollment to receive one of four chemotherapy combinations, abbreviated as CVD, KA/VE, TEC, and TEE, during an initial treatment period of 8 to 24 weeks. Thereafter, response-based assignment to the second stage treatment was made. Patients with a favorable response to the initial treatment stayed on the same treatment during the second stage (“respond ↦ stay”), while patients who did not have a favorable response were randomized among the three remaining treatments (“no response ↦ switch”). Since 47 patients did not follow this protocol due to severe toxicities or progressive disease or other reasons, Wang et al [17] defined viable dynamic treatment regimes including such discontinuation and accounting for both efficacy and toxicity. This evaluation was based an expert score defined from the bivariate outcomes of efficacy and toxicity in each stage. The scores for the first and second stages were denoted by Y₁ and Y₂ respectively. It was further specified that patients who went off treatment during the first stage received a score of Y₂ = 0 for stage 2. We used the modified Q-learning to identify the optimal treatments for the two stages that maximized Y = Y₁ + Y₂. The data set included the following covariates: patient age, radiation treatment (yes or no), length of time hormone therapy was received (in months) before registration, location of evidence of disease at enrollment, strata (low or high risk), baseline PSA level, and alkaline phosphatase hemoglobin concentrations.

4.1. Stage-2 estimation

By design, patients with a favorable response in stage 1 had that treatment repeated, and we assumed that they received the optimal A₂. Since patients whose first stage treatment failed were re-randomized, this produced a saturated factorial design with twelve different two-stage treatment sequences. Due to the limited sample size, we fit a model with twelve indicators for the twelve treatment sequences, without including their interactions with patients’ characteristics. The fitted model showed that, for patients who received TEC in stage-1 and did not have a favorable response, the best stage-2 treatment was CVD. For patients who did not receive TEC in stage-1 and did not have a favorable response, the best stage-2 treatment was TEC. The computation of potential stage-2 scores under the above optimal stage-2 treatment is shown in Table 3. If the stage-1 treatment failed, the score indicated in Table 3 is added to each patient’s actual stage-2 score, Y₂, to obtain a hypothetical optimal score, R₂, which is used in the next step of the analysis. For patients who had a favorable response in stage-1 treatment, we set R₂ = Y₂. For patients who went off treatment during the first stage, since they did not receive any stage-2 treatment, they could not be used in the estimation of stage-2 treatment effects. They were still included in the analyses for stage 1 and overall outcomes by assigning R₂ = 0. This had an impact on the interpretation of the identified optimal regimes, as shown in the next Subsection.

Table 3.

Estimates of Δ₂ in computation of optimal potential stage-2 score R₂ = Y₂ + Δ₂

Stage-1 treatment	Optimal stage-2 treatment conditional on stage-1 treatment	Actual stage-2 treatment
		CVD	KA/VE	TEC	TEE
CVD	TEC	NA	0.03	0	0.24
KA/VE	TEC	0.5	NA	0	0.55
TEC	CVD	0	0.175	NA	0.25
TEE	TEC	0.125	0.125	0	NA

4.2. Stage-1 estimation

After the stage-2 estimation, we defined

$$Q_1^M=Y_1+R_2.$$

For the four stage-1 treatments, we fit a linear regression model for all main effects and interactions associated with the stage-1 treatment with response $Q_1^M$. All covariates mentioned at the beginning of this Section 4 were considered. Using the Akaike information criterion (AIC) to conduct a stepwise variable selection, we found that age seemed to be the only significant covariate. Interactions between age and treatments were not statistically significant. Age was centered at 65 years, which is roughly the mean. The fitted model given in Table 3 and 4 shows that the stage-1 treatments may be ranked in the following order: TEC, KA/VE, TEE, and CVD, and they roughly can be put into two groups, {TEC, KA/VE} and {TEE, CVD}, with substantial difference between the groups, but not much difference within either group. Combining these results with those in Table 3, which show the optimal stage-2 treatment conditional on stage-1 treatment, we conclude that the optimal treatment sequence (strategy) for these patients is as follows. Start with initial treatment TEC. If a patient achieves a favorable response, then continue to treat with TEC in the second stage. Otherwise, i.e., if a patient does not achieve a favorable response to the initial treatment, then treat with CVD in the second stage. We denote this regime by (TEC, CVD). Other regimes are denoted similarly.

Table 4.

Linear regression for the effects of stage-1 treatments on the potential final outcome if their corresponding optimal stage-2 treatments had been received

	Estimate	SE	p-value
Intercept	1.248	0.1004	< 0.001
Age	−0.0109	0.0053	0.039
KA/VE vs. CVD	0.2366	0.1286	0.066
TEC vs. CVD	0.2757	0.1294	0.033
TEE vs. CVD	0.0475	0.1370	0.729

The estimates in Table 4 are not for stage-1 outcomes only, but rather for the mean final rewards if the stage-2 treatments had been optimized conditional on the stage-1 treatment. For example, compared with CVD, the initial treatment TEC could have improved mean final outcome score by 0.2757 (standard deviation = 0.1294), if all subjects had received their respective optimal stage-2 treatments conditional on their stage-1 treatments. Referring to Table 3, the optimal two-stage treatment strategy is (TEC, CVD) for subjects who receive TEC in stage 1, and is (CVD, TEC) for subjects whose stage-1 treatments are CVD. The noted difference of 0.2757 in Table 4 between initial treatments TEC and CVD is actually the difference between the two regimes (TEC, CVD) and (CVD, TEC). This difference is statistically significant (p=0.033).

4.3. Estimation for the mean rewards of 16 regimes

Similar to standard Q-learning, the modified Q-learning does not require fully specified reward functions for all possible treatment strategies. For the above example, combining the results in Tables 3 and 4, we have estimated the mean rewards of the following four regimes: (TEC, CVD), (KA/VE, TEC), (TEE, TEC) and (CVD, TEC). However, we have not obtained estimates for other regimes, e.g., (TEC, TEE). There are 12 such regimes. This might be viewed as an inconvenience for Q-learning or the modified Q-learning. One may try to introduce some extra models to estimate the mean rewards for the other 12 regimes. However, we show below that this is unnecessary.

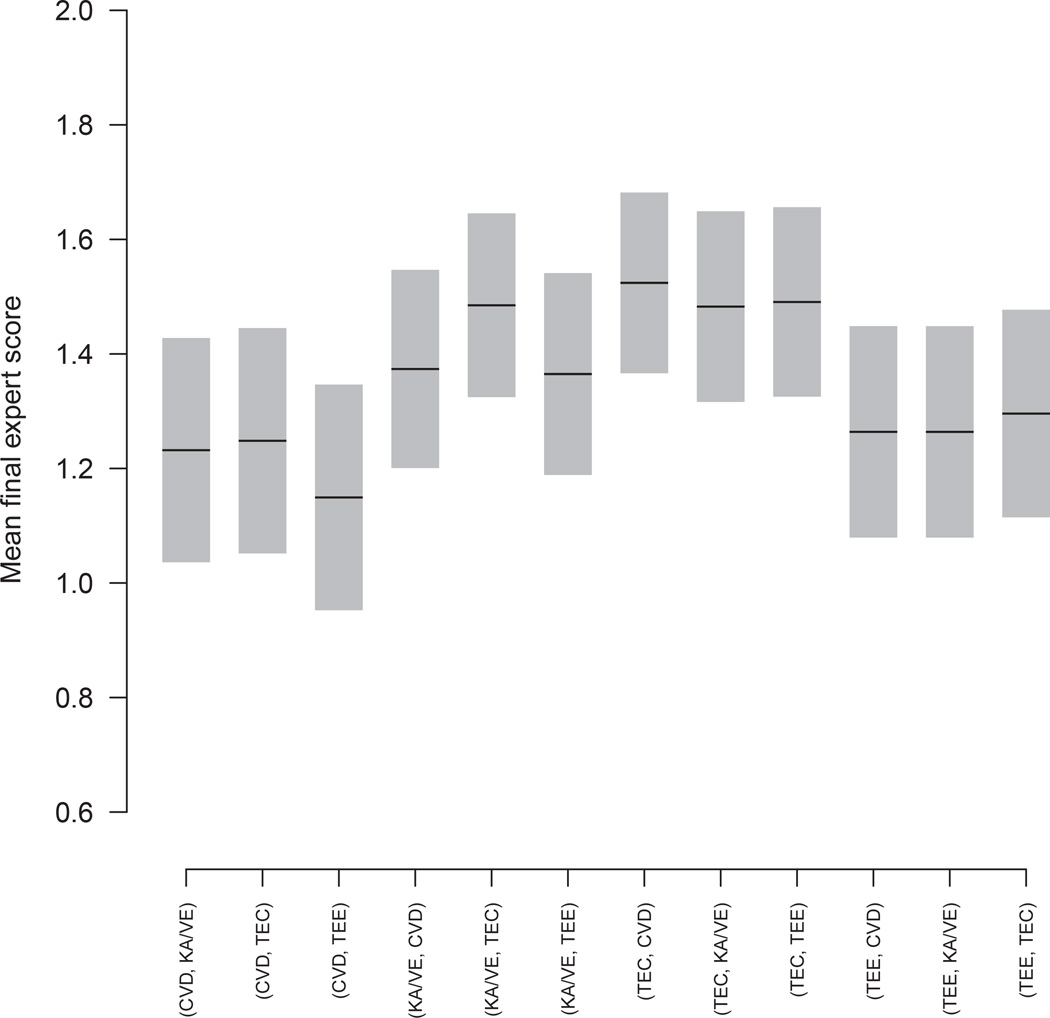
In Table 3, our purpose was to identify the optimal regimes, thus we used the optimal stage-2 treatments as references, and computed the potential loss Δ₂ due to not talking the optimal stage-2 treatment. When our purpose is to compute mean final rewards for other regimes rather than identifying optimal regimes, we replace those optimal stage-2 treatments in Table 3 by the treatments for which we intend to estimate and use them as the new references. Then we figure out the new potential loss (or gain) ${\mathrm{\Delta }}_2^{\prime }$ due to not taking the new reference treatments in stage 2, and finally compute the final reward for regimes using the new reference treatments in stage 2. We put these ${\mathrm{\Delta }}_2^{\prime }$ values in Table 5. For convenience, we copy Table 3 to the top of Table 5. The middle part of Table 5 shows the new ${\mathrm{\Delta }}_2^{\prime }$ values for estimating the mean final rewards for the following regimes, (CVD, KA/VE), (KA/VE, CVD), (TEC, TEE) and (TEE, CVD), which are referred to as target regimes. With these ${\mathrm{\Delta }}_2^{\prime }$, we define a new final reward $Q_1^{M\prime }=Y_1+R_2^{\prime }$, with $R_2^{\prime }=Y_2+{\mathrm{\Delta }}_2^{\prime }$, and then proceed similarly to use regression models for $Q_1^{M\prime }$ as we do for $Q_1^M$. The bottom part of Table 5 uses another different set of stage-2 reference treatments to estimate the final mean rewards for regimes (CVD, TEE), (KA/VE, TEE), (TEC, KA/VE) and (TEE, KA/VE). Throughout Table 5, the stage-2 reference treatments have ${\mathrm{\Delta }}_2^{\prime }=0$ (or Δ₂ = 0). If the label for a stage-2 reference treatment is j (hence ${\Delta }_{2j}^{\prime }=0$), then a different stage-2 treatment k has ${\mathrm{\Delta }}_{2k}^{\prime }={\mathrm{\Delta }}_{2k}-{\mathrm{\Delta }}_{2j}$. Both Tables 3 and 5 are intended to be used for patients who had a unfavorable stage-1 response, consequently their diagonal elements are not given due to the trial design that only those patients who achieved a successful stage-1 response could receive a stage-2 treatment same as stage-1. The results for 12 possible regimes are shown in Figure 2.

Table 5.

Estimates for Δ₂ and ${\mathrm{\Delta }}_2^{\prime }$ with different stage-2 treatments as references

Target regimes	Stage-1 treatment	Reference stage-2 treatment	Actual stage-2 treatment
			CVD	KA/VE	TEC	TEE
Δ2
(CVD, TEC)	CVD	TEC	NA	0.03	0	0.24
(KA/VE, TEC)	KA/VE	TEC	0.5	NA	0	0.55
(TEC, CVD)	TEC	CVD	0	0.175	NA	0.25
(TEE, TEC)	TEE	TEC	0.125	0.125	0	NA
${\mathrm{\Delta }}_2^{\prime }$
(CVD, KA/VE)	CVD	KA/VE	NA	0	0–0.03	0.24–0.03
(KA/VE, CVD)	KA/VE	CVD	0	NA	0–0.5	0.55–0.5
(TEC, TEE)	TEC	TEE	0–0.25	0.175–0.25	NA	0
(TEE, CVD)	TEE	CVD	0	0.125–0.125	0–0.125	NA
${\mathrm{\Delta }}_2^{\prime }$
(CVD, TEE)	CVD	TEE	NA	0.03–0.24	0–0.24	0
(KA/VE, TEE)	KA/VE	TEE	0.5–0.55	NA	0–0.55	0
(TEC, KA/VE)	TEC	KA/VE	0–0.175	0	NA	0.25–0.175
(TEE, KA/VE)	TEE	KA/VE	0.125–0.125	0	0–0.125	NA

Figure 2.

Means and 90% confidence intervals of the final outcome (expert score) for the 12 treatment strategies in the form of (A, B), which means to start with treatment A, if success, stay with A; otherwise switch to treatment B, with A and B each takes one of the four values CVD, KA/VE, TEC and TEE, and A ≠ B.

For this particular example, standard Q-learning gives very similar results (not shown). An advantage of both standard and modified Q-learning is that they can identify optimal dynamic treatment regimes for each individual. This can be done by including interactions between individual level covariates and treatments. For example, if in the above analysis we include an interaction between patient age and stage-1 treatment, then we can identify the age-specific optimal treatment regimes. If we include an interaction between stage-1 score and stage-2 treatment in the model in Subsection 4.1, then such an identified optimal stage-2 treatment will depend on stage-1 score. These are all desirable explorations to maximize benefit for each patient. However, due to the limited sample size, this may not yield stable results and thus is not presented here.

Recall that, for patients who went off treatment during stage 1 due to toxicity or progressive disease, and thus did not receive any stage-2 treatment, we set R₂ = 0. By doing this, all 150 patients were included in the above analyses. This practical modification of the original treatment plan is consistent with the idea of “viable treatment regimes” of Wang et al [17]. For example, a patient received TEC as in stage 1, then went off treatment due to toxicity or progressive disease or other reasons and did not receive any stage-2 treatment, the data from this patient are used in the estimation of final reward for three regimes, namely (TEC, CVD), (TEC, KA/VE) and (TEC, TEE).

5. Discussion

We have demonstrated a robust modification of Q-learning for optimizing a multi-stage treatment sequence in settings where the payoff is a cumulative outcome and intermediate values at each stage are available. The modified Q-learning preserves more randomness in the observed outcomes, and thus is more robust against model mis-specification, has higher power to identify optimal treatments, and satisfies the consistency assumption. If the treating physician happens to adopt the treatment regime that is optimal for a given patient’s condition, the optimal outcome assumed by the modified Q-learning is precisely the observed outcome.

Optimization of a K-stage treatment regime is difficult, since conditioning on the treatment history can result in very complicated models. This is a common problem with all optimization algorithms for multi-stage treatments [6, 5]. We handle this problem by making a Markov assumption. This kind of assumption also was used in others’ simulation studies [6]. In reality, this assumption may be violated. The degree of robustness of model results against this assumption is unknown. In such a case, if sample size permits, it is best to explore models without this Markov assumption, i.e., include a large number of interaction terms to involve earlier stage history into the reward models. In cancer research, practical values for K are about 2 to 5, corresponding to disease recurrences. In other areas of application where the value of K may be much larger, the advantages of the modified Q-learning, i.e., satisfying the consistency assumption and being robust against model mis-specifications, may become more prominent.

An attractive feature of both standard and the modified Q-learning is that they do not need model treatment selection probabilities. Most other methods require this additional structure, including the history-adjusted marginal structural models [35] and A-learning [6]. There are very subtle arguments required with the use of modeling treatment selections. It has been argued that small mis-specifications in such selection models can accumulate over treatment stages and thus cause severe bias and convergence problems [36]. Therefore, there is an advantage to avoid using such treatment selection models.

Appendix A

Regression Model for the Modified Q-Function

For each s = 1,⋯, K, let β_s be a parameter vector of the main effects of ${\overline{H}}_{i,s}^M$ on $Q_{i,s}^M$. Using j = 1 as the reference treatment group, for each j = 2,⋯, J_s, where J_s is the number of treatment options at stage s, let ${\psi }_s^{(j)}$ be a parameter vector of the interactive effects of action A_i,s = j and ${\overline{H}}_{i,s}^M$ on $Q_{i,s}^M$. Let {e_i, i = 1,⋯, n} be a vector of i.i.d. random errors. Denoting the indicator of an event E by I(E), the regression model for $Q_{i,s}^M$ is

$$Q_{i,s}^M={\beta }_s^T{\overline{H}}_{i,s}^M+\sum _{j=2}^{J_s}I(A_{i,s}=j){\psi }_s^{{(j)}^T}{\overline{H}}_{i,s}^M+e_i,$$ (15)

where the main effects are

$${\beta }_s^T{\overline{H}}_{i,s}^M={\beta }_{s,0}+{\beta }_{s,1}{Z}_{i,s-1}+{\beta }_{s,2}{Z}_{i,s}+{\beta }_{s,3}{Y}_{i,s-1}+\sum _{l=2}^{J_s-1}{\beta }_{s,4,l}I(A_{i,s-1}=l)$$

and the multiplier of I(A_i,s = j) in the sum of the interaction terms is

$${\psi }_s^{{(j)}^T}{\overline{H}}_{i,s}^M={\psi }_{s,0}+{\psi }_{s,1}^{(j)}{Z}_{i,s-1}+{\psi }_{s,2}^{(j)}{Z}_{i,s}+{\psi }_{s,3}^{(j)}{Y}_{i,s-1}+\sum _{l=2}^{J_s-1}{\psi }_{s,4,l}^{(j)}I(A_{i,s-1}=l).$$

Thus, each parameter indexed by j is the comparative effect of A_i,s = j versus action A_i,s = 1. Under the model (15), we define the cumulative causal effect of treatment j versus l at stage s, where j > l, as

$$D_{i,s}(j,l)=Q_{i,s}^M(A_{i,s}=j,{\overline{H}}_{i,s}^M)-Q_{i,s}^M(A_{i,s}=l,{\overline{H}}_{i,s}^M)=\{\begin{array}{cc}{\{{\psi }_s^{(j)}-{\psi }_s^{(l)}\}}^T{\overline{H}}_{i,s}^M,\hfill & \text{if}l\ne 1\hfill \\ {\psi }_s^{{(j)}^T}{\overline{H}}_{i,s}^M,\hfill & \text{if}l=1,\hfill \end{array}$$ (16)

which depends on the interaction parameters ${\psi }_s^{(j)},{\psi }_s^{(l)}$, and recent history ${\overline{H}}_{i,s}^M$, but not on the main effects β_s.

Given estimates β̂_s and ${\hat{\psi }}_s^{(j)},j=2,\cdots ,J_s$ of the parameters in (15), denote the resulting estimates of $Q_{i,s}^M$ by ${\hat{Q}}_{i,s}^M$, estimated causal effects by D̂_i,s(j, l), and estimated cumulative future rewards by R̂_i,s.

Appendix B

Asymptotic Properties

The linear models in (15) are easy to fit. However, due to the use of later stage estimates in models for earlier stages, the covariance formulas for the estimated regression parameters are not straightforward. Below we provide closed-form sandwich formula estimators for the covariance matrices. For simplicity, we assume the total number of treatment stages K = 2 in the following derivation, denote by S_k the matrix formed by ${\overline{H}}_{i,k}^M,i=1,\cdots ,n$, and assume treatment A_k is binary, for k = 1, 2. The results can be generalized to K > 2.

Rewrite the right-hand side of the regression model in (15) as

$${𝒬}_k(S_k,A_k;{\beta }_k,{\psi }_k)={\beta }_k^T{S}_{k1}+({\psi }_k^T{S}_{k2})A_k,$$ (17)

where S_k1 ∈ ℝ^p_k and S_k2 ∈ ℝ^q_k are sub-vectors of S_k. We allow variable selection so that the model in (15) may not include the full set of variables in ${\overline{H}}_{i,k}^M$. Denote ${\theta }_k={({\beta }_k^T,{\psi }_k^T)}^T$, and θ_k0 its true value, where β_k ∈ ℝ^p_k is the main effect of the current state variables on the outcome, and ψ_k ∈ ℝ^q_k are the interactions between current state variables and treatment. Note that $Q_{i,2}^M=Y_2$, and $Q_{i,1}^M$ is the potential cumulative outcome given S_1,i, A_1,i and $A_{2,i}^{\mathit{\text{opt}}}$. The two-stage backward induction proceeds as follows. Start with the second stage, we have

$${\hat{\theta }}_2={({\hat{\beta }}_2^T,{\hat{\psi }}_2^T)}^T={\text{arg min}}_{{\beta }_2,{\psi }_2}{\mathbb{P}}_n{\{Q_2^M-{𝒬}_2(S_2,A_2;{\beta }_2,{\psi }_2)\}}^2={[X_2^T{X}_2]}^{-1}{X}_2^T{\overrightarrow{Y}}_2,$$

where $X_2={(S_{21}^T,A_2{S}_{22}^T)}^T$ is the stage-2 design matrix and Y⃗₂ = (Y₂₁, …, Y_2n)^T. Then estimate the second stage individual optimal outcome by R̂₂ = (R̂₂₁,…, R̂_2n)^T, where

$${\hat{R}}_{2i}=Y_{2i}+|{\hat{\psi }}_2^T{S}_{22i}|I\{A_{2i}\ne I({\hat{\psi }}_2^T{S}_{22i}>0)\}.$$ (18)

With this optimized outcome at stage 2, the potential cumulative outcome, given S_1,i, A_1,i and $A_{2,i}^{\mathit{\text{opt}}}$, is ${\overrightarrow{Q}}_1^M={(Q_{1,1}^M,\dots ,Q_{n,1}^M)}^T$, where $Q_{i,1}^M({\hat{\psi }}_2)=Y_{1i}+{\hat{R}}_{2i}$. After this, we estimate the first stage parameters by

$${\hat{\theta }}_1={({\hat{\beta }}_1^T,{\hat{\psi }}_1^T)}^T={\text{arg min}}_{{\beta }_1,{\psi }_1}{\mathbb{P}}_n{\{Q_1^M({\hat{\psi }}_2)-{𝒬}_1(S_1,A_1;{\beta }_1,{\psi }_1)\}}^2={[X_1^T{X}_1]}^{-1}{X}_1^T{\overrightarrow{Q}}_1^M,$$

where $X_1={(S_{11}^T,A_1{S}_{12}^T)}^T$.

The asymptotic properties of these parameter estimates are presented below, under the following technical conditions.

• A1. The true value for θ₂, denoted by ${\theta }_{20}={({\beta }_{20}^T,{\psi }_{20}^T)}^T$, minimizes

  $${𝒫}_0{\{Q_2^M-{𝒬}_2(S_2,A_2;{\theta }_2)\}}^2,$$

  and the true value for θ₁, denoted by ${\theta }_{10}={({\beta }_{10}^T,{\psi }_{10}^T)}^T$, minimizes

  $${𝒫}_0{\{Q_1^M({\hat{\psi }}_2)-{𝒬}_1(S_1,A_1;{\theta }_1)\}}^2,$$

  where 𝒫₀ = lim_n ℙ_n denotes the true probability measure. We assume that the limits exists and is finite in the above expressions.

• A2. ${\theta }_0={({\theta }_{10}^T,{\theta }_{20}^T)}^T$ is is an interior point in a bounded, open, convex subset Θ ⊂ ℛ^m, where m = ∑_k(p_k + q_k). For k = 1, 2, with probability one, 𝒬_k(S_k, A_k; θ_k) is at least twice continuously differentiable with respect to θ_k, and the Hessian matrix, ${ℐ}_{k0}={𝒫}_0[{\nabla }_{{\theta }_k{\theta }_k}^2{\{Q_k^M-{𝒬}_k(S_k,A_k;{\theta }_k)\}}^2]$ exists and is positive-definite.

• A3. With probability one, $\text{Pr}({\psi }_k^T{S}_{k2}=0)=0$ for k = 1, 2.

Condition A1 says that θ₁₀ and θ₂₀ are true values that minimize loss function in each step. If Q_k takes the form of the linear model (17), condition A2 is equivalent to non-singularity of the design matrix $X_k={(S_{k1}^T,A_k{S}_{k2}^T)}^T$ for k = 1, 2. From condition A3, we assume there is no possibility of non-regularity. In case of $\text{Pr}({\psi }_k^T{S}_{k2}=0)>0$, it has been verified that multi-stage estimation, including standard Q-learning, may be biased and the above asymptotic properties may be inappropriate, and thus requiring special treatment [13, 37]. Here, we do not consider such complications.

Denote the estimating equation for θ₂ as ℙ_nΨ₂(θ₂; S₂, A₂) = 0, where

$${\mathrm{\Psi }}_2({\theta }_2;S_2,A_2)={\{{𝒬}_2(S_2,A_2;{\theta }_2)/(\partial {\theta }_2)\}}^T\{Y_2-{𝒬}_2(S_2,A_2;{\theta }_2)\}.$$

Theorem 1

Under conditions A1–A3,

$$\sqrt{n}({\hat{\theta }}_2-{\theta }_{20})~N\{0,V_2({\theta }_{20})\},\mathit{\text{as}}n\to \infty ,$$

where V₂(θ₂) = D₂(θ₂)⁻¹B₂(θ₂){D₂(θ₂)⁻¹}^T with D₂(θ₂) = −E[∂Ψ₂(θ₂; S₂, A₂)/(∂θ₂)] and B₂(θ₂) = E[Ψ₂(θ₂; S₂, A₂)Ψ₂(θ₂; S₂, A₂)^T].

Proof

It is a direct application of the “Sandwich” formula [33], so omitted.

Since the estimation of θ₁ depends on ψ̂₂, let Ψ_2,2 denote the sub-equation of Ψ₂ and D_2,2 denote the sub-matrix of D₂, both corresponding to ψ₂ at β₂ = β₂₀. Then, ψ̂₂ − ψ₂₀ ≈ D_2,2(ψ₂₀)⁻¹ℙ_n[Ψ_2,2(ψ₂₀; S₂, A₂)], where β₂₀ and ψ₂₀ are true values of β₂ and ψ₂.

$$\sqrt{n}{({\hat{\psi }}_2-{\psi }_{20})}^T{S}_{22}~N(0,{\mathrm{\Sigma }}_2),{\mathrm{\Sigma }}_2=D_{2,2}^{-1}E\{{\mathrm{\Psi }}_{2,2}(S_{22}^T{S}_{22}){\mathrm{\Psi }}_{2,2}^T\}{D}_{2,2}^{-1}.$$

The estimating equation for θ₁ is

$${\mathbb{P}}_n{\mathrm{\Psi }}_1({\theta }_1;S_1,A_1,{\hat{\psi }}_2)={\mathbb{P}}_n[{\{\partial {𝒬}_1(S_1,A_1;{\theta }_1)/(\partial {\theta }_1)\}}^T\{{\overrightarrow{Q}}_1^M-{𝒬}_1(S_1,A_1;{\theta }_1)\}]={\mathbb{P}}_n[{\{\partial {𝒬}_1(S_1,A_1;{\theta }_1)/(\partial {\theta }_1)\}}^T\times \{Y_1+Y_2+|{\hat{\psi }}_2^T{S}_{22}|I(A_2\ne I({\hat{\psi }}_2^T{S}_{22}>0))-{𝒬}_1(S_1,A_1;{\theta }_1)\}]={\mathbb{P}}_n[{\mathrm{\Psi }}_1({\theta }_1;S_1,A_1,{\psi }_{20})+{\{\partial {𝒬}_1(S_1,A_1;{\theta }_1)/(\partial {\theta }_1)\}}^T\times \{|{\hat{\psi }}_2^T{S}_{22}|I(A_2\ne I({\hat{\psi }}_2^T{S}_{22}>0))-|{\psi }_{20}^T{S}_{22}|I(A_2\ne I({\psi }_{20}^T{S}_{22}>0))\}]={\mathbb{P}}_n[{\mathrm{\Psi }}_1({\theta }_1;S_1,A_1,{\psi }_{20})+{\{\partial {𝒬}_1(S_1,A_1;{\theta }_1)/(\partial {\theta }_1)\}}^T\times [I(A_2=0)\{|{\hat{\psi }}_2^T{S}_{22}{|}_{+}-|{\psi }_{20}^T{S}_{22}{|}_{+}\}+I(A_2=1)\{|{\hat{\psi }}_2^T{S}_{22}{|}_{-}-|{\psi }_{20}^T{S}_{22}{|}_{-}\}].$$

Let

$${\overline{S}}_2\equiv {[S_{21}^T,S_{22}^T\{I(A_2=0)I({\psi }_{20}^T{S}_{22}\ge 0)+I(A_2=1)I({\psi }_{20}^T{S}_{22}\le 0)\}]}^T.$$

Theorem 2

Under conditions A1–A3,

$$\sqrt{n}({\hat{\theta }}_1-{\theta }_{10})\sim N\{0,V_1({\theta }_{10},{\theta }_{20})\},\mathit{\text{as}}n\to \infty ,$$

where V₁(θ₁₀, θ₂₀) can be estimated by

$${\hat{V}}_1({\theta }_{10},{\theta }_{20})=D_1{({\theta }_{10})}^{-1}[{\mathbb{P}}_n\{{\mathrm{\Psi }}_1{\mathrm{\Psi }}_1^T\}+{\mathbb{P}}_n\{X_1{\overline{S}}_2^T{\hat{V}}_2({\theta }_{20}){\overline{S}}_2{X}_1^T\}]D_1{({\theta }_{10})}^{-1},$$

with D₁(θ₁) = −E[∂Ψ₁(θ₁; S₁, A₁)/(∂θ₁)].

Proof

Again it is a direct application of the “Sandwich” formula [33], so omitted.

Appendix C

Simulation Model

In general, suppose we have random variables X₁,⋯, X_p, and Y, and we would like to do regression of Y on X₁,⋯, X_p with model $Y={\sum }_{i=1}^p{\beta }_i{X}_i+\epsilon$. If X₁,⋯, X_p are orthogonal to each other, then we have ${\beta }_i=\frac{E(X_{i}Y)}{E(X_i^2)}$.

In Section 3, we have Z₁ ~ Normal(0, 1), A₁ ~ Bernoulli(0.5), V ~ Normal(0, 2²), Y₁ = Z₁(A₁ − 0.5) + V + ε₁ with ε₁ ~ Normal(0, 1). A₂ ~ Bernoulli(0.5), Y₂ = −2Z₁(A₁ − 0.5) + (A₁ − 0.5)(A₂ − 0.5) − V + ε₂ with ε₂ ~ Normal(0, 1). We use the following model to do regression analysis.

$$Q_2^M=Y_2={\beta }_{20}+{\beta }_{21}{Z}_1+{\beta }_{22}{A}_1+{\beta }_{23}{Y}_1+A_2({\psi }_{20}+{\psi }_{21}{Z}_1+{\psi }_{22}{A}_1+{\psi }_{23}{Y}_1)+e_2.$$

To find out the true values for β’s in the above model, we consider regressing Y₂ on the following orthogonal set of random variables {1, Z₁, (A₁ − 0.5), Y₁, (A₂ − 0.5), (A₂ − 0.5)Z₁, (A₂ − 0.5)(A₁ − 0.5), (A₂ − 0.5)Y₁}. That is to say, we consider the model

$$Y_2={\beta }_{20}^{\prime }+{\beta }_{21}^{\prime }{Z}_1+{\beta }_{22}^{\prime }(A_1-0.5)+{\beta }_{23}^{\prime }{Y}_1+(A_2-0.5)({\psi }_{20}^{\prime }+{\psi }_{21}^{\prime }{Z}_1+{\psi }_{22}^{\prime }(A_1-0.5)+{\psi }_{23}^{\prime }{Y}_1)+e_2.$$

By using the formula ${\beta }_i=\frac{E(X_{i}Y)}{E(X_i^2)}$ mentioned at the beginning of this Appendix, we obtain

$$Y_2=0+0Z_1+0(A_1-0.5)-0.857Y_1+(A_2-0.5)(0+0Z_1+(A_1-0.5)+0Y_1)+e_2.$$

For the above coefficients, the only one that is not straightforward is

$${\beta }_{23}^{\prime }=E(Y_1{Y}_2)/E(Y_1^2)=\frac{-E(V^2)-2E[Z_1^2{(A_1-0.5)}^2]}{E(V^2)+E[Z_1^2{(A_1-0.5)}^2]+E({\epsilon }_1^2)}=\frac{-4.5}{5.25}\approx -0.857.$$

Note e₂ = ε₂ − 2Z₁(A₁ − 0.5) − V + 0.857Y₁. It can be verified that e₂ is orthogonal to all explanatory variables on the right hand side of the above equation, justifying its validity as a residual term.

Appendix D

An Illustration for > 2 Stages and > 2 Treatment Options in Each

Stage Section 2 and Appendix A provide a general description for any number of stages (K), and any number of treatment options in each stage (J_s), for s = 1,⋯, K. As suggested by a referee, for easy understanding, we illustrate through an example below. We skip the data generation and pick a particular regression model for each stage. Suppose we observe (Z_s, A_s, Y_s) for each stage s = 1, 2, 3, with A_s = 1, 2 or 3 indicating three different treatment options for each stage s. Here A_s = 1 and A_s′ = 1 do not necessarily mean the same medical treatment for stages s ≠ s′. The modified Q-learning proceeds as follows.

Let $Q_3^M=Y_3$. Fit a linear regression model as below to find out the optimal treatment for stage 3 conditional on current covariates Z₃, previous treatment A₂ and outcome Y₂.

$$Q_3^M=\sum _{j=1}^{3}I(A_3=j)\{{\psi }_{30,j}+{\psi }_{31,j}{Z}_3+\sum _{l=1}^3{\psi }_{32,jl}I(A_2=l)+{\psi }_{33,j}{Y}_2\}+e_3.$$

Then the conditional optimal treatment is just the one that maximize the mean reward in stage 3, which is mathematically described as,

$${Â}_3^{\mathit{\text{opt}}}={\text{argmax}}_{j=1,2,3}\{{\hat{\psi }}_{30,j}+{\hat{\psi }}_{31,j}{Z}_3+\sum _{l=1}^3{\hat{\psi }}_{32,jl}I(A_2=l)+{\hat{\psi }}_{33,j}{Y}_2\}.$$ (19)

Then we estimate the potential optimal reward R₃ in stage 3 each individual would have achieved had he/she received his/her conditional optimal treatment as indicated above. If an individual actually received his/her conditional optimal treatment, the estimated reward R̂₃ is set to be the observed Y₃ by our modified Q-learning. Otherwise, R̂₃ is set to be Y₃ plus the difference between the rewards for the optimal and actual treatments.

$${\hat{R}}_3=Y_3+I(A_3\ne {Â}_3^{\mathit{\text{opt}}})\left[\underset{j=1,2,3}{\text{max}}\right\{{\hat{\psi }}_{30,j}+{\hat{\psi }}_{31,j}{Z}_3+\sum _{l=1}^3{\hat{\psi }}_{32,jl}I(A_2=l)+{\hat{\psi }}_{33,j}{Y}_2\}-\sum _{k=1}^{3}I(A_3=k)\{{\hat{\psi }}_{30,k}+{\hat{\psi }}_{31,k}{Z}_3+\sum _{l=1}^3{\hat{\psi }}_{32,kl}I(A_2=l)+{\hat{\psi }}_{33,k}{Y}_2\left\}\right].$$

By doing the above, the optimal stage 3 treatments conditional on historical information are identified. Here the Markov assumption is used in the above linear regression model so that it depends on A₂ and Y₂, but does not go further to depend on A₁ or Y₁.Without such an assumption, the above linear regression would have too many predictors and require an extremely large sample size to have a reasonable fit. This Markov assumption is for practical rather than theoretical consideration.

Now consider optimizing treatments for stage 2. Define $Q_2^M=Y_2+{\hat{R}}_3$. Similarly as above, first fit a linear model as below,

$$Q_2^M=\sum _{j=1}^{3}I(A_2=j)\{{\psi }_{20,j}+{\psi }_{21,j}{Z}_2+\sum _{l=1}^3{\psi }_{22,jl}I(A_1=l)+{\psi }_{23,j}{Y}_1\}+e_2.$$

Then find out the optimal stage-2 treatment conditional on current covariates Z₂, previous treatment A₁ and outcome Y₁, as below.

$${Â}_2^{\mathit{\text{opt}}}={\text{argmax}}_{j=1,2,3}\{{\hat{\psi }}_{20,j}+{\hat{\psi }}_{21,j}{Z}_2+\sum _{l=1}^3{\hat{\psi }}_{22,jl}I(A_1=l)+{\hat{\psi }}_{23,j}{Y}_1\}.$$ (20)

The potential total reward from stage 2 onwards (i.e., sum of rewards from stages 2 and 3), R₂, had a subject received his optimal stage 2 treatment and his corresponding optimal stage 3 treatment, can be estimated as below,

$${\hat{R}}_2=Y_2+I(A_2\ne {Â}_2^{\mathit{\text{opt}}})\left[\underset{j=1,2,3}{\text{max}}\right\{{\hat{\psi }}_{20,j}+{\hat{\psi }}_{21,j}{Z}_2+\sum _{l=1}^3{\hat{\psi }}_{22,jl}I(A_1=l)+{\hat{\psi }}_{23,j}{Y}_1\}-\sum _{k=1}^{3}I(A_2=k)\{{\hat{\psi }}_{20,k}+{\hat{\psi }}_{21,k}{Z}_2+\sum _{l=1}^3{\hat{\psi }}_{22,kl}I(A_1=l)+{\hat{\psi }}_{23,k}{Y}_1\left\}\right].$$

For stage 1, similarly as above, define $Q_1^M=Y_1+{\hat{R}}_2$. Then fit a linear regression model

$$Q_1^M=\sum _{j=1}^{3}I(A_1=j)({\psi }_{10,j}+{\psi }_{11,j}{Z}_1)+e_1.$$

This will give estimates for the optimal treatment stage-1 treatments conditional on Z₁ as below,

$${Â}_1^{\mathit{\text{opt}}}={\text{argmax}}_{j=1,2,3}\{{\hat{\psi }}_{10,j}+{\hat{\psi }}_{11,j}{Z}_1\}.$$ (21)

Under this optimal stage-1 treatment, and corresponding optimal stages 2 and 3 treatments, the total optimal reward is R₁, which can be estimated by,

$${\hat{R}}_1=Y_1+I(A_1\ne {Â}_1^{\mathit{\text{opt}}})[\underset{j=1,2,3}{\text{max}}\{{\hat{\psi }}_{10,j}+{\hat{\psi }}_{11,j}{Z}_1\}-\sum _{k=1}^{3}I(A_1=k)\{{\hat{\psi }}_{10,k}+{\hat{\psi }}_{11,k}{Z}_1\}].$$

The above procedures are to derive the optimal treatments using a backward induction. After the estimation results are obtained, to apply them in practice, the optimal treatment decision rules are determined as follows. First use (21) to find out the optimal treatment conditional on covariate Z₁. Suppose this gives A₁ = 1. After receives this treatment A₁ = 1, the observed stage-1 outcome is Y₁. At the beginning of stage 2, covariate Z₂ is observed. Then at this moment, the optimal stage 2 treatment can be determined by (20) based on Z₂, A₁ = 1 and the observed Y₁. Suppose the optimal treatment conditional on these variables is A₂ = 3. After receives this treatment A₂ = 3, the observed stage-2 outcome is Y₂. At the beginning of stage 3, covariate Z₃ is observed. At this time, the optimal stage-3 treatment is determined by (19) based Z₃, A₂ = 3 and the observed Y₂. Suppose the observed stage-3 outcome is Y₃. The above optimal treatment identification method is supposed to maximize Y = Y₁ + Y₂ + Y₃.