Remodelling of extracellular matrix due to solid stress accumulation during tumour growth

Abstract

Solid stresses emerge as the expanding tumour displaces and deforms the surrounding normal tissue, and also as a result of intratumoural component interplay. Among other things, solid stresses are known to induce extensive extracellular matrix synthesis and reorganization. In the present study, we developed a mathematical model of tumour growth that distinguishes the contribution to stress generation by collagenous and non-collagenous tumour structural components, and also investigates collagen fibre remodelling exclusively due to solid stress. To this end, we initially conducted in vivo experiments using an orthotopic mouse model for breast cancer to monitor primary tumour growth and derive the mechanical properties of the tumour. Subsequently, we fitted the mathematical model to experimental data to determine values of the model parameters. According to the model, intratumoural solid stress is compressive, whereas extratumoural stress in the tumour vicinity is compressive in the radial direction and tensile in the periphery. Furthermore, collagen fibres engaged in stress generation only in the peritumoural region, and not in the interior where they were slackened due to the compressive stress state. Peritumoural fibres were driven away from the radial direction, tended to realign tangent to the tumour-host interface, and were also significantly stretched by tensile circumferential stresses. By means of this remodelling, the model predicts that the tumour is enveloped by a progressively thickening capsule of collagen fibres. This prediction is consistent with long-standing observations of tumour encapsulation and histologic sections that we performed, and it further corroborates the expansive growth hypothesis for the capsule formation.

Introduction

Tumour growth and progression are characterized by an increase in the amount of tumour structural components, such as cancer cells and extracellular matrix constituents. Growth in the confined space of the host (normal) tissue, along with tissue stiffening often observed in tumours, results in the generation of solid stress exerted by the deformed host tissue on the tumour, and accumulation of residual solid stress in tumour structural components persisting even after the tumour has been excised (1-5). Solid and fluid stresses are physical forces per unit area by non-fluid and fluid components of the tumour, respectively. Solid stresses have profound effects on the mechanobiology of the tumour microenvironment as they are sufficiently high to compress blood and lymphatic vessels, thus reducing perfusion and inducing hypoxia, which, in turn, contribute to compromised immune response, promote malignant progression and impede the efficacy of treatments (3-8). Furthermore, solid stresses also compress cancer and stromal cells resulting in altered gene expression, cancer cell proliferation, increase of their invasive and metastatic potential, and extensive extracellular matrix synthesis and reorganization (9-13).

Matrix reorganization by means of cancer and stromal cell proliferation and contraction is augmented by the activation or overexpression of transforming growth factor-β (TGF-β). The latter can regulate the production of matrix-modifying metalloproteinases and lysil oxidase in order to increase matrix protein synthesis and crosslinking, and decrease matrix proteinase activity, thereby increasing matrix stiffness (14-16). Stiffening of the matrix and the subsequent increase of stress levels increase cytoskeletal contraction further by Rho/Rock signalling activation (17, 18). Moreover, mechanical stress and TGF-β activation can convert fibroblasts or other quiescent precursor cells into contractile myofibroblasts, also known as cancer associated fibroblasts, that produce extracellular molecules (collagen-I, fibronectin, glycosaminoglycans) and also remodel the extracellular matrix (19, 20). Production of new matrix material increases its density and, again, tissue stiffness and solid stress, while myofibroblast contraction further activates latent TGF-β from the matrix, creating a positive feedback loop (16). The extracellular matrix is also significantly remodelled directly by growth-induced solid stresses that deform the tumour microenvironment since matrix components, such as collagen and hyaluronic acid, can store and transmit stress in a manner dependent on their mechanical properties (2). Collagen fibres in particular, which are the principal load bearing component of most soft tissues and furnish them with tensile strength, contribute to solid stress due to their remarkable stiffness in tension and resistance to stretching.

In previous studies, several phenomena pertaining to solid stress in tumours were addressed both experimentally and with use of biomechanical modelling. In particular, we demonstrated that solid stresses are compressive at the tumour interior and tensile at the peripheral host tissue, provided estimates of their magnitudes and showed that they are high enough to compress blood vessels, and quantified residual stresses and the interstitial fluid pressure (2, 21); we have further shown that the intratumoural stress state is largely determined by the stiffness of the host tissue (22), calculated the osmotic pressure in the tumour interstitial space (23), and delineated specific strategies to improve perfusion and facilitate drug delivery in solid tumours (5, 8).

The predictions of the models in the aforementioned investigations, although consistent to experimental observations, were based on the examination of the gross mechanical behaviour of a tumour, without distinction between the contributions of individual solid components. Here, we build on previous studies by developing a structural biomechanical model for tumour growth, informed by experimental data, which incorporates distinct accounts of collagenous and non-collagenous constituents to solid stress generation, and focuses on the collagen remodelling elicited by the latter. The computational model comprises two distinct domains, namely, a tumour domain contained within a host tissue domain. The materials in both domains are considered to be reinforced by collagen fibres embedded in the extracellular matrices of the tumour and host. Treating the tumour and host as continua, assuming isotropic tumour growth and isotropic fibre distribution throughout, and considering a collective response for all non-collagenous matter, the model demonstrates the advancing tumour expansion and concomitant host tissue displacement, and predicts a compressive bulk stress state at the tumour interior and a tensile bulk stress state in the peritumoural region. Due to intratumoural compression, when the direct effect of solid stress alone is considered as cause for fibre remodelling, collagen fibres do not contribute to intratumoural solid stress as they are unable to support any compression. On the other hand, as the bulk solid stress transitions from compressive to tensile across the tumour-host interface, significant extracellular matrix remodelling and concerted collagen fibre realignment is predicted in the tumour vicinity and confirmed with immunohistochemical analysis. In particular, according to the model tumour growth drives fibres close to the tangent to the interface direction, in concert with the expansive growth hypothesis of tumour encapsulation (24, 25).

Materials and Methods

Mathematical model

A tumour was represented by a sphere growing at the centre of a much larger cube corresponding to the surrounding host tissue (Figs. 1, S2). To incorporate volumetric growth within the tumour and describe kinematics in both domains, we used the multiplicative decomposition of the total deformation gradient tensor F (28, 29), according to which

$$\mathbf{F}={\mathbf{F}}_e{\mathbf{F}}_g,$$ (1)

where F_g is a prescribed (see Supplement) non-stress-generating deformation gradient tensor accounting for cancer cell proliferation and the subsequent mass growth of each material element from the initial stress-free configuration, and F_e accounts for the stress-generating elastic interactions within and between the tumour and the host tissue from the grown configuration to the current. Note that in the tumour exterior F_g ≡ I, where I is the second order identity tensor. The elastic component of F was readily obtained from Eq. (1) as F_e = F F_g⁻¹. Further, we assumed that in both domains collagen fibres are embedded in an isotropic, compressible, pseudoelastic matrix collectively representing the mechanical behaviour of all non-collagenous material and characterized by the neo-Hookean strain energy density function

$$W_m=\frac{1}{2}\mu ({\overline{I}}_1-3)+\frac{1}{2}\kappa {(J_e-1)}^2,$$ (2)

where μ, κ are the shear and bulk moduli, respectively, J_e = detF_e, and ${\overline{I}}_1=I_1{J}_e^{-2∕3}$ with I₁ = trC_e being the first invariant of the right Cauchy-Green deformation tensor C_e = F_e^T F_e. The shear and bulk moduli of the tumour were determined experimentally (see later in text) and set to μ = 1.22 kPa and κ = 11.87 kPa, respectively, corresponding to a Poisson ratio of ν ≈ 0.45. For the host tissue, the values μ = 0.3 kPa and ν = 0.20 were used; the pertinent bulk modulus was subsequently calculated from the relation κ = 2μ(1 + ν) / 3(1 − 2ν). We also assumed that collagen fibres in both domains are equally distributed in all directions (isotropic distribution), such that their mechanical behaviour is determined by the hyperelastic strain energy density function (30):

$$W_{\mathit{cf}}=\{\begin{array}{cc}\hfill \frac{k_1}{2k_2}\left\{\exp \left[\frac{k_2}{9}{\left({\overline{I}}_1-3\right)}^2\right]-1\right\},\hfill & \hfill \text{when}{\overline{I}}_1>3\hfill \\ \hfill 0,\hfill & \hfill \text{when}{\overline{I}}_1\le 3\hfill \end{array}\phantom{\}},$$ (3)

where k₁, k₂ are fibre stiffness parameters, identically valued for both tumour and host. The piecewise Eq. (3) expresses the premise that collagen fibres cannot support compression and would buckle under compressive load. Thus, fibres contribute to the total strain energy W = W_m + W_cf only when stretched, that is, only when ${\overline{I}}_1>3$ (30). Finally, the solid Cauchy stress tensor was defined as (29, 31):

$$\sigma =J_e^{-1}{\mathbf{F}}_e\frac{\partial W}{\partial {\mathbf{F}}_e^{\mathrm{T}}}.$$ (4)

Figure 1.

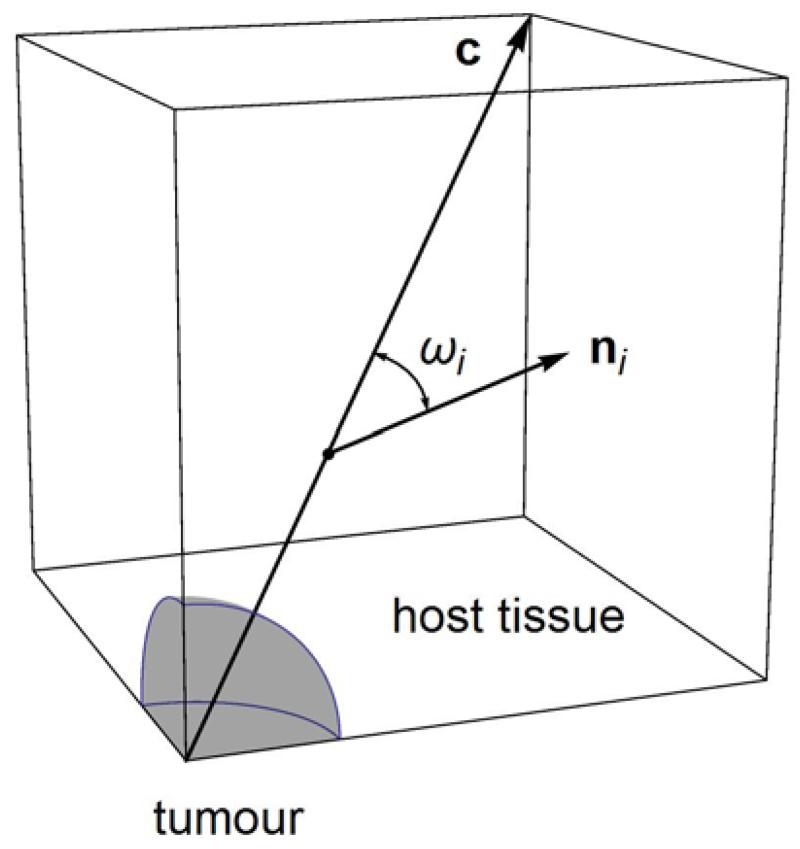
Geometry of the model’s tumour and host tissue domains. Due to symmetry, only one eighth is illustrated and was employed in the computations. The vector c, from the origin at the tumour’s centre to the opposite vertex, is identified as the direction along which results are presented in the following. The angular distance (dot product angle) ω_i between c and an arbitrary vector n_i, at an arbitrary point along c, is used to determine the orientation of n_i with respect to the radial direction. The values ω_i = 0°, 90° correspond to the radial and circumferential directions, respectively. (Figure not to scale.)

In formulating the model, we focused exclusively on solid stresses and assumed that the fraction of collagen was constant throughout the simulation; matrix production or degradation, nutrient availability and oxygen supply were not taken into account; and cell contractility and death were neglected, as well. The model equations were solved using the commercial finite element software COMSOL Multiphysics v. 4.4 (COMSOL, Inc., Burlington, MA, USA). To this end, the growth of a murine tumour developing within a period of 16 days was simulated (Fig. 2), and from comparison with experimental data the model parameters pertinent to growth were specified. Complementary information regarding the mathematical model and values for all parameters are provided in the Supplement (Table S1).

Figure 2.

Experimental data (dots) and model prediction (curve) of tumour growth.

Mathematical description of fibre remodelling

To study collagen fibre remodelling we performed, both in the tumour interior and the exterior, the following analysis. We approximated the isotropic collagen fibre distribution with a custom set of vectors that initially (t = 0) were of unit magnitude (length) and at each point in space formed 0° and 45° angles with the axes of the Cartesian coordinate frame (Fig. 3a; see also Table S2 and Figs. S3, S4a in Supplement for more details on the initial vector distribution). In other words, the initial (reference) vector distribution comprised 13 pairs of opposite unit vectors, each pair describing the orientation of a material line element, which represented a family (direction) of collagen fibres. Growth-induced deformation and solid stress modify the reference distribution such that, at a given point in space and time instant, each reference vector ${\widehat{\mathbf{n}}}_i$ (i = 1 to 26) is mapped to its corresponding deformed vector n_i ≡ F_e ${\widehat{\mathbf{n}}}_i$. To monitor fibre remodelling, we calculated the spatiotemporal evolution of the deformed distribution in terms of the change in length of each vector n_i, and the change in angular distance ω_i between each n_i and the constant radial vector c spanning from the tumour centre to the opposite vertex of the host tissue domain, along the direction of c (Fig. 1). The angular distances ω_i are readily obtained by means of the dot products of the n_i with c (Fig. S3). The value ω_i = 0° corresponds to the radial direction (parallel to c), whereas ω_i = 90° represents all directions perpendicular to c, for example, the circumferential directions tangent to the tumour-host interface.

Figure 3.

(a) Three-dimensional representation of the reference distribution (t = 0) of unit vectors approximating the isotropic distribution of collagen fibres both in the tumour interior and exterior. The reference distribution is identical at every point in the solution space and, therefore, at every point along the direction of the constant radial vector c, which is also presented for comparison. (b) Reference (solid lines) and deformed (dashed lines) vector distributions at the radially outermost intratumoural solution point along c, at t = 16 days. The directions of the reference vectors and their deformed counterparts coincide, however, the latter have been contracted compared to the former, resulting in a double headed arrow illustration (inner arrowheads correspond to deformed vectors). (c) Reference (solid lines) and deformed (dashed lines) vector distributions at the radially innermost extratumoural solution point along c, at t = 16 days. [Solution points for (b), (c) are sequential on opposite sides of the tumour-host interface.] Concerted realignment of deformed distribution vectors towards the plane perpendicular to c, along with stretching (increase in length) evident by the “blot” in the centre depicting the reference distribution. To observe directionality, here, c has been scaled with the longest of the deformed distribution vectors.

Cell culture and animal tumour models

The human breast cancer cell line MCF10CA1a (26) was cultured in DMEM F/12 medium supplemented with 5% heat-inactivated horse serum, insulin (10 g/ml), epidermal growth factor (20 ng/ml), cholera enterotoxin (0.1 μg/ml), and hydrocortisone (0.5 μg/ml), under standard conditions (37°C, 5% CO₂). Orthotopic mammary fat pad animal tumour models were established using 6-week old CD1 nude mice (n = 6), that were housed and cared in a pathogen–free environment in accordance to the European Commission Recommendations 2007/526 and the European Directive 2010/63. Initially, mice were anesthetized by intraperitoneal injection of avertin (200 mg/kg). MCF10CA1a breast cancer cells (5×10⁵) were resuspended in 40 μl PBS and were implanted in the mammary fat pad under the third nipple on the left, as previously described (27). Tumour growth was monitored daily and its planar dimensions (x, y) were measured every 48 h during the course of the experiment using a digital calliper. Tumour volume was calculated using the expression V = 4πr³/3, where r was the average of x and y. Animals were sacrificed 16 days post-implantation and thereafter each tumour was excised and cut in two pieces in order to perform histological and unconfined compression analysis, respectively. All in vivo experiments were conducted according to the animal welfare regulations and guidelines of the Republic of Cyprus and the European Union under a protocol license (No CY/EXP/PR.L1/2014) approved by the Cyprus Veterinary Services, the Cyprus national authority for monitoring animal research.

Fluorescent immunohistochemistry

Solid breast tumours were excised from all 6 mice used in this study. Half of each tumour was fixed with 4% paraformaldehyde in PBS for 20 min at room temperature (RT), and incubated overnight at 30% sucrose in PBS at 4°C. The samples were then embedded in optimal cutting temperature (OCT) compound (Tissue-Tek) and frozen. Transverse 40μm-thick tumour sections were produced using the Tissue-Tek Cryo₃ (SAKURA) and immunostained. At first, the cryo tumour sections were rehydrated in 1x Phosphate Buffered Saline (PBS) for 30 min at RT, blocked using blocking solution (1% Fetal Bovine Serum and 3% Goat serum in PBS) for 2 hours at RT and then incubated with the primary antibody collagen I antibody (ab4710, 1:100 dilution) overnight at 4°C. The sections were subsequently washed twice in 1xPBS and incubated with Alexa Fluor-647 Goat Anti-Rabbit IgG (H+L) secondary antibody (A-21244, 1:800 dilution) for 2 hours at RT, followed by incubation with DAPI (nuclear marker) for 15 min at RT. After several washes with 1xPBS (at RT), the sections were then mounted, inspected and documented under the Olympus fluorescence microscope (U-RLF-T model) using the cellSens software.

Unconfined compression experiment

Unconfined compression, stress-relaxation experiments were carried out using a commercial high precision mechanical testing system (Instron 5944, Norwood, MA, USA). The specimens were cut in an orthogonal shape with dimensions 5×5×3 mm (length × width × thickness). According to the stress relaxation protocol, specimens underwent four cycles of testing for each of which a 5% strain was applied for 1 min, followed by a 10 min hold. Stress was calculated as the force measured on the load cell divided by the initial surface area of the specimen (i.e., 1^st Piola-Kirchhoff stress), and displacement data were converted to strain (i.e., ε = Δl / l₀). Stress-strain curves were determined by selecting relaxation points after 10 min of hold (Fig. S1 in Supplementary Material).

Results

Experimental measurements and specification of model parameters

The biomechanical model was used to simulate the unconfined compression experiments in order to determine the values of the tumour’s mechanical properties that provided the best fit to experimental stress-strain curves. Specifically, a three-dimensional finite elements model of orthogonal geometry was constructed, identical in size to the actual specimens. The model was compressed in one axis and was free to deform in the other two, according to the unconfined compression experimental protocol. The tumour’s shear and bulk moduli were calculated via optimization by COMSOL, so that the sum of squared errors

$${\chi }^2=\frac{1}{n}\sum _{i=1}^n\left[{\left(P_{\mathit{exp}}-P_m\right)}_i^2\right],$$ (5)

was minimized, where P_exp, P_m are experimentally measured and model predicted 1^st Piola-Kirchhoff stresses, respectively, and n is the number of experimental data (Fig. S1). In particular, we obtained μ = 1.220 ± 0.095 kPa and κ = 11.87 ± 0.93 kPa, with χ² = 0.043 ± 0.011. Since collagen fibres were assumed unable to support compression, the fibre stiffness parameters were undetermined by the experiments (see Supplement) and the ad hoc values k₁ = 0.5 kPa and k₂ = 0.6 were chosen, based on data from arterial wall collagen (30). Tumour growth parameters were also determined by fitting the model to experimental data (Fig. 2; see also Supplement). Specifically, using the mouse model reported above, we found that tumour growth followed an exponential profile reaching, on average, 550 mm³ in size by day 16 post-implantation.

Radial solid stress is compressive inside the tumour and in the peritumoural region

The radial component of solid stress (σ_rr) was compressive both inside the tumour and in its proximity, in the surrounding host tissue (Fig. 4). According to the stress profiles of Fig. 4, intratumoural compressive solid stress in the radial direction also presented gradual temporal increase and it was spatially almost homogeneous. In the surrounding tissue σ_rr was still compressive, increased with time, it obtained its maximum value at the tumour-host interface and then decreased progressively with increasing radial distance until it vanished away from the tumour.

Figure 4.

Spatial distribution of radial (σ_rr) and circumferential (σ_θθ, σ_φφ) solid stress components at selected times. All three curves coincide in the tumour interior, whereas the circumferential components coincide in the tumour exterior. Vertical dashed lines indicate the tumour-host interface at the given time instant.

Circumferential solid stresses are compressive inside the tumour and tensile in the peritumoural region

The circumferential components of solid stress (σ_θθ, σ_φφ) presented indistinguishable qualitative and quantitative behaviours throughout the tumour and host domains (Fig. 4). Additionally, in the tumour interior they were compressive and their magnitudes and spatiotemporal evolution were identical to the radial stress response. Across the tumour-host interface, however, the circumferential solid stress components transformed to tensile, increased with time, obtained their maximum value at the interface and then decreased progressively with increasing radial distance until they vanished away from the tumour.

Peritumoural collagen and matrix contributions are antagonistic in radial and complementary in circumferential solid stress

Collagen fibres in the tumour interior did not generate any stress and, therefore, did not contribute to solid stress either in the radial or the circumferential directions (Figs. 5, 6 and Fig. S5), that is, σ_rr^c = σ_θθ^c = σ_φφ^c = 0. In turn, intratumoural solid stress was uniquely determined by stress generated by the non-collagenous matrix component (σ_rr ≡ σ_rr^m, σ_θθ ≡ σ_θθ^m, σ_φφ ≡ σ_φφ^m).

Figure 5.

Matrix (σ_rr^m) and collagen fibre (σ_rr^c) contributions to radial solid stress (σ_rr). In the tumour interior, no stress is generated by collagen fibres and, thus, σ_rr^m coincides with σ_rr. Vertical dashed lines indicate the tumour-host interface at the given time instant.

Figure 6.

Matrix (σ_θθ^m) and collagen fibre (σ_θθ^c) contributions to circumferential solid stress (σ_θθ). In the tumour interior, no stress is generated by collagen fibres and, thus, σ_θθ^m coincides with σ_θθ. Vertical dashed lines indicate the tumour-host interface at the given time instant. The σ_φφ stress component and individual contributions are identical (see Supplement).

By contrast, peritumoural solid stress build-up resulted from both fibre- and matrix-generated stress. In particular, fibre-generated stress in the radial direction was compressive, increased with time, maximum at the interface and decreased down to zero with increasing radial distance from the tumour. Matrix-generated radial stress, other than being tensile, presented the same spatiotemporal features as its collagen-generated counterpart. Since the latter appeared to be greater in magnitude than the former at all times, it follows that radial solid stress was compressive as observed, i.e., σ_rr = σ_rr^c + σ_rr^m < 0 (Figs. 4, 5). On the other hand, peritumoural fibre- and matrix-generated stresses in the circumferential directions were all tensile, increased with time, attained their maximum values at the interface and decreased with radial position until they vanished away from the tumour (Fig. 6).

Intratumoural collagen fibres are relaxed but do not realign

In the tumour interior, growth and the emergence of compressive solid stress deformed the vector distribution employed to monitor collagen fibre remodelling such that vectors in all directions were shortened at approximately equal amounts (Figs. 3b and S4b). This decrease in vector magnitude, however, was not associated with any change in orientation direction. Vector shortening took place concomitantly with tumour growth and it was more pronounced at later stages, when significant compressive solid stress had also developed. According to this picture, spatially homogeneous intratumoural compression would not allow an initially stress-free collagen fibre to extend beyond its natural length or reorient, but would rather result in relaxation (slackening) of the fibre.

Peritumoural collagen fibres are stretched and realign perpendicular to the radial direction

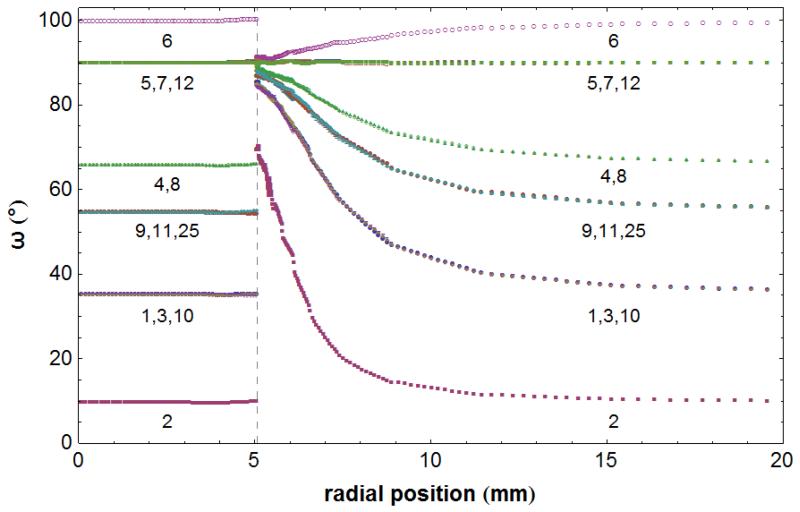
In the host region adjacent to the tumour, growth-induced tissue displacement and the differential development of radial and circumferential solid stresses (compressive and tensile, respectively) deformed the vector distribution such that vectors in all directions were progressively and concurrently stretched and realigned almost perpendicularly to the radial direction (Figs. 3c and S4c). At a given time instant, the closer the vectors initially were to the perpendicular orientation in terms of their angular distances, the more they were stretched and the faster they had converged perpendicularly to the radial direction (Figs. 7 and S4c). Conversely, vectors initially closer to the radial direction converged slower and less, and their stretching was also less pronounced (Figs. 8 and S4c). It should be pointed out that realigned vectors do not, in general, share the same orientation in three-dimensional space, rather, they are all oriented differently but they also tend to occupy the same plane perpendicular to c at the given radial distance. Importantly, in the tumour proximity, deformation and solid stresses resulted in vectors realigning almost tangentially to the spherical tumour-host interface. The propensity of vectors to realign was detectable even from the earliest stages of tumour growth (Fig. S6), and significant realignment took place promptly (Fig. S7). Furthermore, tumour growth and the associated development of solid stresses were also correlated with the spatial extent of the realignment response at different times (Figs. 7, S6 and S7). Farther into the host tissue, where the effects of growth-induced deformation and solid stress gradually subsided, the remodelling behaviour previously sketched also declined gradually (data not shown), until it vanished away from the tumour vicinity as illustrated by the fact that the deformed distribution coincides with the reference at all times (Fig. 7). According to the above, collagen fibres in the peritumoural region are remodelled such that they are progressively stretched while simultaneously reoriented towards the perpendicular to the radial direction. To confirm experimentally the localization of collagen in the peritumoural region, we performed immunohistochemical analysis in our breast tumour samples. Despite that during the excision part of the surrounding host tissue was inevitably removed, our data showed a distinct band of collagen in the tumour periphery (Fig. 9).

Figure 7.

Spatial evolution of the angular distance ω_i between each deformed distribution vector n_i and the constant radial vector c, along the direction of c, at t = 16 days. Due to symmetry, angular distances for only the first of two opposite vectors from each of the 13 pairs are presented, namely, for i = 1 to 12, and 25 (Table S2). The vertical dashed line denotes the position of the tumour-host interface position at the given time instant. The angular distance values ω_i = 0°, 90° correspond to the radial and circumferential directions, respectively.

Figure 8.

Temporal evolution of the angular distance ω_i between each deformed distribution vector n_i and the constant radial vector c, at the radially innermost extratumoural solution point along c (first solution point past the interface, inside the host). Due to symmetry, angular distances for only the first of two opposite vectors from each of the 13 pairs are presented, namely, for i = 1 to 12, and 25 (Table S2). The angular distance values ω_i = 0°, 90° correspond to the radial and circumferential directions, respectively.

Figure 9.

Immunohistochemical analysis of tumour collagen expression in breast tumours. (a, b) Fluorescent views of transverse section samples from two different tumours showing collagen localization (green fluorescence) and nuclei (blue fluorescence). Notice the accumulation of collagen in the periphery (white arrowheads) indicating the tumour-host boundary. Scale bar: 100 μm in both (a), (b).

Discussion

Solid stresses developing during the growth of a tumour elicit a host of biophysical responses that regulate the broader tumour microenvironment and its pathophysiology. In the present study, we elaborated our preceding modelling methods by discriminating between the contributions of collagenous and non-collagenous tumour structural elements in solid stress generation, and by investigating the effect of solid stress accumulation in the reorganization of extracellular matrix, specifically, in the remodelling of collagen fibres. On that account, the present model predicts that intratumoural solid stress is homogeneously compressive, whereas extratumoural solid stress in the tumour proximity is compressive in the radial direction and tensile in the circumferential ones. Moreover, intratumoural solid stress is determined exclusively by the matrix component of the tumour, and collagen fibres participate in stress generation only in the peritumoural region. These findings are in accordance with the common assumption that collagen fibres cannot support compression and contribute to the stress state only when extended, which was further supported by our investigation of fibre remodelling. According to the latter, as a result of intratumoural compression, collagen fibres were progressively and increasingly slackened, therefore, did not engage in stress generation. On the other hand, fibres in the peritumoural region were driven away from the radial direction and tended to align perpendicular to it, where they were also significantly stretched by tensile circumferential solid stresses.

According to model predictions, peritumoural collagen fibre remodelling develops early in tumour growth progression when fibres farthest from the radial direction converge to new orientations that are perpendicular to the radial; that is, they are progressively realigned tangentially to the tumour-host interface. With time, marked remodelling takes place in the other orientation directions as well, until even fibres initially closer to the radial direction also realign towards the perpendicular orientation. Due to symmetry, the reported remodelling behaviour takes place in all (radial) directions which, in turn, suggests that the tumour is enveloped by a progressively thickening capsule of collagen fibres. From the mathematical point of view, the capsule is in place as soon as the first family of collagen fibres is realigned almost tangentially to the interface; realignment of subsequent fibre families by means of increasing growth-induced deformation and solid stresses augments the thickness of the capsule further. This theoretical account of the fibre remodelling process was also substantiated by our experimental observations which revealed marked accumulation of collagen tracing the periphery of the tumour (Fig. 9), indicating that a collagen capsule might originally had been in place. The capsule formation prediction of the model and our experimental data are consistent with long-standing observations of tumour encapsulation (24, 32).

Tumour-encasing capsules, primarily composed of dense fibrillar collagen, are a salient morphological feature most frequently associated with, but not limited to, benign tumours (32). The capsule is considered to contain the tumour and suppress its growth. Capsule-induced growth suppression is accounted for indirectly in the model when considering the sensitivity of growth on the parameters k₁, k₂ of the collagen fibre strain energy density function. Specifically, increasing the stiffness of collagen fibres by increasing any of the k₁, k₂ values results in tumours with decreased volumes, and vice-versa (Fig. S8). This model prediction is in concert with experimental observations that documented the inhibition of growth of cultured avascular multicellular tumour spheroids within agarose gels when the stiffness of the surrounding medium was increased (9), and also with previous modelling approaches by us and others (22, 33, 34).

Although the precise mechanism of capsule formation is still under debate, two complementary theories have been postulated for its interpretation (24, 25). According to the expansive growth hypothesis, tumour growth compresses collagen in the surrounding extracellular matrix, without eliciting new matrix production. On the other hand, per the foreign body hypothesis, the host identifies the tumour as a foreign body and cells under compression issue an immune response by overexpressing collagen and other fibrous extracellular matrix material. Encapsulation has been theoretically addressed in the past by continuum, multiphasic biomechanical models that traced species concentration (35), and by mathematical models that treated the capsule as a pulse in a travelling wave of extracellular matrix (36, 37). These models investigated the plausibility of both capsule formation hypotheses and favoured expansive growth, as the foreign body response alone was considered insufficient. Additionally, they accounted for matrix degrading metalloproteinases that compromise the integrity of the capsule and facilitate cancer cell invasion. Such features lay beyond the scope of the present study, albeit they can be incorporated to the model owning to the generality of its formulation. In cases where the disrupting effect of matrix metalloproteinases on the capsule is pronounced, our current approach would still generally be valid but it would probably also overestimate the amount of solid stress generated during growth. The present study, unlike the aforementioned one-dimensional models, focused on the development of solid stresses and their effect on collagen fibre and extracellular matrix in a fully three-dimensional setting. Furthermore, our aim was not to negotiate tumour encapsulation per se, however, the formation of the capsule emerges as a natural consequence of collagen fibre remodelling. In this respect, our model is in line with the expansive growth hypothesis but cannot refute its alternative.

Simplifying assumptions adopted in the present study along with limitations to our mathematical approach are critically discussed in the following. The tumour in our model was set to be proliferating in an isotropic fashion, which might not be true given the highly heterogeneous nature of solid tumours. A non-uniformly advancing tumour would, nonetheless, displace the surrounding host tissue and induce remodelling of collagen fibres that would still be subject to the general framework delineated by our model; albeit, it would result in non-uniform solid stress distributions and remodelling. In other words, we expect the principal remodelling mechanism due to solid stress accumulation sketched herein to be valid under non-uniform growth, but we also expect pronounced local variations of stresses and fibre remodelling — i.e., extent of realignment, stretching and capsule thickness — depending on growth non-uniformity. On the other hand, the adoption of isotropic growth is a common approximation in literature, and we consider it sufficient for the purposes of the present study in the sense that it offers simplicity and mathematical transparency that facilitate the investigation and description of the physical mechanism of remodelling. Furthermore, the model can be easily modified to accommodate non-isotropic growth. As most biological tissues, tumours have a complex and heterogeneous structure so that the use of the neo-Hookean constitutive equation might not be sufficient to fully describe their mechanical response. However, in previous research we showed that growth and the state of stress of a tumour is largely determined by the mechanical properties of the host tissue, in particular its stiffness, and not from the constitutive equation that is used (22). The model parameters were either obtained experimentally or from data available in literature; in the absence of data, some parameter values were chosen ad hoc.

In formulating the model we intentionally neglected any explicit effects of fluid stresses, cell contractility, biochemical agents affecting tumour progression, and changes in the fractions of collagen and other extracellular proteins. The impact of some of these factors has been documented in separate studies (e.g., 21, 23, 34), whereas others can be incorporated in future, more sophisticated iterations of the model, when pertinent experimental data are also collected. For example, cell-fibre interactions in the tumour interior might generate in tension in the fibres at the microscopic level even though at the macro-scale the tissue is in compression, thus resulting in remodelling of intratumoural fibres not detectable by the present model. On the other hand, although the aforementioned factors may individually influence tumour evolution drastically, incorporating some of them would only affect our results quantitatively as previously discussed for mellatoproteinases. Despite these omissions, the model predictions are reasonable, physiologically feasible and consistent with experimental observations. In any case, we consider the assumptions and limitations of the current model acceptable, as a first approximation, for investigating the generation and development of distinct contributions to solid stresses of a growing tumour, and delineating their consequences on the biophysically complex tumour microenvironment, without allowing the complexity to obscure the stress-driven mechanism of the observed remodelling. Conversely, the results and conclusions of the present study will facilitate the understanding of the more complex interactions with the surrounding tissue taking place concomitantly with in vivo tumour evolution.