Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2014 Dec 7;6(1):13–21. doi: 10.1021/jz5022087

Qualitatively Incorrect Features in the TDDFT Spectrum of Thiophene-Based Compounds

Antonio Prlj †, Basile F E Curchod †,‡,*, Alberto Fabrizio †, Leonard Floryan †,§, Clémence Corminboeuf †,*
PMCID: PMC4598019  PMID: 26263085

Abstract

graphic file with name jz-2014-022087_0007.jpg

Ab initio molecular electronic structure computations of thiophene-based compounds constitute an active field of research prompted by the growing interest in low-cost materials for organic electronic devices. In particular, the modeling of electronically excited states and other time-dependent phenomena has moved toward the description of more realistic albeit challenging systems. We demonstrate that due to its underlying approximations, time-dependent density functional theory predicts results that are qualitatively incorrect for thiophene and thienoacenes, although not for oligothiophene chains. The failure includes spurious state inversion and excitation characters, wrong distribution of oscillator strengths and erroneous potential energy surfaces. We briefly analyze possible origins of this behavior and identify alternative methods that alleviate these problems.

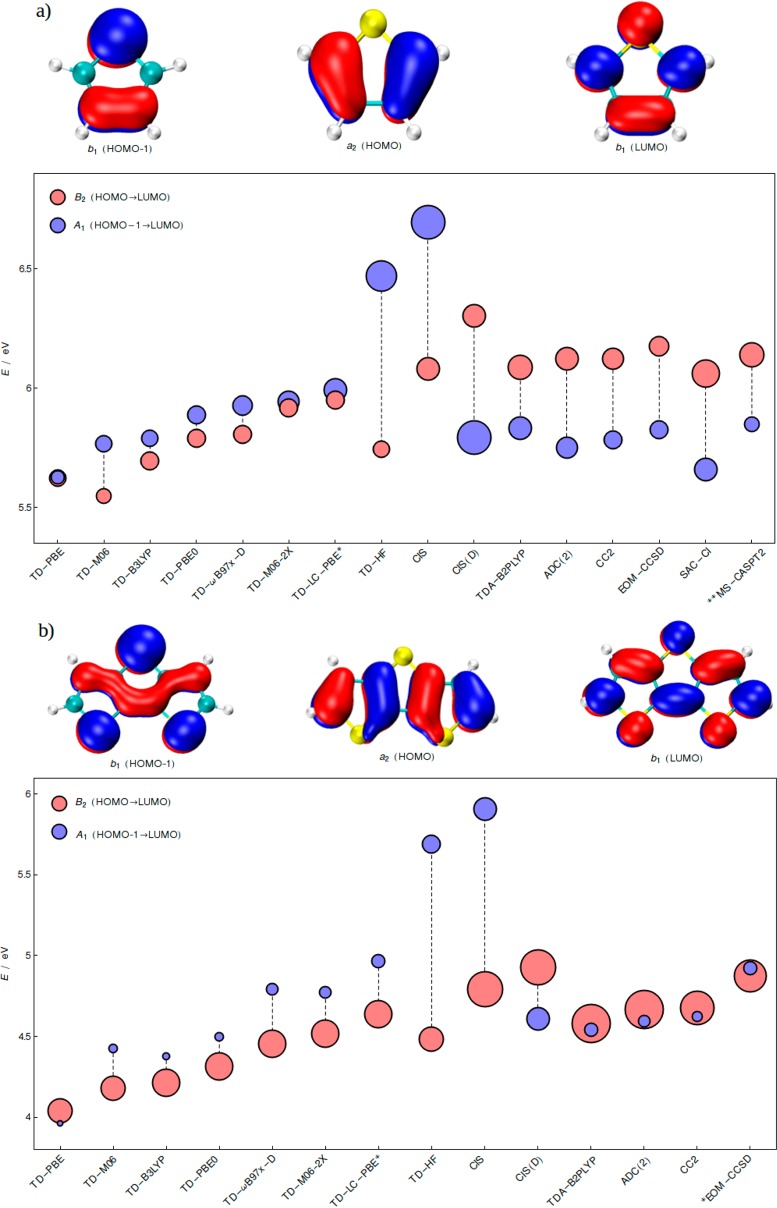
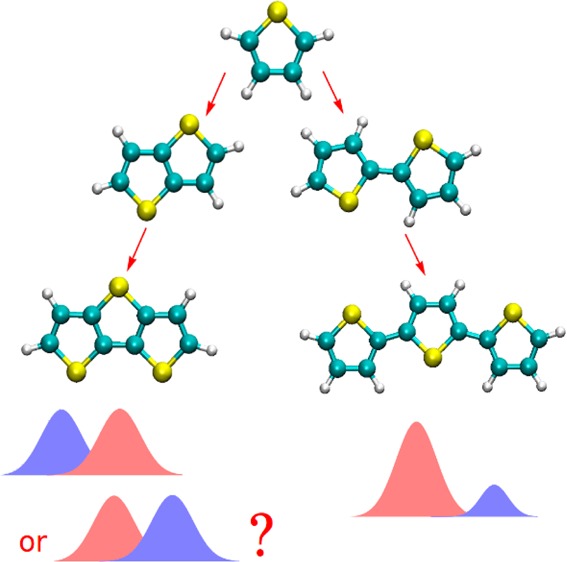
Thiophene-based materials play a central role in the field of organic electronics.1−3 Derivatives of thiophene, oligothiophenes and oligothienoacenes are extensively used in organic photovoltaics,4−10 light emitting diodes,11−15 field effect transistors,16−21 and so forth. Typically high extinction coefficients make them particularly suitable for solar cell materials. As a matter of fact, organic dyes, which do not contain thiophene motifs, seem to be in minority. This is part of the reason why excited states of simple thiophene compounds have drawn interest from numerous theoretical perspectives, including spectroscopy,22−36 excited state geometries,24,30,34 and nonadiabatic molecular dynamics.37,38 In this Letter, we discuss the computational conundrum associated with the low-lying bright ππ* singlet excited states of thiophene, short oligothiophenes, and oligothienoacenes (planar fused oligomers). Figure 1 compares the absorption spectra of thiophene computed with linear response time-dependent density functional theory (TDDFT) and a post-Hartree–Fock (post-HF) formalism. The overall band structure appears rather similar, yet decomposition into individual states (vide infra) reveals an inversion that could dramatically impact the computational prediction of photochemical and photophysical processes of thiophene-based compounds. We believe that this dichotomy and especially its consequences have been overlooked in the literature. The following analysis discusses the underlying origin for this contrasting behavior and identifies methods that alleviate the problem.

Figure 1.

Figure 1

Open in a new tab

Photoabsorption spectra computed from the Wigner distribution (red line) of thiophene. The spectra were decomposed into contributions from two lowest excited states, S1 and S2. The red peak is mainly due to the excitations from highest occupied to the lowest unoccupied molecular orbital (HOMO → LUMO, B2), whereas the blue peak is dominated by HOMO-1 → LUMO, A1, character. The cc-pVTZ basis set was used.

TDDFT,39 or more precisely linear response TDDFT within the adiabatic approximation,40 has emerged as the most widely used method for molecular excited states.41 Its exalted status certainly arises from the combination of low computational cost and, in many cases, amazing predictive power for both excitation energies42 and excited state properties43 of fairly large systems. This contrasts sharply with highly accurate multireference methods, such as CASPT2 (complete active space second order perturbation theory)44 and MCQDPT2 (multiconfigurational quasi-degenerate second order perturbation theory),45 which can be applied only to small systems that appear particularly challenging (of relevance to the present study, we point out the controversy with CASPT2 results for bithiophene32). Although TDDFT is a formally exact theory, standardly employed approximations result in several limitations. These include the underestimation of charge-transfer and Rydberg excitations,46 underestimation of triplet excitation energies,47 and a general inapplicability for high-lying excited states.48 The ubiquitous adiabatic approximation is responsible for the inaccurate description of conical intersections as well as the absence of doubly and multiply excited states49,50 (though it also underlies the charge-transfer problem51). Valence ππ* states with mainly single excitation character (which are studied here) are usually considered less problematic, although exceptions do exist. Grimme and Parac studied the two lowest singlet ππ* states of oligoacenes,52 short-axis polarized La (HOMO → LUMO) and long-axis polarized Lb (HOMO-1 → LUMO, HOMO → LUMO+1). They found La to be strongly underestimated by hybrid and GGA (generalized gradient approximation) functionals, with spurious inversion of states in case of naphthalene. La was later described as an “ionic”,52 “charge-transfer in disguise”53 and “charge-transfer-like”54 excitation. Substantial improvements were found with range separated hybrid functionals.55,56 Most recently, by employing a range separated hybrid functional with optimally tuned parameter,57 Baer, Kronik et al.54 reported excellent agreement with reference CC2 (approximate coupled cluster singles and doubles)58 results, thereby restoring the predictive power of TDDFT for the oligoacene series.

Here we focus upon the ππ* state inversion in related categories of π-conjugated thiophenes and oligothienoacenes that are, nevertheless, distinct in nature due to the presence of third row heteroatoms (i.e., low-lying d-orbitals close in energy) and lower symmetry. The problem illustrated for thiophene in Figure 1 is further examined by computing the vertical excitation energies of the two lowest ππ* states at various TDDFT and post-Hartree–Fock levels (Figure 2a). TDDFT generally predicts that two states, one dominated by the HOMO → LUMO (B2) and another by the HOMO-1 → LUMO (A1) transition, appear in a reversed order (or nearly degenerate) when compared to more accurate post-HF methods. The dependence on the specific exchange-correlation kernels and especially on the fraction of exact exchange is assessed via consideration of different categories of functionals: PBE (GGA), B3LYP and PBE0 (global GGA hybrid), M06 (meta-GGA hybrid), M06-2X (meta-GGA hybrid with 54% Hartree–Fock exchange), long-range corrected hybrid, ωB97x-D as well as optimally tuned long-range corrected hybrid LC-PBE*. Despite their conceptual differences, each of these functionals gives the same qualitative results: two transitions of similar intensities with B2 being slightly lower than A1. Including an implicit polar solvent does not alter the ordering of the transitions and only slightly affects the excitation energies (see Supporting Information). This state ordering is amplified with the CIS (configuration interaction singles) approach, and its response analogue TD-HF (time dependent Hartree–Fock).59 However, the energy of the HOMO-1 → LUMO (A1) state drops by more than 1 eV, and the sequence reverses when correlation is added to CIS by means of doubles and approximate triples using the CIS(D) method.60 This indicates that A1 is highly sensitive to the correlation effects introduced by CIS(D). CC2 and the second order algebraic diagrammatic construction, ADC(2),61 predict the same ordering as CIS(D). This post-HF picture is further solidified by the computationally more involved EOM-CCSD (equation of motion coupled cluster singles doubles),62 SAC–CI (symmetry adapted cluster–configuration interaction)63 and multi state MS-CASPT2 of ref (34). Additionally, the agreement achieved by the double hybrid TDA-B2PLYP with wavefunction-based methods is excellent. Similar in spirit to CIS(D), the double hybrid approach of Grimme and Neese64 adds perturbative second-order corrections to the CIS-like representation of TDDFT (i.e., TDDFT in Tamm-Dancoff approximation; TDA). Although less dramatic, an inversion similar to CIS/CIS(D) is found for the two excited states of thiophene with the double hybrid after introducing the perturbative correction (for details, see Table 1 in Supporting Information).

Figure 2.

Figure 2

Open in a new tab

Excitation energies of the two lowest ππ* states (S1 and S2) of (a) thiophene and (b) dithieno[2,3-b:2′,3′-d]thiophene. Radii of the circles are proportional to the oscillator strengths, and the colors indicate the dominant character. Relevant M06 orbitals are shown. Note that there is no qualitative difference between Kohn–Sham and Hartree–Fock orbitals. The cc-pVQZ basis set was employed. *EOM-CCSD indicates that the energies of dithienothiophene were computed with the cc-pVTZ basis set. The **CASPT2 results for thiophene are taken from ref (34) and correspond to experimental geometry of Bak et al.65

Similar patterns are seen for the A1 and B2 representations of fused dithienothiophene (Figure 2b), which belongs to the same symmetry point group, C2v, as the thiophene example discussed above. Transiting from CIS to CIS(D) inverses the energy ordering of the two ππ* excitations. The TDDFT computations generally match the CIS trend, with the exception of pure PBE, which still gives too low excitation energies. On the other hand, wavefunction-based methods, along with TDA-B2PLYP, slightly improve the CIS(D) results through reduction of the energy gap between the two states. The possibility of double excitations playing a role can be excluded as diagnostic tools associated with ADC(2) and CC2 indicate that both states are dominated by single excitations from the single configurational ground state. The origin of the TDDFT problems is more subtle than that of CIS (i.e., correlation effects). In fact, from the energetic perspective the HOMO-1 → LUMO state is reasonably well positioned by both the reference wavefunction methods and TDDFT, especially when functionals with moderate amount of exact exchange are chosen. By carefully examining Figure 2a and b and drawing a parallel with the oligoacene example discussed above,52−56 it appears that the HOMO → LUMO state is underestimated by TDDFT. Inclusion of exact exchange shifts the energy of this transition; however, it simultaneously shifts the other state, which is affected by correlation effects. The overall result being that no qualitative improvement is observed. Optimally tuned long-range corrected functional54 performs no better than hybrid and long-range corrected hybrid functionals. The state inversion in the TDDFT context is certainly caused by interplay of different effects that influence each of the two states. Because none of the standard functionals (within the strict linear response TDDFT) that are tested here provides a suitable description and the “single state engineering” through increasing the amount of exact exchange is ineffective, the error is inherently connected with subtler effects in the description of correlation for the excited state. The trends obtained with the double hybrid are qualitatively correct, emphasizing the importance of perturbative doubles corrections applied to TDA. Upon inclusion of virtual orbitals, the CIS(D)-like correction captures nonlocal correlation effects missed by conventional approximate functionals in the adiabatic approximation, as advocated by Grimme et al.64,66,67 We note, however, that the (D) correction term is only a pragmatic fix in the context of TDDFT. The mechanisms leading to an improvement between uncorrected TDDFT and TDDFT/CIS(D), in the framework of exact TDDFT, are surely more complex to grasp than those between CIS and CIS(D). In this context, we notice that even the Tamm–Dancoff approximation applied to certain functionals (for instance PBE0) may improve the results of the parent TDDFT approach.

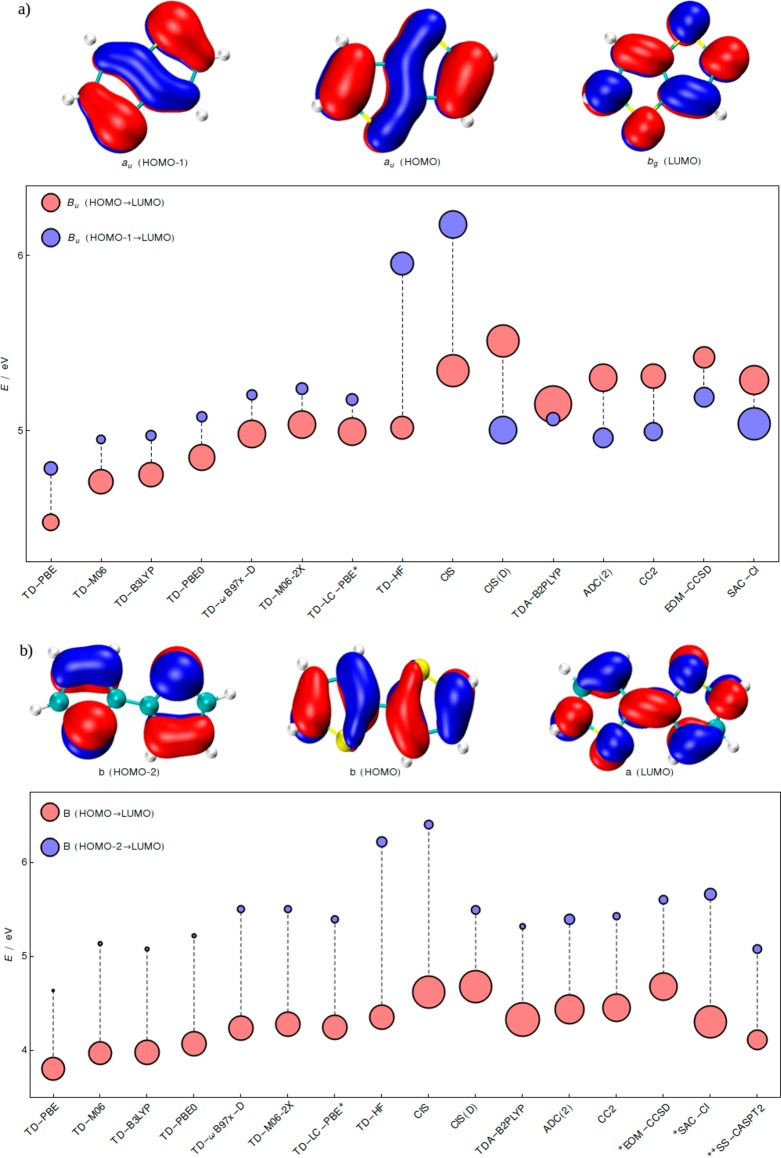
C2h thienothiophene (Figure 3a) is a somewhat more complicated example. CIS(D) again inverts CIS, and so does the double hybrid with respect to its underlying TDA energies. Yet the TDA-B2PLYP excitation energies do not align well with those from the post-Hartee–Fock methods. The TDDFT picture contrasts with the wavefunction-based methods with the intense state lying slightly below the second weaker state. Becaues of symmetry reasons (two states of Bu representation close in energy), our analysis of relaxed density differences reveals a large degree of character mixing, rather than the clear-cut inversion implied by the simplified orbital representation. The character ambiguity arises from the different extents of density increase/depletion at sulfur atoms and the central CC bond (see Supporting Information). Nevertheless, the problematic behavior of TDDFT concerning both the excitation energies and the corresponding oscillator strengths of thienothiophene ππ* states is fully in line with the two former examples (Figure 2). In sharp contrast, nonplanar bithiophene (Figure 3b) and terthiophene (Supporting Information) are rather unproblematic, at least qualitatively. The small dependence on the exact exchange fraction and the energy lowering of the second bright state when moving from CIS and CIS(D) still holds, yet the energy gap between the two ππ* states is consistently large and no inversion occurs. Such a separation arises from the limited conjugation between flexible oligothiophene units. Unlike in thiophene and thienoacenes, where we always refer to S1 and S2, for bithiophene and terthiophene, the two bright transitions are typically S1 and S3/S7, respectively (see Supporting Information).

Figure 3.

Figure 3

Open in a new tab

Excitation energies of the two lowest bright ππ* states of (a) thieno[3,2-b]thiophene (S1 and S2) and (b) 2,2′-bithiophene (S1 and S3/S4). As in Figure 2, radii of the circles are proportional to the oscillator strengths, and colors denote the orbital excitations with largest coefficients. The cc-pVQZ basis set was employed. The *EOM-CCSD and SAC–CI energies of bithiophene were computed at the cc-pVTZ level. The **CASPT2 results of bithiophene are taken from 32 and correspond to the ground state structure optimized at CASPT2 level with C2h symmetry.

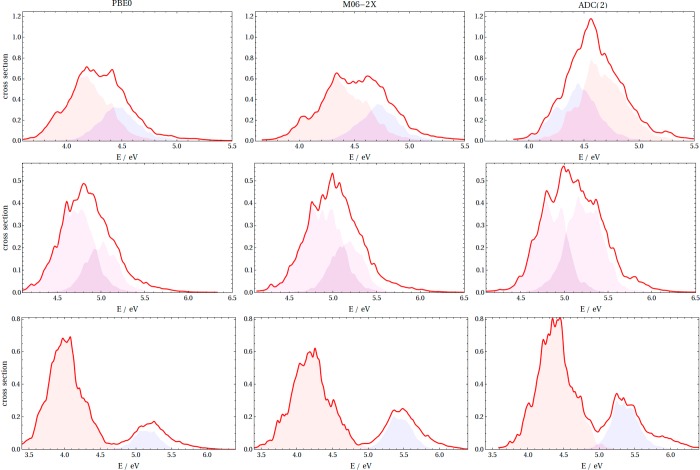
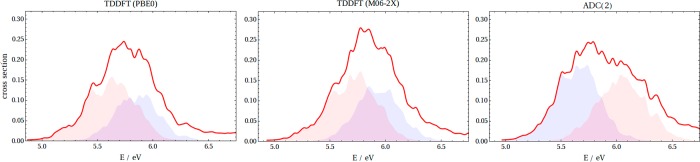
The consequence of the state inversion is best illustrated by the absorption spectra of thiophene highlighted earlier (Figure 1) and its derivatives (Figure 4), which are computed using the geometries sampled from semiclassical Wigner distribution (see Computational Methods) at three illustrative levels, PBE0, M06-2X, and ADC(2). Despite the use of an identical set of 500 initial structures generated from a Wigner distribution in the ground electronic state, the TDDFT spectra of thiophene and dithienothiophene contrast with the ADC(2) spectra. The decomposition of the spectrum into the relevant state contributions (color coding is the same as in Figures 1 and 2) reveals that the inversion is not just an artifact of the optimized geometries: the overall peak intensities largely follow the trends given by the oscillator strengths in the static computations. For thiophene, both functionals predict two overlapping peaks, which results in a single unstructured hill, whereas the ADC(2) spectrum shows both a different state ordering and a longer tail at higher energies, consistent with experimentally measured cross sections.36 The situation is similar for dithienothiophene, where ADC(2) places two states close in energy resulting in an intense peak differing from TDDFT predictions. The seemingly reliable TDDFT spectra of thienothiophene actually emerge from a peculiar mixing of states. Although we intentionally do not attribute the dominant character from the orbital contributions, the contrast between the methods is clearly visible from the small TDDFT intensities of S2, which is consistent with the oscillator strengths computed at the optimized geometry (Figure 3a). On the other hand, the dichotomy does not apply to bithiophene, for which all three methods give similar pictures with only minor difference in the position and peak intensity. Note that the two functionals give similar results in all four cases.

Figure 4.

Figure 4

Open in a new tab

Photoabsorption spectra computed from the Wigner distribution (red line) of dithienothiophene (first row), thienothiophene (second row), and bithiophene (third row). The dithienothiophene and thienothiophene spectra were decomposed into contributions from S1 and S2 and S1 and S3+S4 in the case of bithiophene. The color code reflects the main excitation character (in line with Figures 1 and 2). The same color is used for the bands of thienothiophene to reflect the character ambiguity. The cc-pVTZ basis set was used.

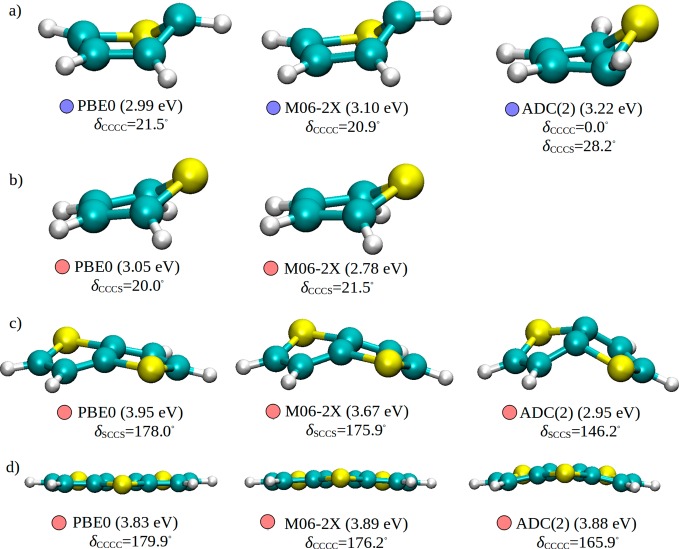
Finally, it is instructive to examine the impact of the preceding observations on the excited state geometries. The inversion of the states seen for ground state equilibrium geometries has little meaning as molecules that relax in the excited state can adopt conformations far from the Franck–Condon region. The PBE0, M06-2X, and ADC(2) optimized minima of the excited state with the initial A1 symmetry (Figure 2) of thiophene are displayed in Figure 5a. ADC(2) predicts the S-puckered minimum, whereas TDDFT converged to the C-puckered structures. The Cs-symmetric S-puckered geometry is a transition state at the TDDFT level, as pointed out by Marian et al.30 On the other hand, both DFT-MRCI30 and CASPT234 (δCCCS = 26.7°) optimizations confirm the S-puckered structure as being a minimum. Slightly different S-puckered minima are found when the B2 state is optimized with both PBE0 and M06-2X (Figure 5b), albeit not with ADC(2). Actually, reoptimization of the TDDFT structures with ADC(2) leads to an intersection with the ground state, consistent with CASPT2 computations of Stenrup,34 suggesting that B2 may be unbound. Even more surprising are the S1 geometries of thienothiophene and dithienothiophene (Figure 5c and d), for which large discrepancies exist for both the geometries and the vertical excitation energies when the two functionals are compared to ADC(2). For both systems, ADC(2) leads to tilted structure, whereas the two functionals prefer nearly planar frameworks. These systems were recently investigated by Jacquemin et al., who looked at how solvation models affect excited state geometries.68 Despite the different purpose of that work, we noticed that the quality of the results obtained with the usually reliable M06-2X functional should be taken with care. In contrast to previous examples, good agreement is achieved for the S1 minimum of bithiophene. All three methods predict the well-known planar quinoidal structure that shows the characteristic alternation of single and double bonds with only slight disagreement in the lengths of the terminal C–C bonds (see Supporting Information).

Figure 5.

Figure 5

Open in a new tab

Minima at the S1 adiabatic potential energy surface of: (a, b) thiophene, (c) thienothiophene, and (d) dithienothiophene. We report the vertical excitation energies (in parentheses), the dominant orbital excitations at given geometry (denoted by red and blue circles as in Figures 2 and 3), and the relevant dihedral angles. δCCCC of dithienothiophene denotes the dihedral angle between the middle and the side ring. The cc-pVTZ basis set was used.

To summarize, we demonstrated the problematic performance of TDDFT for the two lowest ππ* states of thiophene and short thienoacenes. The failures include incorrect state ordering, poor distribution of oscillator strengths, and erroneous descriptions of critical points on the excited state potential energy surfaces. Similar trends are also identified for furan and its fused derivative (see Supporting Information), but without the spurious inversion. What makes the thiophene example unique with respect to the furo- and oligoacene compounds is the large oscillator strengths of the two states involved and the experimental relevance. The incorrect state ordering and oscillator strengths thus notably impact the computed absorption spectra. In addition, serious discrepancies were found between TDDFT and ADC(2) optimized excited state geometries. These qualitative failures directly affect the possible prediction of adiabatic excitation energies and photoemission properties. Achieving accurate potential energy surfaces is also crucial for excited state molecular dynamics simulations, for which inexpensive TDDFT is often the method of choice. More generally, the present study emphasizes the importance of systematically carrying out careful comparisons with more accurate wavefunction-based methods.

Computational Methods

Ground state optimized structures and vibrational frequencies were obtained at the M06/DGDZVP69 level with the Gaussian0970 program package. Excited states were analyzed in their respective point groups: C2v for thiophene, furan, and dithienothiophene, C2h for thienothiophene and furofuran, C2 for bithiophene, and Cs for terthiophene. Excitation energies were computed with Gaussian09 (M06, M06-2X, ωB97x-D, LC-PBE, LC-PBE*, TD-HF, CIS/CIS(D), EOM-CCSD, SAC–CI), Turbomole 6.571 (PBE, PBE0, TDA(PBE0), B3LYP, ADC(2), CC2), and Orca 3.0.272 (TDA-B2PLYP), and numerical values are given in Supporting Information (Tables 1 and 2). In ADC(2) and CC2 computations, we apply the resolution of identity and the frozen core approximations. For the B2PLYP computations, the resolution of identity was employed. M06 and M06-2X computations use an ultrafine integration grid. SAC–CI is performed with the default parameters and convergence criteria of the Gaussian09 program. The CIS(D) oscillator strengths in Figures 2 and 3 are taken from CIS. LC-PBE* computations were performed by tuning the range separation parameter γ to match the HOMO energy and the difference between the total energies of the cation and neutral molecule. All the excitation energies were converged at the cc-pVQZ level, unless otherwise specified. Comparisons with smaller and augmented basis sets show a small and systematic deviation for two valence excitations. To reduce the computational burden, the photoabsorption spectra and excited state geometry optimizations were performed with the cc-pVTZ basis set. Excited state geometries were optimized with Turbomole 6.5 (PBE0, ADC(2)) and Gaussian09 (M06-2X) with tight convergence criteria and no symmetry constraints. The nuclear configurations used for spectral simulations were sampled by an uncorrelated Wigner distribution in the ground sate,73,74 as implemented in Newton-X package.75 A total of 500 structures were taken for each compound and vertical excitation energies and oscillator strengths were computed. Each transition was broadened by a Lorentzian using a phenomenological width of 0.05 eV. The spectra were decomposed into contributions from different states and the main character was assigned according to the dominant orbital excitations. Molecules, orbitals, and difference densities were visualized with VMD 1.9.1 program package.76

Acknowledgments

The authors acknowledge funding from the European Research Council (ERC Grants 306528, “COMPOREL”) and the Swiss National Science Foundation (no. 137666).

Supporting Information Available

Details on the excitation energies, density differences, spectra or excited state geometries of thiophene, thienothiophene, bithiophene, dithienothiophene, and terthiophene. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Supplementary Material

jz5022087_si_001.pdf (5.2MB, pdf)

References

  1. Perepichka I. F.; Perepichka D. F.. Handbook of Thiophene-Based Materials: Applications in Organic Electronics and Photonics; John Wiley & Sons Ltd: Chichester, U. K., 2009. [Google Scholar]
  2. Takimiya K.; Shinamura S.; Osaka I.; Miyazaki E. Thienoacene-Based Organic Semiconductors. Adv. Mater. 2011, 23, 4347–4370. [DOI] [PubMed] [Google Scholar]
  3. Mishra A.; Ma C.; Bäuerle P. Functional Oligothiophenes: Molecular Design for Multidimensional Nanoarchitectures and Their Applications. Chem. Rev. 2009, 109, 1141–1276. [DOI] [PubMed] [Google Scholar]
  4. Zhang F.; Wu D.; Xu Y.; Feng X. Thiophene-Based Conjugated Oligomers for Organic Solar Cells. J. Mater. Chem. 2011, 21, 17590–17600. [Google Scholar]
  5. Wang Z.; Koumura N.; Cui Y.; Takahashi M.; Sekiguchi H.; Mori A.; Kubo T.; Furube A.; Hara K. Hexylthiophene-Functionalized Carbazole Dyes for Efficient Molecular Photovoltaics: Tuning of Solar-Cell Performance by Structural Modification. Chem. Mater. 2008, 20, 3993–4003. [Google Scholar]
  6. Rupert B. L.; Mitchell W. L.; Ferguson A. J.; Köse M. E.; Rance W. L.; Rumbles G.; Ginley D. S.; Shaheen S. E.; Kopidakis N. Low-Bandgap Thiophene Dendrimers for Improved Light Harvesting. J. Mater. Chem. 2009, 19, 5311–5324. [Google Scholar]
  7. Mishra A.; Pootrakulchote N.; Wang M.; Moon S. J.; Zakeeruddin S. M.; Grätzel M.; Bäuerle P. A Thiophene-Based Anchoring Ligand and Its Heteroleptic Ru(II)-Complex for Efficient Thin-Film Dye-Sensitized Solar Cells. Adv. Funct. Mater. 2011, 21, 963–970. [Google Scholar]
  8. Gao P.; Tsao H. N.; Grätzel M.; Nazeeruddin M. K. Fine-Tuning the Electronic Structure of Organic Dyes for Dye-Sensitized Solar Cells. Org. Lett. 2012, 14, 4330–4333. [DOI] [PubMed] [Google Scholar]
  9. Ellinger S.; Graham K. R.; Shi P.; Farley R. T.; Steckler T. T.; Brookins R. N.; Taranekar P.; Mei J.; Padilha L. A.; Ensley T. R.; et al. Donor-Acceptor-Donor-based π-Conjugated Oligomers for Nonlinear Optics and Near-IR Emission. Chem. Mater. 2011, 23, 3805–3817. [Google Scholar]
  10. Sun X.; Zhou Y.; Wu W.; Liu Y.; Tian W.; Yu G.; Qiu W.; Chen S.; Zhu D. X-Shaped Oligothiophenes as a New Class of Electron Donors for Bulk-Heterojunction Solar Cells. J. Chem. Phys. B 2006, 110, 7702–7707. [DOI] [PubMed] [Google Scholar]
  11. Gigli G.; Inganäs O.; Anni M.; De Vittorio M.; Cingolani R.; Barbarella G.; Favaretto L. Multicolor Oligothiophene-Based Light-Emitting Diodes. Appl. Phys. Lett. 2001, 78, 1493–1495. [Google Scholar]
  12. Mazzeo M.; Pisignano D.; Favaretto L.; Barbarella G.; Cingolani R.; Gigli G. Bright Oligothiophene-Based Light Emitting Diodes. Synth. Met. 2003, 139, 671–373. [Google Scholar]
  13. Lim E.; Jung B.; Shim H. Synthesis and Characterization of a New Light-Emitting Fluorene-Thieno[3,2-b]thiophene-Based Conjugated Copolymer. Macromolecules 2003, 36, 4288–4293. [Google Scholar]
  14. Evenson S. J.; Mumm M. J.; Pokhodnya K. I.; Rasmussen S. C. Highly Fluorescent Dithieno[3,2-b:2′,3′-d]pyrrole-Based Materials: Synthesis, Characterization, and OLED Device Applications. Macromolecules 2011, 44, 835–841. [Google Scholar]
  15. Zhao Z.; Deng C.; Chen S.; Lam J. W. Y.; Qin W.; Lu P.; Wang Z.; Kwok H. S.; Ma Y.; Qiu H.; et al. Full Emission Color Tuning in Luminogens Constructed from Tetraphenylethene, Benzo-2,1,3-thiadiazole and Thiophene Building Blocks. Chem. Commun. 2011, 47, 8847–8849. [DOI] [PubMed] [Google Scholar]
  16. Zhang L.; Tan L.; Wang Z.; Hu W.; Zhu D. High-Performance, Stable Organic Field-Effect Transistors Based on trans-1,2-(Dithieno[2,3-b:3,2-d]thiophene)ethene. Chem. Mater. 2009, 21, 1993–1999. [Google Scholar]
  17. Liu Y.; Wang Y.; Wu W.; Liu Y.; Xi H.; Wang L.; Qiu W.; Lu K.; Du C.; Yu G. Synthesis, Characterization, and Field-Effect Transistor Performance of Thieno[3,2-b]thieno[2′,3′:4,5]thieno[2,3-d]thiophene Derivatives. Adv. Funct. Mater. 2009, 19, 772–778. [Google Scholar]
  18. Kang M. J.; Miyazaki E.; Osaka I.; Takimiya K.; Nakao A. Diphenyl Derivatives of Dinaphtho[2,3-b:2′,3′-f]thieno[3,2-b]thiophene: Organic Semiconductors for Thermally Stable Thin-Film Transistors. ACS Appl. Mater. Interfaces 2013, 5, 2331–2336. [DOI] [PubMed] [Google Scholar]
  19. Li R.; Dong H.; Zhan X.; Li H.; Wen S. H.; Deng W. Q.; Han K. L.; Hu W. Physicochemical, Self-Assembly and Field-Effect Transistor Properties of anti- and syn- Thienoacene Isomers. J. Mater. Chem. 2011, 21, 11335–11339. [Google Scholar]
  20. Kim H.; Kim Y.; Kim T.; Noh Y.; Pyo S.; Yi M. H.; Kim D.; Kwon S. Synthesis and Studies on 2-Hexylthieno[3,2-b]thiophene End-Capped Oligomers for OTFTs. Chem. Mater. 2007, 19, 3561–3567. [Google Scholar]
  21. Zhang Y.; Cai X.; Bian Y.; Li X.; Jiang J. Heteroatom Substitution of Oligothienoacenes: From Good p-Type Semiconductors to Good Ambipolar Semiconductors for Organic Field-Effect Transistors. J. Phys. Chem. C 2008, 112, 5148–5159. [Google Scholar]
  22. Serrano-Andrés L.; Merchán M.; Fülscher M.; Roos B. O. A Theoretical Study of the Electronic Spectrum of Thiophene. Chem. Phys. Lett. 1993, 211, 125–134. [Google Scholar]
  23. Rubio M.; Merchán M.; Ortí E.; Roos B. O. A Theoretical Study of the Electronic Spectrum of Bithiophene. J. Chem. Phys. 1995, 102, 3580–3586. [Google Scholar]
  24. Beljonne D.; Cornil J.; Friend R. H.; Janssen R. A. J.; Brédas J. L. Influence of Chain Length and Derivatization on the Lowest Singlet and Triplet States and Intersystem Crossing in Oligothiophenes. J. Am. Chem. Soc. 1996, 118, 6453–6461. [Google Scholar]
  25. Wan J.; Hada M.; Ehara M.; Nakatsuji H. Electronic Excitation Spectrum of Thiophene Studied by Symmetry-Adapted Cluster Configuration Interaction Method. J. Chem. Phys. 2001, 114, 842–850. [Google Scholar]
  26. Rubio M.; Ortí E.; Pou-AméRigo R.; Merchán M. Electronic Spectra of 2,2′-Bithiophene and 2,2′:5′,2″-Terthiophene Radical Cations: A Theoretical Analysis. J. Phys. Chem. A 2001, 105, 9788–9794. [Google Scholar]
  27. Della Sala F.; Heinze H. H.; Görling A. Excitation Energies of Terthiophene and Its Dioxide Derivative: A First-Principles Study. Chem. Phys. Lett. 2001, 339, 343–350. [Google Scholar]
  28. Rubio M.; Merchán M.; Pou-AméRigo R.; Ortí E. The Low-Lying Excited States of 2,2′-Bithiophene: A Theoretical Analysis. ChemPhysChem 2003, 4, 1308–1315. [DOI] [PubMed] [Google Scholar]
  29. Malavé Osuna R.; Zhang X.; Matzger A. J.; Hernández V.; López Navarrete J. T. Combined Quantum Chemical Density Functional Theory and Spectroscopic Raman and UV-Vis-NIR Study of Oligothienoacenes with Five and Seven Rings. J. Phys. Chem. A 2006, 110, 5058–5065. [DOI] [PubMed] [Google Scholar]
  30. Salzmann S.; Kleinschmidt M.; Tatchen J.; Weinkauf R.; Marian C. M. Excited States of Thiophene: Ring Opening as Deactivation Mechanism. Phys. Chem. Chem. Phys. 2008, 10, 380–392. [DOI] [PubMed] [Google Scholar]
  31. Aragó J.; Viruela P. M.; Gierschner J.; Ortí E.; Milián-Medina B. Oligothienoacenes Versus Oligothiophenes: Impact of Ring Fusion on the Optical Properties. Phys. Chem. Chem. Phys. 2011, 13, 1457–1465. [DOI] [PubMed] [Google Scholar]
  32. Andrzejak M.; Witek H. A. The Elusive Excited States of Bithiophene: A CASPT2 Detective Story. Theor. Chem. Acc. 2011, 129, 161–172. [Google Scholar]
  33. Seigert S.; Vogeler F.; Marian C. M.; Weinkauf R. Throwing Light on Dark States of α-Oligothiophenes of Chain Lengths 2 to 6: Radical Anion Photoelectron Spectroscopy and Excited-State Theory. Phys. Chem. Chem. Phys. 2011, 13, 10350–10363. [DOI] [PubMed] [Google Scholar]
  34. Stenrup M. Theoretical Study of the Radiationless Deactivation Mechanisms of Photo-Excited Thiophene. Chem. Phys. 2012, 397, 18–25. [Google Scholar]
  35. Stendardo E.; Avila Ferrer F.; Santoro F.; Improta R. Vibrationally Resolved Absorption and Emission Spectra of Dithiophene in the Gas Phase and in Solution by First-Principle Quantum Mechanical Calculations. J. Chem. Theory Comput. 2012, 8, 4483–4493. [DOI] [PubMed] [Google Scholar]
  36. Holland D. M. P.; Trofimov A. B.; Seddon E. A.; Gromov E. V.; Korona T.; de Oliveira N.; Archer L. E.; Joyeux D.; Nahon L. Excited Electronic States of Thiophene: High Resolution Photoabsorption Fourier Transform Spectroscopy and Ab Initio Calculations. Phys. Chem. Chem. Phys. 2014, 16, 21629–21644. [DOI] [PubMed] [Google Scholar]
  37. Köppel H.; Gromov E. V.; Trofimov A. B. Multi-Mode-Multi-State Quantum Dynamics of Key Five-Membered Heterocycles: Spectroscopy and Ultrafast Internal Conversion. Chem. Phys. 2004, 304, 35–49. [Google Scholar]
  38. Cui G.; Fang W. Ab Initio Trajectory Surface-Hopping Study on Ultrafast Deactivation Process of Thiophene. J. Phys. Chem. A 2011, 115, 11544–11550. [DOI] [PubMed] [Google Scholar]
  39. Runge E.; Gross E. K. U. Density-Functional Theory for Time-Dependent Systems. Phys. Rev. Lett. 1984, 52, 997–1000. [Google Scholar]
  40. Casida M. E.Time-Dependent Density-Functional Response Theory for Molecules. In Recent Advances in Density Functional Methods, Part I; Chong D. P., Ed.; World Scientific: Singapore, 1995; pp 155–193. [Google Scholar]
  41. González L.; Escudero D.; Serrano-Andrés L. Progress and Challenges in the Calculation of Electronic Excited States. ChemPhysChem 2012, 13, 28–51. [DOI] [PubMed] [Google Scholar]
  42. Laurent A. D.; Adamo C.; Jacquemin D. Dye Chemistry with Time-Dependent Density Functional Theory. Phys. Chem. Chem. Phys. 2014, 16, 14334–14356. [DOI] [PubMed] [Google Scholar]
  43. Adamo C.; Jacquemin D. The Calculations of Excited-State Properties with Time-Dependent Density Functional Theory. Chem. Soc. Rev. 2013, 42, 845–856. [DOI] [PubMed] [Google Scholar]
  44. Andersson K.; Malmqvist P. Å.; Roos B. O.; Sadlej A. J.; Wolinski K. J. Second-Order Perturbation Theory with a CASSCF Reference Function. J. Phys. Chem. 1990, 94, 5483–5488. [Google Scholar]
  45. Nakano H. Quasidegenerate Perturbation-Theory with Multiconfigurational Self-Consistent-Field Reference Functions. J. Chem. Phys. 1993, 99, 7983–7992. [Google Scholar]
  46. Dreuw A.; Weisman J. L.; Head-Gordon M. Long-Range Charge-Transfer Excited States in Time-Dependent Density Functional Theory Require Non-Local Exchange. J. Chem. Phys. 2003, 119, 2943–2946. [Google Scholar]
  47. Tozer D. J.; Handy N. C. On the Determination of Excitation Energies Using Density Functional Theory. Phys. Chem. Chem. Phys. 2000, 2, 2117–2121. [Google Scholar]
  48. Casida M. E.; Jamorski C.; Casida K. C.; Salahub D. R. Molecular Excitation Energies to High-Lying Bound States from Time-Dependent Density-Functional Response Theory: Characterization and Correction of the Time-Dependent Local Density Approximation Ionization Threshold. J. Chem. Phys. 1998, 108, 4439–4449. [Google Scholar]
  49. Maitra N. T.; Zhang F.; Cave R. J.; Burke K. Double Excitations within Time-Dependent Density Functional Theory Linear Response. J. Chem. Phys. 2004, 120, 5932–5937. [DOI] [PubMed] [Google Scholar]
  50. Levine B. G.; Ko C.; Quenneville J.; Martínez T. J. Conical Intersections and Double Excitations in Time-Dependent Density Functional Theory. Mol. Phys. 2006, 104, 1039–1051. [Google Scholar]
  51. Ziegler T.; Krykunov M. On the Calculation of Charge Transfer Transitions with Standard Density Functionals Using Constrainted Variational Density Functional Theory. J. Chem. Phys. 2010, 133, 074104. [DOI] [PubMed] [Google Scholar]
  52. Grimme S.; Parac M. Substantial Errors from Time-Dependent Density Functional Theory for the Calculation of Excited States of Large π Systems. ChemPhysChem 2003, 4, 292–295. [DOI] [PubMed] [Google Scholar]
  53. Richard R. M.; Herbert J. M. Time-Dependent Density-Functional Descriptions of the 1La State in Polycyclic Aromatic Hydrocarbons: Charge-Transfer Character in Disguise. J. Chem. Theory Comput. 2011, 7, 1296–1306. [DOI] [PubMed] [Google Scholar]
  54. Kuritz N.; Stein T.; Baer R.; Kronik L. Charge-Transfer-Like π→π* Excitations in Time-Dependent Density Functional Theory: A Conundrum and Its Solution. J. Chem. Theory Comput. 2011, 7, 2408–2415. [DOI] [PubMed] [Google Scholar]
  55. Peach M. J. G.; Benfield P.; Helgaker T.; Tozer D. J. Excitation Energies in Density Functional Theory: An Evaluation and a Diagnostic Test. J. Chem. Phys. 2008, 128, 044118. [DOI] [PubMed] [Google Scholar]
  56. Wong B. M.; Hsieh T. H. Optoelectronic and Excitonic Properties of Oligoacenes: Substantial Improvements from Range-Separated Time-Dependent Density Functional Theory. J. Chem. Theory Comput. 2010, 6, 3704–3712. [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Stein T.; Kronik L.; Baer R. Reliable Prediction of Charge Transfer Excitations in Molecular Complexes Using Time-Dependent Density Functional Theory. J. Am. Chem. Soc. 2009, 131, 2818–2820. [DOI] [PubMed] [Google Scholar]
  58. Christiansen O.; Koch H.; Jørgensen P. The Second-Order Approximate Coupled Cluster Singles and Doubles Model CC2. Chem. Phys. Lett. 1995, 243, 409–418. [Google Scholar]
  59. Dreuw A.; Head-Gordon M. Single-Reference ab Initio Methods for the Calculation of Excited States of Large Molecules. Chem. Rev. 2005, 105, 4009–4037. [DOI] [PubMed] [Google Scholar]
  60. Head-Gordon M.; Rico R. J.; Oumi M.; Lee T. J. A Doubles Correction to Electronic Excited States from Configuration Interaction in the Space of Single Substitutions. Chem. Phys. Lett. 1994, 219, 21–29. [Google Scholar]
  61. Trofimov A. B.; Schirmer J. An Efficient Polarization Propagator Approach to Valence Electron Excitation Spectra. J. Phys. B: At. Mol. Opt. Phys. 1995, 28, 2299–2324. [Google Scholar]
  62. Sekino H.; Bartlett R. J. A Linear Response, Coupled-Cluster Theory for Excitation Energy. Int. J. Quantum Chem. Symp. 1984, 18, 255–265. [Google Scholar]
  63. Nakatsuji H.; Hirao K. Cluster Expansion of the Wavefunction. Symmetry-Adapted-Cluster Exapansion, Its Variational Determination, and Extension of Open-Shell Orbital Theory. J. Chem. Phys. 1978, 68, 2053–2065. [Google Scholar]
  64. Grimme S.; Neese F. Double-hybrid Density Functional Theory for Electronic Excited States of Molecules. J. Chem. Phys. 2007, 127, 154116. [DOI] [PubMed] [Google Scholar]
  65. Bak B.; Christensen D.; Hansen-Nygaard J.; Rastrup-Andersen J. The Structure of Thiophene. J. Mol. Spectrosc. 1961, 7, 58–63. [Google Scholar]
  66. Goerigk L.; Moellmann J.; Grimme S. Computation of Accurate Excitation Energies for Large Organic Molecules with Double-Hybrid Density Funcionals. Phys. Chem. Chem. Phys. 2009, 11, 4611–4620. [DOI] [PubMed] [Google Scholar]
  67. Goerigk L.; Grimme S. Double-Hybrid Density Functionals. WIREs Comput. Mol. Sci. 2014, 4, 576–600. [Google Scholar]
  68. Chibani S.; Laurent A. D.; Blondel A.; Mennucci B.; Jacquemin D. Excited-State Geometries of Solvated Molecules: Going Beyond the Linear-Response Polarizable Continuum Model. J. Chem. Theory Comput. 2014, 10, 1848–1851. [DOI] [PubMed] [Google Scholar]
  69. Kantchev E. A. B.; Norsten T. B.; Sullivan M. B. Time-Dependent Density Functional Theory (TDDFT) Modeling of Pechmann Dyes: from Accurate Absorption Maximum Prediction to Virtual Dye Screening. Org. Biomol. Chem. 2012, 10, 6682–6692. [DOI] [PubMed] [Google Scholar]
  70. Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Mennucci B.; Petersson G. A.. et al. Gaussian 09, Revision (A.02), ; Gaussian, Inc.: Wallingford, CT, 2009. [Google Scholar]
  71. Furche F.; Ahlrichs R.; Hättig C.; Klopper W.; Sierka M.; Weigend F. Turbomole. WIREs Comput. Mol. Sci. 2014, 4, 91–100. [Google Scholar]
  72. Neese F. The ORCA Program System. WIREs Comput. Mol. Sci. 2011, 2, 73–78. [Google Scholar]
  73. Barbatti M.; Aquino A. J. A.; Lischka H. The UV Absorpion of Nucleobases: Semi-Classical ab Initio Spectra Simulations. Phys. Chem. Chem. Phys. 2010, 12, 4959–4967. [DOI] [PubMed] [Google Scholar]
  74. Crespo-Otero R.; Barbatti M. Spectrum Simulation and Decomposition with Nuclear Ensemble: Formal Derivation and Application to Benzene, Furan and 2-Phenylfuran. Theor. Chem. Acc. 2012, 131, 1237. [Google Scholar]
  75. Barbatti M.; Ruckenbauer M.; Plasser F.; Pittner J.; Granucci G.; Persico M.; Lischka H. Newton-X: A Surface-Hopping Program for Nonadiabatic Molecular Dynamics. WIREs Comput. Mol. Sci. 2014, 4, 26–33. [Google Scholar]
  76. Humphrey W.; Dalke A.; Schulten K. VMD – Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 33–38. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

jz5022087_si_001.pdf (5.2MB, pdf)

Articles from The Journal of Physical Chemistry Letters are provided here courtesy of American Chemical Society

RESOURCES