Effects of Lys to Glu mutations in GsMTx4 on membrane binding, peptide orientation, and self-association propensity, as analyzed by molecular dynamics simulations

Abstract

GsMTx4, a gating modifier peptide acting on cationic mechanosensitive channels, has a positive charge (+5 e) due to six Lys residues. The peptide does not have a stereospecific binding site on the channel but acts from the boundary lipids within a Debye length of the pore probably by changing local stress. To gain insight into how these Lys residues interact with membranes, we performed molecular dynamics simulations of Lys to Glu mutants in parallel with our experimental work. In silico, K15E had higher affinity for 1-palmitoyl-2-oleoyl-glycero-3-phosphocholine bilayers than wild-type (WT) peptide or any other mutant tested, and showed deeper penetration than WT, a finding consistent with the experimental data. Experimentally, the inhibitory activities of K15E and K25E were most compromised, whereas K8E and K28E inhibitory activities remained similar to WT peptide. Binding of WT in an interfacial mode did not influence membrane thickness. With interfacial binding, the direction of the dipole moments of K15E and K25E were predicted to differ from WT, whereas those of K8E and K28E oriented similarly to that of WT. These results support a model in which binding of GsMTx4 to the membrane acts like an immersible wedge that serves as a membrane expansion buffer reducing local stress and thus inhibiting channel activity. In simulations, membrane-bound WT attracted other WT peptides to form aggregates. This may account for the positive cooperativity observed in the ion channel experiments. The Lys residues seem to fine-tune the depth of membrane binding, the tilt angle, and the dipole moments.

Graphical abstract

1. Introduction

GsMTx4 is a 34-residue peptide isolated from tarantula (Grammostola spatulata) venom and acts as a gating inhibitor on mechanosensitive channels (MSCs) that are activated by membrane tension [1,2]. Although the molecular structure of eukaryotic MSCs is still underway, GsMTx4 has been shown to be a specific modulator with high specificity toward cationic MSCs like Piezo1 [3]. It may also have activity against TRPC5 [4] and TRPC6 [5] cation channels, but has no activity against the K-selective 2-P domain TREK-1 MSCs [3]. At low concentrations (10⁻⁷–10⁻⁶ M), GsMTx4 inhibit cationic MSCs although it has shown some potentiation of the prokaryotic MSCs at higher concentrations. GsMTx4 belongs to the inhibitory cysteine knot (ICK) family [6,7] of venom peptides, and like other ICK peptides, it has a hydrophobic protrusion that is thought to facilitate bilayer penetration. While other ICK peptides interact stereospecifically with their targets, GsMTx4 is active in the L and D enantiomers [8] and hence inhibits gating by shifting the gating curves to higher tension.

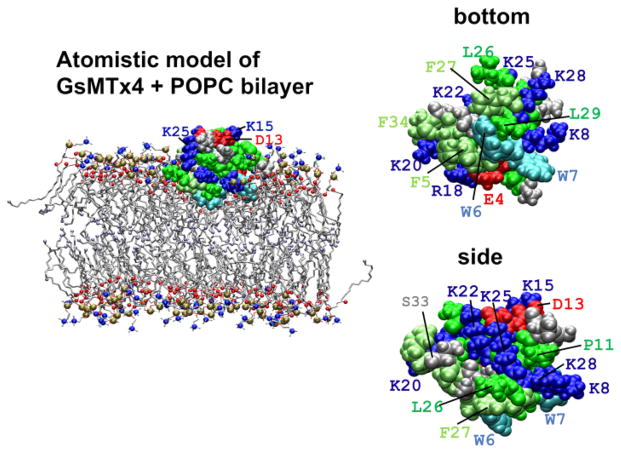
GsMTx4 has been subjected to several computational analyses [9,10], but the interactions with membranes remain poorly understood. We expected that peptide binding would produce local deformation and local changes in membrane thickness and curvature [8,10], but these effects have not been systematically evaluated. One notable feature of GsMTx4 is that it has high net positive charge (+5 e). When the peptide is viewed from the side of the hydrophobic protrusion, six Lys residues and one Arg residue form a ring-like structure encircling the periphery (Figure 1). Our previous simulations suggested that GsMTx4 could interact with the lipid bilayer through a shallow (interfacial) binding mode and a deeper mode [9] wherein some Lys residues interacted with lipid head groups of the inner monolayer while the remaining Lys interacted with head groups of the outer monolayer. At low concentrations GsMTx4 inhibits bacterial channels MscS and MscL, but at higher concentrations there may be potentiation which might reflect a concentration-dependent transition from shallow to deep binding mode [11,12].

Figure 1.

Van der Waals rendering of GsMTx4 structure and the simulation configuration. Left: a representative snapshot from an AT 60/64-WT free simulation of WT GsMTx4 and a POPC bilayer membrane. Trp residues are cyan, Phe residues are lime, other hydrophobic residues (Ala, Cys, Ile, Leu, Met, Pro and Val) are green, basic residues (Arg ad Lys) are blue, and acidic residues (Asp and Glu) are red. For the POPC head group, the nitrogen atoms are blue, phosphorus atoms are ocher, and carbonyl oxygen atoms are red spheres. The terminal carbon atoms of the lipid acyl tails are ice blue spheres. Water molecules and chloride ions are not shown. Right: a bottom and side view of WT GsMTx4 sampled from an in-water simulation. The bottom view illustrates the hydrophobic protrusion that contains W6. The graphical representation is similar to the panel on the left.

To better understand the role of the positively charged residues, we mutated each Lys to Glu (KtoE: K8E, K15E, K20E, K22E, K25E, and K28E) and we examined the effect on channels and the physical chemistry of the peptide lipid interactions; these results are reported in another paper [13]. Briefly, the six mutants inhibited MSCs to variable degrees, but the bilayer affinities did not correlate with inhibition. For example, K15E had the most compromised inhibitory activity relative to WT, but had higher affinity for membranes. We also observed that, in general, all peptides reside at a shallow, apparently surface absorbed, position in membranes at resting tension occupying only a small surface area. The depth and surface area occupied by the peptides increases as the membrane tension increases so that the peptides act as “area clamps”. The tension dependent penetration was the strongest predictor of inhibitory activity. The deeper penetration of the mutants at resting tensions would compromise their capacity to buffer changes in membrane free volume as tension changes during stretch.

To try and gain detailed insight into the interaction of GsMTx4 with the bilayer, unless otherwise noted, we undertook a blinded simulation study of what the KtoE mutations would do to the bilayer. The simulations were done only knowing the mutations, but not the experimental results. Here, we discuss the blinded computational analyses in light of the experimental work [13]. The experiments also served as a test of the predictive power of the combined atomistic (AT) and coarse-grained (CG) molecular dynamics (MD) simulations.

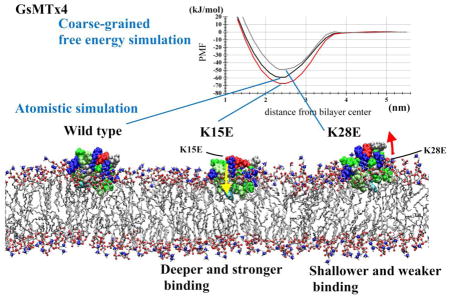
In brief, we found that the most compromised mutant, K15E, bound more tightly to a 1-palmitoyl-2-oleoyl-glycero-3-phosphocholine (POPC) bilayer in the AT and CG simulations relative to the WT and the other mutants. Perturbation of membrane structure induced by WT binding in the shallow binding mode was not as intense as previously reported. Peptide penetration depth showed that mutants with compromised activity tended to penetrate deeper at resting membrane tension, consistent with experimental results. WT peptide penetrated deeper upon increasing membrane tension (increasing free volume) which was predicted by the experimental displacement of the peptide under changing monolayer compression. The dipole moments of compromised mutants tended to show greater directional differences with respect to the plane of the bilayer which may have greater significance in charged bilayers composed of POPG. The tendency to aggregate and the tension-dependent changes in binding were also consistent with experimental results. We conclude that the Lys residues are particularly important in controlling peptide tilt angle, penetration depth, and in defining the equilibrium between the shallow and deep binding modes.

2. Computational details

To ensure an unbiased study, the authors were blinded with respect to the outcome of experiments when they performed computational analyses, unless otherwise noted. GROMACS 4.5.4 [14] was used for simulations and data analysis. Graphical representations were created using Visual Molecular Dynamics [15]. All the simulations in this study are described in Table 1. The size of the simulation box is represented by the x, y, and z-dimensions, and in simulations containing a bilayer, the z-axis was defined as the bilayer normal. We refer to the z-coordinate of an atom as the ‘z-position’ of the atom. The distance between two atoms projected onto the z-axis is referred to as the ‘z-distance.’ The GsMTx4 structural model contained 34 residues, including G47 to F80 of UniProt ID: Q7YT39 [16,17].

Table 1.

Descriptions of performed molecular dynamics simulations

Simulation	Force field	Composition*	Initial box size (Å)	Run type/Configuration	Time
PMF analysis of membrane-binding energy
CG-pmf-WT	MARTINI	124 POPC/2439 w/WT	65×65×110	z-restrained	4μs for each z-position
CG-pmf-K8E	MARTINI	124 POPC/2439 w/K8E	65×65×110	z-restrained	4μs for each z-position
CG-pmf-K15E	MARTINI	124 POPC/2439 w/K15E	65×65×110	z-restrained	4μs for each z-position
CG-pmf-K20E	MARTINI	124 POPC/2439 w/K20E	65×65×110	z-restrained	4μs for each z-position
CG-pmf-K22E	MARTINI	124 POPC/2439 w/K22E	65×65×110	z-restrained	4μs for each z-position
CG-pmf-K25E	MARTINI	124 POPC/2439 w/K25E	65×65×110	z-restrained	4μs for each z-position
CG-pmf-K28E	MARTINI	124 POPC/2439 w/K28E	65×65×110	z-restrained	4μs for each z-position
AT-pmf-WT	Berger/OPLS-AA	124 POPC /8317 w /WT	66×66×98	z-restrained at 1.5–2.8nm	300ns for each z-position
AT-pmf-K15E	Berger/OPLS-AA	124 POPC /8317 w /K15E	66×66×98	z-restrained at 1.5–2.8nm	300ns for each z-position
AT-pmf-K28E	Berger/OPLS-AA	124 POPC /8317 w /K28E	66×66×98	z-restrained at 1.5–2.8nm	300ns for each z-position
AT free run †
60/64-WT	Berger/OPLS-AA	124 POPC/5696 w/WT	66×66×80	free run	300ns
60/64-K8E	Berger/OPLS-AA	124 POPC/5696 w/K8E	66×66×80	free run	300ns
60/64-K15E	Berger/OPLS-AA	124 POPC/5696 w/K15E	66×66×80	free run	300ns
60/64-K20E	Berger/OPLS-AA	124 POPC/5696 w/K20E	66×66×80	free run	300ns
60/64-K22E	Berger/OPLS-AA	124 POPC/5696 w/K22E	66×66×80	free run	300ns
60/64-K25E	Berger/OPLS-AA	124 POPC/5696 w/K25E	66×66×80	free run	300ns
60/64-K28E	Berger/OPLS-AA	124 POPC/5696 w/K28E	66×66×80	free run	300ns
34/34-WT	Berger/OPLS-AA	68 POPC/3180 w/WT	49.5×49.5× 79	free run	600ns
34/34-K28E	Berger/OPLS-AA	68 POPC/3182 w/K28E	49.5×49.5× 79	free run	600ns
30/34-WT	Berger/OPLS-AA	64 POPC/2560 w/WT	47×47×76	free run	15 × 150ns
30/34-K8E	Berger/OPLS-AA	64 POPC/2560 w/K8E	47×47×76	free run	15 × 150ns
30/34-K15E	Berger/OPLS-AA	64 POPC/2560 w/K15E	47×47×76	free run	15 × 150ns
30/34-K20E	Berger/OPLS-AA	64 POPC/2560 w/K20E	47×47×76	free run	15 × 150ns
30/34-K22E	Berger/OPLS-AA	64 POPC/2560 w/K22E	47×47×76	free run	15 × 150ns
30/34-K25E	Berger/OPLS-AA	64 POPC/2560 w/K25E	47×47×76	free run	15 × 150ns
30/34-K28E	Berger/OPLS-AA	64 POPC/2560 w/K28E	47×47×76	free run	15 × 150ns
CG PMF analysis of dimerization in water
in-water-2WT	MARTINI	1684 w/2 WT/13 Na/23 Cl	59.5×59.5× 59.5	Umbrella sampling	3×20μs for each distance1)
in-water-2K28E	MARTINI	1691 w/2 K28E/15 Na/21 Cl	59.5×59.5× 59.5	Umbrella sampling	3×20μs for each distance1)
CG run for peptide self-association near membrane
1-to-1-free-WT	MARTINI	256 POPC/5444 w /2WT/20Na/30Cl	92×92×118	free; initially one in water and one on membrane	100 × 800ns runs
1-to-1-free-K28E	MARTINI	256 POPC/5444 w/2 K28E/22 Na/28 Cl	92×92×118	free; initially one in water and one on membrane	100 × 800ns runs

^*For the CG and AT PMF simulations, as well as the AT free runs, chloride ions, but not other ions, were added to adjust the total charge zero.

^†The 30/34 series were performed after knowing the experimental data as described in Text S1.

¹⁾These analyses based on 3×20μs simulations for each distance were performed after knowing the experimental data as described in Text S1.

2.1 Coarse-grained simulations

For coarse-grained (CG) simulations, we used the MARTINI force field (version 2.0) [18]. CG POPC was modeled as done previously [19], and water was represented using the Yesylevskyy model [20]. For the peptides, atomistic models derived from structures produced in our previous work [9] were coarse-grained with Martinize (version 2.3) using the default topological parameters. As recommended by the developers [18], elastic bonds with force constants of 500 kJ/nm²/mol were applied to all those pairs of the backbone beads which were located within 0.7 nm. The Lennard-Jones interactions were shifted smoothly to zero between 0.9 and 1.2 nm, and the electrostatic interactions were smoothly shifted to zero between 0 and 1.2 nm. The relative dielectric constant was set to 2.5. The non-bonded neighbor list was updated every 10 steps. The integration time step was 20 fs, but for monolayer simulations (see below), we used 10 fs. The pressure was semi-isotropically coupled using the Berendsen algorithm at 1 bar with τ_P = 1 ps and compressibility at 3 × 10⁻⁴ bar⁻¹. The temperature was controlled at 320K with a constant τ_T of 1 ps. For this study, CG simulation time is presented after multiplication by a factor of four [18]. POPC bond lengths were restrained using LINCS [21]. The protonation states of titratable side chains of amino acids were the same as for the AT simulations. The backbone of the N-terminal Gly was represented by a Qd bead and was assigned +1 charge. The backbone of the C-terminal amino acid was represented by an uncharged P5 bead.

2.2 Atomistic simulations

For the atomistic (AT) simulations, the united-atom Berger force field for lipids [22], in combination with an adapted Optimized Potentials for Liquid Simulations all-atom (OPLS-AA) for proteins [23] were used along with the simple-point charge (SPC) water model [24]. The pair of Berger force fields for lipids and OPLS-AA force field for proteins have been used in several studies [e.g., 25, 26] and the energy of water-to-lipid membrane transfer and that of the solvation by cyclohexane have been calculated for amino acid analogues [27, 28]. The bond lengths for water and lipids were restrained using SETTLE and LINCS, respectively [21,29]. The Particle-Mesh Ewald (PME) algorithm [30] was used with a real-space cutoff of 1.4 nm and a maximal grid size of 0.125 nm. Berendsen coupling was used to regulate the temperature [31]. Other parameters were set as described previously [32]. The N-terminus was protonated and the C-terminus was capped with a carboxamide group. All titratable amino acid side chains were assumed to be in their ionized forms, because they were all solvent-exposed, and Glu residues introduced in place of Lys were predicted to have pKa values between 4.3 and 5.3, based on calculations with the H++ server [33]. Furthermore, our CG analyses suggested that membrane binding energy changed only slightly (0.5–8.0 kJ/mol) with changes in protonation state for all mutants tested, which would be insufficient energy to change the protonation state upon membrane binding [34].

2.3 Free energy for binding of peptides to membrane

The profiles of the potential of mean force (PMF) for peptide binding to the membrane were derived using a system containing a peptide and the POPC bilayer (Table 1). For both CG PMF and AT PMF analyses, z-position (i.e., the position along the membrane normal) of the center of mass (COM) of the peptide was restrained using the constraint mode of GROMACS; we measured the vertical mean force needed to impose this constraint. For CG PMF analysis, the target z-position from the bilayer midplane was varied from 2.2 to 5.4 nm in 0.2 nm intervals. For the CG PMF simulations, we performed a 200 ns equilibration run followed by an 800 ns production run for each z-position. For the AT PMF analysis, the z-positions were varied from 1.6 to 3.8 nm, in 0.2 nm intervals, plus an additional run at 1.5 nm. Two independent 300 ns production runs following a 100 ns equilibration run were performed for each z-position. Note that the thickness of the POPC bilayer is different between the CG and AT systems; the mean z-position of the PO₄ atoms of the CG bilayer was 2.1 nm whereas that of the phosphorus atoms of the AT bilayer was 1.85 nm above the bilayer center. For CG PMFs, the PMF curves were vertically shifted so that the 5.2–5.4 nm range, where the vertical mean force was negligible, was defined as zero. Binding free energy was calculated using a method similar to the one used by Neale et al. [23]. Briefly, the Boltzmann factor was integrated and the ratio of the integrals was calculated using the following equation:

$$exp[-\beta \mathit{\Delta }{\mathrm{G}}^{\text{bind}}]=\{{\int }_{min\_\text{memb}}^{max\_\text{memb}}exp[-\beta {\mathrm{G}}^{\text{PMF}}(\mathrm{z})]\text{dz}\}/\{{\int }_{min\_\text{water}}^{max\_\text{water}}exp[-\beta {\mathrm{G}}^{\text{PMF}}(\mathrm{z})]\text{dz}\}$$

where ΔG^bind is the standard free energy of peptide binding to the bilayer, G^PMF(z) is the PMF value at the given z, and β is (RT)⁻¹, where R is the gas constant and T is the temperature. For the CG PMFs, the min_memb and max_memb parameters were set to 0 and 4.0 nm, respectively, whereas min_water and max_water were set to 4.0 and 8.0 nm, respectively. Due to computational limitations, the PMF for 5.4–8.0 nm in the water layer, and for 0–1.4 nm in the membrane, were assumed to be zero. The z-range corresponding to the opposing monolayer was excluded from the calculation, as we regarded peptide residence at the upper (outer) lipid-water interface or within the upper monolayer as the only membrane-bound state relevant to this analysis. While this assumption appears drastic, the Boltzmann factor for the deep part of the membrane is very small; for example, a layer with zero PMF value has no more than 10⁻³-fold of the Boltzmann factor for a layer with −25 kJ/mol. However, the width of the water layer affects ΔG^bind; a change in width from 3 to 4 nm leads to a RTln(4/3) difference in ΔG^bind. As reported previously, the choice of the boundary height also has a non-negligible effect on ΔG^bind [23].

2.4 CG PMF of peptide dimerization in water

The CG PMF analysis for peptide aggregation and dimerization was carried out as described in Table 1. The inter-peptide distance (the distance between COMs) was used to define the reaction coordinate. This set of analysis was performed after knowing the experimental data based on the procedure described in Text S1.

2.5 1-to-1 free runs

In 1-to-1 free runs, CG simulations were configured such that one peptide was introduced in a membrane-bound position (referred to as the pre-bound peptide), and a second peptide was introduced in bulk water (Table 1). Simulations were run free of restraints. To prepare the initial system, the second peptide (WT or K28E) was placed at varying positions in the xy-plane located 4 nm above the bilayer midplane, and the overlapping water molecules were removed. The pre-bound peptide resided at about ~2.35 nm from the midplane of the CG POPC bilayer. We performed a 10-ns preparative run in which the position of each of the peptides was harmonically restrained, followed by 1μs of unrestrained production run.

2.6 Langmuir-type simulations

CG model-based Langmuir-type simulations, with a configuration of vacuum/POPC monolayer/water (henceforth, ‘monolayer simulations’) were carried out and analyzed as described previously [35,36]. Briefly, the surface tension/pressure was calculated using the formula γ_s = h_z {P_zz − (1/2)(P_xx + P_yy)}, where h_z is the z-component of the box size and P_zz and (1/2)(P_xx +P_yy) are the pressures normal to the monolayer and tangential to the monolayer, respectively. For all monolayer simulations, surface tension coupling was used.

CG monolayer simulation systems contained a monolayer of 128 POPC molecules placed in the xy plane, 6435 water molecules [20], chloride ions, and GsMTx4 in a box with a fixed z-component of 20 nm. For monolayer simulations, PMF was analyzed as above, but to reduce error due to the flexibility of the monolayer, we used the cylinder mode (radius of 1 nm), in which the COM of the lipids located within the cylinder was used for the calculation of monolayer-peptide distance.

2.7 Other analyses

The dipole moments for WT and mutant GsMTx4s were calculated using the g_dipole module of GROMACS using coordinates sampled from trajectories for either in-water or interfacial binding mode simulations. Ten structures each for the in-water and membrane-bound states were randomly sampled from trajectories. After aligning each set of structures, the dipole moment vectors were calculated and averaged.

3. Results

3.1 Compromised activity mutant K15E strongly binds to the POPC bilayer

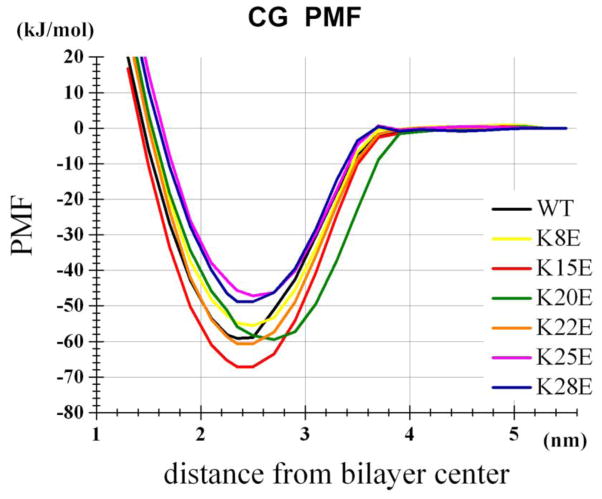
To gain insight into the dynamics of WT and mutant peptide binding, we carried out CG and AT MD simulations (Table 1). To estimate the binding energy between the peptide and the surface of a POPC bilayer, we carried out potential of mean force (PMF) analyses using the distance (z) from the peptide center of mass (COM) to the bilayer center as the reaction coordinate (CG-pmf series of Table 1). We calculated the depth of the PMF profile and the integrated binding energy ΔG^bind (Table 2, Figure 2). K15E interacted with the membrane with higher affinity than WT, and K25E and K28E interacted with lower affinity than WT. For all peptides, ΔG^bind fell within the range of −18–27 kJ/mol. These results are consistent with binding energies determined by fluorescence quenching in the physical experiments and Isothermal titration calorimetry (ITC) [Tables 1 of 13].

Table 2.

Summary of PMF analysis

Simulation	Position of energy minimum relative to bilayer center (nm)	Depth of PMF well ± S.E. (kJ/mol)†	ΔGbind ± S.E. (kJ/mol)*
CG-pmf-WT	2.35	−57.8 ± 0.7	−23.2 ± 0.3
CG-pmf-K8E	2.5	−55.2 ± 1.3	−21.7 ± 0.7
CG-pmf-K15E	2.35	−65.8 ± 0.5	−26.8 ± 0.3
CG-pmf-K20E	2.5	−57.9 ± 0.8	−23.3 ± 0.4
CG-pmf-K22E	2.35	−59.3 ± 1.3	−24.0 ± 0.7
CG-pmf-K25E	2.5	−49.5 ± 0.7	−18.1 ± 0.4
CG-pmf-K28E	2.35	−49.3 ± 0.4	−18.8 ± 0.2
AT-pmf-WT	1.7	−61.2 ± 4.5	n.t.
AT-pmf-K15E	1.7	−72.2 ± 4.7	n.t.
AT-pmf-K28E	2.1	−40.1 ± 5.0	n.t.

^*n.t. = not tested

^†For the AT series, the PMF depth relative to the PMF value at z = 3.8 nm is shown. The mean force at this position was smaller than 3.0 kJ/nm and our estimation based on the CG PMF curve suggested that the systematic error in the PMF depth resulting from ignoring the z = 3.8 – 5.0 nm range was smaller than 0.5 kJ/mol for all three peptides.

Figure 2.

CG PMF profiles for WT and mutant peptides within the POPC bilayer.

Due to computational limitations, the AT simulation-based PMF analysis was performed only for the WT peptide, K28E, and K15E, and for z between 1.6 and 3.8 nm. For WT peptide, the CG and AT PMFs yielded similar PMF depths, which were also consistent with the results of the CHARMM36-based analysis by Chen and Chung, who reported a PMF depth of −26 kT [10]. Binding strengths for these peptides were also consistent with our AT and CG analyses, suggesting that these force fields are reliable, at least for this application. Overall, in silico binding energies were consistent with those in the experiment [13]. In particular, the simulations correctly predicted the strongest binding of K15E (inhibition kinetics and ITC energies) and the weaker binding of K28E (inhibition kinetics). Hereafter, we will refer to the binding position of peptides (the depth in the membrane) in the unrestrained WT peptide and POPC bilayer runs, as the ‘normal’ binding position.

3.2 Peptide penetration depth

To examine membrane penetration depth and properties of the local bilayer in atomistic detail, we performed unrestrained atomistic simulations of membrane-bound peptide in a POPC bilayer system (60/64-WT etc., of Table 1; Figure 1, left). The distance of the peptide COM from the bilayer center differed among WT and mutant peptides; this measurement fluctuated greatly, producing large standard deviations (0.14–0.24 nm) suggesting the peptide’s position in the shallow mode may be available to transition to deeper modes during membrane stress (Table 3). Nonetheless, K15E, K20E, and K22E, all of which displayed compromised inhibitory activities [13], exhibited relatively deep membrane penetration, while peptides that showed WT levels of inhibition (K8E and K28E) showed similar penetration depths to WT. K25E was an outlier in that, while showing compromised activity, it showed penetration depths similar to WT.

Table 3.

Averaged peptide penetration depth based on the AT 60/64 and 30/34 simulation series

Peptide	COM from bilayer center ± S.D. (nm)		Trp residue COM from bilayer center ± S.D. (nm)		Trp residue COM from peptide COM ± S.D. (nm)
	60/64	30/34*	60/64	30/34	60/64	30/34
WT	1.84 ± 0.16	1.78 ± 0.12	1.20 ± 0.16	1.14 ± 0.11	−0.64 ± 0.06	−0.64 ± 0.07
K8E	1.88 ± 0.24	1.89 ± 0.20	1.39 ± 0.32	1.44 ± 0.35	−0.49 ± 0.12	−0.44 ± 0.18
K15E	1.70 ± 0.15	1.71 ± 0.11	1.08 ± 0.17	1.08 ± 0.12	−0.63 ± 0.06	−0.64 ± 0.06
K20E	1.62 ± 0.15	1.70 ± 0.12	1.06 ± 0.18	1.19 ± 0.20	−0.56 ± 0.11	−0.51 ± 0.11
K22E	1.69 ± 0.14	1.71 ± 0.11	1.07 ± 0.17	1.10 ± 0.15	−0.62 ± 0.09	−0.51 ± 0.09
K25E	1.90 ± 0.17	1.81 ± 0.10	1.23 ± 0.17	1.14 ± 0.10	−0.67 ± 0.06	−0.67 ± 0.06
K28E	1.84 ± 0.16	1.82 ± 0.21	1.28 ± 0.19	1.27 ± 0.30	−0.56 ± 0.09	−0.55 ± 0.12

^*For the peptide penetration depth based on the 30/34 simulations, S.D. (nm) of the means of the fifteen simulations was as follows; WT, 0.09; K8E, 0.17; K15E, 0.08; K20E, 0.09; K22E, 0.08; K25E, 0.07 and K28E, 0.20. The depths of the mutants based on the latter set were significantly different from that of WT with p<10⁻⁷ (t-test) for K25E and with smaller p-values (i.e., greater significances) for the other mutants.

The above 60/64 analysis was based on a single simulation for each peptide. To improve the sufficiency of sampling, we added fifteen independent 150ns simulations using a smaller bilayer after knowing the experimental data (AT 30/34 series in Table1). Time development of all trajectories are shown in Figure S1, but the final 50ns segments were analyzed as described in Text S1. This set reproduced the trends observed with the 60/64 set (Table 3). The fluctuation of z-position of peptide COM reflected by SD is smaller than those observed in the 60/64 set, likely due to the reduced undulation of the small bilayer. The SD of the means of the fifteen independent 50ns trajectories was large (footnote of the Table 3), reflecting slow changes in the penetration depth for all peptides and, in particular, for K8E and K28E. This observation also highlights the importance of analysis based on many independent trajectories, instead of a single run, for sufficient sampling.

Quenching of Trp fluorescence by aqueous, and membrane, resident quenching agents is sensitive to the depth of the residues in the membrane. Gnanasambandam et.al. measured the quenching of the two adjacent Trp residues (Trp6 and Trp7) in GsMTx4 WT and KtoE mutants, and found that, in general the Trp residues on KtoE mutants bound deeper, though the sensitivity of the measurements did not allow precise positioning [Figures 7 and 8 from ref 13]. We determined the Trp COM in these simulations (i.e., the COM of the atoms belonging to Trp6 or Trp7), and found that, consistent with the fluorescence data, the Trp residues of compromised mutants (K15E, K20E, and K22E) showed deeper penetration than WT, and mutants with WT activity (K8E and K28E) had depths similar to WT (Table 3). As above, the compromised K25E mutant did not follow this pattern exhibiting Trp depths similar to WT. Also, K28E showed deeper binding depth in the fluorescence quenching experiments. These differences in the COM depth (either whole peptide or Trp residues) at resting tension may be only one factor contributing to the inhibition mechanism.

Assuming the analysis of the tilt angle was statistically reliable (see below), we calculated the z-position of the Trp COM relative to the peptide COM (Trp-Pep z-distance) (the two rightmost columns of Table 3). For WT, this distance was 0.64 nm with a standard deviation (SD) of 0.06–0.07 nm. Intriguingly, K8E showed a relatively short Trp-Pep z-distance (−0.44 – 0.49 nm) with large SD (0.12–0.18 nm). This short Trp-Pep z-distance may be associated with the side of the peptide containing Trp6 and Trp7 tilting away from the membrane (see the next section). The large SD indicates large motions of the Trp residues relative to the peptide COM. In contrast, K15E and K25E, which have most compromised inhibitory activities, have Trp residues that are deeply buried in the membrane with relatively small SD. Given their small SD and the deep penetration of the Trps, we expect that K15E and K25E are stably oriented in the membrane, with the hydrophobic protrusion firmly sticking into the hydrophobic core (Table 3). The implication is that the Trp residues of K15E and K25E may be better engaged by lipids than those of the other mutants, an idea that is consistent with the fluorescence quenching data for K15E and K25E [Table 1 in 13].

3.3 K to E mutations alter tilt orientation of GsMTx4 in the membrane-bound state

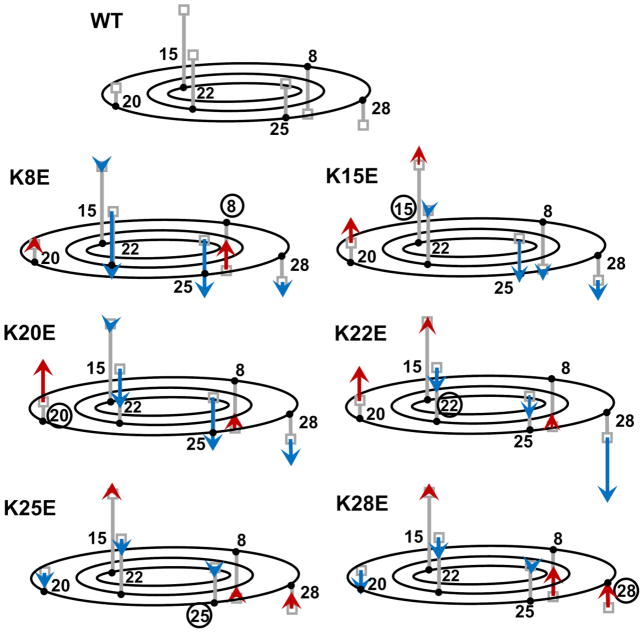
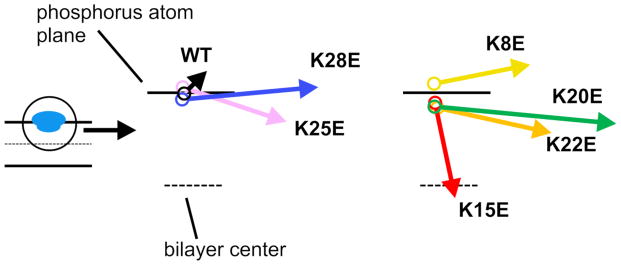
The tilt angle of the peptides was analyzed for the free simulations (AT 60/64 series of Table 1). The tilt is represented by the z-position of Cγ (the carbon atom two bonds away from the Cα) of each amino acid residue relative to that of the peptide COM. Despite large fluctuations in the penetration depth, the tilt angle of the peptides exhibited an unexpectedly consistent trend (Table S1 of Supplementary Material). All KtoE mutations caused the mutated side of the peptide to tilt away from the membrane, in a seesaw-like manner. Figure 3 summarizes the results of Table S1. For example, in the K8E simulation (AT 60/64-K8E), the z-position of Cγ of the eighth (mutated) residue relative to the peptide COM was 2.25 Å shallower in the membrane than the corresponding value for WT peptide (in bold in Table S1), whereas the similarly analyzed z-positions of the residues on the opposite side (K22 and K25) were ~5 Å deeper in the membrane compared to WT (Table S1 and Figure 3). A similar trend was observed when we performed the complimentary analysis using the AT 30/34 simulations that were carried out after knowing the experimental data as discussed in Table S2 and Text S1. A similar trend was also observed for the CG simulation tilt analysis (data not shown). The other mutant with WT like activity, K28E, also cause K8 to become shallower, which is the closest Lys to the Trp residues and is predicted to interact with lipid headgroups on the opposite leaflet in deeper bound states.

Figure 3.

Schematic representations of tilt angles for WT and mutant peptides in AT simulations. Top: WT peptide. Small grey boxes at the tip of the vertical bars indicate the mean z-position of the Lys Cγ atom. To represent the Cγ positions in 3-dimensions, grey vertical lines were anchored to the horizontal plane that represents the height of the COM for the peptide. The root positions of the bars are not accurate, but indicate that K8, K28, K25, K22 and K20 are arrayed in a counterclockwise order when viewed from the bottom, and that K22 and K15 are located somewhat internally compared to K20 and K25. The remaining figures: Results for each mutant are indicated by red and blue arrows that are superimposed on the WT data. Arrows start from the Cγ position observed for WT (i.e., grey boxes) and end at the positions observed in the simulation of each mutant. Red and blue colors indicate increase and decrease, respectively, in the z-position relative to the position in WT. Bold numbers denote native residues, whereas encircled numbers denote mutated residues.

We also analyzed the dipole moments of the WT and mutant peptides. In Figure S1, the moment vector is represented as an arrow originating from the peptide COM. For the structures sampled from in-water simulations, the moment vector generally points from the mutated residue toward the opposite side of the peptide. For the structures sampled from the membrane bound state (shallow binding mode), the moment vectors were quite different among WT and mutant peptides (Figure 4). Intriguingly, K15E and K25E, which had the most compromised functional activity [Figure 3 of 13], produced the greatest angular changes in their dipole moments, while K8E and K28E, whose activities were unaffected, produced the least change in moment vectors. This raises the possibility that the positioning of the charged residues in the membrane, in addition to the direction of the dipole moment vector, play an important role in the inhibitory activity of the peptide.

Figure 4.

Dipole moment vectors for WT and mutant peptides in the normal membrane-bound state. Arrows indicate the dipole moment vectors calculated for representative WT and mutant peptides bound to the POPC bilayer in the AT simulations. Note that the maximum angle is shown; i.e., the peptides were rotated around the z-axis, such that the arrows aligned onto the xz-plane. The starting point of each vector represents the time-averaged position (depth) of the COM from the AT simulations.

3.4 Binding of GsMTx4 causes a minor change in membrane thickness and undulations

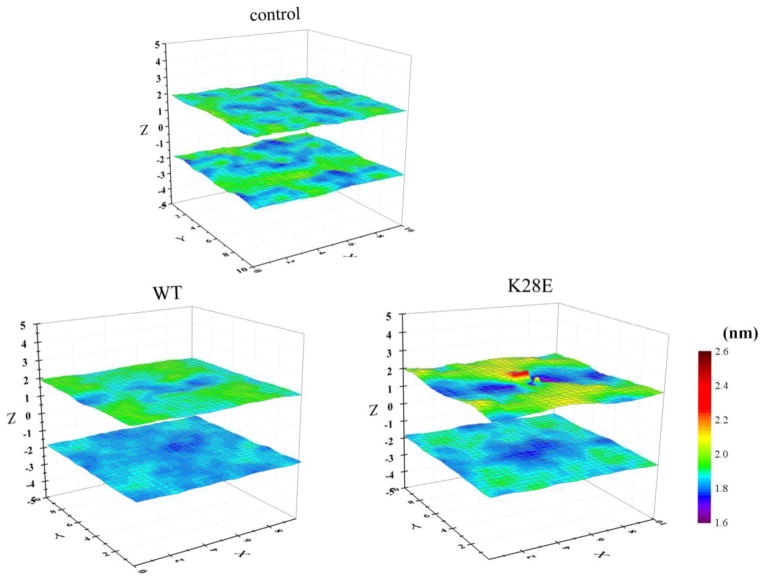
To examine the effect of peptide binding on membrane thickness and dynamics, we analyzed the z-positions of the lipid phosphorus atoms averaged within a small vertical column of membrane for peptide-free (control), WT-bound, and K28E-bound POPC bilayers (Figure 5). There were minimal changes to membrane thickness for the K28E peptide in comparison to WT peptide, however, in comparison to the peptide-free POPC bilayer, a region of higher positioning was observed. For K28E, the upper-monolayer phosphorus heights averaged over nine adjacent 4 Ų bilayer patches ranged from 1.38 to 2.47 nm, whereas the corresponding values for the control bilayer ranged from 1.76 to 2.01 nm. Thus, K28E binding increased the heterogeneity in membrane thickness for the upper monolayer. However, the heterogeneity in membrane thickness for the WT peptide-bound bilayer was similar to the peptide-free bilayer (Figure 5). The ratio of the average distance of the phosphorus atoms from the bilayer midplane for the upper and lower monolayers, in nm was 1.88/1.88 for the control POPC bilayer, 1.90/1.84 for the WT peptide, and 1.93/1.86 for K28E. Together with the PMF results (Table 2) and discussions of the tension-induced change in binding [Figure 10 of 13], the K28E-induced perturbation of the upper monolayer may explain the lower affinity of K28E for POPC (discussed below). Nonetheless, it is difficult to explain the inhibitory activity of the WT peptide and K28E against MSCs based solely on these small effects on the upper monolayer undulation or on membrane thickness. It is also difficult to imagine that the time-averaged thicknesses presented in Figure 5 would be a major determinant of inhibitory impact on channel conductance given the vertical fluctuations in peptide position, as well as the normal peristaltic and undulatory fluctuations of the lipid bilayer [e.g., 37]. Rather, pronounced membrane thinning induced by multiple peptides binding to the bilayer is more likely to have an impact on the peptide activity, as discussed below.

Figure 5.

Three-dimensional representations of the averaged z-positions of phosphorus atoms of the upper and lower POPC monolayers over the AT simulations. Control (i.e., no peptide), 60/64-WT, and 60/64 K28E runs were analyzed. 2 × 2 Ų monolayer patches were analyzed, but for clarity, the mean value for 3 × 3 pixels² (the central pixel plus the surrounding 8 pixels) was plotted.

3.5 Propensity to form multimers/aggregates in water and on the membrane

Dynamic light scattering and nondenaturing electrophoresis suggested that GsMTx4 had a propensity to form large aggregates [Figure 13 in 13]. In addition, an extra peak at 228 nm in the mutants’ CD spectra suggested peptide aggregation in solution and when weakly bound to membranes [Figure 1 and S1 in 13]. Aggregate size was concentration dependent and most mutants showed a greater tendency to form larger aggregates than WT. Dimer and/or multimer formations may affect peptide structure and possibly explain the 228 nm peak observed in the CD spectra for the aqueous and weakly bound mutant peptides to POPC vesicles. The 228 nm peak disappears when bound more strongly to negatively charged vesicles of POPG:POPC [Figure 1 in 13] which may force the formation of bound monomers, though this was not tested here. Multimers of these peptides may also affect Trp quenching in solution and in superficially membrane bound states.

Here we assessed the tendency for peptides to dimerize using the CG simulation system (‘in-water’ series of Table 1). Of note, this set of analysis was carried out after knowing the experimental data as discussed in Text S1. When two WT peptides were placed in water at varying distances from each other, the PMF profile of dimerization suggested that the mean force was attractive for ~1.6–2.6 nm (Figure S2). For WT peptide, the depth of the PMF profile (mean ±SD) was −44.5 ±1.3 kJ/mol, while for K28E, the depth was −52.8 ±3.4 kJ/mol (Text S1, Figure S2). Thus, both WT and K28E peptides had a propensity to self-associate in water, but K28E had a greater propensity, which is consistent with the experimental data [Figure 13 of 13]. In contrast, membrane-bound peptides yielded largely flat PMF attraction profiles for WT and K28E, implying that dimerization was not favorable when these peptides were placed in the interfacial (shallow) binding mode (data not shown).

We then examined whether pre-bound peptides affected the subsequent binding of other peptide molecules from the bulk water. The simulation system contained a WT (or K28E) peptide in the pre-bound position and one additional WT (or K28E) peptide in the bulk water at varied xy-positions (1-to-1 free runs) (Figure 6A). For the WT peptide, a quarter of the 100 trials resulted in the aqueous peptide binding to the pre-bound peptide (Table 4; Figure 6C). For K28E, about half of the 100 runs resulted in peptide-peptide interaction. As we used the periodic boundary condition, in some runs, the peptide moved away from the membrane, entered the adjacent simulation box and bound to the bilayer therein (‘Bound to the opposite side of the bilayer’ column of Table 4). Once binding occurred (either peptide-peptide or peptide-bilayer), it persisted until the end of the simulation. Binding in cis-configuration (independent binding events of the two peptides to the bilayer) was less frequently observed than peptide-peptide binding. After the peptide-peptide binding event, the second peptide resided at a higher position (~3.5–3.9 nm above the bilayer center) than the normal binding position (~2.35 nm for the CG system) for both the WT peptide and K28E. In these and other CG simulations, both WT and K28E peptides appeared to exert a trapping effect, in which the pre-bound peptide attracted a peptide from bulk water to the vicinity of the bilayer to form stable aggregates, hindering the second peptide from proceeding to the normal binding position. GsMTx4 shows weak cooperativity [n_H = 1.5, Figure 4 of 13], so that this finding could be relevant to the inhibitory mechanism, but we have not yet explored this idea experimentally.

Figure 6.

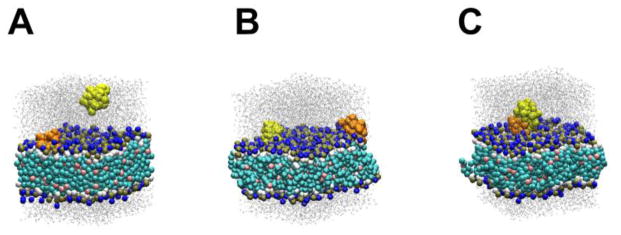
Representative snapshots of the 1-to-1 free runs for WT peptide. The first (pre-bound) peptide is orange and the second peptide (in water) is yellow. Dark blue spheres are NC3 particles. (A) An initial structure. (B) The cis-binding configuration. (C) The second peptide is bound to the first peptide.

Table 4.

Analysis of the 1-to-1-free simulations.

Simulation	Peptide	Bound to pre-bound peptide	Bound to bilayer in cis configuration	Bound to the opposite side of bilayer	Remained in water
1-to-1-freeWT	WT	25	5	9	61
1-to-1-freeK28E	K28E	51	4	15	30

3.6 Impact of applied membrane tension on peptide binding in the shallow binding mode

In the Langmuir experiments [Figure 9–11 of 13], the pressure-area curves for WT, K8E and K28E (active peptides) exhibited a break near the monolayer-bilayer equivalence pressure (πB) in the range between 36 and 40 mN/m showing a remarkable increase in membrane compressibility compared to control monolayers at 37–45 mN/m, where π is the membrane pressure. This shows that the area per molecule of membranes containing these peptides is responsive to small changes in lateral pressure (π). In contrast, π-area isotherms measured in the presence of K15E and K25E peptides (with compromised inhibitory activities) rose steadily up until the collapse and produced lower compressibilities in that range, meaning that for these mutants, the area per molecule was less responsive to membrane pressure [Figure 11 of 13]. The strong binding observed for K15E is likely reflected in the reduced compressibility modulus of the K15E-bound membranes due to the lower probability of K15E expulsion under increasing lateral pressure.

We performed several analyses in which membrane surface tension was varied. In a Langmuir-like CG monolayer system (a monolayer of 128 POPC surrounded by 6435 CG water molecules (Yesylevskyy model) on one side and a vacuum (air) on the other, for 2000 ns), a tension-dependent increase in xy-area was observed [35,36]. When the monolayer was coupled to a surface tension of γ_s = 60mN/m (equivalent to the membrane pressure that brings the area per lipid of the peptide-free monolayer to 0.628 nm², close to 0.64 nm² reported for 1 bar, i.e. resting tension) [35,36], the depth of the PMF profile for WT binding (derived similarly to Figure 2) was −70.7 kJ/mol. When the surface tension was raised to 75 mN/m (corresponding to an area per lipid of 0.721 nm², without peptide, i.e. stretched), the PMF well was deepened to −77.4 kJ/mol. These results suggest that WT binding strength increased as the applied tension expanded the CG monolayer. We have not yet examined the mutants nor have we systematically addressed membrane compressibility.

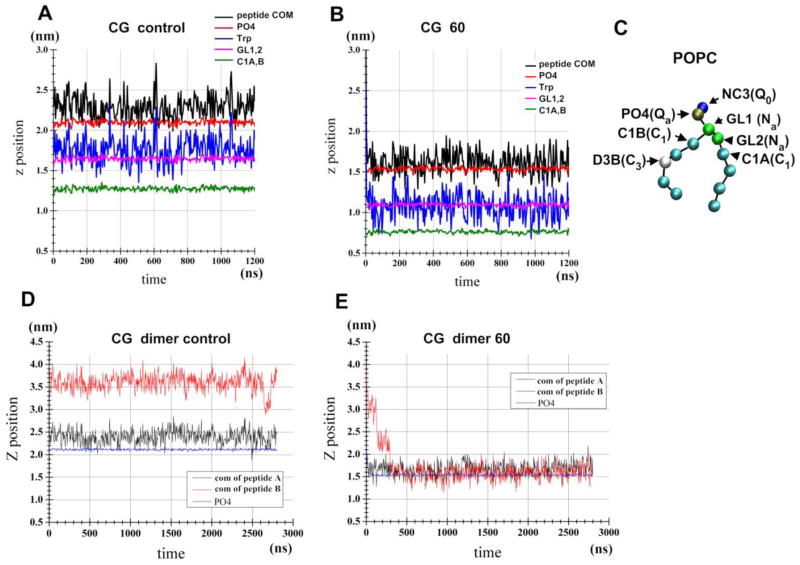
The effect of applied tension on the WT penetration depth in a CG POPC bilayer was also examined. A WT peptide was placed at the water-bilayer interface and the membrane tension was set at 60 mN/m (Figure 7). Note that the run with no applied tension (control run) and the run with tension of 60 mN/m produce an area per lipid of 0.664 and 1.130 nm², respectively, for the peptide-free bilayer. The mean ± SD of z-position of the peptide COM was 0.180 ± 0.14 nm above the z-position of PO₄ for the control run (Figure7A, black line) and the corresponding value was 0.075 ± 0.14 nm for the 60 mN/m run (Figure 7B). Similarly, for the control run, the z-position of the Trp6 and Trp7 COM was 0.11± 0.16 nm above the GL1/GL2 COM (Figure 7C), the corresponding value was only 0.02 ± 0.15 nm for the 60 mN/m run. Thus, the applied tension caused the deeper positioning of the WT. The change in COM appears small (~1Å), but may be associated with changes in the binding energy or transitions to deeper states in a different lipid environment.

Figure 7.

Tension-induced changes in the penetration depth of WT peptide in the POPC bilayer. (A) CG WT/POPC bilayer. (B) CG WT /POPC bilayer with an applied tension of 60 mN/m. (C) MARTINI model of POPC. Atom names and, in parenthesis, atom types are shown. (D) CG WT dimer/POPC bilayer. (E) CG WT dimer/POPC bilayer with an applied tension of 60 mN/m.

The effects of applied tension were clear when the CG POPC bilayer carrying two WT peptides (dimer) was examined. Initial structures were representative of the 1-to-1 free runs, in which the second peptide was leaning on the upper surface of the first (pre-bound) peptide (Figure 6C). At 0 ns, the second peptide was placed at a high z-position, but, in the presence of high tension, it quickly (< ~300ns) moved to the height of the first peptide (black line, Figure 7E). The two peptides remained attached to each other in the interface for the remainder of the simulation (data not shown), suggesting that dissociation occurs on a much longer timescale. In contrast, without the applied tension, the height of the two peptides remained unchanged (Figure 7D). Therefore, at least in this CG system, the applied tension facilitates the movement of the second peptide from the loosely associated state to the normal binding position. Further analyses are necessary to investigate whether the dimers observed in the 1-to-1 simulations merely represent a kinetic trap or whether they are in equilibrium with individual peptides bind in the interfacial (shallow) binding mode that break and reform.

4. Discussion

Before considering the in silico results, we’ll provide a brief summary of the experimental results. The mutants exhibited differences of inhibitory activity against Piezo1 in outside-out patches [13]. However, binding energies did not predict the inhibitory activities of mutants and were actually paradoxical to our expectations. For example, the compromised K15E had a lower equilibrium dissociation constant (K_D from Piezo1 inhibition rates) relative to WT peptide, while the unaffected mutant K28E exhibited a significantly higher K_D [Figure 2 of 13]. Together with the results on membrane penetration depth and the effects of the tension on peptide binding, we propose a model in which the K8E and K28E mutations cause destabilization of the deeper binding states, thereby stabilizing the shallow mode binding, which is likely to be the mode with inhibitory activity [13]. Since the WT peptide and K8E, but not K15E, were easily expelled from the monolayer/bilayer by lateral compression applied in the Langmuir experiment [Figure 10 of 13], we also propose that the WT-like activity of K8E and K28E is enabled by their area-buffering ability, whereas K15E (tight binder) is poorly expelled from the membrane and may suffer the loss of the area-buffering function, causing the loss of the activity [13].

4.1 Membrane Binding energy

ITC was used to show that K15E (lowest K_D) interacted with POPG (1-palmitoyl-2-oleoyl-phosphatidylglycerol):POPC (3:1) liposomes with a higher affinity than WT or any of the other mutants [Table 2 of 13]. These results are consistent with the high affinity binding of K15E observed in our CG and AT PMF analysis. On the other hand, liposome experiments showed that the binding energy to POPC was rather similar among all peptides (e.g., −26.8, −26.4 and −25.9 kJ/mol for the WT, K15E and K28E, respectively) [Table 1 of 13]. While peptide binding to the POPG:POPC (3:1) liposomes produced a blue shift in Trp fluorescence, suggesting that Trp residues became buried in the hydrophobic interior of the membrane, binding to pure POPC liposomes caused no such blue-shift [13]. It is possible that aggregation or loose binding to the membrane surface could be a confounding factors in the experiments using POPC liposomes.

4.2 Penetration depth

Although the penetration depth showed fluctuations in the z-position of the peptides (with SD ranging 1.4–2.4 Å, Table 3), AT simulations produced interesting results (Table 3). In particular, the Trp-Pep z-distance and its SD implied that K15E (with compromised activity) deeply penetrates and stably interacts with lipids compared to K8E and K28E (active mutants). Trp fluorescence quenching experiments suggested that K28E was more deeply positioned in the membrane than WT [Figure 8 of 13]. Our preliminary analyses showed that a system with a thinner membrane (specifically 34/34 POPC) yielded better resolution and a result more consistent with the experimental data, likely because the small system can suppress membrane undulations [data not shown]. However, even though K28E appears to penetrate deeper experimentally, it has a significantly higher K_D than WT suggesting lower affinity that may be the result of altered tilt, local membrane heterogeneities and/or higher aggregation states.

4.3 Dipole moment and tilt orientation

The direction of the dipole moments of K15E and K25E (mutants with compromised functional activity) were quite different from WT, while those of K8E and K28E (with unaffected activity) were similar to that of the WT (Figure 4). We surmise that the position of the charged residues and the direction of the dipole moment vector may be critical determinants of inhibitory activity. Tilt angle analysis suggested that KtoE caused the mutated end of the peptide to tilt away from the membrane and the opposite side to tilt toward the membrane, like a seesaw. The distribution of the charged residues is thus a determinant of the orientation and position of the peptide in the membrane. Phosphatidylcholine bilayers have a zone of high electrostatic potential at the level of the choline group [38]. This zone may cause the shallow positioning of the Glu relative to Lys at the same position. Another possibility is that the Glu side chain is shorter than Lys and might favor the shallow positioning for better hydration. POPG:POPC bilayers order water to a greater extent than POPC and may have a more significant affect on peptide tilt and inhibitory activity [39].

4.4 Effects on membrane thickness

In our analysis of thickness, we obtained a ‘negative’ result in that no clear change in membrane thickness nor curvature was seen upon WT (and K28E) binding (Figure 5), arguing that such changes are not important for the inhibitory activity of the peptides. Using the CHARMM36 force field, Chen and Chung reported thickening of POPC bilayer in the proximity of GsMTx4 and thinning in more distal parts of the POPC bilayer [10]. However, our similar analyses using the CHARMM36 force field uncovered slow undulatory motions of the membrane and vertical drifts of the peptides, but did not show the membrane thickening reported by the latter paper.

We preliminarily replicated the findings of Chen and Chung related to membrane thinning with binding of multiple peptides to the membrane [10] (our unpublished results). Using AT (Berger and OPLS-AA force fields), when two WT peptides were placed at normal binding positions at the center of a bilayer of 256 (125/131) DPPC (dipalmitoylphosphatidylcholine) molecules, thinning was prominent in the close vicinity of GsMTx4. The thickness of the bilayer (divided into cylinders with radius r parallel to the membrane normal) was 2.52 nm (r < 2nm), 2.70 nm (r = 2–3.5 nm), 2.71 nm (r = 3.5–5.5 nm), and 2.73 nm (r >5.5 nm). Thickness was measured as the C2–C2 distance, where C2 is the carbon atom that is bonded to the carbon atom belonging to the carbonyl groups of the acyl chains of DPPC. The membrane thickness of the peptide-free bilayer was 2.73 nm. When four WT molecules were placed at r < 2.0 nm, in the normal binding position, the membrane thinning was pronounced near GsMTx4; the C2–C2 distance was 2.43 nm (r < 3 nm), 2.70 (r = 3–4.5 nm), 2.72 (r = 4.5–6.5 nm) and 2.74 (r > 6.5 nm). Our CG analysis also suggested similar thinning (data not shown). These data suggest that membrane thinning becomes prominent with increasing numbers of bound GsMTx4 peptides, which is in agreement with previous results [10]. This thinning effect may explain the phenomenon that potentiation, but not inhibition, becomes prominent with very high concentrations of GsMTx4 [11,12].

4.5 The shallow and deep binding modes

We previously reported that GsMTx4 could bind in at least in two modes, shallow and deep [9]. As force fields have improved over time, the Lennard-Jones interactions between protein and lipid acyl chains atoms may have weakened [32,40], and the deep binding mode currently appears to be less stable than with previous force fields (unpublished result). Using CHARMM36, the deep binding mode was found to be unstable relative to the shallow (interfacial) binding mode [10]. Nonetheless the deep binding mode could be relevant in some cases. The asymmetry of local pressure between the two monolayers generated by normal peptide binding at modest densities (~3–5 molecules per 100 nm² bilayer) may confer inhibitory activity to GsMTx4. At higher peptide densities, membrane thinning may become predominant, causing facilitation of channel opening as seen previously in prokaryotic channels [11,12]. In this regime, the transition to the deep binding mode may be facilitated through both membrane thinning and local pressure asymmetries between the two monolayers. Intriguingly, in our additional AT simulations containing eight WT peptides and a 64/64 DPPC bilayer, two peptides moved to the membrane core and interacted in the deep binding mode spontaneously (data not shown). Furthermore, our experimental results support the view that the applied membrane tension facilitates the transition from the shallow binding mode to the deep binding mode [13].

Prior to this work, we performed a self-reconstitution analysis in which lipids and peptides starting in randomized configurations were allowed to spontaneously aggregate during AT simulations. Bilayer defects formed in many runs due to the limited time length of simulations (100 ns), and water carrying pore(s) often emerged. If such cases are also counted as successful reconstitution events, WT assumed the deep binding mode in 61 out of 150 runs. Of note, ~59% of the 61 (deep mode) runs produced one of the following results: ~36% adopted the configuration in which K8, K25 and K28 were segregated from the other charged residues, and ~23% adopted the configuration in which K8, K15 and K28 were segregated from the other charged residues. This suggests that K8 and K28 are probably important for the deep mode binding; These mutations which leave WT activity intact, introduce Glu side chains that are shorter than Lys side chains and contain partial negative charges, likely destabilize the deep binding mode.

5. Conclusion

We have described our computational and experimental work on GsMTx4, a peptide that modifies the gating of mechanosensitive channels. The computational simulations were overall consistent with experimental results, demonstrating the predictive power of MD simulations. Both the AT and CG simulations predicted high affinity binding of K15E to the membrane compared to WT and mutant peptides, which was similarly observed in both electrophysiological and calorimetric analyses. Self-reconstitution analyses indicated that K8 and K28 had a tendency to split from the other charged residues during the formation of the deep binding mode. This lends support to the view that K8E and K28E destabilize the deep binding mode [13]. In silico measures of membrane penetration depth were consistent with fluorescence quenching results (Table 3). Tilt angle and the dipole moment analyses raised the possibility that appropriate tilt angle, dipole moment orientation and appropriate locations of charged residues on the peptide surface are important to inhibitory activity, but their relative impacts remain unclear. Of technical relevance, the AT PMF profiles were in agreement with the CG PMF profiles (Table 2). Importantly, no gross membrane deformations or changes in thickness were observed upon a single WT peptide binding to the surface of the bilayer in the AT system.

As discussed in the accompanying paper, the shallow binding mode is likely the functionally relevant inhibitory mode. In the presence of applied tension, the peptide’s action as an area buffer (i.e., reservoir that provides materials to fill free space) should be relevant because it would serve as a mechanism to maintain pressure asymmetry between the two monolayers in the presence of tension. The minimal amount of deep binding would be consistent with the observation that GsMtx4 acts from the extracellular surface and probably the gating mechanics of the channel are based in the outer monolayer. Future studies should address the possibility that peptides can loosely associated with membrane (or with pre-bound peptides) and act as reservoirs when the membrane is stretched. Our CG simulations support this interpretation, but much longer simulations are necessary to examine whether or not the loosely associated peptides are in equilibrium with the peptides that are independently residing in the shallow binding mode. The physiological relevance of the deep binding mode is also unclear. Future analyses should address the extent to which membrane tension stabilizes the deep binding mode relative to the shallow binding mode.

Highlights.

• Simulations and experiments on GsMTx4 conducted in a double-blind approach

• Simulations correctly predicted the strong binding of K15E mutant to membrane

• K-to-E mutations affect tilt orientation of GsMTx4 in the membrane-water interface

• Simulations show no gross changes of lipid bilayer structure upon GsMTx4 binding