Simultaneous Treatment of Missing Data and Measurement Error in HIV Research using Multiple Overimputation

Abstract

Background

Both CD4 count and viral load in HIV infected persons are measured with error. There is no clear guidance on how to deal with this measurement error in the presence of missing data.

Methods

We used multiple overimputation, a method recently developed in the political sciences, to account for both measurement error and missing data in CD4 count and viral load measurements from four South African cohorts of a Southern African HIV cohort collaboration. Our knowledge about the measurement error of lnCD4 and log₁₀ viral load is part of an imputation model that imputes both missing and mismeasured data. In an illustrative example we estimate the association of CD4 count and viral load with the hazard of death among patients on highly active antiretroviral therapy by means of a Cox model. Simulation studies evaluate the extent to which multiple overimputation is able to reduce bias in survival analyses.

Results

Multiple overimputation emphasizes more strongly the influence of having a high baseline CD4 counts compared to a complete case analysis and multiple imputation (hazard ratio for >200 cells/mm³ vs. <25 cells/mm³: 0.21 [95%CI: 0.18;0.24] vs. 0.38 [0.29;0.48] and 0.29 [0.25;0.34] respectively). Similar results are obtained when varying assumptions about the measurement error, when using p-splines, and when evaluating time-updated CD4 count in a longitudinal analysis. The estimates of the association with viral load are slightly more attenuated when using multiple imputation instead of multiple overimputation. Our simulation studies suggest that multiple overimputation is able to reduce bias and mean squared error in survival analyses.

Conclusions

Multiple overimputation, which can be used with existing software, offers a convenient approach to account for both missing and mismeasured data in HIV research.

Background

It is well known that both CD4 count and viral load in HIV infected persons are measured with error, due to physiologic and biologic variation and to assay performance^1,2. Biologic variation includes intrapersonal fluctuations of CD4 cell count over the course of a circadian cycle and from day to day as a result of psychological stresses, intercurrent illnesses, alcohol, caffeine, exercise, and other factors ^1,3,4. Assay variation in CD4 measurements refers to flow cytometry itself and variation attributed to the assays used, their accuracy, specimen preparation techniques, the age of the sample at the time of preparation, and sample conditions during transport to a laboratory ^2,3. Measured CD4 count may therefore not represent the true underlying CD4 count. The same applies to the accuracy of HIV RNA (viral load) measurements: biological variation, related to disease progression, illnesses and lifestyle factors as well as technical variation due to different assays, laboratory standards, technician's skills and storage temperatures can cause a considerable amount of measurement error ^3,5-8.

Failure to appreciate the extent of measurement error may lead to biased results, for example regression estimates can either be attenuated or strengthened ⁹. This makes adjustment for measurement error a topic of considerable interest in the statistical analysis of HIV data ¹⁰. Suggestions for CD4 count measurement error correction include regression calibration ^11-13, and approaches which correct the likelihood function ^14-18. However, these methods have been rarely used in practice because of either their complicated implementation or their construction for a particular regression model or study question^19-21. Furthermore, these approaches require complete data, which limits application in low-income high-burden programmatic care settings where missing data - often related to missed laboratory visits, lost records, or incomplete data capture - is common ^22,23. We are aware of only one approach which accounts for missing data in the presence of measurement error ¹⁵, using a particular non-ignorable missingness assumption for the outcome of a nonlinear mixed effect model. However, this specific setting would typically not be relevant to most HIV research as its motivation and assumptions relate only to long-term viral dynamics modelling.

To address the problem of missing data in HIV research several approaches can be considered. A general and relatively straightforward approach to deal with missing data is multiple imputation, which is implemented in many statistical software packages ²⁴. Based on the user's assumptions about the data distribution (imputation model) missing values can be filled in (imputed) by means of draws from the posterior predictive distribution of the unobserved data given the observed data. This procedure is repeated to create M imputed datasets, the analysis is then conducted on each of these datasets and the M results are combined by a set of simple rules. Multiple imputation yields valid inference under the missing-at-random assumption which states that the probability of any value to be missing from the data set depends only on the observed data ²⁵.

We show how multiple overimputation ¹⁹, recently proposed in the political sciences and closely related to multiple imputation, can be used to account for both missing at random data and measurement error in HIV research under a general framework. Multiple overimputation treats mismeasured data as an extreme case of missing data: values measured with error are replaced with values obtained from an imputation model that incorporates the mismeasured values, as well as knowledge and assumptions about the measurement error process, in prior distributions on individual measurements. After generating multiple overimputed datasets, standard multiple imputation combining rules can be applied to obtain valid inference under assumptions which are similar to missing at random. The method has the main advantages of (i) being easy to implement with existing software, (ii) being applicable to a wide range of analysis models and settings, including longitudinal data analyses, and (iii) addressing measurement error and missing data simultaneously.

While the method has been tested in the political sciences and first simulations showed promising results in the context of linear and logistic regression models, little is known about the assumptions, behaviour, and success of the method in the context of HIV analyses, particularly survival analyses.

We therefore aim to 1) identify an appropriate measurement error model for CD4 count and viral load, 2) to investigate the implications, assumptions, and challenges related to the implementation of multiple overimputation in HIV research, using South African HIV treatment cohort data from patients starting on highly active antiretroviral treatment (HAART), and 3) to quantify the association of both baseline and follow-up CD4 count and viral load with all-cause mortality and to explore the possible bias resulting from ignoring measurement error and missing data in this illustrative example. In addition, 4) simulations are used to evaluate the extent to which multiple overimputation is able to reduce bias arising from measurement error and missing data in a wide range of survival analysis settings

Methods

Framework of multiple overimputation in general and for HIV research

Multiple Overimputation

Multiple Overimputation builds on multiple imputation by interpreting mismeasured values as missing data but including the mismeasured values as prior information in the imputation model. The procedure is as follows:

1. Multiply impute (say M=5 times) missing values and multiply overimpute (replace, overwrite) mismeasured values based on an appropriate imputation model which uses assumptions about the mismeasured data as prior information.

2. Conduct any statistical inference (Cox model, Kaplan-Meier estimator,…) on each overimputed set of data.

3. Combine the M estimates related to the M overimputed sets of data according to standard multiple imputation combining rules (“Rubin's rules”) ²⁶.

For example, if we had 1000 patients and 800 of them had available baseline CD4 counts, we would impute the remaining 200; the 800 measured CD4 counts would be treated as mismeasured, as we know that they don't exactly represent the true CD 4 count of a patient, but rather randomly differ from the true value. We would thus overwrite these values from an imputation model which uses our assumptions about the measurement error process as prior information. Subsequently we would perform our analysis on each overimputed dataset and combine the results accordingly.

Multiple imputation with Amelia II

It is known from multiple imputation theory that proper multiple imputations (yielding valid inference under the missing-at-random assumption) are realized via draws from the posterior predictive distribution of the unobserved data given the observed data ²⁵. These draws can, for example, be generated by specifying a multivariate distribution of the data and simulating the predictive posteriori distribution with a suitable algorithm. For our analysis, we consider the Expectation Maximization Bootstrap (EMB) algorithm ²⁷ from the R-package Amelia II ²⁸, which assumes a multivariate normal distribution for the data D∼N(μ, Σ) (possibly after suitable transformations beforehand). In this algorithm B bootstrap samples of the data (including missing values) are drawn and in each bootstrap sample the EM algorithm ²⁹ is applied to obtain estimates of μ and Σ which can then be used to generate proper imputations by means of the sweep-operator ^27,30. Of note, the algorithm can handle highly skewed variables by imposing transformations on variables (log, square root,…) and recodes categorical variables into dummies based on the knowledge that for binary variables the multivariate normal assumption can yield good results ³¹.

Multiple Overimputation with Amelia II

We assume (i) a classical measurement error model, meaning that for any observation: $x_{ij}^{\ast }=\mathit{\text{true}}{x}_{ij}+u_{ij},u_{ij}\sim N(0,{\sigma }_{u_{ij}}^2)$ With ${\sigma }_{u_{ij}}^2$ known or estimated and (ii) that the data are mismeasured at random, meaning that the presence of a mismeasured and/or missing value may depend only on observed quantities (and not the unobserved value itself), see eText 1 for a formal definition.

Consider the unobserved data to consist of both the missing data and the true latent values x_ij. Blackwell et al. ¹⁹ extend the predictive posterior distribution of the unobserved data given the observed data so that both missing and latent values are treated as unobserved. Using this extended predictive posterior distribution, applying the Expectation Maximization Bootstrap algorithm onto this distribution to obtain imputations, and incorporating the classical measurement error assumptions, $x_{ij}^{\ast }\sim N(x_{ij},{\sigma }_{{\mathrm{U}}_{\text{ij}}}^2)$, into the E-step of the algorithm, allows the use of a multiple imputation framework ¹⁹. Most crucially, the authors show that this modified Expectation Maximization Bootstrap algorithm leads to identical solutions when compared to using this algorithm implemented in Amelia II when prior distributions on mismeasured values that relate to $x_{ij}\sim N(x_{ij}^{\ast },{\sigma }_{{\mathrm{U}}_{\text{ij}}}^2)$ are used. The reason why multiple overimputation is different from multiple imputation and has the potential to correct for measurement error is because the draws are based on a modified predictive posterior distribution which incorporates the classical measurement error assumptions; see eText 1 and the appendices of Blackwell et al. and Honaker et al. for more details ^19,27.

Thus, in summary, using existing software for multiple imputation (Amelia II) and specifying observation level priors for each mismeasured value (normal distribution with the mean relating to the mismeasured value and the variance known or estimated), accounts for both missing and mismeasured data under the above-mentioned assumptions.

After creating M overimputed datasets, the analysis model (e.g. the Cox proportional hazards regression model) can be fitted in each overimputed dataset. The M estimates can then be combined easily either with existing commands contained in most statistical software packages or by hand: the point estimate is just the average of the M point estimates whereas the variance reflects both the uncertainty in each overimputed dataset and between imputed datasets (eText 1).

A measurement error model for CD4 count and viral load

Multiple overimputation can be applied to correct for measurement error in both baseline and follow-up HIV RNA and CD4 count with the following assumptions:

i) A classical measurement error model for both natural logarithm CD4 count (cells/mm³) as well as log₁₀ viral load (copies/μl):

$$\begin{array}{cc}lnC{D}_{4_i}^{\ast }=lnC{D}_{4_i}+u_i,& u_i|lnC{D}_{4_i}\sim N(0,{0.26}^2)\\ {\mathit{log}}_{10}V{L}_i^{\ast }={\mathit{log}}_{10}V{L}_i+u_i,& u_i|{\mathit{log}}_{10}V{L}_i\sim N(0,{0.225}^2)\end{array}$$

ii) The data are mismeasured at random.

The first assumption is a classical measurement error model. This assumption has been used before in methodological work ^12,14,17 and implies increased measurement error for higher absolute (non-log) CD4 count and (non-log) viral load measurements which is in line with clinical knowledge ^2,3,6,32. The measurement error variance for the natural logarithm CD4 was obtained from an estimate of a study with a large sample ³. The estimated variance was similar in a studies with smaller samples (0.275², ¹⁴ and 0.25², ³²); other studies report slightly lower estimates but do not necessarily reflect all sources of measurement error ^1,8.

The measurement error variance for log₁₀ viral load is based on Lew et al. ⁶ who conclude that variation due to biological and technical factors is fairly consistent and in the range of 0.3 to 0.6 log₁₀ copies/ml. Based on this observation we may assume that the upper and lower limits of a 95% confidence interval for the measured viral load correspond to the true viral load±0.5. This yields a measurement error variance of approximately 0.255² (where 0.255 = 0.5/1.96). This is in line with another report (0.264² for viral loads >500 copies/ml) ².

The second assumption states that the probability of a missing or incorrectly measured value depends only on observed quantities, see eText1 for a detailed definition. In line with previous work¹⁹ we therefore use the term “mismeasured at random” to mean that both the missingness process and the measurement error process must not depend on any unobserved values.

In situations where clerical or administrative errors cause a value to be missing, such as in large cohorts where data capturing capacity may be limited, this assumption is certainly fulfilled. If the probability of missingness (or occurrence of measurement error) depends on captured information, such as treatment facility, region, or date of treatment initiation, the assumption would also be fulfilled. In the case where unobserved values determine the probability of missingness (or occurrence of measurement error) the assumption would be violated; for example if particularly high CD4 or viral load measurements were missing or incorrectly measured, or if the missing data relates to a specific healthcare worker and this is not captured. Possible consequences of such situations are described in the discussion.

Simulation studies

Generation of data

We generated data of sample size n=5000 for the main setting, and n=1000, 2500, 7500, 10000 for further settings. Two covariates, representing true log CD4 count and true log viral load, were drawn from log-normal distributions with mean and standard deviations (adapted from the data analysis below) as follows: X₁∼logN(4.286,1.086) and X₂∼logN(10.76,1.8086).We used a Clayton Copula (with copula parameter θ=1 indicating moderate association) to model the dependency between these two variables ^33,34. Survival times Y were simulated as follows:

$$Y=-\frac{log(U)}{h_0\{exp(X\beta )\}}$$

where U is drawn from a distribution that is uniform on the interval [0,1], h₀=0.1, and the linear predictor Xβ is defined as -0.3 ln X₁ + 0.3 log₁₀X₂. Higher values of X₁ are therefore associated with a lower risk of a (death) event, as is the case for CD4 count, while higher values of X₂ are associated with a higher risk of an event, as is the case with viral load. The censoring times were simulated as

$$C=-\frac{log(U)}{0.2}$$

The observed survival time T in our simulation was thus T=min(Y,C).

Measurement error and missing data

To both log-transformed variables we added measurement error, as in our data, with mean 0 and variances of 0.26² and 0.255² respectively.

X₁ and X₂ were assumed to be missing at random and the missing indicator was simulated by means of the following missingness function:

$${\pi }_X(T)=1-{\{1+exp(1-4T)\}}^{-1}$$

This yields approximately 9% missing values per variable. Since, in this simulation, the probability of missingness depends on the outcome, one would expect parameter estimates in a regression model of a complete case analysis to be biased ³⁵.

Simulation studies: estimators and model

We compare the performance of (i) a complete case analysis (omitting observations with missing values), (ii) multiple imputation, and (iii) multiple overimputation when estimating the parameters in a Cox proportional hazards model. We also compare (i) the naïve estimator and multiple overimputation for the setting without missing data. The multiple (over)imputation model included all variables, but T on a log scale.

Measures of performance

We evaluate the bias, mean squared error (MSE), and distribution of each estimator of β_i via R=1000 runs of the simulation study. The bias is estimated as $\frac{1}{R}{\sum }_{r=1}^R{\widehat{\beta }}_{ir}-{\beta }_{ir},$, the MSE as $\frac{1}{R}{\sum }_{r=1}^R{({\beta }_{ir}-{\widehat{\beta }}_{ir})}^2$.

Sensitivity

To explore the sensitivity of our simulation we varied our assumptions with respect to the amount of measurement error, the missingness process, the correct specification of the measurement error variance, and the linear predictor.

Results

Results of simulation studies

One can see that a complete case analysis yields biased results both when dealing only with mismeasured data (Table 1a) and when dealing with mismeasured and missing data (Table 1b). Multiple imputation also yields biased results in our missing-at-random setting when confronted with measurement error (Table 1b). Multiple overimputation considerably reduces bias when compared to the two aforementioned approaches (Table 1). Comparing the distribution of parameter estimates from the different methods by means of Wilcoxon tests leads to rejection of the null hypotheses of identical distributions, confirming the shift of multiple overimputation estimates towards the true parameter.

Table 1.

Bias, Variance, and Mean Squared Error in the main simulation study: results are reported for both β₁ and β₂ - for a naïve/complete case analysis (CC), multiple imputation (MI), and multiple overimputation (MO) respectively. The left panel lists results for the setting without missing data; the right panel lists the results for the setting with missing data.

(a) no missing data	naïve	MI	MO	(b) missing data	CC	MI	MO
Bias β1	0.034	-	0.023	Bias β1	0.033	0.029	0.017
Bias β2	-0.048	-	-0.019	Bias β2	-0.045	-0.042	-0.009
Variance β1	0.0006		0.0009	Variance β1	0.0007	0.0007	0.0010
Variance β2	0.0010		0.0017	Variance β2	0.0011	0.0011	0.0019
MSE β1	0.0018	-	0.0014	MSE β1	0.0017	0.0015	0.0012
MSE β2	0.0033	-	0.0021	MSE β2	0.0031	0.0029	0.0020

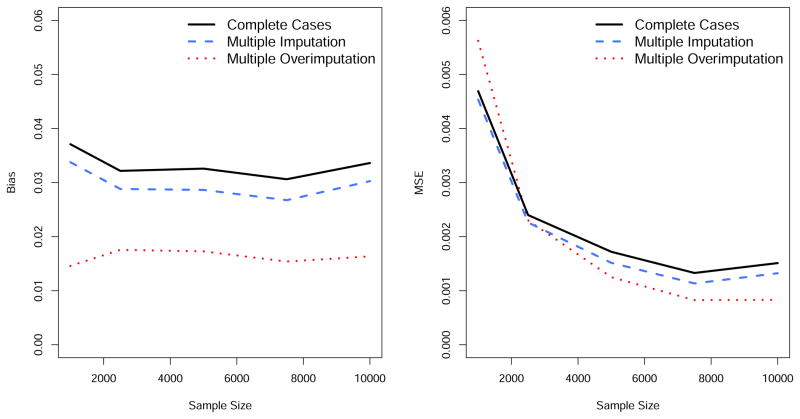
The MSE is smaller for multiple overimputation when compared to a naïve or complete case analysis and multiple imputation, but the variance is larger (Table 1). However, the success of the three methods with respect to the MSE depends on the sample size as highlighted in Figure 1: the larger the sample size, the better the performance of multiple overimputation relative to the other methods. If the sample size is small, multiple overimputation does not outperform the two other methods with respect to the MSE. The bias can always be reduced using multiple overimputation, regardless of the sample size (Figure 1).

Figure 1.

Results of the simulation studies: estimated bias and Mean Squared Error (MSE) of β₁ depending on the sample size, in the setting where the data are missing at random.

Sensitivity analyses show that under a correctly specified measurement error variance, changing the assumptions to allow for a higher amount of missing data, a different missingness process, a larger amount of measurement error, a smaller effect of each variable, and the inclusion of more variables, yields similar conclusions (eFigure 2).

Illustrative Example: HIV-treatment Data from IeDEA-SA

We used data from the International epidemiological Databases Southern Africa cohort collaboration (IeDEA-SA) to illustrate the practical application of multiple overimputation in HIV treatment data. IeDEA Southern Africa is a collaboration of 19 mostly programmatic cohorts in five southern African countries 36. Data were collected at each site as part of routine monitoring and were transferred to the coordinating data centre at the University of Cape Town, South Africa. All contributing facilities obtained ethical approval from the institutional review boards before submitting anonymized patient data to the collaboration.

We limited data to four South African cohorts as those were the only ones with routinely assayed viral loads. Our dataset contained data on nearly 30,000 patients, initiating HAART between 1 January 2001 and 1 January 2010; all were followed from the time of first starting HAART (baseline).

Multiple Overimputation (M=10) was implemented using the “amelia” function of the R-package Amelia II ²⁸. The (over)imputation model included the mortality outcome, time to event or censoring, cohort, sex, age, year of HAART initiation, baseline ln CD4, baseline log₁₀ viral load. Our prior knowledge about the measurement error process was specified by means of the “priors” and “overimp” options of the amelia function, adding a prior normal distribution to each measured ln CD4 count and log₁₀ viral load where the mean corresponded to the mismeasured value and the measurement error variance was set to 0.26² and 0.255² respectively. In sensitivity analyses, the measurement error variance was specified as 0.20² and 0.30² for CD4 and as 0.15² and 0.31² for viral load.

We used the Cox proportional hazards model to estimate the relationship between baseline CD4 count, baseline log₁₀ viral load, year of treatment initiation, sex, cohort, and age with the hazard of death, based on the 10 overimputed datasets and applying multiple imputation-combining rules. Baseline CD4 count and baseline log viral load were included in the model first by categorizing the variables and, secondly, non-linearly via p-splines ³⁷. In addition, as a reference, results from multiple imputation and a complete case analysis were estimated.

This example shows how regression estimates of CD4 count and viral load can vary depending on whether missing data and measurement error are taken into account. We have therefore excluded other variables with high missingness percentages (haemoglobin, WHO stage, creatinine, platelets) and under-reporting (tuberculosis, cryptococcal meningitis, among others) to ensure that comparisons between the different methodological approaches are not complicated by the missingness and measurement error related to these variables.

We also performed a similar analysis for the same data with time-updated CD4 counts and viral loads being included. If a patient did not have a CD4 count/viral load measurement for 6 months, then the respective values were treated as missing. The imputation model included the same variables as above, time-updated CD4 and virologic suppression (viral load <1000 copies/μl), and took the longitudinal structure of the data into account. The prior information for time-updated CD4 count was specified as for baseline CD4 count. Time-updated virologic suppression was preferred over time-updated viral load due to the bimodal distribution of the latter; the corresponding measurement error variance was assumed to be 0.23² which related to an assumption of about 1.5% misclassification (which we assume based on simulated viral loads similar to our data, see eText 2).

To address the fact that patients lost to follow-up are more likely to die, we linked lost patients to the national South African vital registry to obtain the vital status of these patients. The linkage was performed by a trusted third party, the South African Medical Research Council. Lost patients with recorded IDs could thus be linked (and their outcome ascertained and corrected); these patients were up-weighted to represent all patients lost to follow-up: we took the inverse of the modelled probability of having an ID, based on a logistic regression model including age, sex, year of treatment initiation and cohort, in order to account for any differences between linkable and other patients lost to follow-up (patients with and without ID are known to be very similar though there are typically differences by cohort and year ^38,39). Patients not lost to follow-up received a weight of one, while those lost to follow-up and not linkable received a weight of zero. ³⁹ Alternatively, missing outcome data of patients lost to follow-up could have been imputed with multiple overimputation.

From the 29,256 patients included in our analysis more than 10% had a missing baseline CD4 count and more than 60% had a missing baseline viral load. Median follow-up time (1^st; 3^rd quartile) was 498 (197; 878) days. The Expectation Maximization Bootstrap algorithm utilizing multiple overimputation converged successfully for both the cross-sectional and longitudinal data examples.

The results of the Cox regression analysis are presented in Figure 2 and eTable 1. Multiple overimputation emphasizes more strongly the relationship between a high baseline CD4 count and a decreased hazard of death compared to the complete case analysis and multiple imputation (hazard ratio for CD4>200 cells/mm³ versus CD4<25 cells/mm³: 0.21[95%CI: 0.18;0.24] vs. 0.38 [0.29;0.48] for the complete case analysis and 0.29 [0.25;0.34] for multiple imputation). Looking at the nonlinear association of CD4 count with the hazard of death, or excluding baseline viral load from the analysis, or adding additional variables leads to the same conclusions (Figure 2a, eTable 2, eTable 3): the higher the CD4 count, the lower the hazard of death; similarly, the larger the number of viral copies the greater the risk of death, which is more pronounced for multiple overimputation when compared to multiple imputation (Figure 2b). The sensitivity analyses show that different assumptions about the measurement error variance yield an almost identical non-linear association of CD4 count with mortality after applying multiple overimputation. Assuming a much smaller measurement error variance for log₁₀ viral load yields similar results for multiple overimputation and multiple imputation (eFigure 1). Regression coefficients of covariates without measurement error and missing data did not vary much between the three different approaches.

Figure 2.

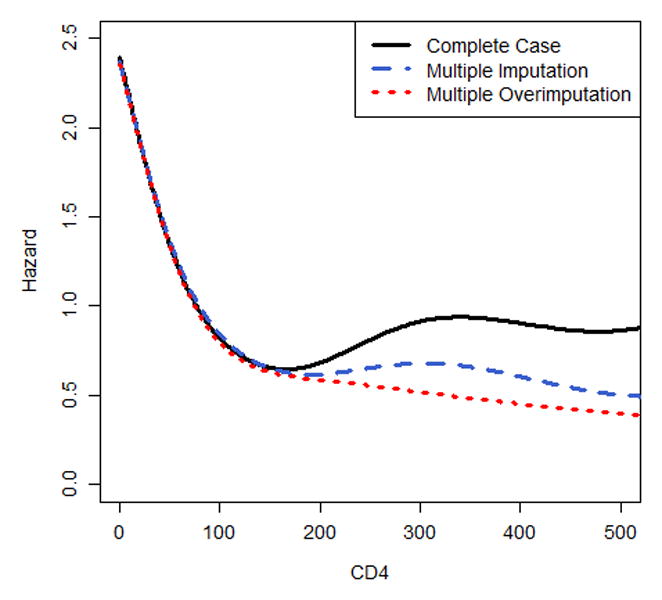
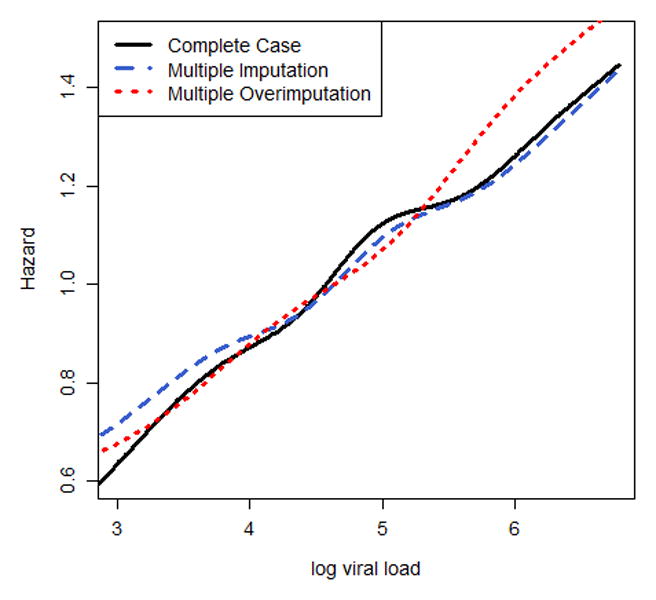
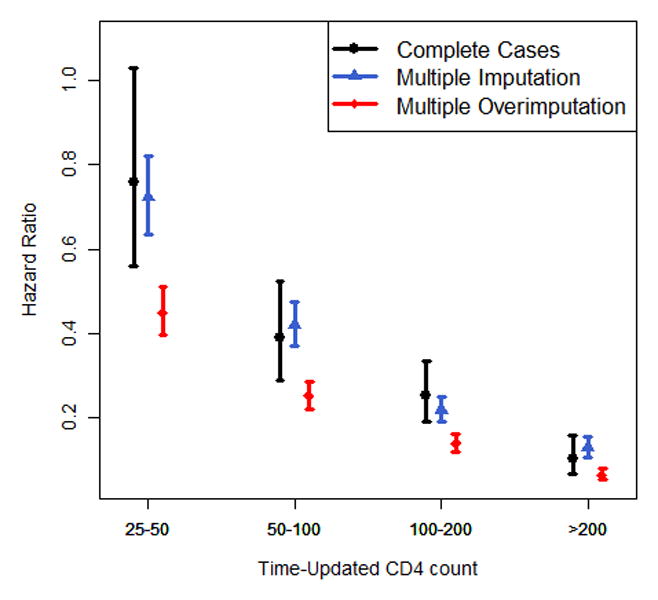
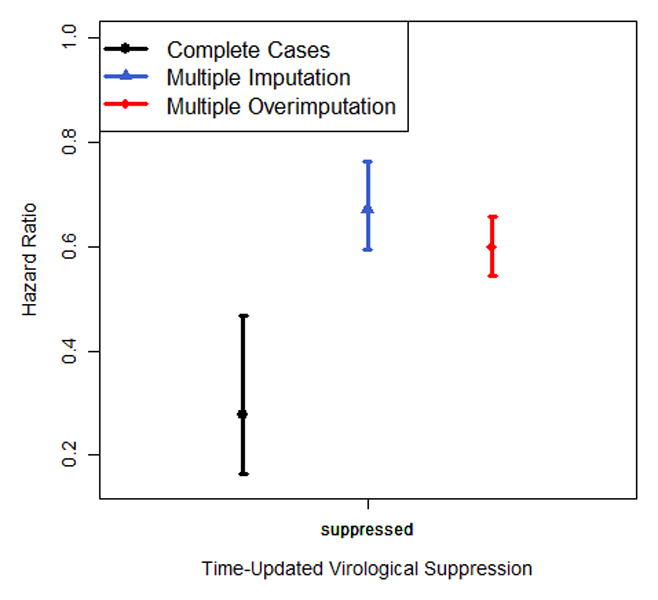
Nonlinear association of (a) baseline CD4 and (b) baseline log₁₀ viral load with the hazard of death, modelled via p-splines. The estimates of (c) categorical time-updated CD4 (reference category: <25 cells/mm³) and (d) categorical time-updated virological suppression (reference category: unsuppressed) are obtained from a Cox model fitted onto the longitudinal data. Results are reported for a complete case analysis, multiple imputation and multiple overimputation and relate to the illustrative data example. The intervals reported in (c) and (d) are 95% confidence intervals.

The longitudinal Cox regression analysis (Figure 2c/d, eTable 4) yields attenuated estimates for CD4 count in the complete case analysis and multiple imputation compared to multiple overimputation (HR for CD4>200 cells/mm³ vs CD4<25 cells/mm³: 0.10 and 0.13 vs. 0.06); this analysis also shows that a complete case analysis yields very different results from the imputation approaches when assessing the estimates of viral suppression (HR 0.28 vs. 0.67 and 0.60).

In both analyses the confidence intervals for all point estimates of multiple imputation and multiple overimputation were similarly wide (eTable 1, eTable 3). It can also be seen that in all analyses the correction made for measurement error was at least as great as the correction made to account for missing data (Figure 2, eTables 1-3).

The above analyses demonstrate that multiple overimputation for both baseline and follow-up CD4 count and viral load data can be easily incorporated into existing software (Amelia II for R), that the overimputation algorithm converges successfully for this data, that results may vary depending on whether one adjusts for missing data and measurement error or not, and that attenuation due to measurement error can occur, but this may not always be the case.

Discussion

Statement of principal findings

We have demonstrated that multiple overimputation offers a convenient approach to address both measurement error and missing data and can be implemented easily for a variety of situations relevant to HIV research. Our simulation studies suggest that this approach is able to reduce bias and MSE in the context of survival analyses.

Strengths of the study

This is, to the best of our knowledge, the first attempt to address simultaneously the the treatment of missing data and measurement error in HIV research under a general framework. It is fast and easy to implement and, after applying multiple overimputation, many estimators relevant to HIV research can be obtained: for example the Kaplan-Meier estimator, and estimates from survival models such as the Cox proportional hazards model and parametric survival models, among many others. We have demonstrated that existing clinical knowledge about the accuracy of CD4 measurements can be used to specify the measurement error process, model and variance, which we have shown to be crucial for the success of method; moreover, our simulations highlight that not only for generalized linear models (as partially investigated by Blackwell et al. ¹⁹) but also in survival analyses multiple overimputation can be successful.

Limitations

There remain, however, some limitations: As with multiple imputation, multiple overimputation cannot necessarily address situations where data are mismeasured not at random because the overimputed values drawn with the Expectation Maximization Bootstrap algorithm may not properly reflect the joint distribution of both the data and the missingness/mismeasurement process (eText 1, formula (1)). In this case, the application of multiple overimputation can lead to biased estimates. Using a complete case analysis (and possibly correcting for measurement error in the respective sample) can also yield biased estimates in this setting, i.e. when the probability of a missing value depends on the outcome or external variables ^31,40. However, if the probability of missingness depends on the unobserved values of the variable itself, a complete case analysis still yields valid inference and may be preferable to multiple overimputation ⁴⁰. As we have argued above, in many cases, we would expect CD4 and viral load data to be mismeasured at random; however, time-updated viral load may be missing not at random if unobserved treatment interruptions due to non-adherence predict missingness.

We also have assumed that a successful specification of the imputation model is straightforward. The implementation of multiple overimputation is closely related to the joint modelling approach of Amelia II and thus natural constraints relate to specifying suitable transformations for skewed variables, additional imputation uncertainty with respect to categorical variables, and restrictions regarding complex longitudinal data ^28,41. An inappropriate imputation model or incorrect assumptions about the measurement error process can potentially cause multiple overimputation to be inferior compared to naïve estimators.

Meaning of the results

Our results suggest that regression estimates related to true CD4 count and true viral load may be biased in many studies. Both markers are a cornerstone in HIV research and thus it may be advisable to consider accounting for error in their measurement. Our data example illustrates how the application of multiple overimputation can change regression estimates: for example, the association of CD4 count with the hazard of death was more strongly pronounced under multiple overimputation compared to the approaches which neglected measurement error. This does not, however, imply that for any regression analysis the estimates of a complete case analysis are biased towards the null, nor does it imply that corrected estimates of CD4 count are necessarily better just because their estimates yield stronger associations than naïve analyses.

While our data example is illustrative and descriptive in nature, and none of the reported regression coefficients report a causal relationship, there are several applications for which our findings are of interest. For example, predictive models can be used to inform mathematical modelling studies that require mortality rates stratified by true CD4 count and viral load ^42,43. It is evident from both our simulation studies and the data example that adjusting for missing data and measurement error can yield different predicted mortality rates; indeed, fitting the predictive model of May et al. ⁴⁴ to our data shows that the differences between multiple overimputation and naïve approaches found in our illustrative example persist in this context (eTable 5).

Our numerical investigations confirm previous studies showing that even a moderate amount of measurement error and/or missing data can cause bias in regression estimates ^9,45. Multiple overimputation reduced the bias in these estimates and also improved the MSE if the sample size was not too small. The latter observation implies that multiple overimputation may yield estimators with a higher variance compared to a naïve analysis (reflecting the underlying uncertainty) and the success with respect to the MSE depends on the sample size. This is in line with the literature on measurement error correction in the case of complete data ^9,45,46. Generally, multiple overimputation yields asymptotically unbiased estimates under the mismeasured at random assumption (eText 1) given an appropriate imputation model is used, but its performance may vary from context to context.

Research in context

Methods dealing with measurement error in CD4 count have already been suggested for particular applications and models under the assumption of no missing data ^10-18. One could think of applying these methods in the appropriate context in conjunction with multiple imputation. Since these methods are often very specific, combining the more general simulation extrapolation method ⁴⁷ with multiple imputation might be a fruitful alternative. An implementation of simulation extrapolation in the statistical software R⁴⁸ is already available for (generalized) linear models, allows for both homoscedastic and heteroscedastic measurement error and can be naturally combined with existing multiple imputation procedures in R²⁸; similar implementations are available for Stata ⁴⁹. However, it is an open question whether the imputations generated from mismeasured data yield valid inference or not.

It also remains important to check model assumptions after applying multiple overimputation: for example, when assessing the proportional hazards assumption of a Cox proportional hazards model, one may evaluate graphical diagnostics in each overimputed dataset; or, alternatively, the estimates of an interaction of analysis time with the covariate of interest can be easily combined by means of Rubin's rules.

We have concentrated our investigations on measurement error and missing data in CD4 counts and viral load measurements. There are however many more variables prone to measurement error and missing data and relevant in HIV research: CD4 percentage, haemoglobin, creatinine, p24 antigenemia, concentrations of antiretroviral drugs, among others. Existing knowledge can be used to account for both measurement error and missing data in many of these variables ^1,2,8. We stress, however, that an overestimated measurement error variance may yield biased estimates when applying multiple overimputation, see eFigure2l and Blackwell et al.¹⁹. Complicated measurement processes such as in pharmacokinetics, where metabolism, concomitant medication, and genetic factors influence measurement error, may, however, require special care and knowledge.

Conclusion

In conclusion, our investigations show that multiple overimputation is a convenient and possibly promising approach to account for both missing and mismeasured data in HIV research. Further studies are needed to explore the implications, feasibility, and challenges of multiple overimputation for other models and applications.