Short-selling constraints as cause for price distortions: An experimental study

Abstract

In this paper we explore the influence of the possibility to short stocks and/or borrow money in laboratory markets. A key innovation of our study is that subjects can simultaneously trade two risky assets on two double-auction markets, allowing us to differentiate between assets with relatively high versus low capitalization. Divergence of opinions is created by providing each trader with noisy information on the intrinsic values of both assets. We find that when borrowing money or shorting stocks is restricted prices are systematically distorted. Specifically, stocks with high (low) capitalization are traded at lower (higher) prices than their fundamental value. Lifting the restrictions leads to more efficient prices and more liquidity, thereby also lowering volatility and bid-ask spreads.

1. Introduction

After the sudden demise of Lehman Brothers in September 2008 several stock exchanges, including London and New York restricted the short selling of stocks of finance companies. This move – argued to be necessary to stop speculators from driving stocks prices to artificially low levels – was not uncommon in the history of finance. Nobody likes a “spoiler”, and short-sellers are bearish, while most “common” people bet on rising stock prices. The bears who, during a boom (or bubble) argue that prices are too high are ridiculed, and if they dare to make money on their opinion by selling short, they are called economic vandals when a bubble pops. Thus, bans on short selling are neither uncommon nor unpopular – the public is usually easily convinced that “speculators” need to be tamed.

However, the story is probably not so easy – bears serve an invaluable function in markets, as they may keep prices from rising too far. Markets are supposed to aggregate all information available and incorporate it in prices. When this is possible without constraints, markets should properly reflect all available information, in the vein of Fama’s efficient market hypothesis (Fama, 1970, Fama, 1991). The key question is thus how good markets are at aggregating and disseminating information (Hayek, 1945). The question whether and how short-selling constraints and limits of arbitrage influence price aggregation is central to this issue and is therefore hotly debated. This is particularly relevant since, on a global scale, constraints on short-selling vary between and within markets. Bris et al. (2007) give a comprehensive overview on the differences of short-selling restrictions across markets before the financial crisis of 2008. Subsequently, additional (temporary and/or sector-specific) bans on short-selling were imposed in numerous countries (e.g. in the US in 2008 and Germany in 2010). Since it is still not clear whether isolated bans on short-selling are an appropriate measure to “protect” markets against speculators, further insights in the effects of short-selling constraints on price aggregation are of high importance from a regulatory point of view.

In a seminal paper Miller (1977) argues that when investors disagree about the value of a stock, the optimistic buy while the pessimistic sell. When no constraints exist, prices reflect the average opinion. However, in the presence of short-selling constraints, divergence of opinions leads to higher-than-justified prices, as pessimists are unable to sell a stock once they no longer hold it, while optimists can buy without any limitations other than the money they have. As a consequence prices will be set by the optimists and thus too high. This is called the “overvaluation hypothesis” (see Duffie et al., 2002, Jiang, 2005, Scheinkman and Xiong, 2003, Shleifer and Vishny, 1997; for more literature supporting this view). In contrast, Diamond and Verrecchia (1987) claim that prices will not be biased because of short-selling constraints if traders have rational expectations. According to their analytical model, short-selling constraints only decrease the speed of price adjustment to private information.

The empirical evidence on the issue is mixed.¹ We attribute this to the difficulties in measuring relevant variables. Specifically, to explore the effect of short-selling constraints on market efficiency researchers have to (i) measure the degree to which shorting is constrained, (ii) estimate the intrinsic value of the stock, and (iii) measure the degree of divergence of opinions. None of the three is easy, but especially the last two are extremely tricky. Calculating the correct intrinsic value of a stock (if it exists at all) is the goal of a whole profession and so far no generally accepted model has been found. Similarly, collecting the different opinions on the market is virtually impossible. Thus, for both questions empirical research has to rely on proxies, which are noisy at best, biased at worst.

Given the methodological challenges to empirical studies, we think this issue lends itself naturally to experimental exploration. In laboratory markets we can control the institutional rules, intrinsic values of the contracts traded, and the fundamental information available to participants, thus solving all three of the tricky estimation problems that hamper empirical studies in this field.

We are aware of four studies that have explored the effects of short-selling restrictions in an experimental setting: Ackert et al., 2002, Haruvy and Noussair, 2006, and King et al. (1993) are all based on the classical Smith et al. (1988) setting and find (weak) support for Miller’s overvaluation hypothesis. However, in all three studies participants receive symmetric information, while asymmetry is an important feature of real markets. Fellner and Theissen (2011) set up a model with asymmetric information with results corroborating the overvaluation hypothesis, but they restrict the number of tradable assets to only one (as do Haruvy and Noussair, 2006, King et al., 1993). Only Ackert et al. (2002) implement trading in two assets. However, while one asset is intended to replicate a stock, the other is likened to a lottery ticket, as it has only a 4-percent-chance of generating a positive payoff. Thus, also in this study the important issue of investment decisions between different stocks, which is central to real financial markets, is not addressed.

A static equilibrium model proposed by Jacobsen et al. (2000) indicates that short-selling constraints on stocks will lead to a systematic bias, notably the overvaluation of low-capitalized stocks, while high-capitalized stocks will be undervalued.² This suggests that the mechanism Miller describes is likely to be affected by the capitalization of a specific stock. In our experiments short-selling constraints are independent of market capitalization, thus disentangling these two variables.³ Our design allows for the first time to differentiate between high- versus low-capitalized stocks and the interaction effects between relative capitalization of a stock and constraints to shorting money and/or stocks.

Based on the existing literature we implement experiments where two risky assets with differing capitalization are traded. Having two assets we examine whether any systematic mispricing in settings with/without short-selling constraints can be observed. Divergence of opinion is created by supplying participants with noisy information about the intrinsic values of the assets traded.

We find that allowing short-selling of stocks does increase efficiency in our markets. In sessions where short-selling is constrained we observe systematic overvaluation (undervaluation) of stocks with relatively low (high) capitalization. When only borrowing money is allowed this result remains unchanged but the overall price level is higher. However, when borrowing money and shorting stocks is allowed, no such bias can be observed. In addition, liquidity is higher and volatility is lower when borrowing money and shorting stocks is allowed. General overvaluation is not present when shorting money is forbidden.

The paper is structured as follows: in Section 2 we derive several testable conjectures on the impact of short-selling restrictions on price distortions. Section 3 presents the experimental setup, while Section 4 discusses the methodology for testing our conjectures. Section 5 presents the main results, and Section 6 concludes.

2. Conjectures

Jacobsen et al. (2000) suggest that short-selling constraints will cause overvaluation of low-capitalized stocks as well as undervaluation of high-capitalized stocks. The main reason is that, lacking the ability to go short, traders with relatively low expectations for the stock no longer influence its price once they have sold all their respective holdings. Thus, a few traders with particularly high expectations set the price and through their readiness to buy they can stabilize the stock price at a level above the median expectation. This is especially relevant for low-capitalized stocks, as here the limited amount of money that traders have allows them to buy a higher share of the total number of stocks available.⁴ When borrowing money is possible this problem is not resolved, but the unlimited access to cash is likely to lead to higher average prices. Only allowing to short stocks will resolve this systematic bias, as then traders with relatively low expectations for a stock can short it and thus counterbalance the traders with the highest expectations. Consequently the first set of conjectures reads:

• Conjecture 1a:

  When borrowing money and shorting stocks is forbidden, low-capitalized stocks will be overpriced relative to their intrinsic value while high-capitalized stocks will be underpriced.

• Conjecture 1b:

  When borrowing money is allowed, but shorting stocks is not, low-capitalized stocks will be overpriced relative to their intrinsic value while high-capitalized stocks will be underpriced, but overall prices will be higher.

• Conjecture 1c:

  When borrowing money and shorting stocks is possible there will be no systematic price distortions.

If Conjecture Set 1 is confirmed, then this is likely due to a few traders with the highest expectations buying most of the low-capitalized stocks. Thus, holdings of such stocks will be more concentrated than those of stocks with comparably high capitalization, as long as borrowing money and shorting stocks is not allowed. When borrowing money is allowed, the cash limitation on buying the stocks with high capitalization no longer holds, so for these stocks as well the traders with the highest expectation can buy most of the stocks outstanding. Thus, the stock concentration should be the same across all stocks. This line of argumentation holds as well when shorting stocks is also possible. Conjecture Set 2 therefore reads:

• Conjecture 2a:

  If borrowing money and shorting stocks are forbidden, stock holdings will be more concentrated for stocks with low capitalization than for stocks with high capitalization.

• Conjecture 2b:

  With the possibility to borrow money, concentrations of stock holdings will be more similar across different capitalization levels.

• Conjecture 2c:

  When borrowing money and shorting stocks are possible there will be no differences in concentrations of stock holdings.

Trading activity is also likely to be influenced by the market setting: when borrowing money and shorting stocks are constrained, traders with relatively low expectations for a specific stock can only sell their initial endowment of this stock, but not short it. Similarly, traders with the highest expectations for the value of a stock cannot buy unlimitedly, as their cash is restricted. Consequently they cannot trade as much as they would possibly like to. When shorting stocks and borrowing money are possible no such constraints exist. This leads to

• Conjecture 3:

  Trading activity will be lowest in sessions with constraints on money and stocks, and highest when borrowing money and shorting stocks is possible.

When borrowing money is not allowed, the amount of money provided initially allows to buy a relatively larger share of low-capitalized stocks. E.g., 200 in cash allows to buy 40 stocks priced at 5, but only 4 stocks priced at 50. When the number of outstanding stocks is the same for each asset, the relative trading volume (number of shares traded divided by shares outstanding) will be higher for low-capitalized stocks. However, when borrowing money is possible this no longer holds – and even less so when shorting stocks is also possible. Consequently we formulate Conjecture Set 4:

• Conjecture 4a:

  In the setting with constraints on borrowing money and shorting stocks trading volume will be higher for stocks with low capitalization than for stocks with high capitalization.

• Conjecture 4b:

  When the money constraint is lifted, no such pattern will emerge.

In the laboratory as well as in real markets, bid-ask-spreads and volatility are strongly driven by liquidity and trading volume. If Conjecture 3 holds we should see lower bid-ask-spreads and lower volatility when shorting stocks is possible than when it is constrained. Our final conjectures 5 and 6 are therefore:

• Conjecture 5:

  The bid-ask-spread is higher when shorting stocks is constrained.

• Conjecture 6:

  Volatility of prices is higher when shorting stocks is constrained than when it is possible.

3. Experimental setup

We run laboratory experiments where we control the intrinsic values of the stocks traded as well as the information signals given to traders.⁵ Subjects trade one period assets that have an intrinsic value between 5 and 95. In each period two assets (A and B), whose values add up to 100, are traded on two separate continuous double-auction markets. This is an important modification to earlier studies with only one risky asset (e.g. Fellner and Theissen, 2011, King et al., 1993), because it allows to distinguish between stocks with relatively high and relatively low intrinsic values, which is essential to test our conjectures.

We create three settings distinguished by whether borrowing money and/or shorting stocks is possible. Specifically, in setting 1 (labeled BMF_SSF for Borrowing Money Forbidden_Shorting Stocks Forbidden, throughout the text) going short in money or stocks is not possible. In setting 2 (BMA_SSF, Borrowing Money Allowed_Shorting Stocks Forbidden) it is possible to take out loans to buy stocks on margin without limitations and extra costs. Finally, in setting 3 (BMA_SSA, Borrowing Money Allowed_Shorting Stocks Allowed) borrowing money and shorting stocks is possible without limitations at no extra cost at no extra cost (see Table 1 for a detailed description of all settings).⁶

Table 1.

Settings of the experiment distinguished by whether shorting money and or stocks is allowed.

	Short money	Short stocks	Label
Setting 1	No	No	BMF_SSF
Setting 2	Yes	No	BMA_SSF
Setting 3	Yes	Yes	BMA_SSA

Each market is populated by 20 subjects who trade for 20 independent periods (p). In 10 periods the intrinsic values are calculated as

$$v_{A,p}=\frac{100}{x}=100-v_{B,p},x\in \left\{2,4,6,\dots ,20\right\},$$ (1)

while in the other 10 periods v_A and v_B are interchanged. As a benchmark we always set the sum of the intrinsic values of the two stocks to 100. The sequence of periods is randomized and is shown in Table 2.

Table 2.

Intrinsic values of stock A and B in the 20 periods of each session.

p	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
vA	16.67	92.86	25.00	5.56	6.25	90.00	87.50	8.33	50.00	95.00	91.67	7.14	50.00	83.33	5.00	94.44	10.00	75.00	93.75	12.50
vB	83.33	7.14	75.00	94.44	93.75	10.00	12.50	91.67	50.00	5.00	8.33	92.86	50.00	16.67	95.00	5.56	90.00	25.00	6.25	87.50

The set in Table 2 allows us to compare cases when the two intrinsic values differ widely (e.g., 95 vs. 5) to others where the difference is smaller (75 vs. 25) or even zero (50 vs. 50). Most cases intentionally have a large difference in capitalization between the two stocks, as we are interested in the interaction between relative capitalization (high versus low) and constraints on shorting money and/or stocks.

Each trader starts each period with 4 shares of A, 4 shares of B, and 200 in cash. Traders therefore hold 400 in stocks and 200 in cash for a starting wealth of 600. The market is a zero-sum game – whatever one trader wins is at the expense of another trader, and an end-of-period wealth of 600 reflects a net return of zero. As the total number of stocks in the market is equal for A and B, a stock with an intrinsic value of 5 or 10 is relatively low-capitalized, while a stock with an intrinsic value of 90 or 95 is high-capitalized and we use the terms “stock with low (high) intrinsic value” and “low-(high-)capitalized stock” synonymous.

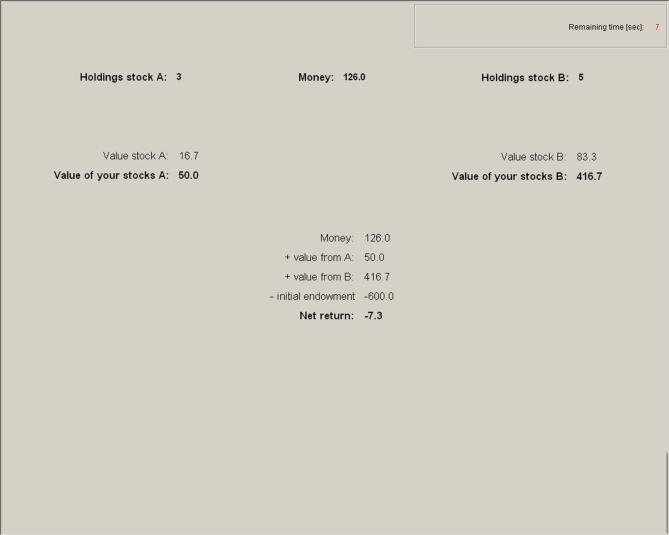
Prices are set exclusively by actions of the traders in two continuous double-auction markets with open order-books (see screenshot in the Appendix). Similar to most stock exchanges all orders are executed according to price and then time priority. Market orders have priority over limit orders in the order-book and are always executed instantaneously. Each transaction is for one stock.

The exact intrinsic values are not public knowledge, but to provide subjects with information on the intrinsic values of the stocks and create divergence of opinions at the same time, each trader receives a noisy signal on the value of each stock. To ensure that the median signal is an unbiased estimate of the intrinsic value, we predetermine the deviations from a normal distribution with a standard deviation of 2. Specifically, we draw ten positive deviations and “mirror” them (take the respective negative deviation) for the other ten subjects in the market. The same absolute deviations are used for all periods. The quality of information each individual receives (determined by deviation of fundamental information and intrinsic value) is different in each period. As the intrinsic values of A and B always add up to 100, which is public knowledge, the two signals a trader receives also add up to 100, i.e. if his signal for A is upward biased by x, his signal for B is downward biased by −x.⁷

Holdings of money and stocks are not carried over from one period to the next, but all stocks are bought back by the bank (the experimenter) at their intrinsic values at the end of each period. At this time, the intrinsic values of both stocks are revealed to all traders and gains or losses in experimental currency are balanced with the traders’ total payouts (€0.02 for every unit of experimental currency). At the start of the next period each trader is again endowed with 4 stocks A and B and with 200 units of money.

We conducted a total of twelve sessions, four sessions for each treatment. In each session 20 subjects, all students of business or economics students, traded for 20 periods of 120 s each. Several sessions were conducted at Yale University and the others at the University of Innsbruck (Austria). On average each session lasted about 60 min and average earnings were $ 22 in the U.S. and €18 in Austria. No person participated in more than one of the experimental sessions reported here. The experiments were programmed with z-Tree (Fischbacher, 2007) and participants were recruited with ORSEE (Greiner, 2004).

4. Method

To shed light on the conjectures formulated in Section 2, we apply OLS regressions on period data gathered in the experiments. As we conducted twelve sessions m, each covering two stocks st in 20 independent periods p, we have 480 observations for each dependent variable.

We consider several possible explanatory variables. First, we separate the three settings by introducing dummies.⁸ Additionally, we examine whether some of our results are influenced by the intrinsic value of a stock. For a more convenient interpretation, we introduce a normalized proxy for the intrinsic value, given by:

$$V_{m,st,p}=\frac{v_{m,st,p}-50}{45},$$ (2)

hence V_m,st,p takes values between −1 (for a stock with v = 5) and 1 (for a stock with v = 95). To test whether effects differ for sessions with or without restrictions on shorting stocks or money we interact V with BMF_SSF, BMA_SSF, and BMA_SSA. The resulting coefficients are β_{BMF_SSF,V}, β_{BMA_SSF,V}, and β_{BMA_SSA,V}, respectively.

It is also reasonable to expect traders to change their behavior over the course of the experiment. We therefore use period p to detect possible learning effects. As p 1,2,…,20, we normalize this variable by subtracting the mean:

$$\text{PER}=p-10.5\Rightarrow \text{PER}\in -9.5,-8.5,\dots ,\mathrm{9.5.}$$ (3)

PER is used as an independent variable and the basic regression equation then reads:

$$y_{m,st,p}={\beta }_{\text{BMF}\_\text{SSF}}·\text{BMF}\_\text{SSF}+{\beta }_{\text{BMA}\_\text{SSF}}·\text{BMA}\_\text{SSF}+{\beta }_{\text{BMA}\_\text{SSA}}·\text{BMA}\_\text{SSA}+{\beta }_{\text{BMF}\_\text{SSF},V}·\text{BMF}\_\text{SSF}·V+{\beta }_{\text{BMA}\_\text{SSF},V}·\text{BMA}\_\text{SSF}·V+{\beta }_{\text{BMA}\_\text{SSA},V}·\text{BMA}\_\text{SSA}·V+{\beta }_{\text{PER}}·\text{PER}+u_{m,st,p},$$ (4)

with u_m,st,p = ρu_m,st,p−1+ε_m,st,p to account for possible autocorrelation in the residuals.⁹ The resulting AR(1) coefficient will be reported with the regression results. To deal with the econometric problems resulting from heteroscedasticity as well as autocorrelation in our data, we apply the period SUR method to compute robust covariances (Beck and Katz, 1995).

Depending on our research questions, we introduce the dependent variables used in these regressions in Section 5. Considering our experimental design, we cannot assume that the observations for stock A and stock B are independent. Hence, we use separate regressions for each stock.

5. Results

5.1. Over/undervaluation

According to Jacobsen et al. (2000) and to Conjecture 1, the over/undervaluation of a stock in our experiment should depend on its intrinsic value when borrowing money and/or shorting stocks is constrained, i.e. we should see overvaluation of low-capitalized stocks and undervaluation of high-capitalized stocks. To analyze this relationship, we start by calculating the average price of all transactions, P_m,st,p, for each stock in each period.¹⁰ Taking into account the intrinsic value v, we calculate the over/undervaluation for each observation by

$$M_{m,st,p}=P_{m,st,p}-v_{m,st,p}\text{.}$$ (5)

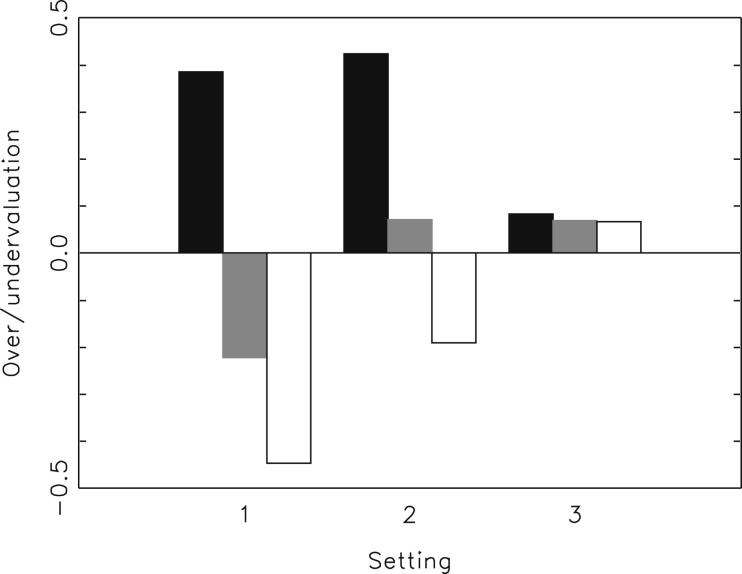
For a first graphical impression on the over/undervaluation, we divide our sample into three categories according to the intrinsic value v. The categories are zero to 24.9 (category 1, shown in black in Fig. 1), 25–75 (category 2, gray in Fig. 1), and 75.1 to 100 (category 3, white in Fig. 1). Fig. 1 shows the results for the three settings.

Fig. 1.

Over/undervaluation of stocks separated by settings: setting 1, BMF_SSF, without shorting money or stocks (left), setting 2, BMA_SSF, where shorting money was allowed (center), and setting 3, BMA_SSA, where going short was possible in money and stocks (right); and categories: black bars for intrinsic values from 5 to 24.9 (category 1), gray for values from 25 to 75 (category 2), and white for values from 75.1 to 95 (category 2).

The first 3 bars in Fig. 1, referring to setting 1, where neither borrowing money nor shorting stocks was allowed, confirm the postulated relationship between intrinsic value and over/undervaluation: in category 1, combining stocks with relatively low intrinsic values, we observe the highest average overvaluation, while the highest average undervaluation can be found in category 3, covering the stocks with the highest intrinsic values. This is in line with Conjecture 1a. Also note that on average we observe slight undervaluation in setting 1, in contrast to Miller (1977).

With borrowing money allowed in setting 2, the overall pattern stays the same, i.e. the overvaluation is highest for the stocks with the lowest intrinsic values and negative (i.e. undervaluation) for the stocks with the highest intrinsic values. But here we see that the average overvaluation across the three categories is positive, as the unlimited supply of money increases average prices and consequently the average overvaluation. This confirms Conjecture 1b.

For setting 3, with borrowing money and shorting stocks allowed, we find a moderate average overvaluation that is almost constant across all three categories, giving support to Conjecture 1c.

To assess the overall accuracy of prices in our experiments, we analyze the descriptive statistics of the squared mispricing (defined as ${\text{SQM}}_{m,st,p}=M_{m,st,p}^2$) as shown in Table 3.

Table 3.

Mean and standard deviation for squared mispricing $M_{m,st,p}^2$ across the three settings of the experiment.

	BMF_SSF	BMA_SSF	BMA_SSA
Mean	0.719	0.579	0.417
Std. Dev.	0.985	1.176	0.640

Considering the mean squared error of prices, the mispricing observed in setting 3 is not only less systematic than in the other two settings, it is also less pronounced. Hence, we conclude that allowing short selling and borrowing money increases informational efficiency in our experimental markets.

To test for the relation between intrinsic value and over/undervaluation, we use over/undervaluation M_m,st,p as the dependent variable in the regression described in Eq. (4). The results are given in Table 4.

Table 4.

Over/undervaluation – results for the regression Eq. (4) with M_m,st,p as the dependent variable, p-values for two-sided tests.

Coeff.	Stock A		Stock B
	Est.	p− val.	Est.	p− val.
BMF_SSF	−0.120	0.141	−0.049	0.708
BMA_SSF	0.175	0.006	0.007	0.955
BMA_SSA	0.102	0.307	0.044	0.671
βBMF_SSF,V	−0.571	0.000	−0.506	0.000
βBMA_SSF,V	−0.344	0.000	−0.370	0.001
βBMA_SSA,V	−0.076	0.478	−0.048	0.587
βPER	−0.014	0.195	0.003	0.864
AR (1)	0.076	0.392	0.216	0.013
R2	0.241		0.199
n	228		228

The results of the regression do not confirm the overvaluation hypothesis of Miller (1977): When borrowing money and shorting stocks is forbidden, overall mispricing in our experiment is economically and statistically not different from zero. However, unlimited access to money in setting 2 leads to higher prices in this setting and for stock A we find significant overvaluation (p = 0.006). When in addition shorting stocks becomes possible in setting 3, the significant overvaluation disappears, so the ability to short stocks seems to reduce prices, giving some support to Miller’s hypothesis.

More importantly, in line with Conjectures 1a and 1b, the slope coefficients β_{BMF_SSF,V} and β_{BMA_SSF,V} for the two settings where shorting stocks was not possible are negative for both stocks (all four are significant at the 1% level). This indicates that the over/undervaluation depends on market capitalization – the higher the intrinsic value, the higher the undervaluation and vice versa. Relative to the average level, the stocks with the lowest capitalization were overpriced by averages of 0.34–0.57, while stocks with the highest capitalization were underpriced. In contrast, this does not hold for setting 3, where borrowing money and shorting stocks was possible, and where β_{BMA_SSA,V} is insignificant for both stocks, again in line with Conjecture 1c: only the possibility to short stocks eliminated the systematic overpricing (underpricing) of stock with relatively low (high) capitalization.

The insignificant value for β_PER shows that the extent of over/undervaluation does not depend on the period; i.e. no learning effects are visible. We consider this important because it suggests that the observed pattern is persistent. We also checked for cross-dependencies by interacting PER with the treatment dummies and V. Again, we find no significant effects. We observe significant positive autocorrelation (AR1) for stock B, indicating that a high (low) overvaluation in a trading session may partly persist from one period to another.

We conclude that in our markets constraints on shorting money and stocks proved to be the main factor causing systematic deviations in prices.

5.2. Stock concentration

We have seen that in sessions with constraints on shorting stocks prices are distorted, as stocks with low intrinsic values are systematically overpriced. The most likely reason for this is that traders with the highest expectations for the intrinsic values of these stocks buy most of them, and thereby keep prices high. Conjecture 2 is a logical consequence of this: holdings of low-capitalized stocks will be more concentrated among a small number of traders than holdings of high-capitalized stocks, as long as money constraints exist. When borrowing money is possible no such effect should be observed. Hence, settings 2 and 3 should deliver similar results.

Fig. 2 presents the respective Lorenz curves for setting 1 (top left), setting 2 (top right) and setting 3 (bottom left).¹¹ For setting 1 we find that concentration of holdings clearly depends on the intrinsic value of a stock: it is largest in categories 1 (where the stocks with the lowest intrinsic values are comprised), next is category 2, and finally category 3, as predicted by Conjecture Set 2. The panels for settings 2 and 3 look quite different from setting 1: when the restrictions on borrowing money are lifted no systematic relationship between capitalization and stock concentrations can be found, thus supporting Conjecture Set 2.

Fig. 2.

Lorenz curves for categories. Short dashes: category 1 (low-capitalized stocks with values between 5 and 24.9), dashes: category 2 (values between 25 and 75), solid line: categories 3 (high-capitalized stocks with values above 75) in setting 1 without shorting money or stocks (top left), in setting 2 where shorting money was allowed (top right), and in setting 3 where going short was possible in money and stocks (bottom left).

To test the significance of these results, we sort holdings for each stock at the end of each period. Aggregating the number of stocks owned by the five traders with the highest holdings gives us a testable proxy CON for stock concentration.¹² CON is then used as the dependent variable in Eq. (4).

Considering the coefficients BMF_SSF,BMA_SSF, and BMA_SSA in Table 5, we observe the stock concentration to be highest for setting 3, where borrowing money and shorting stocks was possible. A Wald-test shows that in this setting the average number of stocks in the portfolio of the five largest holders is significantly larger than in settings 1 and 2. This can be attributed to the fact that the maximum number of stocks held by five traders is unlimited in the sessions where shorting stocks is possible, thus the concentration can be expected to be higher in this setting.

Table 5.

Stock concentration – results for the regression Eq. (4) with CON_m,st,p as the dependent variable, p-values for two-sided tests.

Coeff.	Stock A		Stock B
	Est.	p− val.	Est.	p− val.
BMF_SSF	39.112	0.000	38.956	0.000
BMA_SSF	40.112	0.000	40.351	0.000
BMA_SSA	43.558	0.000	41.789	0.000
βBMF_SSF,V	−5.943	0.000	−5.768	0.000
βBMA_SSF,V	−1.213	0.006	−1.194	0.012
βBMA_SSA,V	−2.883	0.000	−1.376	0.068
βPER	0.026	0.675	−0.021	0.754
AR (1)	0.109	0.265	0.168	0.106
R2	0.341		0.326
n	228		228

The results for the interaction terms, presented in Table 5 give further support to Conjecture 2: while all coefficients are significant, we clearly see that the coefficients for setting 1 (−5.9 and −5.8 respectively for stocks A and B) are several times larger than those for the other two settings (betas from −1.2 to −2.9). We think this result can be attributed to the fact that – as in real markets – not all traders make use of the possibility to go short in stocks or borrow money.

To sum up, we find that especially in setting 1 holdings of low-capitalized stocks are more concentrated than holdings of high-capitalized stocks. In settings 2 and 3 the difference is much smaller.

5.3. Trading activity

We observed lively trading in all twelve sessions, with an average volume (VOL) of more than 1,000 trades per session. Partly confirming Conjecture 3, the average volume was highest in setting 3 (1,130 trades per session) where shorting stocks was possible. Surprisingly, trading volume in setting 2 (995 trades per session) was lower than in setting 1 (1,066 trades per session).

Fig. 3 compares the number of transactions dependent on intrinsic value without shorting stocks or borrowing money (top left), with borrowing money (top right), and with borrowing money and shorting stocks (bottom left). Confirming Conjecture 4, we see significantly higher trading activity in low-capitalized stocks when short-selling is constrained, but almost no effect when shorting is possible in either money, or money and stocks.

Fig. 3.

Average trading volume sorted by the intrinsic value of the stock traded in setting 1 without shorting money or stocks (top left), in setting 2 where shorting money was allowed (top right), and setting 3 where going short was possible in money and stocks (bottom left).

To shed further light on this issue, we run the regression from Eq. (4) with VOL_m,st,p as the dependent variable. The results for this regression also support Conjecture 4 (see Table 6): in setting 1, without short-selling, β_{BMF_SSF,V} is highly significantly negative for both stocks, i.e. trading volume falls with a higher intrinsic value. For the other two settings no such effect can be observed – the betas are negative, but less pronounced and only one of the four betas is significant.

Table 6.

Volume – results for the regression Eq. (4) with VOL_m,st,p as the dependent variable, p-values for two-sided tests.

Coeff.	Stock A		Stock B
	Est.	p− val.	Est.	p− val.
BMF_SSF	27.455	0.000	25.867	0.000
BMA_SSF	25.731	0.000	24.136	0.000
BMA_SSA	30.113	0.000	26.478	0.000
βBMF_SSF,V	−6.594	0.000	−6.972	0.000
βBMA_SSF,V	−0.996	0.145	−1.047	0.073
βBMA_SSA,V	−2.410	0.005	−0.461	0.604
βPER	−0.157	0.145	−0.187	0.033
AR (1)	0.201	0.023	0.198	0.024
R2	0.25		0.277
n	228		228

As is often observed in experiments, trading activity decreases over time, i.e. β_PER is negative for both stocks and significantly negative for stock B. As we observe more orders posted over time (see Table 7) the lower trading volume hints at participants becoming more careful in accepting offers in later periods. Significant positive AR(1) terms can be attributed to session effects as well as persistence of trading activity: a period with high trading volume is likely to be followed by another period of high volume.

Table 7.

Orders posted – results for the regression Eq. (4) with ORD_m,st,p as the dependent variable, p-values for two-sided test.

Coeff.	Stock A		Stock B
	Est.	p− val.	Est.	p− val.
BMF_SSF	55.581	0.000	53.809	0.000
BMA_SSF	56.757	0.000	54.955	0.000
BMA_SSA	72.296	0.000	67.283	0.000
βBMF_SSF,V	−9.485	0.000	−7.591	0.000
βBMA_SSF,V	0.402	0.601	1.558	0.113
βBMA_SSA,V	−3.490	0.005	−1.634	0.089
βPER	−0.023	0.954	0.446	0.014
AR(1)	0.647	0.000	0.446	0.000
R2	0.569		0.444
n	228		228

As a second measure for trading activity we take a look at the orders posted (ORD). Considering the regression results presented in Table 7 we again find that setting 3, with shorting in money and stocks possible, is significantly more active with 2,775 orders (average per session) vs. 2,175 orders in setting 1 and 2,236 in setting 2. According to those results, Conjecture 3 can be fully confirmed for orders posted. Our results also go in line with other studies (see Daouk and Charoenrook, 2005), who state that the ability to short stocks will improve liquidity.

The significantly negative coefficients for β_{BMF_SSF,V} (setting 1) tells us that fewer orders are posted for the stocks with higher intrinsic values, as the constraints on money and stocks bind traders. With the restriction on borrowing money removed in setting 2 we see an (insignificant) positive coefficient β_{BMA_SSF,V}, meaning that more orders were posted for high-capitalized stocks than for low-capitalized ones. The corresponding coefficients for setting 3 turn out to be negative again, but values are much smaller compared to setting 1. All these results support Conjecture 4, which states that trading activity should be higher for low-capitalized stocks when shorting constraints for money are present, but no such effect should be visible when borrowing money is possible.

Autocorrelation is highly significant in this regression, and is responsible for almost half of the fit in terms of R². This indicates that the number of orders posted is prone to persistence effects, e.g. due to a few very active traders that provide high liquidity in one session.

5.4. Use of information

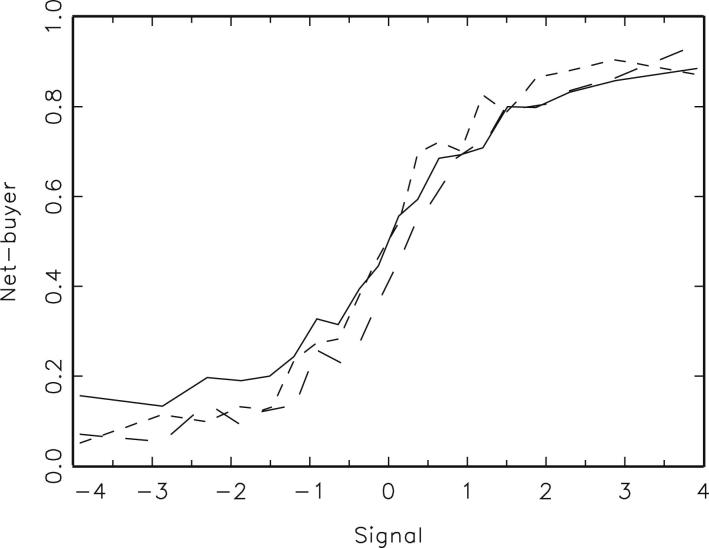
We now explore how much subjects traded on their private signals. Remember that subjects did not get the true value of a stock, but a signal that could deviate by up to +/−3.9 from the true value. Subjects receiving a very low signal (e.g. 6.1 when the true value is 10) are likely to sell, e.g. at a price of 10, while those receiving the highest signal (in this case 13.9) are likely to buy – assuming that subjects do take their signals into account when trading. Fig. 4 shows that the observed frequency of a subject being net-buyer of an asset at the end of a period (vertical axis) strongly depends on the deviation of the private signal from the intrinsic value provided to this subject (horizontal axis). E.g. in settings 2 and 3 less than 10% of the subjects who received the lowest private signal (being) were net-buyers, while more than 90% of those receiving the highest signal (v+3.9) were net buyers. From the data provided in Fig. 4 we conclude that subjects tended to follow the private signals they received. This finding holds across all three settings.

Fig. 4.

Relative number of observations where a trader was net-buyer of an asset at the end of a period for setting 1 (solid line), setting 2 (long dashes) and setting 3 (short dashes).

5.5. Short positions

Giving our subjects the opportunity to hold short positions in a session does not necessarily mean that subjects made use of it. One might assume that business students are aware of the risk induced by shorting stocks or cash and therefore avoid it. To get an impression of how extensive traders used the opportunity to hold short positions we analyze in how many cases a trader finished a period with a short position in stocks or money, and how many of the subjects used the possibility to go short at least once during their session.

As shown in Table 8 we find that around 11% of the cash holdings at the end of a period were negative in T2 as well as T3. When shorting stocks was allowed we observe that only in 5% of all cases traders had a negative position in stocks. But bear in mind that we have twice as many observations for stocks and it is relatively unlikely that a subject goes short in stock A and B at the same time as she will receive contrarily biased signals for the two stocks. Concerning the relative number of subjects that held a short position at least one time during the experiment it becomes obvious that a majority of subjects made use of the possibility to go short in stocks and cash as well.

Table 8.

Percentage of cases where a subject had a short position at the end of a period and percentage of subjects that had short positions at least once during their session.

Treatment	Percentage of cases		Percentage of subjects
	Money	Stocks	Money	Stocks
T2	10.6%		61.2%
T3	11.5%	5.1%	65.0%	58.7%

Considering the cumulative distribution of stock holdings, as shown in Fig. 5, we can furthermore see that extreme positions in stock holdings rarely occurred. In fewer than 1% of all cases a trader finished a period with less than −4 stocks in T3 or with more than 15 stocks in any treatment. Note that the distribution was cut off at −4; 12 to improve visibility.

Fig. 5.

Cumulative distribution of subjects’ stock holdings at the end of a period in setting 1 without shorting money or stocks (solid line), in setting 2 where shorting money was allowed (long dashes), and setting 3 where going short was possible in money and stocks (short dashes).

5.6. Bid-ask-spreads

Next, we look at a proxy for liquidity, the bid-ask-spread. We calculate the bid-ask-spread at the end of each period as

$${\text{SPR}}_{m,st,p}={\text{Ask}}_{m,st,p,t=120}-{\text{Bid}}_{m,st,p,t=120},$$ (6)

and run regression Eq. (4).

We find that bid-ask-spreads are significantly lower in setting 3, where shorting money and stocks was possible, than in the other two settings (see Table 9). This is significant at the 1% level for both stocks (Wald-test), supporting Conjecture 5. We have already seen that the number of orders posted is significantly higher when short-selling is possible and this obviously drives down bid-ask-spreads. When short-selling is not possible only traders who own a stock can post asks for it and only those who have money available can post bids. This limitation constrains especially those active traders who sell all their stocks of A or B and are then no longer able to post asks for the respective stock. Again, short-selling constraints seem more like a distorting factor than a useful regulation to ensure the smooth functioning of markets.

Table 9.

Bid-ask-spread – results for the regression Eq. (4) with SPR_m,st,p as the dependent variable, p-values for two-sided test.

Coeff.	Stock A		Stock B
	Est.	p− val.	Est.	p− val.
BMF_SSF	2.701	0.000	3.026	0.000
BMA_SSF	2.808	0.000	2.814	0.000
BMA_SSA	1.910	0.000	2.044	0.000
βBMF_SSF,V	0.288	0.106	0.532	0.001
βBMA_SSF,V	0.356	0.051	0.457	0.037
βBMA_SSA,V	0.310	0.000	0.163	0.242
βPER	−0.120	0.000	−0.129	0.000
AR (1)	0.180	0.034	−0.058	0.567
R2	0.358		0.334
n	224		218

All six slope coefficients are positive, three of them significant, showing that bid-ask-spreads are higher for stocks with relatively high intrinsic values (and thus prices) than for stocks with relatively low intrinsic values. This is not surprising, as spreads can be expected to be higher for stocks trading at 95 than for stocks trading at 5.

The significantly negative coefficients of β_PER are in line with our results on orders posted – this number increases over time and thus lowers bid-ask-spreads.

5.7. Volatility

We measure volatility per period by calculating the standard deviation σ_m,st,p of absolute price changes within each period. With the resulting 240 data points per stock we run the OLS regression Eq. (4).

In Table 10 we see that volatility is lower in setting 3, where borrowing money and shorting stocks was possible, than in the other two settings (a Wald-test shows that three out of four differences are significant at the 1% or 5% level), supporting Conjecture 6 and corroborating the overall impression that allowing short-selling improves market efficiency rather than harming it.

Table 10.

Volatility – results for the regression Eq. (4) with σ_m,s,t,p as the dependent variable, p-values for two-sided tests.

Coeff.	Stock A		Stock B
	Est.	p− val.	Est.	p− val.
BMF_SSF	2.062	0.000	2.184	0.000
BMA_SSF	2.199	0.000	2.032	0.000
BMA_SSA	1.681	0.000	1.775	0.000
βBMF_SSF,V	0.153	0.237	0.078	0.435
βBMA_SSF,V	0.296	0.008	0.204	0.035
βBMA_SSA,V	0.167	0.060	0.263	0.016
βPER	−0.051	0.000	−0.053	0.000
AR (1)	0.127	0.177	0.233	0.008
R2	0.229		0.241
n	228		228

All slope coefficients are positive, three of them significant, showing – similar to bid-ask-spreads – that volatility is higher for stocks with higher intrinsic values. We attribute this to the higher bid-ask-spreads reported above.

As indicated by the significantly negative factor for β_PER, volatility decreases over the course of the experiment. This pattern is commonly observed in laboratory markets and is usually explained by learning of the participants (see Kirchler and Huber, 2007).

6. Conclusion

In this paper we used laboratory experiments to explore the effects of short-selling constraints on information aggregation in markets. Our main finding is that allowing short positions in stocks and money increases efficiency and reduces volatility and bid-ask-spreads. When shorting stocks is constrained we observe a systematic bias in prices. This bias works in different directions for stocks with low and high capitalization – while the former are systematically overpriced, the latter usually trade below their intrinsic value. When going short in stocks and borrowing money are possible, no systematic pattern is observed and prices are close to intrinsic values. We examined portfolio data, trading activity, and liquidity to explain the observed bias.

We found that the concentration of stock holdings depends strongly on the capitalization of a stock when borrowing money is not possible, but not when it is allowed. With respect to trading activity we see that the number of orders posted is significantly higher for setting 3, where borrowing money and shorting stocks is allowed, thereby also driving down the bid-ask-spread and volatility. Trading activity is significantly higher for low-capitalized stocks than for high-capitalized ones when borrowing money is not possible, while this effect is not observable in settings 2 and 3 where borrowing money was allowed. The issues discussed here are highly relevant from a regulatory point of view. Today, on a global scale, constraints of shorting and borrowing vary, and relative capitalizations vary between and within markets. Ignoring such differences may result in unwanted effects.

Caveats when trying to draw conclusions from our results for real capital markets include: in our experiments borrowing money and shorting stocks – when allowed – was free of costs, while in reality borrowing money as well as short selling of stocks is limited and costly. Furthermore we did not vary divergence of opinions, which we leave to future research.¹³ However, with two risky assets we consider our market setting to be closer to real markets than earlier experiments where only one asset was traded (Haruvy and Noussair, 2006, Fellner and Theissen, 2011, King et al., 1993). The clarity of our results may help to shed light on the divergent empirical results on short-selling constraints: apart from the degree of divergence of opinions among investors and the degree of the short-selling constraints, relative market capitalization was found to be a third crucial factor for the price level of a stock.

Funding

Financial support by the Wirtschaftskammer Tirol and the Austrian Science Foundation FWF (grant P20609-G11) is gratefully acknowledged. Beside of financial support, sponsors played no role in study design, in the collection, analysis, and interpretation of data, in the writing of the report, and in the decision to submit the paper for publication.

Appendix. Instructions of the experiment

Background of the experiment

This experiment is concerned with replication of an asset market where traders can trade stocks of two fictitious companies for 20 independent periods.

Characteristics of the market

Each period is independent from the others. Stock and money holdings are not carried over, but liquidated at the end of each period. As a participant, you start each period with 200 units of experimental currency, 4 stocks of company A, and 4 stocks of company B. The intrinsic value of the two stocks always adds up to 100. The value of your stocks before trading is therefore 400 and your total wealth is 600. At the start of each period each participant receives private information about the intrinsic value of the two stocks. This private information differs for each participant and is distributed normally around the intrinsic value with a standard deviation of 2. The quality of information you receive (closeness to real intrinsic values) changes randomly from period to period. Sometimes you will know the exact intrinsic values, while at others your estimate will deviate more from the intrinsic values. At the end of each period all stocks are bought back by the bank at their intrinsic value. Profits and losses are calculated by deducting the initial endowment of 600 (see screenshot “history screen” for further details).

Trading

The trading mechanism is implemented as a double auction. This means that you can buy and sell stocks, whereby each transaction is for one stock (see screenshot “trading screen” for further details). Only in Setting 1 (borrowing money and shorting stocks forbidden):

You can enter as many bids and asks within the price range of 0 and 100 (with a precision of one decimal place) as you wish. However, you can only sell/enter as many asks for a stock as the number of respective stocks you own. Bids can only be entered as long as you have enough money to honor those bids. Only in Setting 2 (borrowing money allowed, shorting stocks forbidden):

You can enter as many bids and asks within the price range of 0 and 100 (with a precision of one decimal place) as you wish. However, you can only sell/enter as many asks for a stock as the number of respective stocks you own. Negative holdings of money are possible without limitations or additional costs. Only in Setting 3 (borrowing money and shorting stocks allowed):

You can enter as many bids and asks within the price range of 0 and 100 (with a precision of one decimal place) as you wish. Negative holdings of stock or money are possible without limitations or additional costs. When you end a period with negative holdings of stocks the intrinsic value of the stock multiplied with the (negative) number you hold will be deducted from your total wealth.

Final payment

The average payment for all participants is $ 22. Gains/losses in experimental currency will raise/lower your individual payment by 0.02 $ per unit of experimental currency.

Important details

• •Payout-creating trading will be preceded by 4 trial periods.
• •The experiment will run for 20 periods.
• •The sum of the two intrinsic values is always 100.
• •Each trading period lasts for 120 s.

Fig E1.

Trading screen.

Fig E2.

History screen.