A bio-economic analysis of harvest control rules for the Northeast Arctic cod fishery

Abstract

Harvest control rules (HCRs) have been implemented for many fisheries worldwide. However, in most instances, those HCRs are not based on the explicit feedbacks between stock properties and economic considerations. This paper develops a bio-economic model that evaluates the HCR adopted in 2004 by the Joint Norwegian–Russian Fishery Commission to manage the world's largest cod stock, Northeast Arctic cod (NEA). The model considered here is biologically and economically detailed, and is the first to compare the performance of the stock's current HCR with that of alternative HCRs derived with optimality criteria. In particular, HCRs are optimized for economic objectives including fleet profits, economic welfare, and total yield and the emerging properties are analyzed. The performance of these optimal HCRs was compared with the currently used HCR. This paper show that the current HCR does in fact comes very close to maximizing profits. Furthermore, the results reveal that the HCR that maximizes profits is the most precautionary one among the considered HCRs. Finally, the HCR that maximizes yield leads to un-precautionary low levels of biomass. In these ways, the implementation of the HCR for NEA cod can be viewed as a success story that may provide valuable lessons for other fisheries.

Highlights

► We examine harvest control rules (HCRs) for Northeast Arctic cod, the world's largest cod stock. ► The bio-economic model is detailed and estimated with long-term data. ► The currently used HCR is compared with alternatives optimizing profit, welfare or yield. ► The currently used HCR comes very close to the one that maximizes profits. ► Maximizing yield leads to un-precautionary low levels of biomass.

1. Introduction

1.1. Northeast Arctic cod and its current management plan

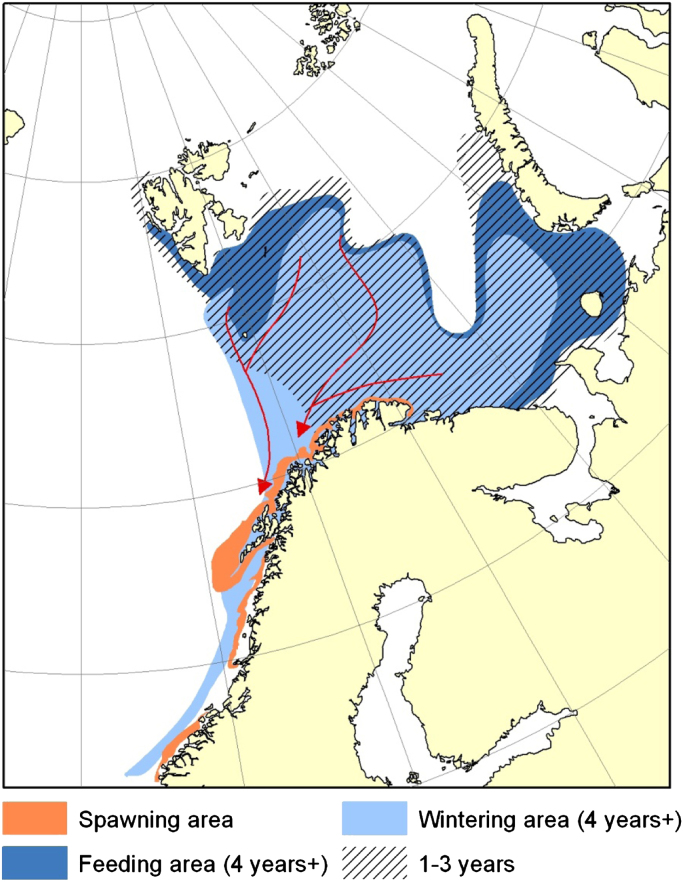
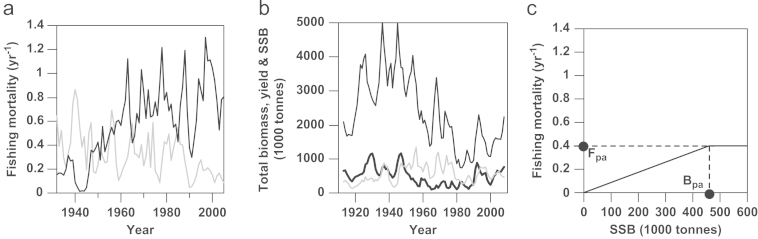
Northeast Arctic (NEA) cod (Gadus morhua) is currently the world's largest cod stock, distributed from its feeding grounds in the Barents Sea to its spawning grounds off the Lofoten islands in the Norwegian Sea [1]. The fishery consists of two parts that are geographically separate: the feeding-ground fishery in the north and the spawning-ground fishery further south (Fig. 1). Humans have been fishing on the spawning grounds for more than a thousand years, beginning with the export of cod during the Viking Age [2]. Until the 1930s, the spawning-ground fishery dominated catches, due to its proximity to coastal villages and ports. However, during the 1930s the advent of industrial fishing technology facilitated the expansion of the NEA cod fishery into the Barents Sea. This expansion led to a shift of catches toward the stock's feeding grounds, as well as to an increase in the total fishing mortality (Fig. 2a). In 2010, ICES (the International Council for Exploration of the Sea) estimated the spawning-stock biomass (SSB) of NEA cod to reach 1,145,000 t, the highest amount that has been observed since 1947 [3]. The stock's total biomass has also increased, even though not concomitantly with the SSB (Fig. 2b). In addition to possible climate effects, this recent increase in SSB could have at least two explanations: First, illegal fishing has been reduced from the maximum of 166,000 t in 2005 to approximately zero in 2009 [4]. This decline is most likely due to the introduction of port control in 2007, requiring all vessels to document that their landings are legally caught. Second, a joint Norwegian–Russian harvest control rule (HCR) that determines the total allowable catch (TAC) has been implemented since 2004, to ensure that the stock is not at “risk of being harvested unsustainably” or “suffering reduced reproductive capacity” [5], [6].

Fig. 1.

Distribution of NEA cod, with feeding grounds in the Barents Sea and spawning grounds along the Norwegian coast. The figure has been developed by the Norwegian Institute of Marine Research.

Fig. 2.

(a) Historic fishing mortality rates in the feeding grounds (black line) and spawning grounds (grey line) for 1932–2005. (b) Time series of total biomass for individuals aged 3 years or older (black line), reported yield (grey line), and spawning-stock biomass (SSB, thick black line), as reported by ICES AFWG 2009. (c) Current HCR (continuous line), as determined by the two parameters B_pa and F_pa (dashed lines).

NEA cod is an economically very important fish resource [7], [8] mostly situated in the exclusive economic zones of Norway and Russia (Fig. 1). For years, NEA cod has been managed jointly by those two countries, though not without scientific and political disagreements [9]. To enable more farsighted management and to simplify the annual negotiations on harvest levels, an HCR was agreed upon by the two countries in 2004 (Fig. 2c). In general, an HCR is an algorithm and a tactical management tool that translates biological information, such as a stock's current SSB, into management information such as a TAC for that stock during the next fishing season. An HCR is often designed with the help of reference points for target biomass and fishing mortality. In particular, the precautionary reference points for biomass and fishing mortality, B_pa and F_pa, respectively, act as buffers to account for natural variability and uncertainty in the stock assessment: B_pa implements a “safety margin” to reduce the risk that the true SSB falls below a limit reference point B_lim below which the stock is expected to suffer from reduced reproductive capacity. Likewise, F_pa is meant to avoid a true fishing mortality that exceeds the limit reference point F_lim above which SSB is expected to drop below B_lim [5]. The range of these buffers depends on the level of uncertainty and on the level of risk fisheries managers are willing to accept on behalf of society.

In autumn 2004, the 33rd session of the Joint Norwegian–Russian Fishery Commission adopted a HCR stipulating that the fishing mortality is allowed to be at F_pa as long as SSB exceeds B_pa, but is required linearly to decrease from F_pa to 0 as SSB decreases from B_pa to 0 (Fig. 2c). Therefore, fishing can take place at all SSB levels [10]. The HCR contains additional elements that aim to restrict how much the TAC can change from one year to the next. However, the TAC advised by the adopted HCR is not always followed. For example in 2009, due to the high SSB, the TAC was decided by the Joint Norwegian–Russian Fishery Commission to be 525,000 tonnes, while the adopted HCR advised 473,000 tonnes [11]. Today, the NEA stock is classified as having “full reproductive capacity” and being “harvested sustainably” [6], [12].

1.2. Need for adaptive management and clear objectives

Despite considerable attention to the management of marine ecosystems, most fisheries have yet to be optimized to reach management goals [13], [14], [15], [16]. Political obstacles and roadblocks play an important role in failures of fisheries management [17]. Also, some scientific models for optimal management are not easily applicable to real-world situations, and may be based on hidden and/or overly simple assumptions [18].

Another obstacle for successful fisheries management is the fact that it is often not explicit, or evident a priori, which particular objectives should be pursued [16], [19], [20]. At a very basic level, a specific fish stock can provide income to society, but also serves as an important food source. Therefore, one may favour a harvesting rate that provides the highest perpetual yield, known as the maximum sustainable yield (MSY), and this objective has been endorsed in various international agreements [19]. Economic science has added an important refinement to the purely biological consideration of MSY by accounting for the costs and benefits associated with resource extraction [21], [22]. This allows deriving an exploitation path that maximizes profits from harvesting, but is based on the simplifying assumption that the government, at least theoretically, is the “sole owner” of the resource. The contrast between these two basic approaches already shows that a crucial prerequisite for achieving optimal exploitation is the clear specification of management goals. A policy-maker may, for instance, take into account that parts of society are concerned about nature conservation in general, or about a specific species or ecosystem in particular. Accordingly, the policy-maker may decide to harvest less than what would be optimal if only yields or profits were to be maximized. The opposite can be true when fishing is considered part of a region's cultural heritage, which society finds worth preserving even at the expense of reducing profits through subsidies or over-fishing.

It is important to acknowledge that fisheries management—just as every other part of public policy—is, inherently political. Nevertheless, objectives that politicians consider important should be clearly defined; otherwise, hidden objectives can sneak in through the backdoor and take precedence [18]. It is therefore desirable to devise models that are flexible enough to evaluate realistic political options and transparent enough to communicate their consequences effectively to all stakeholders.

Technically, an HCR is a feedback control that links one or more control variables (e.g., catch) to one or more state variables (e.g., SSB) of the stock. If an operational biological model is in place and is sufficiently simple, such a feedback control can be derived analytically [24], [25], [26], [27]. There is, however, a critical trade-off between analytic tractability and realistic complexity, implying that sufficiently detailed biological models will often be too complicated for deriving an optimal HCR analytically. In such cases, it is necessary to sacrifice analytical rigor for biological realism and use numerical analyses instead.

When setting up an HCR, policy-makers can express their resource-management objectives by emphasizing quantitative goals, which different scientific disciplines can then jointly help to assess. HCRs are readily based on such an approach, and accordingly offer various advantages for modern fisheries management, including (i) a reduced need for annual negotiations on how to set harvest quotas, (ii) the integration of interdisciplinary research into policy-making, and (iii) the strengthening of a constructive dialogue between policy-makers, stakeholders, and the scientific community. Harvest policies formulated through HCRs therefore represent an ideal platform for policy makers and scientists on which to interact. Positive practical experiences with the HCR framework have been highlighted in recent reviews [28], [29], [30].

1.3. Aims of this study

The approach here is to use a detailed bio-economic model for the NEA cod fishery to evaluate the current HCR and to inform policy-makers about how this HCR performs compared to alternative HCRs that are optimized for different objectives. The purpose of this study is to provide an overview of the strengths and weaknesses associated with HCRs devised to meet the different objectives. In doing so, this study aims to examine how these alternate HCRs for the management of NEA cod perform in comparison with the currently implemented HCR.

Kovalev and Bogstad in 2005 [12] addressed the performance of the current HCR, however, their model is purely biological and thus does not include economic objectives. While their biological model operates at the population level, ours is individual-based. This allows us to incorporate more biological detail and realistic complexity than other biological models used in previous bio-economic studies. This level of realism is needed: to evaluate the merits of any HCR, the used biological model must match the observational data it represents sufficiently well, if inferences for future fishing pressures are to be trusted. Analogous considerations apply to the used economic model. The bio-economic model presented below is the most detailed such model developed for NEA cod, and the first applied to evaluating HCRs.

2. Materials and methods

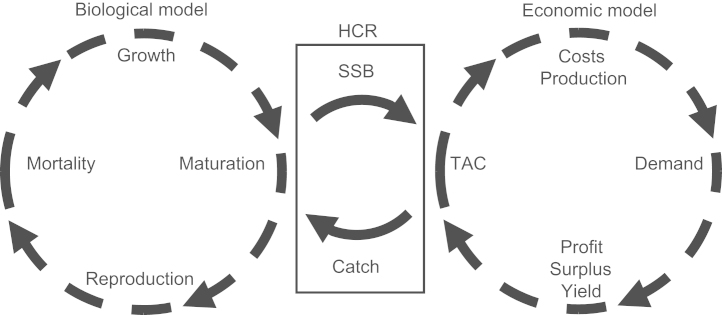
The bio-economic model considered here consists of two sub-models linked through an annual feedback loop (Fig. 3). The biological sub-model describes biological details such as processes of growth and maturation specific to NEA cod, while the economic sub-model describes economic details such as costs and harvest functions. The biological model delivers information about the stock's SSB, which is fed into the considered HCR to calculate a total allowable catch (TAC), which consequently determines fleet profits, yield, etc. in the economic model. The total catch feeds then back into the biological model affecting the stock dynamics. The two sub-models have been specifically estimated and calibrated for the NEA cod fishery using data from the time period 1978–2007 (Table 1).

Fig. 3.

Overview of the bio-economic model, its main components, and the feedback links between the two sub-models. The biological sub-model predicts spawning-stock biomass (SSB). This enters a harvest control rule (HCR), characterized by a pair of parameter values, that determines the total annual catch (TAC). This feeds into the economic sub-model, where functions for demand, costs, and production predict annual total profit and total welfare. The total catch then feeds into the biological model, affecting the development of the stock. Depending on the considered management objective, the parameter pair that maximizes either total welfare, total profit, or total yield determines the optimal HCR and its resultant catch.

Table 1.

Parameter values and data sources for the bio-economic model.

Parameter	Value	Eq.	Source
Biological sub-model
Probabilistic maturation reaction norm slope, s	0.0 cm yr−1	1	[36]⁎
Probabilistic maturation reaction norm intercept, i	64.0 cm	1	[36]⁎
Probabilistic maturation reaction norm width, w	18.9 cm	1	[36]⁎
Strength of density dependence in growth, x	2.08×10−5 kg−1	2	[36]⁎
Reproductive investment, G	0.17	3	[63]
Reproductive-investment conversion factor, γ	0.60241	3	[38], [39]
Allometric proportionality constant, k	4.9×10−6 kg cm−j	4	[64]
Allometric exponent, j	3.18	4	[64]
Weight-specific oocyte density, D	4.45×106 kg−1	4	[40]
Maximum growth increment, g	13.0 cm	–	[11]
Natural mortality rate	0.2 yr−1	–	[11]
Spawning-ground fishing mortality before 1990	0.13 yr−1	–	[3]⁎
Immature feeding-ground fishing mortality before 1990	0.52 yr−1	–	[3]⁎
Size-selectivity midpoint, l50	49.34 cm	–	[45]
Size-selectivity range, SR	10.47 cm	–	[45]
Factor for conversion of total fishing mortality to feeding-ground fishing mortality, η	1.15	–	[3]⁎
Factor for conversion of total fishing mortality to spawning-ground fishing mortality, k	0.215	–	[3]⁎
Economic sub-model
Intercept of demand function, $\overline{p}$	18.88 NOK kg−1	5	[27]
Slope of demand function, b	1.19257×10−8 NOK kg−2	5	[27]
Stock-output elasticity, α	0.58	5	[27]
Effort-output elasticity, β	0.85	5	[27]
Catchability coefficient, q	6.17×10–4 tonnes−1 day−1	5	[27]
Fixed costs per vessel, cf	1.55×106 NOK	6	[27]
Coefficient of variable costs per vessel, cv	131.6 NOK tonnes−1 day−1	6	[27]
Optimal number of tonnage days, e*	66,712 tonnes day	9	[27]

^⁎M. Heino and O.R. Godø (unpublished data).

2.1. Biological sub-model

The biological sub-model is based on a previously published model [31], which is parameterized for NEA cod. The biological model is individual-based, age- and length-structured, and describes an individual's life-cycle from birth to death through annual processes of maturation, growth, reproduction, and mortality [31], [32]. This model includes stock-specific estimated relationships for maturation tendency, density-dependent growth, stock–recruitment, and energy allocation. Individuals vary in age, body size, and maturation status, which are tracked on an annual basis. Unlike some previous models [31], [32], [33], [34], this model reduces complexity by keeping life-history traits monomorphic and by not considering their evolutionary dynamics. The included life-history traits describe an individual's maturation tendency, growth, and reproductive investment. All model parameters are based on empirical data (Table 1).

Each year, the tendency that an immature individual will mature depends on a probabilistic maturation reaction norm [35], [36], [37], which describes maturation probability p_m(a,l) as a function of age a and body length l. This probability equals 50% at the length at age l_P50(a)=i+sa, and is given by

$$p_{\mathrm{m}}(a,l)=1/(1+\exp (-\left(l\right(a)-l_{\mathrm{P}50}(a\left)\right)/c\left)\right)$$ (1)

The probabilistic maturation reaction norm thus has intercept i and slope s. Its width w, spanning from the 25% to the 75% percentile of maturation probability [31], [32], is determined by the parameter c where $c=w/\left[\text{logit}\right(p_{\mathrm{u}})-\text{logit}(p_{\mathrm{l}}\left)\right]$, and p_u and p_l are the probabilities for the upper and lower bounds of the PMRN.

The growth rate of individuals depends on the total biomass of the population, to account for reductions in growth expected when population density is high and resource availability consequently is low. Data from 1978–2009 on annual growth increments g_D,t in year t, together with data on total stock biomass B_t of individuals aged 3 years or older in year t, were used to estimate the two parameters g and x of an exponential relationship for density-dependent growth,

$$g_{\mathrm{D},t}=g\exp (-x{B}_t),$$ (2)

where g is the maximum growth increment (realized at B_t=0) and x determines the strength of density dependence in growth (Table 1). For immature individuals, denoted by a superscript I, body length in year t is determined by their length in the previous year enhanced by the corresponding growth increment, $l_t^{\mathrm{I}}=l_{t-1}^{\mathrm{I}}+g_{\mathrm{D},t-1}$.

Mature individuals, denoted by a superscript M, allocate a proportion of their resources to reproduction. In this model, reproductive investment is measured by the gonado-somatic index G, defined as the ratio between an individual's gonadic and somatic mass. A conversion factor γ accounts for the higher energy content of gonadic tissue relative to somatic tissue [38], [39]. Consequently, the length of a mature individual is given by

$$l_t^{\mathrm{M}}=3(l_{t-1}^{\mathrm{M}}+g_{\mathrm{D},t-1})/(3+\gamma G)$$ (3)

An individual's fecundity f depends on its body length l,

$$f=k{l}^{j}GD,$$ (4)

where D is the weight-specific packing density of oocytes [40], and k and j are allometric constants relating body length to somatic body mass. Sex is assigned randomly at birth based on a 1:1 primary sex ratio.

The density-dependent newborn mortality is determined by an estimated Beverton–Holt stock–recruitment relationship for 3-year-olds [32], depending on SSB and climate. The climatic variable, the sea-surface temperature from the Kola meridian transect (33°50′ E, 70°50′ N to 72°50′ N) has been shown to be an important factor for recruitment [41], [42], [43], [44]. This annual climatic data is used as input to the modelled stock–recruitment relationship (prior to 1990, the mean value from 1980–1989, while from 2004 onwards, the mean value from 1990–2007). Back-calculating from the predicted number of 3-year-olds, the number of 1-year-olds is determined by setting instantaneous natural mortality rate to 0.2 yr⁻¹, as conventionally done for that stock [11].

Individuals die from natural mortality or fishing mortality. Natural mortality is parsimoniously held constant and set equal to an instantaneous rate of 0.2 yr⁻¹, as routinely assumed in the stock assessment of NEA cod [11]. In terms of fishing mortality, immature fish can only get captured on the feeding grounds, while mature fish may also experience fishing mortality on the spawning grounds (Fig. 2a). Fishing mortality rates F from the stock-assessment model [3] are translated into harvest probabilities $1-\exp (-\eta F)$ in the feeding grounds and $1-\exp (-\kappa F)$ in the spawning grounds, where the parameters η and κ convert the total fishing mortality rate into those in the feeding grounds and spawning grounds, respectively. Also taken into account is that only mature fish migrate out of the Barents Sea for about ¼ of the year, and therefore reduced their harvest probabilities thereto.

A selectivity curve accounting for the lower catchability of smaller-sized fish, estimated for the commercial trawling gear used in the NEA cod fishery [45] was also implemented. Initially, fishing mortality is held constant in the model at the 1932–1989 average, in order to allow the population to reach demographic equilibrium (in terms of stable total biomass, SSB, individual growth, and age and length at maturation). After that equilibration, the stock's observed annual fishing mortality rates for each year between 1990 and 2003 were implemented, resulting in very good matches between model-predicted and observed SSB values. From 2004 onwards, one of the alternative HCRs was introduced, as described in more detail below.

The individual-based model simulations have only computational capacity to follow about 50,000 super-individuals [46], [47]. We therefore scale up this modelled population by a scaling factor of 80,000 which can recreate the appropriate stock levels in the natural population [3]. All model predictions reported below, such as SSB and catch, are given for this scaled population, and thus are directly comparable to the observed data.

2.2. Economic sub-model

The main components of the economic sub-model are the functions describing demand, costs, and production. All analyses in this section are further explained in Richter et al. [27]. Individual vessel data for 1990–2000 were used to estimate costs and production for the component of the Norwegian trawler fleet that caught cod north of 62°N. These data, collected by the Norwegian Directorate of Fisheries (Bergen, Norway), are described in more detail in Sandberg [48].

The NEA cod fishery contributes a large part of the world's cod landings and therefore affects the international market price for cod. To describe this relationship, a linear demand function is given by

$$P_t=\overline{p}-b{H}_t,$$ (5)

where P_t is the price for cod in year t, H_t is the total harvested biomass in year t (as determined by the TAC), and $\overline{p}$ and b are parameters. The production function is estimated as a Cobb–Douglas function [49], [50]; accordingly, the catch of vessel i in year t is given by

$$h_{i,t}=q{e}_{i,t}^{\beta }{B}_t^{\alpha },$$ (6)

where q is a catchability coefficient, and e_i,t is the fishing effort of vessel i in year t. In this model, effort is measured in efficiency units and given by the number of days a vessel is fishing cod north of 62°N multiplied by the vessel's gross tonnage, so that differences in operational intensity are taken into account [51]. The parameter α is the stock-output elasticity and β is the effort-output elasticity, describing, respectively, the percentage change in harvests caused by a percentage change in stock biomass or fishing effort. The costs C_i,t incurred by vessel i in year t are given by the inflation-corrected sum of cost components multiplied by the fraction of days the vessel has fished cod, as opposed to other species; the result is split into fixed costs c_f and variable costs c_ve_i,t according to

$$C_{i,t}=c_{\mathrm{f}}+c_{\mathrm{v}}{e}_{i,t}$$ (7)

Multiplying the catch h_i,t of vessel i with the price of cod P_t yields the revenue P_th_i,t of vessel i. The profit π_i,t of vessel i is then given by offsetting this revenue with the costs C_i,t of vessel i,

$${\pi }_{i,t}=P_t{h}_{i,t}-C_{i,t}$$ (8)

For NEA cod, the effort-output elasticity β is smaller than 1, so there is a trade-off between allowing more vessels to enter the fishing grounds (vessels can then harvest less on average, but do so more efficiently) and allowing larger individual catches per vessel (vessels can then invest their fixed costs more economically). For each year t, an optimal number $n_t^{⁎}$ of vessels harvesting an optimal number e^⁎ of tonnage days for a given TAC and total stock biomass (for details see [27]) were identified, where

$$n_t^{⁎}=H_t{q}^{-1}{e}^{⁎-\beta }{B}_t^{-\alpha }$$ (9)

This optimal number of vessels could reflect a system of individual transferable quotas that will be allocated in the most efficient way. The total fleet profit Π_t in year t is given by

$${\prod }_t=n_t^{⁎}(P_t{h}_t-C_t),$$ (10)

with $h_t=H_t/n_t^{⁎}$ and C_t=c_f+c_ve^⁎. From society's point of view, it is desirable to consider that consumers and fish processors benefit from buying cheap fish, and hence, policy-makers may take consumer surplus into account. Consumer surplus in year t is given by

$$S_t=\frac{1}{2}(\overline{p}-P_t)H_t$$ (11)

Total welfare is given by the sum of total fleet profit and consumer surplus,

$$W_t={\prod }_t+S_t$$ (12)

2.3. Harvest control rules

This study analyzes the performance of several HCRs. First, the HCR that has been implemented in 2004 [6], will be referred to as the “current HCR”. We only consider the core of the HCR that relates TAC to SSB; in order to facilitate comparisons between alternative HCRs, we have ignored the additional elements in the current HCR that aim at reducing annual variability in TACs. Second, alternative HCRs that result from the optimization of specific objectives will be analyzed and referred to as “optimized HCRs”.

The current HCR for NEA cod is determined by two parameters in the form of reference points, B_pa and F_pa. The optimized HCRs are also characterized by two parameters: (i) the maximum fishing mortality F_max, and (ii) the level B_max of SSB at which the maximum fishing mortality F_max starts to apply. Each of the optimized HCRs were derived by allowing F_max and B_max to vary across a wide range of values (see below), without constraining them to existing reference points, and by then choosing those combinations of F_max and B_max that best fulfil the specific objective aimed to optimize. The current HCR is recovered as a special case by setting F_max=F_pa and B_max=B_pa. For all considered HCRs, the fishing mortality rate resulting for a particular SSB is determined as follows: if the SSB is between 0 and B_max, the instantaneous fishing mortality rate for that year is F_max SSB/B_max; otherwise, the instantaneous fishing mortality rate is F_max (Fig. 2c).

The HCR parameters were optimized for three different objectives, maximizing either total welfare, total profit, or total yield. For all considered combinations of B_max (varied over the range 0–800,000 tonnes in steps of 20,000 tonnes) and F_max (varied over the range 0.1–1.3 yr⁻¹ in steps of 0.01 yr⁻¹), the discounted total welfare, total profit, and total yield over the period 2004–2053 were calculated. This gives a grid of 4961 different HCRs. The particular parameter combination that maximizes one of these three measures is identified as the corresponding optimal HCR. To account for demographic stochasticity inherent to individual-based models, all results shown are averages over 15 independent simulation runs.

3. Results

3.1. Different objectives lead to different harvest control rules

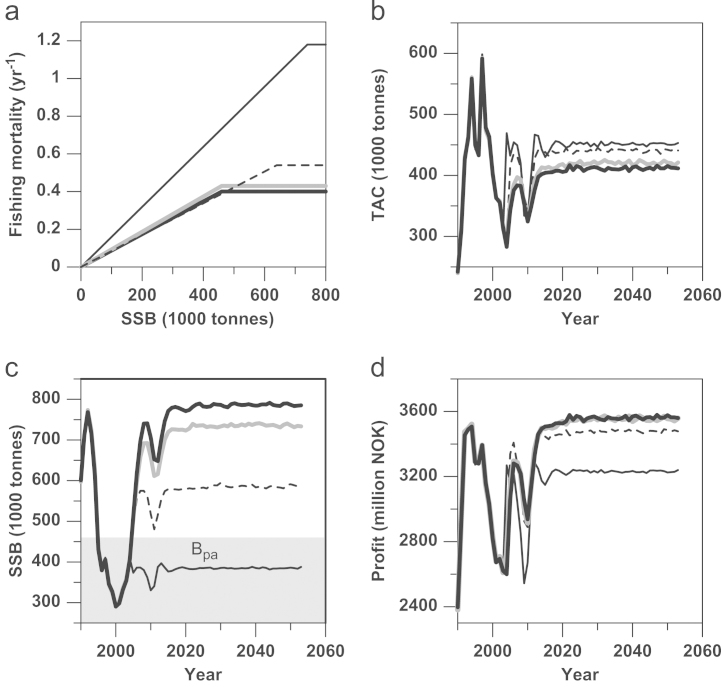
Here follows a description and comparison of the results for the optimized HCRs with the current HCR, for a discount rate of 0, while the effect of different discount rates will be analyzed in Section 3.3. Not surprisingly, the results show that the optimized HCRs depend markedly on the specific objective that is maximized (Fig. 4a).

Fig. 4.

Optimal harvest control rules (HCRs) for different management objectives, maximizing either total welfare (dashed black line), total profit (grey line), or total yield (thin black line). The current HCR is shown for comparison (thick black line). (a) Each HCR maps a certain fishing mortality for a given level of SSB. The resultant emerging harvesting properties are shown as (b) annual total allowable catch (TAC), (c) spawning-stock biomass (SSB), and (d) total profit. The shaded area indicates SSB levels below the precautionary reference point B_pa determined by ICES.

The yield-maximizing HCR allows for much higher fishing mortality than the current HCR (F_max=1.18 yr⁻¹ instead of 0.4 yr⁻¹; Table 2), but implies a significantly more precautionary SSB safety margin than the current HCR (B_max=740,000 tonnes instead of 460,000 tonnes; Table 2). The HCR that maximizes total welfare implies a higher maximum fishing mortality than the current HCR (F_max=0.54 yr⁻¹ instead of 0.4 yr⁻¹; Table 2) and also results in a more precautionary SSB buffer than the current HCR (B_max=640,000 tonnes instead of 460,000 tonnes; Table 2). Strikingly, the profit-maximizing HCR is almost identical to the current HCR, even though the latter is slightly more precautionary in terms of maximum fishing mortality (F_max=0.4 yr⁻¹ instead of 0.43 yr⁻¹; Table 2).

Table 2.

Optimal harvest control rules (HCRs) for three alternative management objectives, maximizing either total welfare, total profit, or total yield, for a discount rate of 0%. Emerging harvesting properties for 2004–2053 are given as temporal means (with coefficients of temporal variation in parentheses) for catch ratio, total allowable catch (TAC), spawning-stock biomass (SSB), total profit, and total welfare. The catch ratio is the emerging ratio between TAC and total biomass of individuals aged 3 years or older.

Objective	Fmax (yr−1)	Bmax (1000 tonnes)	Catch ratio	TAC (1000 tonnes)	SSB (1000 tonnes)	Total profit (million NOK)	Total welfare (million NOK)
Maximize total welfare	0.54	640	0.248 (0.039)	431 (0.064)	571 (0.058)	3410 (0.049)	4520 (0.065)
Maximize total profit	0.43	460	0.214 (0.027)	408 (0.062)	709 (0.09)	3466 (0.053)	4465 (0.067)
Maximize yield	1.18	740	0.301 (0.038)	445 (0.057)	383 (0.029)	3190 (0.043)	4374 (0.058)
Current HCR	0.4	460	0.200 (0.025)	399 (0.066)	756 (0.095)	3468 (0.057)	4424 (0.071)

3.2. Emerging properties of stock and fishery

This section examines how the optimized HCRs would have performed had they been implemented in 2004 (Fig. 4 and Table 2), again for a discount rate of 0%. The HCR that maximizes total yield gives the highest average TAC over time, even though the HCR that maximizes total welfare allows for almost the same catch (Fig.4b). The HCR that maximizes total profit and the current HCR both give lower TACs than the HCR optimized for total welfare.

The HCR that maximizes total yield results in a level of SSB that is constantly below the level ICES considers as precautionary (Fig. 4c). This indicates that maximum sustainable yield (MSY) as a sole management target may not necessarily result in sufficiently precautionary harvesting. The HCR that maximizes total welfare results in SSB levels that stay above the precautionary reference point most of the time. The HCR that maximizes total profit and the current HCR both produce SSB levels between 700,000 and 800,000 tonnes, which can be considered very precautionary.

Perhaps most surprisingly, the current HCR produces total profits that are almost identical to those resulting from the HCR that maximizes total profits (Fig. 4d). The HCR that maximizes total welfare delivers slightly lower total profits, while the HCR that maximizes total yield produces even lower total profits.

The HCR that maximizes total yield has the highest catch ratio (TAC divided by total biomass of individuals aged 3 years or older) and must therefore be recognized as the most aggressive harvest strategy, exploiting the largest portion of the stock; the lowest catch ratio is observed for the current HCR, with HCRs maximizing total welfare and total profit lying in between. The coefficient of variation in the TAC is almost identical for all considered HCRs (Table 2).

3.3. Discounting

Society may prefer short-term benefits over longer-term benefits, and this study therefore derives optimal HCRs also for discount rates of 2% and 4% (Table 3). Perhaps surprisingly, the HCR that maximizes total profit is identical for all discount rates. At the resolution considered for F_max and B_max, the HCRs that maximize total welfare are indistinguishable for discount rates of 0% and 2%. For a discount rate of 4%, a slightly higher F_max and a smaller B_max are optimal, implying a more aggressive harvesting pattern resulting in lower SSB and higher TAC. While only results are shown for discount rates of up to 4%, even higher discounting does not affect the results qualitatively; see also [27]. Two mechanisms are important for explaining the relative unimportance of discounting. First, more aggressive harvesting today leads to lower recruitment in the future. Even when discounting the future, those benefits from harvesting today do not offset the relative losses that occur in the future. Second, increasing harvests will result in lower sales prices. At a certain point, the profit loss resulting from lower prices outweighs the profit gain resulting from catching more fish.

Table 3.

Optimal harvest control rules (HCRs) for three alternative management objectives, maximizing either total welfare, total profit, or total yield, for different discount rates (0%, 2%, and 4%). Emerging harvesting properties for 2004–2053 are given as temporal means (with coefficients of temporal variation in parentheses) for catch ratio, total allowable catch (TAC), spawning-stock biomass (SSB), total profit, and total welfare. The catch ratio is the emerging ratio between TAC and total biomass of individuals aged 3 years or older.

Objective	Fmax (yr−1)	Bmax (1000 tonnes)	Catch ratio	TAC (1000 tonnes)	SSB (1000 tonnes)	Total profit (million NOK)	Total welfare (million NOK)
Maximize total welfare
0% discount ratea	0.54	640	0.248 (0.039)	431 (0.064)	571 (0.058)	3410 (0.049)	4520 (0.065)
2% discount ratea	0.54	640	0.248 (0.039)	431 (0.064)	571 (0.058)	3410 (0.049)	4520 (0.065)
4% discount rate	0.58	160	0.260 (0.026)	436 (0.051)	526 (0.057)	3375 (0.042)	4512 (0.055)
Maximize total profit
0% discount ratea	0.43	460	0.214 (0.027)	408 (0.062)	709 (0.09)	3466 (0.053)	4465 (0.067)
2% discount ratea	0.43	460	0.214 (0.027)	408 (0.062)	709 (0.09)	3466 (0.053)	4465 (0.067)
4% discount ratea	0.43	460	0.214 (0.027)	408 (0.062)	709 (0.09)	3466 (0.053)	4465 (0.067)
Maximize yield
0% discount rate	1.18	740	0.301 (0.038)	445 (0.057)	383 (0.029)	3190 (0.043)	4374 (0.058)
2% discount rate	0.79	200	0.307 (0.028)	445 (0.047)	367 (0.044)	3164 (0.04)	4347 (0.051)
4% discount rate	0.84	360	0.316 (0.03)	444 (0.049)	340 (0.052)	3110 (0.04)	4288 (0.053)

^aThe same optimal HCR is obtained for different discount rates.

For maximizing yield, the impact of discount rates on the HCR parameters F_max and B_max is not monotonic: F_max first decreases for higher discount rates, and so does B_max. For a discount rate of 4%, both F_max and B_max increase again. Overall, the catch ratio increases, meaning that discounting makes the emerging harvesting pattern more aggressive. Average SSB decreases, even though this does not lead to a higher average TAC.

4. Discussion

The most striking result from the analysis of this bio-economic model is that the currently implemented HCR for NEA cod is almost identical with the one that maximizes profits. The current HCR confers not only near-maximal profits, but also the highest, and hence safest, SSB levels. This is an unusually encouraging finding, given that on a global scale management failures appear to be more common than management successes [52], [53]. The results confirm that achieving economic objectives does not necessarily come at the expense of sacrificing biological sustainability [19]. The common key to reach high profits and high SSB levels is a low fishing mortality. This study finds that when a high catch has a negative effect on the price, low harvesting rates are favoured even more. Indeed, in many circumstances “a monopolist is the conservationist's friend” [54]. It is an inherently political question whether maximizing profits is a desirable management target: higher prices are then paid by all fish consumers, while a small number of fishers benefit [55].

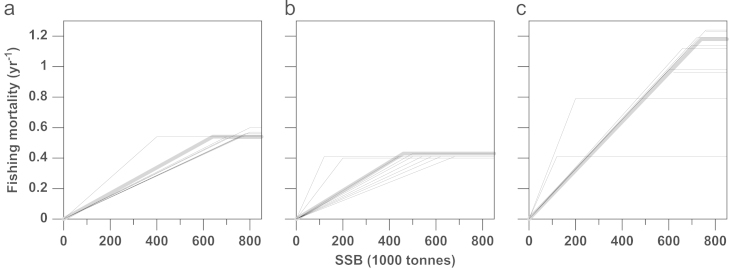
Having established that low fishing mortality is economically optimal, one can, in principle, ensure such low fishing mortality by setting a low reference point for F_max or a high precautionary buffer B_max. With the former setting, one tries to avoid breaking safe biological limits in the first place. With the latter setting, one tries to ensure that biomass levels will recover once low SSB levels are reached. The 10 best HCRs for each of the different management objectives are overall very similar; yet, there are some HCRs that stand out (Fig. 5). This is due to the trade-off between F_max and B_max, which is clearly exemplified for the objective of maximizing yield: if F_max increases, then the optimal B_max also increases. For the HCRs that maximize profit and welfare, especially in one case (Fig. 5a, b), the B_max is lower, while the F_max is more or less unchanged (Fig. 5). However, the resultant catch ratio and cash-flow are very similar. This is because these HCRs avoid the low SSB levels at which B_max affects TACs.

Fig. 5.

Top 10 harvest control rules (HCRs) for each of the different management objectives, maximizing either (a) total welfare, (b) total profit, or (c) total yield, for a discount rate of 0%. The best HCRs are shown in grey.

An important additional advantage of a low fishing mortality, given by a low F_max, is that it produces a more stable harvest pattern, which is usually preferred over a more volatile one (the current HCR for NEA cod includes an explicit clause to promote stable catches [3]). An advantage of a strict precautionary buffer, given by a high B_max, is that it accounts for factors other than fishing mortality that might reduce SSB. If such cases occur, it will usually still be important to reduce harvest pressure, even if fishing has not been causing the stock decline. The harvest pattern that arises from the current HCR gives an SSB that consistently lies above the precautionary biomass limit B_pa (Fig. 4). However, this does not imply that precautionary buffers are not needed, because uncertainty is always present and risks can never be fully controlled [56]. The good news is that these results suggest that adopting these precautionary buffers will most likely not come at the expense of profits. These buffers are comparable to a fire insurance, which most home owners consider to be a worthwhile investment, yet hope that they are never actually needed.

Maximizing yield can lead to a harvesting pattern that is not consistent with what ICES considers to be precautionary, with SSB levels falling below the precautionary reference point B_pa (Fig. 4c). There is a consensus among economists and biologists that maximum sustainable yield (MSY) is not a perfect management target [49], [50], [57], [58], [59]. This suggests that if managers decide to target MSY, it will be crucial to define a strict limit reference point B_pa that ensures safe SSB levels [60].

A disadvantage with the model presented here is the computational cost required for evaluating HCRs. Also, these results are only numerical approximations of optimal HCRs, and thus do not offer the precision of analytical solutions. Although the model simulations already search over an extensive and fine-grained grid of HCR parameter values, the grid's resolution could be enhanced, or a final step of gradual local optimization could be added. However, the emerging harvest patterns implied by the best models (Fig. 5) exhibit relatively small differences, which suggests that not much could be gained by further numerical precision. Therefore, this approach offers a decent compromise between complexity and tractability. In fact, in designing this model, great emphasis is placed on integrating sufficient process-based biological and economic detail. Owing to its resulting flexibility, this bio-economic model could easily be employed to address related additional questions, such as predicting the effects of climate change, fisheries-induced evolution, or oil spills on the performance of the current HCR and its alternatives.

The developed model includes several simplifying assumptions. An empirically derived size–selectivity curve has only been estimated for the Norwegian trawlers in the cod fishery [45], and it would be interesting to account separately for the size–selectivity curve of the Russian trawlers, which however appears to be unavailable at present. Also, temperature only varies in our model from 1990–2004, contributing to the initial stock fluctuations, and this model do not further specifically account for the role climatic changes. Furthermore, if there is a non-negligible probability that a stock will collapse, this ought to be reflected in the evaluation of the corresponding management decisions. In particular, if one optimizes profits while insufficiently accounting for risk, it is likely that precautionary buffers will be too permissive for coping with actual risk, and one will typically end up with a stock poised “at the edge of the cliff” [61]. The acceptable level of risk, as well as the chosen discount rate, remain key political choices. The purpose and promise of detailed, quantitative, process-based bio-economic models, such as the one presented here, is to strengthen the rational and transparent translation of these political choices into policies such as HCRs.

5. Conclusions

This bio-economic model predicts that the current HCR rule is practically identical with the economically optimal one, suggesting that economic and biological sustainability can go hand in hand. A relatively low fishing mortality is a major factor in achieving both. Also, yield maximization alone has been demonstrated to potentially result in a lack of precaution.

The design of HCRs provides a platform for promoting and structuring the dialogue between policy-makers, managers, scientists, and stakeholders. With this in mind, HCRs can be tailored according to a variety of management objectives. The benefits of translating a harvest policy into an HCR are epitomized by the phrase “quantification leads to clarification” [62]: unclear objectives and “gut-feeling” policies do not lend themselves to being quantified as part of harvest-strategy evaluation. Nonetheless, it is important to realize that quantification alone might increase the precision, but not necessarily the accuracy, of results. Therefore, intensive and open dialogue between managers, who set operational fisheries objectives, and scientists, who aid in designing and testing management strategies, will remain essential in pursuing the sustainable management of aquatic resources.