Automatic Dendritic Length Quantification for High Throughput Screening of Mature Neurons

Abstract

High-throughput automated fluorescent imaging and screening are important for studying neuronal development, functions, and pathogenesis. An automatic approach of analyzing images acquired in automated fashion, and quantifying dendritic characteristics is critical for making such screens high-throughput. However, automatic and effective algorithms and tools, especially for the images of mature mammalian neurons with complex arbors, have been lacking. Here, we present algorithms and a tool for quantifying dendritic length that is fundamental for analyzing growth of neuronal network. We employ a divide-and-conquer framework that tackles the challenges of high-throughput images of neurons and enables the integration of multiple automatic algorithms. Within this framework, we developed algorithms that adapt to local properties to detect faint branches. We also developed a path search that can preserve the curvature change to accurately measure dendritic length with arbor branches and turns. In addition, we proposed an ensemble strategy of three estimation algorithms to further improve the overall efficacy. We tested our tool on images for cultured mouse hippocampal neurons immunostained with a dendritic marker for high-throughput screen. Results demonstrate the effectiveness of our proposed method when comparing the accuracy with previous methods. The software has been implemented as an ImageJ plugin and available for use.

1. Introduction

High-throughput screening of cultured neurons has become an increasingly important tool for investigation of neuronal mechanisms and drug discovery, such as efficient identification of synaptogenic genes and pathways (Fox, 2003) (Hawker, 2007) (Dunkle, 2003) (Sharma, et al., 2013). Traditionally, the scale of screens had been held back by culturing and staining techniques but it is rapidly changing with the advances in high-content culturing, immunolabeling, and image acquisition (Al-Ali, Blackmore, Bixby, & Lemmon, 2013). For example, a recent high-throughput genetic screen allowed for over-expression of any set of genes or shRNA targeting the genes in a 96-well format, using mature primary neurons that are beyond simpler cellular systems (Sharma, et al., 2013).

A critical step in such screening is the identification of phenotypic changes, which requires an efficient and reliable quantification of important metrics. One such critical metric to be quantified in a neuronal genetic screen is the length of neuronal dendrites. Dendritic length has a profound influence over the neuronal system function (Pittenger & Duman, 2008) (Faherty, Kerley, & Smeyne, 2003). It has also been combined with other metrics (such as synapse distribution) to explore various mechanism of neuronal activity, development and disease (Glausier & Lewis, 2013) (Becker, Armstrong, & Chan, 1986) (Patt, Gertz, Gerhard, & Cervós-Navarro, 1991). Therefore, an automated quantification tool is essential for high-throughput screening. However, currently, such quantification has been limited to young neurons with short dendrites that have minimal intersections. For mature neurons where dendrites are significantly long and form a complex network, a common practice is to select regions of interest manually in the high-throughput multi-well images and perform the analysis. The length of this region is then measured using a tool that requires a lot of user interaction, e.g. NeuronJ (Meijering, et al., 2004). Such practice is laborious and unpractical for a large-scale screen. Moreover, manual selection of region of interest can also introduce subjective bias.

While length quantification based on methods such as image skeletonization have been attempted recently, the lack of an effective image analysis tool to automatically process mature neurons for quantitative measure remains a bottleneck for large scale screening (Sharma, et al., 2013) (Nieland, et al., 2014). This is because images of mature neurons, such as mammalian pyramidal neurons, typically contain many cultured neurons, each of which has a complex dendritic arbor. Due to the size and complexity of the images, they may have areas of dendrite branches with varying levels of illumination, contrast, and arbor-density. They may also have different levels of artifact noises, especially at the cross points of multiple dendritic branches. In consequence, the signal-to-noise ratio is typically low. The big contrast variation and arbor characteristics in different parts of the image of a neuron or multiple neurons makes it unlikely that a single length quantification algorithms and/or a single set of parameters of image analysis will be a cure-all for the entire image.

In this paper, we develop algorithms that tackle the complexity of the mature neuronal images and provide an open tool, DendriteLengthQuantifier, as an ImageJ plugin to automatically estimate total dendritic length in high-throughput setting. After reviewing the related work in Section 2, we detail the methodology for automatic dendritic length quantification. Experimental results are given in Section 4, followed by discussions.

2. Related Work

The aim of this research is to provide automatic and reliable dendritic length quantification for a high-throughput image with multiple neurons. In addition to related methods that focus on dendritic length estimation, we will also discuss several popular neuron reconstruction tools which can be used for length quantification in low-throughput settings.

2.1 Tools for Dendritic Quantification

Existing tools and methods that yield neuronal length metric vary on the degree of automation.

A popular example of a semi-manual tool is an ImageJ plugin called NeuronJ (Meijering, et al., 2004), which is among a class of methods that use searching-based algorithms to trace the dendrite in order to get quantification metrics. In NeuronJ, the user utilizes a computer mouse to select a starting point and an ending point. NeuronJ makes use of a minimal cumulative cost search algorithm to determine a path between the two points. The algorithm is highly resilient against varying levels of noise and neurite intensity contrast. The drawback is that semi-manual methods are time consuming and labor intensive, which make them impractical in dealing with high-throughput data sets. Due to this drawback, it is a typical practice for researchers to just trace selective parts of the dendritic arbor. This approach is inherently non-holistic and dependent on subjective judgment.

In addition to neurite estimates, NeuronJ provides a partial digital reconstruction of the neuronal morphology. Similar recent efforts on reconstruction of two dimensional and three dimensional neuron images have yielded many tools such as NeuroMantic (Myatt, Hadlington, Ascoli, & Nasuto, 2012), Vaa3D (Peng, Ruan, Long, Simpson, & Myers, 2010), NeuronStudio (Rodriguez, Ehlenberger, Hof, & Wearne, 2006), and some commercial candidates such as NeuroLucida and Imaris. While the reconstruction tools are achieving different levels of automation with ongoing motivations including DIADEM competition (Liu, 2011), in practice they are not used as often as semi-manual ones. As an indication of reality, a majority of neuron morphology of the online neuron morphology database NeuronMorph.org still come from manual instead of automatic reconstruction (Myatt, Hadlington, Ascoli, & Nasuto, 2012). One major reason is because the results still require a lot of labor-consuming proof-reading which is manual post processing that fills missing segments or fixes other issues (Peng, Long, Zhao, & Myers, 2011). This is inappropriate for high-throughput demands.

Different from tools which need human-machine interactions during or after, some methods are designed for extracting and quantifying neurites of cultured neurons in high-throughput settings. For example, NeuriteTracer (Pool, Thiemann, Bar-Or, & Fournier, 2008), CellProfiler (Nieland, et al., 2014) and some others (Vallotton, et al., 2007) (Narro, et al., 2007). NeuriteTracer and similar software binarize images before extracting the neurites by skeletonization to calculate the centerline of the neurites. The method described by Zhang et al. (Zhang, et al., 2007) quantifies the length of the neurite segments by a live-wire search method that link the detected seed points. The method described by Wu et al. (Wu, Schulte, Sepp, Littleton, & Hong, 2010) uses a contrast-limit adaptive histogram equalization method to overcome the non-uniform illumination in high-throughput screening images. The method then uses orientation-guided neurite tracing to carry out neurite quantification. These tools typically require minimal interaction. However, they only work effectively with neurons of simple morphologies. In these neurons, the neurite segments coming out of cell bodies are short with little branching and minimal branch intersecting, lacking the complex arbor structure and branching pattern of mature neurons.

2.2 Algorithms for Dendritic Quantification

Among the above tools with varying levels of automation and application, there are several main algorithms employed for dendritic estimation.

One line of investigation involves the use of stereological principles to acquire length estimates (Rønn, et al., 2000). This approach, designed to be less labor-intensive than direct tracing, uses grids superimposed on images obtained from fluorescence microscopy. The intersections between the grid lines and the dendrites are counted and subjected to statistical analyses to produce length per neuron estimates. This approach has been applied to both primary and secondary neurites. Higher order neurites are generally ignored. The method works best with less densely plated cells; difficulties develop when attempting to analyze overlapping and extensively branching arbors.

The exploratory tracing algorithm guided by direction (Al-Kofahi, et al., 2002) uses the peak response from a set of directional two-dimensional (2-D) correlation kernels to determine the direction of the branch as it progresses forward. The method was initially used in applications with similar tree-like morphology (e.g. retinal vasculature) (Can, Shen, Turner, Tanenbaum, & Roysam, 1999) before being associated with neuroscience applications. This approach is attractive because the processing is performed at the local level, therefore it scales with the complexity of the neurons rather than image size. The algorithm can work with the gray-level image directly without the binarization of the entire image first. Overall the method is robust against curvature and discontinuous branches. The direction estimation is, however, sensitive to noise. The design of stopping conditions for tracing can encounter issues when the dendrites have dense branches with a lot of crossovers. Tracing using a shortest path algorithm, as employed by NeuronJ, is a minimal cumulative cost search algorithm that determines a path between the two points of source and destination. It has often being used as the interactive algorithms in semi-automatic tools with cost functions defined based on foreground pixel intensity and/or the flow of the structure (Meijering E., 2010).

Another alternative to automated tracing methods is the segmentation approach. One of the major differences between segmentation and other approaches is that it involves the processing of every pixel in the image. For example, NeuriteTracer (Pool, Thiemann, Bar-Or, & Fournier, 2008) and NeuronMetrics (Narro, et al., 2007) both utilize skeletonization, which contains two very important steps. The first step is the binarization of the image based on an automated estimation of the background threshold. Next, the foreground is stripped until the diameter is only one pixel across. The length estimate is then derived by counting the total number of the foreground pixels. Skeletonization has a significant time advantage as it is fully automated and works well with crowded images that have high contrast. However, the limitation of global threshold detection methods restricts its ability to handle low-contrast images. To remedy the issue, some tools (e.g. NeuronMetrics) have an optional manual post-processing feature that fills in the gaps caused by faint segments. As previously mentioned, this is inappropriate for high-throughput demands.

3. Materials and Methods

3.1 High-Throughput Experiments

Neurons were prepared from E17 mouse embryos and plated in 96-well optical plates by automated dispensing at the density of 9500 neurons per well. Media was changed to a serum-free condition and cultures were maintained as described earlier (Brewer & Cotman, 1989). Neurons were fixed with 4% paraformaldehyde and 4% sucrose in PBS, followed by permeabilization in 0.25% Triton X-100. After blocking in 10% BSA-PBS, neurons were incubated in primary antibodies against MAP-2 (NOVUS) at 1:20,000 dilution on PBS-3%BSA overnight at 4 °C. Neurons were washed in PBS and incubated in Alexa Fluor conjugated secondary antibodies (Life Technologies). In the end after washing, neurons were maintained in a fixation solution.

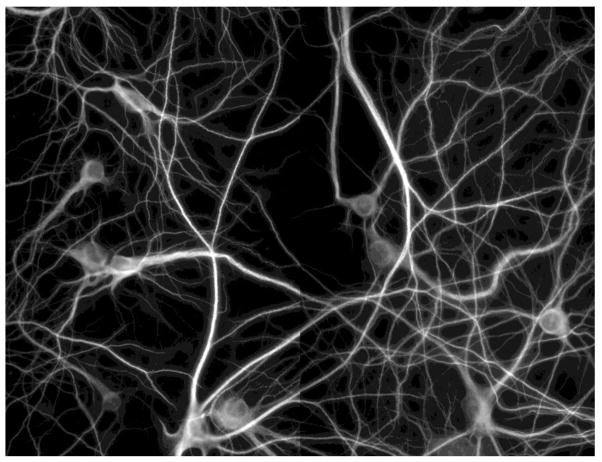
Automated imaging was carried out on a BD Pathway Imaging Platform (BD Biosciences) with a 40× objective in 2×2 montages from each well with 1×1 binning. Figure 1 shows examples of the images obtained by the high-throughput system. The contrast differences among the sub-images were caused by uneven staining, bleaching, or the camera’s automated adjustment.

Figure 1. Example of high-throughput images of cultured mature mouse hippocampal neurons.

This is a 2*2 montage obtained by BD Pathway Imaging system. Size: 2688*2048. Scale: 0.15622 micron/pixel.

3.2 Quantification Process Flow

High-throughput screen images of cultured mature neurons typically have varying levels arbor-density, non-uniform contrasts, and artifact noises. As a consequence, global processing of these images using one algorithm with a single set of parameters is often ineffective. A single length estimation algorithm, either tracing-based or thinning-based, does not deliver desirable performance. This is due to different properties of the algorithms and the fact that different areas of the dendrite may present different branch characteristics.

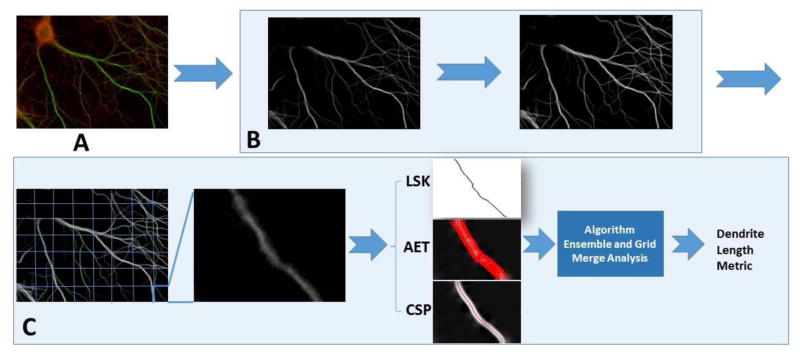
To address the challenges and obtain automatic, robust dendritic length estimates for mature neurons, we employed several new approaches at different stages of the process. The flow of our novel method is described in Figure 2 with highlights described below:

Figure 2. The schematic illustration of our methodology.

A. The raw image. Green channel is the MAP2 stained dendrite channel. B. Preprocessing of the dendrite channel including soma removal and image enhancement. C. The divide-and-conquer framework for dendrite length quantification.

1. A divide-and-conquer strategy that divides the images into grid windows is utilized. Each grid window is processed automatically and independently, and then the results are merged together resulting in an overall estimate. This enables the adaptive processing of each grid window to tackle the unique complexity that it presents.

2. Fully automatic estimation algorithms are developed for each grid. The three algorithms used are: Localized Skeletonization (LSK), Adaptive Exploratory Tracing (AET) and Curvature-preserving Shortest Path (CSP). The need to interactively specify starting and/or ending points is eliminated. In AET, stopping criterion based on adaptive threshold selection is incorporated in the direction-guided tracing. CSP uses a cost function to find the shortest path that avoids taking shorting cuts when tracing curved, branching arbors.

3. An ensemble approach for length estimate at each grid window that takes advantage of both tracing-based and thinning-based algorithms to achieve a higher degree of reliability. LSK, AET and CSP are combined in our process, which leads to an improved overall efficacy.

Each highlight, namely the divide-and-conquer, adaptive tracing, and ensemble estimation, will be detailed in sections 3.3 to 3.7.

3.3 The Divide-and-Conquer Strategy

The microscopic image of mature neurons acquired during the high-throughput process is divided into M rows and N columns, resulting in M*N grids, where M and N are positive integers. Both M and N are set by default to 10, and are adjusted dynamically based on the size of the image (more details below). Each grid window is the base unit for preprocessing, enhancement, and dendritic length estimation. The length estimate quantification is done independently in each grid window. A post-processing merging analysis unit merges the individually estimated lengths together while avoiding the counting of branches along the boundaries of neighboring grids more than once. The total dendritic length, L_total, in a neuronal image is given by Equation 1.

$${\mathrm{L}}_{\text{total}}={\mathrm{\sum }}_{\mathrm{m}=\mathrm{1..}\mathrm{M}}{\mathrm{\sum }}_{\mathrm{n}=1\dots \mathrm{N}}{\mathrm{L}}_{\text{mn}}={\mathrm{\sum }}_{\mathrm{m}}{\mathrm{\sum }}_{\mathrm{n}}({\mathrm{r}}_{\mathrm{m}.\mathrm{n}}-{\mathrm{e}}_{\mathrm{m},\mathrm{n}})$$ (1)

where r_m.n is the raw length estimate in the grid window in row m and column n, e_m,n is the duplicated estimation detected during the boundary analysis with its neighboring windows, which is subtracted from r_m,n to yield the final estimate L_mn for a given grid window at (m,n). The details of boundary analysis are described later in this section. The summation of L_mn over the grids provides the total neuronal length of the image.

One essential advantage of such a strategy is that the processing is limited to the local grid window. Therefore, it overcomes great contrast variation in an image and helps to extract higher order branches that are often quite dim. More importantly, localizing the estimation lowers the complexity of the branch pattern being processed in each particular window. For example, when direction-guided tracing is used to estimate the length, the direction change of the branches within the window of interest is limited. This allows us to employ more reliable, automatic, and adaptive tracing without the need for user interaction. Ultimately, the divide-and-conquer strategy provides the flexibility of applying either one or multiple estimation algorithms (and parameters) in a manner that is independent to its neighboring windows. Note that although grids have been used in image analysis (Al-Kofahi, et al., 2002), they differ from our strategy in that they are typically used for localized preprocessing instead of algorithm independence. It is also worth mentioning that such an approach allows for parallel implementation, which may lead to further improvement in the speed of high-throughput processing.

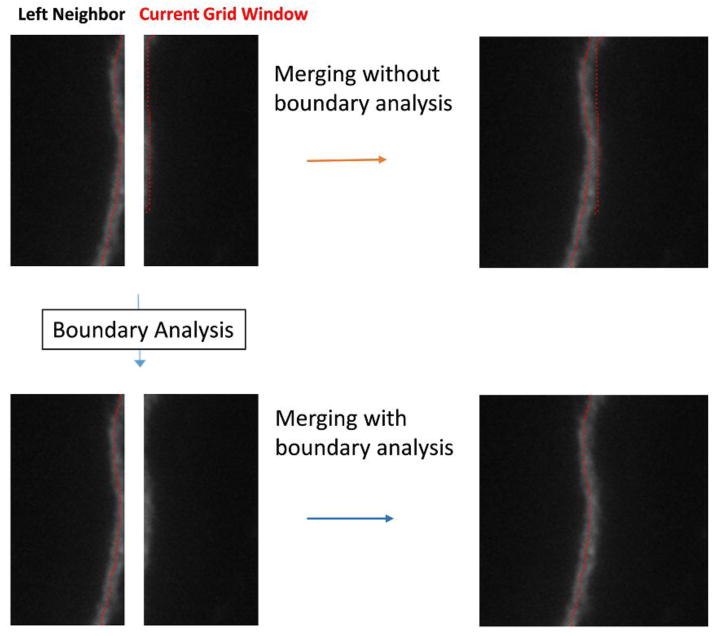
The main task of the merging process in the divide-and-conquer framework is to sum up the individual estimates of each grid window. Occasionally, there may be branches that run along the boundaries of two neighboring grid windows. This may cause double tracing. A boundary analysis module is used to resolve this issue. The grid windows of a neuronal images are processed from top to bottom and left to right. For each window, a boundary analysis is performed to check if there are any dendrites along its upper and left boundaries that have already been detected by the grid windows that are directly above and to the left of it, respectively. If, for example, the right boundary of the current window’s left neighbor and the left boundary of the current window both have a dendrite detected along the boundary (as illustrated in Figure 3), then the branch in the current window is considered as a duplicated estimate (e_m,n in Eq. 1), and it is removed from the total length count for the current window. Meanwhile, the dendrites detected along the right and bottom boundaries in the current window are saved and used in the boundary analysis of the windows directly below it and to the right of it.

Figure 3.

An illustrative example for boundary analysis that reduces duplicate estimation.

The size of the grid window is set to be between 50 and 100 pixels in size. The program dynamically calculates the grid based on the image’s size: By default it first sets M and N to 10 (i.e. 10*10 of 100 grid windows). If the default setting makes either dimension of a grid window outside of the desired range (50–100 pixels), the values of M and N are incremented (if initial size is larger than 100 pixels) or decremented (if the initial size is less than 50 pixels) until both dimensions fall within the range of [50, 100]. This setting was chosen based on parameter analysis (see Results).

The algorithms in this paper are implemented in the DendriteLengthQuantifier as a plugin for the freely available NIH ImageJ.

3.4 Preprocessing and Localized Skeletonization (LSK)

Preprocessing is performed at both global level and the individual grid window level.

At the global level, a rolling ball algorithm is used to detect and remove soma from the dendritic image unless a soma channel has been provided separately (Sternberg, 1983). The soma masks, provided or calculated, are also used in the quantification step to validate the detected dendrite traces by making sure that the detected dendrites are not in the area where the somas were. The image is denoised using a 3×3 median filter. It is then enhanced using contrast-limited adaptive histogram equalization (CLAHE) (Zuiderveld, 1994) for background correction and to improve local contrast (Fig. 2B). Different from traditional histogram equalization, CLAHE corrects the background and improves the contrast with non-uniform illumination at different local areas, which is suitable for the images we process.

At each grid level, different preprocessing techniques are performed based on the specific length estimation algorithm employed on the grid (i.e. LSK, AET or CSP). For the localized skeletonization (LSK) algorithm, the grid image is first inverted to be black-on-white. Then binarization is performed by automatic, histogram-based thresholding (Otsu, 1975). Image dilation is performed followed by erosion to fill in holes in the binarized image. A thinning operation is then performed to reduce the foreground structure to 1 pixel wide in all directions. Five rounds of pruning are performed after the thinning operation to remove the spurious details, yielding a cleaner centerline. For AET and CSP, preprocessing starts with denoising the grid window using a 3×3 median filter. The following enhancements are then performed:

1. The grid window is subject to contrast enhancement using histogram stretching. Four percent of the pixels are allowed to become saturated.

2. Hessian-based enhancement highlights the curvilinear structure of the dendrites. The post-Hessian image is obtained by eigenvector analysis of the Hessian matrix, which is a square matrix of second-order partial derivatives of the greyscale intensity function. The Hessian-transform has been a beneficial step for neuronal tracing (Meijering, et al., 2004). We use largest Eigenvalue of the Hessian matrix, which yields the post-Hessian image for the next step processing (Figure 4B).

3. Histogram stretching is then applied to the post-Hessian image to clear up artifacts and fuzzy boundaries caused by Hessian transform (Figure 4B). This is done by chopping the histogram below a background intensity value and then stretching the resulting minimum and maximum intensity values to 0 and 255. The value is conservatively chosen to avoid removing foreground. The resulting image is used for AET and CSP tracing.

Figure 4. Dendrite length estimation Based on AET.

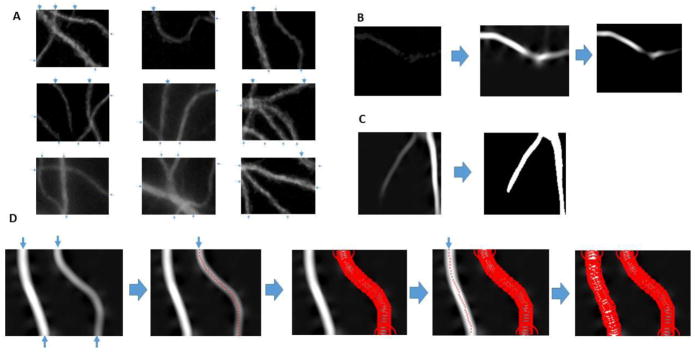
A. Examples of grid window images. The detected initial points as indicated using blue arrows. B. Preprocessing to highlight the faint and/or broken dendrites using Hessian transform and histogram stretching. C. Stopping mask generation using RATS. D. Estimation algorithm flow. The branch on the right is traced first because it is thinner.

3.5 Adaptive Exploratory Tracing (AET): Direction-Guided Tracing with Adaptive Stopping Criterion

3.5.1 Direction-Guided Tracing

Direction-guided tracing (Can, Shen, Turner, Tanenbaum, & Roysam, 1999) is an exploratory tracing method that does not process every pixel in the image and works with a gray-level image. It needs one starting position and an initial direction for tracing. The tracing goes on until one of the stopping criteria is satisfied, e.g., reaching the end of a dendrite. We adopt the direction-guided exploratory tracing and make it adaptive and robust for our purpose.

The algorithm uses the peak response of a pair of two-dimensional correlation kernels to determine the direction of the dendrite branch. For each direction, we have a pair of kernels correspond to the left and right edges of the branch it is currently tracing. There are 16 pairs of kernels defined corresponding to 16 directions, 22.5 degrees apart. For example, the left kernel of the horizontal x-axis direction is defined as:

$$\left[\begin{array}{rrrrrr}1& 1& 1& 1& 1& 1\\ 2& 2& 2& 2& 2& 2\\ 0& 0& 0& 0& 0& 0\\ -2& -2& -2& -2& -2& -2\\ -1& -1& -1& -1& -1& -1\end{array}\right]$$

The response is defined as the convolution between the kernel and the post-Hessian image intensity. For example, for the kernel above, the response is (Al-Kofahi, et al., 2002):

$$\frac{1}{48}\{-\delta (y-2)-2\delta (y-2)+\delta (y-1)+2\delta (y+1)+\delta (y+2)\}\ast \sum _{k=0}^5\delta (y-k)$$

The kernels are defined such that they have a maximal response when oriented over an edge. When a summed response of left and right edges reaches a maximum, it reveals the direction to follow during tracing. The exploratory tracing also yields the radius of the dendrite, which is half of the distance between the detected left and right edges of the dendrite.

3.5.2 Dendrite Estimation Algorithm Based on AET

The length estimate algorithm is a self-initiating quantification algorithm in the sense that it does not need any interaction. The algorithm involves the following steps:

1. Grid window preprocessing and dendrite enhancement using Hessian transform followed by histogram normalization.

2. Automatic initial point detection along grid boundaries.

3. Sort the initial points based on their radii.

4. Start tracing from the first initial point (thinnest branch), until it meets at least one stopping criterion. Save the length of the trace and clear the traced area.

5. Repeat 4 until initial points are exhausted.

6. Sum the total length of the traces to get the estimate for the dendritic length in the grid window.

For dendrite tracing in a given grid window, we assume initial points can be detected along the grid boundary. This is a reasonable assumption due to the continuity of dendrites and the small size of the divided grid window we process. Figure 4A shows several common cases of the traces in a window with detected initial points highlighted as arrows. Figure 4D shows the flow of the estimation algorithm using AET.

To perform initial point detection, thin strips that are four pixels wide along the four boundaries are cropped and binarized. If there are at least three foreground pixels for a line vertical to the boundary direction, we get a potential part of a branch, or a candidate initial point for start tracing in the grid. Getting the width of a continuous foreground section on the boundary yields the diameter of a branch candidate. This candidate is subject to a branch diameter thresholding. If the branch has a diameter/radius greater than a set minimum, then the midpoint of the branch is used as an initial point. All the initial points are sorted based on their diameters. Tracing is done for each automatically detected initial point on the four borders of the edge window, starting from the one of smallest diameter (thinnest). This is to prevent the area removal of a thick branch impact nearby thin branches. For each tracing, the initial direction is perpendicular to the border. We then use eight directions surrounding the current direction, 22.5 degrees apart, to explore the next direction of the trace. The direction with the highest response is considered the direction for next trace point. Once a dendrite branch is traced, the structure is removed from the image by clearing a circular region of interest around each trace point, to prevent multiple tracing of the same branch. The radius of the circular region of interest is determined by adding a fixed buffer to the calculated radius of the dendrite branch obtained during exploration.

If the divide-and-conquer was not used and the tracing was done on an entire image, one potential issue with direction-based tracing would be that tracing could be discontinued at crossovers or branching joints in the middle of the image. In the case of our grid-based quantification, the tracing starts from initial points along the boundaries of each grid. Different initial points can lead to the joint, so such situations will not affect the overall length estimates.

3.5.3. Adaptive Stopping Criteria

Four stopping criteria were used in AET to stop the tracing. They include:

• #1Reaching the background (end of a trace);
• #2Reaching one of the four borders;
• #3Reaching an infinite loop.
• #4Maximum response of all directions is lower than a threshold.

Criterion #1 is import to ensure the trace being on the track. Traditional methods such as Otsu’s method for detecting the background were found to be ill-suited for crowded, high contrast grid segments: If multiple branches had highly variant greyscale intensities, the fainter branches could be mistaken for background pixels. In order to deal with this issue, a more adaptive approach was required to prevent the trace from entering the background. We used the Robust Adaptive Threshold Selection (RATS) method (Wilkinson, 1998). RATS recursively divides the input image into a quadtree hierarchy of sub-regions. It uses the gradient weighted sum of the pixels to automatically determine a local threshold. The Sobel operator is used to estimate the gradient. If the sum of the gradients fails to exceed a noise estimate input parameter, the regional threshold of the parent region is used instead. The thresholds are bilinearly interpolated across the image to form the binary mask. Note that RATS is used here to provide a binary mask for stopping criterion #1, instead of image segmentation. As a result, we use RATS to produce an overmask, which detects the foreground area that can be slightly bigger than the actual area covered by dendrites, but not smaller. This avoids prematurely stopping the tracing of faint branches. Figure 4C gives an example of a binary stopping mask generated by RATS.

Criterion #2 is encountered when a trace starts from an initial point and then reaches to one of the grid window’s borders. Infinite looping described in #3 happens rarely but it is possible with an abrupt change of branch angle. If there are any remaining parts to be traced for that branch, they will be captured from the other end of the branch starting from a different initial point. The overall length is not comprised when a branch is traced from both sides. Criterion #4 could happen with dense branching or thick joint. When it is encountered, the same strategy described for #3 is used to measure the branch(es) by performing multiple tracing from different initial points.

3.6 Self-Initiating Length Estimation Using Curvature-Preserving Shortest Path (CSP)

As one of the automatic algorithms applied to a grid window, we use the shortest-path algorithm to get all the traces in the grid. The backbone of the CSP is the Dijkstra’s path search algorithm (Dijkstra, 1959), which requires two points: the source node and the destination node. Initial point detection is performed along the boundary as described in Section 3.5. Shortest paths between each pair of these points, with one being the source and another being the destination, are found. The pairing of these points is arbitrary, other than the condition that the source and destination notes cannot be on the same edge of the grid window. Therefore, the algorithm will find a path as long as there is a way to reach from source to destination, sometimes via branching. After the trace points between each legitimate pair are obtained, the trace is removed from the image to prevent multiple traces on the same branch. The summation of the path length gives the dendritic length metric. Figure 5 illustrates the CSP algorithm.

Figure 5. Dendrite length estimation Based on CSP.

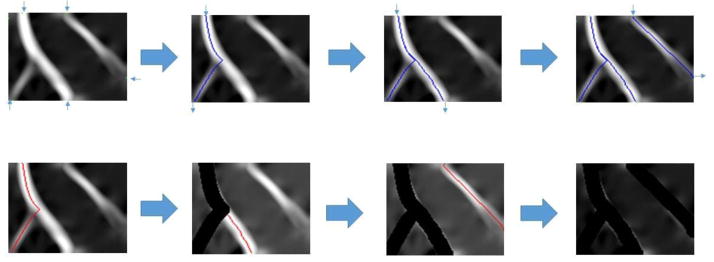
The flow starts from finding initial points on post-Hessian grid window, followed by calculating and storing paths from legitimate pairs of initial points. The path placement is then repeated and traces are removed until all points are processed.

One concern for such a search-based tracing algorithm is its computational efficiency, which is highly related to both the computational data structure and the cost function for the search. The primary data structure used is a binary heap implemented as a priority queue. Asymptotically, the best implementation of the priority queue for Dijkstra’s algorithm is the Fibonacci heap (Fredman & Tarjan, 1987). However, the advantage of using a Fibonacci heap only materializes when using a very large, dense graph, due to the large constants involved in the required operations. Consequently, a binary heap is used instead. The binary heap has logarithmic amortized time for the delete minimum operation, but smaller constants compared to the Fibonacci heap. Another data structure used is a hash set which offers constant time performance for adding and lookup operations given a properly implemented hash function. In addition, efficiency is dependent on the size of the searched region (area of wavefront), which is related to the cost-function defined for the optimal search, as we will explain next.

3.6.1 Curvature-preserving cost-function

The Hessian processing step yielded a processed neuronal image which contained the eigenvalues of the Hessian matrix that represents the likelihood of the curvilinear structure for each pixel. Such values have been described as the “neuriteness” of the pixel (Meijering, et al., 2004). A shortest path algorithm was used in that tool to link manually selected starting and ending points. Because those were interactively chosen, the cost function was simply defined to be neuriteness plus a term that favors the “smooth flow” of the trace. It was because an interactively selected pair of points were expected to correspond to the actual starting and ending points of a branch without acute angle changes.

However, it is not suitable for our automatic algorithm to use such a cost function due to the self-initiating nature of our tracing: It is possible that a path will need to be found between a pair of two points that are not natural starting and ending points of an arbor. In such cases, the algorithm needs to be able to go through sharp angle changes of branching in order to reach the destination. Instead of favoring smooth flow, we want to preserve the curvature of such angle changes to avoid short-cutting the path, and to get a more accurate length estimate of the dendrite centerline. Thus, the cost function needs to be reexamined.

Initially, a cost function was developed that had a linear relationship with neuriteness as existing literature:

$$\mathit{cost}(x,y)=\{\begin{array}{ll}255-{\lambda }_{x,y}\hfill & if{\lambda }_{x,y}>t\hfill \\ \infty \hfill & if{\lambda }_{x,y}\le t\hfill \end{array}$$

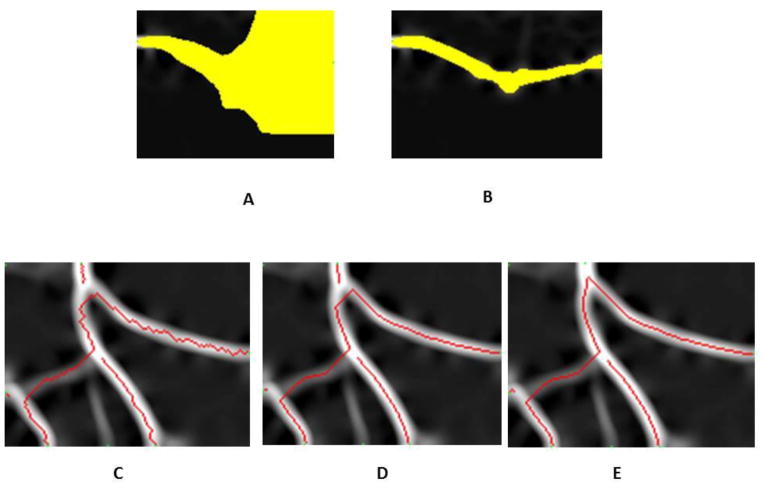
The neuriteness λ_x,y is subtracted from 255 as that is the maximal intensity value of an eight bit image after Hessian preprocessing. The threshold value t is used to prevent the wavefront from expanding into the background which is not only computationally expensive, but could cause false positives. This is because Dijkstra’s algorithm has a tendency to settle nodes in a circular wavefront pattern. As a result, any path of final cost between two initial points will be traced regardless of the magnitude. Truncating the function to infinity at the threshold intensity has the effect of constructing a barrier that funnels the wave function down the dendrite branch. Figure 6A shows the search wave front when using a cost function without the background truncating (t set to zero), while Figure 6B has the threshold set by Otsu’s method which has a much smaller search region for improved efficiency.

Figure 6. Comparison of different search waves and choices of the cost function in CSP.

A. Shortest path wavefront without threshold truncating. The yellow wavefront indicates the area where the pixels are searched. B. Shortest path wavefront with threshold truncating. C. Tracing results (in red) when using cost function with a logarithmic growth rate. D. Tracing results when using a cost function with linear growth rate. E. Tracing results when using a cost function with cubic growth rate. The branching curvature is better preserved compared with C and D.

An investigation into the nature of the cost function led to the discovery of an interesting relationship between the growth rate of the function and the tracing method’s bias for shorter Euclidean distance. The higher the growth order of the cost function, the more costly it became to traverse the dim portions of the branch. The resulting path will trace the brightest part of the Hessian image, which will correspond to the curvature of the dendrite. Observing the tracing with cost functions having different growth rates will illustrate the effect, as shown in Figure 6. The cost function used in Figure 6C had a logarithmic growth rate (i.e. log(255 – λ_x,y)). The resulting tracing method had a tendency to take short cuts through lower intensity regions of the image. The higher cost of tracing lower intensity pixels was offset by tracing less of them. The ideal cost function was one that made short-cut paths expensive compared to longer paths that traversed higher intensity pixels. This was achieved by using cost functions with higher growth rates. The initial cost function had a linear growth rate, as shown in Figure 6D. It can be observed that the tracing methods still retain a bias for lower Euclidean distance. However, the method better traced the curvature of the dendrite compared to the method with a logarithmic cost function. Cost functions with rates greater than polynomial can be ruled out based on restrictions of numerical precision due to arithmetic underflow. Based on heuristic experiments, the best performing growth rate for a cost function was found to be cubic, which is the cost function used in our algorithm as defined in Equation (2) where λ_x,y is the pixel intensity in post-Hessian grid image. These traces preserved the curvature very well, and avoided taking shortcuts.

$$\mathit{cost}(x,y)=\{\begin{array}{ll}{(255-{\lambda }_{\mathrm{x},\mathrm{y}})}^3\hfill & if255>{\lambda }_{\mathrm{x},\mathrm{y}}>t\hfill \\ \hfill \infty \hfill & if{\lambda }_{\mathrm{x},\mathrm{y}}\le t\hfill \\ 0\hfill & if{\lambda }_{\mathrm{x},\mathrm{y}}=255\hfill \end{array}$$ (2)

3.7 Automatic Dendritic Length Estimate Based on Ensemble of Multiple Approaches

Instead of using a single estimation algorithm as in traditional work, we employed three length estimation algorithms for each grid window, namely Localized SKeletonization (LSK), Adaptive Exploratory Tracing (AET), and Curvature-preserving Shortest Path search (CSP). The first is based on segmentation, and the latter two are considered tracing-based methods. The resulting estimate is an ensemble of the three methods. One possible ensemble is a weighted sum of individual estimates from the different algorithms:

$${\mathrm{L}}_{\text{mn}}={\mathrm{w}}_{\text{SK}}\ast {\mathrm{L}}_{\text{mn},\text{LSK}}+{\mathrm{w}}_{\text{AET}}\ast {\mathrm{L}}_{\text{mn},\text{AET}}+{\mathrm{w}}_{\text{CSP}}\ast {\mathrm{L}}_{\text{mn},\text{CSP}};$$

In reality, individual algorithms have respective biases as reviewed in related work. For example, the thinning operation is performed in all directions including the one perpendicular to the branch growth. Therefore, it may yield spurious lines that over-estimate the length. On the other hand, tracing can have premature stops that under-estimate the dendritic length. Ideally, if the combined result can compensate each algorithm’s weakness, the resulting L_mn can give a more reliable estimate. Considering their different types of biases, one simple ensemble is to use the average of all three methods. We thus employ a statistical average of three individual estimates, essentially setting w_LSK = w_AET = w_CSP = 1/3. We get the length estimate by average ensemble as following:

$${\mathrm{L}}_{\text{ens}\_\text{avg}}={\mathrm{\sum }}_{\mathrm{m}}{\mathrm{\sum }}_{\mathrm{n}}({\mathrm{L}}_{\text{mn},\text{LSK}}+{\mathrm{L}}_{\text{mn},\text{AET}}+{\mathrm{L}}_{\text{mn},\text{CSP}})/3)$$ (3)

The divide-and-conquer strategy provides a framework to allow other ways of algorithm ensemble. For comparison, we performed a multi-variate regression analysis on ten randomly chosen neuronal images, with each algorithm being one variable and the length being the prediction. The model was fitted with the golden standard estimate. The highest coefficient of determination (R²) compared with the R² from individual estimates is obtained when it set the L_mn,LSK, L_mn,AET and L_mn,CSP to 0.51, 0.24 and 0.25 respectively.

$${\mathrm{L}}_{\text{Ens}\_\text{weighted}}={\mathrm{\sum }}_{\mathrm{m}}{\mathrm{\sum }}_{\mathrm{n}}(0.51{\mathrm{L}}_{\text{mn},\text{LSK}}+0.24{\mathrm{L}}_{\text{mn},\text{AET}}+0.25{\mathrm{L}}_{\text{mn},\text{CSP}}))$$ (4)

4. Results

We tested our results on a set of 50 high-throughput neuronal images obtained using the system described in Section 3.1 and shown in Figure 1. The images were of size 1344×1024 pixels, and each image contained a varying number of neurons with total dendritic length ranging from thousands to tens of thousands pixels, at a scale of 0.15622 μm/pixel.

4.1 Qualitative Results

Figure 7 gives an example of Localized Skeletonization (LSK) using divide-and-conquer method. In comparison with Figure 7b, which uses global skeletonization, the grid-based approach (Figure 7c) is able to extract the dim branches that would otherwise be missed due to contrast variation among different regions. This illustrates an advantage in using the grid window approach which is adaptive to local contrast difference.

Figure 7. Comparison of the LSK method with global alternative.

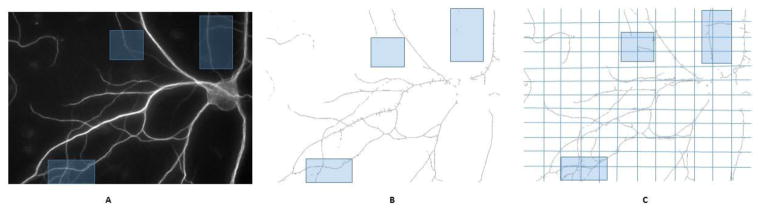
A. Original image (raw image has been enhanced for better visualization). Blue masks indicate the area with dim branches. B. Global skeletonization. C. LSK with the divide-and-conquer strategy. The improved local adaptiveness allows better capturing of dim branches.

Figure 8 shows examples of how the three individual estimation methods work on the images. In general, both LSK and CSP handle branching and rapid change of direction well, as illustrated in Figure 8a and Figure 8c. LSK also effectively worked with discontinued branches, but it only worked the best when binarization and soma removal were performed well. Adaptive exploratory tracing (AET, Figure 8b) had some advantages of its own. The stopping criteria made it a conservation tracing algorithm that resulted in fewer false positives. AET requires only one initial point as input, as opposed to the shortest path algorithm which requires a source point and a target point. This allowed AET to trace dendrite branches that lack a clearly defined end point. The fact that different algorithms had different strengths made it possible for the ensemble methodology to provide more accurate results.

Figure 8. Examples of results.

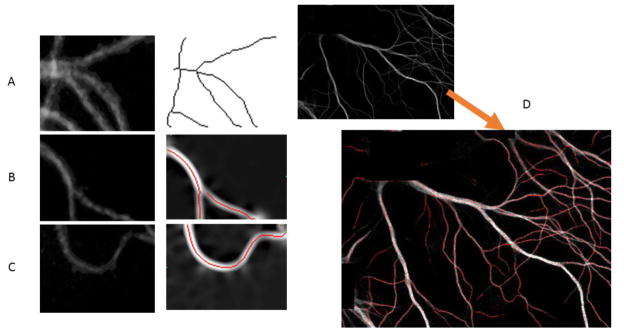
A. LSK works with a grid window with multiple branches; B. AET works with a grid window with dim and broken branches; C. CSP works with a grid window of big curve change. D. An example of tracing results overlaid in the original image. The dotted red line indicates the trace. The small gaps between dots represent the step size of exploration tracing algorithm (set to 3 by default).

Figure 8D visualizes the tracing results of AET and CSP overlaid on an image of three neurons. The estimations are in agreement with the actual dendrite branches except the false positives near the soma area.

4.2 Quantitative Results

The quantitative validation process requires gold-standard estimates from each image. Following literature (Pool, Thiemann, Bar-Or, & Fournier, 2008), the gold-standard estimates were generated manually using NeuronJ.

We calculated the quantification accuracy of overall length estimate as:

$$\mathit{Accuracy}=1-\frac{\mid \mathit{estimated}\mathit{length}-\mathit{standard}\mathit{length}\mid }{\mathit{Standard}\mathit{Length}}$$ (5)

As listed in Table 1, our fully automatic pipeline for dendritic length estimation achieved an average accuracy of 88.8% on 50 images for cultured mature mouse hippocamal neurons. The results are reported as Ens_AVG, which is the ensemble obtained by getting the average of LSK, AET and CSP in each grid segment calculated based on Equation (3). Among the 50 images, about half (23 out of 50) of the results yielded an accuracy of 90% or better. For more than a quarter images (13 out of 50), the algorithm obtained an estimation with an accuracy higher than 95%, with three images obtaining higher than 99% accuracy. For 31 out of 50 images, lower estimates than the gold standard were obtained. This left 19 out of the 50 images that had estimations higher than the gold standard. These statistics will be discussed in Section 5. The results in Table 1 also showed that our tool can effectively detect the differences of dendritic length in different images (regions). For example, for image #21 and #46, the tool reported dendritic lengths different from each other. Our method validated that the difference was 13,044 (pixels). This was very close to what NeuronJ reported at 13,224 pixels. The discrepancy between our tool and NeuronJ was only 1.4%, despite our tool being automatic while NeuronJ is semi-automatic. The results indicated the effectiveness of our proposed approach, which will be further demonstrated by comparison with other methods in the next section.

Table 1.

Results on high-throughput neuronal images. GS: dendrite length based on gold standard; Length: Estimated length based on algorithm ENS_AVG. ACC: accuracy in %.

#	GS	Length	ACC
1	11520	10752	93.3
2	17465	16061	92.0
3	20066	16991	84.7
4	25054	20168	80.5
5	10128	8035	79.3
6	12379	10436	84.3
7	12478	13222	94.0
8	6917	4609	66.6
9	23606	20607	87.3
10	28826	23218	80.5
11	5746	6006	95.5
12	10561	10227	96.8
13	29952	25136	83.9
14	14194	12547	88.4
15	3908	4119	94.6
16	9421	7875	83.6
17	24865	22083	88.8
18	18937	15277	80.7
19	12246	11105	90.7
20	22355	19568	87.5
21	8940	8924	99.8
22	12929	12313	95.2
23	12126	11338	93.5
24	16634	14626	87.9
25	23057	19523	84.7
26	30080	24307	80.8
27	11769	14315	78.4
28	14236	15381	92.0
29	9060	9098	99.6
30	6976	6208	89.0
31	10769	12782	81.3
32	5614	6734	80.1
33	5981	5884	98.4
34	8547	9486	89.0
35	26897	25178	93.6
36	15211	16451	91.8
37	8267	7337	88.7
38	15177	15668	96.8
39	26241	26787	97.9
40	12088	14677	78.6
41	3276	3367	97.2
42	21449	24229	87.0
43	28883	25699	89.0
44	19376	18964	97.9
45	12289	16425	66.3
46	22164	21968	99.1
47	27477	27997	98.1
48	24114	26032	92.0
49	17694	18699	94.3
50	18346	20091	90.5
AVG			88.8

Equation (5) is used to quantify the estimation accuracy of the overall length of dendrites. It is meaningful under the condition that few falsely traced dendrites are generated. To verify this, we examined the dendritic image in Figure 8D to count the over estimation and under estimation for the three tracing algorithms (LSK, AET, CSP). Compared with gold standard from semi-manual tracing, total over-estimation of dendrites (false positive traces) ranged from 239 pixels to 376 pixels for the three tracing algorithms with detected dendritic length being 17K to 18K pixels. The average precision rate of three algorithms was 97.5%. These results confirmed that the accuracy defined in Equation (5) is a suitable measure for our method. For Figure 8D, the average recall rate of the three algorithms, calculated using underestimation, was 82%. These results indicated that when conservative, our algorithms are precise.

4.3 Comparison with Other Methods

In Table 2, we compare the results of several methods for dendritic length estimation on the same set of images. The table displays the individual methods (AET, CSP, LSK) and two ensemble methods (Ens_AVG and Ens_Weighted) in our divide-and-conquer framework. It also shows the results of a third-party tool, NeuriteTracer (Pool, Thiemann, Bar-Or, & Fournier, 2008). NeuriteTracer was chosen for comparison because it is publicly available and based on global skeletonization after binarization, which is a representative method for current automated estimation methods. NeuriteTracer requires the user to manually choose a threshold for binarization. Based on the recommendation of its user guide, we adjusted the parameter of NeuriteTracer using histogram and visual inspection in order to find the best threshold for the images. Based on these findings, the threshold limit was set to 20. We tried several settings and reported its best performance in Table 2. NeuriteTracer also requires the user to supply a separate soma channel, while our tool provides the option of automatically extracting the soma mask. The same soma masks were used in each of the methods to ensure a fair comparison.

Table 2.

Comparison of several methods in accuracy (%). The highest average accuracy is in bold and the lowest average is in italic.

#	AET	CSP	LSK	Ens_Wei	Ens_AVG	Neurite Tracer
1	87.8	90.0	97.4	95.4	93.3	85.4
2	82.5	92.7	98.9	93.6	92.0	57.6
3	77.5	89.1	87.7	84.9	84.7	75.7
4	72.7	82.0	87.1	82.0	80.5	78.7
5	78.0	78.9	81.3	79.2	79.3	99.3
6	88.3	80.6	84.4	83.4	84.3	94.8
7	98.0	97.5	86.2	92.6	94.0	88.5
8	71.0	66.6	62.7	64.5	66.6	85.8
9	79.5	90.8	91.9	87.7	87.3	88.1
10	73.9	82.8	85.2	81.1	80.5	75.7
11	98.4	96.6	84.2	93.1	95.5	91.5
12	96.9	85.9	91.8	99.0	96.8	82.7
13	75.5	85.5	91.0	85.2	83.9	66.9
14	85.7	87.3	92.7	88.2	88.4	90.1
15	97.8	100.0	85.5	93.0	94.6	83.6
16	87.1	78.5	85.5	83.2	83.6	90.5
17	81.9	90.5	94.3	89.7	88.8	79.5
18	81.1	76.8	84.5	81.5	80.7	83.7
19	89.8	89.5	93.1	90.5	90.7	81.8
20	80.2	90.9	91.8	87.9	87.5	72.2
21	89.9	94.0	96.0	99.8	99.8	87.9
22	97.2	96.2	92.5	93.9	95.2	95.4
23	94.9	90.8	95.1	93.1	93.5	96.0
24	83.3	92.0	88.8	87.6	87.9	84.5
25	79.7	82.0	92.6	85.9	84.7	61.8
26	76.1	80.9	85.7	81.3	80.8	67.8
27	83.9	81.0	69.7	76.8	78.4	93.7
28	94.3	98.0	83.1	90.7	92.0	75.9
29	99.3	96.6	97.6	99.2	99.6	99.2
30	93.6	82.5	91.4	88.6	89.0	95.1
31	81.9	94.0	67.5	78.4	81.3	79.4
32	80.2	81.3	78.0	80.2	80.1	99.4
33	95.2	87.4	96.5	98.7	98.4	98.6
34	91.8	87.4	87.3	89.1	89.0	80.9
35	82.8	99.0	97.2	93.7	93.6	73.4
36	95.3	88.8	91.1	93.0	91.8	90.2
37	82.7	93.4	90.7	88.3	88.7	81.5
38	91.1	85.5	95.6	97.0	96.8	91.4
39	86.6	88.6	91.5	97.2	97.9	70.2
40	92.2	71.2	72.0	78.2	78.6	78.6
41	97.9	94.3	99.1	98.6	97.2	85.2
42	97.6	79.4	79.0	85.7	87.0	69.8
43	76.4	94.4	96.3	89.9	89.0	71.1
44	84.2	97.6	92.7	99.7	97.9	73.8
45	83.0	54.7	60.9	66.1	66.3	63.6
46	83.0	88.2	97.0	99.2	99.1	63.0
47	86.2	92.5	87.7	96.3	98.1	55.2
48	90.4	85.3	80.8	90.4	92.0	54.9
49	95.7	95.4	88.1	93.9	94.3	76.1
50	99.6	85.8	85.8	90.2	90.5	82.3
AVG	86.99	87.42	87.69	88.73	88.84	80.96

From the average accuracy, we can see that all of our methods (AET, CSP, LSK, Ens_AVG, and Ens_Weighted) were more effective than the results reported by NeuriteTracer. Overall, the best performing methods were the ensemble methods, Ens_Weighted and Ens_AVG. Ens_AVG achieved the highest average accuracy of 88.8%. The average accuracy of Ens_AVG was 8 percent higher than that of NeuriteTracer. The p-value for the paired t-test between Ens_AVG and NeuriteTracer was 0.0002, indicating that the difference was statistically significant.

The reason that our results were superior to those of NeuriteTracer can likely be attributed to the divide-and-conquer framework. NeuriteTracer uses global skeletonization as the foundation of its algorithm, which can encounter obstacles when working with complex branch patterns with high local variation. To further validate the effectiveness of the divide and conquer strategy, we also ran the global skeletonization algorithm without using the divide-and-conquer strategy on all of the 50 testing images. We measured the dendritic lengths using skeletonization on the entire images and computed the accuracies. The results were then compared with those of LSK, which is also a skeletonization-based algorithm but uses the divide-and-conquer strategy. For the algorithm without using divide-and-conquer, the accuracies ranged from 39.85% (image 9) to 92.10% (image 41), with an average accuracy of 63.90%. The results were significantly lower than the results of LSK which had an average accuracy of 87.69%. This comparison strongly supported the effectiveness of the adopted strategy.

The results also confirmed that AET, CSP and LSK can have different performance biases on different images. For example, LSK has a lower accuracy than those obtained from AET and CSP on image 15. However, for image 43, AET had lower accuracy than the other two methods. We found that the accuracy difference associated with image 15 was because LSK has an over estimation of dendritic length. Image 43 is a crowded image, and AET, being a conservative exploratory tracing method, yielded an under-estimation.

Compared with Ens_Weighted, which needs to perform multivariate regression on images to estimate the weights, Ensemble_AVG is simpler to implement and avoids image-dependent bias. Supported by quantitative results and practice considerations, we chose Ens_AVG as the method implemented in the dendrite quantification tool DendriteLengthQuantifier available for download (see link in Supplemental Results).

4.4 Parameter Analysis

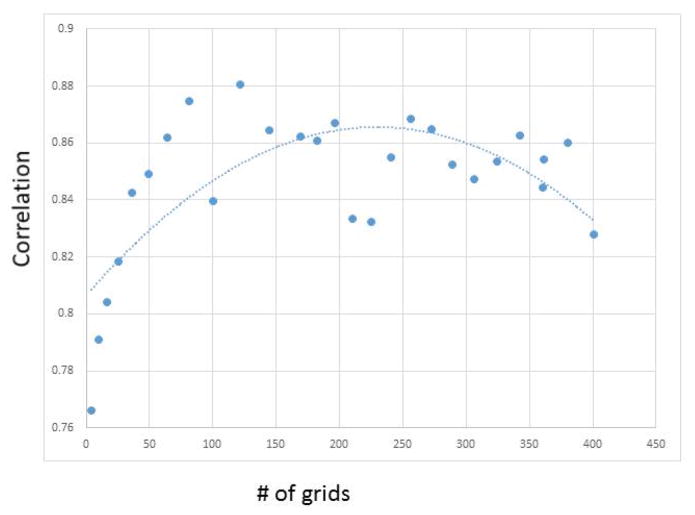
In our methodology of grid-based divide-and-conquer, a critical parameter is the size of the grid segments. To adapt to local characteristics, it is obvious that the grid window size should not be large. However, it may not be the case that a smaller grid window size is better under all circumstances. For example, RATS, being a recursive method based on quadrant trees, requires a reasonable sized image to work effectively. To understand the grid segment’s impact on length estimation, we conducted grid size analysis using a representative example image shown in Figure 2. We then calculated its Pearson correlation with gold standard on each grid segment. Figure 9 shows that when fitted using second order polynomial, the best performance is achieved in the middle range of grid size between roughly 50 and 100 pixels in both width and height. Therefore, the DendriteLengthQuantifier tool dynamically calculates the grid size using the method explained in Section 3.2 to ensure that the grid size falls into this range.

Figure 9. Performance versus number of grids.

The x coordinate is number of grids starting from 2*2 = 4, 3*3 =9, …, 20*20 = 400. The trendline is fitted using second order polynominal.

For the results reported in Table 1 and 2 of images sized 1344×1024, grid was set as 14 columns and 11 rows. The Hessian transform’s smoothing factor was set to 5. For AET, the tracing step size was set to 3. For each of the tested images (with more than 1 million pixels per image), the processing time of our algorithm was 15 seconds on a regular PC with default settings of ImageJ 1.48q. Since our approach is automatic, the algorithm is suitable for high-throughput processing of neuronal images. Parallelized implementation on grids is expected to further speed up the algorithm in future work.

5 Discussion

The qualitative and quantitative results have shown the effectiveness of processes and algorithms employed in our method. Such algorithms include divide-and-conquer and several preprocessing and tracing strategies to improve local adaptation. The motivation behind developing an ensemble approach is to exploit the advantages of each algorithm. The algorithms performed differently on image segments with varying characteristics such as noise, crowdedness, and contrast differences, as explained in Section 4.1. In particular, using a weighted ensemble of the three algorithms yields the highest length estimate accuracy. One justification for using a combined estimate on such images is the fact that there are typically different sources of error common in each method. The idea is similar to using an ensemble classifier in machine learning where a committee is used to get a balanced view that can lead to improved reliability. For example, one algorithm may overestimate in some cases where another algorithm would underestimate. When the average of the results of each of the algorithms is used to yield the overall estimate, errors from different sources may be balanced out and the combined accuracy on the image could potentially be higher. Visual inspection and quantitative validation on high-throughput images confirm our proposed methodology.

5.1 Remaining Issues

Despite that quantitative results demonstrated the efficacy of our method, it still has some remaining problems. Images that show an underestimation of dendritic length may due to dim branches that are not accounted for by the automatic approach although they could be recognized manually. We have incorporated modules to mitigate some causes of false positives, but they can be further improved. One impact is related to the area around somas. Removal of the soma area is a pre-requisite for automatic length estimation. If somas were not completely removed, they could influence the dendrite length estimate. While rolling ball soma detection on the dendrite channel was used for general applicability of the tool, having a separate channel of soma staining can help improve the accuracy of the estimate. Another source of error or ambiguity comes from thick branches that sometimes cause trace over-count. Shortest path (CSP) appears to be more robust than the other methods in such situations. A merging analysis component also helps resolve this issue to some extent, but it is not eliminated. In addition, the Hessian-transform may introduce artifacts when a region is mostly black with subtle texture. We employed a pre-detection strategy for such a situation. If the entire image was largely black, it would not be processed. If the image had a very low mean, then histogram was chopped in order to remove the texture at low intensity.

Algorithm validation is another issue worth further consideration. Length accuracy based on the gold standard is a straightforward and meaningful measure. However, several limitations need to be mentioned. First of all, the tool that was used to generate the gold standard, NeuronJ, is a semi-automated tool. Although it is often used in literature for validation purpose, its traces were computationally generated based on human interaction. This may have resulted in algorithm bias as well as human bias. Secondly, the current measure of length is a global measure that does not imply the quality of connectivity or agreement with the actual branches. For example, it is possible that some areas over-estimation overcome other areas underestimation.

5.2 On Divide-and-Conquer

One important potential advantage of the grid-based divide-and-conquer strategy, in addition to those illustrated in the paper (e.g., better local adaptation), is that it opens up various possibilities of algorithm ensemble. The simple weighted combination we adopted already brings significant improvement over state-of-the-art methods. In future work, we will explore other possibilities of fusing different methods, which may lead to further improved efficacy.

We also need to point out that the divide-and-conquer strategy requires consideration to overcome the interference of the generated boundary edges during dendrite tracing and quantification, as explained in Section 3.3. The focus of the current work is to yield dendrite length automatically. This goal allows us to make use of the average of the results of multiple algorithms in the ensemble-based dendritic length estimation. It can also avoid the confusion between crossover and branching, which is a challenging issue for 2D images (it is less an issue for 3D images because crossovers do not overlap in 3D). For the individual tracing methods, such as AET and CSP, the strategy is expected to be extensible to calculating other morphometric conditions with additional effort. For example, the seed points along the boundary for AET and CSP can be examined and the traces can be linked over the neighboring grid windows, which can potentially yield morphometrics such as branch points and numbers.

In summary, this paper developed automatic algorithms as well as an open and free tool for dendritic length quantification in cultured mature mammalian neurons. The proposed method uses a divide-and-conquer strategy to tackle the complexity of the dendritic arbor and local variation. It also provides a framework for algorithm fusion. Proposed algorithms and ensemble strategy achieved improved efficacy for dendrite length estimation on high-throughput images of cultured mammalian neurons.