Fourier transform coupled to tryptophan-scanning mutagenesis: Lessons from its application to the prediction of secondary structure in the acetylcholine receptor lipid-exposed transmembrane domains

Abstract

Although Fourier transform (FT) and tryptophan-scanning mutagenesis (TrpScanM) have been extremely useful for predicting secondary structures of membrane proteins, they are deemed to be low-resolution techniques. Herein, we describe the combined use of FT and TrpScanM (FT-TrpScanM) as a more reliable approach for the prediction of secondary structure. Five TrpScanM studies of the acetylcholine receptor lipid-exposed transmembrane domains (LETMDs) were revisited and analyzed by FT-TrpScanM. FT analysis of the raw data from the aforementioned TrpScanM studies supports and validates the conclusions derived from their tryptophan-periodicity profiles. Furthermore, by FT-TrpScanM, we were able to determine the minimum number of consecutive tryptophan substitutions necessary for more robust prediction of α-helical secondary structures and evaluate the quality of structure predictions by α-helical character curves. Finally, this study encourages future utilization of FT-TrpScanM to more reliably predict secondary structures of the membrane protein LETMDs.

1. Introduction

Unlike globular proteins, high-resolution three-dimensional structures of membrane proteins as determined by x-ray crystallography are seldom found in protein structure databases, reflecting the difficulties associated with their crystallization. As preferred alternatives to x-ray crystallography for structural assessment, NMR and cryo-electron microscopy have been typically used; however, they are limited by protein size and reachable resolution, respectively. In this scenario, the tryptophan-scanning mutagenesis (TrpScanM) has emerged as another option for predicting the secondary structure and packing arrangement of the lipid-exposed transmembrane domains (LETMDs), which can then be used to model their overall spatial orientation [1]. Although TrpScanM has been successfully applied to several ion-channel proteins such as nicotinic AChR channels [1-5], inward rectifier potassium channels [6-8], voltage-activated potassium channels [9-15], glutamate receptor channels [16], γ-aminobutyric acid type A receptor channels [17, 18], voltage-gated sodium channels [19], N-methyl-D-aspartate receptor channels [20], P2X₄ receptor channels [21] mechanosensitive channels MscL [22, 23], human ether-a-go-go-related gene (HERG) K⁺ channels [24] and epithelial Na⁺ channels [25], the TrpScanM is, nevertheless, deemed a low-resolution method for predicting secondary structure and packing arrangement because it does not provide direct structural information. The rationale for choosing TrpScanM is that tryptophan systematic substitutions in the transmembrane domain of the ion-channel protein should result in a loss of function and/or functional expression when facing the interior of the protein. Conversely, when the tryptophan substitution faces the lipid environment the mutation could be tolerated, thus, the tryptophan systematic substitutions give rise to periodic patterns of perturbations in ion-channel function and functional expression. Herein, we coupled Fourier transform (FT) to TrpScanM (FTTrpScanM) to predict reliable secondary structures of the acetylcholine receptor (AChR) LETMDs. The focus of the present study is not to determine the secondary structure of the AChR LETMDs because these have already been determined. Indeed, the main objective of this study is to convey the use of FT-TrpScanM as a valuable alternate tool to make reliable predictions of secondary structures of the membrane protein LETMDs for which high-resolution structures are not yet available. It is noteworthy that we took advantage of the recently reported structure of the Torpedo AChR, which was determined at 4 Å resolution using cryo-electron microscopy in order to corroborate our predictions [26]. Interestingly, the TrpScanM predicted α-helical structures for the LETMDs [1-5] even when a lower-resolution cryo-electron microscopy structure mistakenly predicted the LETMDs to be arranged as β-sheets [27]. Thus, the AChR serves as an excellent model to test the validity of the FT-TrpScanM approach and provides reassurance on its capacity to generate trustworthy predictions of the secondary structures of membrane protein LETMDs in general. Furthermore, FT-TrpScanM supports and validates the conclusion from previous TrpScanM [1-5] and biochemical [28-30] studies, which predicted that the LETMDs are arranged as α-helical structures. In addition, using this approach, we were able to provide additional structural information, estimate mean periodicities, determine the minimum number of consecutive tryptophan substitutions required to reliably predict α-helical structures, and assess the quality of structure predictions.

2. Materials and methods

2.1. General Experimental Procedures

Xenopus laevis oocytes were microinjected with complementary RNAs from mouse muscle adult-type or Torpedo californica AChR (see also refs. [1-5]). Mutations were engineered with the QuikChange^® Site-Directed Mutagenesis kit (Stratagene, La Jolla, CA, USA) and were confirmed by automated DNA sequencing. All mutagenic primers were designed with the tryptophan codon (TGG) instead of the wild type (WT) codon at the desired position. Muscle-type or Torpedo AChR cRNA transcripts were synthesized with the mMESSAGE mMACHINE^® kit (Ambion, Inc., Austin, TX, USA). Oocytes were incubated for 3-5 days with fresh liquid medium at 19 °C.

2.2. Voltage Clamp

Macroscopic ACh-induced currents were recorded at room temperature with a whole-cell two-electrode voltage clamp configuration using a Gene Clamp 500B amplifier (Axon Instruments, Inc., Union City, CA, USA). Electrodes were filled with 3 M KCl and had resistances of < 2 mega ohms. Impaled oocytes were automatically perfused with a MOR-2 buffer [82.5 mM NaCl, 2.5 mM KCl, 5 mM MgCl₂, 1 mM Na₂HPO₄, 0.2 mM CaCl₂, 5 mM HEPES, and 0.5 mM EGTA (pH 7.4)] at a rate of 0.43 mL/s and a solution exchange of < 3 s using a Perfusion Valve Controller VC-8 (Warner Instruments, Inc., Hamden, CT, USA). Membrane potential was held at −70 mV. Membrane currents were filtered at 100 Hz and digitized at 1 kHz using Gene Clamp 500B amplifier and DigiData 1322A interface (Axon Instruments, Inc., Union City, CA, USA), respectively. Data acquisition was conducted through the Clampex 9.2 program (Axon Instruments, Inc., Union City, CA, USA). Dose-response curves were generated from macroscopic peak currents (I) obtained from seven different ACh concentrations (1, 3, 10, 30, 55, 100, and 300 μM ACh). Dose-response curves were fitted through a sigmoidal dose-response equation with variable slope using GraphPad Prism 4 program (GraphPad Software, Inc., San Diego, CA, USA),

$$I\left(nA\right)=I_{min}+\frac{I_{max}-I_{min}}{1+{10}^{(LogE{C}_{50}-Log\mid ACh)\times HillSlope}}$$ (1)

where I is the macroscopic peak ionic current at a given ACh concentration, I_min and I_max are the smallest and the largest currents observed, respectively, EC₅₀ is the concentration of acetylcholine that provokes a response halfway between I_min and I_max, and the Hill Slope is the steepness of the dose-response curve [31].

2.3. Periodicity Profiles

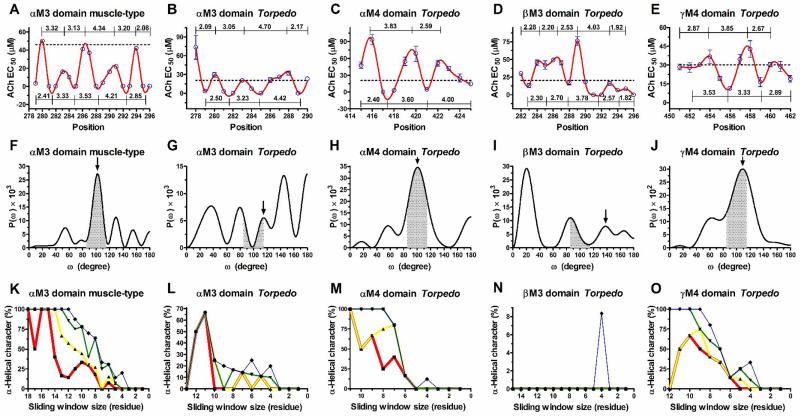
The oscillation patterns of the TrpPPs were generated from the reported ACh EC₅₀ values from five LETMDs (αM4, βM3, γM4, and two αM3 domains). TrpPPs were plotted with ACh EC₅₀ values as a function of the tryptophan substitution positions. TrpPP curves were fitted through a cubic spline method with 3,000 segments to interpolate the points using GraphPad Prism 4 program. The number of residues per helical turn of the periodicity profiles was estimated as the number of amino acids between adjacent maximums and minimums peaks (see Fig. 1 A-E).

Figure 1. Tryptophan-periodicity profiles, Fourier transform power spectra, and α-helical character curves generated from tryptophan-scanning mutagenesis data of the AChR lipid-exposed transmembrane domains.

(A-E) are TrpPPs. Values along the lines indicate the number of residues per helical turn between adjacent maximums and minimums peaks. The black dashed line indicates the ACh EC₅₀ value of the wild-type AChR. (F-J) are FT power spectra from entire sequences of the ACh EC₅₀ values shown in the TrpPPs (A-E). The black headed arrows indicate the peaks that correspond to mean periodicities of the TrpPPs (A-E). Grey shadings demarcate the region 85° ≤ ω ≤ 115° that is used to calculate peak ratio values. (K-O) are α-helical character curves of different periodicity intervals as a function of the number of residues in the sliding window; red line (3.5 – 3.7) residues/turn; yellow line (3.4 – 3.8) residues/turn; green line (3.3 – 3.9) residues/turn; or blue line (3.2 – 4.0) residues/turn.

2.4. Fourier Transform

The FT power spectra from ACh EC₅₀ data were generated using a least-squares discrete FT equation [13, 21, 32-36]. The FT power spectrum P(ω) were plotted as a function of angular frequency ω (rotation angle between residue around a helical axis) using,

$$P\left(\omega \right)={\left[{\sum }_{j=1}^N(V_j-\langle V_j\rangle )\cos \left(j\omega \right)\right]}^2+{\left[{\sum }_{j=1}^N(V_j-\langle V_j\rangle )\sin \left(j\omega \right)\right]}^2$$ (2)

where V_j is the ACh EC₅₀ values at a given position j, <V_j> is the mean value of V_j in the sliding window, and N is the number of ACh EC₅₀ values in the sliding window (see Fig. 1 F-J). The sliding windows of the ACh EC₅₀ values must follow the order presented in the original sequence. For instance, the FT analysis of a sequence of values from an ideal α-helical pattern (3.6 residues per turn) should give a prominent peak at ~100° in the FT power spectrum, given that the ω parameter is related to the number of residues per turn (d) by the expression ω = 360°/d. The mean periodicities of the sequences of ACh EC₅₀ values were estimated from the peak localized in the vicinity of the rotation angle as indicated by the mean periodicities of their TrpPPs. The expected rotation angles (ω) of the TrpPPs’ mean periodicities were calculated by the abovementioned equation, ω = 360°/d. The reliability of the sequences of ACh EC₅₀ values for predicting α-helical periodicities was evaluated by calculating the ratio of P(ω) in the α-helical range (85° ≤ ω ≤ 115°) relative to P(ω) over the whole spectrum using,

$$Peakratio=\left[(1∕30){\int }_{85°}^{115°}P\left(\omega \right)d\omega \right]∕\left[(1∕180){\int }_{0°}^{180°}P\left(\omega \right)d\omega \right]$$ (3)

where P(ω) is the FT power spectrum. Peak ratio values greater than 2, which represent at least 33% of the whole power spectrum, have been considered as a very good indicator of an α-helical secondary structure [21, 32-34, 36]. The algorithm templates developed to plot the FT power spectra and calculate the peak ratio values were generated using the MATLAB^® 7.4 program (The MathWorks, Inc., Natick, MA, USA) with a precision of 1×10⁻⁴. The algorithm templates are available in the appendix 1.

2.5. α-Helical character curves

To generate the α-helical character curves, different sequences of ACh EC₅₀ values were partitioned as a squared triangle to form the sliding windows of different sizes. The number of sliding windows was determined using a triangular number equation; number of sliding windows = n(n+1)/2, where n is the number of values in the sequence. The partitions of sequences, as triangular numbers, satisfy the condition that the sub-sequences generated should be unique and also follow the consecutive order of the original sequences. The FT power spectra generated from different sliding windows were evaluated to determine the percent of FT power spectra per sliding window size that fulfilled two characteristic parameters of α-helical secondary structures: (i) peak ratio > 2 and (ii) prominent peak inside several frequency intervals such as 102.9° ≤ prominent peak ≤ 97.3° for 3.5-3.7 periodicities; 105.9° ≤ prominent peak ≤ 94.7° for 3.4-3.8 periodicities; 109.1° ≤ prominent peak ≤ 92.3° for 3.3-3.9 periodicities; or 112.5° ≤ prominent peak ≤ 90° for 3.2-4.0 periodicities. The percent of the FT power spectra that fulfilled the aforementioned parameters were plotted as a function of sliding window size to generate α-helical character curves of the different frequency intervals (see Fig. 1 K-O). For instance, a value of 100% α-helical character for a sliding window size of 12 residues implies that each one of the seven FT power spectra (see Fig. 1 K; blue curve), which were generated from seven partitions composed of 12 consecutive and different values, has a peak ratio value > 2 and a prominent peak maximum inside the range 90°-112.5°. In this example, the sliding window size of 12 values was moved seven times along a sequence of 18 values in total to generate the seven different partitions that were used to generate the seven FT power spectra (see Appendix 2; Table A2).

3. Results and discussion

In this study, we revisited the reported TrpScanM from five LETMDs (αM4, βM3, γM4, and two αM3 domains) of two different AChR species (Table 1). The raw data of these studies, which predicted helical structures with diverse periodicities and packing arrangements for the LETMDs [1-5], were used to generate the FT power spectra and the α-helical character curves. By coupling FT to TrpScanM, we achieve a more reliable prediction for secondary structures of the LETMDs and provide initial support of this valuable alternative tool to the future scanning mutagenesis studies.

Table 1.

Amino acid sequences of the studied AChR LETMDs.

AChR type	Sequence																		Ref.
αM3 Muscle-type	L	F	T	M	V	F	V	I	A	S	I	I	I	T	V	I	V	I	[1]
αM3 Torpedo	M	L	F	T	M	I	F	V	I	S	S	I	I						[3]
αM4 Torpedo	M	L	I	C	I	I	G	T	V	S	V								[2]
βM3 Torpedo	R	Y	L	M	F	I	M	I	L	V	A	F	S	V	I				[4]
γM4 Torpedo	C	F	W	I	A	L	L	L	F	S	I	G							[5]
Position	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18

3.1. Tryptophan-periodicity profiles of the αM4, βM3, γM4, and two αM3 domains

We used TrpScanM to predict the secondary structures and packing arrangements of the LETMDs. The periodic patterns of the functional consequences due to the tryptophan substitutions were displayed in the TrpPPs (Fig. 1 A-E). The TrpPPs were plotted with ACh EC₅₀ values derived from dose-response curves of the mutations generated in the AChR LETMDs [1-5]. The TrpPPs, which have been previously reported, display different oscillation patterns and different frequencies, indicating that LETMDs form helical structures with different periodicities and different helical packings. These findings have been supported by a refined structure of the Torpedo marmorata nicotinic acetylcholine receptor at 4 Å resolution determined by cryo-electron microscopy method [26].

3.2. Fourier transform power spectra of the αM4, βM3, γM4, and two αM3 domains

Generally, the discrete Fourier transform analysis is used for converting a sequence of values into a frequency spectrum and thus, it may be used to detect periodic variations in the sequence. Therefore, we coupled FT to TrpScanM to estimate mean periodicities and peak ratios of the sequences of ACh EC₅₀ values of the LETMDs that are displayed in the TrpPPs (Fig. 1 A-E). Using FT equation (Eq. 2), the sequences of ACh EC₅₀ values were decomposed into multiple peaks with different frequencies and abundances at the FT power spectra, suggesting that TrpPPs may be divided as well into several periodicities with diverse oscillation patterns (Fig. 1 F-J). The similarities in the periodicity values from the mean periodicities determined by rotation angle of the peaks and the mean periodicities of the TrpPPs reveal that FT supports and validates TrpScanM data (see Table 2). Interestingly, the prominent peaks of the Torpedo αM3 and βM3 AChRs were not found in the expected vicinity of the rotation angle indicated by the mean periodicities of their TrpPPs. The unexpected location of these prominent peaks could be due to the contribution of anomalous oscillations in their TrpPPs. For instance, the anomalous amplitudes displayed by the values in the 278 and 284-287 positions in the TrpPPs (Fig. 1 B and D, respectively), have considerable weight on the fitting of the sequences of values, causing a bias on the abundance of the peaks. Therefore, these anomalous oscillations populate peaks at frequencies which are not characteristic of the periodicity of an α-helical secondary structure. A notorious example of this is the abovementioned value in the 278 position. The value in the 278 position contributes extensively to delocalizing the prominent peak from the α-helical frequency intervals (see Appendix 2; Fig. A1 A, B, and D). However, this contribution is not reflected in the FT power spectra generated from sub-series (partitions) that do not bear the value of the 278 position (see Appendix 2; Fig. A1 C, E, and F).

Table 2.

Secondary structure parameters of AChR LETMDs determined by TrpPPs and FT power spectra.

		TrpPPs		FT power spectra
AChR type	No residues	Periodicity	Expected rotation angle	Rotation angle	Peak ratio	Mean periodicity
		residues/turn	Degree	degree		residues/turn
αM3 Muscle-type	18	3.24 ± 0.70	111.11	102.25	2.94	3.52
αM3 Torpedo	13	3.17 ± 1.04	113.56	115.00	0.53	3.13
αM4 Torpedo	11	3.28 ± 0.74	109.76	100.76	3.15	3.57
βM3 Torpedo	15	2.61 ± 0.74	137.93	138.06	0.75	2.61
γM4 Torpedo	12	3.19 ± 0.45	112.85	108.88	2.67	3.31

Given values correspond to analysis performed on the entire sequence of ACh EC₅₀ values from the AChR LETMDs. Periodicities of the TrpPPs are given as mean ± SD. Expected rotation angles of the TrpPPs and the mean periodicities of the peaks that correspond to mean periodicities of the TrpPPs were calculated using periodicity (residues/turn) = 360°/rotation angle.

3.3. α-helical character curves of the αM4, βM3, γM4, and two αM3 domains

We used α-helical character curves as complementary tool to the prediction of secondary structure by TrpScanM. The peak ratio from FT power spectra has been used as a parameter of reliability for predicting α-helical structures, however, it is not enough for a clear prediction because the maximum of the prominent peak could be located outside the α-helical frequency interval (85° ≤ ω ≤ 115°) and yet have a peak ratio > 2. In order to avoid this problem and to make more reliable predictions of secondary structures, we have generated the α-helical character curves (Fig. 1 K-O). The α-helical character curves provide us a tracking quality map of structure predictions. The α-helical character curves of the muscle-type αM3 domain, and the Torpedo αM4 and γM4 domains show that the α-helical structures predicted by FT-TrpScanM method were more reliable than those of the Torpedo αM3 and βM3 domains because they maintain a level of 100% α-helical characters even while reducing the size of the sliding windows at different periodicity intervals. A level of 100% α-helical character indicates that all the FT power spectra, generated from TrpScanM data, for a given sliding window size and periodicity interval fulfill both parameters that characterize an α-helix structure (see “2. Material and methods”). The Torpedo αM3 and βM3 domains displayed low percents in the α-helical character curves, presumably due to two factors: (i) insufficient amount of tryptophan substitutions to predict an α-helix structure and/or (ii) the sequence of values predicted a mixture of α- and 3₁₀-helix structures or a 3₁₀-helix structure. The size of the smallest sliding window displaying a level of 100% α-helical character can be considered indicative of the minimum number of consecutive tryptophan substitutions necessary to predict reliable α-helix structures at a given periodicity interval. For instance, the amount of 12 residues is suitable to predict a reliable α-helical structure that would have periodicities between 3.2 and 4.0 residues per turn (Fig. 1 K; blue curve), whereas in the Fig. 1 L more residues are required to predict a reliable α-helix structure using the studied periodicity intervals (Appendix 2; Table A1 and A2). Also, from the α-helical character graphs, it is evident that the prediction of extremely reliable α-helical structures requires shorter periodicity intervals and larger sliding windows. In addition, the predictions of the LETMDs could be ranked according to the following order: αM3 muscle-type > αM4 Torpedo ≈ γM4 Torpedo > αM3 Torpedo >> βM3 Torpedo through the use of the α-helical character curves. In essence, the quality of structure predictions by TrpScanM could be examined by α-helical character curves at different periodicity intervals.

4. Conclusions

FT-TrpScanM may be a useful tool for predicting reliable secondary structures of membrane protein LETMDs, shedding light into their overall spatial orientation. The α-helical character curves may be used to fingerprint the quality of structure predictions and determine the minimum of substitutions required for reliable structure predictions. Finally, this work corroborates the predictions from previous TrpScanM studies, demonstrates that similar results could have been reached with even fewer substitutions and encourages future utilization of FTTrpScanM as a means of predicting the secondary structure of LETMDs.

Abbreviations

AChR

acetylcholine (ACh) receptor

FT

Fourier transform

FT-TrpScanM

Fourier transform coupled to tryptophan-scanning mutagenesis

LETMDs

lipid-exposed transmembrane domains

TrpPPs

tryptophan-periodicity profiles

TrpScanM

tryptophan-scanning mutagenesis

APPENDIX 1

The script 1 of the algorithm template to plot the FT power spectra, calculate the peak ratios values and determine the maximum of the prominent peaks using the MATLAB^® program with a precision of 1×10⁻⁴is located below. This script is designed to use with the Microsoft Office Excel program.

%------------------------------------------------------------------------------------------------------------------

function[]=FOURIERTRANSFORMRESULTS(DATAFILENAME,DATARANGE,STORAGE FILE)

clc;

dirtemp=cd;FILENAME=strcat(cd,'\',STORAGEFILE);

data=xlsread(strcat(cd,'\',DATAFILENAME),DATARANGE);

n=length(data);N=n*(n+1)/2;K=cell(n-1,1);

[omega p]=fftspectra(data');T=[omega'p'];MM=length(omega);

for j=1:n-1

[T1]=windowareafft(data',j);K(j)={T1};

end

DK=[{'Window Size'};{'Average'};{'Peak Ratio'};{'Max omega'};{'P(Max omega)'}];

HK=cell2mat(K);[a b]=size(HK);H=cell2mat(K);

for jj=2:n

C1(jj-1)=length(find(H(:,4)<=360/3.5&H(:,4)>=360/3.7&

H(:,3)>=2&H(:,1)==jj))/length(find(H(:,1)==jj));

C2(jj-1)=length(find(H(:,4)<=360/3.4&H(:,4)>=360/3.8&

H(:,3)>=2&H(:,1)==jj))/length(find(H(:,1)==jj));

C3(jj-1)=length(find(H(:,4)<=360/3.3&H(:,4)>=360/3.9&

H(:,3)>=2&H(:,1)==jj))/length(find(H(:,1)==jj));

C4(jj-1)=length(find(H(:,4)<=360/3.2&H(:,4)>=360/4.0&

H(:,3)>=2&H(:,1)==jj))/length(find(H(:,1)==jj));

end

Tabla=[[2:n]' C1' C2' C3' C4'];[c d]=size(Tabla);

DKTabla=[{'Window Size'};{'3.5 - 3.7'};{'3.4 - 3.8'};{'3.3 - 3.9' };{'3.2 - 4.0'}];

xlswrite(FILENAME,T,strcat('A2:B',num2str(MM+1)));

xlswrite(FILENAME,[{'omega'};{'P(omega)'}]','A1:B1');

xlswrite(FILENAME,DK','D1:H1');

xlswrite(FILENAME,HK,strcat('D2:H',num2str(a+1)));

xlswrite(FILENAME,DKTabla','J1:N1');

xlswrite(FILENAME,Tabla,strcat('J2:N',num2str(c+1)));disp('Finish');

end

function[omega,P]=fftspectra(data)

omega=0:.0001:180;n=length(data);dbar=sum(data)/n;

h=data-dbar;P=(h*cosd([1:n]'*omega)) ^2+(h*sind([1:n]'*omega)) ^2;

end

function[M]=windowareafft(v,k)

n=length(v);m=n-k+1;M=zeros(n-m+1,5);P=partition(n,m);

for i=1:(n-m+1)

data=v(P(i,:));

if ~(sum(data~=0)==0)

[omega p]=fftspectra(data);

Area=6*trapz(omega(find(omega>=85&omega<=115)),

p(find(omega>=85&omega<=115)))/trapz(omega,p);

Average=mean(data);M(i,:)=[m Average Area omega(find(p==max(p))) max(p)]

else

M(i,:)=[m 0 0 0 0];end;end;

function[H]=partition(n,m)

Residue=1:n;t=1;

while t<=(n-m)+1

tmp=(1:m)+t-1;H(t,:)=Residue(tmp);t=t+1;

end;end;end

%------------------------------------------------------------------------------------------------------------------

The script 2 for the directory of the files is located below. All files should be inside a folder. Replace “Put you data file name” and “Put you storage file name” with the desired data file name and storage file name, respectively. The data should be placed and saved in a Microsoft Office Excel file. The data should be along the column B beginning with the cell B2. The number signs “##”should be replaced with the number of the cell from the last data.

%------------------------------------------------------------------------------------------------------------------

DATAFILENAME='Put you data file name.xls';

DATARANGE='B2:B##';

STORAGEFILE='Put you storage file name.xls';

FTRESULTS(DATAFILENAME,DATARANGE,STORAGEFILE)

%------------------------------------------------------------------------------------------------------------------

APPENDIX 2

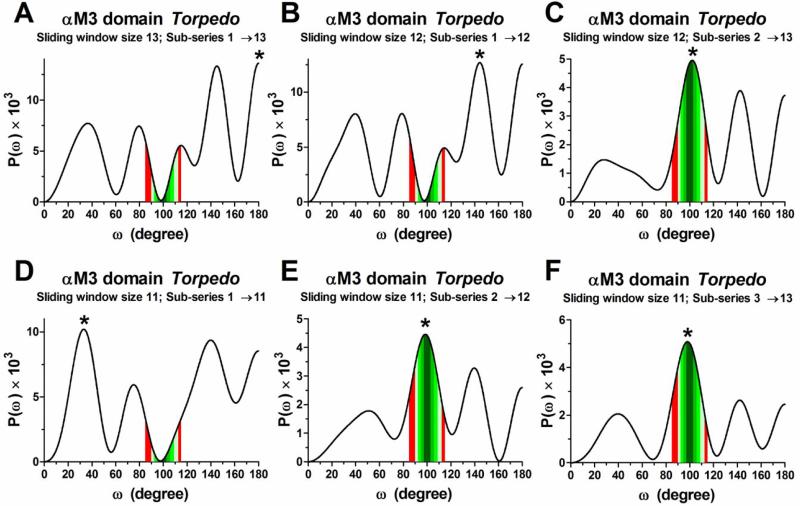
In this appendix, we illustrate extracts of the Fourier transform power spectra data from αM3 Torpedo AChR and the α-helical character data from αM3 Torpedo and αM3 Muscle-type AChRs for a clear comprehension of the FT-TrpScanM method. In Fig. 1A, we show the FT power spectra of the sliding window sizes 11 through 13. When the value of the 278 position is included on the partition to generate a FT power spectrum (i.e. the sub-series 1→13, 1→12, and 1→11), the prominent peak is not localized inside α-helical frequency intervals and neither into peak ratio interval (see Fig. A1 A, B, and D). In Table A1, we show the contribution of the value in the 278 position of the αM3 Torpedo to the α-helical character curves. The contribution of the value in the 278 position to the α-helical character curves at the sliding window sizes of 11 to 13 residues is shown by the sub-series 1→13, 1→12, and 1→11 (see red shading boxes; Table A1). In these sub-series the value of the 278 position is included to generate their respective FT power spectrum. From these FT power spectra, it is determined the peak ratio value and rotation angle of the prominent peak resulting on FT power spectra not characteristics of an α-helical secondary structure (see No=0; Table A1). Hence, these sub-series do not contribute positively to α-helical character from their sliding window size. Overall, the anomalous oscillations in the TrpPPs take more notoriety in sliding window sizes that are composed of few sub-series (e.g. the sub-series 1→13, 1→12, and 1→11 from αM3 Torpedo; see Table A1) because these sub-series individually represent a portion larger than in sliding windows of many sub-series (i.e. the increase in the number of sub-series decrease the proportion that is contributed by each sub-series in the sliding window). In the Table A2, we show the minimum number of substitutions that is required to predict a reliable α-helical secondary structure at a level of 100% α-helical character. The αM3 Muscle-type data show that to predict an α-helical secondary structure of mean periodicities between 3.2 and 4.0 residues per turn at a level of 100% α-helical character at least 12 substitutions are necessary, while for mean periodicities between 3.3 and 3.9, 3.4 and 3.8, or 3.5 and 3.7 at least 13, 14, or 15 substitutions, respectively, are necessary (see red shading boxes; Table A2).

Note: Sub-series are partitions from the sequence of values. Out or In represents wheather the localization of the maximum of the prominent peak is outside or inside of the frequency interval. 0=No or 1=Yes represent if the FT power spectrum generated from the sub-series fulfill the two parameters characteristic of an α-helical secondary structure: i) Peak ratio value > 2 and ii) Localization of the maximum of the prominent peak is inside frequency interval. 0=No represents that one of the two parameters is not fulfilled. 1=Yes represents that both parameters are fulfilled (see gray shading boxes; Table A1 and A2). % is the percent of α-helical character per sliding window. % represents the percent of sub-series per sliding window that fulfill the characteristic parameters of an α-helical structure.

Figure 1A. Extract of the Fourier transform power spectra data from αM3 Torpedo AChR.

(A-F) are FT power spectra generated from sub-series 1→13, 1→12, 2→13, 1→11, 2→12, and 3→13 of the αM3 Torpedo data. Asterisks indicate the localization of the prominent peaks. Different intensities of green shadings demarcate the different frequency intervals; dark green (97.3°-102.9°); green; (94.7°-105.9°); bright green (92.3°-109.1°); light green (90.0°-112.5°). Red shadings demarcate the region 85° ≤ ω ≤ 115° that is used to calculate peak ratio values.

Table A1.

Extract of the α-helical character data from αM3 Torpedo AChR.

Sliding window	Fourier transform power spectra			α-Helical character curves
	Partition	Peak ratio	Prominent Peak	Periodicity interval (3.5-3.7)			Periodicity interval (3.4-3.8)			Periodicity interval (3.3-3.9)			Periodicity interval (3.2-4.0)
	Sub series		Rotation angle	Frequency interval (97.3°-102.9°)			Frequency interval (94.7°-105.9°)			Frequency interval (92.3°-109.1°)			Frequency interval (90.0°-112.5°)
Residue	Position		Degree	Out or In	0=No 1=Yes	%	Out or In	0=No 1=Yes	%	Out or In	0=No 1=Yes	%	Out or In	0=No 1=Yes	%
13	1→13	0.53	180	Out	0	0	Out	0	0	Out	0	0	Out	0	0
12	1→12	0.50	144.22	Out	0	50	Out	0	50	Out	0	50	Out	0	50
12	2→13	2.12	102.17	In	1		In	1		In	1		In	1
11	1→11	0.28	33.18	Out	0	66	Out	0	66	Out	0	66	Out	0	66
11	2→12	2.06	98.64	In	1		In	1		In	1		In	1
11	3→13	2.36	98.17	In	1		In	1		In	1		In	1
10	1→10	0.35	130.15	Out	0	0	Out	0	25	Out	0	25	Out	0	25
10	2→11	1.60	99.36	In	0		In	0		In	0		In	0
10	3→12	2.28	95.09	Out	0		In	1		In	1		In	1
10	4→13	1.88	94.40	Out	0		Out	0		In	0		In	0
9	1→9	0.29	134.08	Out	0	0	Out	0	0	Out	0	0	Out	0	20
9	2→10	2.57	110.58	Out	0		Out	0		Out	0		In	1
9	3→11	1.83	93.54	Out	0		Out	0		In	0		In	0
9	4→12	1.71	88.69	Out	0		Out	0		Out	0		Out	0
9	5→13	1.69	154.98	Out	0		Out	0		Out	0		Out	0

Table A2.

Extract of the α-helical character from αM3 Muscle-type AChR.

Sliding window	Fourier transform power spectra			α-Helical character curves
	Partition	Peak ratio	Prominent Peak	Periodicity interval (3.5-3.7)			Periodicity interval (3.4-3.8)			Periodicity interval (3.3-3.9)			Periodicity interval (3.2-4.0)
	Sub series		Rotation angle	Frequency interval (97.3°-102.9°)			Frequency interval (94.7°-105.9°)			Frequency interval (92.3°-109.1°)			Frequency interval (90.0°-112.5°)
Residue	Position		Degree	Out or In	0=No 1=Yes	%	Out or In	0=No 1=Yes	%	Out or In	0=No 1=Yes	%	Out or In	0=No 1=Yes	%
18	1→18	2.94	102.25	In	1	100	In	1	100	In	1	100	In	1	100
17	1→17	2.75	103.24	Out	0	50	In	1	100	In	1	100	In	1	100
17	2→18	3.08	101.26	In	1		In	1		In	1		In	1
16	1→16	2.75	101.82	In	1	100	In	1	100	In	1	100	In	1	100
16	2→17	2.90	102.11	In	1		In	1		In	1		In	1
16	3→18	3.37	98.02	In	1		In	1		In	1		In	1
15	1→15	2.51	102.31	In	1	100	In	1	100	In	1	100	In	1	100
15	2→16	2.93	100.41	In	1		In	1		In	1		In	1
15	3→17	3.11	98.69	In	1		In	1		In	1		In	1
15	4→18	3.23	98.94	In	1		In	1		In	1		In	1
14	1→14	2.62	105.38	Out	0	40	In	1	100	In	1	100	In	1	100
14	2→15	2.70	100.60	In	1		In	1		In	1		In	1
14	3→16	3.18	96.66	Out	0		In	1		In	1		In	1
14	4→17	2.91	100.14	In	1		In	1		In	1		In	1
14	5→18	3.32	95.99	Out	0		In	1		In	1		In	1
13	1→13	2.31	107.10	Out	0	16	Out	0	66	In	1	100	In	1	100
13	2→14	2.85	103.59	Out	0		In	1		In	1		In	1
13	3→15	2.80	94.40	Out	0		Out	0		In	1		In	1
13	4→16	2.95	97.49	In	1		In	1		In	1		In	1
13	5→17	2.97	96.43	Out	0		In	1		In	1		In	1
13	6→18	3.23	95.80	Out	0		In	1		In	1		In	1
12	1→12	2.30	109.32	Out	0	14	Out	0	57	Out	0	86	In	1	100
12	2→13	2.54	104.32	Out	0		In	1		In	1		In	1
12	3→14	2.97	98.12	In	1		In	1		In	1		In	1
12	4→15	2.52	94.42	Out	0		Out	0		In	1		In	1
12	5→16	3.02	92.65	Out	0		Out	0		In	1		In	1
12	6→17	2.91	96.29	Out	0		In	1		In	1		In	1
12	7→18	3.23	96.43	Out	0		In	1		In	1		In	1
11	1→11	2.26	109.41	Out	0	25	Out	0	50	Out	0	75	In	1	87
11	2→12	2.53	106.47	Out	0		Out	0		In	1		In	1
11	3→13	2.59	96.69	Out	0		In	1		In	1		In	1
11	4→14	2.66	100.66	In	1		In	1		In	1		In	1
11	5→15	2.59	88.16	Out	0		Out	0		Out	0		Out	0
11	6→16	3.01	92.61	Out	0		Out	0		In	1		In	1
11	7→17	2.90	97.37	In	1		In	1		In	1		In	1
11	8→18	2.87	95.09	Out	0		In	1		In	1		In	1
10	1→10	2.09	112.6	Out	0	33	Out	0	44	Out	0	77	Out	0	77
10	2→11	2.52	106.48	Out	0		Out	0		In	1		In	1
10	3→12	2.59	101.2	In	1		In	1		In	1		In	1
10	4→13	2.16	100.56	In	1		In	1		In	1		In	1
10	5→14	2.80	92.71	Out	0		Out	0		In	1		In	1
10	6→15	2.44	87.23	Out	0		Out	0		Out	0		Out	0
10	7→16	3.01	93.74	Out	0		Out	0		In	1		In	1
10	8→17	2.42	95.86	Out	0		In	1		In	1		In	1
10	9→18	3.35	101.19	In	1		In	1		In	1		In	1
9	1→9	1.79	112.61	Out	0	30	Out	0	30	Out	0	40	Out	0	70
9	2→10	2.37	109.8	Out	0		Out	0		Out	0		In	1
9	3→11	2.39	100.72	In	1		In	1		In	1		In	1
9	4→12	2.16	107.3	Out	0		Out	0		In	1		In	1
9	5→13	2.22	82.29	Out	0		Out	0		Out	0		Out	0
9	6→14	2.71	92.2	Out	0		Out	0		Out	0		In	1
9	7→15	2.44	88.03	Out	0		Out	0		Out	0		Out	0
9	8→16	2.46	90.79	Out	0		Out	0		Out	0		In	1
9	9→17	2.86	102.83	In	1		In	1		In	1		In	1
9	10→18	2.80	98.15	In	1		In	1		In	1		In	1