Abstract
Purpose:
Accurate segmentation and quantification of liver metastases on CT images are critical to surgery/radiation treatment planning and therapy response assessment. To date, there are no reliable methods to perform such segmentation automatically. In this work, the authors present a method for semiautomatic delineation of liver metastases on contrast-enhanced volumetric CT images.
Methods:
The first step is to manually place a seed region-of-interest (ROI) in the lesion on an image. This ROI will (1) serve as an internal marker and (2) assist in automatically identifying an external marker. With these two markers, lesion contour on the image can be accurately delineated using traditional watershed transformation. Density information will then be extracted from the segmented 2D lesion and help determine the 3D connected object that is a candidate of the lesion volume. The authors have developed a robust strategy to automatically determine internal and external markers for marker-controlled watershed segmentation. By manually placing a seed region-of-interest in the lesion to be delineated on a reference image, the method can automatically determine dual threshold values to approximately separate the lesion from its surrounding structures and refine the thresholds from the segmented lesion for the accurate segmentation of the lesion volume. This method was applied to 69 liver metastases (1.1–10.3 cm in diameter) from a total of 15 patients. An independent radiologist manually delineated all lesions and the resultant lesion volumes served as the “gold standard” for validation of the method’s accuracy.
Results:
The algorithm received a median overlap, overestimation ratio, and underestimation ratio of 82.3%, 6.0%, and 11.5%, respectively, and a median average boundary distance of 1.2 mm.
Conclusions:
Preliminary results have shown that volumes of liver metastases on contrast-enhanced CT images can be accurately estimated by a semiautomatic segmentation method.
Keywords: image segmentation, marker-controlled watershed, liver metastasis, CT image
1. INTRODUCTION
The liver is the second most common site for metastatic spread after the lymph nodes.1–5 Nearly, all primary tumor sites can deposit metastases in the liver due to its rich and dual blood supply. For instance, about 50% of colorectal cancer, the third most common type of cancer and the second most common cause of cancer death in the USA, will eventually develop liver metastases.3,4
CT is routinely performed in patients with liver cancer; tumor size measured on CT images is critical for surgery/therapy planning, disease monitoring, and therapy response assessment. Despite lacking accuracy and reproducibility, liver metastases are measured manually by radiologists in clinical settings. This is particularly impractical when dealing with tumor volumes.
A few studies have been reported on the development of semiautomated/automated segmentation methods for liver lesions on contrast-enhanced CT images.6–15 Williams et al. made use of edge detection and linking techniques to delineate the liver tumor boundary on CT images.6 Liver CT images can often be noisy and this method was known to be sensitive to noise. In Refs. 7, 8, and 10, some models such as ellipse, ellipsoid, and alpha shape were employed to extract and highlight liver lesions on CT images. However, these models did not always conform to actual growth patterns of the liver metastases. Chemouny et al. gave a tool for liver and hepatic tumors and location and volumetry in 3D space.9 Zhao et al. developed a shape-constrained region-growing method for the delineation of liver metastases.11 Experimentally determined parameters used in this algorithm need to be validated if the algorithm is applied to the liver images acquired using different imaging protocols. Hong et al. proposed an algorithm combining an adaptive thresholding, a contour correction, and a fuzzy C-means clustering technique for automated identification and segmentation of tumor candidates in the liver.12 The algorithm’s assumption on tumor intensities, i.e., tumor intensities should be either greater or lower than those of the liver parenchyma, may not always hold true. Another fuzzy C-means algorithm for volumetric analysis of liver metastases on CT images proposed by Yim et al.13 required manual determination of a mask including the target lesion and an approximately 0.5 cm margin surrounding the lesion. Bellon et al. developed a semiautomated region partitioning method with watershed model.14 Yim and Foran compared the segmentation results obtained by watershed, active contour, and dual-scale active contour for hepatic metastases on CT images and concluded that the dual-scale active contour method was promising.15 For the watershed model, because of the oversegmentation that is associated with this model, the algorithm demanded manual operations to correct the results, especially the results of heterogeneous lesions. For the active contour method, the requirement on the initial contour was strict, i.e., it should be as close as possible to the target boundary.
In this paper, we propose a method, based on marker-controlled watershed transformation, to segment liver metastases on contrast-enhanced volumetric CT images. The markers, i.e., the internal and the external markers, introduced to the conventional watershed method can resolve the oversegmentation problem. Marker-controlled watershed transformation is a well-known segmentation method based on watershed transformation and morphological reconstruction.16–18 It has been widely applied due to its ability to detect the target boundary allocated between the markers (i.e., an internal marker that is a region inside the target object and an external marker that is a region contained within the background), even if there is no clearly defined edge between the target and its surroundings.16–21 Successful use of marker-controlled watershed transformation depends on successful determination of the two markers, which was the focus of this work. Our method requires manual selection of a seed region-of-interest (ROI) inside the liver metastasis on one slice. It can then automatically determine both the internal and the external markers for automated delineation of the lesion contours on all lesion slices. Details of the method will be illustrated in Sec. 2, followed by Secs. 3 and 4.
2. METHODS
Liver lesions that are metastasized from colorectal cancer often possess relatively hypoattenuated values compared to liver parenchyma on contrast-enhanced CT images that are acquired during the portal venous phase. Difficulty arises in the segmentation when lesion’s attenuations are heterogeneous or when a lesion resides at the edge of the liver where attenuations of the surrounding tissues may overlap with those of the lesion. Our marker-controlled watershed algorithm for segmentation of liver metastasis on volumetric CT images consists of the following three steps: (1) estimation of the dual threshold values based upon a manually chosen seed ROI on a reference slice, (2) determination of the internal and external makers with the estimated threshold values, and (3) segmentation of the 3D liver metastasis. All these steps are shown in Figs. 1–4 and described in detail.
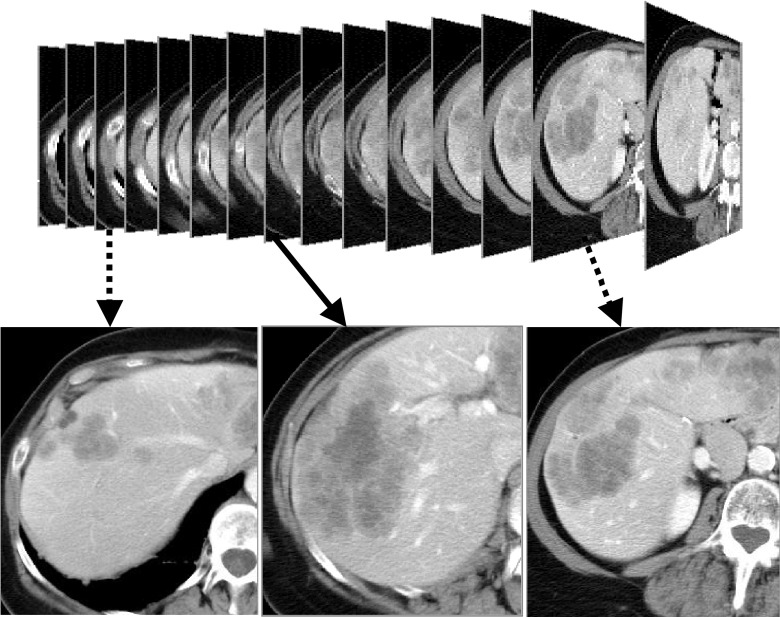
FIG. 1.
Selection of the reference slice from volumetric liver metastasis CT images.
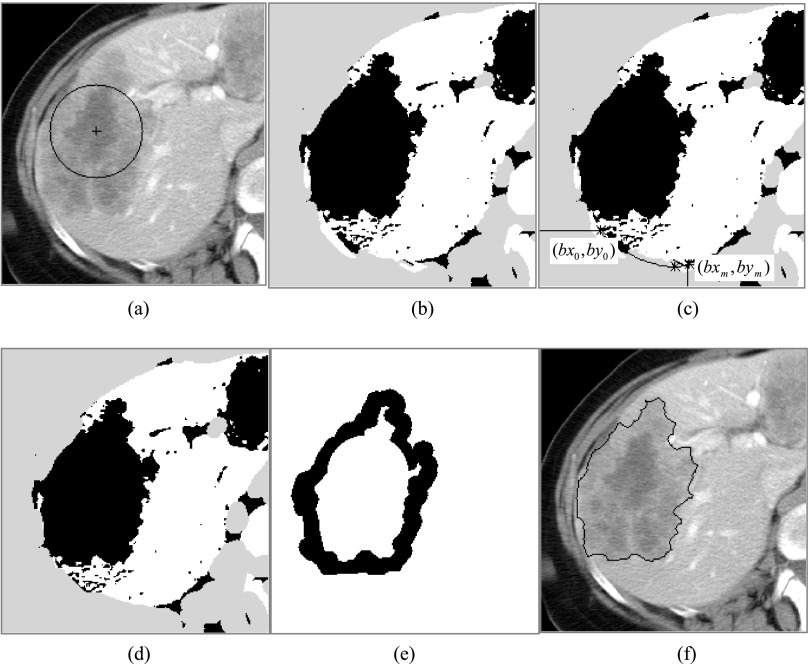
FIG. 2.
Rough segmentation of the target liver metastasis on the selected 2D reference slice. (a) The given circle; (b) the threshold result, in which the white, gray, and black represent the high-intensity, low-intensity, and middle-intensity regions, respectively; (c) illustration of deleting the rib bones; (d) the threshold result of deleting the rib bones; (e) the internal and the external markers; (f) the marker-controlled watershed segmentation results.
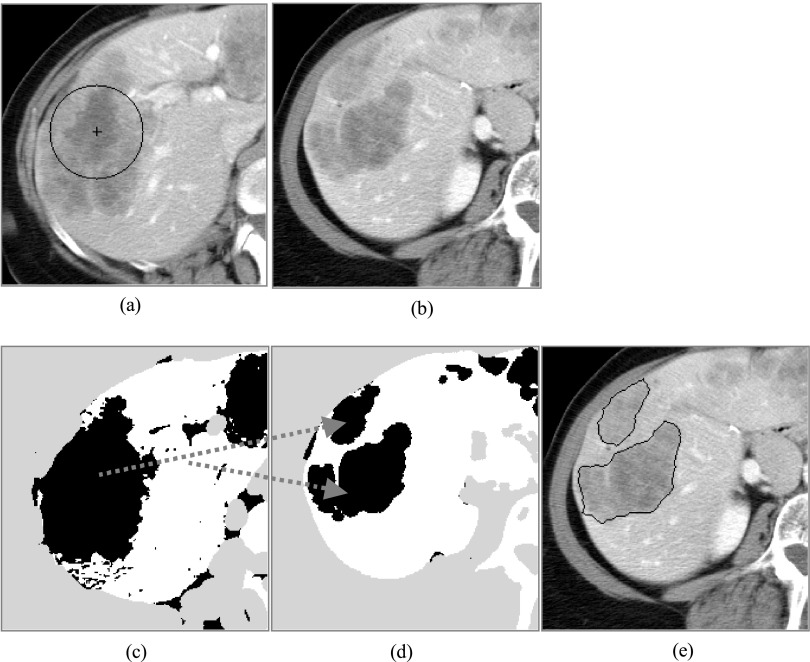
FIG. 3.

Histogram used to estimate the dual threshold values for the 3D target liver metastasis. (a) The roughly delineated contour and the expanded contour overlapped on the 2D reference slice; (b) the intensity histogram of the pixels inside the roughly delineated contour; (c) the intensity histogram of the pixels between the roughly delineated contour and the expanded contour; (d) the combined intensity histogram.
FIG. 4.
Segmentation of the 3D target liver metastasis. (a) The selected reference slice; (b) the example slice, in which the target liver metastasis is connected with that in the reference slice in 3D space; (c) and (d) are the threshold images of (a) and (b), and the arrows represent the 3D connectivity; (e) the segmentation result of (b).
2.A. Estimation of the threshold values
For a segmentation task, it is acceptable that a lesion is identified manually (with a single click-and-drag of the computer mouse) by drawing a circle inside the lesion on the reference slice (the slice where the segmentation starts). Such an initiation can not only allocate the lesion but also provide information about intensity distribution of the lesion on that slice, assisting in determination of the internal and the external markers for segmenting the lesion on the reference slice.
2.A.1. Estimation of dual threshold values for the lesion on reference slice
The reference slice should be in the middle of the consecutive CT slices containing the lesion so that the lesion area on the slice is relatively large (Fig. 1). Meanwhile, a seed ROI should contain as much heterogeneous information (if the lesion is heterogeneous) as possible [Fig. 2(a)]. In this way, the intensity distribution estimated based upon the ROI should approximately represent that of the lesion on the slice. In order to determine the markers for the lesion on the reference slice, a threshold technique is used.
Our data show that the intensity of a liver lesion follows Gaussian distribution. Thus, two threshold values (i.e., a lower value Tlower and a higher value Tupper) that roughly span the entire range of the lesion intensity can be estimated with the following Eqs. (1) and (2):
| (1) |
| (2) |
where Imean is the average intensity and Istd is the standard deviation calculated using the pixels in the lesion ROI. The parameters w1 and w2 are weighting factors which are constant. They had the experimentally determined values of 2.0 and 1.732 in the present paper.
2.A.2. Determination of the markers for the lesion on reference slice
With the estimated dual thresholds, the reference image can be divided into three regions: (a) the low-intensity regions [gray areas in Fig. 2(b)] in which pixels’ intensities are lower than Tlower, (b) the high-intensity regions [white areas in Fig. 2(b)] in which pixels’ intensities are higher than Tupper, and (c) the intermediate-intensity regions [gray areas in Fig. 2(b)] in which pixels’ intensities are between Tlower and Tupper.
Considering that the right ribs may have an influence on the following steps if the lesion is located at the periphery of the liver and connects with right intercostal muscles, we forcedly classified the region including the right ribs into the low-intensity regions. In this presented paper, we first use threshold technique (the threshold value is fixed 180 HU) to extract the bones in the right part of the body. Then, we find the point nearest to the center of the given ROI for every bone. Sort these points from the front to the back of the body in turns and according to the distance of these points to the center of the given ROI, we can interpolate the other points between them. Let the positions of the interpolated points be {(bx0, by0), (bx1, by1), …, (bxm, bym)}. The region closed by polygon {(0, 0), (0, by0), (bx0, by0), …, (bxm, bym), (bxm, 0), (0, 0)} is the region that needs to be forcedly classified into the low-intensity regions [Figs. 2(c) and 2(d)].
One area from the intermediate-intensity regions that has the largest intersection with the given circular ROI is chosen as an area-of-interest (AOI). Holes inside the AOI are filled prior to further processing. The boundary pixels of the AOI can be grouped into two sets: one consisting of the pixels lying between the AOI and the high-intensity regions and the other consisting of the pixels between the AOI and the low-intensity regions. In the former set, almost all of the pixels are located in the near of or at the edge of the lesion because of the hyperintensity values of the normal liver parenchyma captured during the portal venous phase. In the latter set, pixels can belong to different structures such as muscle and fat if the lesion resides at the periphery of the liver that is adjacent to the chest wall.
Based upon this analysis, a strategy is developed to obtain the internal and the external markers to restrict the search area for the lesion boundary on the reference slice. The external marker is obtained by dilating the AOI with a certain filter width (8 pixels in this work) and taking the outside region of the expanded AOI. Then, the boundary points of the nondilated AOI that neighbor the normal liver parenchyma are connected, creating a new area. This area will be eroded with a certain width (5 pixels in this work) to obtain the internal marker.
2.A.3. Rough segmentation of the target liver metastasis on the selected reference slice
The watershed transform treats the gray image as a topographic surface where light pixels are high and dark pixels are low. We flood the surface from its local minima. In order to prevent the merging of waters from different sources, dams must be built at certain points. These dams are called watersheds. The regions enclosed by the watersheds are water basins. In practice, the traditional watershed transform often produces heavy oversegmentation due to noise or local heterogeneity in the image. In order to solve this problem, marker-controlled watershed was proposed.22 In marker-controlled watershed transform, some markers are first defined. The marker inside the object is called internal marker and outside is called external maker. Once the internal and external markers are determined, a gray scale reconstruction algorithm22 is used to modify the gradient image (in this paper, the gradient image is obtained with the Sobel operator) to allow the local minima only occur in the regions of the two markers.22 Then, the traditional watershed transform can be applied to the modified gradient image to obtain the target lesion boundary in the belt between the internal and the external markers [Fig. 2(f)].
2.A.4. Estimation of the threshold values for the 3D target liver metastasis
After roughly segmenting the target liver metastasis on the selected reference slice, it seems that we can simply use the intensity inside the delineated contour to estimate the dual threshold values for the 3D target liver metastasis with the similar method in Sec. 2.A.1. Unfortunately, through lots of experiments, we find that while the estimated lower threshold value works well, the higher threshold often fails. In order to solve this problem, the iterative threshold selection method23 is used. Because the higher threshold is used to separate the target liver metastasis and the normal liver parenchyma, if we have a histogram only counting the intensities of the target liver metastasis and its surrounding normal liver parenchyma, we can utilize it to estimate the threshold with the iterative threshold selection method. This is also due to the attenuation difference between the liver metastasis and the normal liver parenchyma.
In order to construct a histogram counting only the intensities of the target liver metastasis and its surrounding normal liver parenchyma, we must first define their regions (Fig. 3). For the target liver metastasis, we directly use the rough segmentation result. For the surrounding normal liver parenchyma, we use some points outside and within a certain distance (for all our experiments, the distance is 10 pixels) of the delineated target liver metastasis. At the same time, the intensity of the points should be higher than the average intensity of the segmented target liver metastasis.
According to the intensity inside the segmented target liver metastasis and the constructed histogram, we can refine the dual threshold values: T3Dlower and T3Dupper for the target 3D liver metastasis with Eqs. (3) and (4),
| (3) |
| (4) |
where ITmean is the mean intensity and ITstd is the standard deviation in intensity of the segmented target liver metastasis on the selected 2D reference slice. w3 is a weighting parameter, which has a constant value of 2.5 in this paper. Toptimal is the threshold calculated by the iterative threshold selection method.
2.B. Determination of the markers for the target 3D liver metastasis
At present, the CT data scanned for the clinical application are still not isotropic. The resolution along the scanning axis is often several times to in-plane resolution. Thus, in the presented paper, we still deal with 3D data slice by slice. The fortunate thing is that we can automatically determine the range of the 3D data with 3D connectivity, rather than manually give the start and end slices. The other advantage of utilizing 3D connectivity is that the algorithm can effectively solve the branch problem for the 3D object.
Similarly, for 3D data, we first use the refined dual threshold values (T3Dlower and T3Dupper) to divide the entire 3D data into three classified regions: (a) the low-intensity regions, inside which the image intensities are lower than T3Dlower, (b) the middle-intensity regions, inside which the image intensities are between T3Dlower and T3Dupper, and (c) the high-intensity regions, inside which the image intensities are higher than T3Dupper. Then, we also use the same method to eliminate the influence of the right rib.
After that, we choose one 3D connected region from the middle-intensity regions, which has the largest common area with the circular ROI, and use it as a volume-of-interest (VOI). With VOI, we can easily determine those slices including the target lesion regions and the AOIs on each of them [Figs. 4(c) and 4(d)]. For every AOI on each slice, we use the same method described in Subsection 2.A.2 to determine the corresponding internal and external markers.
2.C. Segmentation of the target 3D hepatic lesion
Once all the corresponding internal and external markers are determined, we just need to use the method of Subsection 2.A.3 for every AOI on each slice [Fig. 4(d)]. All these operations will make up the segmentation for the target 3D liver metastasis.
3. EXPERIMENTS AND RESULTS
3.A. Imaging data
We retrospectively collected portal venous phase CT scans of 15 patients from a clinical trial database of patients with liver metastases. The CT imaging protocol used in the trial is listed in Table I. Retrospective Institutional Review Board (IRB) approval was received for the study. The CT images (LightSpeed QX/I, GE Medical Systems, Milwaukee, WI) were first retrieved from the hospital picture archiving and communication system (PACS) to our research PACS (rPACS) where the DICOM format images were stored with patient identification information deidentified. The images in the rPACS were then read for the automated segmentation and quantification analysis.
TABLE I.
Contrast-enhanced CT imaging protocol.
| Items | Parameters |
|---|---|
| Slice thickness | 7.5 mm |
| Table speed | HQ 11.25–15.0 mm/rotation |
| Coverage | 1 breath hold: from diaphragm domes to iliac crests |
| Time (s) | Unique to patient |
| Injection [(rate/time)/volume] | (2.5 cm3/s)/125 cm3 |
| Injection to scan delay | 70 s |
| Oral contrast | Yes |
3.B. Performance evaluation
The performance of a segmentation algorithm can be assessed by comparing the computer-generated contours to the “gold standard” contours, which generally are the contours drawn by human observers.24,25 In the present study, the gold standard was generated by an experienced radiologist who manually delineated the contours of all liver metastases without seeing the computer results. As discussed in Ref. 25, several quantitative measurements were calculated to measure the deviations of the computer results from the gold standard. These included the contour distance-based measurements such as average distance and Hausdorff distance between the computer-segmented contours and the radiologist-generated contours,25,27–29 as well as area/volume matching-based measurements such as the ratios of overlap, overestimation, and underestimation of the computer-segmented areas/volumes and the radiologist-generated areas/volumes.24–26 For convenience, all the measurement definitions used in this paper are rewritten as follows.
The average boundary distance and Hausdorff boundary distance are defined in Eqs. (5) and (6), respectively,
| (5) |
| (6) |
where the set of points A = {a1, a2, …, am} is the contour to be evaluated (e.g., the computer-generated contour in this work) and B = {b1, b2, …, bn} is the gold standard contour (e.g., the radiologist-generated contour in this work), each ai or bi is a point on the contours, and
| (7) |
is the distance from ai to the closest point on the contour B.
Let R_A and R_B be the set of points inside the contours to be evaluated and the gold standard contours, respectively, and the overlapped (overlap_ratio), overestimated (over_ratio), and underestimated (under_ratio) ratios can be defined as
| (8) |
| (9) |
| (10) |
where ∩ is the “AND” operator and ∪ is the “OR” operator.
To assess the reproducibility of the proposed method, which may be affected by variations in seed ROI placement, and the pairwise agreement between the radiologist and the computer, the concordance correlation coefficient (CCC)30 was used. The CCC quantifies reproducibility, taking into account both the correlation between two measurements and the deviation from the 45° line of the best-fit line in a plot of one measure by the other. Suppose that Yil and Yi2 are two measurements for the ith liver metastasis and that the Yil and Yi2 pairs are independent and follow a bivariate distribution with means μ1 and μ2 and covariance matrix,
Then, the CCC is defined as
| (11) |
The CCC has a few of advantages over other methods used to assess reproducibility: (1) it takes into account both accuracy and precision; (2) it is a nonparametric statistic and does not assume the data that follow a particular distribution (i.e., the data do not have to be normally distributed); (3) it easily accommodates clustered data.11 In the present paper, the CCC was calculated with the software MedCalc version 15.6.1 (https://www.medcalc.org).
3.C. Results and discussion
In order to validate the proposed method, we applied it to 69 liver metastases (size range, 1.1–10.3 cm in diameter) from 15 patients’ image data described in Sec. 3.A. Then, we asked an experienced radiologist to manually delineate the contours for all cases without seeing the computer-generated results. The deviation between the computer-generated and manually delineated contours was analyzed in detail.
The experiments demonstrated that almost all 69 liver metastases were successfully segmented using the proposed algorithm. Figures 5 and 6 show two segmentation results: one of the liver metastases is relatively heterogeneous (Fig. 5) and the other one is relatively homogenous (Fig. 6). These examples visually demonstrate the ability of our algorithm to accurately delineate the liver metastasis in volumetric CT images even when the liver metastasis is located at the periphery of the liver and/or the boundaries between the liver metastasis and the surrounding structures are unclear. The other advantage of the proposed method is that it deals with the branching problem by utilizing the connectivity in 3D space. Quantitative evaluation results are provided in Table II. The CCC between the volumes of the liver metastases defined by the computer-generated contours and the gold standard contours is 0.9976 (95% confidence interval: 0.9967–0.9983). The statistic data (1.2 mm for the median boundary distance and 82.3% for the median volume overlap percentage) indicate the accuracy of the proposed method for the segmentation of liver metastasis. By comparing the overestimated and underestimated ratios, we find that the algorithm seems to be prone to underestimation.
FIG. 5.
Segmentation results obtained with the proposed method. (a) The original images and the given circle (see the arrow). (b) The computer-generated segmentation results. (c) The radiologist’s manual results.
FIG. 6.
Segmentation results obtained with the proposed method. (a) The original images and the given circle (see the arrow). (b) The computer-generated segmentation results. (c) The radiologist’s manual results.
TABLE II.
Summary statistics for the performance of the proposed segmentation method based on the comparison of the computer segmentation results and the radiologist’s manual delineation results.
| Comparison items | Mean | Standard deviation | Minimum | Median | Maximum |
|---|---|---|---|---|---|
| Average distance (mm) | 1.3 | 0.7 | 0.3 | 1.2 | 3.7 |
| Hausdorff distance (mm) | 8.5 | 4.6 | 1.5 | 8.8 | 21.2 |
| Overlap ratio (%) | 81.4 | 4.9 | 70.4 | 82.3 | 90.5 |
| Overestimated ratio (%) | 7.5 | 5.3 | 1.1 | 6.0 | 21.9 |
| Underestimated ratio (%) | 12.6 | 4.8 | 5.5 | 11.5 | 28.7 |
The overlap ratio is a widely used method to evaluate the performance of image segmentation algorithms. From a visual inspection of segmented objects, radiologists agree that a volume nonoverlap of 30% is good, 30%–60% is acceptable, and 60% is poor.31 In Ref. 31, Jolly and Grady pointed out that for their algorithm, 90% of the segmented cases fell into the good to acceptable zone. For our method, all the segmented liver metastases fell into the good to acceptable zone. This may be because the method proposed in Ref. 31 is a general method, rather than specific for liver metastasis segmentation.
In Ref. 32, an intraobserver difference of 15.2% ± 7.7% was obtained for the volumes of 102 liver metastases in 45 patients. The mean overlap, overestimated ratio, and underestimated ratio of 81.4%, 7.5%, and 12.6% (Table II) of our method indicate that the difference between the computer-generated contours to the gold standard contours is similar to the intraobserver difference.
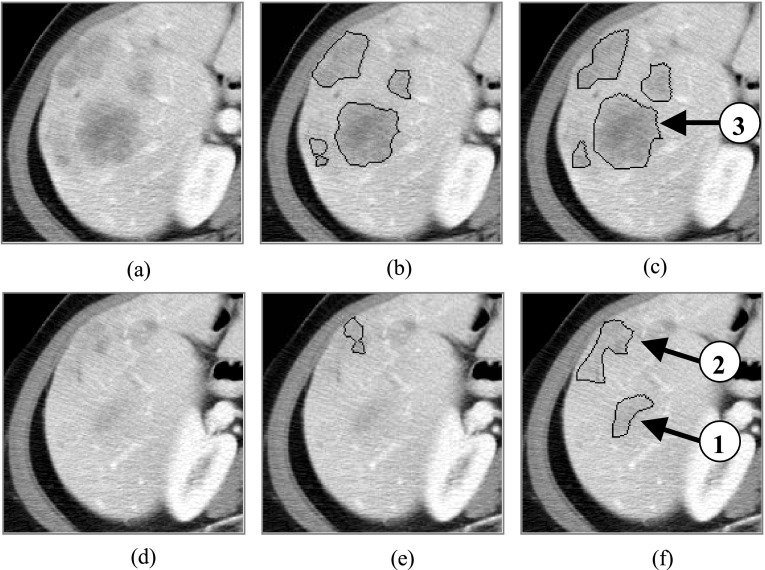
From the statistic data of Table II, we can also see that the Hausdorff distance seems to be large. By comparing the computer-generated results to the radiologist’s manual results, we found that the large distances often happen at the two terminals of the target liver metastases (Figs. 5 and 6). In order to bring the reasons to light, we chose two adjacent terminal slices of the case in Fig. 5 in which the distances between computer-generated contours and those drawn by the radiologist are large (15.0 mm for Hausdorff distance). From Fig. 7, it is not difficult for us to find that the liver metastasis intensity in the terminal part of every branch [arrows 1 and 2 in Fig. 7(f)] becomes very similar to that of the surrounding normal liver parenchyma, rather than that of liver metastasis in the middle part [arrow 3 in Fig. 7(c)]. Moreover, there is nearly no boundary between the terminal part of the target liver metastasis and its surrounding normal liver parenchyma [Fig. 7(d)]. Thus, it is very difficult for the proposed method to detect the liver metastasis boundary correctly [Figs. 7(e) and 7(f)]. This will inevitably result in a large boundary distance. The definition of Hausdorff distance specifies that it only considers the worst situation. Therefore, even though such a large distance only happens at the terminal slice, the Hausdorff distance is large for the entire target object. For our experiments of all 69 liver metastases, this is the main reason for the large Hausdorff distance. Apparently, this will enlarge the average distance to some extent.
FIG. 7.
Illustration of the large distances between the computer-generated contours and those drawn manually by the radiologist. (a) and (d) are the original images. (b) and (e) are computer-generated contours corresponding to (a) and (d). (c) and (f) are radiologist-delineated contours corresponding to (a) and (d). In this example, the Hausdorff distance is 15.0 mm.
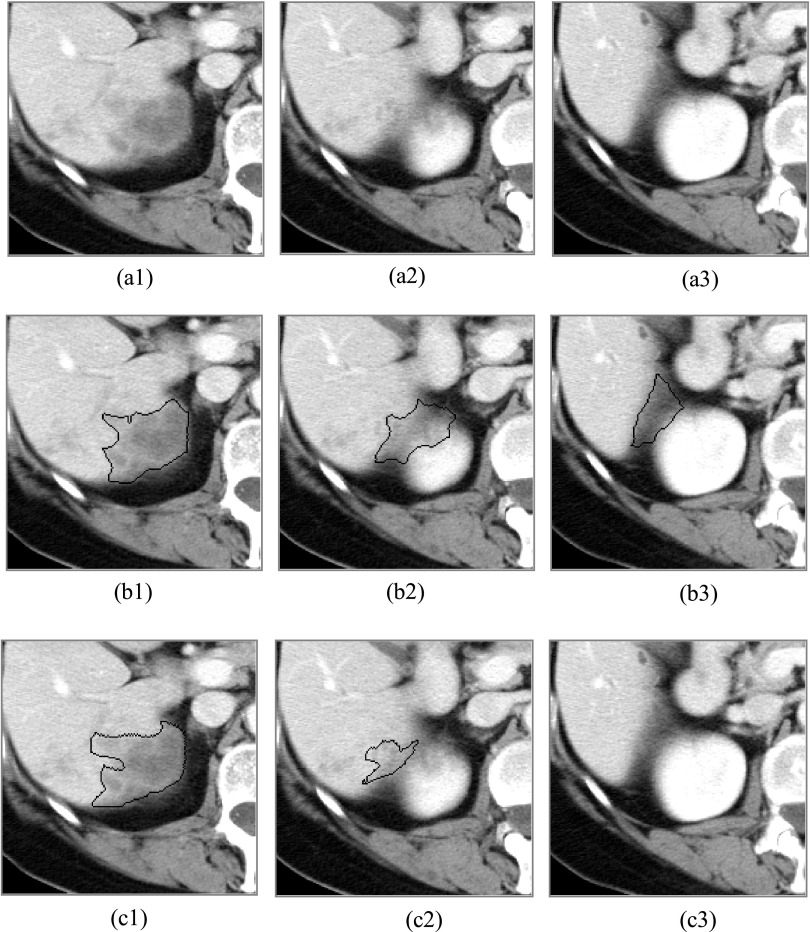
The other reason that the proposed method cannot correctly detect the boundary of the target liver metastasis is that the intensity of surrounding structures is too similar to that of the metastasis, especially for metastases located at the periphery of the liver. This sometimes lets the computer-generated contour leak out and produces large boundary distances. This will also enlarge the average boundary distance. Figure 8 is such an example, in which the Hausdorff distance is about 21.2 mm. For this case, it also produces the maximal average distance (3.7 mm). What we want to point out is that this is a rare phenomenon. For all 69 liver metastases, there are only three such cases, and this (Fig. 8) is the worst one. In each of the three cases, boundary leakage happens in only one or two slices. It is easy for the user to correct them.
FIG. 8.
Illustration of the computer-generated leaking out contours. [(a1)–(a3)] The original images. [(b1)–(b3)] The computer-generated contours. [(c1)–(c3)] The radiologist’s manually delineated contours.
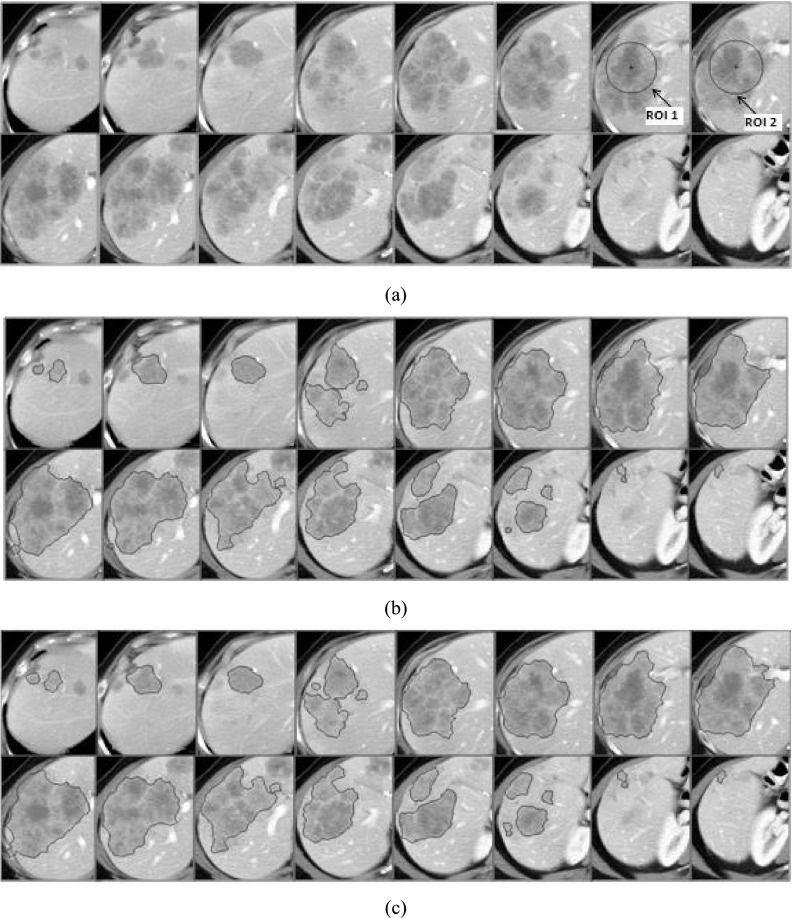
For a semiautomatic segmentation algorithm, results are often affected by manual selection of an initial ROI. To validate the robustness of our algorithm to the variations in manually given initializations, i.e., the seed circles, we reran the algorithm on all 69 cases with a different ROI and blinded to the initializations of that first round. The pairwise agreement between the two measurements was evaluated with the overlap ratio and the CCC. For the 69 liver metastases in 15 patients, the algorithm achieved a median overlap ratio of 92.6% and a CCC of 0.9990 (95% confidence interval: 0.9984–0.9994). This is better than that obtained by the method proposed in Ref. 11. Figure 9 illustrates a typical case. The two different seed ROIs are provided in Fig. 9(a) (ROI 1 and ROI 2). Figure 9(b) shows the segmentation result obtained with ROI 1 in Fig. 9(a). Figure 9(c) shows the segmentation result obtained with ROI 2 in Fig. 9(a). The volumes of the liver metastases in Figs. 9(b) and 9(c) are 335.5 and 343.5 cm3. The overlap ratio is about 96.8%.
FIG. 9.
Segmentation results obtained with the different seed ROIs. (a) The original images and the given seed circles (see the arrows). (b) The segmentation result with the seed ROI (ROI 1). (c) The segmentation result with the other seed ROI (ROI 2).
For the proposed method, the parameters w1, w2, and w3 in Eqs. (1)–(3) are weighting factors. Throughout this paper, for all the demonstrated cases and experiments, w1, w2, and w3 were fixed with the constant values of 2.0, 1.732, and 2.5, which were experimentally determined. From the results, we can see that the algorithm is robust to these parameters.
Once the seed ROI was provided, the proposed liver metastasis segmentation algorithm took about 15 s to segment one 3D liver metastasis (programmed with idl Version 6.4 Win32 and run on a laptop of 2.5 GHz CPU and 4 GB RAM).
The proposed segmentation algorithm focuses on liver metastases with hypointensity. One limitation of the algorithm is that it has not considered cases with a hyperintense lesion or an enhanced ring. In the future, we will enhance our algorithm by incorporating information of liver parenchyma so that it can handle liver lesion with hypointense, or when there is an enhanced ring.
4. CONCLUSIONS
Based on marker-controlled watershed transformation, we developed a semiautomatic method for the segmentation of 3D liver metastases in volumetric CT images. The only manual requirement of the algorithm is an initialization circle inside the target liver metastasis in a selected reference slice. By combining techniques including thresholding, morphological operations, and 3D connectivity, we proposed a reliable method to automatically determine the internal and the external markers for every region on each slice. The algorithm was applied to 69 liver metastases in 15 patients and received a median overlap, overestimation ratio and underestimation ratio of 82.3%, 6.0%, and 11.5%, respectively, and a median average boundary distance of 1.2 mm. Preliminary results have demonstrated that the proposed algorithm is accurate and promising.
ACKNOWLEDGMENT
This work was in part supported by Grant No. U01 CA140207 from the National Cancer Institute (NCI). The content is solely the responsibility of the authors and does not necessarily represent the funding sources.
REFERENCES
- 1.Cancer Facts & Figures, American Cancer Society, 2005, available at http://www.cancer.org.
- 2.Colorectal Cancer Facts and Figures, American Cancer Society, 2005, available at http://www.cancer.org.
- 3.Fusai G. and Davidson B. R., “Strategies to increase the respectability of liver metastases from colorectal cancer,” Dig. Surg. 20, 481–496 (2003). 10.1159/000073535 [DOI] [PubMed] [Google Scholar]
- 4.Geoghegan J. G. and Scheele J., “Treatment of colorectal liver metastases,” Br. J. Surg. 86, 158–169 (1999). 10.1046/j.1365-2168.1999.01013.x [DOI] [PubMed] [Google Scholar]
- 5.Siegel R., Ma J., Zou Z. H., and Jemal A., “Cancer statistics,” Ca-Cancer J. Clin. 64(1), 9–29 (2014). 10.3322/caac.21208 [DOI] [PubMed] [Google Scholar]
- 6.Williams D. M., Bland P., Liu L., Farjo L., Francis I. R., and Meyer C. R., “Liver-tumor boundary detection: Human observer vs Computer edge detection,” Invest. Radiol. 24, 768–775 (1989). 10.1097/00004424-198910000-00008 [DOI] [PubMed] [Google Scholar]
- 7.Gao L., Heath D. G., Kuszyk B. S., and Fishman E. K., “Automatic liver segmentation technique for three-dimensional visualization of CT data,” Radiology 201, 359–364 (1996). 10.1148/radiology.201.2.8888223 [DOI] [PubMed] [Google Scholar]
- 8.Soler L., Delingette H., Malandain G., Montagnat J., Ayache N., Koehl C., Dourthe O., Malassagne B., Smith M., Mutter D., and Marescaux J., “Fully automatic anatomical, pathological, and functional segmentation from CT scans for hepatic surgery,” Comput. Aided Surg. 6(3), 131–142 (2001). 10.3109/10929080109145999 [DOI] [PubMed] [Google Scholar]
- 9.Chemouny S., Joyeux H., Masson B., Borne F., Jaeger M., and Monga O., “Advanced 3D image processing techniques for liver and hepatic tumor location and volumetry,” Proc. SPIE 3661, 761–771 (1999). 10.1117/12.348633 [DOI] [Google Scholar]
- 10.Bilello M., Gokturk S. B., Desser T., Napel S., Jeffrey R. B., and Beaulieu C. F., “Automatic detection and classification of hypodense hepatic lesions on contrast-enhanced venous-phase CT,” Med. Phys. 31(9), 2584–2593 (2004). 10.1118/1.1782674 [DOI] [PubMed] [Google Scholar]
- 11.Zhao B. S., Schwartz L. H., Li J., Colville J., Moskowitz C., Wang L., Leftowitz R., Liu F., and Kalaigian J., “Shape-constrained region-growing for delineation of hepatic metastases on contrast-enhanced CT scans,” Invest. Radiol. 41, 753–762 (2006). 10.1097/01.rli.0000236907.81400.18 [DOI] [PubMed] [Google Scholar]
- 12.Hong J. S., Kaneko T., Sekiguchi S., and Park K. H., “Automatic liver tumor detection from CT,” IEICE Trans. Inf. Syst. 84(6), 741–748 (2001). [Google Scholar]
- 13.Yim P. J., Vora A. V., Raghavan D., Prasad R., McAullife M., Ohman-Strickland P., and Nosher J. L., “Volumetric analysis of liver metastases in computed tomography with the fuzzy C-means algorithm,” J. Comput. Assisted Tomogr. 30, 212–220 (2006). 10.1097/00004728-200603000-00008 [DOI] [PubMed] [Google Scholar]
- 14.Bellon E., Feron M., Maes F., Van Hoe L., Delaere D., Haven F., Sunaert S., Baert A. L., Marchal G., and Suetens P., “Evaluation of manual vs semi-automated delineation of liver lesions on CT images,” Eur. Radiol. 7(3), 432–438 (1997). 10.1007/s003300050180 [DOI] [PubMed] [Google Scholar]
- 15.Yim P. J. and Foran D. J., “Volumetry of hepatic metastases in computed tomography using the watershed and active contour algorithm,” in 26th IEEE Symposium on Computer-Based Medical Systems–CBMS (IEEE, New York, NY, 2003), pp. 329–335. [Google Scholar]
- 16.Meyer F. and Beucher S., “Morphological segmentation,” J. Visual Commun. Image Representation 1(1), 21–46 (1990). 10.1016/1047-3203(90)90014-M [DOI] [Google Scholar]
- 17.Roerdink J. B. and Meijster A., “The watershed transform: Definitions, algorithms and parallelization strategies,” Fundamenta Informaticae 41, 187–228 (2001). [Google Scholar]
- 18.Xu S. Z., Liu H., and Song E. M., “Marker-controlled watershed for lesion segmentation in mammograms,” J. Digital Imaging 24(5), 754–763 (2011). 10.1007/s10278-011-9365-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Rogowska J., Batchelder K., Gazelle G., Halpern E., Connor W., and Wolf G., “Evaluation of selected two-dimensional segmentation techniques for computed tomography quantization of lymph nodes,” Invest. Radiol. 31(3), 138–145 (1996). 10.1097/00004424-199603000-00004 [DOI] [PubMed] [Google Scholar]
- 20.Mancas M. and Gosselin B., “Fuzzy tumor segmentation based on iterative watersheds,” in Proceedings of STW Conference on ProRISC (2003). [Google Scholar]
- 21.Lapeer R. J., Tan A. C., and Aldridge R., “A combined approach to 3D medical image segmentation using marker-based watersheds and active contours: The active watershed method,” in Medical Image Understanding and Analysis, MIUA (BMVA, Durham, UK, 2002), pp. 165–168. [Google Scholar]
- 22.Vincent L., “Morphological grayscale reconstruction in image analysis: Applications and efficient algorithms,” IEEE Trans. Image Process. 2, 176–201 (1993). 10.1109/83.217222 [DOI] [PubMed] [Google Scholar]
- 23.Ridler T. W. and Calvard S., “Picture thresholding using an iterative selection method,” IEEE Trans. Syst., Man, Cybern. 8(8), 630–632 (1978). 10.1109/TSMC.1978.4310039 [DOI] [Google Scholar]
- 24.Horsch K., Giger M. L., Venta L., and Vyborny C. J., “Automatic segmentation of breast lesion on ultrasound,” Med. Phys. 28(8), 1652–1659 (2001). 10.1118/1.1386426 [DOI] [PubMed] [Google Scholar]
- 25.Yan J. Y., Zhao B. S., Wang L., Zelenetz A., and Schwartz L. H., “Marker-controlled watershed for lymphoma segmentation in sequential CT images,” Med. Phys. 33(7), 2452–2460 (2006). 10.1118/1.2207133 [DOI] [PubMed] [Google Scholar]
- 26.Zhang Y. J., “Evaluation and comparison of different segmentation algorithms,” Pattern Recognit. Lett. 18, 963–974 (1997). 10.1016/S0167-8655(97)00083-4 [DOI] [Google Scholar]
- 27.Chalana V. and Kim Y. M., “A methodology for evaluation of boundary detection algorithms on medical images,” IEEE Trans. Med. Imaging 16(5), 642–652 (1997). 10.1109/42.640755 [DOI] [PubMed] [Google Scholar]
- 28.Alberola-López C., Martín-Fernández M., and Ruiz-Alzola J., “Comments on: A methodology for evaluation of boundary detection algorithms on medical images,” IEEE Trans. Med. Imaging 23(5), 658–660 (2004). 10.1109/tmi.2004.826358 [DOI] [PubMed] [Google Scholar]
- 29.Huttenlocher D. P., Klanderman G. A., and Rucklidge W. J., “Comparing images using the Hausdorff distance,” IEEE Trans. Pattern Anal. Mach. Intell. 15(9), 850–863 (1993). 10.1109/34.232073 [DOI] [Google Scholar]
- 30.Li L., “A concordance correlation coefficient to evaluate reproducibility,” Biometrics 45, 255–268 (1989). 10.2307/2532051 [DOI] [PubMed] [Google Scholar]
- 31.Jolly M. P. and Grady L., “3D general lesion segmentation in CT,” in 5th International Symposium on Biomedical Imaging: From Nano to Macro, ISBI (IEEE, New York, NY, 2008), pp. 796–799. [Google Scholar]
- 32.Rothe J. H., Grieser C., Lehmkuhl L., Schnapauff D., Fernandez C. P., Maurer M. H., Mussler A., Hamm B., Denecke T., and Steffen I. G., “Size determination and response assessment of liver metastases with computed tomography-comparison of RECIST and volumetric algorithms,” Eur. J. Radiol. 82, 1831–1839 (2013). 10.1016/j.ejrad.2012.05.018 [DOI] [PubMed] [Google Scholar]