Abstract
Purpose:
The motivation of this study was to find and eliminate the cause of errors in dose-averaged linear energy transfer (LET) calculations from therapeutic protons in small targets, such as biological cell layers, calculated using the geant 4 Monte Carlo code. Furthermore, the purpose was also to provide a recommendation to select an appropriate LET quantity from geant 4 simulations to correlate with biological effectiveness of therapeutic protons.
Methods:
The authors developed a particle tracking step based strategy to calculate the average LET quantities (track-averaged LET, LETt and dose-averaged LET, LETd) using geant 4 for different tracking step size limits. A step size limit refers to the maximally allowable tracking step length. The authors investigated how the tracking step size limit influenced the calculated LETt and LETd of protons with six different step limits ranging from 1 to 500 μm in a water phantom irradiated by a 79.7-MeV clinical proton beam. In addition, the authors analyzed the detailed stochastic energy deposition information including fluence spectra and dose spectra of the energy-deposition-per-step of protons. As a reference, the authors also calculated the averaged LET and analyzed the LET spectra combining the Monte Carlo method and the deterministic method. Relative biological effectiveness (RBE) calculations were performed to illustrate the impact of different LET calculation methods on the RBE-weighted dose.
Results:
Simulation results showed that the step limit effect was small for LETt but significant for LETd. This resulted from differences in the energy-deposition-per-step between the fluence spectra and dose spectra at different depths in the phantom. Using the Monte Carlo particle tracking method in geant 4 can result in incorrect LETd calculation results in the dose plateau region for small step limits. The erroneous LETd results can be attributed to the algorithm to determine fluctuations in energy deposition along the tracking step in geant 4. The incorrect LETd values lead to substantial differences in the calculated RBE.
Conclusions:
When the geant 4 particle tracking method is used to calculate the average LET values within targets with a small step limit, such as smaller than 500 μm, the authors recommend the use of LETt in the dose plateau region and LETd around the Bragg peak. For a large step limit, i.e., 500 μm, LETd is recommended along the whole Bragg curve. The transition point depends on beam parameters and can be found by determining the location where the gradient of the ratio of LETd and LETt becomes positive.
Keywords: geant4, Monte Carlo, proton therapy, LET, LET spectrum, step limit
1. INTRODUCTION
As currently defined, the clinical relative biological effectiveness (RBE) of protons compared to photons is assumed to be 1.1 for all conditions. This value is based on experimental results obtained with passive-scattering proton therapy (PSPT) beams.1–3 In reality, RBE is a complex variable and a function of dose, linear energy transfer (LET), tissue and cell type (α/β), endpoint, etc.3–5 Recent experiments have documented significant variability in the RBE of protons as a function of depth or particle energy in the beam.6–9 The sharp increase of RBE at the proton end of range is presumably due to the increase in LET. With the development of new beam delivery methods, such as scanning techniques to implement intensity-modulated proton therapy (IMPT), the importance of variations of RBE along the proton beam path has increased. Disregarding the RBE variation in treatment planning may lead to bias in selecting the plans for proton therapy.10 This warrants an in depth understanding of the LET values utilized.
RBE values for the estimation of biological effect of the computed particle dose distributions and planning of particle therapy are calculated using various models such as the LEM-model,11–14 the MKM-model,15 the Wilkens–Oelfke-model,16,17 or a mechanism based approach.18–20 The LET in a variety of flavors (such as track-averaged LET, LETt or dose-averaged LET, LETd) of the particles serves as a main input parameter in these models; therefore, the accuracy of the calculated LET and the manner of calculation can significantly affect the reliability of the calculated RBE.
LET is not a physical quantity that can be easily measured, and therefore, values are usually estimated by calculating stopping power using computer programs, based on the corrected Bethe equation.21,22 Such theoretical calculations can be used to computationally generate stopping power tables but cannot be applied in a complete radiation transport problem. The Monte Carlo (MC) technique is treated as the most accurate method in simulating complex radiation transport problems; however, as a computation method, the accuracy and precision of the MC calculation results depend strongly on the physics interaction cross sections applied as well as the simulation algorithms used. MC calculations of LET have been investigated in a variety of previous studies using different codes.23–33 MC calculated LET values have been implemented in the optimization of proton treatment planning systems.11,23,31,34,35 Most of these works focused on the calculations in relative large targets, such as CT voxels (mm scale), but the feasibility of MC method in calculating LET in small targets, such as biological cell layers (μm scale), was rarely investigated.
To experimentally correlate the in vitro RBE of protons with dose and LET, we performed a novel high-resolution and high-throughput single-cell-layer irradiation experiment using scanned proton beams at our institution.9 The MC technique was used to calculate the spatial dose and LET distributions in different target cell layers (5 μm thickness) in the culture plates with different preabsorber thicknesses. The calculated LETd values, however, showed an unexpected variation, first decreasing and then increasing as preabsorber thickness increased; this trend was not reported in any previous studies. The calculated LETt values followed an expected trend, first increasing slowly and then increasing rapidly, as the preabsorber thickness increased. This discrepancy in variation trends between LETt and LETd motivated us to address the following questions: (1) does the variation in the trends arise from physics or calculation methods; (2) what is the applicability and appropriateness of available LET calculation methods (MC or deterministic) for different target sizes, such as a single cell or a patient CT voxel; and (3) what is the appropriate selection of LETt or LETd to explain experimentally observed cell kill effects at our institution.9
To address the stated problems, we selected six different particle tracking step limits increasing from 1 to 500 μm in the MC simulations. The step limit is defined as the upper limit of a tracking step length. In a random sampling process, the sampled tracking step length cannot be longer than the preset step limit. LETt and LETd were calculated in a step-by-step mode during the transport of protons. We termed the accuracy of dependence of the calculated average LET (LETt and LETd) on the preset particle tracking step limit “step limit effect” in this study. To investigate the step limit effect, we scored the stochastic spectra of energy-deposition-per-step at a variety of locations in the water phantom. Please note that this study was performed only with the geant 4 (Refs. 36 and 37) code, which is a popular MC system used by a large community. Whether this step limit effect is also apparent in other codes has to be evaluated.
The detailed energy-deposition-per-step spectra information explains how the step limits set in MC simulations affect the variations of the averaged LET along the proton beam path. The authors hope that the findings in this study will help to improve LETd and LETt predictions for small scale biology experiments, and also to facilitate the development of models predicting RBE of charged particles which can be utilized in next-generation particle treatment planning systems.
2. MATERIALS AND METHODS
The accuracy of the developed algorithms relies on the interpretation of the physics quantities by the program developers and users. Thus, it is necessary to introduce a strict definition of the theoretical LET and reiterate its importance to guide the developers and users to apply correct algorithms to calculate LET in practical problems (such as in patient CT voxels) following its original physics meaning. We will introduce different algorithms to calculate the average LET but focus on the MC particle tracking algorithm in this study.
2.A. Original and derived definitions of linear energy transfer
The definition of LET can be found in ICRU Report No. 85.38 It was defined as a nonstochastic quantity to describe the average energy “transfer” from purely “electronic” interactions (ionization or excitation) per unit length traveled by charged primary particles. LET is strictly defined at a spatial point.38 The mean energy transferred locally is equal to the mean energy lost by the primary charged particles minus the mean sum of energy carried away (energy cutoff, denoted as Δ, in units of keV) by energetic secondary electrons (delta rays) with initial kinetic energies greater than Δ. As such, LET with an energy cutoff is usually denoted by LΔ. If no energy cutoff of delta rays is imposed, the “unrestricted” LET is equal to what is known as the electronic stopping power, Sel, which describes only the energy “loss” per unit of length traveled by charged particles. The unrestricted LET is denoted as L∞, or simply L.
The strict definition of LET limits its application because in a practical problem, irradiation targets always have a finite volume, rather than being a dimensionless point, and the monoenergetic pre-requisite of the primary particles is not easy to be met. Hence, LET is commonly averaged over a target volume and an energy spectrum of the specified type of charged particles. Two different practical LET concepts, LETt and LETd, are derived from the original definition of LET. LETt is the arithmetic mean value of the fluence spectrum of LET. Although LETt is derived from a spectrum scored in a volume, it is essentially very close to the physics meaning of the LET concept defined by ICRU. However, when biological outcome is the focus of a study, both dose and LET should be considered. LETd is a quantity taking into consideration both factors. The relative dose contribution of each individual energy deposition event is treated as the weighting factor in calculating LETd, which may serve as a candidate quantity to predict biologic effects.3,23 Both LETt and LETd can be calculated using MC techniques.
Because the energy loss (termed as dEΔ) counted in LET is only from electronic interactions such as ionization and excitation,38 the energy loss of primary charged particles due to generating secondary recoil nuclei or nuclear fragments should be excluded when stating the LET of the primary charged particles. These secondary nuclei can also make contributions to the total dose; however, their LET should be indicated separately from the primary charged particles.23 In this study, we only focus on the LET from the primary protons. The influence of secondary nuclei (including secondary protons) in LET calculations has been investigated in other studies.3,23
2.B. Deterministic algorithms to calculate the averaged LET
The spatial distribution of a physical quantity such as dose is the main interest in radiotherapy. Similarly, the spatial distributions of LETt and LETd in the irradiated target are investigated as well. Wilkens and Oelfke have defined a “stopping power” based method to calculate the spatial distributions of LETt and LETd.26 A modified calculation formula for LETt is expressed in Eq. (1). It can be seen from the calculation method that the name “fluence-averaged LET” (LETf) is more intuitive, but it is called “track-averaged LET” due to historical reasons,26
| (1) |
where Sel(E) is the electronic stopping power of primary charged particles with kinetic energy E and is the fluence of primary charged particles with kinetic energy E at location z. The relative fluence is used as the weighting factor to calculate LETt. Essentially, it is the arithmetic average value from a spectrum distribution. The electronic stopping power is used in the calculation, which implies that unrestricted LET is calculated without the production of delta rays.
The dose-averaged LET is calculated as follows:
| (2) |
where is the electronic stopping power of primary charged particles with kinetic energy E and is the absorbed dose contributed by primary charged particles with kinetic energy E at location z.
Because relative dose is used as the weighing factor to calculate this averaged LET, it is called dose-averaged LET. Obviously, with similar lengths traveled, a high-LET particle track can contribute a higher dose than a low-LET particle track. Hence, we can assume that a high-LET track can provide a higher contribution to cell kill, viz., a higher biological effect. In simple terms, the higher the LET, the higher the probability for cell kill, unless the so-called “cell overkill” takes effect.5
Dose can be estimated by using the electronic stopping power and fluence based on the continuously slowing down approximation (CSDA) assumption of energy loss and by neglecting the nuclear stopping power and the escape of delta rays,39 given as
| (3) |
where is the mass density of the current medium where energy is deposited.
Substituting dose with Eq. (3), Eq. (2) can be written as
| (4) |
In the above equations, nonstochastic quantities (electronic stopping power, dose, and fluence) are used. We therefore treat the strategy developed by Wilkens and Oelfke as a deterministic method. Using Eqs. (1) and (4) can simplify the problems to determining the fluence spectrum of energy ( vs E) only. Mathematically, Eqs. (1) and (2) show that LETt is the first moment of the fluence spectrum, and LETd is the second moment over the first moment. LET is a function of the charged particle energy. Therefore, once the energy spectrum at a point or averaged over a volume is determined, it can be converted to the LET spectrum using the electronic stopping power table provided by programs, such as pstar for protons.40 Afterward, LETt and LETd can be calculated by integration over all energies.
Although it is a deterministic strategy, the energy spectrum is usually obtained from MC simulations. One disadvantage of this strategy is that both the energy spectra and LET spectra are not strictly continuous but discrete. The energy bin width of the spectra is a main uncertainty source of the calculated LET values. For medium- and high-energy therapeutic protons (usually lower than 250 MeV), the uncertainty is small due to the slow variation of LET with energy. For low-energy protons (lower than 10 MeV), the bin width effect is prominent because the LET can vary sharply with the variation of energy. This energy spectrum to LET spectrum conversion process is not adopted in this study. We will introduce another way to implement the method developed by Wilkens and Oelfke.
The general purpose MC code geant 4 (Refs. 36 and 37) provides a built-in function (ComputeElectronicDEDX() function of the class G4EMCalculator) to convert energy of charged particles to unrestricted LET directly. Three parameters: energy, particle name, and medium are used. This function adopts the Bethe formula21,22 to calculate LET. This can eliminate the uncertainty caused by energy bin width because the LET of each particle is obtained from a single energy value, rather than from an energy spectrum. The biggest advantage of this method is that it simplifies the problem to scoring the distribution of unrestricted LET only.
Although the deterministic method follows the definition of LET, it has limitations in solving practical problems in finite volumes. Using the physics quantity LET averaged at a point within the target may not correlate the biological effect to the whole target accurately, especially close to the end of the penetration range of protons, where LET varies sharply. Using the LET averaged over a finite trajectory length, i.e., a tracking step may provide a more accurate radiation effect. To investigate the effect averaged in a target volume, detailed MC tracking processes are needed. Nevertheless, we also provide the averaged LET values calculated using the deterministic method for comparison.
2.C. Monte Carlo particle tracking algorithms to calculate the averaged LET
In this study, we used the geant 4 (version 10.0) MC toolkit to perform particle tracking to calculate LETt and LETd. In the geant 4 physics algorithm, the binding energy of electrons is treated as a “local” (at a spatial point) energy deposition; hence, based on the energy conservation and the definition of LET, the energy transferred during a tracking step by a charged particle is simplified to be equal to the total energy deposited (along the step and at the starting point of a step) by this charged particle. Both the total energy deposition, ε, during a discrete tracking step and the true step length, l (taking into account any differences of the particles path from the length of a straight line), can be obtained using geant 4 built-in functions in the particle tracking process. Therefore, in this study, we defined the quotient ε/l as “energy deposition per step” in a specified target volume. Due to the stochastic nature of the MC method and analogous physics meaning between ε/l and LET, ε/l can be treated as the random variable form of LET.
Here, the definition of ε/l is quite similar to the stochastic quantity lineal energy (), which is extensively used in microdosimetry, with the following differences: first, ε refers to the energy deposit only from a primary charged particle trajectory, but εs refers to the total energy deposits from the primary particle and all of its secondary particles (any types of ionizing radiation) in a “single” event within the target volume;41 and second, l refers to the true tracking step length of the primary charged particle and it is a variable, but refers to the mean chord length in a spherical or cylindrical target geometry (equals to two thirds of the diameter of the sphere or cylinder) and it is a fixed value for any events and any types of ionizing radiation.41
If the relative tracking step length contribution is used as the weighting factor for each step within the target geometry, LETt can be expressed as
| (5) |
where εi is the energy deposition by the ith charged particle with the tracking step length li, n is the total number of charged particles of the specified type within the sensitive volume, and wi,t is the track-length weighting factor for the ith event, expressed as
| (6) |
Equation (5) can be written as
| (7) |
Equation (7) shows that LETt is the ratio of the total energy depositions and total track lengths from all primary charged particles of the specified type. This calculation clearly expresses the meaning of track-averaged LET. The tracking step length li is sampled randomly and influenced by factors, such as the interaction cross section, the geometry boundary, and the user-defined step size limit.42 The step lengths are not necessarily equal for any two particles tracked. Strictly speaking, εi and li are not independent variables. In the geant 4 tracking algorithm, li is first determined by random sampling, and second, εi is determined based on the length of li and the random sampling algorithm of energy deposition.42
In calculating LETd, the relative dose contribution is used as the weighting factor for each ε/l event,
| (8) |
where wi,d is the dose weighting factor for the ith event, expressed as
| (9) |
where Di is the dose deposited by the ith charged particle of the specified type within the sensitive volume with the mass of m.
Equation (8) can be written as
| (10) |
Using Eqs. (7) and (10), one can calculate LETt and LETd in any sensitive volume after all the particle histories are tracked in a MC simulation.
2.D. Scoring of the fluence and dose spectra of energy deposition per step and LET
Based on the similarity of ε/l and (either one refers to the energy deposition in a unit traveling distance of particles), in this study, we performed the data scoring and processing methods for ε/l similar to the ones used for in microdosimetry.
During the tracking process, the energy deposition per step (ε/l) within each sensitive volume was obtained for each charged particle of the specified type. Then, each obtained spectrum of ε/l was normalized by the total fluence from the specified type of charged particle to form a new spectrum with , where is the relative fluence; thus, the new spectrum is referred to as the fluence spectrum of ε/l.
By using ε as the weighting factor for each ε/l event, the dose spectrum of ε/l can be scored. In the dose spectrum, the product of the counts within each ε/l bin and the bin width is proportional to the dose contribution from the events within the ε/l bin.
The fluence and dose spectra of LET obtained using the deterministic method introduced in Sec. 2.B were also recorded and compared with the spectra of ε/l.
Similar to obtaining the microdosimetric quantity, frequency mean lineal energy, , we used the fluence spectrum of energy deposition per step, Φ(ε/l) vs ε/l, to investigate LETt, and the dose spectrum. Equivalent to obtaining dose-mean lineal energy, , we used vs ε/l to investigate LETd, where is the probability density function of ε/l with ( is the bin width of ε/l) and 2.3/LETt is the normalization factor. The fluence and dose spectra of LET using the deterministic method are also provided, replacing the ε/l with LET in the spectra. Details of the processing method for the fluence spectra and dose spectra in microdosimetry have been described by Rossi and Zaider.41
Please note that although we used the microdosimetry method to investigate LETt and LETd, essentially they have different meanings from and due to differences in the definition of ε/l and discussed above.
2.E. Basic settings in Monte Carlo simulations
We modeled the spot-scanning nozzle of the Proton Therapy Center at our institution43 using the geant 4 MC toolkit in this study. The dose simulation results were crossvalidated with a commissioned MCNPX-44 based MC model developed at our institution.45
A 79.7-MeV single beamlet was used to irradiate an 80 × 80 × 40 cm3 water phantom. The selected energy is consistent with beam energy used in the proton biology experiments performed at our institution.9 The doses were scored in a stack of cylinders (800 in total), with a radius of 40 cm and a length of 0.5 mm each. The energy spectra, LET spectra, and particle fluence were scored at the entrance surface of each cylinder. The energy spectrum bin width was set to 100 keV. In addition, the beamlets from two other energies 146.9 and 201 MeV were selected to test the generality of step limit effect on calculated LET. If it is not pointed out explicitly, the results are from the 79.7 MeV proton beamlet.
Within each 0.5-mm-thick cylinder, a sensitive layer (with a radius of 40 cm) was defined to start at the entrance plane and extend to a specified thickness. Six different sensitive layer thicknesses (1, 5, 10, 50, 100, and 500 μm) were used, respectively, to calculate the average LET and score the spectrum of ε/l. In geant 4, a “sensitive volume” refers to a volume used to record the quantity of interest, such as the energy deposition and the particle fluence. A step limit equal to the sensitive layer thickness was specified for each sensitive layer to limit the maximum particle tracking step length within. In geant 4, a prestep point refers to the starting point of a tracking step, and a poststep point refers to the ending point of a tracking step. The continuous energy loss along the tracking step is processed by a function, AlongStepDoIt(), in the classes of physics processes in geant 4. The scoring geometry and particle tracking process are illustrated in Fig. 1.
FIG. 1.
Illustration of the scoring geometry and particle tracking process. Cylindrical sections with a radius of r = 40 cm and a thickness of t = 0.5 mm were used to score doses, and the LET was evaluated from fluence spectra scored in the sensitive layers (red sections) which had a thickness corresponding to the step size limit.
The FTFP_BERT physics package was selected for the current proton beam tracking calculations, as recommended by the geant 4 Collaboration.42 This package contains both standard electromagnetic (EM) and advanced hadronic physics processes. The basic “EM standard” option is used for EM Physics. Bertini-style cascade46 is used when hadrons energy is below 5 GeV, and Fritiof model47 is used when hadrons energy is above 4 GeV. The default production cut (i.e., the penetration range in all media) of secondary particles (only photons, electrons, positrons, and protons) is set to 0.7 mm in this physics package. During a tracking process, the production cut is converted to the corresponding energy threshold in the medium. The electron energy cutoff corresponds to 276 keV for the 0.7 mm production cut in water. The maximum energy of secondary electrons produced from 79.7 MeV protons is about 180 keV in liquid water according to the “hard-collision” theory,39 lower than the preset energy cutoff, 276 keV; consequently, there are no delta rays produced by 79.7-MeV protons in water in the simulations. Hence, the calculated LET is an unrestricted LET. As indicated by the geant 4 Collaboration, the simulation results are strongly affected by the preset production cut value,42 the selection of which depends on the user’s needs. A smaller production cut can cause more standalone secondary electrons. The production of a secondary electron from a primary charged particle is treated as a discrete energy loss process; however, the LET calculation over a tracking step is a continuous energy loss process.42 Obviously, the discrete process can result in a spike in the calculated average LET along the particle trajectory. Therefore, if the production cutoff value for secondary electrons is low enough, some spikes may be observed in the LET curve.33 The authors do not recommend introducing delta rays in the LET calculations for therapeutic protons at this moment because (1) delta rays may result in the discontinuity of the LET curves as a function of penetration depth and (2) to clearly analyze a problem, it is best to only change one parameter at one time. The step limit effect is the object of the current study, and the discussion of the production cut effect is beyond the scope of this study. The default value 0.7 mm was used in all simulations. It must be kept in mind that if the user is intended to obtain smooth unrestricted LET curves, the production cut must be set longer than the maximum range of the secondary electrons possibly generated by the initial primary protons. As mentioned above, the maximum energy of the secondary electrons can be calculated using the hard-collision theory, and then, the penetration range can be calculated using the estar program.40
The number of primary histories was set to 1 × 107 in all cases to make the simulation results meet the statistical uncertainty requirement (relative error of the mean value <1%). The data analysis tool—root (Ref. 48) was applied in geant 4 simulations to define 1D and 2D histograms to store the quantities of interest in binary format. After the simulations, all data were analyzed using root. All simulations were performed on our institutional high-performance computing cluster and the Lonestar cluster at the Texas Advanced Computational Center.
2.F. RBE calculation
RBE values were calculated according to an implementation of the repair-misrepair-fixation (RMF) model described by Polster et al.49 In this framework, the primary RMF model parameters are the RBE of double-strand break (DSB) induction (RBEDSB) and the frequency-mean specific energy (), both of which may be obtained through the use of the Monte Carlo damage simulation (mcds) software developed by Semenenko et al.19,50–52 RBEDSB values for protons were calculated relative to 137Cs γ-rays with a DSB yield of 8.3 DSB Gy−1 Gbp−1. Because LET information was obtained from geant 4 directly, the information necessary for performing a dose-averaged RBE calculations for every step length and LET averaging method was not available. In order to facilitate the calculations, energy spectra at each depth were used to calculate LETd, RBEDSB, and . The latter two parameters were then fit to the LETd values over the range of depths with first order and second order polynomials, respectively. These relationships were then used to calculate RBEDSB and for each LET value obtained from the simulations. Alpha (αp) and beta (βp) for protons were then calculated according to the equations
| (11) |
| (12) |
where the values for αx and βx (0.29 Gy−1 and 0.083 Gy−2, respectively) were from 137Cs γ-ray irradiations of H460 lung cancer cells previously performed at our institution.9 All RBE calculations were performed for a dose corresponding to 10% surviving fraction which was determined by solving the linear quadratic survival equation for dose and performing the computation with the αp and βp obtained from the aforementioned calculations. All components were then incorporated into the linear quadratic RBE formalism described by the equation
| (13) |
which is simply a ratio of the linear quadratic survival curves for photons and protons.17
3. RESULTS AND DISCUSSION
Distributions of LETt and LETd as a function of depth were investigated for the different step limits. To better understand differences in the distributions caused by choice of a step limit, the fluence and dose spectra of ε/l were compared. As reference, the calculation results using the determin istic strategy developed by Wilkens and Oelfke were also provided.
3.A. Track-averaged LET distributions as a function of depth
The distributions of LETt as a function of depth with six different step limits and obtained from the deterministic method are compared in Fig. 2. The abscissa of each LETt data point is the center of the sensitive layer for six different step limits and the entrance plane of the layer for the deterministic method. Relative dose (total dose from all types of particles) and proton fluence (from primary protons only) curves are also included for reference.
FIG. 2.
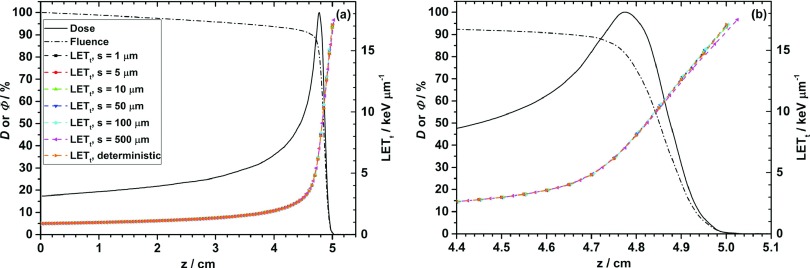
Distributions of LETt as a function of depth with different step limits and obtained using the deterministic method. (a) Depth z from 0 to 5.4 cm; (b) depth z from 4.4 to 5.1 cm. D describes dose, and the fluence is represented by Φ. No error bars have been plotted because they would obstruct the curves and they are generally very small (on the order of 0.1%, see Table I). The legend in (a) also refers to (b).
Dose and fluence did not exhibit dependence on the step limit because the dose was scored in a series of cylinders of fixed thickness (0.5 mm), and fluence was scored at the entrance plane of the cylinder. Distal to the Bragg peak (at z = 4.75 cm), fluence expectedly decreases sharply. The LETt curves with six different step limits are very close to each other in Fig. 2(a) and show that the step limit dependence is small in LETt. The LETt curve obtained using the deterministic method is also close to the curves obtained using the MC particle tracking method. The expanded scale comparison around the Bragg peak is shown in Fig. 2(b). In the dose plateau region, proton energy is high and the spread is small. The LET variation with energy is small; and LETt is thus independent on the step limit. However, close to the Bragg peak, proton energy becomes low, and LET is highly sensitive to variations in energy. Hence, the LETt averaged in a longer step length such as 500 μm can be different from the value averaged in a smaller step length or from the deterministic method calculated on a plane. It implies that close to the end of penetration range, the LETt obtained using the deterministic method may not reveal the real radiation effect within the whole target when target is relatively large.
The comparisons of LETt from three different energies 79.7, 146.9, and 201 MeV are shown in Fig. 3. To avoid the issue of a large amount of data in one plot, only the results from the step limit of 5 and 500 μm were provided. The results show that for different initial beam energies, the LETt always has small dependence on the step limit. Figure 3 also shows that with the increase of the initial beam energy, the maximum LETt decreases. The longer traveling path from a higher-energy beam can result in more energy straggling close to the maximum range, and hence, the energy spectrum is also broadened at the corresponding locations, resulting in a higher mean energy and a lower LETt accordingly. The energy spectrum analysis will be shown in Sec. 3.C.
FIG. 3.
Distributions of LETt as a function of depth from 79.7, 146.9, and 201 MeV protons with two different step limits of 5 and 500 μm.
3.B. Dose-averaged LET distributions as a function of depth
The distributions of LETd as a function of depth with six different step limits and obtained from the deterministic method are compared in Fig. 4. Relative dose (total dose from all types of particles) and proton fluence (from primary protons only) curves are also included for reference.
FIG. 4.

Distributions of LETd as a function of depth with different step limits and obtained using the deterministic method. (a) Depth z from 0 to 5.4 cm; (b) depth z from 4.4 to 5.1 cm. D describes dose, and the fluence is represented by Φ. The legend in (a) also refers to (b).
Proximal to the Bragg peak, with step limits of 1, 5, and 10 μm, LETd results show an obvious decreasing trend with depth, which leaves the entrance LETd as the highest. However, no such high-LET values were observed at the entrance or in the plateau region in previous published data and calculations. Obviously, the calculated LETd results are incorrect at these locations for the small step limits. With step limits of 50 and 100 μm, our calculated LETd in the plateau region shows a slightly decreasing trend (cannot be distinguished in the curves). With the step limit 500 μm, LETd in the plateau region increases slightly with depth in agreement with previous studies.24,26,28 At all depths, we found that the smaller the step limit the larger the LETd.
Around the Bragg peak, the differences among the curves with different step limits are small, and all the curves show a rapid increase in LETd with increasing depth until fluence drops to zero. The expanded scale comparison around the Bragg peak is shown in Fig. 4(b). The results also show that close to the end of penetration range, the LETd values obtained using the deterministic method may not accurately reveal the radiation effect averaged in the whole target (on the scale of the preset step limit), overestimating for large step limits and underestimating for small step limits. The reason for the erroneously calculated high LETd values using the MC particle tracking method at the entrance and in the plateau region is discussed in more detail in Sec. 3.D.
The comparisons of LETd from three different energies 79.7, 146.9, and 201 MeV with 5 and 500 μm step limits are shown in Fig. 5. The curves clearly show a difference of LETd with different step limits proximal to the Bragg peak for all the energies. The lower maximum LETd from the beam with a higher initial energy is also caused by the broader proton energy spectrum and higher mean energy at the corresponding locations close to the maximum range, as explained in Sec. 3.A for LETt.
FIG. 5.
Distributions of LETd as a function of depth from 79.7, 146.9, and 201 MeV protons with two different step limits of 5 and 500 μm.
3.C. Kinetic energy spectra and LET spectra of protons at different depths
The kinetic energy spectra and the LET spectra (obtained using the deterministic method) of primary protons at five selected depths [z = 0, 1.9, 3.95, 4.75 (Bragg peak), and 4.85 cm] are shown in Fig. 6. The coordinate D(LET) in the LET spectra is the differential dose contribution of the events with the specified LET. The details of the LET spectra are explained in Sec. 3.D. The spread of the energy spectra increases with depth. The mean energy, , at each depth was determined and converted to the mean electronic stopping power (denoted as ) using the pstar program.40 The calculated LETt with 500-μm step limit and the are compared in Table I. The mean energy of protons at the entrance of the water phantom is 76.6 MeV, which indicates that the mean energy loss is 3.1 MeV in the proton nozzle with the injection energy of 79.7 MeV. Because LET is a function of particle energy, the broadening of the energy spectra causes the spread of the LET spectra, clearly shown in Fig. 6(b). In the plateau region, proton energy is high and the spread of the energy spectrum is small, and thus, the derived from the mean energy agrees well with LETt. This agreement validates the accuracy of the calculated LETt using Eq. (7). However, close to the Bragg peak, the mean proton energy is low and the spread of the energy spectrum is large as is the spread of the corresponding LET spectrum, which makes the use of the mean energy to derive the mean stopping power, , inappropriate. Therefore, the comparison of and the calculated LETt becomes meaningless.
FIG. 6.
(a) Kinetic energy spectra of primary protons at different depths. P(Ep) describes the probability of an event per energy bin and total probability is normalized to unity; (b) LET spectra of primary protons at different depths. D(LET) stands for the differential dose contribution of the events with the specified LET.
TABLE I.
Comparison between the mean electronic stopping power and the calculated LETt.
| z(cm) | (MeV) | (keV μm−1)a | LETt(keV μm−1)b | s.e.m. (keV μm−1)c |
|---|---|---|---|---|
| 0 | 76.6 | 0.89 | 0.89 | 4.6 × 10−5 |
| 1.9 | 57.9 | 1.1 | 1.1 | 7.3 × 10−5 |
| 3.95 | 29.7 | 1.9 | 1.9 | 1.5 × 10−4 |
| 4.75 | 8.3 | 5.3 | 7.3 | 2.0 × 10−3 |
| 4.85 | 5.0 | 7.9 | 13.8 | 5.7 × 10−3 |
The mean electronic stopping power, , was calculated using the pstar program (Ref. 40) for the mean kinetic energy of protons, .
LETt was calculated from the fluence spectra of ε/l with the step limit of 500 μm.
s.e.m stands for “standard error of mean.” Here, value is the absolute error of LETt from MC calculations.
The energy spectra at different depths were recorded for the three beams with different initial energies 79.7, 146.9, and 201 MeV. The energy spectra at the depths with 10% dose level in the distal edge of Bragg peak for these three beams were compared in Fig. 7. The corresponding depths in the water phantom are 4.9, 15.2, and 26.4 cm, respectively. The curves clearly show that with the increase of the initial energy of the beam, the spread of the energy spectrum increases and the mean energy increases as well. According to the relationship between the particle energy and the electronic stopping power, the energy spectra shown in Fig. 7 can explain why the beam with a higher energy can have a lower maximum LETt and LETd at the maximum range.
FIG. 7.
Kinetic energy spectra of primary protons at the depths with 10% dose level in the distal edge of Bragg peak from 79.7, 146.9, and 201 MeV. The corresponding depths are 4.9, 15.2, and 26.4 cm. The mean energies at these locations are 4.0, 6.5, and 8.5 MeV. P(Ep) has the same meaning as in Fig. 6.
3.D. Fluence and dose spectra of energy deposition per step and LET at different depths
At the five selected depths introduced in Sec. 3.C, we found that the shapes of spectra at the three shallower depths were similar, as were the shapes of spectra at the two largest depths. Therefore, only the spectra at z = 0 cm and z = 4.85 cm are presented.
Figure 8 shows the fluence spectra of ε/l for different step limits or the fluence spectrum of LET at z = 0 cm and z = 4.85 cm [(a) and (b), respectively]. In Fig. 8(a), at the entrance, as the step size limit increases, the spread (standard deviation, σ) of the fluence spectrum decreases, but the mean value (μ) remains constant (see LETt values in Table III). Because the proton energy spread at z = 0 cm is very narrow [see Fig. 6(a)], the corresponding LET spectrum has a narrow spread as well, as can be seen in Fig. 8(a). In Fig. 8(b), beyond the Bragg peak, the mean value (see LETt values in Table III) is no longer independent of the step limit. This can be attributed to the large variation of LET with energy along the tracking step or due to the large fluctuations in the statistics. Near the end of the penetration range, particle energy is low and the spread of the energy spectrum is broad; therefore, the spread of the fluence spectrum of ε/l or LET is broad as well, irrespective of the step limit.
FIG. 8.
Fluence spectra of ε/l with different step limits and the fluence spectrum of LET at two selected depths. (a) z = 0 cm; (b) z = 4.85 cm. The mean can be treated as LETt, and all mean values are listed in Table III.
TABLE III.
LETt, LETd, and the standard deviation from the fluence spectrum of ε/l or LET using the deterministic method at different depths.
| z = 0 cm | z = 1.9 cm | z = 3.95 cm | z = 4.75 cm | z = 4.85 cm | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S (μm) | LETt | LETd | σ | LETt | LETd | σ | LETt | LETd | σ | LETt | LETd | σ | LETt | LETd | σ |
| 1 | 0.89 | 10.9 | 3.0 | 1.1 | 8.6 | 2.9 | 1.9 | 6.1 | 2.9 | 6.1 | 10.0 | 4.8 | 10.3 | 17.1 | 8.3 |
| 5 | 0.89 | 2.9 | 1.3 | 1.1 | 2.7 | 1.3 | 1.9 | 2.8 | 1.3 | 6.2 | 8.9 | 4.2 | 10.4 | 16.3 | 8.2 |
| 10 | 0.89 | 1.9 | 0.94 | 1.1 | 1.9 | 0.93 | 1.9 | 2.4 | 0.94 | 6.2 | 8.8 | 4.3 | 10.6 | 16.1 | 8.5 |
| 50 | 0.89 | 1.1 | 0.42 | 1.1 | 1.3 | 0.44 | 1.9 | 2.0 | 0.54 | 6.5 | 8.6 | 5.1 | 11.9 | 15.6 | 10.2 |
| 100 | 0.89 | 1.0 | 0.30 | 1.1 | 1.2 | 0.38 | 1.9 | 2.0 | 0.85 | 6.8 | 8.6 | 5.6 | 12.9 | 15.1 | 10.8 |
| 500 | 0.89 | 0.9 | 0.14 | 1.1 | 1.1 | 0.23 | 1.9 | 2.0 | 0.44 | 7.4 | 9.9 | 5.7 | 13.8 | 16.0 | 10.7 |
| Deterministic | 0.88 | 0.89 | 0.06 | 1.1 | 1.1 | 0.15 | 1.9 | 1.9 | 0.30 | 6.1 | 8.6 | 3.9 | 10.3 | 15.9 | 7.6 |
Note: S stands for step limit. σ is the standard deviation of the random variable ε/l or the deterministic quantity LET, calculated from the fluence spectrum of ε/l or LET. The units of LETt, LETd, and σ are keV μm−1. The symbols also refer to Table IV.
Figure 9 shows the dose spectra of ε/l with different step limits or the dose spectrum of LET at z = 0 cm and z = 4.85 cm [(a) and (b), respectively]. In a dose spectrum, the area under the curve is proportional to the relative dose contribution. In Fig. 9(a), at the entrance, as the step limit decreases, the proportion of high-ε/l events increases. Hence, the calculated LETd is higher with a smaller step limit at the entrance and in the plateau region. In Fig. 9(b), the proportion of high-ε/l or LET events, i.e., LET ≥ 10 keV μm−1, is high in all curves because of the high proportion of low-energy protons. Hence, the calculated LETd is no longer strongly dependent on the step limit. The discontinuities at the end of the spectra are explained later in the text.
FIG. 9.
Dose spectra of ε/l with different step limits and the dose spectrum of LET at two selected depths. (a) z = 0 cm; (b) z = 4.85 cm. LETd is the mean value calculated from each dose spectrum.
Edges and peaks are seen in Figs. 8(b) and 9(b). They are probably caused by calculation artifacts or from protons with specific energies, explained as follows. Close to the end of a proton range, if the residual range of the current proton is equal to or shorter than the specified step limit, the proton loses all of its remaining energy during the current step, which becomes the final tracking step. Hence, the calculated quotient of the remaining energy and the residual range (denoted as , a constant for each specified step limit) has a significantly larger value than events scored from protons that have energy large enough to travel beyond the step limit. As a result, these events are shifted to the high-ε/l region, leading to the observed artifacts. This shift is the main cause of variation in the LETt and LETd values calculated from these spectra as functions of step limit size. The values of observed edges and peaks and the calculated are listed in Table II. The maximum LET value in the abscissa (deterministic method) can be observed at 82 keV μm−1, which corresponds to the maximum LET of protons in liquid water with an energy of 80 keV obtained using the pstar program.40
TABLE II.
Edge or peak values in the fluence and dose spectra of ε/l.
| Step limit (μm) | KER(keV)a | Sel(keV μm−1)b | (keV μm−1)c | First edge (keV μm−1) | Second peak (keV μm−1) |
|---|---|---|---|---|---|
| 1 | 50 | 77.4 | 50 | NA | NA |
| 5 | 320 | 53.2 | 64 | NA | 63 |
| 10 | 550 | 38.9 | 55 | 55 | 63 |
| 50 | 1560 | 19.0 | 31.2 | 31 | 63 |
| 100 | 2400 | 13.9 | 24 | 24 | 63 |
| 500 | 6000 | 6.85 | 12 | 23 | 63 |
KER stands for the kinetic energy of protons with a residual range equal to the step limit set in the simulation.
The electronic stopping power, Sel, was calculated using the pstar program (Ref. 40) for the kinetic energy of protons, KER.
is the quotient of KER and step limit set in the simulation.
The larger spread of the fluence spectra of ε/l for a smaller step limit can be explained as follows. With a fixed step length, the number of electronic interactions such as ionizations or excitations is a random variable following a Poisson distribution. Therefore, a longer step length results in a larger number of ionizations or excitations along this step, which in turn results in a smaller fluctuation due to the fact that in a Poisson distribution, the variance equals the mean. In the geant 4 algorithm used to calculate ε/l for each tracking step, the mean value of all ε/l events is the electronic stopping power calculated using the Bethe formula,21,22 and fluctuation is sampled from a Gaussian distribution related to the step length. This processing method explains why in the plateau region the calculated LETt is consistent with mean electronic stopping power, listed in Table I.
Obviously, in a series of events with mixed ε/l, the relative dose contribution from a high-ε/l event is higher than its relative track-length contribution explaining why at the same depth the calculated LETd is always higher than LETt with the same step limit. An exception is the case in which the step limit is 500 μm, proximal to the Bragg peak, where LETt is equal to LETd. This result can also be attributed to the spectra. In the curves with a step limit of 500 μm in Figs. 8(a) and 9(a), no high-ε/l events were found in either fluence spectrum or dose spectrum (the maximum ε/l is even smaller than 3 keV μm−1). Figures 8(b) and 9(b) show that close to the penetration range, even if we use the deterministic method, the LET spectrum has a large spread as well as using the MC particle tracking method. The calculated LETt and LETd and the standard deviation from the fluence spectrum of ε/l or LET using the deterministic method at five different depths are compared in Table III.
The analysis for the detailed ε/l or LET spectra information also reveals that using the mean quantity LETt or LETd may not be appropriate in modeling the biologic effects when the energy spectrum is broadened, as it is close to the Bragg peak. A model utilizing the detailed ε/l or LET spectrum distribution may be more comprehensive, but this would make the calculation for biologic effects more complicated.38
3.E. RBE results
In order to quantify the potential impact on biological dose for the different LET calculation methods, RBE calculations were performed. For each depth, Table IV displays the RBE for each combination of LET and tracking step length. In the plateau region (depths of 0, 1.9, and 3.95 cm), the greatest differences in RBE between LETt and LETd occur for the shortest tracking step and are equivalent to 37%, 27%, and 15% increases over the value of the LETt, respectively. For the depths near the Bragg peak (4.75 and 4.85 cm), the LETd remains higher than the LETt at values 12% and 20% higher than the LETt, respectively. These differences correspond directly to differences that would be observed in RBE-weighted dose and thus would constitute a noticeable effect on biological dose calculations. For the tracking step limit of 500 μm, the largest difference in RBE due to LET calculations occurs close to the maximum depth where the RBE from LETd is 6% higher than that from LETt.
TABLE IV.
RBE values at different depths for H460 nonsmall cell lung cancer cell line. The surviving fraction level is 10%. The calculated RBE values are based on the LET values in Table III. The bold values show enhanced RBE based on erroneous LETd values.
| z = 0 cm | z = 1.9 cm | z = 3.95 cm | z = 4.75 cm | z = 4.85 cm | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| S (μm) | RBE (LETt) | RBE (LETd) | RBE (LETt) | RBE (LETd) | RBE (LETt) | RBE (LETd) | RBE (LETt) | RBE (LETd) | RBE (LETt) | RBE (LETd) |
| 1 | 1.02 | 1.39 | 1.02 | 1.30 | 1.05 | 1.21 | 1.21 | 1.35 | 1.37 | 1.64 |
| 5 | 1.02 | 1.09 | 1.02 | 1.08 | 1.05 | 1.08 | 1.21 | 1.31 | 1.37 | 1.61 |
| 10 | 1.02 | 1.05 | 1.02 | 1.05 | 1.05 | 1.07 | 1.21 | 1.31 | 1.38 | 1.60 |
| 50 | 1.02 | 1.02 | 1.02 | 1.03 | 1.05 | 1.06 | 1.22 | 1.30 | 1.43 | 1.58 |
| 100 | 1.02 | 1.02 | 1.02 | 1.03 | 1.05 | 1.06 | 1.23 | 1.30 | 1.47 | 1.56 |
| 500 | 1.02 | 1.02 | 1.02 | 1.02 | 1.05 | 1.06 | 1.25 | 1.35 | 1.50 | 1.60 |
| Deterministic | 1.02 | 1.02 | 1.02 | 1.02 | 1.05 | 1.05 | 1.21 | 1.30 | 1.37 | 1.59 |
3.F. Recommendations to select LET for cell irradiation experiments
Figures 2 and 4 have shown the obvious differences between the calculated LETt and LETd. It is challenging to select a proper LET as an input parameter for RBE modeling or as an indicator to explain biological experiment results.9 In this study, we proposed a method to select the LET from calculations. The theoretical basis for our recommendation is that as the beam energy decreases along the path, the averaged LET increases continuously until the particle fluence decreases to zero.
Our results indicate that in the dose plateau region, LETt shows minor but LETd shows strong dependence on step limit. The results from proton biology experiments have shown that in the dose plateau region, the role of LET in determining cell kill is small.9 Therefore, we recommend the use of LETt in the dose plateau region due to its characteristics of continuous increase along beam path and step-limit independence. Around the Bragg peak, LETd shows minor dependence on step limit. Therefore, we recommend the use of LETd around the Bragg peak. A spatial transition point to switch between the use of LETt and LETd to quantify the LET is needed. The studies by Wilkens and Oelfke,26 and Kempe et al.,53 indicated that LETd is equal to or larger than LETt, and the difference increases with the penetration depth. This means that the ratio of LETd over LETt must be monotonically increasing with depth. Hence, to obtain a smooth transition from LETt to LETd, this point should be selected where the gradient of the ratio of LETd and LETt becomes positive.
The ratios of LETd and LETt as a function of depth are shown in Fig. 10(a). The determination of the transition point around the Bragg peak is illustrated in Fig. 10(b). The determined depths for the transition points and the smallest ratios of LETd and LETt with different step limits and the deterministic method are listed in Table V. For the large step limit of 500 μm, or the deterministic method, no such transition point can be found because the LETd-to-LETt ratio monotonically increases with depth from the entrance plane (z = 0 cm). This indicates that LETd can be used along the whole Bragg curve.
FIG. 10.
The ratio of LETd and LETt with different step limits and the deterministic method as a function of depth in water. (a) Depth z from 0 to 5.4 cm; (b) depth z from 4.0 to 5.2 cm.
TABLE V.
The LETd-to-LETt ratios and transition depths to switch LETt and LETd.
| Step limit (μm) | LETd/LETt | Transition depth (cm) |
|---|---|---|
| 1 | 1.57 | 4.7 |
| 5 | 1.22 | 4.6 |
| 10 | 1.15 | 4.55 |
| 50 | 1.07 | 4.2 |
| 100 | 1.05 | 4.2 |
| 500 | 1.03 | 0 (entrance plane) |
| Deterministic | 1.0 | 0 (entrance plane) |
Obviously, both calculated LETt and LETd as a function of depth depend on the initial proton beam source characteristics, such as energy and angular divergence. Therefore, the transition point for different initial beam energies should be determined according to the actual LETd-to-LETt ratio curves.
4. CONCLUSIONS
In this study, we investigated the step limit effect in geant 4 by calculating LETt and LETd for a 79.7-MeV proton beam. To explain the observed incorrect LETd calculation results with small step limits in the dose plateau region, we investigated the fluence spectra and dose spectra of ε/l at different depths along the Bragg curve. The results using the deterministic method were also provided for comparison.
From our data, we conclude that the step limit effect is negligible for LETt but strongly affects LETd results for targets smaller than 500 μm. This dependency was based on differences in the fluence spectra and dose spectra of ε/l from protons along the proton beam path. Based on the results of the RBE calculations, it is clear that the dependency of LETd on target size will affect the calculation of RBE-weighted dose in the plateau region. Based on our results, we recommend that for small targets (<0.5 mm), LETt be used in the dose plateau region and LETd be used close to the Bragg peak. The transition depth to switch between the use of LETt and LETd to quantify LET is dependent on the irradiation target size and the initial beam source characteristics. In order to determine the transition point, one needs to calculate the ratio of LETd and LETt as a function of depth and find the location where the gradient of the ratio becomes positive. In the case of large target sizes (500 μm), no such point can be found and it is valid to use LETd over the whole path length. Our findings are in agreement with the results of Grassberger and Paganetti3,23 when one considers to compute LETd and LETt in relatively large target volumes (such as CT voxels) but show that artifacts are affecting the results when small targets are investigated. In particular, one may need to pay attention when cell experiments are simulated, where target sizes can be on a micrometer scale. The erroneous LETd calculation results in small targets can be attributed to the algorithm to determine fluctuations in energy deposition along the particle tracking step in geant 4. As we have shown, this can further result in incorrect RBE values when LETd is used as an input parameter in modeling.
We also conclude that using MC particle tracking method may be better suited to investigate radiation effect than the deterministic method for targets located at the end of the penetration range.
From the spectra information of ε/l or LET, we conclude that the usage of average LET may not be the optimum parameter to model biologic effects especially in small scale targets and when protons reach the end of the penetration range where the energy spectrum and the LET spectrum have a large spread. Prospectively, the authors hope that incorporating more detailed radiation field information, i.e., energy spectrum, LET spectrum, or ε/l spectrum, into the design and optimization of intensity-modulated particle therapy may provide more optimal treatment plans for patients.
Due to the complexities of biological response to ionizing radiations, it is challenging to select an appropriate physics quantity to partially or completely quantify the biological effectiveness observed in biological experiments. For low energy particles and small scale targets down to DNA molecular scale, analyzing the detailed interactions between radiation and molecules may provide better explanations. Incorporating the geant 4-DNA physics list54–56 in the cell targets to perform more detailed interaction analysis will be our future work.
ACKNOWLEDGMENTS
This work was partly supported by National Cancer Institute Grant Nos. U19 CA021239-35 and R21 CA187484-01. The authors would like to thank Dr. Michel Maire and Dr. Sebastien Incerti from the National Institute of Nuclear and Particle Physics, France (IN2P3) for discussing the energy deposition fluctuation algorithms in geant 4 simulations and geant 4-DNA physics. The authors thank Dr. Leslie Braby from Texas A&M University for discussing the application of physics quantities in biological effectiveness of radiations. The authors thank Dr. Makoto Asai and Dr. Joseph Perl from SLAC National Accelerator Laboratory for discussing geant 4 particle tracking algorithms. The authors also appreciate Dr. Gabriel Sawakuchi for discussing in LET calculations.
REFERENCES
- 1.ICRU, “Prescribing, recording, and reporting proton-beam therapy (ICRU Report 78),” J. ICRU 7, 1–210 (2007). 10.1093/jicru/ndm021 [DOI] [Google Scholar]
- 2.Paganetti H., Niemierko A., Ancukiewicz M., Gerweck L. E., Goitein M., Loeffler J. S., and Suit H. D., “Relative biological effectiveness (RBE) values for proton beam therapy,” Int. J. Radiat. Oncol., Biol., Phys. 53, 407–421 (2002). 10.1016/S0360-3016(02)02754-2 [DOI] [PubMed] [Google Scholar]
- 3.Paganetti H., “Relative biological effectiveness (RBE) values for proton beam therapy. Variations as a function of biological endpoint, dose, and linear energy transfer,” Phys. Med. Biol. 59, R419–R472 (2014). 10.1088/0031-9155/59/22/R419 [DOI] [PubMed] [Google Scholar]
- 4.Paganetti H., “Four-dimensional Monte Carlo simulation of time-dependent geometries,” Phys. Med. Biol. 49, N75–N81 (2004). 10.1088/0031-9155/49/6/N03 [DOI] [PubMed] [Google Scholar]
- 5.Hall E. J. and Giaccia A. J., Radiobiology for the Radiologist (Lippincott Williams & Wilkins, Philadelphia, PA, 2006). [Google Scholar]
- 6.Calugaru V., Nauraye C., Noel G., Giocanti N., Favaudon V., and Megnin-Chanet F., “Radiobiological characterization of two therapeutic proton beams with different initial energy spectra used at the Institut Curie Proton Therapy Center in Orsay,” Int. J. Radiat. Oncol., Biol., Phys. 81, 1136–1143 (2011). 10.1016/j.ijrobp.2010.09.003 [DOI] [PubMed] [Google Scholar]
- 7.Britten R. A., Nazaryan V., Davis L. K., Klein S. B., Nichiporov D., Mendonca M. S., Wolanski M., Nie X., George J., and Keppel C., “Variations in the RBE for cell killing along the depth-dose profile of a modulated proton therapy beam,” Radiat. Res. 179, 21–28 (2013). 10.1667/RR2737.1 [DOI] [PubMed] [Google Scholar]
- 8.Chaudhary P., Marshall T. I., Perozziello F. M., Manti L., Currell F. J., Hanton F., McMahon S. J., Kavanagh J. N., Cirrone G. A. P., Romano F., Prise K. M., and Schettino G., “Relative biological effectiveness variation along monoenergetic and modulated Bragg peaks of a 62-MeV therapeutic proton beam: A preclinical assessment,” Int. J. Radiat. Oncol., Biol., Phys. 90, 27–35 (2014). 10.1016/j.ijrobp.2014.05.010 [DOI] [PubMed] [Google Scholar]
- 9.Guan F., Bronk L., Titt U., Lin S. H., Mirkovic D., Kerr M. D., Zhu X. R., Dinh J., Sobieski M., Stephan C., Peeler C. R., Taleei R., Mohan R., and Grosshans D. R., “Spatial mapping of the biologic effectiveness of scanned particle beams: Towards biologically optimized particle therapy,” Sci. Rep. 5, 1–10 (2015). 10.1038/srep09850 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Wedenberg M. and Toma-Dasu I., “Disregarding RBE variation in treatment plan comparison may lead to bias in favor of proton plans,” Med. Phys. 41, 091706 (8pp.) (2014). 10.1118/1.4892930 [DOI] [PubMed] [Google Scholar]
- 11.Kramer M., “Treatment planning for heavy-ion radiotherapy: Biological optimization of multiple beam ports,” J. Radiat. Res. 42, 39–46 (2001). 10.1269/jrr.42.39 [DOI] [PubMed] [Google Scholar]
- 12.Scholz M. and Kraft G., “Calculation of heavy ion inactivation probabilities based on track structure, x ray sensitivity and target size,” Radiat. Prot. Dosim. 52, 29–33 (1994). [Google Scholar]
- 13.Scholz M. and Kraft G., “Track structure and the calculation of biological effects of heavy charged particles,” Adv. Space Res. 18, 5–14 (1996). 10.1016/0273-1177(95)00784-C [DOI] [PubMed] [Google Scholar]
- 14.Scholz M., Kellerer A. M., Kraft-Weyrather W., and Kraft G., “Computation of cell survival in heavy ion beams for therapy,” Radiat. Environ. Biophys. 36, 59–66 (1997). 10.1007/s004110050055 [DOI] [PubMed] [Google Scholar]
- 15.Inaniwa T., Furukawa T., Kase Y., Matsufuji N., Toshito T., Matsumoto Y., Furusawa Y., and Noda K., “Treatment planning for a scanned carbon beam with a modified microdosimetric kinetic model,” Phys. Med. Biol. 55, 6721–6737 (2010). 10.1088/0031-9155/55/22/008 [DOI] [PubMed] [Google Scholar]
- 16.Frese M. C., Wilkens J. J., Huber P. E., Jensen A. D., Oelfke U., and Taheri-Kadkhoda Z., “Application of constant vs. variable relative biological effectiveness in treatment planning of intensity-modulated proton therapy,” Int. J. Radiat. Oncol., Biol., Phys. 79, 80–88 (2011). 10.1016/j.ijrobp.2009.10.022 [DOI] [PubMed] [Google Scholar]
- 17.Wilkens J. J. and Oelfke U., “A phenomenological model for the relative biological effectiveness in therapeutic proton beams,” Phys. Med. Biol. 49, 2811–2825 (2004). 10.1088/0031-9155/49/13/004 [DOI] [PubMed] [Google Scholar]
- 18.Frese M. C., Yu V. K., Stewart R. D., and Carlson D. J., “A mechanism-based approach to predict the relative biological effectiveness of protons and carbon ions in radiation therapy,” Int. J. Radiat. Oncol., Biol., Phys. 83, 442–450 (2012). 10.1016/j.ijrobp.2011.06.1983 [DOI] [PubMed] [Google Scholar]
- 19.Semenenko V. and Stewart R., “Fast Monte Carlo simulation of DNA damage formed by electrons and light ions,” Phys. Med. Biol. 51, 1693–1706 (2006). 10.1088/0031-9155/51/7/004 [DOI] [PubMed] [Google Scholar]
- 20.Carlson D. J., Stewart R. D., Semenenko V. A., and Sandison G. A., “Combined use of Monte Carlo DNA damage simulations and deterministic repair models to examine putative mechanisms of cell killing,” Radiat. Res. 169, 447–459 (2009). 10.1667/rr1046.1 [DOI] [PubMed] [Google Scholar]
- 21.Bethe H., “Zur theorie des durchgangs schneller korpuskularstrahlen durch materie,” Ann. Phys. 397, 325–400 (1930). 10.1002/andp.19303970303 [DOI] [Google Scholar]
- 22.Bethe H., “Bremsformel für elektronen relativistischer geschwindigkeit,” Z. Phys. 76, 293–299 (1932). 10.1007/BF01342532 [DOI] [Google Scholar]
- 23.Grassberger C. and Paganetti H., “Elevated LET components in clinical proton beams,” Phys. Med. Biol. 56, 6677–6691 (2011). 10.1088/0031-9155/56/20/011 [DOI] [PubMed] [Google Scholar]
- 24.Chen Y. and Ahmad S., “Empirical model estimation of relative biological effectiveness for proton beam therapy,” Radiat. Prot. Dosim. 149, 116–123 (2012). 10.1093/rpd/ncr218 [DOI] [PubMed] [Google Scholar]
- 25.Romano F., Cirrone G. A., Cuttone G., Rosa F. D., Mazzaglia S. E., Petrovic I., Fira A. R., and Varisano A., “A Monte Carlo study for the calculation of the average linear energy transfer (LET) distributions for a clinical proton beam line and a radiobiological carbon ion beam line,” Phys. Med. Biol. 59, 2863–2882 (2014). 10.1088/0031-9155/59/12/2863 [DOI] [PubMed] [Google Scholar]
- 26.Wilkens J. J. and Oelfke U., “Analytical linear energy transfer calculations for proton therapy,” Med. Phys. 30, 806–815 (2003). 10.1118/1.1567852 [DOI] [PubMed] [Google Scholar]
- 27.Cirrone G. P., Cuttone G., Mazzaglia S. E., Romano F., Sardina D., Agodi C., Attili A., Blancato A. A., De Napoli M., and Di Rosa F., “Hadrontherapy: A geant4-based tool for proton/ion-therapy studies,” Prog. Nucl. Sci. Technol. 2, 207–212 (2011). 10.15669/pnst.2.207 [DOI] [Google Scholar]
- 28.Perles L. A., Mirkovic D., Anand A., Titt U., and Mohan R., “LET dependence of the response of EBT2 films in proton dosimetry modeled as a bimolecular chemical reaction,” Phys. Med. Biol. 58, 8477–8491 (2013). 10.1088/0031-9155/58/23/8477 [DOI] [PubMed] [Google Scholar]
- 29.Sawakuchi G. O., Sahoo N., Gasparian P. B., Rodriguez M. G., Archambault L., Titt U., and Yukihara E. G., “Determination of average LET of therapeutic proton beams using Al2O3:C optically stimulated luminescence (OSL) detectors,” Phys. Med. Biol. 55, 4963–4976 (2010). 10.1088/0031-9155/55/17/006 [DOI] [PubMed] [Google Scholar]
- 30.Kantemiris I., Karaiskos P., Papagiannis P., and Angelopoulos A., “Dose and dose averaged LET comparison of 1H, 4He, 6Li, 8Be, 10B, 12C, 14N, and 16O ion beams forming a spread-out Bragg peak,” Med. Phys. 38, 6585–6591 (2011). 10.1118/1.3662911 [DOI] [PubMed] [Google Scholar]
- 31.Giantsoudi D., Grassberger C., Craft D., Niemierko A., Trofimov A., and Paganetti H., “Linear energy transfer-guided optimization in intensity modulated proton therapy: Feasibility study and clinical potential,” Int. J. Radiat. Oncol., Biol., Phys. 87, 216–222 (2013). 10.1016/j.ijrobp.2013.05.013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Cortés-Giraldo M. and Carabe A., “A critical study of different Monte Carlo scoring methods of dose average linear-energy-transfer maps calculated in voxelized geometries irradiated with clinical proton beams,” Phys. Med. Biol. 60, 2645–2669 (2015). 10.1088/0031-9155/60/7/2645 [DOI] [PubMed] [Google Scholar]
- 33.Granville D. A. and Sawakuchi G. O., “Comparison of linear energy transfer scoring techniques in Monte Carlo simulations of proton beams,” Phys. Med. Biol. 60, N283–N291 (2015). 10.1088/0031-9155/60/14/N283 [DOI] [PubMed] [Google Scholar]
- 34.Wilkens J. J. and Oelfke U., “Fast multifield optimization of the biological effect in ion therapy,” Phys. Med. Biol. 51, 3127–3140 (2006). 10.1088/0031-9155/51/12/009 [DOI] [PubMed] [Google Scholar]
- 35.Kramer M. and Scholz M., “Treatment planning for heavy-ion radiotherapy: Calculation and optimization of biologically effective dose,” Phys. Med. Biol. 45, 3319–3330 (2000). 10.1088/0031-9155/45/11/314 [DOI] [PubMed] [Google Scholar]
- 36.Agostinelli S. et al. , “ geant4—A simulation toolkit,” Nucl. Instrum. Methods Phys. Res., Sect. A 506, 250–303 (2003). 10.1016/S0168-9002(03)01368-8 [DOI] [Google Scholar]
- 37.Allison J. et al. , “ geant4 developments and applications,” IEEE Trans. Nucl. Sci. 53, 270–278 (2006). 10.1109/TNS.2006.869826 [DOI] [Google Scholar]
- 38.ICRU, “Fundamental quantities and units for ionizing radiation (ICRU Report 85),” J. ICRU 11, 1–31 (2011). 10.1093/jicru/ndr012 [DOI] [PubMed] [Google Scholar]
- 39.Attix F. H., Introduction to Radiological Physics and Radiation Dosimetry (Wiley, New York, NY, 1986). [Google Scholar]
- 40.Berger M. J., Coursey J. S., Zucker M. A., and Chang J., estar, pstar, andastar: Computer Programs for Calculating Stopping-Power and Range Tables for Electrons, Protons, and Helium Ions (version 1.2.3), National Institute of Standards and Technology, Gaithersburg, MD, 2005, available at http://physics.nist.gov/Star [July 23, 2014].
- 41.Rossi H. H. and Zaider M., Microdosimetry and Its Applications (Springer, New York, NY, 1996). [Google Scholar]
- 42.geant4 Collaboration, geant4 User’s Guide for Application Developers (2014), see http://geant4.web.cern.ch/geant4/UserDocumentation/UsersGuides/ForApplicationDeveloper/fo/BookForAppliDev.pdf. [Google Scholar]
- 43.Gillin M. T., Sahoo N., Bues M., Ciangaru G., Sawakuchi G., Poenisch F., Arjomandy B., Martin C., Titt U., Suzuki K., Smith A. R., and Zhu X. R., “Commissioning of the discrete spot scanning proton beam delivery system at the University of Texas M.D. Anderson Cancer Center, Proton Therapy Center, Houston,” Med. Phys. 37, 154–163 (2010). 10.1118/1.3259742 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Waters L. S., McKinney G. W., Durkee J. W., Fensin M. L., Hendricks J. S., James M. R., Johns R. C., and Pelowitz D. B., Presented at the Hadronic Shower Simulation Workshop, 2007.
- 45.Sawakuchi G. O., Mirkovic D., Perles L. A., Sahoo N., Zhu X. R., Ciangaru G., Suzuki K., Gillin M. T., Mohan R., and Titt U., “An MCNPX Monte Carlo model of a discrete spot scanning proton beam therapy nozzle,” Med. Phys. 37, 4960–4970 (2010). 10.1118/1.3476458 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Heikkinen A., Stepanov N., and Wellisch J. P., “Bertini intra-nuclear cascade implementation in geant4,” preprint arXiv:nucl-th/0306008 (2003).
- 47.Yarba J., Presented at the Journal of Physics: Conference Series, 2012.
- 48.Brun R. and Rademakers F., “ root—An object oriented data analysis framework,” Nucl. Instrum. Methods Phys. Res., Sect. A 389, 81–86 (1997). 10.1016/S0168-9002(97)00048-X [DOI] [Google Scholar]
- 49.Polster L., Schuemann J., Rinaldi I., Burigo L., McNamara A. L., Stewart R. D., Attili A., Carlson D. J., Sato T., and Méndez J. R., “Extension of TOPAS for the simulation of proton radiation effects considering molecular and cellular endpoints,” Phys. Med. Biol. 60, 5053–5070 (2015). 10.1088/0031-9155/60/13/5053 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Semenenko V. and Stewart R., “A fast Monte Carlo algorithm to simulate the spectrum of DNA damages formed by ionizing radiation,” Radiat. Res. 161, 451–457 (2004). 10.1667/RR3140 [DOI] [PubMed] [Google Scholar]
- 51.Semenenko V., Stewart R. D., and Ackerman E. J., “Monte Carlo simulation of base and nucleotide excision repair of clustered DNA damage sites. I. Model properties and predicted trends,” Radiat. Res. 164, 180–193 (2005). 10.1667/RR3402 [DOI] [PubMed] [Google Scholar]
- 52.Semenenko V. and Stewart R., “Monte Carlo simulation of base and nucleotide excision repair of clustered DNA damage sites. II. Comparisons of model predictions to measured data,” Radiat. Res. 164, 194–201 (2005). 10.1667/rr3414 [DOI] [PubMed] [Google Scholar]
- 53.Kempe J., Gudowska I., and Brahme A., “Depth absorbed dose and LET distributions of therapeutic 1H, 4He, 7Li, and 12C beams,” Med. Phys. 34, 183–192 (2007). 10.1118/1.2400621 [DOI] [PubMed] [Google Scholar]
- 54.Incerti S., Ivanchenko A., Karamitros M., Mantero A., Moretto P., Tran H., Mascialino B., Champion C., Ivanchenko V., and Bernal M., “Comparison of geant4 very low energy cross section models with experimental data in water,” Med. Phys. 37, 4692–4708 (2010). 10.1118/1.3476457 [DOI] [PubMed] [Google Scholar]
- 55.Incerti S., Baldacchino G., Bernal M., Capra R., Champion C., Francis Z., Guèye P., Mantero A., Mascialino B., and Moretto P., “The geant4-DNA project,” Int. J. Model., Simul., Sci. Comput. 1, 157–178 (2010). 10.1142/S1793962310000122 [DOI] [Google Scholar]
- 56.Karamitros M., Incerti S., and Champion C., “376 the geant4-DNA project,” Radiother. Oncol. 102, S191–S192 (2012). 10.1016/S0167-8140(12)70325-0 [DOI] [Google Scholar]










