Systems biology and mechanics of growth

Abstract

In contrast to inert systems, living biological systems have the advantage to adapt to their environment through growth and evolution. This transfiguration is evident in embryonic development, when the predisposed need to grow allows form to follow function. Alterations in the equilibrium state of biological systems breed disease and mutation in response to environmental triggers. The need to characterize the growth of biological systems to better understand these phenomena has motivated the continuum theory of growth and stimulated the development of computational tools in systems biology. Biological growth in development and disease is increasingly studied using the framework of morphoelasticity. Here we demonstrate the potential for morphoelastic simulations through examples of volume, area, and length growth, inspired by tumor expansion, chronic bronchitis, brain development, intestine formation, plant shape, and myopia. We review the sytems biology of living systems in light of biochemical and optical stimuli and classify different types of growth to facilitate the design of growth models for various biological systems within this generic framework. Exploring the systems biology of growth introduces a new venue to control and manipulate embryonic development, disease progression, and clinical intervention.

MOTIVATION

Growth is a phenomenon unique to biological living systems. Specifically soft tissue growth, as is seen in early embryonic stage development or disease, is classified as the volumetric increase in mass, as opposed to changes in density (Ambrosi et al. 2011). This noticeable alteration in shape and structure gives rise to the often-explored notion in mechanics, the pursuit of understanding how form follows function (Kuhl 2014). Differential growth, the phenomenon of different growth rates of neighboring regions, is a vital ingredient to embryogenesis (Gasser 2006), but also a characteristic hallmark of inflammatory disease (Coussens and Werb 2002). Whether in the natural stages of embryonic development or in defensive response to disease progression, the iteration between functionality and form has long been of interest to basic sciences of various disciplines (Taber 1995). However, it still remains a mystery how organs know when to cease or continue development and how they modulate their structure and shape by differential growth (Vogel 2013).

Soft tissue growth can be classified as two types (Taber 1995): mechanically driven growth, where stress or strain provoke growth, for example, in patients with high blood pressure who develop thickened heart walls to sustain the increased pressure; and biochemically, optically, or generally non-mechanically driven growth, that is frequently observed in embryonic development or disease (Kuhl 2014). Here we focus on the latter type of growth, commonly referred to as morphogenetic growth or morphoelasticity (Goriely and Ben Amar 2007). In morphoelasticity, the underlying biological system drives the tissue to change form; this growth alters the mechanics of the system and its function (Dervaux and Ben Amar 2008). For example, in pulmonary disease, inflammation and remodeling of asthmatic airway walls result in airway collapse due to the growth-induced mechanical instability of cells flooding the mucosal lining (Eskandari, Kuschner, and Kuhl 2015). During embryonic development, growth-induced folding of the cortex may dictate the difference between schizophrenia and healthy function (Budday, Raybaud, and Kuhl 2014). While understanding the underlying biochemistry that causes morphogenetic growth is important, it is equally critical to understand how the tissue takes shape and how instabilities are caused by residual stresses generated by the growing tissue (Ben Amar and Goriely 2005; Volokh 2006).

Characterizing the mechanics of growth has long been used as a method of capturing bodily development and progression of disease (Menzel and Kuhl 2012). The numerous mechanisms of differential growth including the imbalance of homeostasis, the excessive or lacking hormonal signals, the defensive responses to toxins and pollutants, or the general embryonic formation lead to cell proliferation, hypertrophy, and migration. Biological systems are often modeled as continua where the tissue layers, embedded vessels and veins, influx of cells, and passing of proteins across the cellular membrane are viewed as sub-systems within a larger biological system of the organ-level analysis, defined by an overarching governing behavior (Jones and Chapman 2012; Nelson et al. 2005). In growth mechanics, we often characterize the overall behavior of the tissue or organ using solid and continuum mechanics, assuming an overall elastic response (Böl and Bolea Albero 2014; Dervaux and Ben Amar 2008). Table 1 summarizes selected examples of growing systems in development and disease. For each system, we highlight the biological description and suggest a morphoelastic model, which captures its behavior via volumetric, area, and length growth.

Table 1. Examples of morphogenetic growth in development or disease.

Asterisk indicates simulations illustrated in this publication. Biological phenomena highlight the growth concept from a medical and scientific perspective: development describes organogenesis and morphogenesis, growth driven by genetic signaling for development of bodily organs; disease indicates growth or deterioration signaling in response to infection or disorder. Growth can occur in volume, area, or length. Some morphogenetic models account for mechanical driving forces in addition to the non-mechanical driving forces highlighted throughout this monograph.

System	Biological Phenomenon	Mechanical Model
Brain*	Development and Disease (Callen et al. 2001; Hofman 1989; Welker 1990; Xu et al. 2010)	Length (Bayly et al. 2013; Holland, Miller, and Kuhl 2015) Area (Bayly Taber, Kroenke 2014; Budday, Steinmann, and Kuhl 2014; Budday, Raybaud, and Kuhl 2014; Toro and Burnod 2005; this study) Volume (Richman et al. 1975)
Ear	Development (Wright 1997)	Area (Kagurasho et al. 2012)
Eye*	Development and Disease (Cui, Trier, and Munk Ribel- Madsen 2013; Dolgin 2015; Grytz et al. 2012; McBrien, Jobling, and Gentle 2009)	Length (Kimpton 2015; this study) Area (Hosseini, Beebe, and Taber 2014)
Heart	Development (Lin 1994; Taber 2001; Taber 2001)	Length (Göktepe et al. 2010a) Volume (Göktepe, Abilez, and Kuhl 2010; Taber 1995)
Intestines*	Development (Savin et al. 2011)	Area (Ciarletta and Ben Amar 2012; Balbi and Ciarletta 2013; Balbi, Kuhl, and Ciarletta 2015)
Lung*	Disease (Tony R Bai and Knight 2005; Eskandari, Pfaller, and Kuhl 2013; Kamm 1999)	Volume (Li, Cao, Feng, and Yu 2011; Moulton and Goriely 2011; Eskandari, Kuschner, and Kuhl 2015)
Plant*	Development (Srivastava 2002)	Length (Holland et al. 2013; Thimann and Schneider 1938; Vandiver and Goriely 2009)
Tumor*	Disease (Coussens and Werb 2002; Hanahan and Weinberg 2000)	Volume (Ambrosi and Mollica 2002; Ciarletta 2013; Ambrosi, Preziosi, and Vitale 2012)

One concerning type of undesirable growth is projected to affect 2.5 billion people by the end of this decade: growth leading to an elongated eye which causes myopia or shortsightedness (Dolgin 2015). The optical stimulus, or lack thereof, inhibits biochemical signaling pathways responsible for preventing excessive eye growth; children’s shortage of exposure to the outdoors and bright sunlight suppresses the hormone dopamine, which is vital to stop the disproportionate growth of the eye (Cui, Trier, and Munk Ribel-Madsen 2013). In addition to these kinematic changes, myopic eyes display remodeling via marked increase in elasticity (McBrien, Jobling, and Gentle 2009, Grytz et al. 2012). Figure 1 illustrates a finite element simulation of growth-induced geometric changes in the eye motivated by a recent monograph on eye growth (Kimpton et al. 2015). The focal point of the light passing through the cornea and focusing through the lens is no longer located on the retina. The altered geometry disrupts the optical environment necessary for proper vision. To address this problem, more and more children and teenagers are being fitted with glasses and contact lenses—growth has dictated the form of the system and the form of the system has modified the function. This example of myopia illustrates how morphological alterations or changes of physiological growth can give rise to abnormalities and even cause disease.

Figure 1. Axial growth of the eyeball.

During myopia, the elongation of the eye causes the light to focus prior to reaching the retina. This shift of focus results in blurry vision and shortsightedness. Growth mechanics can illustrate this phenomenon.

We classify the interplay of form and function for selected living systems in Table 1. We distinguish between developmental growth and diseased growth for the brain, ear, eye, heart, intestines, lung, plant, and tumor. While many biological systems have well-established morphoelastic models to explore development and disease, other systems, such as the developing ear or the disesed eye, remain underexplored from a mechanical perspective. To illustrate the potential to model novel systems, we categorize morphoelastic growth to be primarily in volume, area, or length. We highlight the general continuum model and the computational model for these growing systems. We discuss developmental and diseased non-mechanical biological systems that undergo volumetric, area, and length growth, subsequently reviewing the approaches applicable to each kind of system. All simulations use the framework proposed in this review and serve as exclusive examples of growth-driven mechanics. Our overall objective is to illustrate the impact of growth on mechanics and to provide a framework and reference, which enables the reader to classify different types of growth and understand how to simulate the systems biology of growth.

METHODS

To model the systems biology of growth in developmental or diseased, we illustrate the continuum and computational modeling of growth. We view the biological system as composed of many sub-systems, which we look at from a higher-level: within the organ scale, we assume that tissues composed of veins, cells, and various substructures are perceived as a uniform continuum (Garikipati et al. 2004). We define growth of living systems as an increase in mass, which can occur through either an increase in volume or an increase in density, or both (Kuhl and Steinmann 2003). For most soft tissues, growth is characterized as an increase in volume through kinematic alterations (Epstein and Maugin 2000).

Continuum Modeling of Growth

The motion of a growing body is defined through the deformation φ as shown in Figure 2. Particles located at X in the material or undeformed, stress-free configuration β_o are mapped to x in the spatial deformed configuration β_t, via x = φ(X,t), where φ is a function of the particles’ original location X and the current time t. The deformation gradient F is fundamental to characterize finite growth. At a fixed time, the gradient of the deformation φ with respect to X defines F:

$$\mathit{F}={\nabla }_X\mathit{\phi }.$$ (1)

Figure 2. Kinematics of growth.

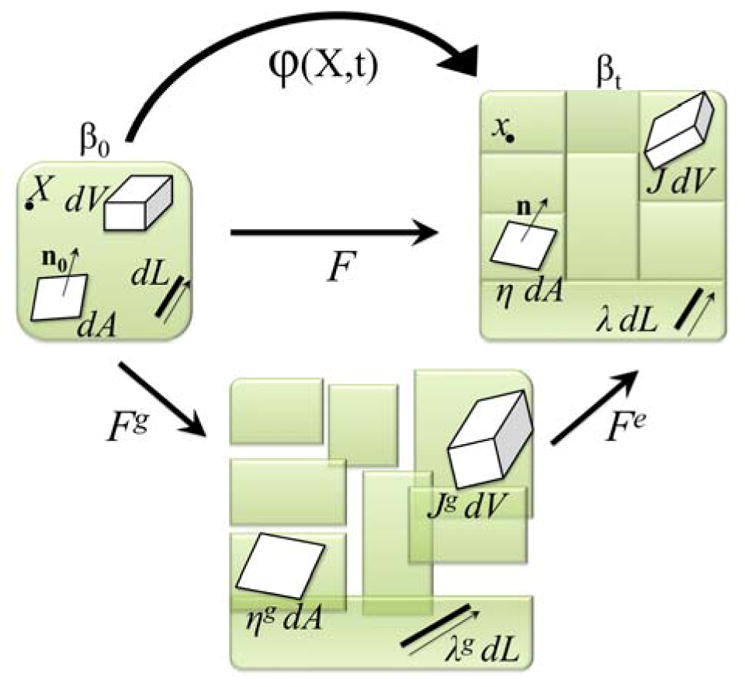
Undeformed configuration β₀, incompatible grown configuration, and deformed configuration β_t. Line elements associated with λ, area elements associated with η, and volume elements associated with J are shown in the overall multiplicative decomposition of F = F^e · F^g.

In the case of finite growth, the deformation due to growth manifests itself in the deformation gradient F, which would otherwise be purely elastic and reversible upon removal of the loads. However, F is now multiplicatively composed of an elastic and growth part (Rodriguez, Hoger, and McCulloch 1994):

$$\mathit{F}={\mathit{F}}^e·{\mathit{F}}^g.$$ (2)

Figure 2 shows the initial configuration β_o, grown to an incompatible configuration via the growth tensor F^g, and made to fit back together as shown in the current configuration β_t via the elastic deformation tensor F^e; together forming the overall deformation gradient F. The growth tensor follows from the underlying systems biology.

The stress required to make the incompatible grown pieces compatible and fit back together is conceptually understood as the residual stresses unique to biological systems (Taber 1995, Rausch and Kuhl 2013). The change in volume, area, and length between elements of the undeformed and deformed configurations is defined using F. Its Jacobian denotes the total change in volume, which can also be decomposed multiplicatively as

$$J=det(\mathit{F})=J^e{J}^g,$$ (3)

where J^e = det(F^e) is reversible and J^g = det(F^g) is irreversible and characterizes the amount of volumetric growth. The surface area change η is defined by Nanson’s formula:

$$\eta =\Vert J{\mathit{F}}^{-t}·{\mathit{n}}_o\Vert ={\eta }^e{\eta }^g.$$ (4)

Similarly, it is decomposed in to a reversible η^e and irreversible part η^g = ||J^g F^g−t · n_o||, where n_o denotes the unit surface normal. To account for lengthwise growth, the change in length λ uses the norm of the stretched unit vector n_o, the microstructural direction of growth, via

$$\lambda =\Vert \mathit{F}·{\mathit{n}}_o\Vert ={\lambda }^e{\lambda }^g$$ (5)

and λ^g = ||F^g · n_o||. Again, the change in length is also multiplicatively decomposable, and λ^e can be found be recalling the relation λ^e = λ · λ^g−1, analogous to area and volume analyses. We further introduce the right Cauchy-Green deformation tensor, generally defined as

$$\mathit{C}={\mathit{F}}^t·\mathit{F}={\mathit{F}}^{gt}·{\mathit{F}}^{et}·{\mathit{F}}^e·{\mathit{F}}^g={\mathit{F}}^{gt}·{\mathit{C}}^e·{\mathit{F}}^g,$$ (6)

where the elastic definition is C^e = F^et · F^e. Similarly, the left Cauchy-Green deformation tensor and elastic tensor are

$$\mathit{b}=\mathit{F}·{\mathit{F}}^t\text{and}{\mathit{b}}^e={\mathit{F}}^e{\mathit{F}}^{et}.$$ (7)

To formulate the constitutive laws, we further need the right Cauchy-Green growth tensor C^g = F^gt · F^g and its inverse which can be related to the left elastic Cauchy-Green deformation tensor b^e via

$${\mathit{C}}^{g-1}={\mathit{F}}^{g-1}·{\mathit{F}}^{g-t}={\mathit{F}}^{-1}·{\mathit{F}}^e·{({\mathit{F}}^{-1}·{\mathit{F}}^e)}^t={\mathit{F}}^{-1}·{\mathit{b}}^e·{\mathit{F}}^{-t}.$$ (8)

For simplicity, we assume that the elastic response of the material is purely isotropic, defined in terms of invariants J^e and $I_1^e$,

$$J^e=det({\mathit{F}}^e)\text{and}{I}_1^e={\mathit{C}}^e:\mathit{I}={\mathit{b}}^e:\mathit{I}.$$ (9)

In the context of growth, viscous effects can usually be neglected because of the separation of ψ time scales (Drozdov and Khanina 1997). For simplicity, we choose a hyperelastic, isotropic material response in the form of the Helmholtz free energy function parameterized by the invariants J^e and $I_1^e$,

$$\psi =\frac{1}{2}\lambda {ln}^2(J^e)+\frac{1}{2}\mu [I_1^e-3-2ln(J^e)],$$ (10)

where λ and μ are the Lamé parameters. In general, most biological systems are anisotropic and an anisotropic free energy function ψ, for example the widely used Holzapfel model would be more appropriate (Holzapfel, Gasser, and Ogden 2000). To define the elastic Piola-Kirchhoff stress, we use standard arguments of thermodynamics and apply the chain rule,

$${\mathit{S}}^e=2\frac{\partial \psi }{\partial {\mathit{C}}^e}=2\left[\frac{\partial \psi }{\partial J^e}\frac{\partial J^e}{\partial {\mathit{C}}^e}+\frac{\partial \psi }{\partial I_1^e}\frac{\partial I_1^e}{\partial {\mathit{C}}^e}\right]=[\lambda ln(J^e)-\mu ]{\mathit{C}}^{e-1}+\mu \mathit{I},$$ (11)

recalling that $\frac{\partial J^e}{\partial {\mathit{C}}^e}=\frac{1}{2}{J}^e{\mathit{C}}^{e-1}$ and $\frac{\partial I_1^e}{\partial {\mathit{C}}^e}=\mathit{I}$. We then obtain the Piola-Kirchhoff stress from the relationship between the overall stress S and the elastic stress S^e.

$$\mathit{S}={\mathit{F}}^{g-1}·{\mathit{S}}^e·{\mathit{F}}^{g-t}=[\lambda ln(J^e)-\mu ]{\mathit{C}}^{-1}+\mu {\mathit{C}}^{g-1}.$$ (12)

We can obtain the corresponding Kirchhoff stress via the standard push-forward,

$$\mathit{\tau }={\mathit{F}}^e·{\mathit{S}}^e·{\mathit{F}}^{et}=[\lambda ln(J^e)-\mu ]\mathit{i}+\mu {\mathit{b}}^e,$$ (13)

where i denotes the spatial unit tensor. The stress-strain relationship is non-linear and requires the tangent operator for the Newton-Raphson iteration to enforce the global equilibrium equations. The Lagrangian tangent moduli result from the derivative of the stress using the chain rule

$${\mathit{L}}^e=\frac{\partial {\mathit{S}}^e}{\partial {\mathit{C}}^e}={\mathit{C}}^{e-1}\otimes {\mathit{C}}^{e-1}-(\lambda ln(J^e)-\mu )[{\mathit{C}}^{e-1}\overline{\otimes }{\mathit{C}}^{e-1}+{\mathit{C}}^{e-1}\stackrel{\sim }{\otimes }{\mathit{C}}^{e-1}]$$ (14)

where L^e denotes the elastic tangent moduli, which are related to overall tangent L by

$$\mathit{L}={\mathit{F}}^{g-1}\overline{\otimes }{\mathit{F}}^{g-1}:{\mathit{L}}^e:{\mathit{F}}^{g-t}\overline{\otimes }{\mathit{F}}^{g-t}.$$ (15)

Finally, the Eulerian tangent moduli are related to the Lagrangian moduli via the standard push-forward,

$$\mathit{e}=\frac{1}{J}[\mathit{F}\overline{\otimes }\mathit{F}:\mathit{L}:{\mathit{F}}^{-t}\overline{\otimes }{\mathit{F}}^{-t}].$$ (16)

For the non-standard fourth order tensor products, we have used the abbreviations

$$\begin{array}{l}{\{\ast \otimes \circ \}}_{\mathit{ijkl}}={\{\ast \}}_{ij}{\{\circ \}}_{kl}\\ {\{\ast \overline{\otimes }\circ \}}_{\mathit{ijkl}}={\{\ast \}}_{ik}{\{\circ \}}_{jl}\\ {\{\ast \stackrel{\sim }{\otimes }\circ \}}_{\mathit{ijkl}}={\{\ast \}}_{il}{\{\circ \}}_{jk}\end{array}$$

to denote the operators. It is important to note that this growth model is purely morphoelastic (Goriely and Ben Amar 2007). Therefore, the tangent is computed with respect to F^e with F^g constant; the complimentary tangent, the derivative of the stress with respect to F^g maintaining F^e constant is zero; this is unique due to the non-mechanical nature of F^g. The tangent would have an additional term should if growth was mechanically driven (Menzel 2005), for example in strain-induced skin growth (Buganza Tepole et al. 2011) or stress-induced cardiac growth (Göktepe et al. 2010).

We have now defined the governing equations of the continuum model. The key kinematic entity that characterizes growth is the second-order growth tensor F^g. Table 2 summarizes the formulation of the growth tensor for different types of growth.

Table 2. Overview of growth kinematics.

Growth can be categorized as volume, area, and length growth. Depending on the biological system, a selection of growth types and corresponding growth tensors for growth factors ϑ₁, ϑ₂, and ϑ₃ and growth directions n₁, n₂, and n₃ is shown. Illustrations of how the growth would change unit volume, area, or length are portrayed. The right column summarizes common forms of growth kinetics, linear and exponential.

Growth Type	Growth Tensor	Growth Evolution
Volume	General Anisotropic Growth ϑ1 n1 ⊗ n1 + ϑ2 n2 ⊗ n2 + ϑ3 n3 ⊗ n3 Simple Isotropic Growth ϑI	Constant Growth Rate: $$\stackrel{.}{\vartheta }=G,$$ Growth: $$\vartheta (t)=1+G·t$$ Exponential Growth Rate: $$\stackrel{.}{\vartheta }=({\vartheta }^{\mathit{max}}-1)\frac{1}{\tau }\left(e^{\frac{-t}{\tau }}\right)$$ Growth: $$\vartheta =1+({\vartheta }^{\mathit{max}}-1)\left(1-e^{\frac{-t}{\tau }}\right)$$
Area	General Anisotropic Growth ϑ1 n1 ⊗ n1 + ϑ2 n2⊗ n2 Simple Isotropic Growth ϑI − ϑn3 ⊗ n3
Length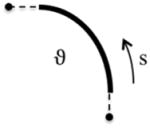	Single Direction Growth ϑ s ⊗ s

Types of Growth

As shown in Table 2, while the form of F^g is specific to the problem, a scalar-values growth factor ϑ is often selected based on clinical observations to represent the history of growth over time. For more complex types of growth, we typically need to introduce more growth parameters ϑ and capture anisotropy, for example, through growth along specific directions using a microsphere approach (Menzel, Harrysson, and Ristinmaa 2008). In the most general case, which we will not consider here, these microstructural directions could also evolve in time (Menzel 2007). The evolution of tissue microstructure, here represented exclusively through the growth factor, should be informed by the subsystems in the body that trigger growth. In addition to the different growth kinematics, growth may differ for different materials. This naturally introduces the notion of differential growth (Vandiver and Goriely 2009, Moulton and Goriely 2011). It is important to consider these specifics in the mechanics of growth. On the smaller scales, growth can be credited to cell proliferation, death, and engorgement, but also to changes in the extracellular matrix (Ambrosi et al. 2011). Considerations of all these factors inform the evolution of the growth value depicted in Table 2.

For most growing systems, there is limited information about the time evolution of growth and longitudinal data; a constant growth rate ϑ̇ can be used for simplicity (Eskandari, Kuschner, and Kuhl 2015). Other more complex temporal evolutions, such as exponential and asymptotic, are also frequently used, including growth criteria that are active only when the applied growth value exceeds a certain threshold (Ambrosi and Mollica 2002). Here, for illustrative purposes, we propose a constant growth rate for all examples, reflected through a linear relation between growth ϑ and time t. However, in Table 2, we also provide the common exponential form of growth.

Computational Modeling of Growth

We solve the governing equations for finite growth using a nonlinear finite element approach, in which the body is discretized and incrementally grown. The growth value ϑ is calculated for each successive time step, depending on the linear relation with time, and used to calculate the individual growth tensor F^g from Table 2. The elastic tensor F^e is then found from equation (2), yielding the elastic left Cauchy-Green deformation tensor b^e from equation (7). Using the constitutive relation in equation (10), the resulting stress definition τ from equation (13), and tangent moduli c from equation (16), we adopt an iterative Newton-Raphson scheme to solve the resulting residual problem. We ensure convergence by automatically adapting the time step size to solve the residual of the global equilibrium equation. Once the current step satisfies equilibrium, we update F^g by the next ϑ value and grow the body further.

VOLUME GROWTH

The simplest version of finite growth is volumetric growth in which growth is seen to occur in all directions. It is habitually compared to thermal expansion (Skalak 1981). This type of growth is applicable to diseased states, such as in tumor growth controlled by nutrient supply to increase the tumor size (Ambrosi and Mollica 2002; Coussens and Werb 2002; Hanahan and Weinberg 2000). The loss of biological homeostasis leads to growth of a stiffer tissue (Ciarletta 2013), often noticeable in ductile carcinoma presenting itself in the mammary glands of what is widely known as breast cancer. Modeling of such a prevalent disease mechanism enables better targeting of interventions such as chemotherapy (Araujo and McElwain 2004). While tumors are often heterogeneous, reacting differently depending on the regions which receive more or less nutrients (Araujo and McElwain 2004), here we illustrate homogenous growth of a tumor lodged inside a duct. For this example, in agreement with the literature, the spherical tumor is stiffer than the surrounding duct (Ciarletta 2013). Upon growth, the tumor grows to nearly the full diameter, pushes against the duct, and eventually migrates through the duct wall. Figure 3 illustrates the stress profile of the duct and the tumor as it grows. Red indicates the region of highest stress and is located at the interface between the tumor surface and duct wall, indicating regions of high rupture risk (Volokh 2006). The duct bulges outwards due to the force induced by tumor growth. This model can readily inform studies of tumor growth and eventually help design treatments focused on preventing the tumor from spreading.

Figure 3. Volume growth of a tumor.

Disease-driven isotropic volume growth of a tumor inside a duct as in the case of breast cancer. The duct is assumed to be free to deform as the tumor grows. Assuming a homogeneous nutrients supply, the tumor grows homogeneously and isotropically, while its overall deformation is constrained by the wall of the duct. Tumor growth causes deformation of the mammary gland. According to this model, the duct-tumor interface, the site of high stress concentrations indicated in red, suggests high risk of rupture.

Similar to tumors, in which a lack of bodily equilibrium initiates a biochemical imbalance, in chronic obstructive lung disease, an inflammatory response triggered by toxins and allergens stimulates growth (Bai et al. 2000; Eskandari, Pfaller, and Kuhl 2013). In contrast to tumors, the cylindrical airway duct itself is the site of growth (Kamm 1999). During inflammation, the thickening of the airway wall folds the perimeter inwards causing airflow obstruction, a typical hallmark of asthma and chronic bronchitis (Eskandari, Kuschner, and Kuhl 2015). Growth drives a mechanical instability caused by increasing wall stresses (Javili, Steinmann, and Kuhl 2014; Moulton and Goriely 2011). The underlying mechanism is a growing stiffer inner layer, the mucosa, enclosed by a softer outer layer, the submucosa (Bai et al. 1994).

The example in Figure 4 illustrates a patient-specific airway model created from magnetic resonance images and its bi-layered branching airway segment (Eskandari, Kuschner, and Kuhl 2015). The outer layer of the submucosa is fixed, imitating the spongy parenchymal tissue that tethers open the airways. The mucosa layer grows isotropically (Li et al. 2012; Moulton and Goriely 2011) and folds in different patterns depending on the airway’s geometry and stiffness. Prior work has analyzed obstruction sensitivity with respect to geometry and stiffness, because fewer large folds are more likely to cause airway obstruction than numerous small folds (Eskandari, Pfaller, and Kuhl 2013; Li et al. 2011; Moulton and Goriely 2011). The morphogenetic growth phenomena considered here illustrate isolated body growth for the single-material tumor and interactive growth for the bi-material airways. These models can be applicable beyond medical implications and provide insight into wrinkling and folding of bi-material layers in material science and manufacturing (Kuhl 2014; Li et al. 2012).

Figure 4. Volume growth of the airway wall.

Patient-specific branch of the human airway where the mucosal layer is subjected to isotropic growth and the outer submucosa layer is constrained. Growth-induced instabilities are shown as the airway experiences an influx of cells, a biochemical bodily reaction to toxins and pollutants. The regions of high displacement are shown in red illustrating the obstruction of the lumen as disease-driven growth folds the airway walls inwards.

AREA GROWTH

In area growth, tissues grow only within the plane while their thickness remains virtually constant. Either a single unified growth factor or two independent growth factors can be assigned to model isotropic or anisotropic area growth, as presented in Table 2. Area growth is characteristic of skin (Buganza Tepole et al. 2011) but also present in the form of surface growth in horns (Skalak, Farrow, and Hoger 1997). Recent mathematical formulations characterize the behavior specific to growing surfaces (Papastavrou, Steinmann, and Kuhl 2013). Similar to the previous section, typical examples include bi-material layers, which grow at different rates. For the example of the brain, there are several competing theories that explain the development of gyri and sulci, the folds that incur peaks and valleys (Xu et al. 2010). One of them, the theory of differential growth, explains brain folding as a growing stiffer outer layer, the cortex, on a soft inner core, the subcortex (Bayly et al. 2013; Holland, Miller, and Kuhl 2015). The formation of these instabilities and wrinkles is critical to proper mental function and lack of folds may indicate disease (Budday, Raybaud, and Kuhl 2014). Surface growth is significant during brain development and decreased or increased surface-to-volume ratios are often associated with malformations including the prominent examples of lissencephaly and polymicrogyria (Budday, Steinmann, and Kuhl 2014). In the brain, growth is induced by a non-mechanical preprogrammed activation during embryonic stages.

Using the methods highlighted in Section 2, Figure 5 shows the cortical folding patterns that evolve during growth. The formation of these folds protrudes away from the center as the elliptical three-dimensional brain appears to increases in overall shape. Once growth reaches a critical stage, folds emerge and form the familiar gyral shapes.

Figure 5. Area growth of the cerebral cortex.

Morphologically driven brain development of growing external cortical layer on elastic subcortical core. The area growth of the expanding cortex triggers mechanical instabilities, which shape the characteristic folding pattern of our brain. As the surface grows, regions of high stress develop in regions of highest curvature. The brain can be simplified as a homogenous bi-layered structure, in which existing or lacking folds are characteristic of healthy or diseased states.

In the example of the intestines, embryonic growth is sectioned into three main stages during development (Balbi and Ciarletta 2013). To model the formation of realistic intestinal structures, the inner layer of the intestine is grown radially and circumferentially (Balbi, Kuhl, and Ciarletta 2015). Figure 6 illustrates a two-dimensional view of the circular cross-section, where the innermost layer grows thicker eventually buckling inwards and creating folds characteristic of the gut. During this temporal evolution, we see folds appearing throughout the length of intestines (Ciarletta, Balbi, and Kuhl 2014). Given a stiff inner layer and the geometric parameters, the instability and fold formation are naturally occurring and would be altered for different material and geometric properties (Ciarletta and Ben Amar 2012). Area growth is naturally visible as surface growth of thin biological membranes. However, it can also appear as cross-sectional area growth of three-dimensional structures, for example in skeletal muscle (Wisdom, Delp, and Kuhl 2015).

Figure 6. Area growth of the intestinal lining.

The development of ridges in the gut is caused by area growth in the radial and circumferential directions. The inner stiff mucosa layer is grown on a soft submucosa core. The instabilities that occur in an enclosed cylindrical geometry are characteristic of intestinal morphogenesis during embryonic development. The resulting surface patterns are directly comparable to clinical endoscopies.

In contrast to the folding of diseased airways, the mechanical instabilities during organogenesis of the brain and the intestine are essential for appropriate bodily function. Both types of biological growth can be classified as area growth. Typically, the non-growing direction is characterized by the surface normal, which can be subtracted from the isotropic three-dimensional form of the growth tensor to obtain isotropic two-dimensional growth as shown in Table 2.

LENGTH GROWTH

Fiber growth is the elongation along a single material direction regardless of whether this is a straight line or a curvilinear path. Mechanically induced lengthwise growth may be seen in muscle (Wisdom, Delp, and Kuhl 2015), where the strain induced by overstretching the muscle and its unitary sarcomere components triggers biological growth. This type of axial directional growth leads to elongated or shortened shape in a single direction. In the case of a plant or leaf growth, both nutrient-driven and genetically-programmed growth can be understood as the non-mechanical driver for the growth response (Hathway 1990). Classical examples in plant physiology including growing rhubarb or curly dock can be modeled using this framework (Vandiver and Goriely 2008; Holland et al. 2013).

The Rumex Crispus leaflet is a tri-material strip, with distinct growth rates for each material. The plant has three different material characteristics, a stiff outermost layer, growing at a much faster rate than the stem, located at the joint of the two leaf planes, which is deemed the stiffest part. The remaining middle body is softer and elastic, but not growing. Figure 7 illustrates the evolution of instabilities and the resulting folding patterns in the Rumex Crispus leaflet. The color indicates the growth value of the outer layer. As the outer layer grows, the initially flat surface forms the characteristic folded contours of the Rumex Crispus plant. This example illustrates the ability to increasingly enhance the desired model with additional materials and varying growth rates to create morphogenetic growth models capable of reproducing biological structural form.

Figure 7. Length growth of a plant leaf.

Initial configuration of the leaf (left) morphing into Rumex Crispus shape (right). The outermost edge of the leaf is subjected to growth; increasing growth value over time shown through the color scheme. The intersection of the two planar sections forms the stiff stem and grows slower than the outer edges. The intermediate material is softer than the stem and the edge, but does not grow. Simulation of the Rumex Crispus leaf is possible through fiber or lengthwise growth.

For the myopic eye, growth is aligned with the axial direction. In contrast to the Rumex Crispus leaf, the eye ball can be considered as a single material. We fix a single point on the external edge of the cornea and the thicker wall region in space and allow the entire eye to undergo uniform growth. The result is an elongated eyeball as seen in myopia (Kimpton et al. 2015). Growth alters the optically optimal geometry and the location of focus, which ultimately causes shortsightedness. Understanding the systems biology of the eye through the lense of mechanics allows novel insight into a growing disease phenomenon that already affects billions of people (Dolgin 2015).

While a plant is macroscopically uni-directional whereas the eye is not, the growth of both systems is conceptually similar. The nutrient driven photosynthesis process resulting in leaf shape is analogous to the optically driven axial elongation of the myopic eyeball. Once we have identified the growth-inducing mechanism, we can isolate the tissues responding to these alterations, and assign them a specific growth law. Conceptually, it is simply a matter of classifying the type of growth, adding complexities of different growth rates, and locating regions of various material properties to accurately model the morphoelasticity of living systems.

CONCLUSION

Growth and adaptation are distinguishing features of all living things. In this review, we have extensively revisited morphogenetic growth stimulated by biochemical and optical factors during development and disease. We have presented a continuum and computational framework to model volume, area, and length growth, and reviewed the systems biology of growth to identify and classify the different growth mechanism. We have highlighted the systems biology of growth using various examples including growth of the brain, lung, intestines, plants, tumors and the eye. While longitudinal experimental data to inform these models are still rare, our first prototype simulations yield realistic shapes and patterns that agree with observations. In understanding the growth and adaptation of living systems, it is critical to comprehend how function and form are intertwined. Through selected simulations, we elucidate how to simulate and understand growing systems through computational modeling to provide deeper insight into the systems biology of growth.