Learning feedback and feedforward control in a mirror-reversed visual environment

Abstract

When we learn a novel task, the motor system needs to acquire both feedforward and feedback control. Currently, little is known about how the learning of these two mechanisms relate to each other. In the present study, we tested whether feedforward and feedback control need to be learned separately, or whether they are learned as common mechanism when a new control policy is acquired. Participants were trained to reach to two lateral and one central target in an environment with mirror (left-right)-reversed visual feedback. One group was allowed to make online movement corrections, whereas the other group only received visual information after the end of the movement. Learning of feedforward control was assessed by measuring the accuracy of the initial movement direction to lateral targets. Feedback control was measured in the responses to sudden visual perturbations of the cursor when reaching to the central target. Although feedforward control improved in both groups, it was significantly better when online corrections were not allowed. In contrast, feedback control only adaptively changed in participants who received online feedback and remained unchanged in the group without online corrections. Our findings suggest that when a new control policy is acquired, feedforward and feedback control are learned separately, and that there may be a trade-off in learning between feedback and feedforward controllers.

humans have the remarkable ability to adjust movements to novel tasks or environments. To achieve desired motor actions, the system needs to modify both feedforward and feedback control processes. Better feedforward control enables successful open-loop control during fast movements, whereas the feedback controller is necessary to make online error corrections when unexpected visual or dynamic disturbances occur (Desmurget et al. 1999; Pruszynski et al. 2011).

The relationship between feedforward and feedback control is still a matter of debate. A number of studies have shown that, after adaptation of feedforward control, motor feedback responses to unanticipated errors become task appropriate, indicating that feedback and feedforward control are tightly coupled (Ahmadi-Pajouh et al. 2012; Cluff and Scott 2013; Wagner and Smith 2008). However, other studies have suggested that the two can be dissociated. In the framework of structural learning (Braun et al. 2009, 2010a, 2010b), a study demonstrated that responses to dynamic perturbations during reaching movements can be modified in a structural manner, and that these modifications are at least partly dissociable for feedback and feedforward control (Yousif and Diedrichsen 2012).

The coupling between feedforward and feedback control may therefore depend on whether an existing motor skill is adapted within the existing structure, or whether a new motor skill is acquired, i.e., a new structure needs to be learned. A recent study (Telgen et al. 2014) compared learning of visuomotor rotations to learning of mirror reversals. For mirror reversal, both feedforward and feedback commands required initially more time to be computed correctly, indicating that a new control policy had to be acquired. In contrast, no time-accuracy tradeoff was found for visual rotations, indicating a parametric change within an existing control policy, which thereby can inherit the established automaticity of the underlying computational processes.

Here we ask whether feedforward and feedback control need to be learned separately when a new control policy is acquired. Participants were trained to reach under left-right mirror-reversed (MR) visual feedback. We quantified learning of feedforward control using the relationship between reaction time (RT) and initial movement accuracy. Feedback control was assessed by the amplitude and direction of force responses to sudden visual perturbation of the cursor (Telgen et al. 2014). During reaches to the lateral targets, one group was provided with online feedback, allowing them to make visually driven online corrections. The other group only received endpoint feedback.

If feedback control and feedforward control are learned separately, only the online-feedback group should adapt their feedback corrections during the reaches to the central target. If feedback control is adapted automatically with feedforward learning, the two groups should show equivalent improvements in both feedforward and feedback control.

MATERIALS AND METHODS

Ethics statement.

This study was conducted according to the Declaration of Helsinki. The experimental procedures were approved by the ethical committees of the Faculty of Science and Technology, Keio University. Written, informed consent was obtained from all participants prior to the experiments.

Participants.

Twenty-three neurologically healthy individuals (8 women and 15 men, aged 19–31 yr) participated in the experiments. All participants were right-handed (laterality quotient = 83.9 ± 3.4; all data values are means ± SE), as assessed by the Edinburgh Handedness Inventory (Oldfield 1971). They were randomly assigned to one of the following three groups: the endpoint feedback group (N = 9), the online feedback group (N = 9), and the control group (N = 5). All participants were naive to the purpose of the experiments.

Apparatus.

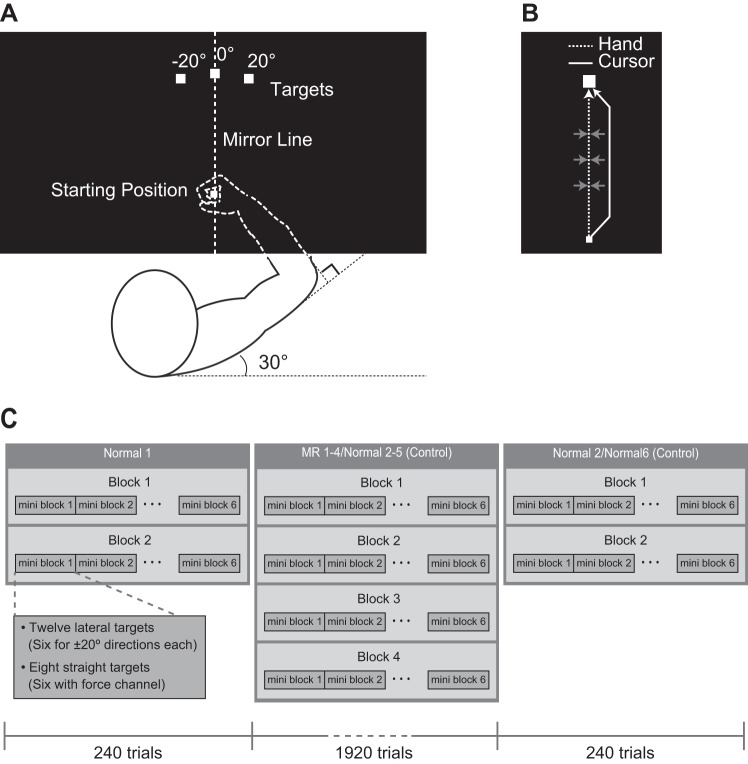
The experiment was performed using the KINARM endpoint robotic device (BKIN Technologies, Kingston, Ontario, Canada; Scott 1999). Participants sat in a chair and moved their right arm in the horizontal plane holding a robotic handle. They viewed a virtual reality display through a half mirror (72 cm × 35 cm) that showed a white cursor indicating a handle position (circle of 6-mm diameter) and visual targets in the same plane (Fig. 1A). A screen under the display prevented the participants from directly seeing their arms. The participants controlled the cursor by performing reaching movements from a starting position (5 mm square) toward three targets (10 mm square, 15 cm distance from the start, either straight ahead or in a ±20° rotated direction). At the starting position the shoulder angle was ∼30° and the elbow angle ∼90° (Fig. 1A). The position and velocity of the endpoint was analog/digital converted at 1.129 kHz and then recorded at 1 kHz for offline analysis.

Fig. 1.

Experimental setup. A: visual information was displayed on a horizontal virtual reality display above the hand. Top middle and ±20° rotated white squares indicate central and lateral targets, respectively, and bottom white square indicates the starting position. The distance from starting target to each target was 15 cm. B: during cursor displacement trials, the robotic arm applied a damped spring force to the subject's hand when the hand was deviated in the lateral direction from the midline. C: each block consisted of six mini-blocks containing 20 trials each. A mini-block consisted of 12 reaches to the lateral target and 8 reaches to the straight-ahead target. Six of these were trials with force channel, and two trials were free movement with endpoint feedback. The participants performed two blocks of non-mirror-reversed (MR) feedback as baseline phase (240 trials in total, Normal 1). In the endpoint, or online, feedback group, the following 16 blocks of MR feedback were divided into four training phases (1,920 trials in total, MR 1 to MR 4), containing four blocks each. In the control group, all training phases were performed with non-MR feedback (1,920 trials in total, Normal 2–5). After the training phases, participants performed two non-MR blocks as a washout phase (240 trials in total, Normal 2 or Normal 6).

Task procedure.

The participants were instructed to move the cursor from the starting position to the target in a fast and straight movement. Before each trial, they needed to place the cursor at the starting position for 1,000–1,250 ms. In all tasks, they were asked to perform a movement within 400 ms after the target's appearance. The color of the target changed to blue if a participant did not start within 400 ms.

In the online feedback and control group, the cursor was visible during the whole movement, and participants were encouraged to make online corrections to keep the cursor on the straight line connecting the starting position and the target. The endpoint feedback group only received static visual feedback of the cursor movement after the end of the movement (i.e., when the speed had dropped below 35 mm/s). The feedback was presented for 750 ms. No visual feedback on the way back to the starting position was given in either group.

The movement needed to stop within 800 ms at a distance of >0.65 cm from the center of the target. Furthermore, the participants were asked to maintain the peak speed of the movement within the range of 500–800 mm/s. To provide feedback to the participants as to whether all criteria were met, we changed the color of the target after they stopped moving (i.e., movement speed dropped below 35 mm/s). If all criteria were met, the target turned red. If the movement was not fast enough or was not completed within 800 ms, the target turned blue or pink; if participants moved too fast, the target turned yellow; if participants moved at the right speed but stopped the movement too far from the target, the target turned green.

The general procedure described above was same in all trials, but a subset of the trials (see Experimental procedure for details) were designed to probe the gain of feedback responses to visual perturbations. On these trials, visual feedback about the cursor was given to all participants, including the endpoint feedback group. The cursor was jumped to the left or right after the participants started moving. The cursor displacement started at 1 cm into the movement and was linearly ramped up until it reached 1.5 cm after 3 cm into the movement. The displacement was then linearly ramped down in the similar manner at 12–14 cm into the movement (similar to Franklin and Wolpert 2008). To probe responses to cursor displacements, we used a force channel (Scheidt et al. 2000; Sing et al. 2009; Smith et al. 2006), during which the trajectory of the handle was constrained to a straight line toward the target (Fig. 1B). The channel was created by simulating a very stiff one-dimensional spring (6,000 N/m) and damper to reduce the vibration (75 Ns/m). The force in the y-direction was always zero. This method enabled us to measure directly the lateral force exerted into the channel wall.

After each trial, the robot automatically moved the arm to the starting position by a springlike force without visual feedback. Participants practiced 120 trials under normal visuomotor conditions before the experiment.

Experimental procedure.

The participants performed 20 blocks of 120 trials each. Each block consisted of 6 mini-blocks containing 20 trials each. A mini-block consisted of 12 reaches to the lateral targets (six trials for ± 20° directions each), and 8 reaches to the straight-ahead target. Six of these were trials with force channel (two trials for left, two for right cursor displacements, and two for no displacements), in which visual feedback was given in all groups. The remaining two trials were free movement, and only endpoint feedback was given to all groups (Fig. 1C). The lateral target-reaching trials were performed to probe the adaptive state of feedforward control, while the cursor displacement trials were performed to probe feedback control. The force channel trials without cursor displacements were used to obtain reference force profiles in each block for standardization (see Data analysis).

In the endpoint, and the online-feedback groups, the participants performed two blocks of non-MR feedback as baseline phase (240 trials in total, Normal 1). This was followed by 16 blocks with MR feedback. These blocks were divided into four training phases (1,920 trials in total, MR 1 to MR 4) containing four blocks each. In these phases, the x-coordinate of the cursor was flipped across a line passing through probe target and starting position (Fig. 1A). The participants were given explicit instruction about the onset of the mirror reversal before MR 1. After the training phases, participants performed two non-MR blocks as a washout phase (240 trials in total, Normal 2).

The control group was recruited to clarify whether changes in the visuomotor response to the cursor displacements was due to learning of the MR transformation, or fatigue and/or habituation caused by the long-term experiment. Therefore, the control group performed all blocks under the non-MR visuomotor condition (2,400 trials in total, Normal 1–Normal 6).

The participants had a 3-min break between the blocks and 10-min break between the phases. In the middle of the experiment, they had a 45-min break. The timing and length of the break was the same across participants. The experiment took 5.5 h in total, and participants were paid about $55 as an honorarium.

Data analysis.

The position and velocity data of the hand obtained from KINARM was low-pass filtered with a zero-lag, fourth-order Butterworth filter (cutoff frequency, 20 Hz). Movement onset was defined as the time that the outward movement speed exceeded 35 mm/s. Movement offset was defined as the time point when the hand velocity first dropped below 35 mm/s after the time when the peak velocity of each trial was detected. The initial movement direction was determine as the line connecting the starting position and the average cursor position in the time interval of 100–150 ms after movement onset. The initial angular error was defined as the angle between the initial movement direction and the line connecting the starting position and the target.

As a proxy for the total amount of online corrections during the movement, we calculated the standard deviation (SD) of the position perpendicular to the main movement direction between movement onset and offset.

The force data obtained from KINARM was also low-pass filtered with a zero-lag, fourth-order Butterworth filter (cutoff frequency, 20 Hz). To adjust for intersubject differences in baseline, the lateral hand force that participants exerted in channel trials without cursor displacements was subtracted from the force traces measured with cursor displacements. To quantify the corrective response, we calculated the averaged hand force in 251 ms to 350 ms after the onset of cursor displacement for each participant. We selected this time window because two previous studies (Gritsenko and Kalaska 2010; Telgen et al. 2014) found that the changes in rapid feedback corrections induced by learning of the MR transformation occurred mostly in this time window.

To quantify the improvement in feedforward control during the training phases, we investigated the RT, the time from target appearance to movement onset, and the accuracy of the movements assessed by the absolute initial angular error (averaged over the time interval of 100–150 ms after movement onset). The relationship between RT and accuracy is thought to represent the change of computational load in motor preparation (Saijo and Gomi 2010, Telgen et al. 2014).

Statistics.

A repeated-measures two-way ANOVA (group × training phase) was used to detect changes in the maximal movement speed, the force responses, RT, and the absolute error during experiments and their groups difference. If a significant main effect was detected, we performed a post hoc Bonferroni test. P values represented in the result of post hoc tests were multiplied by the number of test performed (i.e., any difference across groups in any of the four training phases: four times). The significance threshold was set at P < 0.05. Unpaired t-test was used to detect baseline (Normal 1) difference between the groups. Paired t-test was used to detect difference between baseline and washout (Normal 2) phase, or the first (MR 1) and last mirror-reversal (MR 4) phase in each group. One-sample t-tests were used to detect significant difference against zero for the force response in the online feedback group to investigate reversal of the response within the single training session.

RESULTS

Feedback corrections.

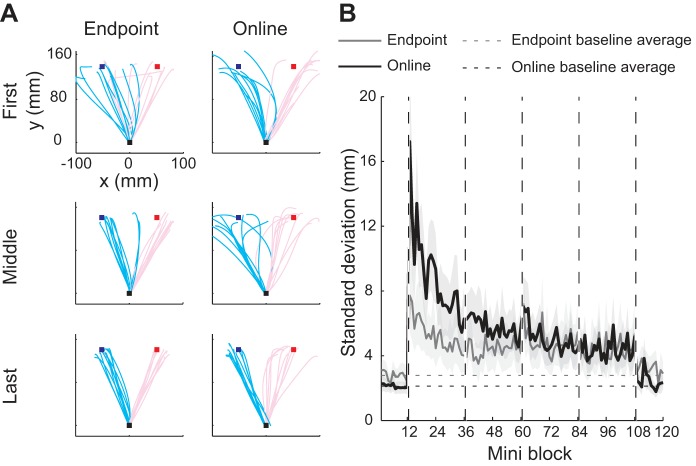
Figure 2A shows movement trajectories to the lateral targets from two exemplary participants in the first, middle, and last 20 trials of the MR 1 phase. The trajectories indicate that both participants showed adapted (reversed) movements in the end of the phase. An inspection of individual trials reveals that the participant with endpoint feedback exhibited relatively straight trajectories, while the participant with online feedback showed substantial deviations from straight movements. Based on the assumption that participants intend to make visually straight trajectories (Wolpert et al. 1995b), we ascribed these deviations to online corrections. To quantify their strength, we used the SD of the position perpendicular to the main movement direction across the movement duration for each trial.

Fig. 2.

Online correction during the first phase of MR learning. A: movement trajectories from a representative participant from the endpoint (left column) and online (right column) feedback groups. The top panels indicate the first 20 trials of MR 1, the middle panels indicate the middle 20 trials of MR 1, and the bottom panels indicate the last 20 trials of MR 1. Red lines indicate individual trajectories for trials aiming to the red target, and blue lines indicate individual trajectories for trials aiming to the blue target. B: standard deviation of the position perpendicular to the main movement direction as a measure of online movement corrections. Solid gray line indicates the endpoint feedback group, and solid black line indicates the online feedback group. Dashed horizontal lines indicate baseline average of each group.

Using this measure of online corrections, we indeed found a significant group difference during the training phases (F_1,56 = 16.85, P < 0.0001; Fig. 2B). Furthermore, there was a significant main effect of phase (F_3,56 = 14.04, P < 0.0001) and an interaction effect (F_3,56 = 6.68, P = 0.001). A post hoc test indicated that SD was significantly larger in the online group than the endpoint group during the MR 1 (t₁₆ = 8.03, P < 0.0001, significant after Bonferroni corrected) and MR 2 phase (t₁₆ = 3.02, P = 0.016). Thus, especially in the earlier phases of learning, the online feedback group seemed to make substantially more online corrections than the endpoint feedback group.

Feedforward control.

Learning of feedforward control is apparent in the ability of participants to initiate their movement in the right direction, even when reacting very quickly to the target appearance (Lillicrap et al. 2013; Telgen et al. 2014). We, therefore, introduced an RT limit of 400 ms and investigated both RT and the absolute initial error. In both endpoint and online groups, RT and the absolute error increased when the MR transformation was applied (Fig. 3) and then decreased during training. To investigate differences in feedforward learning, we compared both measurements between groups.

Fig. 3.

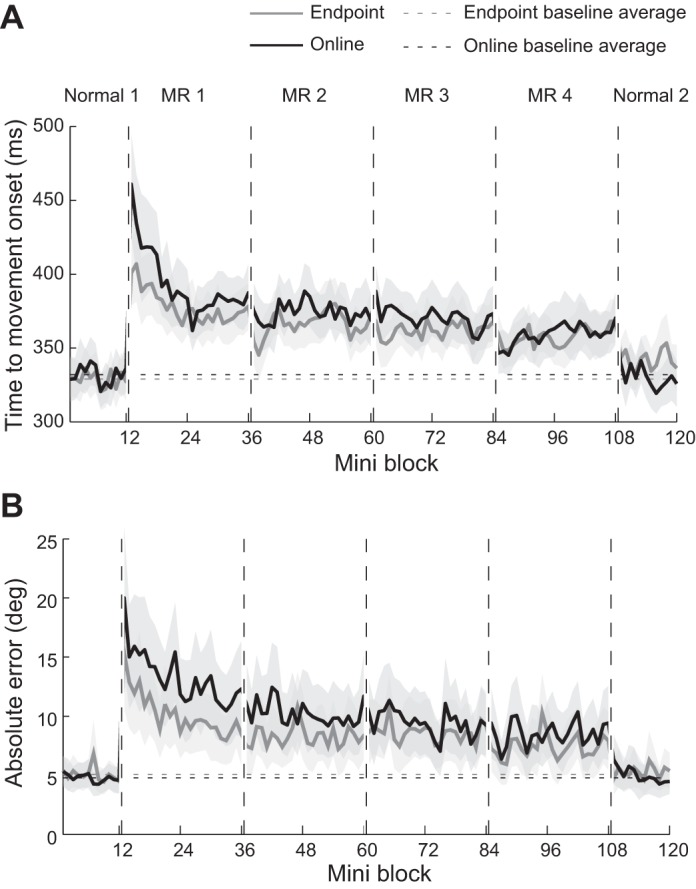
Changes in feedforward control. Solid gray line indicates the endpoint feedback group, and solid black line indicates the online feedback group. Dashed horizontal lines indicate baseline average of each group. The shaded region indicates ± 1 SE across participants. A: changes in reaction time. B: changes in the absolute initial angular error.

For RT (Fig. 3A), no group difference was detected during the baseline phase (t₁₆ = −0.21, P = 0.84). During the training phases, a two-way repeated-measures ANOVA (group × training phase) detected a significant main effect of group (F_1,56 = 5.14, P = 0.027) and phase (F_3,56 = 9.73, P < 0.0001), but no group × phase interaction (F_3,56 = 0.597, P = 0.619). Post hoc tests indicated that RT was significantly shorter in the endpoint group than in the online group during the MR 1 phase (t₁₆ = 2.92, P = 0.04, significant after Bonferroni corrected). Both groups showed significant decrease in RT from the MR 1 to MR 4 phase (endpoint group, t₈ = 2.34, P = 0.047; online group, t₈ = 3.39, P = 0.01). In the washout phase, RT returned to the baseline level, showing that there was no difference between Normal 1 and Normal 2 for both groups (endpoint group, t₈ = −1.83, P = 0.11; online group, t₈ = 0.23, P = 0.83).

For the absolute error (Fig. 3B), there was also no group difference during baseline (t₁₆ = 0.46, P = 0.66). During the training phases, there was a significant main effect of group (F_1,56 = 10.71, P = 0.002) and phase (F_3,56 = 8.66, P < 0.0001). A post hoc test indicated that the absolute error was significantly smaller for the endpoint feedback group than the online feedback group in the MR 1 phase (t₁₆ = 4.13, P = 0.002, significant after Bonferroni corrected). Both groups showed decreases in the absolute error from the MR 1 to MR 4 phase (endpoint group, t₈ = 4.64, P = 0.002; online group, t₈ = 4.70, P = 0.002).

Thus, somewhat surprisingly, the endpoint feedback group showed both faster RTs and lower absolute errors compared with the online feedback group, even though no baseline difference between the groups existed.

Fast feedback control.

We then sought to determine whether the endpoint and online feedback group differed in their ability to generate fast online corrections. If feedback control is not automatically acquired through feedforward learning, but needs to be trained separately, then the online feedback group should have changed their fast corrections to cursor displacements more than the endpoint feedback group.

Figure 4, left and middle, shows temporal profiles of the lateral force produced in response to cursor displacements for the endpoint and online feedback group, respectively. The data are flipped so that the response in the opposite direction to the cursor displacement (i.e., compensatory movements to the visual perturbation) has a positive sign. This means that, if the participants fully learned feedback control under MR environment, the force response should have a negative value. The first feedback response was visible with a latency of around 200 ms.

Fig. 4.

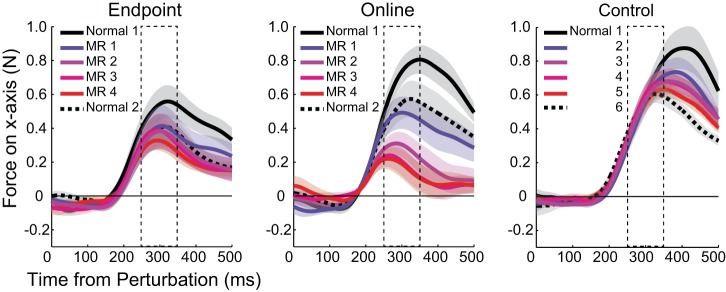
Temporal profiles of visuomotor responses to cursor displacement. Force on x-axis produced in response to cursor displacements in Normal 1 (solid black), MR 1 (blue), MR 2 (purple), MR 3 (magenta), MR 4 (red), and Normal 2 (dotted black) is shown. The solid line indicates the mean responses across participants, and the shaded colored regions represent the SE. The dashed box indicates the time window (251 ms to 350 ms) that is used for the analysis shown in Fig. 5. The endpoint feedback group is shown on the left, the online feedback group is shown in the middle, and control group is shown on the right.

At the baseline phase (Normal 1), the online feedback group showed larger feedback responses compared with the endpoint feedback group, although this difference was not significant (t₁₆ = −1.58, P = 0.135). The difference is likely caused by the fact that the online feedback group relied on the visual feedback provided during the movement, whereas the endpoint feedback group had started to ignore the feedback.

However, over the training phases, this relationship reversed (Fig. 5). A repeated-measures two-way ANOVA (group × training phase) for the averaged force responses during the training phases detected a significant main effect of group (F_1,56 = 5.26, P = 0.026) and phase (F_3,56 = 7.01, P < 0.0001) and an interaction effect (F_3,56 = 3.40, P = 0.024). Post hoc tests indicated that the force was smaller in the online feedback group than the endpoint feedback group during MR 3 (t₁₆ = 3.87, P = 0.003, significant after Bonferroni corrected) and MR 4 phase (t₁₆ = 2.90, P = 0.021). In the endpoint feedback group, it did not change from the MR 1 to MR 4 phase (t₈ = 1.10, P = 0.304). For the online group, the force response increased again in the washout phase, even though it was smaller than in the baseline phase (t₈ = 2.78, P = 0.023).

Fig. 5.

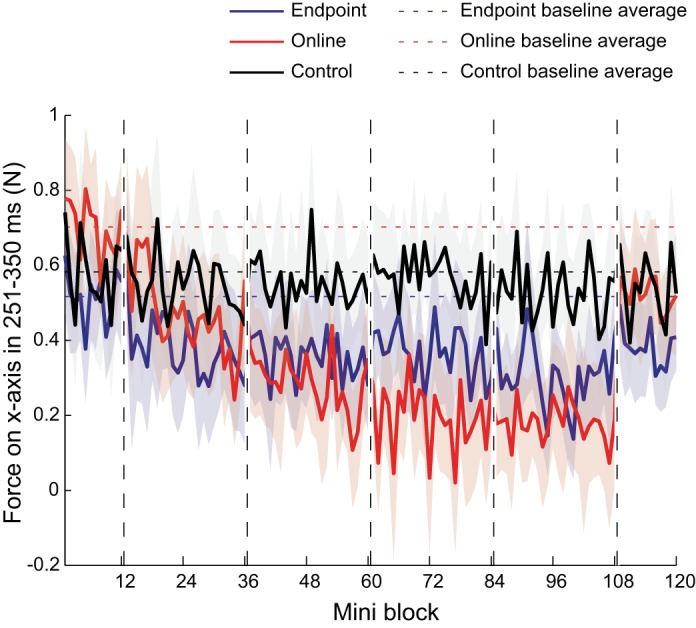
Magnitude of averaged visuomotor responses. Lines indicate mean force on x-axis produced in response to cursor displacements across all participants during the 251- to 350-ms interval after the onset of the perturbation. Solid blue line indicates the endpoint feedback group, solid red line indicates the online feedback group, and solid black line indicates control group. Dashed horizontal lines indicate baseline average of each group. The shaded colored region indicates ± 1 SE across participants.

Despite these reductions in force response, the feedback response of the online feedback group did not reverse within the single training session. The MR 4 phase was significantly larger than zero in one-sample t-test (t₈ = 5.55, P < 0.001). Similar observations have been made in previous studies (Gritsenko and Kalaska 2010), and the feedback response for the corresponding latency only reversed during the second day of training (Telgen et al. 2014).

No change in feedback responses in control group.

To evaluate whether the decreases in the force responses in the online feedback group were related to learning the MR transformation or to the repeated exposure to cursor displacements, we ran a control, which underwent the same protocol as the online feedback group (and received visual feedback), but did not experience mirror reversal.

Figure 4, right, shows temporal profiles of the lateral force for the control group produced in response to the cursor displacement in different phases of the experiment. During the baseline phase, the control group did not differ significantly from the online feedback group (t₁₂ = 1.12, P = 0.284). During the training phases, the feedback responses did not decrease as much as in the online feedback group (Fig. 4, middle). A repeated-measures two-way ANOVA (group × training phase) detected a significant main effect of group (F_1,40 = 10.7, P = 0.002), phase (F_3,40 = 2.91, P = 0.046) and an interaction effect (F_3,40 = 3.07, P = 0.039). In contrast, no group × training phase interaction was found between the control and the endpoint group (F_3,40 = 0.125, P = 0.945). Furthermore, a paired t-test indicated that the force response did not significantly change from the first to last training phase in the control group (t₄ = 0.47, P = 0.66).

Since the maximum force response was observed later for the control group than the other two groups (Fig. 4), we shifted the time window for the control group to 301–400 ms after movement onset, and additionally performed a repeated-measures two-way ANOVA (group × training phase) for the control and the online group, and the control and the endpoint group. The results were similar to the earlier time window. There was no significant interaction for the control and the endpoint group (an interaction effect, F_3,40 = 0.026, P = 0.994). The online group also showed a stronger reduction than the control group over this time window. This, however, led only to a significant main effect of group (F_1,40 = 37.0, P < 0.0001), but in this case not to a significant interaction (F_3,40 = 2.31, P = 0.091).

DISCUSSION

The present study provides evidence that feedforward and feedback control do not always form an inseparable unit, but that they must be trained separately when learning to reach under MR feedback. We found that feedforward control was learned better when participants only received endpoint feedback. In contrast, feedback control was only adjusted when participants had the opportunity to make online corrections in the new environment. These results suggest that, when a new control policy is acquired, both feedforward and feedback control need to be trained.

The contrast between the two groups was clearest for feedback control, which was only learned by the group that received online feedback. The slight decrease in the feedback response observed in the endpoint group was indistinguishable from the control group and, therefore, likely resulted from the habituation to a sudden visual perturbation (Fig. 5). These results indicate that a feedback control policy for MR feedback can only be acquired when the online visual consequences of an action can be observed during training.

Conversely, and somewhat surprisingly, we found that the endpoint feedback group showed significantly more accurate initial movement directions than the online feedback group, indicating more successful feedforward learning. We can exclude the possibility that this difference arose because the endpoint feedback group used longer preparation times, as the RTs were shorter in the endpoint feedback group. Of course, both groups showed significant improvement in feedforward control and successfully reversed the movement directions. Why the online feedback group exhibited less feedforward learning is not entirely clear. It is possible that the online corrections into the wrong direction may have led the online group to adapt their feedforward command. Indeed, there is evidence that subjects confronted with a mirror reversal of the feedback first interpret the feedback as a visual rotation and adapt the next movement into the wrong direction (Lillicrap et al. 2013; Telgen et al. 2014). However, such inadvertent adaptation should also have been occurring in the endpoint feedback group. Alternatively, the greater learning of feedback control may have diverted computational resources away from acquiring the correct feedforward control, or the initial errors were more permissible for the online feedback group, as they were allowed online corrections. Either way, the present study appears to indicate a trade-off between learning of feedback and feedforward controllers.

Changes to the feedback control were assessed via forces in channel trials that were only employed for the central target. Thus we cannot exclude the possibility that the participants regarded this target to be different from the lateral targets; it is possible that, had we measured feedback responses to lateral targets, we may have found a stronger modulation. However, the fact that we find fast, strong and consistent feedback responses throughout the experiment indicates that the 25% of nonchannel trials to the central target were sufficient to maintain a normal feedback response. Furthermore, the visual feedback and frequency of probe trials to the center target were identical across the endpoint and online feedback group (see materials and methods). Therefore, the different feedback responses of the two groups must be explained by the differential influence of learning that occurred to the lateral targets.

One important weakness of the study is that we only observed a faster reduction of the feedback response in the online feedback group, but not the reversal of the response into the correct direction. This is consistent with previous studies (Gritsenko and Kalaska 2010; Telgen et al. 2014) in which the feedback responses did not reverse until the second day of training. It, therefore, would have been more convincing to observe a force reversal and faster increases in the correct response in the online feedback group (as in Telgen et al. 2014). However, our control group indicates that the observed reduction of response was due to active learning processes, rather than due to a passive decay (Scheidt et al. 2000). Therefore, we think there is reasonable evidence that the faster reduction of feedback responses reflected learning of new feedback control policy acquired in the lateral targets.

Overall, the relationship between feedforward and feedback control has been vigorously debated. Traditional theories have emphasized the existence of different controllers for feedforward and feedback control (Desmurget and Grafton 2000; Kawato 1999). In contrast, in many implementations of optimal feedback control (Diedrichsen et al. 2010; Todorov and Jordan 2002), both the open-loop and the closed-loop phase of the movement are controlled by the same control policy. The two phases simply differ by whether the internal state estimate is determined by an internal prediction from the forward model (Wolpert et al. 1995a), or by inflowing sensory information. In this architecture, the transition between feedforward and feedback control is gradual, and adaptation of the early phase of the movement should also lead to adaptation of the feedback command. Indeed, some empirical results seem to indicate that this is the case when the system adapts to a new dynamic environment (Ahmadi-Pajouh et al. 2012; Cluff and Scott 2013; Wagner and Smith 2008) or a new visuomotor rotation (Telgen et al. 2014).

Here we show that this prediction does not hold when learning to reach under MR visual feedback. Our previous study has shown that mirror reversal is learned by establishing a new control policy, as evidenced by a gradually shifting speed-accuracy tradeoff (Telgen et al. 2014). Together these pieces of evidence suggest that feedback and feedforward control need to be acquired separately when a new control policy is being learned, but not when adapting an existing control policy to a new environment.

A second important debate concerning feedforward and feedback control is whether the feedback controller provides the teaching signal that then adjusts the feedforward controller. This is the core tenet in feedback error learning theory (Kawato 1999; Thoroughman and Shadmehr 1999). Supporting this idea is the observation that, in a redundant system, the solution for feedback correction is correlated with the solution for the subsequent adaptation (White and Diedrichsen 2010). In contrast, another study showed that adaptation rates, extent of adaptation, and after-effects were similar whether or not online corrections were possible, suggesting that online corrective movements do not contribute to visuomotor adaptation (Schaefer et al. 2012; Tseng et al. 2007).

The partial dissociability of feedforward and feedback control raises the question if these two processes are subserved by different neural substrates. There is good evidence that the cerebellum is involved in the adaptation of predictive feedforward commands based on sensory prediction error (Shadmehr and Krakauer 2008; Smith and Shadmehr 2005; Tseng et al. 2007). In contrast, Huntington's disease patients show aberrant responses during movement corrections to force pulses (Smith et al. 2000), suggesting an important role of the basal ganglia in feedback control. However, cerebellar ataxia can also be understood as a dysfunction of feedback control (Diedrichsen and Bastian 2014; Hore and Flament 1988). Furthermore, a number of researchers have suggested that feedforward and feedback control share the same neural substrate, including primary motor cortex (Pruszynski et al. 2011; Scott 2004). Thus a clear dissociation in terms of different neural regions is unlikely. Rather, feedforward and feedback control most likely involve processing of different types of information in overlapping areas, with feedforward control being more reliant on goal-related information, and feedback control on dynamic feedback of limb position. When learning a new skill, however, these processes seem to have to be learned separately.

GRANTS

This work was supported by Grant-in-Aid for Young Scientists (B) and the Ministry of Education, Culture, Sports, Science, and Technology (no. 25750267) to S. Kasuga.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: J.D., S.K., S.T., J.U., and D.N. conception and design of research; S.K. performed experiments; J.D., and S.K. analyzed data; J.D., S.K., S.T., J.U., and D.N. interpreted results of experiments; J.D. and S.K. prepared figures; J.D., S.K., S.T., and D.N. drafted manuscript; J.D., S.K., S.T., J.U., and D.N. edited and revised manuscript; J.D., S.K., S.T., J.U., and D.N. approved final version of manuscript.