Lack of depth constancy for grasping movements in both virtual and real environments

Abstract

Recent studies on visuomotor processes using virtual setups have suggested that actions are affected by similar biases as perceptual tasks. In particular, a strong lack of depth constancy is revealed, resembling biases in perceptual estimates of relative depth. With this study we aim to understand whether these findings are mostly caused by a lack of metric accuracy of the visuomotor system or by the limited cues provided by the use of virtual reality. We addressed this issue by comparing grasping movements towards a spherical object located at four distances (420, 450, 480, and 510 mm) performed in three conditions: 1) virtual, in which the target was a virtual object defined by binocular cues, 2) glow-in-the-dark, in which the object was painted with luminous paint but no other cue was provided, and 3) full-cue, in which the movement was performed with the lights on and all the environmental information was available. Results revealed a striking effect of object distance on grip aperture equally in all three conditions. Specifically, grip aperture gradually decreased with increase in object distance, proving a consistent lack of depth constancy. These findings clearly demonstrate that systematic biases in grasping actions are not induced by the use of virtual environments and that action and perception may involve the same visual information, which does not engage a metric reconstruction of the scene.

retinal disparities, arising from the slightly different images of an object falling on the two eyes, could yield the veridical metric representation of an object three-dimensional (3D) structure, if appropriately scaled through an accurate estimate of the fixation distance (Johnson 1991; Rogers and Bradshaw 1993). Information about the egocentric distance of an object can be entirely determined by extraretinal signals, like ocular vergence and accommodation. However, empirical evidence shows that distance information carried by these binocular signals is not immune to systematic distortions: near objects are seen further than they are and far objects are seen closer than they are (Foley 1980; Johnston 1991; Servos 2000). This pattern of distortions is compatible with biases observed in depth judgments. The depth of an object is overestimated at closer distances and underestimated at further distances, denoting a failure in perceptual depth constancy (Johnston 1991; Norman et al. 1996; Brenner et al. 1997; Brenner and van Damme 1999; Volcic et al. 2013).

Although binocular information is fundamental for guiding reaching and grasping movements, the accuracy with which we interact with the world seems to indicate that motor actions are unaffected by the biases afflicting perception. Goodale and Milner's (1992, 1993) dual stream theory has accounted for this dissociation by hypothesizing the existence of two separate streams for the elaboration of visual stimuli: a ventral path involved in visual perception and subject to visual distortions and illusions, and a dorsal path immune to these biases, where visual information yields accurate metric estimates of object structure and spatial location. However, more recent findings seem to contradict and challenge this hypothesis. In reaching tasks without haptic feedback spatial distortions were found in both egocentric distance and object size estimation (Bingham et al. 2000, 2001). Furthermore, errors similar to those in perceptual estimates were also found for grasping movements towards target objects only defined by binocular information (Bingham et al. 2007; Hibbard and Bradshaw 2003; Bozzacchi et al. 2014). In particular, by using virtual reality setups, we observed that even at the presence of both visual and haptic feedback, the grip aperture (GA) decreases with the increase of object egocentric distance, a clear index of depth constancy failure (Bozzacchi et al. 2014). Remarkably, the effects reported in our previous study are strongly consistent with findings from perceptual paradigms. In a task where participants judged the depth of a disparity defined object, Volcic et al. (2013) observed a decrement in the estimation of the object depth as function of distance. The same object viewed at different distances within a range of 150 mm appeared on average 4.5 mm shallower at the farthest distance than at the closest distance, indicating a flattening of 3 mm per 100 mm of distance separation (i.e., slope = 0.03). In a grasping task we found the same decrease in the maximum grip aperture (MGA-slope = 0.027), suggesting that the same mechanisms leading to a lack of depth constancy in perceptual tasks is also governing the execution of grasping actions.

On the basis of these controversial effects on action tasks, in the present study we aim to test for the two possible interpretations of these distortions. The first one attributes the incorrect execution of grasping movements to cue conflicts, which affect virtual stimuli (Wann et al. 1995), and to the lack of additional 3D information such as vertical disparities and prospective cues. Therefore, according to this interpretation, richer stimuli in which cues-to-flatness have been eliminated should allow movements that reflect correct estimates of the visual scene (see also Sousa et al. 2010). The second interpretation, instead, questions the assumption that reach-to-grasp actions are based on a veridical metric reconstruction of the scene. According to this view both perception and action engage the same visual information, which is subject to distortions because lacks of metric accuracy.

A similar question was previously addressed by Bingham and colleagues (2000, 2001), who compared reaching movements in virtual and real setups while keeping the same visual information in both conditions (in the “real” condition the object was painted with luminous paint and showed in complete darkness). The authors did not report any significant effect between conditions on shape estimates but only more inaccurate egocentric distance estimation in the virtual than in the real environment (Bingham et al. 2000, 2001).

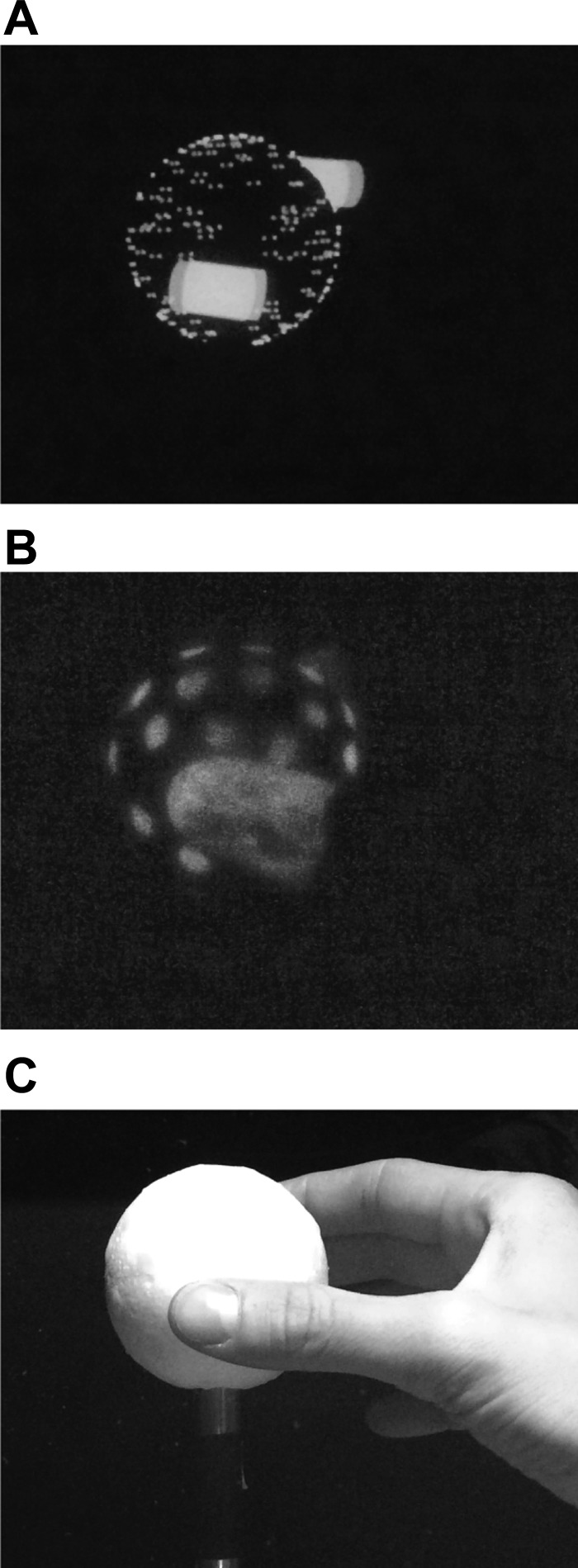
In the present study we extended these findings to the grasping domain and compared three viewing conditions: 1) virtual condition, in which the target was a virtual object defined by binocular cues; 2) glow-in-the-dark condition, in which the object was painted with luminous paint but no other cue was provided; and 3) full-cue condition, in which the movement was performed with the lights on and all the environmental information was available (Fig. 1). Therefore, the glow-in-the-dark condition presented the same binocular-disparity information as the virtual condition, with the addition of the blurring gradient, which is always present when viewing a real object. In the full-cue condition the presence of other objects in the laboratory environment and the shading gradient produced by illuminating the scene maximized the number of cues. Importantly, in all conditions the visual feedback of the hand was present throughout the movement duration and the object could always be felt at the end of the action.

Fig. 1.

The grasping of a spherical object was performed in 3 different conditions. A, virtual: sphere and the visual feedback of the fingers were virtually rendered. The virtual sphere was paired with a real one located at the same distance and having the same dimension (ø 60 mm). Visual feedback of the index finger and thumb were rendered by means of virtual cylinders (height: 20 mm; ø: 10 mm). B, glow-in-the-dark: the sphere and the fingers of the participants were covered with luminous material to make them visible in the dark. The start and end of the trials was indicated by the PLATO goggles turning transparent and opaque. C, full-cue: the object was perfectly visible in front of the participants as well as their hand. All cues were available and the light was on for the duration of the experiment. The start and end of the trials was indicated by the PLATO goggles turning transparent and opaque.

Based on the empirical evidence that binocular cues do not yield an accurate metric space representation (Bingham et al. 2001; Volcic et al. 2013; Johnston et al. 1991; Brenner et al. 1997; Brenner and van Damme 1999; Hibbard and Bradshaw 2003), we expect to find a modulation of the MGA as function of distance in the virtual condition, where only binocular cues are available, resembling the effects previously described for perceptual and grasping tasks (Volcic et al. 2013; Bozzacchi et al. 2014). Specifically, we predict a reduction of the MGA of ∼3 mm per 100 mm separating the closest from the furthest object distance (slope: ∼0.03).

If conflicting information present in the virtual condition is responsible for these biases in depth estimates, then the elimination of conflicting cues and the introduction of additional cues in the glow-in-the-dark and full-cue conditions should lead to depth constancy. Alternatively, the assumption that the dorsal pathway is metrically accurate should be revisited. After all, the successful completion of reaching and grasping movements does not necessarily imply that action kinematics is based on a veridical metric reconstruction of environmental objects (Domini and Caudek 2013).

MATERIALS AND METHODS

Subjects

Fifteen undergraduate and graduate students from the University of Trento (mean age 24.4; 10 females) participated in the study. All participants were naive to the purpose of the experiment and were paid eight Euros for their participation. The total duration of the experiment was 1 h, including the calibration procedure. Participants were all right-handed, based on a self-report of hand preference, and all had normal or corrected-to-normal vision. The experiment was approved by the Comitato Etico per la Sperimentazione con l' Essere Vivente of the University of Trento and in compliance with the Declaration of Helsinki.

Apparatus and Design

Participants underwent three separate experimental conditions (virtual, glow-in-the-dark, and full-cues) in 3 separate days. The order of conditions was randomized across subjects. Participants were asked to perform a precision grip of a sphere (ø: 60 mm) with their thumb and index finger without lifting it. The sphere was presented randomly at four distances along the line of sight (420, 450, 480, and 510 mm). Participants were instructed to initiate and perform the movement at their own pace. Each condition, composed of 80 trials combining all the different randomly assigned distances, lasted ∼20 min. All experimental sessions started with the calibration procedure. The position of the head, eyes, wrist, the thumb, and index fingers pads was calculated with respect to infrared-emitting diodes. For the head, three diodes were located on a band surrounding the head of the participant. For the wrist, a single diode was located on the ulnar styloid. Finally, for the thumb and index finger, three diodes were placed on metal plates and fixed on the nail of each finger. During calibration, the position of the center of each finger pad relative to the three markers was determined through a fourth calibration marker. The x, y, and z coordinates of the center of the finger pad recorded during calibration in conjunction with the x, y, and z coordinates of the three markers on the metal plate specified a four-point rigid body. Thus, during the experiment, the x, y, and z coordinates of the three markers on the metal plates of the index and thumb uniquely determined the exact location of the centers of the finger pads. These in turn were used to render the visual feedbacks and for calculating the GA, defined as the Euclidean distance between the two finger pads (Nicolini et al. 2014) (Fig. 2). Head, wrist, index, and thumb movements were acquired online at 100 Hz with submillimeter resolution by using an Optotrak 3020 Certus motion capture system composed of two position sensors (Northern Digital, Waterloo, Ontario, Canada). Haptic feedback of the sphere was always provided in all conditions. Participants were seated in a dark room in front of a high-quality, front-silvered 400 × 300 mm mirror slanted at 45° relative to the participant's' sagittal body mid-line and had his/her head stabilized by a chin rest. The room was entirely illuminated only in the full-cue condition.

Fig. 2.

For both the index finger and thumb 3 markers located at the vertexes of a triangle and the finger pad defined a rigid prism (dashed lines). During calibration, the position of the finger pad relative to the three markers was determined through a fourth calibration marker (gray discs) so that the location of the finger pad was uniquely specified for any orientation of the 3-marker configuration.

Virtual condition.

The mirror reflected the image displayed on a ViewSonic 9613 19-in. CRT monitor placed directly to the left of the mirror. For consistent vergence and accommodative information, the position of the monitor, attached to a linear positioning stage (Velmex, Bloomfield, NY), was adjusted on a trial-by-trial basis to equal the distance from the participants' eyes to the virtual object (Wann et al. 1995). To present visual stimuli in 3D, we used a frame interlacing technique in conjunction with liquid crystal FE-1 goggles (Cambridge Research Systems, Cambridge, UK) synchronized to the monitor frame rate. Stimuli presentation and response recording were controlled by a C++ program. A disparity defined high-contrast random-dot sphere was paired with a real sphere (ø: 60 mm) placed at the same four distances as the virtual sphere by a computer controlled mechanical arm (Velmex). This provided the participants with the veridical haptic feedback of the simulated virtual stimulus. The participant interocular distance and the tracked head position were used to deliver in real time the correct geometrical projection to the two eyes. Visual feedback of the index finger and thumb were rendered by means of virtual cylinders (height: 20 mm; ø: 10 mm) representing the fingers phalanxes (Fig. 1A). The correct position of the thumb and index finger pads for the presentation of the virtual feedback was calculated during the calibration process at the beginning of the experiment (see above). Before running the experiment, subjects were tested for stereo vision and were allowed to perform some practice trials to get accustomed to the virtual environment.

Glow-in-the-dark condition.

The participant saw the polystyrene sphere painted with luminous material to be visible in the dark. To render also the thumb and index fingers visible in the dark, we covered them with latex caps, which were also painted with the luminous material (Fig. 1B).

Full cues condition.

The same polystyrene sphere as in the previous condition was seen with the lights on. Thus the participant had access to all the depth cues typically available during a normal grasp in addition to other information about the surrounding environment (Fig. 1C).

In all conditions, trials started with the presentation of the stimulus at the correct location. In the real and lights-on conditions, participants wore PLATO goggles (Translucent Technologies, Toronto, Ontario, Canada) that were controlled by the C++ software. The PLATO turned transparent only when the object had reached the correct position and turned opaque again at the end of the trial. From the moment the object was visible, participants could start moving towards it and grasp it. For all conditions, the trial ended 1 s after participants had grasped the object.

Data Analysis: Dependent Variables

Data were processed and analyzed offline using custom software. The raw data were smoothed and differentiated with a 2nd order Savitzky-Golay filter with a window size of 41 points. These filtered data were then used to compute velocities and accelerations in 3D space for each finger and the wrist, the Euclidean distance between the finger pads of the thumb and the index finger (GA), and the velocity and acceleration of the change in GA. The dependent measures were the MGA, the movement duration, and the wrist peak velocity. The MGA was defined as the maximum distance between the fingers pads observed during a grasp. The peak velocity was calculated as the maximum velocity reached by the wrist.

RESULTS

The primary goal of this experiment was to study how the MGA varies as function of grasping distance. If depth estimates guiding reach-to-grasp actions are subject to the same systematic distortions found in perceptual tasks then the MGA should decrease with the object distance. Therefore, for each participant and in each condition we fitted a linear regression model on the MGA variable as function of distance (centered by subtracting its mean). For each condition, a one-sample t-test on the slope of this fit determined whether distance had any effect on the MGA. Slopes and intercepts of the model were compared between conditions with a repeated measures ANOVA using condition as main factor. The same analysis was also run for all the other dependent variables. The Bonferroni correction was applied for multiple comparisons.

At first, we run a repeated-measures multivariate ANOVA on the intercepts and slopes from all the different dependent variables with condition (full-cues, real, and virtual) as within-participant factors. The analysis showed a significant effect of condition [F(2,28) = 3.01; P = 0.003]. Below we report the analyses for all the single dependent variables separately.

Maximum GA

One sample t-test on the slope confirmed that the MGA was significantly affected by distance in the virtual [t(14) = −2.84; P = 0.01], the glow-in-the-dark [t(14) = −4.15; P = 0.0009], and the full-cue [t(14) = −3.32; P = 0.004] conditions (Fig. 3A). The values for three slopes were −0.031 (SE = 0.007) for the virtual condition, −0.032 (SE = 0.007) for the real condition and −0.025 (SE = 0.01) for the full-cues condition with an overall effect of distance of ∼2.8 mm over 9 cm. Note that these values are very similar to those found in previous studies with perception (Volcic et. al. 2013) and grasping (Bozzacchi et al. 2014) paradigms. The comparison between the three slopes showed no significant effect of condition [F(2,28) = 0.36; P = 0.69]. Similarly, the comparison of the three intercepts did not reveal any significant difference between the three conditions [F(2,28) = 2.94; P = 0.07; see Fig. 3A]. Although we cannot completely exclude the possibility that these results were due to the effect of biomechanical constraints of the reaching movement extending towards the target (Mon-Williams and Bingham 2011), we consider this option unlikely, because of the very small range of distances at which the objects were located (90 mm). Moreover and most importantly, the amount of change of the MGA as function of distance (average slope = 0.029) is basically identical to that found for perceptual judgments (average slope = 0.03; Volcic et. al. 2013), where biomechanical constraints cannot have any effect. This striking quantitative similarity of the effect of distance on grasp and perception constitute a convincing converging evidence that what was found in this study is likely the result of systematic biases in depth estimates. However, to better verify for this hypothesis, we analyzed the GA performed in earlier phases of the trajectory. In the case a modulation of the GA was already present before reaching the maximum GA, when the arm is not yet extended towards the object, we might better rule out any mechanical issue as responsible for this effect. For this purpose, we computed the GA along the space-normalized trajectory and fitted a regression model for each point of the trajectory. The analysis of the slopes revealed a modulation of the GA as function of distance starting from about half of the traveled path (already from ∼250 mm from the body) for all the three conditions (Fig. 3B).

Fig. 3.

A: averaged maximum grip aperture (MGA) performed in the 3 conditions, virtual (black line), glow-in-the-dark (dark gray line), and full-cues (light gray line) as function of distance. Error bars represent means ± SE. B: plot of the grip aperture along the spaced-normalized trajectory (sampled at 101 points) for the 3 experimental conditions. For each subject and at each points of the trajectory, we fitted a linear regression model as function of distance (centered by subtracting its mean). Separately for the 3 conditions we run a 1-sample t-test on the slopes of the model to test from which point of the trajectory the grip aperture was significantly modulated by the target distance. The frames represent a blow-up of the part of the trajectory in which the grip aperture was modulated as function of the target distance. The shading bar on the bottom of each plot represents the P value of the t-test run on the single slopes.

Peak Velocity

Repeated-measures ANOVA on the three slopes for the peak velocity showed no significant effect of the condition [F(2,28) = 1.44; P = 0.25], indicating that in all the three conditions the peak velocity similarly increased as function of distance. The values of the slope was in fact positive for the virtual (mean = 0.23; SE = 0.14), glow-in-the-dark (mean = 0.52; SE = 0.13), and full-cues (mean = 0.49, SE = 0.15). Instead, the analysis on the intercepts showed a significant effect of condition [F(2,28)=14.18; P < 0.001]. Specifically, the peak velocity of the full-cue condition was higher than in the virtual [t(14) = −4.57; P = 0.001] and in the glow-in-the-dark [t(14) = 3.71; P = 0.006] conditions, which, instead, did not differ from each other [t(14) = 1.79; P = 0.09; Fig. 4].

Fig. 4.

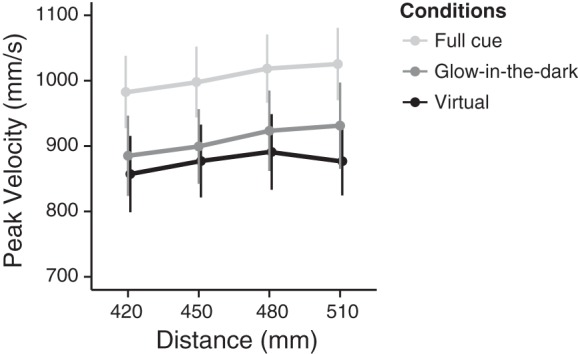
Averaged peak velocity performed in the 3 conditions, virtual (black line), glow-in-the-dark (dark gray line), and full-cues (light gray line) as function of distance. Error bars represent means ± SE.

Movement Duration

The ANOVA run on slope and intercept showed no effect of condition on the slope [F(2,28) = 0.21; P = 0.80], with the value of the three slopes equal to 1.64 (SE = 0.27) for the full-cues condition, 1.88 (SE = 0.24) for the glow-in-the-dark condition, and 1.92 (SE = 0.41) for the virtual condition. On the other hand, a strong effect of condition on the intercept was present [F(2,28) = 22.15; P < 0.001]. Pairwise comparisons showed that the movement in the full-cue condition was significantly faster than in the glow-in-the-dark condition [t(14) = −5.09; P = 0.004] and in the virtual condition [t(14) = −5.5; P = 0.0002]. To better investigate which phase of the movement was more affected by the condition, we decomposed the movement duration into five time phases corresponding to 1) the time to peak acceleration, 2) the time lag from peak acceleration to peak velocity, 3) the time lag from peak velocity to peak deceleration, 4) the time lag from peak deceleration to MGA, and 5) the time lag from MGA to the end of the movement. For each time segment we ran a repeated-measures ANOVA with condition as main factor and found that a difference among the three conditions started to be significant already in the second (from peak acceleration to peak velocity) and third (from peak velocity to the peak deceleration) time phases [F(2,28) = 4.36; P = 0.02]. However, substantial differences between conditions become evident after the peak deceleration, during the time needed for the MGA to form [F(2,28) = 7.83; P = 0.001]. This phase, indeed, was much faster in the full-cue condition than in the glow-in-the-dark [t(14) = −3.16; P = 0.02] and the virtual conditions [t(14) = −3.03; P = 0.02], which in turn were not different from each other [t(14)= −0.01; P = 0.98]. A large difference among conditions was also present in the last phase of the movement [F(2,28) = 20.95; P < 0.0001; Fig. 5].

Fig. 5.

Averaged movement duration of the 3 conditions. Bars are segmented in subsequent movement phases from black to light gray: from movement onset to time of peak acceleration; from time of peak acceleration to time of peak velocity; from time of peak velocity to time of peak deceleration; from time of peak deceleration to time of MGA; and from time of MGA to movement end.

DISCUSSION

In this study we asked whether systematic biases in depth estimates that have been observed in reach-to-grasp actions are due to conflictual cues present in virtual setups or are the result of a lack of metric reconstruction of the scene. We found a clear and consistent effect of object distance on GA, which equally affected all the experimental conditions, whether the stimulus was a stereo display (virtual condition), a real luminous sphere in an otherwise dark environment (glow-in-the dark condition), or a real sphere in a lit environment (full-cue condition).

Even when cues-to-flatness are eliminated and all the information needed for a successful grasp is available, the inspection of the GA exposes a clear signature of a lack of depth constancy, in a way that is indistinguishable to what found in perceptual tasks (Foley 1980; Johnston 1991; Volcic et al. 2013). On this empirical basis we argue the assumption that binocular depth cues allow a veridical metric estimate of 3D structure for guiding actions, which, instead, may be driven by the same mechanisms leading to perceptual biases.

The fact that everyday actions are successful, since we rarely bump into objects or spill coffee when we pick up a cup, does not necessarily mean that the visual system represents accurately and precisely the Euclidean structure of the visual scene (Domini and Caudek 2013). Instead, biased estimates may be present at the start of an action and be corrected online while the movement unfolds. Undoubtedly, the availability of different sources of feedback at the end of an action, like the vision of the hand and the physical presence of a target, plays a crucial role in guiding the limb to the appropriate contact position on the object (Jakobson and Goodale 1991; Gentilucci et al. 1994; Connolly and Goodale 1999; Churchill et al. 2000). As largely demonstrated, the absence of such feedback can induce atypical patterns of movements (Wing et al. 1986; Gentilucci et al. 1994; Churchill et al. 2000; Bingham et al. 2007; Hibbard and Bradshaw 2003; Bozzacchi et al. 2014). These findings are in agreement with a theoretical framework postulating a nonmetric (i.e., non-Euclidean) representation of 3D properties. According to this framework the visual system reconstructs with great fidelity the affine structure of environmental objects, even though visual signals could, in principle, specify their veridical Euclidean structure. The affine structure is in principle ambiguous, since it only determines the shape of an object up to an arbitrary linear stretch along the line of sight. It therefore encodes important ordinal properties, like the depth order of feature points, the parallelism of lines, and the relative length of parallel segments (Lee et al. 2008; Todd et al. 1995). If only affine information is accurately carried on from the earliest stages of 3D processing, then it is possible to predict systematic biases and great variability in perceptual and motor tasks that require Euclidean estimates (Domini and Caudek 2013). The typical result in perceptual studies is that the large variability of Euclidean judgments is observed both within and between observers, whereas such variability is negligible when affine tasks are involved (Lappin and Craft 2000). The systematic distortions that are generally reported are those surfacing when the means are analyzed and are highly dependent on contextual factors (Lee et al 2013).

In our study we attribute these distortions to an incorrect scaling of retinal information with distance, in a way that is identical to that already described in perceptual studies (see Volcic et al. 2013; Johnston 1991; Rogers and Bradshaw 1993). According to Volcic et al. (2013), the Euclidean structure of 3D objects is only veridical at the distance where they are usually grasped and held for inspection. However, their depth is overestimated at closer distances and underestimated at larger distances. Hence, these findings resemble a compression of visual space, as observed in the present study, since the average MGA for grasping the same object decreases with the object distance. On this respect, the analysis of the peak velocity also provides converging evidence of the ineffectiveness of additional depth cues to correct for biases affecting grasps in virtual reality. Although the mean peak velocity was higher in the full-cue condition than in the virtual and glow-in-the-dark conditions, its scaling with viewing distance did not differ among the three conditions. Since peak velocity is an indirect measure of the object distance estimate during the planning phase of a movement (Jeannerod 1984; Glennester et al. 1996; Carey et al. 1998; Churchill et al. 2000; Hibbard and Bradshaw 2003), the fact that in all conditions distance modulated peak velocity in the same way might suggest that the compression of visual space was the same in all conditions as well.

Adding depth cues did play an important role on some aspects of the movement, such as the size of GA, peak velocity, and the movement total duration. Even though equally modulated by the object distance, the GA and the MGA showed an overall reduction (although not significant) in the full-cue condition in respect to the other two conditions. Possibly, seeing the entire hand within a full cue environment yields a more confident movement, which resulted in the adoption of a smaller margin of safety. In the same vein, movements performed with all cues available were much faster than those performed in the dark, indicating that participants achieved more confidence when able to see the object and the surrounding setting (Churchill et al. 2000). In particular, by segmenting the movement in all its phases, we found that the effect of additional depth cues on the movement speed increased from the earlier to the later phases to be largest in the second part of the movement, during the deceleration phase. This shows that, on the one hand, the experimental manipulations of this study were effective and that, on the other, they left systematic biases of depth estimates unperturbed.

These findings seem to be at odds with previous results showing a correct scaling of grasping even for targets subject to perceptual illusions (Aglioti et al. 1995; Goodale and Westwood 2004; Goodale et al. 2004). We reconcile this apparent idiosyncrasy with the fact that, in our experimental setting, participants could only see the front of the object and, therefore, did not have direct access to visual information of both grasp contact points (Smeets and Brenner 1999). However, it is remarkable that in our study the constant exposure to veridical haptic feedback could not correct for the lack of this apparently necessary visual information. In this respect, these results are also consistent with previous findings suggesting that poor shape perception is not calibrated by feedback from reach-to-grasp (Lee at al. 2008, 2010; but see also Coats et al. 2008).

It is worth noting that the present work limited its analysis to only one simple measure of grasping, that is, the GA. It is possible that differences in posture (i.e., orientation of the fingertips) might have occurred when grasping in different conditions. Furthermore, in our experimental condition we manipulated only some cues (i.e., binocular disparities, vergence, blurring and shading gradient, surrounding environment) and the presentation of a static target at eye-height limited the availability of other sources of information important for estimating distance and size of the target object, such as vertical disparity, motion parallax, and linear perspective (Brenner et al. 2001; Dijkerman et al. 1999). Therefore, further research should investigate whether additional cues might help to get rid of these distortions by allowing a more accurate estimation of the target shape and depth.

In conclusion, findings from the present study demonstrate that systematic biases in grasping actions are not exclusive of virtual environments, since they also persist when all depth cues are available. However, more than a demonstration of a failure of the visual system, they indicate that vision for grasping, as vision for perception, is based on mechanisms that bypass a veridical metric reconstruction of the scene.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: C.B. conception and design of research; C.B. performed experiments; C.B. analyzed data; C.B. and F.D. interpreted results of experiments; C.B. prepared figures; C.B. and F.D. drafted manuscript; C.B. and F.D. edited and revised manuscript; C.B. and F.D. approved final version of manuscript.