Lateral Prefrontal Cortex Contributes to Fluid Intelligence Through Multinetwork Connectivity

Abstract

Our ability to effectively adapt to novel circumstances—as measured by general fluid intelligence—has recently been tied to the global connectivity of lateral prefrontal cortex (LPFC). Global connectivity is a broad measure that summarizes both within-network connectivity and across-network connectivity. We used additional graph theoretical measures to better characterize the nature of LPFC connectivity and its relationship with fluid intelligence. We specifically hypothesized that LPFC is a connector hub with an across-network connectivity that contributes to fluid intelligence independent of within-network connectivity. We verified that LPFC was in the top 10% of brain regions in terms of across-network connectivity, suggesting it is a strong connector hub. Importantly, we found that the LPFC across-network connectivity predicted individuals' fluid intelligence and this correlation remained statistically significant when controlling for global connectivity (which includes within-network connectivity). This supports the conclusion that across-network connectivity independently contributes to the relationship between LPFC connectivity and intelligence. These results suggest that LPFC contributes to fluid intelligence by being a connector hub with a truly global multisystem connectivity throughout the brain.

Introduction

Flexible intelligent behavior requires the goal-directed control of a wide variety of potentially goal-relevant brain processes. These processes are distributed throughout the brain, likely making it important for regions that maintain goal representations—such as lateral prefrontal cortex (LPFC) (Braver et al., 2003; Miller and Cohen, 2001)—to have extensive global connectivity to access and influence this wide variety of processes. Supporting this hypothesis, we recently demonstrated that a region in the left LPFC has high global connectivity, and individuals with especially high global connectivity with this region have especially high general fluid intelligence (gF) (Cole et al., 2012).

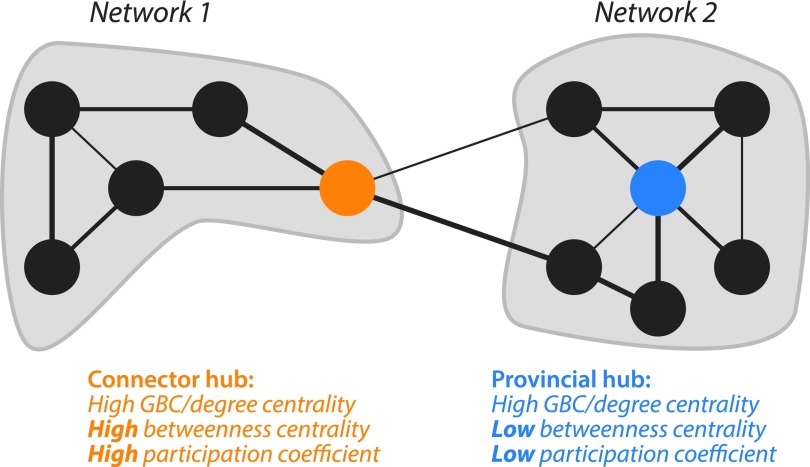
In that study, global connectivity was defined in terms of global brain connectivity (GBC)—the average resting-state correlation of LPFC with all gray matter brain voxels (Cole et al., 2010b). Importantly, GBC does not distinguish between provincial hubs with high within-network connectivity and connector hubs with high across-network connectivity (Fig. 1). This suggests it is possible that the previous result may have resulted from solely within-network connectivity or some combination of within-network connectivity and across-network connectivity.

FIG. 1.

Connector versus provincial hubs. Two hypothetical networks are illustrated, with key nodes highlighted. The left highlighted node is a connector hub, which is critical for across-network communication. In contrast, the right highlighted node is a provincial hub, which is important for within-network communication, but not across-network communication. Both the connector hub and provincial hub have high global brain connectivity (GBC)/degree centrality (number of connections), while the connector hub has high betweenness centrality and a high participation coefficient. Specifically, the provincial hub has a degree of 5, betweenness of 18.7 (calculated based on 7 shortest paths through the node), and participation of 0. In contrast, the connector hub has a degree of 4, betweenness of 50 (calculated based on 24 shortest paths through the node), and participation of 0.5 (half of the node's connections are within network and half across network).

The purpose of the present study is to distinguish among these possibilities by using graph theoretical measures designed to specifically estimate across-network connectivity. For instance, betweenness estimates the number of shortest paths through a region, which tends to be high for regions with extensive across-network connectivity (Rubinov and Sporns, 2010). Alternatively, the participation coefficient measures the proportion of a region's connections that are across network relative to within network (Guimera et al., 2005). We were able to estimate the participation coefficient using a recently identified set of putative functional regions that were partitioned into distinct brain network communities (Power et al., 2011). This set of uniform spherical regions covering every major brain network also allowed us to reduce potential confounds arising from voxel-wise approaches that result in large regions affecting graph theoretical metrics disproportionally (Power et al., 2013; Wig et al., 2011).

We hypothesized that these more direct measures of across-network connectivity would demonstrate that LPFC is a connector hub with extensive across-network connectivity, and individuals with especially high across-network connectivity would have especially high gF. This would suggest an important role for extensive across-network connectivity in supporting higher-order cognition, which relies on the integration of constituent functions to form complex cognitive processes and representations.

Materials and Methods

Participants

The data presented here were collected as part of a larger multifaceted study. Individuals participated in three separate sessions, spaced a few days to few weeks apart, to complete personality tests, mood questionnaires, neuropsychological tests, and the N-back fMRI scanner task. The first session was 3-h long and involved answering several standard paper-and-pencil questionnaires; the second was 2-h long and involved answering computerized questionnaires and cognitive tasks; and the third was 2.5-h long and involved an fMRI scan of the N-back task. The Raven Advanced Progressive Matrices–Set II (Raven, 2000) and the Cattell Culture Fair Test (Cattell and Horn, 1978) were included in the first session as measures of gF. The standard scoring procedures for each test were used to compute measures from these tests. These measures were combined into a single fluid intelligence score by z-scoring the values of each score separately and then averaging them. Data from these participants have been used in other articles to address questions distinct from those in the current study (Burgess et al., 2011; Cole et al., 2012; DeYoung et al., 2009, 2010; Fales et al., 2008; Shamosh et al., 2008).

One hundred twenty-one participants (70 female; mean age=23, range=18–40) were recruited from the undergraduate population at Washington University (n=60) or surrounding communities and received financial remuneration for their participation. The experiment was approved by the Washington University Institutional Review Board. The same 94 participants used in Cole et al. (2012) were used here (see that study for exclusion criteria).

fMRI data acquisition and preprocessing

Whole-brain images were acquired on a 3 Tesla Allegra System (Siemens, Erlangen, Germany). Structural images were acquired using a magnetization-prepared rapid gradient-echo T1-weighted sequence. Functional images were acquired using an asymmetric spin-echo echo-planar sequence sensitive to blood-oxygen-level-dependent magnetic susceptibility (TR=2360 msec, TE=50 msec, flip=90°). Each scanning run gave 149 sets of brain volumes (32 contiguous, 4-mm-thick axial images, 4×4-mm in-plane resolution).

Resting-state fcMRI preprocessing was performed identical to that of Cole et al. (2012). Functional images were extracted from the rest periods between task blocks using a previously validated method (Fair et al., 2007). Although there are some criticisms of using signal between task blocks as rest (Barnes et al., 2009), we minimized these concerns in the following way (see Cole et al., 2012 for further consideration of this issue): We used rest images that were 14.16 sec (six frames) or more past the end of every task block and 4.72 sec (two frames) or fewer into the start of every task block. Furthermore, the mean signal amplitude for each rest block was subtracted for each voxel before rest block concatenation. There were 3 rest blocks per run, resulting in 35 rest frames per run (after removing the first 5 frames of each run). There were 8.26 min of rest total (across the six runs) per participant.

These resting-state functional images were further preprocessed using AFNI (Cox, 1996) with the following steps (in the indicated order): (1) slice-time correction, (2) removal of first five images from each run to reach steady state, (3) rigid body motion correction, (4) removal of a set of nuisance regressors, including signals from the ventricles, deep white matter, whole-brain average, motion correction parameters, and first derivatives of these regressors, (5) additional removal of local white matter (using 16-mm radii spheres) nuisance regressors on a voxel-wise basis (ANATICOR) (Jo et al., 2010), (6) band-pass filtering (0.009<f(t)<0.08), and (7) smoothing with a 6-mm spherical dilation of gray matter voxels (to avoid averaging nonbrain voxel noise with the gray matter). These steps helped to ensure that spurious signal confounds did not impact our results. Finally, following GBC processing, but before group analysis, the images were transformed into atlas space (Talairach and Tournoux, 1988).

Region definition

We used the 264-region set presented by Power et al. (2011) with several modifications. Our hypotheses were specific to the LPFC region identified in Cole et al. (2012), so we added that region as a sphere such that we used a 265-region set. This region was defined based on individual differences in activation amplitudes correlating with N-back task performance (Cole et al., 2012). When adding the 265th region, 2 nearby regions overlapped by a single voxel each. To ensure that each region was independent of every other, we moved these 2 nearby regions by a single voxel for the 265-region set. We also carried out our analyses with the original 264-region set and found that the connectivity of the regions nearby LPFC did not significantly correlate with fluid intelligence. Note that we assigned the LPFC region to the same network as the two nearby regions: the frontoparietal control network.

Power et al. (2011) presented several region network segmentations based on different connection density thresholds. We used their 2% connection density segmentation for our analyses, given that of all the tested segmentations, it best separated networks known to be distinct (such as the auditory network) (Power et al., 2011).

Graph theoretical analyses

Graph theoretical analyses were carried out with MATLAB (version 2008a) using in-house code and the Brain Connectivity Toolbox (Rubinov and Sporns, 2010). Functional connectivity was estimated as the Fisher z-transformed correlation between each pairwise regions' time series (the average of the voxels' time series within each region). GBC was calculated as the average connectivity of each region with all other regions. In graph theoretical terms, GBC was the weighted degree centrality (or strength) divided by the total number of connections. We calculated weighted betweenness centrality as the number of shortest paths through a region (the Brain Connectivity Toolbox function “betweenness-wei”) divided by the total number of connections. The participation coefficient was calculated using the regional community assignments from Power et al. (2011) at the 2% threshold and the Brain Connectivity Toolbox function “participation_coef.” We calculated the participation coefficient results across three connectivity density thresholds: 10%, 5%, and 1%.

We applied transformations on the graph theoretical metrics to achieve normal distributions for the Pearson's correlation tests. The GBC values were nearly normally distributed, but better fit a normal distribution (assessed using histograms and QQ-plots) using a square-root transformation. Weighted betweenness was skewed to the left, but a square-root transformation made it approximately normally distributed. Participation was skewed strongly to the right and we found that only a complex inverse transformation [1/(−1×pc+1)] made it approximately normally distributed. We also performed Spearman's correlation tests (which do not assume a normal distribution) on the nontransformed metrics and achieved similar results.

Results

Using GBC to predict gF with a predefined set of regions

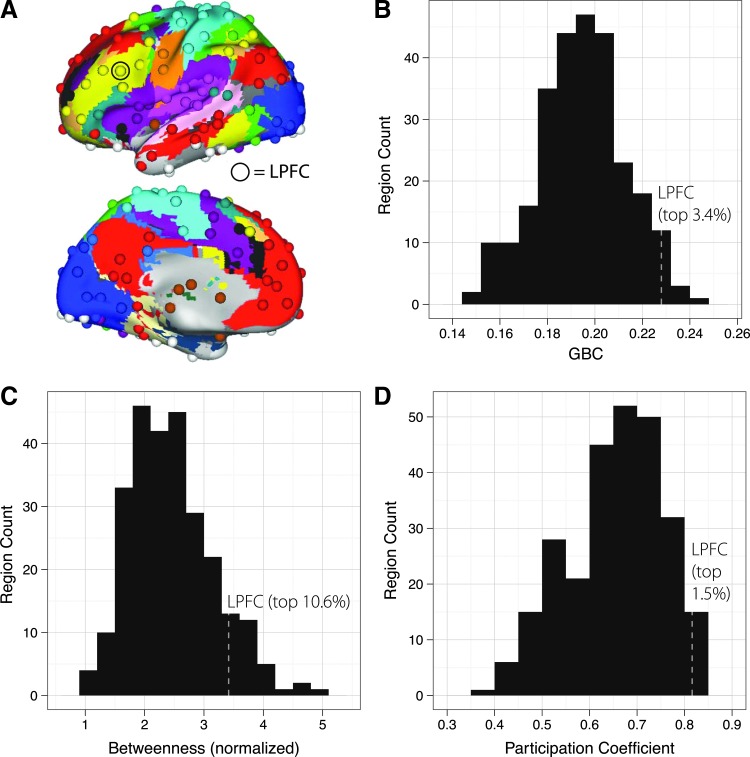
It has recently been argued that using a voxel-wise approach, as in our previous demonstration of an LPFC GBC-gF correlation is problematic for characterizing brain connectivity (Wig et al., 2011). Rather than identifying a region's true graph theoretical properties, a voxel-wise approach can distort results toward large regions. One solution to these issues—which we applied here—is to use a large set of equal-sized functionally defined regions of interest (ROIs) from every major system of the brain (Power et al., 2011) (Fig. 2A).

FIG. 2.

Location and graph theoretical ranking of lateral prefrontal cortex (LPFC). (A) The left hemisphere regions and network segmentations (each network is a different color) from Power et al. (2011). The left LPFC region from Cole et al. (2012) was added and highlighted with a circle. (B) A histogram of GBC values across all 265 regions, with the ranking of LPFC highlighted. (C) A histogram of betweenness, with LPFC's ranking highlighted. (D) A histogram of participation, with LPFC's ranking highlighted. LPFC was within the top ∼10% of all three graph theoretical metrics.

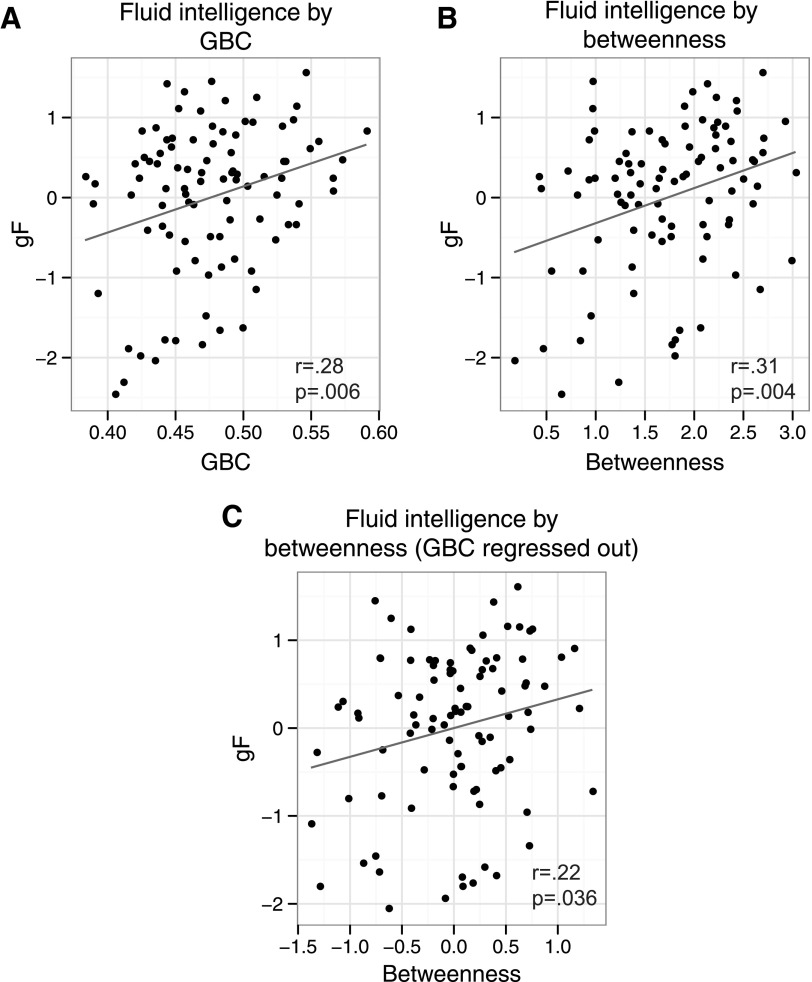
A replication of the LPFC GBC-gF effect would be nontrivial, despite using the same large dataset as our previous study (Cole et al., 2012), given that the GBC calculation now includes only 11.8% of the voxels included in the voxel-wise analysis in the previous study. We first replicated the finding that LPFC is a GBC hub region, defined as being in the top 10% of ROIs. We found that LPFC's GBC was in the top 3.4% for positive connections (top 4.5% for absolute values, including both positive and negative connections). Furthermore, we replicated the finding that LPFC's GBC correlated significantly with gF (r=0.28, p=0.006) (Fig. 3A), suggesting the previous results were not biased by region size and validating the 265 ROI set for subsequent analyses.

FIG. 3.

LPFC graph theoretical correlations with fluid intelligence. (A) The correlation between LPFC GBC and fluid intelligence. (B) The correlation between LPFC betweenness and fluid intelligence. (C) The correlation between LPFC betweenness and fluid intelligence, after regressing GBC variance out of both betweenness and fluid intelligence. The correlation remains significant, suggesting that LPFC multinetwork connectivity independently contributes to fluid intelligence.

Like the previous study, no other regions showed a significant GBC-gF effect (p<0.05, false discovery rate corrected for multiple comparisons). This was also the case when the original 264 ROI set was used. Note that the standard statistical tests used do not provide evidence that LPFC is exclusive in this GBC-gF relationship. Furthermore, it will be important for future studies to explore the possibility of other regions also having this relationship.

Determining if LPFC is a connector hub

LPFC's high GBC could be due to extensive within-network connectivity—consistent with a provincial hub—rather than extensive across-network connectivity—consistent with a connector hub (Fig. 1). We used the participation coefficient to determine if LPFC has an especially extensive amount of across-network connectivity (relative to within-network connectivity) compared to other regions (Guimera et al., 2005). The participation coefficient was calculated across three connectivity density thresholds (top 10% of connections, top 5% of connections, and top 1% of connections) to test for generalizability of the results. Networks were defined using the region community parcellation (density threshold of 2%) from Power et al. (2011). We considered a region to be a connector hub if it was within the top 10% of regions in terms of participation coefficient. LPFC was in the top 8% (for the 10% connectivity density threshold), the top 3% (for the 5% connectivity density threshold), and the top 2% (for the 1% connectivity density threshold). This suggests that LPFC is a connector hub with more across-network (relative to within-network) connections than most brain regions.

We also measured across-network connectivity using betweenness centrality, which estimates the number of shortest paths that goes through a given brain region (Rubinov and Sporns, 2010). Connector hubs typically have high betweenness centrality because regions with many across-network connections tend to provide the shortest paths between many nodes in different networks. Given that GBC is weighted and normalized by the number of connections (i.e., the average of the connection weights/strengths), we sought to parallel the GBC approach by using weighted betweenness centrality normalized by the total number of connections. As expected, we found that LPFC was also a connector hub in terms of betweenness centrality, given that it was in the top 10.6% of regions (just over the 10% cutoff) using positive connections only and top 6.3% of regions using the absolute value of connections (including both positive and negative values). Results were virtually identical when the two regions closest to the LPFC region were excluded for this analysis.

To further establish the LPFC region's broad across-network connectivity, we calculated the percentage of possible connections that the LPFC region actually made with each network (Table 1). There were statistically significant functional connections with every network. The network with the fewest number of LPFC connections was the ventral attention network. Even for this network, over a third of its regions were significantly connected with LPFC, suggesting that LPFC has a strong influence and/or monitoring ability with every major network in the brain.

Table 1.

Percentage of Possible Connections Between Lateral Prefrontal Cortex and Each Network

FPN	SAL	SSM	SSH	DMN	COP	VIS	AUD	DAN	SUB	NONE	MEM	CBM	VAN
84.6%	83.3%	80.0%	76.7%	72.4%	71.4%	71.0%	69.2%	63.6%	61.5%	60.7%	60.0%	50.0%	33.3%

Results were obtained by computing which possible LPFC connections were statistically significant relative to 0 (FDR-corrected) and then dividing the number of significant connections with each network by the total number of regions in each network.

AUD, auditory network; CBM, cerebellum; COP, cingulo-opercular task; DAN, dorsal attention network; DMN, default-mode network; FPN, frontoparietal network; LPFC, lateral prefrontal cortex; MEM, memory retrieval; NONE, uncertain/unidentified regions; SAL, salience network; SSH, somatosensory hand; SSM, somatosensory mouth; SUB, subcortical; VAN, ventral attention network; VIS, visual network.

Identifying a provincial hub for comparison with LPFC

In order for the previous hypothesis (that LPFC has high betweenness, participation, and GBC) to be valid, it must be falsifiable. In other words, betweenness, participation, and GBC cannot be perfectly correlated, and there should be cases in which regions have high GBC, but low betweenness and participation (provincial hubs; Fig. 1). To verify that this is the case, we took the across-subject mean for each region and tested for Spearman's ranked correlations between the metrics across the 265 regions. All three metrics were significantly, but not perfectly correlated, as expected. Specifically, GBC was imperfectly correlated with betweenness at rho=0.82, p<0.00001; GBC was imperfectly correlated with participation (5% density threshold) at rho=0.43, p<0.00001; and betweenness was imperfectly correlated with participation at rho=0.26, p<0.0001.

We looked for provincial hub regions using the relatively strict criteria of a region that is in the top 10% GBC and bottom 90% betweenness and participation. There were a variety of regions that were in the top 10% GBC and the bottom 90% of either betweenness or participation, but only a single region survived all three criteria: left primary auditory cortex (A1; Talairach coordinates: −58, −27, 13). Specifically, A1 was in the top 10.2% GBC, bottom 81% betweenness, and bottom 70.2% participation. This demonstrates that, in contrast to LPFC, it is possible for a region to have high within-network connectivity and low across-network connectivity—consistent with a provincial hub.

Determining if across-network connectivity of LPFC predicts gF

We next more directly tested our hypothesis that the increased across-network LPFC connectivity would be associated with increased gF across individuals. We found that LPFC betweenness correlated strongly with gF (r=0.31, p=0.002 for positive only connectivity, r=0.23, p=0.03 for negative only connectivity, and r=0.32, p=0.001 for absolute value connectivity), supporting our hypothesis (Fig. 3).

We had begun by testing for an LPFC participation coefficient correlation with gF, yet we found that the participation coefficient's statistical properties were not ideal for identifying correlations. In particular, the participation coefficient values tended to be strongly skewed to the right, violating the normality assumption behind Pearson's correlations. Note that, we are referring here to the across-subject distributions used for calculating correlations with gF, not the across-region distributions depicted in Figure 2 (which were approximately normally distributed). Furthermore, the strong clustering of values across participants suggested that even nonparametric tests such as Spearman's correlations might not be effective since the relative ordering of values across participants might not be very meaningful. We nonetheless tested for correlations between the participation coefficient and gF, finding no correlation using an inverse transformation to achieve normality with Pearson's correlation (10% density: r=0.11, p=0.28; 5% density: r=0.17, p=0.09; 1% density: r=0.16, p=0.12). Similarly, there was no correlation when using Spearman's rank-order correlation (10% density: rho=0.07, p=0.5; 5% density: rho=0.14, p=0.19; 1% density: rho=0.15, p=0.15).

In contrast to the participation coefficient, betweenness centrality had better statistical properties for correlation tests. The LPFC betweenness distribution was slightly skewed to the left, but results were similar with (r=0.31, p=0.002) and without (r=0.30, p=0.003) a square root transformation (to achieve normality), when using a nonparametric Spearman's correlation test (rho=0.30, p=0.004) and when using unweighted betweenness (10% and 5% density thresholds; r=0.23, p=0.024). These results suggest that LPFC across-network connectivity is strongly associated with gF across individuals.

Random-walk betweenness centrality

One limitation of standard betweenness centrality is that it assumes that brain activity flows through shortest paths. It is unknown if brain activity actually flows through shortest paths, and it remains unclear how any brain activity would know the shortest path to its destination to take it. We therefore used a recently developed graph theoretical measure—random-walk betweenness centrality—that estimates betweenness centrality based on a large number of random paths rather than shortest paths (Newman, 2005). This may better model how activity flows within brain networks.

We found that fluid intelligence was also correlated with the LPFC region's random-walk betweenness (r=0.26, p=0.01). This was also the case when using Spearman's correlation (rho=0.23, p=0.03), when including only negative connections (r=0.24, p=0.02) and the absolute value of the connections (r=0.29, p=0.004). The consistency of these results with the main betweenness analysis suggests that the shortest path assumption for that analysis was not problematic.

Assessing the independence of LPFC betweenness and GBC

We next hypothesized that the relationship between LPFC across-network connectivity and gF was largely independent of the GBC-gF correlation identified previously (Fig. 3A). Consistent with this hypothesis, we found that the LPFC betweenness-gF correlation—which primarily reflects across-network connectivity—remained statistically significant after regressing out LPFC GBC variance (from both betweenness and gF): r=0.22, p=0.036 (Fig. 3C). In contrast, regressing out LPFC betweenness variance (from both GBC and gF) resulted in a nonsignificant LPFC GBC-gF correlation: r=0.17, p=0.11. We achieved a similar result using multilevel linear modeling, with GBC predicting gF significantly (F(1,92)=7.8, p=0.006) and increasing in significance when including betweenness in the model (F(2,91)=6.3, p=0.003). This increase in predictive power was statistically significant (F(1,91)=4.5, p=0.037). Together, these results suggest that betweenness provided an independent and relatively cleaner estimate than GBC of the connectivity property—likely across-network connectivity—underlying the LPFC connectivity-gF correlation.

Discussion

We previously showed that LPFC is a hub region with especially high global connectivity and this global connectivity can predict individuals' fluid intelligence (Cole et al., 2012). This suggested that LPFC might support fluid intelligence abilities through its extensive brain-wide connectivity. Critically, however, global connectivity reflects local within-network connectivity in addition to across-network connectivity, such that the previous findings may have resulted primarily from local rather than truly global connectivity. In this study, we tested the hypothesis that LPFC is a truly global connector hub with extensive across-network connectivity and this connectivity contributes to fluid intelligence independent of within-network connectivity.

We used two graph theoretical metrics to isolate across-network connectivity: betweenness centrality and participation coefficient. Participation uses a predefined network segmentation to calculate the number of across-network connections relative to the number of within-network connections (Guimera et al., 2005). Betweenness measures the number of shortest paths passing through each region, which tends to be especially high for connector hubs (due to entire networks needing to pass through such hubs to reach other networks) (Rubinov and Sporns, 2010). We also used an alternate betweenness measure (random-walk betweenness centrality) that does not assume activity flows between networks through shortest paths, obtaining similar results. Importantly, unlike participation, betweenness does not require network segmentation, such that any inaccuracies in network segmentation will not affect betweenness. This—along with the observed nonnormal participation coefficient distribution—may explain the less robust results using participation relative to betweenness.

We found that LPFC is a truly global connector hub according to all of these metrics (including participation coefficient). Compatible with our hypothesis, LPFC betweenness predicted fluid intelligence over and above global connectivity, demonstrating a strong relationship between across-network connectivity and fluid intelligence.

Several previous studies have found that regions within the default-mode network and frontoparietal control network have among the highest connectivity in the brain (Buckner et al., 2009; Cole et al., 2010b). It has been recently pointed out, however, that these findings may have been biased by these networks being especially large (resulting in extensive within-network connectivity contributing to global connectivity estimates) and/or by regions within these networks being especially big (resulting in disproportionate numbers of voxels contributing to global connectivity estimates) (Wig et al., 2011). We accounted for the size of LPFC's network using betweenness and participation measures—which primarily estimate across-network connectivity. We further accounted for region size biases to connectivity estimates by using a set of uniform spheres throughout the brain (Fig. 2A). In agreement with our findings, a previous study using these same regions found that regions within the frontoparietal control network (which LPFC is a member of) tended to have high across-network connectivity, while the default-mode network had primarily within-network connectivity (Power et al., 2011).

The finding that LPFC has extensive across-network connectivity that predicts fluid intelligence supports the possibility that LPFC is a truly global flexible hub (Cole et al., 2012, 2013; Miller and Cohen, 2001). This account suggests that LPFC may be able to shift its connectivity in a task-dependent manner (Cole et al., 2010a, 2013; Rowe et al., 2005) to dynamically configure brain networks according to goal representations likely actively maintained within LPFC. According to this account, the present findings based on resting-state functional connectivity likely demonstrate that individuals with greater intrinsic functional LPFC connectivity have a goal-driven access to a wider variety of potentially task-relevant brain regions. Further research is necessary to test if higher across-network resting-state functional connectivity facilitates flexible task-dependent changes in connectivity, as predicted by this flexible hub hypothesis. It will also be critical to explore the role of across-network connectivity of other brain regions (e.g., frontoparietal regions other than the LPFC region used here) in supporting higher-level cognition.

Conclusion

We previously demonstrated a correlation between LPFC global connectivity and fluid intelligence, yet it was unclear if that result might have been biased by local within-network connectivity. We showed here that fluid intelligence was significantly correlated with LPFC across-network connectivity, supporting the conclusion that LPFC's extensive brain-wide connectivity contributes to fluid intelligence. It will be important for future research to investigate the relationship between LPFC's across-network resting-state functional connectivity and LPFC's structural connectivity, task-dependent shifts in connectivity, and the task activity, in addition to how they all relate to LPFC's contribution to fluid intelligence.

Acknowledgments

Research reported in this publication was supported by the National Institute of Mental Health of the National Institutes of Health under Award Numbers MH096801, MH66088, NR012081, MH66078, and MH66078-06A1W1. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.

Author Disclosure Statement

No competing financial interests exist.