Molecular weight–gyration radius relation of globular proteins: a comparison of light scattering, small-angle X-ray scattering and structure-based data

Light scattering and small-angle scattering data indicate that for globular proteins the relation between molecular weight and radius of gyration follows a power law which can be related to the fractal dimension of the proteins.

Abstract

The molecular weight–gyration radius relation for a number of globular proteins based on experimental light scattering data is compared with small-angle X-ray scattering data recently published by Mylonas & Svergun [J. Appl. Cryst. (2007 ▸), 40, s245–s249]. In addition, other recent experimental data and theoretical calculations are reviewed. It is found that the M _W–R _g relation for the globular proteins is well represented by a power law with an exponent of 0.37 (2).

In recent years the structural study of proteins in solution has become a rapidly growing field, thanks to major progress in the interpretation and analysis of solution small-angle X-ray scattering (SAXS) data (Svergun & Koch, 2003 ▸; Mertens & Svergun, 2010 ▸; Blanchet & Svergun, 2013 ▸). Owing to the small scattering contrast between protein and buffer, such studies are mostly performed at synchrotron facilities, in order to access the largest possible range of scattering angles. As there is significant overhead in performing experiments at a synchrotron facility, laboratory-based methods are of interest for the purpose of assessing the protein quality, in order to maximize the chance of success during the limited amount of available beamtime. We show that light scattering data taken in the static and dynamic mode can be useful for quality control. Moreover, the molecular weight M _W and the radius of gyration R _g are efficiently accessible with light scattering and can provide the basis of further in-depth SAXS studies.

A simple lookup table, diagram or equation is useful, in order to check whether incoming data are in a reasonable range. The globular proteins form such a convenient reference, and data from a variety of proteins are available in the literature. Here we compare molecular weight data and gyration radius data obtained by static and dynamic light scattering, respectively, with data from solution SAXS recently compiled by Mylonas & Svergun (2007 ▸). In our case, M _W was obtained by static light scattering using the Zimm method (Folta-Stogniew & Williams, 1999 ▸). The gyration radius R _g was obtained with dynamic light scattering from the hydrodynamic radius R _H by the well known relation

for spheroidal objects. Table 1 ▸ lists the light scattering results for a variety of standard proteins.

Table 1. Light scattering results for standard globular proteins.

Protein	Oligomeric state	M W (kDa)†	R H (nm)‡	R g (nm)§
Aprotinin	Monomer	6.8 (5)	1.35 (6)	1.04 (5)
Cytochrome C	Monomer	12.0 (6)	1.77 (12)	1.37 (9)
-Lactalbumin	Monomer	14.3 (1)	1.91 (8)	1.49 (6)
Myoglobin	Monomer	14.2 (9)	2.12 (7)	1.64 (6)
Carbonic anhydrase	Monomer	29.2 (2)	2.35 (16)	1.82 (12)
Trypsin inhibitor	Monomer	20.5	2.47 (8)	1.91 (6)
-Lactoglobulin	Monomer	20.1 (3)	2.64 (13)	2.04 (9)
Ovalbumin	Monomer	42.5 (7)	2.98 (2)	2.31 (1)
Bovine serum albumine	Monomer	67.1 (10)	3.56 (1)	2.76 (1)
Enolase (yeast)	Dimer	79.5	3.57 (2)	2.76 (1)
Enolase (rabbit)	Dimer	86.4 (19)	3.65 (10)	2.83 (8)
Transferrin	Monomer	76.9 (10)	4.02 (6)	3.11 (5)
Alcohol dehydrogenase	Tetramer	144.0 (9)	4.50 (10)	3.48 (8)
BSA dimer	Dimer	137.1 (39)	3.68 (21)	3.62 (15)
Aldolase (rabbit)	Tetramer	155	4.77 (6)	3.69 (5)

^†Based on static light scattering, averaged over three runs.

^‡Based on ‘in-line’ dynamic light scattering, averaged over three runs.

^§Determined from R _H via equation (1).

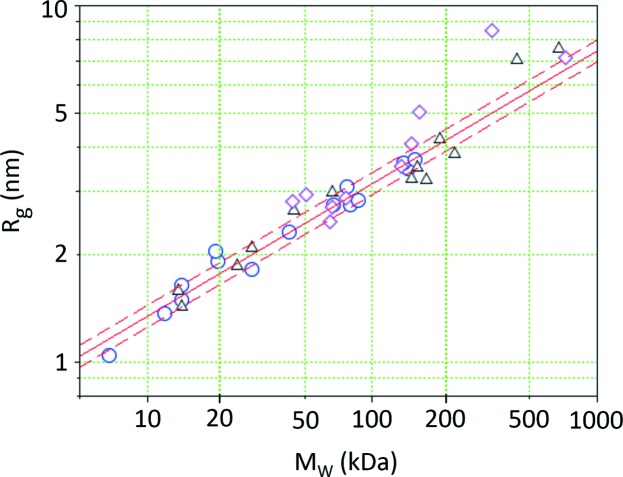
We found that plotting the data in a log–log plot provides a convenient presentation of the M _W–R _g relation over the typical size range of proteins in solution (see Fig. 1 ▸). The globular proteins form the baseline. Proteins featuring a more complex structure (e.g. unfolded, elongated or two domains with a flexible linker) would veer off the main branch: at the same molecular weight they would display a larger gyration radius.

Figure 1.

Gyration radius versus molecular weight for a range of globular proteins. Light scattering data are from this study (circles). The solid line shows the fit to our light scattering data, and the dashed lines indicate the range of confidence based on the standard deviation of the residual. SAXS data were reported by Mylonas & Svergun (2007 ▸) (triangles). Light scattering data on blood components (Armstrong et al., 2004 ▸) show both globular and elongated proteins (diamonds).

The data were fitted by the simple relation

We find that the fitted parameters of the optical and the X-ray measurements agree within error, as listed in Table 2 ▸. The standard deviation of the residual in the log–log plot was determined to be σ = 0.031, which translates into an R _g uncertainty of 7%. The corresponding range of confidence is indicated by dashed lines in Fig. 1 ▸, and most data points fall within these limits. Statistical analysis was done using the reglin routine of Scilab 5.5.2 (Scilab Enterprises, 2015 ▸). Fitting results are summarized in Table 2 ▸. Our parametrization of the light scattering data provides a convenient lookup table for a quick examination of M _W and R _g data. The experimental values still have a certain amount of scatter; however, most experimental values fall within a factor of 1.07 of the fitted curve, as indicated by the dashed parallel lines.

Table 2. Fits of light scattering and SAXS data.

PDB is the Protein Data Bank, DLS is dynamic light scattering.

Technique M w/R g	Parameter a	Parameter b	Correlation coefficient R
Light scattering†	0.25 (3)	0.37 (2)	0.98
Structure/SAXS‡	0.27 (6)	0.39 (3)	0.97
Combined† ‡ §	0.26 (3)	0.38 (2)	0.98
Structure (PDB)¶	0.28 (2)	0.36 (2)	0.97
Structure/SAXS††	0.27 (6)	0.39 (4)	0.98
DLS/SAXS††	0.32 (4)	0.42 (3)	0.99
SAXS/SAXS††	0.31 (5)	0.43 (3)	0.99

^†This study.

^‡Cited from Mylonas Svergun (2007 ▸).

^§No weighting was applied.

^¶Data based on calculations by Abad-Zapatero Lin (1990 ▸).

^††Data compiled by Akiyama (2010 ▸).

In order to assess whether the M _W–R _g relation can be used as a tool to see deviation from globular shape, it is useful to analyze the generalized gyration tensor (Šolc, 1971 ▸). R _g is related to the half-axes A, B, C of the gyration tensor by

A globular protein has A = B = C and R _g is given by 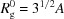. In order to examine the sensitivity of our method to deviations from the globular shape we will assume a prolate shape of the protein, i.e. A = B < C. Introducing the aspect ratio C/A we obtain

Thus we can detect whether a protein is non-globular within the limitations given by the scatter in our data, if the aspect ratio is larger than C/A > 1.25. We find that the method is sensitive to elongated protein shapes, while the effect is too small for oblate shapes. As more data become available, these boundaries and uncertainties should shrink further.

As an example we show data from a dynamic light scattering study of blood components by Armstrong et al. (2004 ▸). Human serum albumin (M _W = 66 kDa), transferrin (76 kDa), ceruloplasmin (135 kDa) and α-2 macroglobulin (725 kDa) lie nicely within our extrapolated range for globular proteins, while the elongated proteins immunoglobulin A (IgA, monomer, 162 kDa) and fibrinogen (340 kDa) have a significantly larger R _g, as would be expected for globular proteins. α-1 acid glycoprotein (44 kDa), α-1 antitrypsin (51 kDa) and immunoglobulin G (IgG, 150 kDa) lie just outside the bounds for globular proteins, which indicates that these proteins may be somewhat elongated. On the basis of our data alone the method should apply for molecular weights ranging from 5 to 200 kDa. Comparison with the experimental data from the literature displayed in Fig. 1 ▸ indicates that this range can be extended up to 1000 kDa, thus covering the typical molecular weight range of proteins.

While SAXS analysis has powerful direct methods such as the Kratky plot (Glatter & Kratky, 1982 ▸; Feigin & Svergun, 1987 ▸; Putnam et al., 2007 ▸) to determine whether a protein is unfolded, partially unfolded or folded, there is no equivalent direct method in light scattering to retrieve this important information. However, with the help of the diagram in Fig. 1 ▸, combined static and dynamic light scattering data can provide an indication of whether a protein in solution has a shape more complex than globular.

We include data from two theoretical studies in Table 2 ▸ for comparison. Abad-Zapatero & Lin (1990 ▸) published a list of theoretical R _g values based on structural data of 45 proteins in the Protein Data Bank (http://www.rcsb.org/pdb/). Fitting these data resulted in a value of b = 0.36 (1), which is still in agreement with the fit of the SAXS data by Mylonas & Svergun (2007 ▸). Recently Akiyama (2010 ▸) reviewed molecular weight determination for seven protein standards, based on theoretical molecular weights from structural data, dynamic light scattering and SAXS compared to measured SAXS values of R _g. Fitting these data sets with equation (2), we obtain values for the exponent b of 0.39, 0.42 and 0.43, respectively. The detailed fit results are also listed in Table 2 ▸.

Dewey (1997 ▸) and more recently Enright & Leitner (2005 ▸) have pointed out that proteins can be considered as mass fractals, with the fractal dimension D = 2.5 (2). A mass fractal scales as M ∝ R ^D, i.e. when the mass M enclosed in a sphere of radius R is plotted as a function of R. For the globular proteins we note that the inverse of our scaling exponent yields 1/b = 2.6 (2), i.e. the scaling behavior of R _g versus M _W is consistent with the fractal nature of proteins. This means that all globular proteins within our sample have similar fractal properties. Our light scattering results match well with the theoretical study by Enright & Leitner (2005 ▸), which was based on a mathematical analysis of 200 protein structures published in the Protein Data Bank.