Single quantum dot controls a plasmonic cavity’s scattering and anisotropy

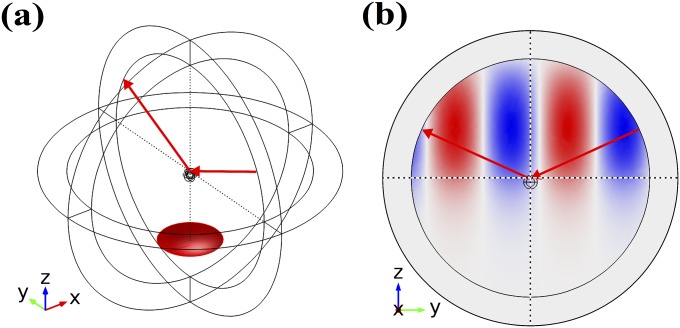
Significance

We experimentally demonstrate that a single semiconductor quantum dot placed in close proximity to a plasmonic cavity (i.e., a spherical metallic nanoparticle) can be used to control the scattering spectrum and anisotropy of the latter. The scattering spectrum of the hybrid structure features a Fano resonance mediated by single photon absorption/scattering. This result is highly counterintuitive because the scattering cross sections of these two nanoparticles differ by four orders of magnitude. Our work represents a critical step toward realizing quantum plasmonic nanostructures that are capable of producing scattered light, which, depending on its polarization state, obeys either quantum or classical statistics. Furthermore, our work enables a hybrid orientation sensor unaffected by photobleaching of quantum dots.

Abstract

Plasmonic cavities represent a promising platform for controlling light–matter interaction due to their exceptionally small mode volume and high density of photonic states. Using plasmonic cavities for enhancing light’s coupling to individual two-level systems, such as single semiconductor quantum dots (QD), is particularly desirable for exploring cavity quantum electrodynamic (QED) effects and using them in quantum information applications. The lack of experimental progress in this area is in part due to the difficulty of precisely placing a QD within nanometers of the plasmonic cavity. Here, we study the simplest plasmonic cavity in the form of a spherical metallic nanoparticle (MNP). By controllably positioning a semiconductor QD in the close proximity of the MNP cavity via atomic force microscope (AFM) manipulation, the scattering spectrum of the MNP is dramatically modified due to Fano interference between the classical plasmonic resonance of the MNP and the quantized exciton resonance in the QD. Moreover, our experiment demonstrates that a single two-level system can render a spherical MNP strongly anisotropic. These findings represent an important step toward realizing quantum plasmonic devices.

Many quantum network and quantum information processing schemes build upon the enhanced light–matter interaction between a single quantum emitter and a cavity, enabling the effective conversion between photonic and matter-based quantum states (1–4). For example, if the absorption of a photon by a single atom placed inside a cavity can render it transparent to a second photon, then a variety of promising quantum information processing devices can be envisioned including quantum phase gates and repeaters (5). Such QED effects require a high atomic cooperativity $c=\frac{g^2}{\gamma k}$, where the coupling strength $g^2\propto 1/V$ is inversely proportional to the volume of the cavity mode V (6). γ and k are the linewidth of the atomic transition and the cavity mode, respectively. Typically, a high cavity quality factor Q (or low k) of conventional photonic cavities is required to compensate for relatively large (diffraction-limited) mode volumes and comes at a cost: The narrow linewidth of cavity modes places stringent requirements on their spectral alignment with the frequencies of quantum transitions. Plasmonic cavities, on the other hand, achieve high values of $C$ while maintaining moderate $Q$ values because of their ultrasmall modal volume (7–10). The relaxed spectral alignment requirements facilitate the experimental realization of various quantum phenomena, such as collective photon emission from a small ensemble of emitters (11) and single photon sources with tunable statistical properties (12).

Prior experiments exploring cavity QED effects associated with single emitters coupled to plasmonic cavities or waveguides focused almost exclusively on the observations of reducing the emitter’s lifetime due to the enhanced radiative (proportional to $F_P$) and nonradiative energy transfers (13–15). The realms of quantum information science and plasmonics have also been bridged by demonstrating that photon emission statistics, such as antibunching behavior in the second-order correlation function for single photon sources, remain intact following the photon–plasmon–photon conversion process (16–19). The possibility of controlling the scattering of a plasmonic nanocavity by a single (and inherently quantum and nonlinear) two-level system has also been proposed (12, 20–22) but never experimentally observed.

In this article we provide, to our knowledge, the first experimental demonstration that a single quantum dot (QD) dramatically modifies the scattering spectrum of a simple plasmonic cavity comprising a single metallic nanoparticle (MNP). The MNP–QD hybrid structure is assembled into a well-controlled geometry using the technique of atomic force microscope (AFM) nanomanipulation. The coupling between the MNP and QD is experimentally confirmed by measuring the exciton lifetime, which is reduced by more than an order of magnitude in the presence of the MNP. Analyzing the polarization and spectral properties of light scattered by the MNP-QD hybrid, we observe that the overall plasmonic cavity scattering is significantly modified over a broad spectral range. A Fano resonance spectrally aligned with the QD’s quantized exciton resonance is clearly identified when the polarization of the scattered photon is along the Fano axis (23) connecting the MNP’s center with the QD. The anisotropic scattering spectrum observed in our experiments suggests that a polarization-controlled, versatile quantum light source may be realized in this simple QD–MNP cavity system.

The calculated polarization-resolved scattering spectra by the QD–MNP (diameters: $2r_{QD}=6$_.nm and $2r_{MNP}=30$ nm) hybrid are shown in Fig. 1A for three polarization angles ${\varphi }_A$ of the analyzer placed in the collection path of the scattering signal to mimic the experimental setup (see Methods and Supporting Information for details). In the absence of the QD, all scattering spectra from a single MNP are independent of ${\varphi }_A$ and possess a single broad peak at ${\lambda }_{MNP}\approx 520$ nm corresponding to the plasmonic dipole resonance of the MNP. The introduction of a QD under the MNP, with the separation gap of $g=1\hspace{0.5em}\text{nm}$, modifies the scattering spectrum: A sharp Fano feature emerges at the exciton transition wavelength ${\lambda }_{MNP}\approx 520$_.nm. The magnitude of the feature is a strong function of the analyzer orientation. If the projection of the Fano axis onto the analyzer plane is perpendicular to the analyzer direction (${\varphi }_A=\pi /2$ in Fig. 1A), then no Fano feature is predicted by our calculation. The strongest Fano feature is observed for ${\varphi }_A=0$, and a weaker but finite Fano feature is observed for intermediate angles. Therefore, what is originally an isotropic scatterer (a spherical MNP) is transformed into a highly anisotropic one by the strong hybridization between the QD and the MNP.

Fig. 1.

Calculation demonstrating how the near-field coupling modifies the far-field scattering spectra of a structure placed on a glass substrate. (A) The scattering spectra of an NP–QD hybrid excited by the unpolarized evanescent wave coming from the glass substrate side in all azimuthal angles. The angle ${\phi }_A$ indicates the orientation of the analyzer in the path of the scattered light. The Fano feature is the most (least) prominent when the orientation of the analyzer is parallel (perpendicular) with the in-plane component of the Fano axis, which connects the QD and MNP centers. (B and C) The field near the NP–QD hybrid at 500 and 552 nm, respectively, as indicated by the black arrows in the scattering spectrum at ${\phi }_A=0$ in A. The scattering signal at these two wavelengths is the same (indicated by the dotted line on the blue curve) whereas the MNP is excited much more strongly in C. This wavelength dependence proves that the presence of the QD indeed controls the MNP’s scattering and anisotropy resonantly.

The ability of a single QD to modify the scattering spectrum of a much larger MNP possessing a scattering cross-section of ${\left(r_{MNP}/r_{QD}\right)}^6\approx \mathrm{15,000}$-fold greater in magnitude than that of the QD seems surprising. Naively, one may expect the effect of a QD on the scattering spectrum of the hybrid system to be very small. As pointed out by a number of theoretical studies (12, 20, 21) and our own numerical calculation shown in Fig. 1, this expectation is not correct. Whereas the exciton dipole moment is too small to produce significant far-field scattering on its own, it is sufficient to depolarize the MNP in the near field, thereby dramatically modifying the electric polarizability of the combined hybrid system at the frequency of the exciton transition.

To illustrate this point, the near-field distributions were calculated for ${\lambda }_1=500$ nm (Fig. 1B) and ${\lambda }_2=552$ nm (Fig. 1C), respectively. These two wavelengths were chosen because the scattering intensities are the same. The much higher (by almost a factor of 2) electric field induced on the MNP’s surface at $\lambda ={\lambda }_2$, is offset by strong near-field depolarization (light-color area near the QD) of the MNP by the exciton’s dipole. Because the electric field of a dipole rapidly decays with distance, such extreme depolarization (which can be alternatively interpreted as the excitation of high-order multipoles of the MNP by an exciton) can only occur if the QD is placed within nanometers from the MNP. Therefore, it is extremely crucial to precisely position the QD near the MNP as accomplished in our experiments.

We assemble the hybrid structure using the technique of AFM nanomanipulation (24–26) (see Methods for details). Whereas other techniques including self-assembly (bottom-up approaches) and lithography (top-down approaches) can be used to create hybrid nanostructures, it is difficult to ensure that only one QD is present in the hybrid structure and to precisely control the distance between the QD and the MNP. AFM nanomanipulation allows us to carefully tailor the dimensions of an individual structure with <5-nm precision and to ensure the presence of only one QD.

The assembly process begins by dispersing MNPs and QDs on a glass substrate randomly. We then simultaneously obtain an AFM topography image and a photoluminescence (PL) image by scanning the sample on a home-built integrated AFM–confocal microscope. We locate isolated MNPs and QDs in close proximity via the AFM topography image. We then manipulate a nearby MNP to approach the chosen QD as illustrated in Fig. 2 A–C. Because of the tip-convolution effect as well as the size difference between the MNP (∼30 nm in diameter) and the QD (∼5 nm in diameter), the lateral resolution of the AFM image is not sufficient to allow direct measurement of the distance between the MNP and QD in a hybrid structure. We push the MNP until the QD is no longer visible in the AFM image (Fig. 2C), and use nearby topography surfaces to estimate the position of the QD underneath with a precision of <5 nm. Ligand molecules on the surfaces of the MNP and QD prevent them from physically touching one another.

Fig. 2.

Assembly and characterization of a strongly coupled MNP–QD hybrid structure. (A–C) Representative steps in a hybrid structure assembly. A single Au NP (A, Left) was placed in the close vicinity of a single CdSe/ZnS QD (A, Right). (D) Representative PL lifetime measurement of a single isolated QD (black) yielding ∼29 ns and lifetime of the assembled hybrid structure (red) with a fast component of ∼1.6 ns. Solid lines are fits to the data. We used a single exponential function to fit the bare QD lifetime and a double exponential function to fit the hybrid structure, yielding a fast decay of ∼1.6 ns and a slow decay of ∼13 ns.

We then measure the lifetime to confirm that the MNP is indeed in the close proximity of the QD. Lifetime is, in fact, a rather accurate way to characterize the distance between the MNP and QD as demonstrated in our previous work (27). For the particular hybrid structure discussed in the rest of the paper, we measure a greatly reduced short lifetime (∼1.6 ns for the fast decay component, red curve in Fig. 2D). Compared with the representative bare QD lifetime of ∼29 ns (shown as the black curve in Fig. 2D), the QD in the hybrid structure shows a lifetime reduction of more than an order of magnitude, thus confirming the strong coupling between the QD and MNP.

Measured ensemble absorption and PL emission spectra (taken in solution) of QDs are shown in Fig. 3B. The absorption spectrum features multiple discrete exciton resonances at lower energies and a continuous absorption spectrum at energies above the band gap of the crystal. Although all absorption resonances may influence the scattering spectrum of the hybrid structure, in the following analysis we focus on the lowest-energy exciton state featuring the strongest absorption resonance. This exciton transition is centered near ${\lambda }_{QD}\approx 615$ nm with an ensemble-averaged spectral FWHM $\mathrm{\Delta }{\lambda }_{1/2}\sim 15$ nm.

Fig. 3.

Scattering and anisotropy of a plasmonic cavity (i.e., an MNP) controlled by a single QD. (A) Experimental schematics for scattering measurements. (B) Experimentally measured absorption (black) and PL emission (red) spectra from an ensemble of colloidal CdSe/ZnS core–shell QDs. (C) Measured scattering spectra of a bare 30-nm-diameter MNP at different analyzer angles. The small changes near 550 nm or below are likely due to deviations from a perfectly spherical shape of the MNP. (D) Measured scattering spectra of the assembled QD–MNP hybrid structure at different analyzer angles. The Fano resonance indicated by the dotted vertical line spectrally aligns with the lowest exciton state measured in the absorption from an ensemble of QDs. The Fano resonance is most pronounced at ${\varphi }_A=30°$.

The dark-field scattering experiments are performed using a home-built optical system optimized for small MNP measurements (Fig. 3A). An unpolarized white-light source incident in a conical geometry generates evanescent fields and excites the hybrid structure from all directions. An analyzer is placed in the scattered light’s path to select the polarization of the collected scattering (see Methods for details of the optical setup and measurement). A series of such spectra $S(\lambda ,{\varphi }_A)$ is displayed in Fig. 3D as a function of the analyzer angle ${\varphi }_A$. A very sharp Fano feature, with $\partial S\left(\lambda ,{\varphi }_A\right)/\partial \lambda$ actually reversing its sign at ${\lambda }_{QD}\approx 627\hspace{0.17em}\text{nm}$, can be clearly observed for ${\varphi }_A={\varphi }_1=30°$. Weaker Fano features are observed for other polarizer orientations, all in qualitative agreement with our theoretical predictions in Fig. 1A. Remarkably, almost no Fano interference between the inherently quantum (single-exciton) and classical (plasmonic) transitions is observed for ${\varphi }_A={\varphi }_2=120°$.

Comparing the spectra which show the strongest and weakest Fano resonance at $30°$ and $120°$, respectively, one observes modifications over a much broader spectral range than the lowest exciton resonance linewidth because other exciton states and absorption features in the QD also contribute to the resonantly enhanced depolarization of the MNP. We note that the numerical calculation presented in Fig. 1 is based on an MNP coupled to a single two-level system and only serves to illustrate the basic principle of QD controlled plasmonic cavity scattering and anisotropy. The calculation has incorporated a dipole moment of 50 Debye for the two-level system, which is an overestimate for a small colloidal QD used in the experiments. A quantitatively accurate model for calculating the scattering spectrum of this simplest MNP–QD hybrid structure remains a challenge. Higher-order multipole effects of the MNP and QD (28), the nanoparticle’s geometrical deviation from a perfect sphere, and all relevant electronic transitions in QDs need to be taken into account to quantitatively reproduce the experimental observations.

To further confirm that the polarization dependence of the scattering spectra of the hybrid structure indeed originates from the coupling between the QD and MNP, we show the scattering spectra of a bare MNP in Fig. 3C. The spectra do not display any Fano features or analyzer angle dependence in the spectral proximity of the exciton resonance ${\lambda }_{QD}$. Therefore, it is indeed the coupling between a single QD and the MNP that turns an otherwise isotropic plasmonic cavity into a strongly anisotropic one. Because a single quantum absorber achieves this effect, one can envision the proposed hybrid system as an experimental platform for observing a plasmonic cavity anisotropy controlled by optical nonlinearity at the single-photon level. The small angular variations of $S(\lambda ,{\varphi }_A)$ at shorter wavelengths (around $550$ nm or below) in Fig. 3 C and D most likely arise from a small intrinsic deviation of the MNP’s shape from an ideal sphere. Unlike the extrinsic anisotropy induced by the QD, it cannot be optically controlled and is not of interest for nonlinear quantum optics.

The control of scattering and anisotropy of the MNP cavity by a single QD is not affected by the common photobleaching that puts severe limits on any fluorescence-based experiment. To confirm this property, we measure the PL of the hybrid structures again after the scattering experiments and find no measurable signal. This observation suggests that the QD has been severely photobleached by the combination of extended atmospheric exposure, strong near-field of the MNP cavity, and prolonged exposure to the halogen lamp used as the excitation source. Our experiments clearly demonstrate that even a photobleached QD may still be used to control the plasmonic cavity scattering by creating the Fano resonance due to its still intact absorption/scattering capability. Furthermore, the polarization-resolved scattering spectra presented here can be used to determine the location of a QD with respect to the nearby MNP based upon the recently developed plasmonic nanoprotractor concept (23). Thus, our work also suggests a hybrid sensor consisting of a nonfluorescent (photobleached) QD and an MNP.

In summary, we have demonstrated that a single semiconductor QD coupled to an MNP cavity can effectively control the scattering spectrum of the latter, as well as render it highly anisotropic. The speculative implications of such extrinsic anisotropy are very intriguing. On the one hand, it serves as an orientation sensor to determine the relative locations of the QD and MNP. On the other hand, it should be possible to observe polarization-dependent photon statistics of light scattered from the QD-MNP nanohybrid. Furthermore, the photon statistics are wavelength tunable as previously proposed (12). By tuning the excitation wavelength to the spectral position corresponding to the destructive (constructive) interference side of the Fano resonance, strong bunching (antibunching) behavior should be observed in second-order correlation function g⁽²⁾ measurements. Furthermore, a single two-level system is intrinsically highly nonlinear. One may modulate the Fano resonance via such nonlinear effects associated with the single QD at higher incident light intensity. The studies presented here demonstrate the feasibility of QD–MNP hybrid nanostructures combined with polarization-sensitive detection schemes as a promising platform for new and exciting opportunities in plasmonic quantum technologies.

Methods

Sample Preparation, AFM, and PL Measurement.

Colloidal Au nanoparticles (BBI Solutions, 30 nm suspended in H₂O) and QDs (Ocean Nanotechnology, CdSe/ZnS core/shell suspended in H₂O with PL maximum at 621 nm) were selected for the structure. These particles were spread onto substrates via a drop-casting technique. SiO₂ markers (∼10 nm thick) were deposited on the glass substrate to aid us in locating individual particles.

We used a home-built, combined AFM/inverted confocal microscope for assembly and characterization. AFM probes used for both imaging and manipulation had a force constant of ∼14 N/m (Mikromasch NSC-35-B). Typical AFM parameters used for manipulating MNPs were the following: servo gain of ∼1, an integral gain of ∼2, a proportional gain of ∼20, a scanning speed of ∼0.3 μm/s for imaging, and a speed of 10 μm/s for manipulation. To obtain simultaneous AFM and confocal images, we aligned the AFM tip at the focus of a 60× 0.95 N.A. microscope objective to focus the excitation laser and to collect PL. A pulsed femtosecond laser centered at 532 nm from an optical parametric oscillator was used for excitation. PL signal from individual QDs was directed toward an avalanche photodiode (APD). The APD signal was fed into a time-correlated single photon counting system, with a measured impulse response function of roughly 800 ps.

Scattering Measurement.

Single-particle scattering measurements were performed with a home-built dark-field microscope consisting of an inverted dark-field microscope (Zeiss AxioObserver m1, with oil immersion dark-field condenser N.A. = 1.4) and an imaging spectrograph (Princeton Instruments, Acton SpectraPro 2150i with Pixis 400BR thermoelectrically cooled back-illuminated CCD) mounted atop a programmatically controlled linear translation stage (Newport Linear Acuator model LTA-HL). A halogen lamp was used as the light source. The unpolarized light from the lamp was focused by the oil-immersion dark-field condenser in a conical geometry to excite nanoparticles with a large incident angle from the normal of the substrate. Due to the large incident angle of 67° (greater than the critical angle of 41° at the glass–air interface) and total internal reflection at the air–substrate interface, the excitation created evanescent waves from all directions with respect to each nanoparticle. The scattered light from a nanoparticle was collected by an air-spaced objective (Zeiss, N.A. = 0.8) and guided through a polarizer into the spectrograph. The scattering images were taken by moving the spectrograph on the translational stage so that the slit of the spectrograph scans through the first image plane of the microscope while taking spectra. Polarized spectra were taken by rotating the polarizer in the collection path. Integration time was 240 s for each spectrum to increase the signal to noise ratio. All measured single-particle spectra were corrected for background scattering and normalized by the intensity of the white light using the following equation:

$$\text{scattering}=\frac{I_S-I_{BG}}{I_{STD}-I_{DC}},$$

where $I_S$ is the spectrum of the nanoparticle, I_BG is the background spectrum with no particle present, $I_{STD}$ is the spectrum of the lamp, and $I_{DC}$ represents the detector dark count spectrum measured with the lamp switched off.

Modeling.

The simulation performed using COMSOL Multiphysics software qualitatively explains the origin of the Fano feature observed in the experiment. The diameters of NP and QD were set up to be $2r_{NP}=30\hspace{0.17em}\hspace{0.5em}\text{nm}$ and $2r_{QD}=6\hspace{0.5em}\hspace{0.17em}\text{nm}$, respectively. The QD was modeled as a sphere with the effective dielectric permittivity ${\mathit{ϵ}}_{eff}\left(\omega \right)$ derived in the semiclassical approximation by introducing the effective polarizability (29):

$$\alpha =\frac{-2{\mu }^2/\hslash \left[2(\omega -{\omega }_{QD})+i\left({\gamma }_{\text{rad}}+{\gamma }_{\text{nonrad}}\right)\right]}{4{\left(\omega -{\omega }_{QD}\right)}^2+{\left({\gamma }_{\text{rad}}+{\gamma }_{\text{nonrad}}\right)}^2}\equiv 4\pi {\mathit{ϵ}}_0{r}_{QD}^3\frac{{\mathit{ϵ}}_{\text{eff}}-1}{{\mathit{ϵ}}_{\text{eff}}+2},$$

where $\mu$ is the exciton’s electric dipole moment, and ${\gamma }_{\text{rad}}$ (${\gamma }_{\text{nonrad}}$_.) is the radiative (nonradiative) damping rate. For illustrative purposes, the following exciton parameters were used: $\mu =1\hspace{0.17em}e\mathrm{\cdot }nm$, ${\gamma }_{\text{rad}}=0$, and ${\gamma }_{\text{nonrad}}=0.01{\omega }_{QD}$, where ${\omega }_{QD}\equiv 2\pi c/{\lambda }_{QD}$ and ${\lambda }_{QD}=550\hspace{0.17em}\hspace{0.5em}\text{nm}$ is the resonant exciton wavelength. The permittivity of the gold NP from ref. 30 was used.

The gap between NP and QD, both resting on a glass substrate with the refractive index n = 1.5 as shown in Fig. 1, was assumed to be $g=1\hspace{0.17em}\hspace{0.5em}\text{nm}$ in all simulations. To model the unpolarized isotropic evanescent excitation from the substrate side, the partial scattering cross-sections $d\sigma ({\theta }_{in},{\varphi }_{in};{\theta }_{out},{\varphi }_{out})$ corresponding to the full range of incident azimuthal angles $0<{\varphi }_{in}<2\pi$ and a fixed off-axis incidence angle ${\theta }_{in}=69°$ were calculated by integrating the out-flux of the scattered field over a small solid angle $\partial {\Omega }_{out}=d\left(\cos {\theta }_{out}\right)d{\varphi }_{out}$ directly above the sample. Scattered light’s polarization with respect to the angular position ${\varphi }_A$ of the analyzer placed above the NP/QD cluster was accounted for. The total cross-section was then obtained by averaging over ${\varphi }_{in}$ and over the s- and p-polarizations of the incident light. The resulting scattering spectra are plotted in Fig. 1A for three values of ${\varphi }_A$. Here ${\varphi }_A=0^{\circ }$ corresponds to the direction of $E_0$ as shown in Fig. 1 B and C, and ${\varphi }_A={90}^{\circ }$ corresponds to the out-of-plane direction in Fig. 1 B and C. Note that the Fano resonance has no effect on the polarized spectrum (black curve) collected with the analyzer set at ${\varphi }_A={90}^{°}$. Fig. 1 B and C simulates the NP–QD cluster electric field (color: $\left|\overrightarrow{E}\right|$) at ${\lambda }_1=500$ nm and ${\lambda }_2=552$ nm, respectively, assuming a single s-polarized incident wave within the $y-z$ incident plane.

Simulation Setup

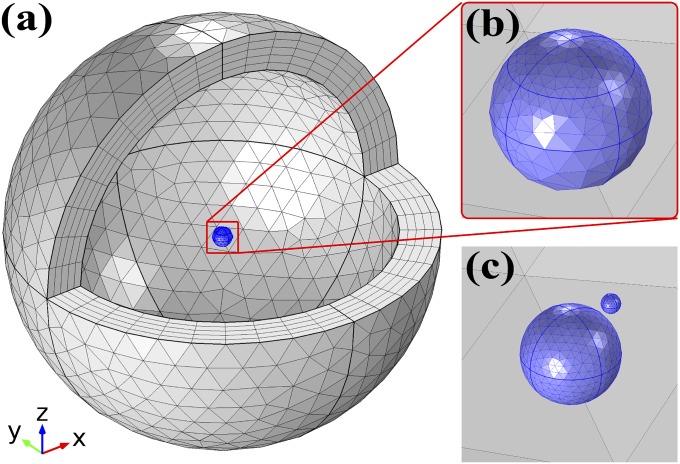
The simulation layout consists of an outer spherical shell set as a perfectly matched layer (PML) surrounding the center of the simulation domain enclosing the scatterer. The scatter, a combination of the QD and NP, is located as shown in Fig. S1A. The standard scattering formalism provided by the COMSOL electromagnetics module is adopted. The size of the simulation domain is chosen to be large enough (the diameter is 860 nm, larger than one wavelength across) so that the scattering formulism gives an accurate result in the evaluation of the scattering cross-section. A test, using merely a background total internal reflection field (created by setting the scatterer’s $\mathit{ϵ}$ to be 1) is carried out as shown in Fig. S1B. The ratio of the scattering cross-section without to that with the scatterer’s effect in this test is only ${10}^{-5}$. This shows the validity of implementing the background total internal reflection field in the scattering formalism.

Fig. S1.

Simulation setup. (A) The layout of the simulation domain. The small red dome spanning the solid angle $0.6\pi$ illustrates the position of the analyzer in the experiment, and it is also where the scattering cross-section is evaluated in the simulation. (B) Modeling of the background s-polarized and p-polarized field of total internal reflection at $\theta =69°$. The color, red and blue, shows $E_y\left(\mathit{r}\right)$ for one case, with s-polarized incidence on the y–z plane.

Meshing Procedure and Convergence Test

The shape function on the mesh is of quadratic accuracy; this is the default setting of COMSOL. The far-field domain (away from the scatterer) has mesh size no bigger than 40 nm, so as to have roughly 15 points to outline one wavelength (one can get a rough idea about the quality of this mesh from Fig. S1B from the simulated field). The meshing procedure is shown in Fig. S2. The PML consists of five layers for effective absorption of the scattering field. The mesh close to the scatterer (near and inside the purple sphere) is much more refined. This is to achieve detailed resolution in the near field, or hot spot, with a characteristic length roughly equivalent to the radius of the QD, $r_{QD}$. To analyze the effect of the mesh choice close to the near field on the far-field evaluation of the scattering cross-section, we vary either the mesh of the QD or the mesh of the NP while keeping the mesh of the other fixed. The QD’s and NP’s mesh sizes are parameterized by $d_{QD}$ and $d_{NP}$, respectively, and their length is expressed as some fraction of $r_{QD}$. The number of mesh elements for modeling the NP and QD is clearly proportional to $d_{QD\left(NP\right)}^{-3}$.

Fig. S2.

Meshing. (A) Overall meshing of the simulation domain. Some domains are hidden to clearly display the inner scatterer. (B) A zoomed-in view of the scatterers. The NP and QD are each embedded within small spheres to provide a finer mesh resolution close to the scatterers. (C) The meshing of the NP and QD with the surrounding sphere hidden.

The mesh sizes adopted in the main text are $d_{QD}/2r_{QD}=0.16$ and $d_{NP}/2r_{QD}=0.5$. To demonstrate how these parameters were chosen, we present the analysis shown in Fig. S3. The scattering cross-sections are evaluated at the Fano dip (552 nm) and peak (556 nm) as the surface integral of the outgoing Poynting flux of the scattering field over the red dome region shown in Fig. S1A. As shown in Fig. S3A, this flux is insensitive to changes in the mesh of the QD ranging from $d_{QD}/2r_{QD}=0.1\hspace{0.17em}\hspace{0.17em}\sim \hspace{0.17em}\hspace{0.17em}0.3$. For the case of changing the NP’s mesh, shown in Fig. S3B, one can see that significant variation from the convergent value happens only when $d_{NP}/2r_{QD}>0.7$. The peak and dip scattering cross-sections are therefore

$$S\left(\lambda =552\hspace{0.17em}\text{nm}\right)=\left(2.898\pm 0.009\right)\times {10}^{-4},$$

$$S\left(\lambda =556\hspace{0.17em}\text{nm}\right)=\left(3.291\pm 0.006\right)\times {10}^{-4}.$$

Because the Fano dip and peak is the finest spectral feature from this result, we deduce that the scattering cross-section in this simulation, with the appropriate meshing procedure, has a deviation as small as $\sim 0.3\%$ compared with any other reasonable choice of mesh.

Fig. S3.

Convergence test. (A) The scattering cross-section at the Fano dip (552 nm, blue dots) and peak (556 nm, red dots) as a function of the QD’s mesh size, $d_{QD}$, with the NP’s mesh fixed at $d_{NP}/2r_{QD}=0.5$. (B) The scattering cross-section as a function of the NP’s mesh size, $d_{NP}$, with the QD’s mesh fixed at $d_{QD}/2r_{QD}=0.16$. The red and blue lines show the convergent value of the scattering cross-section.