Competition and allostery govern substrate selectivity of cyclooxygenase-2

Significance

The cyclooxygenase enzymes perform the initial steps in the synthesis of prostaglandins, potent signaling molecules with diverse physiological functions. Recent data have suggested that these enzymes, although structural homodimers, act as functional heterodimers. Herein, we demonstrate that the heterodimeric nature of cyclooxygenase-2 leads to differential allosteric regulation of the enzyme by two of its substrates, arachidonic acid and the endocannabinoid 2-arachidonoylglycerol. We provide the first evidence (to our knowledge) that fatty acid-based modulation of COX-2 activity occurs in cellular settings. These findings demonstrate the complexity of the interaction of multiple substrates with COX-2, which involves competition for both the catalytic and allosteric sites in addition to differential allosteric regulation.

Abstract

Cyclooxygenase-2 (COX-2) oxygenates arachidonic acid (AA) and its ester analog, 2-arachidonoylglycerol (2-AG), to prostaglandins (PGs) and prostaglandin glyceryl esters (PG-Gs), respectively. Although the efficiency of oxygenation of these substrates by COX-2 in vitro is similar, cellular biosynthesis of PGs far exceeds that of PG-Gs. Evidence that the COX enzymes are functional heterodimers suggests that competitive interaction of AA and 2-AG at the allosteric site of COX-2 might result in differential regulation of the oxygenation of the two substrates when both are present. Modulation of AA levels in RAW264.7 macrophages uncovered an inverse correlation between cellular AA levels and PG-G biosynthesis. In vitro kinetic analysis using purified protein demonstrated that the inhibition of 2-AG oxygenation by high concentrations of AA far exceeded the inhibition of AA oxygenation by high concentrations of 2-AG. An unbiased systems-based mechanistic model of the kinetic data revealed that binding of AA or 2-AG at the allosteric site of COX-2 results in a decreased catalytic efficiency of the enzyme toward 2-AG, whereas 2-AG binding at the allosteric site increases COX-2’s efficiency toward AA. The results suggest that substrates interact with COX-2 via multiple potential complexes involving binding to both the catalytic and allosteric sites. Competition between AA and 2-AG for these sites, combined with differential allosteric modulation, gives rise to a complex interplay between the substrates, leading to preferential oxygenation of AA.

The cyclooxygenase (COX) enzymes catalyze the dioxygenation and subsequent hydroperoxide reduction of arachidonic acid (AA). These reactions comprise the first two steps in the biosynthesis of prostaglandins (PGs), which play a role in a broad range of physiological and pathophysiological processes (1, 2). The COX enzymes are the primary targets of the pharmacologic action of the widely used nonsteroidal antiinflammatory drugs (e.g., aspirin, ibuprofen, and naproxen). There are two COX isoforms, COX-1 and COX-2, which are structurally and kinetically similar. COX-1 is constitutively expressed in most tissues, whereas COX-2 is highly inducible in response to inflammatory and mitogenic stimuli. Thus, it is generally accepted that the primary factor that differentiates the two isoforms is their distinct patterns of expression (1).

Although gene expression clearly is a factor in COX-related physiology, subtle structural differences between the two isoforms result in intrinsic functional distinctions. Specifically, the active site of COX-2 is larger than that of COX-1, allowing COX-2 to oxygenate bulkier amide and ester analogs of AA that are poor COX-1 substrates. Among these COX-2–selective substrates are the endocannabinoids 2-arachidonoylglycerol (2-AG) and arachidonoylethanolamide (3–5). COX-2–dependent oxygenation of these substrates leads to the biosynthesis of prostaglandin glyceryl esters (PG-Gs) and prostaglandin ethanolamides (prostamides), respectively (3, 4). In vitro, COX-2 uses 2-AG and AA with similar kinetic efficiencies (3); however, PG-G production in intact cells is much lower than would be expected based on the relative amounts of cellular AA and 2-AG (6). This discrepancy is partially due to the fact that COX-2 requires activation by hydroperoxides, and higher concentrations of hydroperoxide are required to maintain 2-AG oxygenation than AA oxygenation (7). In addition, compartmentalization of the substrates within the cell might explain the poor utilization of 2-AG.

The homodimeric COX enzymes function as heterodimers, with one subunit that contains the required heme cofactor acting as a catalytic site and the second subunit, which lacks heme, acting as an allosteric site (8, 9). Evidence for allosteric regulation of COX is seen in the ability of various nonsubstrate fatty acids to modulate the activity and inhibitor sensitivity of the COXs, presumably through interaction with the allosteric site (8). A particularly striking example is the ability of 13-methylarachidonic acid to selectively and substantially increase the oxygenation of 2-AG while having no effect on the oxygenation of AA (10). Another example of allosteric regulation is substrate-selective inhibition, the ability of weak reversible inhibitors of AA oxygenation to strongly inhibit 2-AG oxygenation by COX-2 (11). These considerations led us to hypothesize that differential interactions of AA and 2-AG at the allosteric site of COX-2 might result in a complex interplay between the substrates when both are present. Here, we demonstrate that modulation of AA levels inversely affects cellular biosynthesis of PG-Gs. We go on to explore the interaction of the substrates AA and 2-AG during oxygenation by COX-2 in vitro and in silico. We build a mathematical model of COX-2 oxygenation kinetics with multiple ligands that explicitly incorporates the dynamics of all of the chemical intermediates in the reaction network, and we use a Bayesian parameter inference formalism to characterize the multiple reaction pathways that exist between the two substrates, the enzyme subunits, and their products. Our rigorous model calibration approach allows us to determine probability distributions, given our experimental data, for kinetic constants rather than single best-fit values, providing a systems-level understanding of multiple competing interactions in the reaction network and accurate confidence estimates for fitted values. The presented methods are generalizable to other kinetic systems that, like COX-2, can appear deceptively simple. Our findings support the hypothesis that a combination of competition and allosteric regulation controls the selective use of substrates by COX-2 and, to our knowledge, provide the first evidence of the physiologic relevance of this phenomenon in live cells.

Results

AA Enrichment Suppresses 2-AG Oxygenation in RAW264.7 Cells.

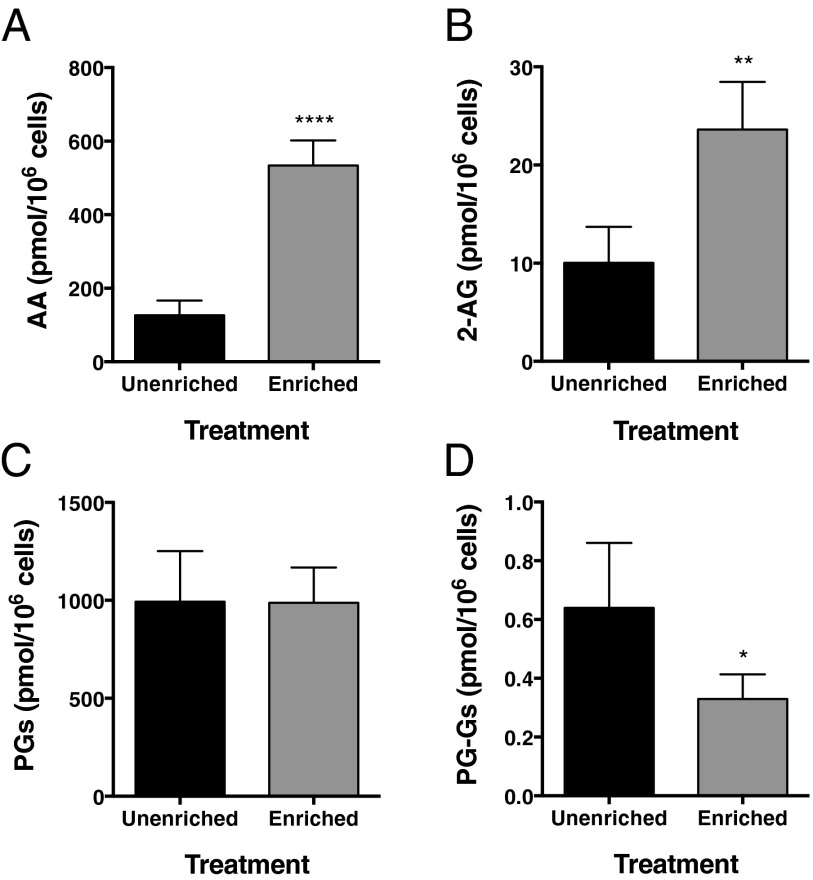
RAW264.7 murine macrophage-like cells exhibit COX-2–dependent PG-G biosynthesis (3). Incubation of RAW264.7 cells overnight with AA complexed to BSA increases their cellular phospholipid AA content by ∼100% (12). We used this enrichment to examine the impact of endogenously released AA on the production of PGs and PG-Gs following zymosan stimulation. AA enrichment resulted in a 4.2-fold (Fig. 1A) and 2.4-fold (Fig. 1B) increase in peak zymosan-stimulated AA and 2-AG release, respectively. However, despite the substantial increase in available substrate, AA-enriched cells produced no more PGs (Fig. 1C) than unenriched cells in response to zymosan, and the quantity of PG-Gs produced by the AA-enriched cells was reduced by ∼50% (Fig. 1D). Thus, AA enrichment in stimulated RAW264.7 cells results in increased release of both AA and 2-AG in response to zymosan, but reduced production of PG-Gs.

Fig. 1.

AA enrichment leads to reduced PG-G levels in zymosan-stimulated RAW264.7 cells. Cells (5 × 10⁵) were enriched with AA, incubated with LPS and IFN-γ to induce COX-2 expression, and then stimulated with zymosan to trigger release of AA (A) and 2-AG (B) and biosynthesis of PGs (C) and PG-Gs (D). Data are the mean ± SD of four independent experiments, each performed in triplicate. Statistical significance was determined by Student’s t test (*P < 0.05, **P < 0.01, ****P < 0.0001 compared with unenriched).

Inhibition of Endogenous AA Release Results in Elevated PG-G Levels.

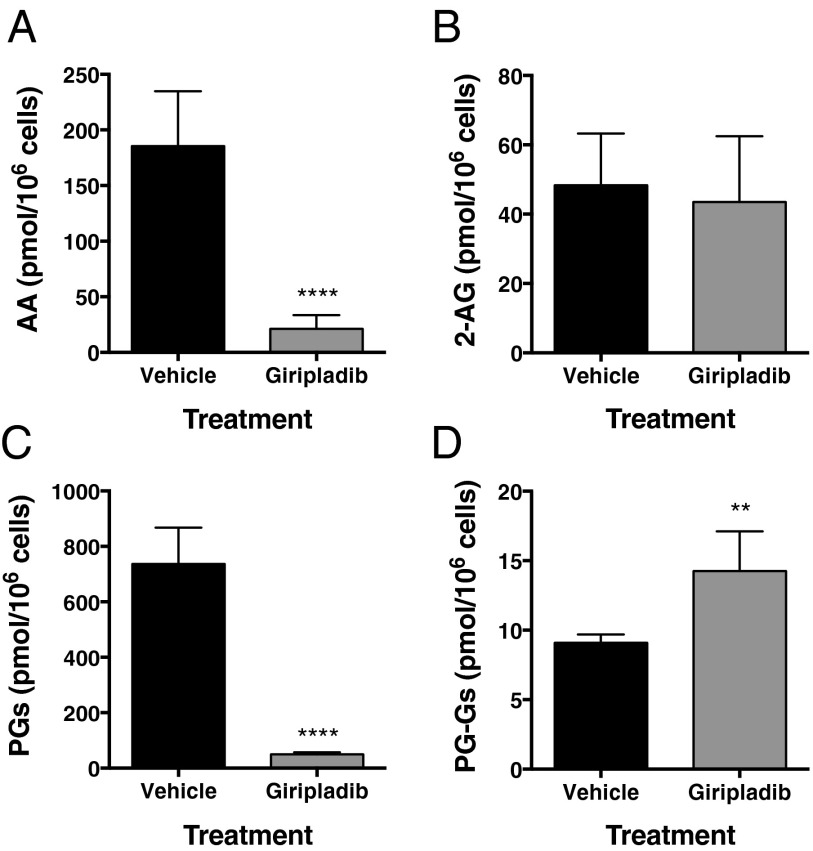
We next used a pharmacologic approach to manipulate the levels of AA in RAW264.7 cells. The major route for the release of AA for PG biosynthesis in macrophages is hydrolysis at the sn-2 position of AA-containing phospholipids by cytosolic phospholipase A₂ α (cPLA₂α) (13–16). Consequently, we explored the effects of giripladib, a selective inhibitor of cPLA₂α (17), on AA release and PG biosynthesis in ionomycin-stimulated RAW264.7 cells. As seen in Fig. 2 A and C, giripladib exposure led to an 89% and 93% decrease in AA release and PG biosynthesis, respectively. Giripladib treatment also resulted in an ∼1.6-fold increase in PG-G levels (Fig. 2D) with no change in the levels of 2-AG (Fig. 2B). When ionomycin-stimulated RAW264.7 cells were incubated with 5 μM PGE₂-G-d₅ under the same conditions as described in the legend to Fig. 2, there was no difference in the recovery of the added PG-G between cells incubated in the absence (92 ± 1%) or presence (89 ± 1%) of giripladib, indicating that the observed increase in endogenously produced PG-Gs was not due to an off-target suppression of PG-G hydrolysis by the inhibitor.

Fig. 2.

Inhibition of cPLA₂α-dependent AA release by giripladib results in increased PG-G biosynthesis in RAW264.7 cells. Cells (3 × 10⁶) were preincubated with LPS and IFN-γ and then stimulated with ionomycin in the presence or absence of giripladib (1 μM). Data show AA (A) and 2-AG (B) levels along with amounts of PGs (C) and PG-Gs (D) formed. Results are the mean ± SD of six determinations. Statistical significance was determined using Student’s t test (**P < 0.01, ****P < 0.0001 compared with vehicle).

AA Suppresses 2-AG Oxygenation by COX-2 in Vitro.

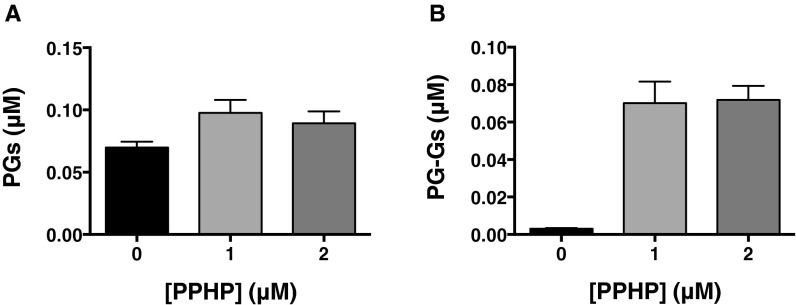
One possible explanation for these cellular observations is that AA suppresses COX-2–dependent 2-AG oxygenation when both substrates are present. To examine this possibility, we characterized the kinetics of oxygenation of AA and 2-AG by purified mouse COX-2 with both substrates present in the reaction mixture. Kinetic analysis of COX activity is complicated by the requirement for product hydroperoxide activation, which results in an early lag phase, and enzyme self-inactivation, which leads to premature termination of the reaction. Consequently, the enzyme does not exhibit a true initial rate, and monitoring oxygen consumption using the maximal rate achieved at the end of the lag phase has been the approach used in most kinetic studies (18). Although multiple previous investigations have yielded kinetic parameters for COX-2 using this approach, it cannot be used to explore the simultaneous metabolism of two COX-2 substrates because oxygen consumption occurs with both. Hence, we used liquid chromatography–tandem mass spectrometry (LC-MS/MS) to distinguish the oxygenation products of AA and 2-AG, necessitating a fixed time point assay. To approximate a true initial rate as closely as possible, substrate–enzyme incubations were limited to 10 s, the shortest time point that yielded reproducible data. The brief incubation period minimized substrate consumption and COX-2 self-inactivation; however, it also increased the likelihood that rates would be underestimated due to incomplete peroxide-dependent activation. This potential problem was eliminated by the inclusion of 5-phenyl-4E-pentenyl-1-hydroperoxide (PPHP) in the substrate mixtures. At a concentration of 1 μM, PPHP maximized COX-2–dependent oxygenation, particularly in the case of 2-AG (Fig. S1).

Fig. S1.

Effect of PPHP on the oxygenation of AA and 2-AG by mCOX-2. Reaction mixtures consisted of mCOX-2, the indicated concentrations of PPHP, and 0.25 μM AA (A) or 0.25 μM 2-AG (B). Results shown are the mean (±SD) of triplicate determinations.

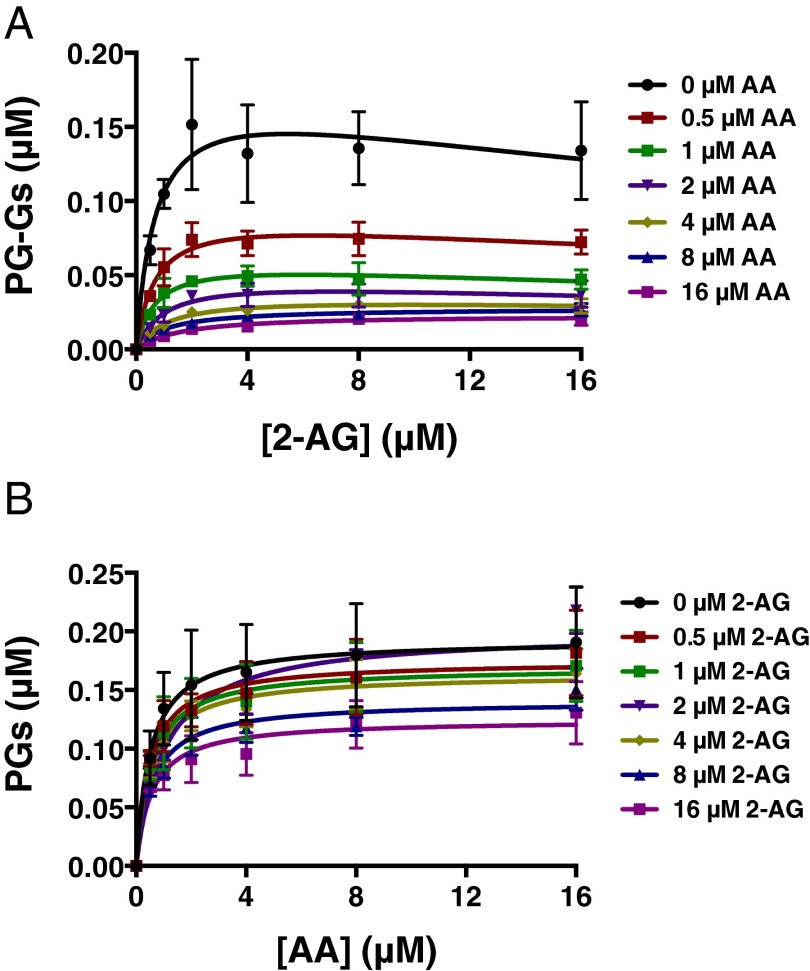
Under the LC-MS/MS assay conditions, AA inhibited 2-AG oxygenation by mCOX-2 in a concentration-dependent manner, reaching >80% inhibition at the highest concentrations of AA tested (Fig. 3A and Fig. S2A). The IC₅₀ for inhibition of 2-AG oxygenation was ∼0.5 μM AA, regardless of the concentration of 2-AG. 2-AG also suppressed AA oxygenation, but to a lesser extent, never achieving >40% inhibition (Fig. 3B and Fig. S2B).

Fig. 3.

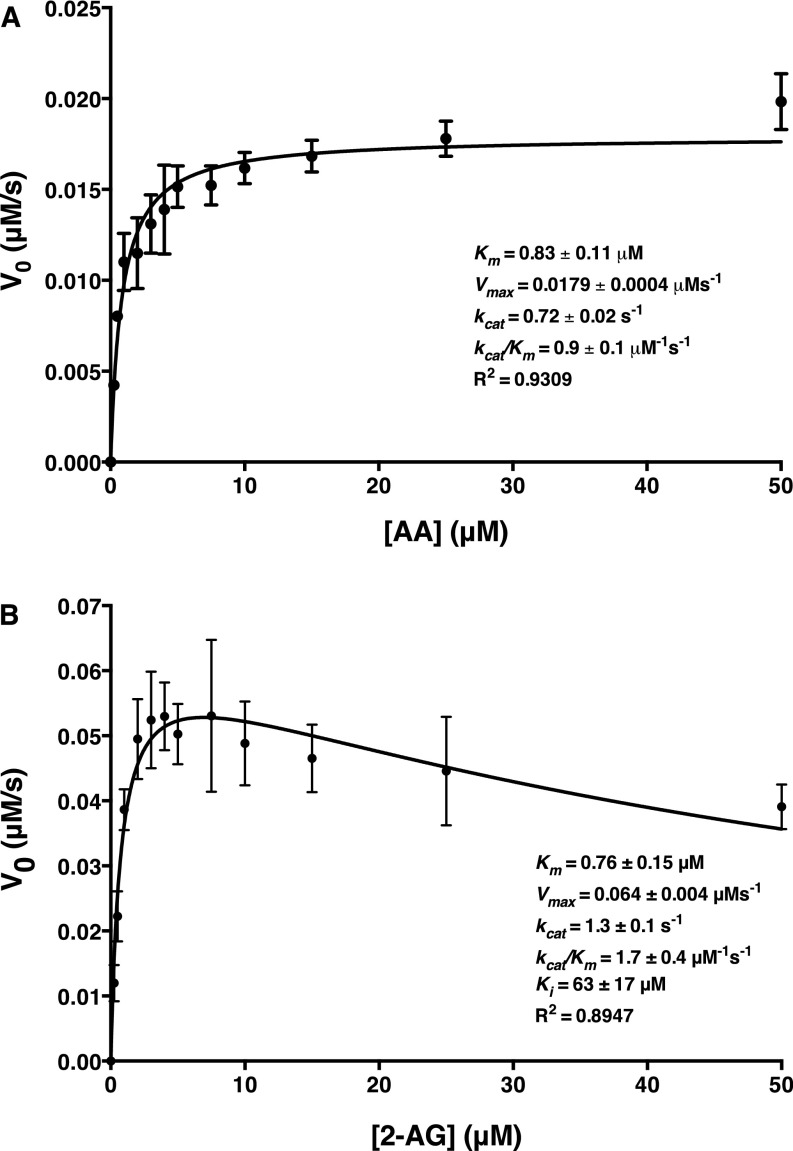
AA suppresses 2-AG oxygenation by mCOX-2 in vitro. The indicated concentrations of premixed 2-AG and AA with 1 μM PPHP were incubated with 15 nM mCOX-2 for 10 s. PGs and PG-Gs were quantified by LC-MS/MS. Results are depicted as PG-G formation as a function of increasing 2-AG concentration in the presence of various amounts of AA (A) and PG formation as a function of increasing AA concentration in the presence of various amounts of 2-AG (B). Results are the mean ± SD of triplicate determinations. Kinetic parameters for oxygenation of 2-AG in the absence of AA were as follows: K_m = 0.71 ± 0.37 μM, k_cat = 1.2 ± 0.2 s⁻¹, and K_I = 42 ± 38 μM. Kinetic parameters for oxygenation of AA in the absence of 2-AG were as follows: K_m = 0.51 ± 0.18 μM and k_cat = 1.3 ± 0.1 s⁻¹.

Fig. S2.

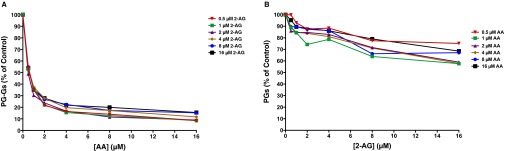
Replot of the data in Fig. 3 showing the inhibition of PG-G (A) and PG (B) synthesis at the indicated substrate concentrations and increasing concentrations of AA and 2-AG, respectively.

Classic Models of Enzyme Inhibition Fail to Explain the Interaction Between AA and 2-AG.

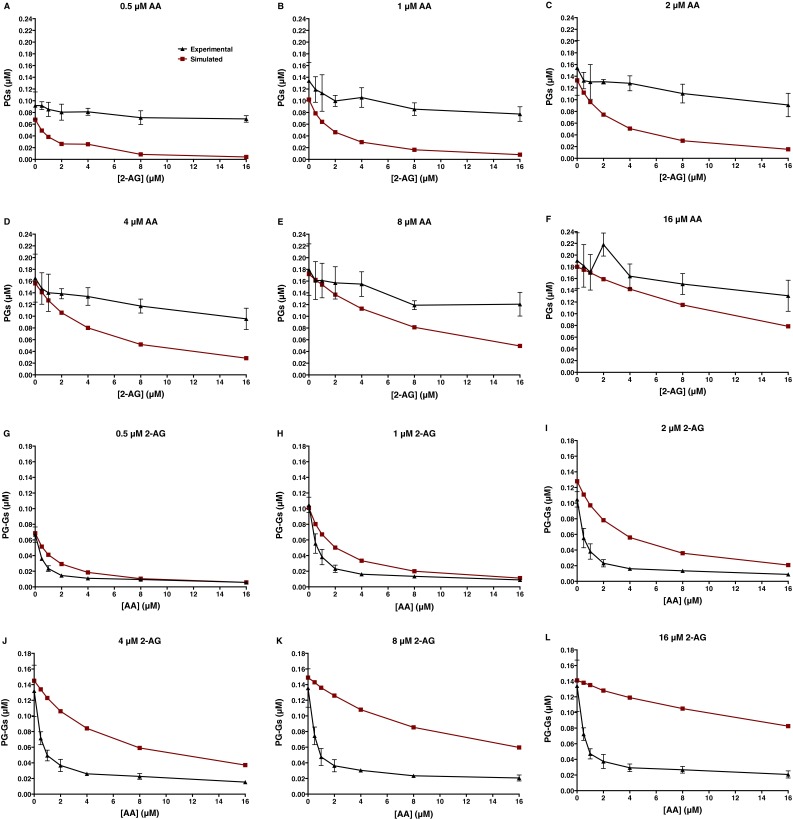
The data presented in Fig. 3 and Fig. S2 suggest that the interaction between the two substrates, which have apparently similar catalytic efficiencies with mCOX-2 (Fig. S3) (3), is inconsistent with simple competition between the substrates for a single active site. We tested this hypothesis by using KinTek Explorer software to simulate the results that would be expected from the experiment depicted in Fig. 3 if the two substrates compete with each other for the catalytic site with affinities estimated by their respective experimental K_m values (Fig. S3). The model also incorporated substrate inhibition in the case of 2-AG (Fig. S3B) (10). As shown in Fig. S4 A–F, experimental levels of PGs far exceeded those predicted by substrate competition alone. Conversely, experimental levels of PG-Gs were much lower than expected based on the competitive model (Fig. S4 G–L).

Fig. S3.

Kinetics of oxygenation of AA and 2-AG by mCOX-2. (A) Kinetic determinations for AA were conducted using 25 nM mCOX-2, and the initial velocity plot is reflective of PGs formed during a 10-s incubation, as determined by LC-MS/MS. (B) Kinetic determinations for 2-AG were conducted in the presence of 1 μM PPHP using 50 nM mCOX-2, and the initial velocity plot is reflective of PG-Gs formed during a 10-s incubation as determined by LC-MS/MS. The data were analyzed using GraphPad Prism 6 software according to the Michaelis–Menten model for AA and a model for substrate inhibition for 2-AG. Results for AA and 2-AG oxygenation are the mean ± SD for one or three independent experiments, respectively, each performed in triplicate.

Fig. S4.

Expected production of PGs and PG-Gs by mCOX-2 incubated with the indicated combinations of AA and 2-AG assuming only a competitive interaction of substrates at the catalytic site of COX-2 and substrate inhibition in the case of 2-AG. The simulated data were obtained using KinTek Explorer software. The experimental data are those obtained from the experiment described in the legend to Fig. 3. Data shown are PGs produced for various concentrations of AA in the presence of increasing concentrations of 2-AG (A–F) and PG-Gs produced for various concentrations of 2-AG in the presence of increasing concentrations of AA (G–L).

We next tested the hypothesis that the observed results might be explained on the basis of classical models for uncompetitive, noncompetitive, or mixed inhibition of 2-AG oxygenation resulting from binding of AA to the allosteric site. These models also assumed competition between the substrates at the active site and substrate inhibition in the case of 2-AG. The best fit was achieved with a model of uncompetitive inhibition of 2-AG oxygenation by AA, which yielded a K_I value of 0.52 μM for AA at the allosteric site (R² = 0.88). The classic uncompetitive model, however, assumes that binding of AA at the allosteric site completely inhibits 2-AG oxygenation, ultimately leading to total blockade of PG-G formation at high AA concentrations. This is inconsistent with the experimentally observed failure of AA to completely suppress PG-G formation (Fig. S5). Furthermore, similar efforts to model the modest inhibitory effects of 2-AG on AA oxygenation were unsuccessful.

Fig. S5.

Analysis of the effects of AA on 2-AG (0.5, 1, 2, 4, 8, and 16 μM; A–F, respectively) oxygenation using classical models of inhibition. The model incorporated classical uncompetitive inhibition based on binding of AA to the allosteric site of COX-2 along with competition between the two substrates for the catalytic site and substrate inhibition of 2-AG. The data points are values obtained in the experiment described in the legend to Fig. 3, and the curves in red are the result of nonlinear regression analysis performed using GraphPad Prism 6 software.

AA Allosterically Curbs 2-AG Oxygenation by COX-2.

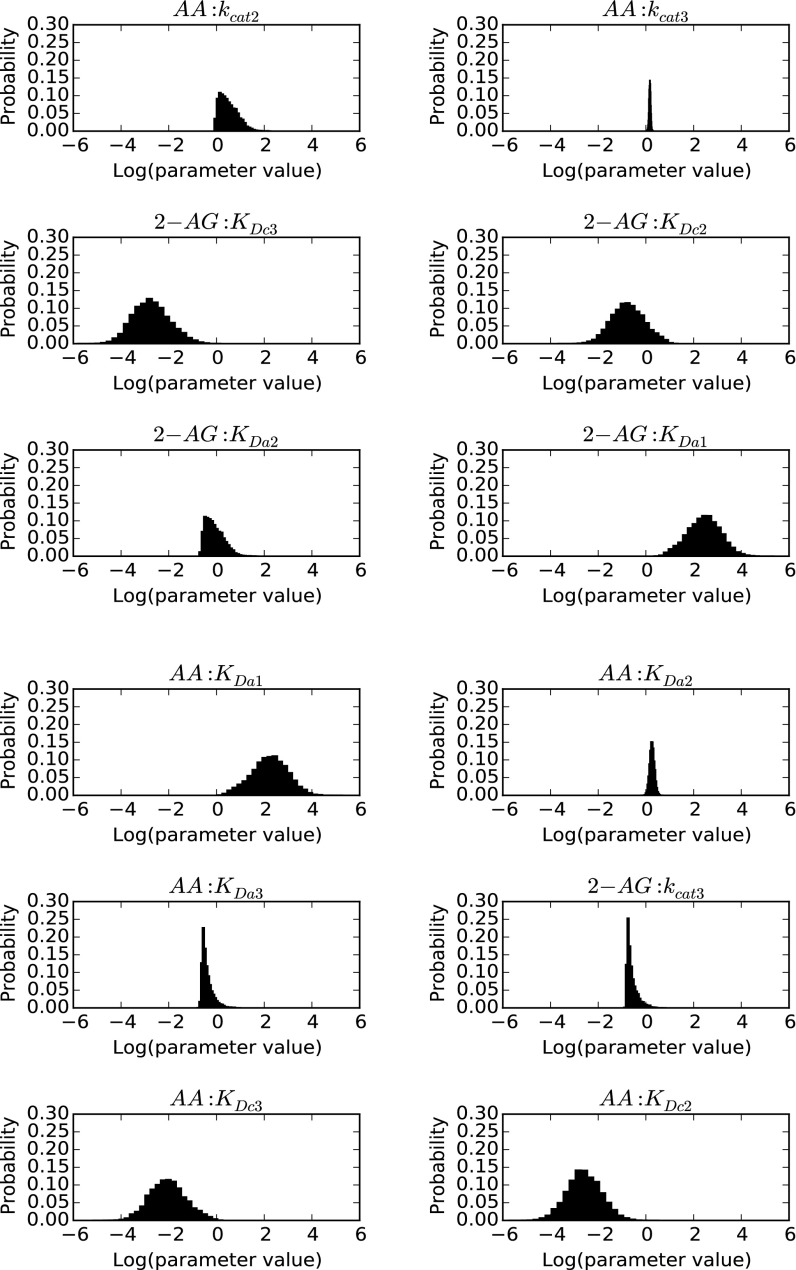
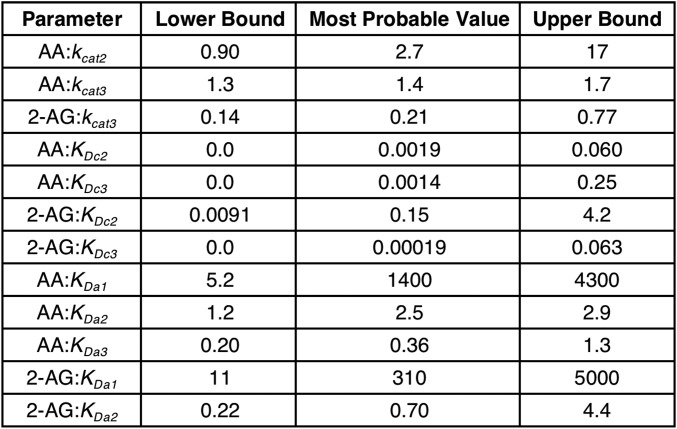
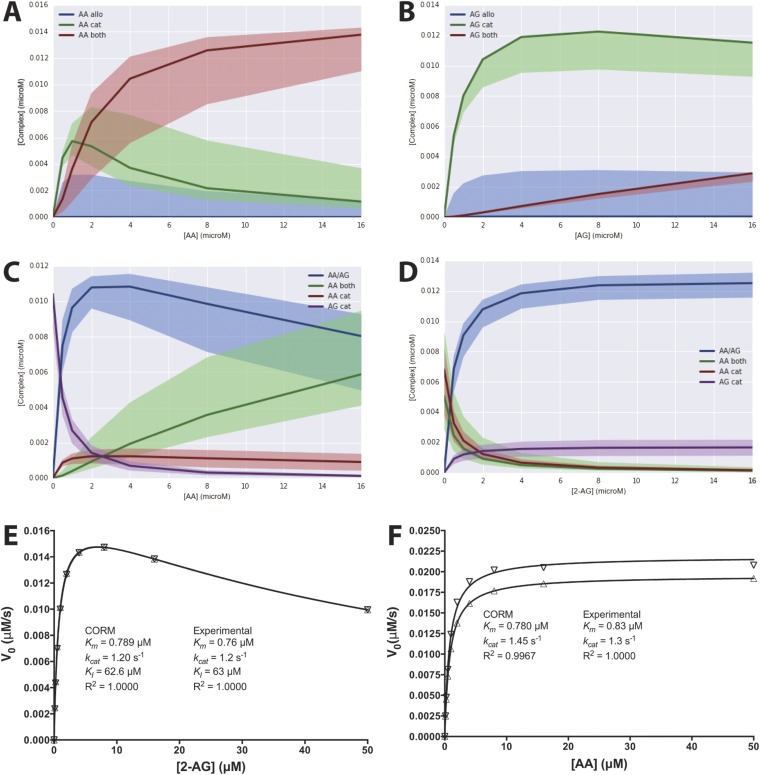
To better explain the effects of combining AA and 2-AG on the oxygenation of each substrate, we hypothesized that both substrates can bind to either the catalytic or the allosteric subunit or both, and that the binding of a substrate in the allosteric subunit modulates, but does not necessarily eliminate, the activity of the catalytic subunit. To test this hypothesis, we created the COX-2 reaction model (CORM), a rule-based ordinary differential equation model encompassing all of the potential binding interactions of each substrate at both the catalytic and allosteric sites of the enzyme (Fig. 4). As some kinetic parameters in CORM are not easily accessible for direct measurement, we used a Bayesian statistics inference approach to determine whether CORM could explain the experimental data and estimate parameter distributions within a probability framework. Bayesian approaches can model systems with parametric uncertainty to interpret observed behavior within constraints of existing knowledge (19). To reduce the number of values to be derived computationally, the experimental K_m for each substrate was used to approximate its K_D for binding to the catalytic site when no ligand is present in the allosteric site, and the K_D for binding of 2-AG to the allosteric site in the presence of 2-AG at the catalytic site was fixed at the experimentally determined K_I value for substrate inhibition (Fig. S3). The catalytic constants for product formation when each substrate is bound only to the catalytic site were fixed to the experimentally determined k_cat values (Fig. 3), and the catalytic constant for the enzyme with 2-AG in both sites was set to zero, as assumed in the model for substrate inhibition. The forward rate constants for formation of the remaining reversible intermediate complexes were fixed at diffusion-limited values. All remaining parameters were fitted to experimental data using a Bayesian Markov Chain Monte Carlo walk, which samples possible parameter values to probabilistically determine the combinations that fit the experimental data (20). Equilibrium constants for intermediate complexes were then calculated from the relevant rate constants. This approach generates both a parameter set of the most probable values and a probability distribution (Fig. S6) for the value of each parameter that indicates its level of constraint, given the experimental data. The 95% credible intervals, which are calculated from the probability distributions, contain the true parameter with a 95% probability (Fig. S7).

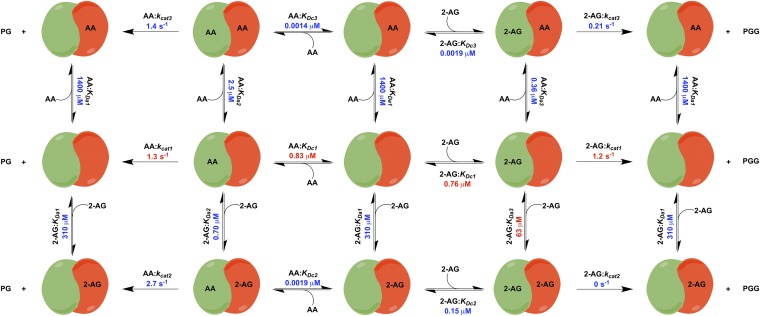
Fig. 4.

COX-2 reaction model (CORM) for the interaction of substrates AA and 2-AG with COX-2, a functional heterodimer comprising a catalytic subunit (Left, green) and an allosteric subunit (Right, red). The model provides values for the equilibrium constants of all intermediate complexes and rate constants for product-forming steps as indicated. Constants depicted in red were fixed to experimentally determined values. Specifically, K_m values, which varied little between experiments, were based on the data in Fig. S3. To optimize fitting to the data in Fig. 3, k_cat values obtained from those data were used. Values depicted in blue are the most probable values for those parameters, based upon computational results.

Fig. S6.

CORM parameter posterior probability distributions. Distributions were obtained using Bayesian Markov Chain Monte Carlo sampling of parameter values as described in SI Methods.

Fig. S7.

CORM 95% credible intervals and most probable parameter values obtained from sampling. These represent the minimum-width credible intervals enclosing the region of highest posterior probability density. All k_cat parameter values are expressed in units of per second, and all K_D parameters are in micromolar concentration.

As seen in Fig. S6, the coefficients of variation for the parameter distributions vary substantially across the model fit, so that some distributions are quite narrow whereas others are much broader. The presence of broad distributions reflects the fact that our current knowledge of the system is insufficient to result in a tight convergence of all values. Those parameters with broad distributions are less likely to play a significant role in the overall kinetics of the system, whereas those with a narrow distribution more strongly affect the observed kinetic behavior. These considerations suggest that the most influential parameters of those modeled computationally are the dissociation constants for the binding of AA in the allosteric site after either AA or 2-AG has bound in the catalytic site, and the rate constants for the formation of PGs or PG-Gs, respectively, from those resulting doubly bound complexes.

The most probable K_D and k_cat values obtained computationally are shown in Fig. 4 and Fig. S7. Fig. 5 and Fig. S8 provide a comparison of the experimental data with those predicted by the model. Clearly, CORM provides a better fit to the experimental data than was observed for any of the classic kinetics models tested, supporting the hypothesis that the COX-2 reaction occurs through the formation of multiple complexes via a variety of pathways. A more detailed analysis of CORM’s parameters suggests that binding of either substrate to the allosteric site is favored only if a ligand is present in the catalytic site. When AA is present alone, the doubly bound complex is favored over the singly bound one at concentrations above ∼1.5 μM, whereas, for 2-AG, the singly bound complex predominates even at very high concentrations (Fig. S9 A and B). When both substrates are present over a wide range of concentrations, complexes with two different ligands are favored over those in which the same molecule is bound to both sites (Fig. S9 C and D). Notably, CORM predicts that the catalytic constant for conversion of 2-AG to PG-Gs when AA is present in the allosteric site is reduced compared with the catalytic constant associated with 2-AG turnover in the absence of a ligand in the allosteric site; based on the kinetic rate distributions returned by CORM, there is a 98% probability that the turnover of 2-AG with no ligand in the allosteric site is greater than when AA is present in the allosteric site. In contrast, the catalytic constant for AA oxygenation by COX-2 is predicted to be higher when 2-AG occupies the allosteric site than when AA or no ligand is present in that site; there is an 85% probability that the 2-AG–bound complex turns over AA more quickly than the complex with no allosteric ligand. Thus, allosteric interactions between substrates and COX-2, as revealed through kinetic modeling, provide a rational explanation for the observed in vitro experimental results.

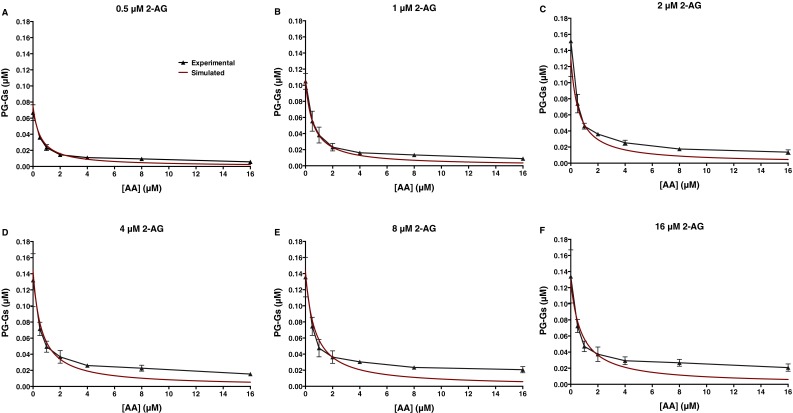
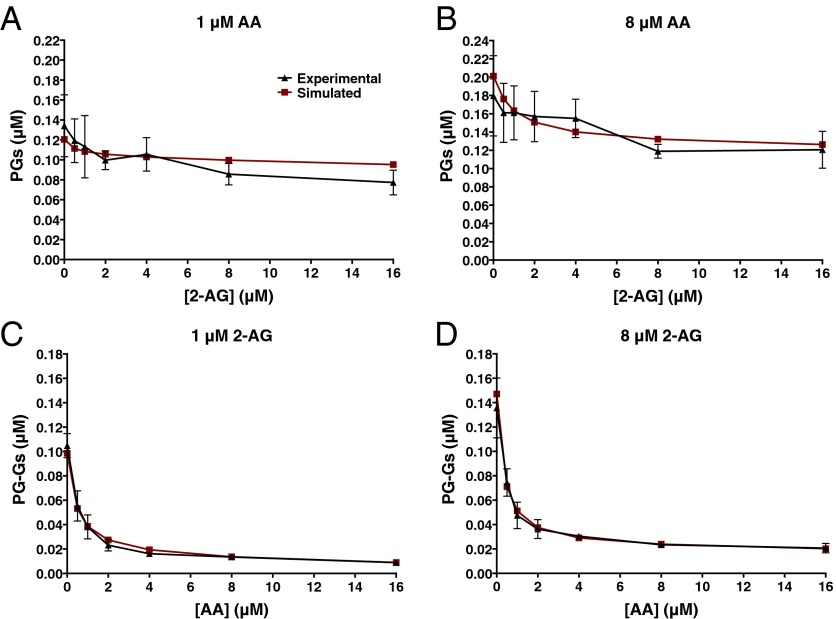
Fig. 5.

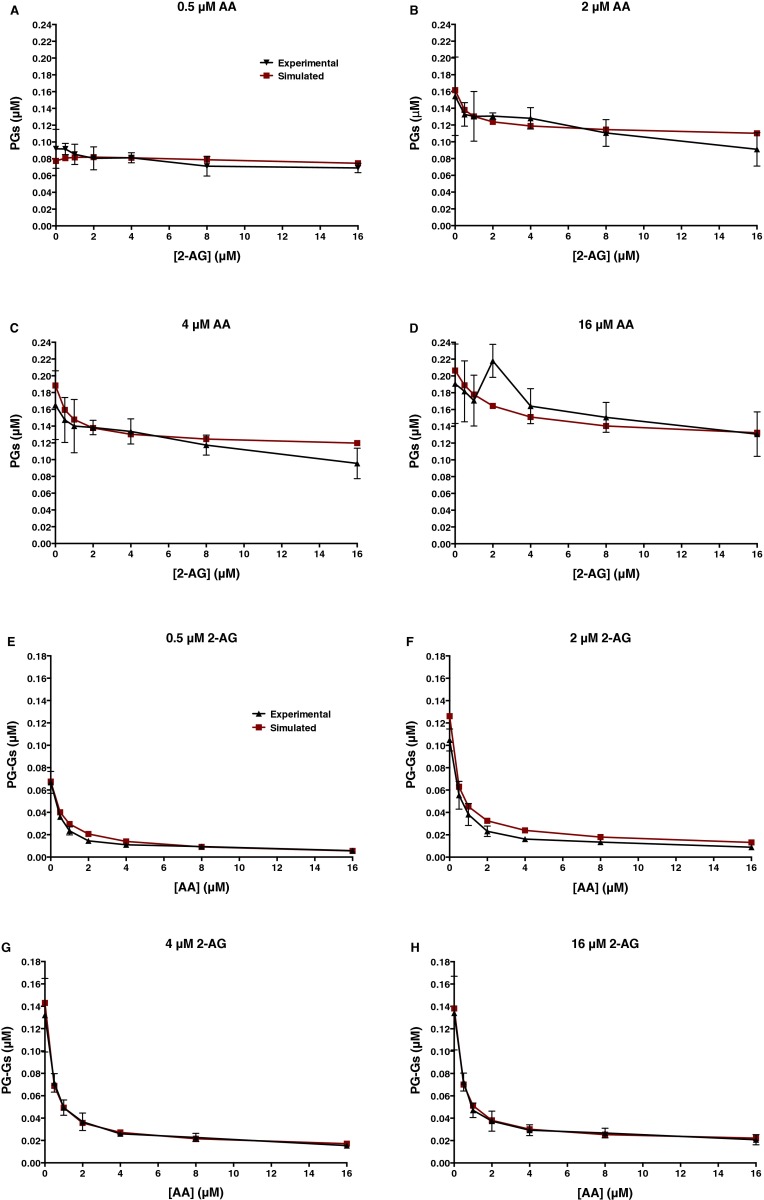
Computational modeling of both the catalytic and allosteric sites of COX-2 enables data fitting. Graphed are the actual data from the experiment described in the legend to Fig. 3 versus those simulated using parameters generated by CORM shown in Fig. 4. Data shown are PG levels produced from low (1 μM) and high (8 μM) concentrations of AA in the presence of increasing concentrations of 2-AG (A and B) and PG-G levels produced from low and high concentrations of 2-AG in the presence of increasing concentrations of AA (C and D). For results from the entire set of data, see Fig. S8.

Fig. S8.

Modeling of both the catalytic and allosteric site of COX-2 enables data fitting. Experimental results versus those simulated using the computational parameters derived from CORM (Fig. 4 and Fig. S7) are presented. Data shown are PG levels produced from the indicated concentrations of AA in the presence of increasing concentrations of 2-AG (A–D) and PG-G levels produced from the indicated concentrations of 2-AG in the presence of increasing concentrations of AA (E–H).

Fig. S9.

CORM-based predictions of COX-2, AA, and 2-AG complex formation. (A and B) Steady-state levels of AA- or 2-AG–containing complexes formed in the absence of the other substrate. Blue, green, and red lines indicate predicted concentrations of COX-2 with AA or 2-AG bound in only the allosteric site, only the catalytic site, or in both sites, respectively, when simulated at the most probable values returned by CORM calibration. Shaded regions delineate possible complex formation as predicted by the entire calibrated parameter ensemble consistent with experimental data. (C and D) Levels of prominent complexes as AA concentration varies in the presence of 2 μM 2-AG (C) or as 2-AG concentration varies in the presence of 2 μM AA (D). Blue, green, red, and purple lines indicate predicted concentrations of COX-2 with both AA and 2-AG bound, with AA bound to both catalytic and allosteric sites, with AA bound only to the catalytic site, and with 2-AG bound only to the catalytic site, respectively. Other low-abundance complexes were present at less than 0.0009 μM at all concentrations and are not shown. Lines indicate most probable value simulations, and shaded regions delineate predictions based on the entire parameter set as in A and B. All simulations were performed in the presence of 15 nM COX-2. (E and F) Simulated substrate concentration versus initial velocity curves for the COX-2 enzyme behaving as predicted by CORM. The most probable parameter values derived from CORM (Fig. 4 and Fig. S7) were used to predict the initial velocity of reaction using 15 nM COX-2 and the indicated concentrations of 2-AG (E) or AA (F) (▽). The resulting values of K_m, k_cat, and K_I generated by curve fitting using the substrate inhibition model (E) or Michaelis–Menten model (F) are shown. Also shown for comparison are the corresponding curves generated from the substrate inhibition model (E) or the Michaelis–Menten model (F) using the experimental parameters that were used in the generation of CORM (△).

Discussion

COX-2 as an Allosteric Enzyme.

In 1997, Swinney et al. (21) reported that COX-1 behaves as an allosteric enzyme with a Hill coefficient of 1.3. Their interpretation of this apparent cooperativity was later disputed by Chen et al. (22), who explained the phenomenon on the basis of COX’s requirement for product hydroperoxide to activate the enzyme’s active site. Since that time, researchers have generally agreed that the COX isoforms do not behave as allosteric enzymes with regard to AA. However, recent evidence strongly supports the concept that the enzymes are functional heterodimers and that activity is modulated by binding of nonsubstrate ligands to the allosteric subunit (8–10). Here, we report that AA and 2-AG, despite similar catalytic efficiencies with COX-2 when measured individually in vitro, differ markedly in their rate of oxygenation in the presence of the other substrate. Furthermore, we present data consistent with the hypothesis that this modulation of COX-2 activity not only occurs with purified protein but also in intact cells.

CORM Explains the Complex Interplay of COX-2 Substrates.

To explain our experimental observations, we hypothesized that AA and 2-AG can bind to both the catalytic and allosteric sites of the enzyme, and that binding in the allosteric site modulates the activity of the catalytic site. This hypothesis is described by CORM, which provides assessments of the affinity of each substrate for COX-2’s catalytic and allosteric sites and the k_cat values associated with each catalytically competent complex. We used a Bayesian statistical approach to characterize CORM within a probabilistic framework that uses prior knowledge to constrain plausible biochemical mechanisms of COX-2 reaction dynamics. To the best of our knowledge, this is the first attempt to use this conditional probability approach to infer mechanisms for small biochemical model systems such as the COX-2 reaction network. CORM suggests that the two substrates compete for the enzyme’s allosteric site. Binding of AA to that site likely results in a decrease in the enzyme’s catalytic efficiency for oxygenation of 2-AG while having little effect on the oxygenation of AA. CORM also suggests that binding of 2-AG to the allosteric site of COX-2 in the presence of AA in the catalytic site increases the enzyme’s catalytic efficiency for oxygenation of AA. These results explain why the suppression of 2-AG oxygenation by AA and the suppression of AA oxygenation by 2-AG are greater and lesser, respectively, than predicted based upon competition at the catalytic site alone. Thus, our mechanistic model and parameter inferences reveal a complex enzyme–substrate interaction that cannot be construed from classical kinetic analyses.

It is important to note that a number of assumptions were made when constructing CORM, including that the forward rate constant for formation of all intermediate complexes is diffusion limited, that the affinity of each substrate binding alone to the catalytic site can be approximated by its experimental K_m, that the respective experimental k_cat value should apply to product formation specifically from this complex, and that the affinity of 2-AG at the allosteric site can be approximated by its experimental K_I. The latter assumptions are reasonable in the case of 2-AG oxygenation, as the experimental values obtained for that substrate were derived from a substrate inhibition model that accounts for binding of 2-AG in both the catalytic and allosteric sites. Consequently, it is not surprising that CORM predicts initial rate values for oxygenation of 2-AG in the absence of AA that are indistinguishable from those predicted from the substrate inhibition model using the same experimentally derived parameters (Fig. S9E). In the case of AA oxygenation, however, the K_m and k_cat values used to derive CORM were obtained from the Michaelis–Menten model, which assumes only a single binding site for substrate. The presence of a catalytically active complex containing AA in both the allosteric and catalytic sites, as modeled in CORM, calls into question how well the Michaelis–Menten model applies to this scenario. As seen in Fig. S9F, initial velocities predicted by the most probable values returned by CORM fit the Michaelis–Menten equation remarkably well. However, the resulting K_m and k_cat values are lower and higher, respectively, than the corresponding experimental parameters applied during the generation of CORM. These results indicate that an enzyme exhibiting the behavior predicted by CORM will appear to follow Michaelis–Menten kinetics, as COX-2 does experimentally; however, the K_m and k_cat values returned will reflect the activity of all catalytically competent complexes rather than any single one. Consequently, some error has likely resulted from the use of experimental K_m and k_cat values to estimate the affinity and activity of the complex containing AA bound only to the catalytic site during the derivation of CORM.

Structural Basis of Allostery.

Previously reported data suggest that the two sequence-identical subunits of COX-2 are distinguished by the presence of heme in the catalytic site and its absence in the allosteric site (8). This difference is not recapitulated in the currently available crystal structures of the holoenzyme, which show heme bound to both subunits. Nevertheless, crystal structures of complexes of the holoenzyme with either AA or 1-AG, a more stable isomer of 2-AG, show different conformations for the binding of the substrate in each subunit (23, 24). In both cases, only one subunit contains a productively bound conformation of the substrate. These observations suggest a functional difference between the two subunits even when heme is bound in both sites. They also confirm that both AA and 2-AG retain affinity for the allosteric site, albeit in a different binding pose than what is observed in the catalytic site. Thus, there is a structural foundation for the allosteric regulation of COX-2 activity by both substrates. Our kinetic model suggests that binding of either AA or 2-AG in the allosteric site is inhibitory to 2-AG oxygenation and mildly stimulatory to AA oxygenation, reinforcing literature reports that AA oxygenation is relatively unaffected by the presence of many nonsubstrate modulators (both inhibitory and stimulatory) at concentrations that markedly affect 2-AG oxygenation (10, 11, 25). We currently do not know the basis for these differences between the substrates, but crystal structure data of 1-AG in the COX-2 active site reveal that binding requires movement of the side chain of leucine-531 that is not required for binding of AA (23). It is possible that the flexibility required to accommodate 2-AG in the active site is highly sensitive to the presence of ligands in the allosteric site.

Role of Allostery in Intact Cells.

Our findings that AA inhibits 2-AG oxygenation in vitro and that cellular AA and PG-G levels are inversely correlated lead one to question the degree to which allosteric control modulates PG-G synthesis in cells. Most studies of cellular PG-G production have used stimuli that trigger the release of high concentrations of free AA, only a portion of which is converted to PGs. In most cases, the ratio of AA to 2-AG in whole-cell lysates is at least 10:1, whereas the ratio of PGs to PG-Gs has been in the range of 500–1,000:1 (6, 26). In the experiments reported here, the PG:PG-G ratio was from 20- to 100-fold higher than the AA:2-AG ratio (Figs. 1 and 2). These findings are consistent with our evidence that AA suppresses 2-AG oxygenation by COX-2. However, allosteric regulation is likely only one of a number of factors contributing to the high PG:PG-G ratio found in cells. Others include the kinetics of release of AA and 2-AG, the local concentrations of each substrate, and the hydroperoxide tone in the immediate vicinity of the enzyme.

Although the heterodimeric nature of COX enzyme function has been described, the impact of substrate binding in the allosteric site on catalytic efficiency or inhibitor potency has not been thoroughly explored. Our data demonstrate that binding of AA or 2-AG in the allosteric site of COX-2 leads to changes in the efficiency of oxygenation of both substrates in the catalytic site, effects that are not easily appreciated through kinetic studies using individual substrates. Our findings also indicate that both substrates are theoretically capable of competing with inhibitors for either site. Clearly, future considerations of the kinetic behavior of the COX enzymes must take into account the potential for substrate and inhibitor binding, and the associated functional consequences, in both subunits of the enzyme.

Methods

Cell Culture.

For AA enrichment studies, RAW264.7 cells were incubated with BSA-complexed AA and granulocyte–macrophage colony-stimulating factor overnight. The cells were subsequently stimulated with lipopolysaccharide/IFN-γ (LPS/IFN-γ) to induce COX-2 expression followed by zymosan to promote substrate release and PG and PG-G biosynthesis. For studies of the effects of inhibition of AA release, RAW264.7 cells were treated with LPS/IFN-γ to induce COX-2 expression, followed by treatment with giripladib to inhibit cPLA₂α. Ionomycin was then added to promote substrate release and PG and PG-G biosynthesis. Further details can be found in SI Methods.

Kinetic Experiments.

Various concentrations of substrate premixed with PPHP were incubated with mCOX-2 as specified in the figure legends. Reactions were quenched and products extracted with acidified ethyl acetate containing internal standards for quantification via LC-MS/MS (see SI Methods for details). Quantitation is based on the production of PGE₂ and PGD₂ or PGE₂-G and PGD₂-G, which are the primary dioxygenated products from AA or 2-AG, respectively. These species comprise a constant proportion of total products under the reaction conditions used. The quantification does not include monooxygenated products of either substrate or other breakdown products of the PG endoperoxide intermediates. Consequently, reported measurements of k_cat are lower than previously reported values based on total oxygen consumption that, for most products, occurs at a rate of two molecules of oxygen per molecule of fatty acid substrate.

Kinetic Modeling.

KinTek Explorer software was used to simulate competitive inhibition. Modeling of uncompetitive, noncompetitive, and mixed inhibition was carried out using GraphPad Prism 6. The rule-based model depicted in Fig. 4 was built in the PySB modeling framework, and parameter fitting was performed with the DREAM_(Z) module in PyMC (27–29). Details are in SI Methods.

SI Methods

Materials.

The expression and purification of recombinant mCOX-2 from Sf9 cells were performed as previously described (30). AA, 2-AG, PPHP, PGE₂-d₄, AA-d₈, and 2-AG-d₈ were purchased from Cayman Chemical. PGE₂-G-d₅ was synthesized as described previously using chemicals from Sigma-Aldrich (3). RAW264.7 cells were obtained from the American Type Culture Collection. Cell culture reagents were purchased from Life Technologies. FBS was purchased from Atlas Biologicals. Fatty acid-free BSA, LPS, zymosan B, ionomycin, and IFN-γ were purchased from Sigma-Aldrich. Granulocyte–macrophage colony-stimulating factor (GM-CSF) was purchased from R&D Systems. Giripladib was synthesized in C.W.L.’s laboratory as described (31).

AA and 2-AG Kinetics with mCOX-2.

For kinetic analyses, mCOX-2 was reconstituted with 2 eq of heme in 195 μL of 100 mM Tris⋅HCl buffer, pH 8, with 500 μM phenol. Following a 3-min preincubation at 37 °C, 5 μL of DMSO containing the specified amounts of AA, 2-AG, and PPHP (final concentrations of 0–16 μM for each substrate and 1 μM for PPHP) was added to the tube, and, after thorough mixing, the reaction was allowed to proceed for 10 s. The reaction was quenched by adding 200 μL of ethyl acetate containing 0.5% glacial acetic acid and internal standards, PGE₂-d₄ and PGE₂-G-d₅. Tubes were frozen, and the organic layer was separated and evaporated to dryness under nitrogen gas. The samples were then reconstituted in 200 μL of methanol and analyzed using liquid chromatography–tandem mass spectrometry (LC-MS/MS) as described below. Initial velocities were plotted versus substrate concentration. In the case of incubations containing a single substrate, kinetic parameters (k_cat, K_m, and K_I) were determined by data fitting to the Michaelis–Menten model (for AA) or a substrate inhibition model (for 2-AG) using GraphPad Prism 6 software. The concentration of enzyme was selected to maintain substrate consumption below 20%. This varied with enzyme preparation, likely due to the presence of variable amounts of inactive enzyme. Accordingly, some variability in k_cat was also noted between enzyme preparations.

Kinetic Modeling: Competitive Inhibition.

Data simulations were carried out with KinTek Explorer, Version 4.0, Student Edition software (32–34) using the following model:

$$\begin{array}{lll}\mathrm{E}+\mathrm{AA}\rightleftharpoons \mathrm{E\cdot AA}\hfill & {\mathit{k}}_{\mathrm{f}}=\mathrm{1,000}\hspace{0.17em}{\mathrm{s}}^{\mathrm{-1}}\mathrm{\cdot \mu }{\mathrm{M}}^{\mathrm{-1}}\hfill & {\mathit{k}}_{\mathrm{r}}=830\hspace{0.17em}{\mathrm{s}}^{\mathrm{-1}}\hfill \\ \mathrm{E\cdot AA}\to \mathrm{E}+\mathrm{PG}\hfill & {\mathit{k}}_{\mathrm{f}}=1.3\hspace{0.17em}{\mathrm{s}}^{\mathrm{-1}}\hfill & {\mathit{k}}_{\mathrm{r}}=0\hspace{0.17em}{\mathrm{s}}^{\mathrm{-1}}\hfill \\ \mathrm{E}+2\text{-}\mathrm{AG}\rightleftharpoons \mathrm{E\cdot }2\text{-}\mathrm{AG}\hfill & {\mathit{k}}_{\mathrm{f}}=\mathrm{1,000}\hspace{0.17em}{\mathrm{s}}^{\mathrm{-1}}\mathrm{\cdot \mu }{\mathrm{M}}^{\mathrm{-1}}\hfill & {\mathit{k}}_{\mathrm{r}}=760\hspace{0.17em}{\mathrm{s}}^{\mathrm{-1}}\hfill \\ \text{E⋅}2\text{-}\mathrm{AG}\to \mathrm{E}+\mathrm{PG}\hfill & {\mathit{k}}_{\mathrm{f}}=1.2\hspace{0.17em}{\mathrm{s}}^{\mathrm{-1}}\mathrm{\cdot \mu }{\mathrm{M}}^{\mathrm{-1}}\hfill & {\mathit{k}}_{\mathrm{r}}=0\hspace{0.17em}{\mathrm{s}}^{\mathrm{-1}}\hfill \\ \text{E⋅}2\text{-}\mathrm{AG}+2\text{-}\mathrm{AG}\rightleftharpoons \mathrm{E\cdot }2\text{-}\mathrm{AG}\mathrm{\cdot }2\text{-}\mathrm{AG}\hfill & {\mathit{k}}_{\mathrm{f}}=\mathrm{1,000}\hspace{0.17em}{\mathrm{s}}^{\mathrm{-1}}\mathrm{\cdot \mu }{\mathrm{M}}^{\mathrm{-1}}\hfill & {\mathit{k}}_{\mathrm{r}}=\mathrm{63,000}\hspace{0.17em}{\mathrm{s}}^{\mathrm{-1}}\hfill \\ \text{E⋅}2\text{-}\mathrm{AG}\mathrm{\cdot 2-AG}\to \mathrm{E\cdot }2\text{-}\mathrm{AG}+\mathrm{PG}\text{-}\mathrm{G}\hfill & {\mathit{k}}_{\mathrm{f}}=0\hspace{0.17em}{\mathrm{s}}^{\mathrm{-1}}\mathrm{\cdot \mu }{\mathrm{M}}^{\mathrm{-1}}\hfill & {\mathit{k}}_{\mathrm{r}}=0\hspace{0.17em}{\mathrm{s}}^{\mathrm{-1}}.\hfill \end{array}$$

The model assumes that each substrate establishes a rapid, reversible equilibrium with the catalytic site before forming product, and that binding of 2-AG to the allosteric site results in substrate inhibition. The experimental values of K_m for AA and 2-AG (0.83 and 0.76 μM, respectively) were assumed to be reasonable estimates of the binding affinity of each substrate for the enzyme’s catalytic site. Similarly, the values of K_I for 2-AG at the allosteric site and k_cat for the formation of PG and PG-Gs were all obtained from the experimental data (Fig. S3 and Fig. 3, respectively). The KinTek program does not allow for entry of equilibrium constants, so values for the rate constants of the forward and reverse reactions were entered to simulate the appropriate rapid, reversible equilibrium for the formation of each enzyme–substrate complex. Simulations were performed using 15 nM enzyme and all combinations of AA and 2-AG (0.5–16 μM) used in the experiment described in the legend to Fig. 3, with reactions carried out for 10-s incubation times.

Kinetic Modeling: Uncompetitive Inhibition.

The effects of AA on the production of PG-Gs from 2-AG by COX-2 were evaluated using classical models of uncompetitive, noncompetitive, and mixed inhibition. In all cases, competition of each substrate with the other at the active site and substrate inhibition of 2-AG were included. The general equation was as follows:

$$V=\frac{V_{\max }\left[\mathrm{AG}\right]}{K_{\mathrm{mAG}}\left(1+\frac{\left[\mathrm{AA}\right]}{K_{\mathrm{mAA}}}+\frac{\left[\mathrm{AA}\right]}{K_{\mathrm{I1}}}\right)+\left[\mathrm{AG}\right]\left(1+\frac{\left[\mathrm{AG}\right]}{K_{\mathrm{I}}}+\frac{\left[\mathrm{AA}\right]}{K_{\mathrm{I2}}}\right)}.$$

In this equation, K_mAG and K_mAA were the experimental values obtained for 2-AG and AA, respectively (Fig. S3). V_max was the experimental value for PG-G formation obtained from the experiment described in the legend to Fig. 3. K_I was the experimental value for substrate inhibition of 2-AG oxygenation (Fig. S3B). The model assumes that binding of either AA or 2-AG to the allosteric site creates an inactive complex. Curve fitting was carried out using the data generated in the experiment described in the legend to Fig. 3. For noncompetitive inhibition, K_I1 was set equal to K_I2. For mixed inhibition, the two values were fit independently. For uncompetitive inhibition, the term including K_I1 was removed.

Kinetic Modeling: Explicit Catalytic and Allosteric Sites.

The COX-2 reaction model (CORM) was implemented as a Python program that, when executed, generates a set of BioNetGen rules that, in turn, generate 13 ordinary differential equations using the mass-action kinetics formalism, within the PySB models-as-programs Python modeling framework (27). Bayesian statistical sampling of possible model parameter values was then performed using the Markov Chain Monte Carlo algorithm DREAM_(z) (29) in the Python package PyMC (28). Experimentally measured parameters were fixed. Fitted parameters included both K_D and k_cat values. Because the ordinary differential equations used to derive CORM require rate constants instead of K_D values, fitted K_D values were converted into rate parameters (k_r/k_f). The reaction k_f was then assumed to be diffusion limited, whereas the k_r was allowed to vary to yield a particular K_D. Parameter prior probabilities were specified as normal distributions, with means set at the parameter values fitted using the uncompetitive inhibition model and SDs of approximately an order of magnitude, reflecting a relative lack of knowledge about likely parameter values. A model likelihood function measured model simulation fit to experimental data as has been described in previous work (20). Additionally, four thermodynamic cycles present in the interaction network (Fig. 4) provided another measure of model likelihood, as the relative values of these parameters must be consistent with energy conservation. The thermodynamic cycles are shown below:

$$\mathrm{E\; +\; AA}\rightleftharpoons \mathrm{E\cdot AA\; +\; AA}\rightleftharpoons \mathrm{AA\cdot E\cdot AA}\rightleftharpoons \mathrm{AA\; +\; AA\cdot E}\rightleftharpoons \mathrm{E\; +\; AA,}$$

$$\text{E}\hspace{0.17em}+\hspace{0.17em}2\text{-}\mathrm{AG}\rightleftharpoons 2\text{-}\mathrm{AG}\mathrm{\cdot E\; +\; AA}\rightleftharpoons 2\text{-}\mathrm{AG}\mathrm{\cdot E\cdot AA}\rightleftharpoons 2\text{-}\mathrm{AG}\hspace{0.17em}\mathrm{+\; E\cdot AA}\rightleftharpoons \mathrm{E\; +\; AA,}$$

$$\text{E + AA}\rightleftharpoons \text{AA}\cdot \text{E}\hspace{0.17em}+\hspace{0.17em}2\text{-}\mathrm{AG}\rightleftharpoons \text{AA⋅E⋅}2\text{-}\mathrm{AG}\rightleftharpoons \text{AA + E⋅}2\text{-}\mathrm{AG}\rightleftharpoons \text{E}\hspace{0.17em}+\hspace{0.17em}2\text{-}\mathrm{AG,}$$

$$\text{E}\hspace{0.17em}+\hspace{0.17em}2\text{-}\mathrm{AG}\rightleftharpoons \text{E⋅}2\text{-}\mathrm{AG}\mathrm{+}2\text{-}\mathrm{AG}\rightleftharpoons 2\text{-}\mathrm{AG}\text{⋅E⋅}2\text{-}\mathrm{AG}\rightleftharpoons 2\text{-}\mathrm{AG}\mathrm{+}2\text{-}\mathrm{AG}\mathrm{\cdot E}\rightleftharpoons \text{E}\hspace{0.17em}+\hspace{0.17em}2\text{-}\mathrm{AG}\text{.}$$

The fit of model simulations to experimental data and the extent to which tested parameters were consistent with energy conservation was measured using the probability density function for a normal distribution:

$$f\left(x,\mu ,\sigma \right)=\frac{1}{\sigma \sqrt{2\pi }}{e}^{-\frac{{(x-\mu )}^2}{2{\sigma }^2}},$$

where x is the simulated value, µ is the observed average value, and σ is the SD. When measuring goodness of fit to experimental data, the average and SD for each experimental measurement were used. When measuring energy conservation, perfect energy conservation (i.e., a ratio of 1:1 for the product of K_D values on each side of a thermodynamic cycle) was used as the average and 0.001 as a SD to allow small deviations from this ideal value. This function was minimized during our parameter scans to find probable parameter values given the network interactions and the experimental kinetics.

The DREAM_(Z) algorithm was initialized with five chains in random locations in parameter space drawn from prior parameter probability distributions. Sampling was performed for 2.5 million iterations; 100,000 samples were discarded as burn-in, and sample matrixes were thinned by a factor of 10. All chains converged to a limiting distribution as assessed by both the Geweke score (35) and Gelman–Rubin convergence criterion (36). Ninety-five percent credible intervals for each parameter were then estimated by determining the narrowest interval that encompasses 95% of the sample distribution. Fig. S9 A–D was plotted using the Python package seaborn (stanford.edu/∼mwaskom/software/seaborn/). All code used to build the model and fit the model parameters is freely available in the GitHub repository of C.F.L.’s laboratory (github.com/LoLab-VU/CORM).

RAW 264.7 Cell Culture.

Low passage number RAW264.7 cells were maintained in Dulbecco’s modified Eagle medium (DMEM) plus GlutaMAX containing 10% heat-inactivated FBS. For studies of the effects of AA enrichment on PG-G biosynthesis, cells were plated at 5 × 10⁵ cells per dish onto 35-mm plates and incubated with AA complexed with BSA and 20 ng/mL GM-CSF for 20 h as described previously (12). The cells were then transferred to fresh DMEM/heat-inactivated FBS with LPS (100 ng/mL, Escherichia coli 011:B4), IFN-γ (10 ng/mL), and GM-CSF (20 ng/mL). Cultures were incubated for 5 h and then washed in PBS and overlaid in fresh serum-free DMEM. Zymosan was added (160 μg/dish), and cells were incubated for 1 or 2 h before harvesting for analysis of AA and 2-AG or PGs and PG-Gs, respectively.

For studies of the effects of inhibition of AA release, RAW264.7 cells were plated at 3 × 10⁶ cells per dish onto 100-mm plates and incubated for 24 h. The medium was then removed and replaced with serum-free DMEM with LPS (1 μg/mL; E. coli 011:B4) and IFN-γ (10 ng/mL). Cultures were incubated for 6 h and then washed and overlaid with fresh serum-free DMEM containing either DMSO or 1 μM giripladib in DMSO. Fifteen minutes later, ionomycin was spiked into the medium to a final concentration of 5 μM, and cells were incubated for an additional 45 min.

LC-MS/MS Analysis.

Following cell treatments as described above, the culture medium was removed and extracted with 2 vol of ethyl acetate containing PGE₂-d₄ and PGE₂-G-d₅. The cells were scraped into 1 mL of ice-cold methanol containing AA-d₈, 2-AG-d₈, and added directly into the ethyl acetate solution. The solution was vigorously mixed, and the organic layer was then removed and dried under a stream of nitrogen gas. The resultant film was reconstituted and analyzed for AA and 2-AG levels using a Luna C18 (2) column (50 × 2 mm, 5 μm) (Phenomenex) with a gradient elution of 83–99% solvent B over 2 min at a flow rate of 300 μL/min (solvent A: 80 μM silver acetate, 0.1% acetic acid in water; solvent B: 118 μM silver acetate, 0.1% acetic acid in methanol). MS/MS analysis was conducted on a QTrap 3200 (AB SCIEX) operated in positive ion mode using selected reaction monitoring for the following transitions: m/z 519→409 for AA, m/z 527→417 for AA-d₈, m/z 485→411 for 2-AG, and m/z 493→419 for 2-AG-d₈ (37). PGs and PG-Gs were quantified in a similar manner with a gradient elution of 25–98% solvent B over 4 min at a flow rate of 300 μL/min (solvent A: 5 mM ammonium acetate, pH 3.6; solvent B: acetonitrile with 6% solvent A) with selected reaction monitoring for the following transitions: m/z 370→317 for PGE₂/D₂, m/z 374→321 for PGE₂-d₄, m/z 444→391 for PGE₂/D₂-G, and m/z 449→396 for PGE₂-G-d₅ (38). This method of PG and PG-G analysis was also applied to kinetic studies with purified mCOX-2 as described in the corresponding methods section.