Direct measurement of the 3-dimensional DNA lesion distribution induced by energetic charged particles in a mouse model tissue

Significance

Charged particles are applied in cancer radiotherapy because they are more efficient than X-rays or γ-rays in tumor cell killing. This efficiency results from the high dose deposition along the path of the particles. However, charged particles damage tissue inhomogeneously, such that many cells not directly hit by the particles receive a low dose and can survive with mutations. Because mutations can lead to secondary malignancies, this effect limits the applicability of charged particles in cancer radiotherapy. We provide the first direct measurement of the 3D DNA lesion distribution induced by energetic charged particles in a mouse model tissue. Our detailed analysis of the dose distribution will serve to benchmark biophysical models currently used for irradiation planning in cancer radiotherapy.

Abstract

Charged particles are increasingly used in cancer radiotherapy and contribute significantly to the natural radiation risk. The difference in the biological effects of high-energy charged particles compared with X-rays or γ-rays is determined largely by the spatial distribution of their energy deposition events. Part of the energy is deposited in a densely ionizing manner in the inner part of the track, with the remainder spread out more sparsely over the outer track region. Our knowledge about the dose distribution is derived solely from modeling approaches and physical measurements in inorganic material. Here we exploited the exceptional sensitivity of γH2AX foci technology and quantified the spatial distribution of DNA lesions induced by charged particles in a mouse model tissue. We observed that charged particles damage tissue nonhomogenously, with single cells receiving high doses and many other cells exposed to isolated damage resulting from high-energy secondary electrons. Using calibration experiments, we transformed the 3D lesion distribution into a dose distribution and compared it with predictions from modeling approaches. We obtained a radial dose distribution with sub-micrometer resolution that decreased with increasing distance to the particle path following a 1/r² dependency. The analysis further revealed the existence of a background dose at larger distances from the particle path arising from overlapping dose deposition events from independent particles. Our study provides, to our knowledge, the first quantification of the spatial dose distribution of charged particles in biologically relevant material, and will serve as a benchmark for biophysical models that predict the biological effects of these particles.

Charged particles, including protons, α-particles, and heavy ions, are increasingly used in cancer radiotherapy and represent a significant component of the natural background irradiation on earth and in space (1–3). Their biological effect is often very different from that of photons (X- or γ-rays), largely because charged particles deposit their energy along a track, whereas photons produce a fairly homogeneous dose distribution. Linear energy transfer (LET; typically given in units of keV/µm) has been introduced as a parameter to describe the amount of energy that charged particles deposit along their track. Particles with high LET are densely ionizing and typically biologically more effective than photons or low-LET particles.

Energy deposition along a particle track is not restricted to the path itself (the so-called “track core”), but extends laterally into an area known as the penumbra of the particle, which can reach considerable distances for high-energy particles. Energy deposition in the penumbra arises from energetic secondary electrons, so-called δ-electrons, which are generated by ionization events of the charged particles and carry energy away from the immediate path into the penumbra. According to classical track structure theory, ∼50% of the total energy is deposited in the penumbra, where it spreads out over a much greater volume than the energy in the track core (4). Thus, the penumbra represents a sparsely ionized region within the track of high-LET particles. Thus, charged particles deposit their energy in a complex 3D manner and typically comprise a spectrum of high- and low-ionization densities. The total biological effect of a charged particle is a result of this complex energy deposition pattern.

Our knowledge about the energy deposition pattern of charged particles is based largely on theoretical predictions and physical measurements in inorganic material. Most information in this respect was gained from microdosimetric experiments with gas-filled detectors (5). In these devices, the dose distribution around an ion trajectory is measured and rescaled to a track structure profile in water by comparing the electron density of the gas with that of water. Such a density scaling approach is expected to fail, however, when the energies of the δ-electrons are in the same order of magnitude as the intermolecular binding energies (6, 7). These limitations call for alternative approaches for assessing the 3D energy deposition pattern of charged particles directly in biologically relevant material.

Computational models, mostly Monte Carlo codes, have been developed to describe the energy deposition patterns of charged particles. Results from such approaches are in reasonable agreement with physical measurements, although track structure modeling at a nanometer or micrometer scale remains a challenge. Computational models are also used to predict the biological effects of charged particles, such as the induction of DNA damage (8–11). Unlike Monte Carlo calculations, amorphous track structure models exploit the radial dose distribution to predict the biological response (12, 13). One of these approaches, known as the local effect model (LEM), is currently applied in particle cancer therapy to predict the biological effects of heavy ions (14, 15). The LEM assumes that the same local dose, independent of the radiation type that deposits this dose, leads to the same biological effect. Essentially, LEM derives the biological effects of charged particles from the response of cells or tissues to photon radiation.

Double-strand breaks (DSBs) are among the most hazardous DNA lesions induced by ionizing radiation (IR) because they can give rise to more complex lesions when occurring in clusters or associated with other lesions (16). On DSB induction, the histone variant H2AX is phosphorylated at the break site to γH2AX (17). This histone modification can be visualized by microscopy and forms so-called γH2AX foci, which arise within minutes after IR in a 1:1 ratio to isolated DSBs and are lost with time due to DSB repair (18, 19). Because this technology detects single isolated DSBs in single cells, it has exceptional sensitivity and can monitor the effect of IR doses of a few mGy (20, 21). Not surprisingly, γH2AX foci analysis has been applied to assess radiation doses encountered by humans during diagnostic medical procedures, such as computed tomography scanning (22–25). Moreover, this technology can be applied to different tissues (26, 27) and is becoming the gold standard for various biodosimetric applications (28, 29).

In the present study, we combined the particular sensitivity of the γH2AX foci technology with its second major advantage, the ability to precisely determine the position of the DNA lesions, to investigate the spatial distribution of γH2AX foci induced by charged particles. Calibration experiments allowed transformation of the lesion distribution into a 3D dose distribution, which could be compared with predictions from the amorphous track structure model, the LEM. Using this procedure, we were able to quantify the lateral (radial) dose profile of titanium (Ti) ions with sub-micrometer resolution and verify the theoretically predicted 1/r² dose decline using a biological model system.

Results

Charged particles deposit high doses in the core (i.e., the inner part) of their track and low doses in the surrounding penumbra (i.e., the outer part). Because the physical dose deposited by δ-electrons in the outer part of the track is predicted to decrease strongly with the distance to the particle path (5, 30), we aimed to biologically quantify the dose in a 3D geometry around the path. We used mouse tissue as a model system and quantified DSBs by counting γH2AX foci, which arise linearly with radiation dose (18, 19, 31). To further enhance the sensitivity of this biodosimetric approach, we investigated the mouse retina with its densely packed and uniformly arranged photoreceptors (32). Lamin B staining showed that mouse photoreceptors contained a low amount of cytoplasm and little intercellular space (Fig. 1A). The nuclei of photoreceptors contained a central heterochromatic chromocenter, which is surrounded by euchromatic DNA (33) (Fig. 1B). This specialized chromatin structure represents a unique adaptation of photoreceptors to optimal vision in low-light conditions (33). Collectively, the various special features of the mouse retina make it an ideal model system for analyzing the spatial dose distribution of charged particles.

Fig. 1.

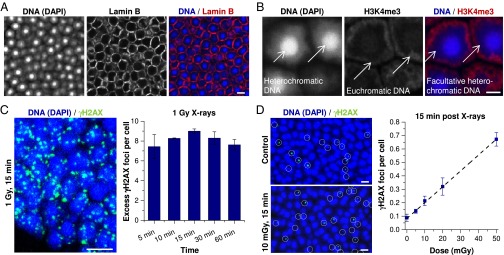
γH2AX foci in mouse photoreceptors after low X-ray doses. (A) IF image of Lamin B in mouse photoreceptors. (Scale bar: 5 µm.) (B) IF image of H3K4me3 in mouse photoreceptors. Different chromatin regions in the nucleus are indicated by white arrows. (Scale bar: 2 µm.) (C) Time-dependent quantification of γH2AX foci per cell after receipt of 1 Gy X-irradiation. Retinae were left unirradiated or were analyzed at 5–60 min postirradiation. (Left) IF image (maximum intensity projection, MIP) of γH2AX in irradiated photoreceptors. (Scale bar: 5 µm.) (Right) Spontaneous γH2AX foci (fewer than 0.1 per cell) were subtracted. Error bars represent the SD between two retinae with 40 cells each. (D) Quantification and regression analysis of γH2AX foci per cell after various X-ray doses. Retinae were left unirradiated or were analyzed at 15 min after receipt of 5–50 mGy. (Left) IF images (MIP) of γH2AX in unirradiated or irradiated photoreceptors. γH2AX foci were framed with white circles for better visualization. (Scale bars: 5 µm.) (Right) Error bars representing the SD among three retinae with 1,500 cells each (R² = 0.994).

γH2AX Foci in Mouse Photoreceptors After Low X-Ray Doses.

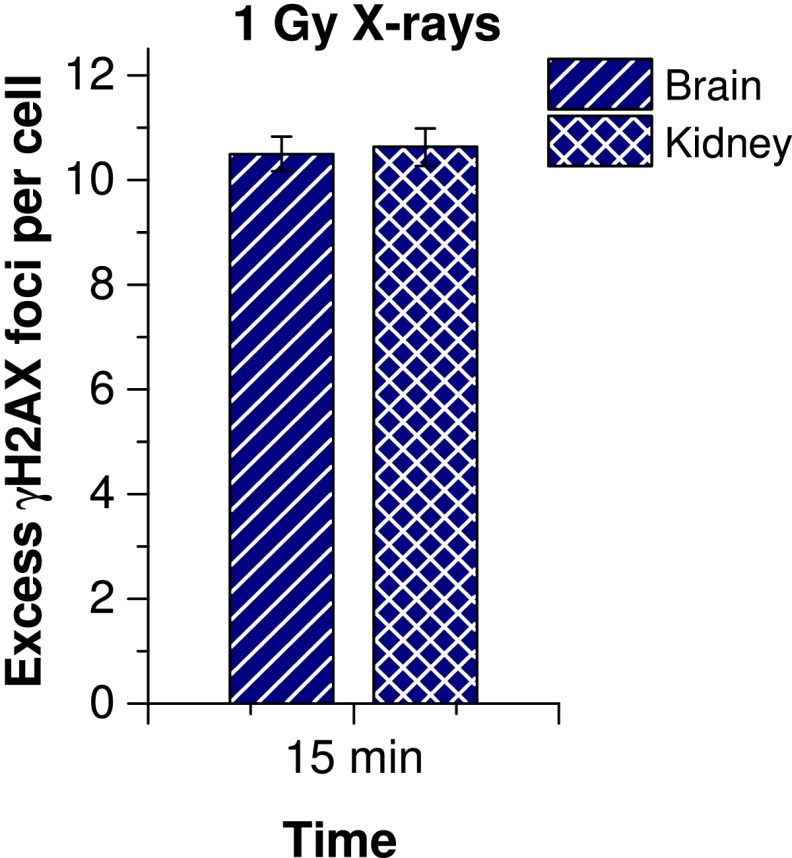
To characterize the formation of γH2AX foci in mouse photoreceptors, we quantified the number of foci per cell at different time points between 5 and 60 min after delivery of 1 Gy of X-irradiation. γH2AX foci were already detected at 5 min and reached their highest value of nine foci per cell at 15 min post-IR before diminishing slightly owing to ongoing repair (Fig. 1C). In all subsequent experiments, we analyzed foci at 15 min post-IR. The maximum number of nine γH2AX foci per photoreceptor is substantially lower than the level of approximately 20 foci per human cell in culture (34). However, other mouse tissues, such as the brain and kidney, with cells of different nuclear architecture and size also exhibit only approximately 10.5 foci per cell, suggesting that the difference with human cells in culture is not a specific phenomenon of photoreceptors (35) (Fig. S1).

Fig. S1.

Quantification of γH2AX foci in mouse brain and kidney tissue at 15 min postirradiation with 1 Gy X-rays. Spontaneous foci of unirradiated brain and kidney tissue (fewer than 0.1 per cell) were subtracted. Error bars represent the SD between two mice with 40 cells each.

Given that radiation doses in the outer part of particle tracks are expected to be on the order of a few tens of mGy, we next characterized the dose–response of γH2AX foci formation after low radiation doses. We exposed mouse photoreceptors to 5–50 mGy of X-rays and quantified foci numbers at 15 min post-IR. We observed a linear correlation between γH2AX foci and dose with an induction rate of 11.8 ± 0.4 foci/cell/Gy (Fig. 1D). This result is in good agreement with the direct measurement at 1 Gy (Fig. 1C), and supports the view that γH2AX foci are induced linearly with dose over a large dosage range. The slight difference between the induction rates obtained at low and high doses might be explained by dosimetric errors and differences in the accuracy of foci counting at low and high doses. In summary, we have characterized the X-ray dose–response using γH2AX foci formation in mouse photoreceptors, and have shown that this tissue represents a biological system well-suited for assessing radiation doses over a substantial dosage range.

γH2AX Foci in Mouse Photoreceptors After Ion Traversals.

When a single high-energy particle penetrates tissue, approximately one-half of the energy is deposited in the inner part of the track close to the particle path (within a few µm), whereas the other half is spread out by δ-electrons over a larger distance in the outer part of the track (4, 14, 36). Thus, a few cells directly hit by the ion receive a high dose, whereas numerous cells surrounding the particle path receive considerably lower doses (typically on the order of a few mGy).

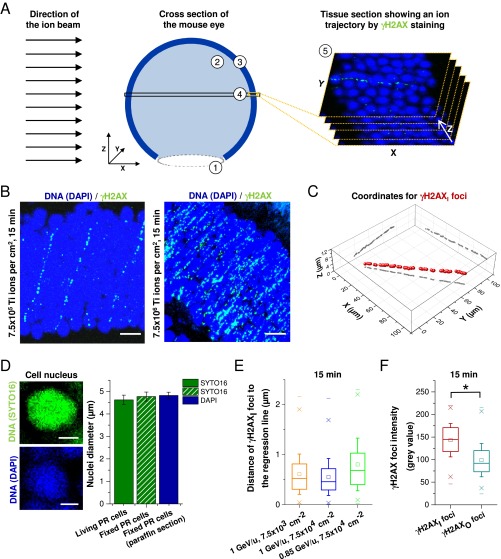
To investigate the dose deposition by δ-electrons in a biological system, we exposed mouse retinae to high-energy Ti ions at very low fluences of 7.5 × 10³ and 7.5 × 10⁴ ions/cm². Owing to the dense packaging of photoreceptor cells, single ion traversals could be readily visualized by a chain of relatively big and bright γH2AX foci over numerous cell nuclei (Fig. 2A; Fig. S2A shows the geometry of an imaged tissue section relative to the ion beam). In addition, smaller and less intense γH2AX foci were observed in the cells surrounding the particle trajectory, representing isolated DSBs induced by δ-electrons (Fig. 2A). The average number of ion traversals visible on a single microscopic image of approximately 100 × 100 × 12 µm³ was less than one after irradiation with 7.5 × 10³ and 7.5 × 10⁴ ions/cm² and increased proportionally with higher fluences (Fig. S2B).

Fig. 2.

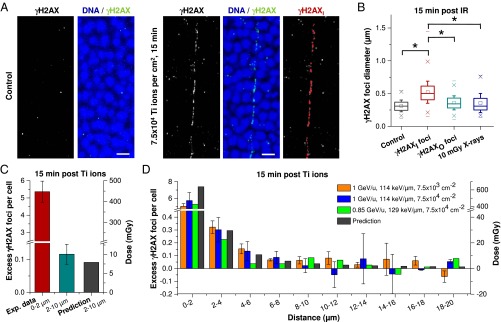
γH2AX foci in mouse photoreceptors after single high LET ion traversals. (A) IF images (MIP) of γH2AX in unirradiated and Ti ion-irradiated mouse photoreceptors. DNA was counterstained with DAPI. (Scale bars: 5 µm.) (Right) γH2AX foci along the trajectory (γH2AX_I foci) that were selected by eye for the calculation of the 3D regression line are marked in red. (B) Analysis of γH2AX foci diameters. Here 400 γH2AX_I and 400 γH2AX_O foci from four retinae exposed to 1 GeV/u Ti ions with 7.5 × 10³ or 7.5 × 10⁴ ions per cm² were analyzed and compared with 100 γH2AX foci from three retinae after 10 mGy X-rays and 100 γH2AX foci from three unirradiated retinae. The whiskers of the box (25–75% of the data points) represent the SD between the measured diameters. The ranges between the “x” below and the “x” above the boxes encompass 98% of the data. Statistical significance was tested by ANOVA; *P < 0.05. (C and D) Quantification of γH2AX foci per cell in different size categories. γH2AX foci and cells were enumerated in categories based on their distance to the trajectory. The number of foci per cell from images without visible ion tracks was subtracted (between 0.1 and 0.3 foci per cell, depending on particle fluence) to provide the dose contribution from a single Ti ion. Between 13 and 15 tracks with approximately 100 cells (for foci within 0–2 µm in C), 1,000 cells (for foci within 2–10 µm in C), or 2,500 cells (for foci at 0–20 µm in D) from one retina (for 0.85 GeV/u Ti ions) or two retinae (for 1 GeV/u Ti ions) were analyzed for each irradiation condition. Error bars represent the SD between five (C) or two (D) retinae. The predicted dose decline was calculated for 0.85 GeV/u Ti ions using the volume integral of the formula for the radial dose distribution (14) and transformed in foci per cell using the X-ray calibration curve (Fig. 1D).

Fig. S2.

γH2AX foci in mouse photoreceptors after high-LET ion traversals. (A) Schematic showing the geometry of an imaged tissue section relative to the ion beam. Numbers within the scheme indicate the subcompartments of the mouse eye, including the lens (1), the vitreous body (2), and the retina containing the photoreceptor cells (3). After the fixation and dehydration process, the eye was embedded in paraffin and tissue sections roughly parallel to the ion beam were obtained (4). This procedure enabled the detection of ion trajectories perpendicular to the imaged Z-stack direction (5). (B) IF images (MIP) of γH2AX in mouse photoreceptors at 15 min postirradiation with high fluences of Ti ions (1 GeV/u). (Scale bar: 5 µm.) (C) Three-dimensional view of the γH2AX_I foci coordinates that are indicated in red in the image shown in Fig. 2A, Right. XY, XZ, and YZ projections of the γH2AX_I foci coordinates are shown in gray for visualization of the 3D arrangement. (D) Quantification of the nuclear diameters of photoreceptors. Freshly isolated retinae were incubated with SYTO16, sliced like a trefoil, and placed on coverslips for image acquisition. Retinae were then fixed, and the DNA was counterstained with DAPI. This control experiment shows that the cellular dimensions are the same at the time of irradiation (i.e., in living tissue) and the time of analysis (i.e., in tissue after the fixation, cutting, and staining procedure). (Left) Fluorescence images of mouse photoreceptors. (Scale bar: 2 µm.) (Right) Nuclear diameters measured by the SYTO16 signal in living or by the SYTO16 and DAPI signals in fixed photoreceptors (PR). Error bars represent the SD between two retinae with 100 cells. (E) Distance analysis of γH2AX_I foci to the 3D regression line. Between 300 and 500 foci from 13–15 tracks of 1 retina (for 0.85 GeV/u Ti ions) or two retinae (for 1 GeV/u Ti ions) were analyzed. (F) Analysis of γH2AX foci intensities. Each γH2AX focus intensity was determined from the average pixel intensity inside the area defining the focus. Here 400 γH2AX_I foci and 400 γH2AX_O foci from foci retinae exposed to 1 GeV/u Ti ions with 7.5 × 10³ or 7.5 × 10⁴ ions per cm² were analyzed. The whiskers of the box (25–75% of the data points) represent the SD between the measured distances. The ranges between the “x” below and the “x” above the boxes encompass 98% of the data. Statistical significance was tested by ANOVA; *P < 0.05.

To reconstruct the trajectory of the particle in the tissue, we approximated the location of each focus by its center and performed a 3D regression analysis of the chain of foci representing the inner part of the track (hereinafter termed γH2AX_I; indicated in red in Fig. 2A, Right, and displayed in 3D in Fig. S2C). We then calculated the distance of all γH2AX foci in the outer region of the track (γH2AX_O) to the approximated ion trajectory. Because irradiation occurred in living tissue, whereas the analysis of foci position was performed in tissue after fixation, cutting, and staining, we performed control experiments to verify that cell dimensions were not altered by this procedure (Fig. S2D).

The first step of our analysis involved distinguishing the γH2AX_I foci in the inner part of the track from the γH2AX_O foci in the surrounding area. For this analysis, we separated γH2AX foci located <2 µm from the regression line from foci located farther away. Approximately 99% of the γH2AX_I foci that were identified by eye to represent the inner part were positioned within 2 µm (Fig. S2E). We then measured the size and intensity of each focus and confirmed our visual impression that γH2AX_I foci along the trajectory were on average larger (Fig. 2B) and brighter (Fig. S2F) than γH2AX_O foci in the surrounding region (diameter, ∼0.5 µm vs. ∼0.3 µm; mean signal intensity, 142 vs. 99). Interestingly, the γH2AX_O foci were similar in size to X-ray–induced foci, consistent with the notion that foci after X-irradiation as well as foci in the outer part of the particle track are induced by sparsely ionizing δ-electrons.

We next determined the number of foci per cell below and above the 2 µm limit. For this, we approximated the location of each cell by its center. Thus, a cell with its center inside the 2 µm border was considered to fall within this region even though it partly protruded beyond the 2 µm limit, whereas a cell with its center outside the 2 µm border was not considered for the 0–2 µm category even if it protruded inside this area. We obtained an average of 5.4 γH2AX foci/cell inside the 2-µm border and 0.12 γH2AX foci/cell at 2–10 µm (Fig. 2C).

Because both γH2AX_O and X-ray–induced γH2AX foci originate from secondary electrons, we converted the number of 0.12 γH2AX foci/cell into a dose of 10 mGy by using the induction rate of 11.8 foci/cell per Gy obtained in Fig. 1D. This dose of 10 mGy, which was evaluated based solely on biological measurements, is in excellent agreement with a theoretical track structure model that predicts an average dose of approximately 8 mGy at 2–10 µm around Ti ion trajectories (14). These results provide proof of principle that our biological dosimetry approach yields meaningful dose estimates in the low-dose range.

In the second step of our analysis, we investigated the radial decline in dose with increasing lateral distance from the particle path. We extended the analysis up to a distance of 20 µm and assessed the number of γH2AX foci per cell in 10 categories with a size of 2 µm each. We observed a decrease in γH2AX foci per cell in the first four categories up to 8 µm, which is in reasonable agreement with the theoretically predicted decline with increasing distance from the approximated trajectory (Fig. 2D). However, the agreement between γH2AX foci and predicted X-ray dose is less convincing in the first category (0–2 µm) where the measured foci arise from the densely ionized inner part of the particle tracks. Moreover, γH2AX foci numbers per cell varied considerably for categories larger than 8 µm, precluding a reliable analysis of the dose profile above this distance. Thus, despite the apparently good correlation between measured foci and predicted doses, this agreement was essentially limited to three size categories.

Radial and Longitudinal Distance Analysis of γH2AX Foci.

To further refine the observed decline of γH2AX foci with increasing distance from the particle trajectory, we enhanced the statistical power in the categories further away from the trajectory where low γH2AX foci numbers resulted in high variations. The enhancement was achieved by defining categories that increase in width with increasing distance from the trajectory. We applied a logarithmic scale in which the distance between 0.1 and 20 µm is divided into 36 categories, with the width of each category increasing proportionally to the distance from the trajectory. This procedure reduces the data scatter in the larger categories, but has limitations for the smaller categories close to the particle trajectory (below approximately 0.5 µm), because the number of cells in these categories is very small. Thus, we introduced a further step in the analysis and reconstructed the analyzed tissue volume using small voxels with a dimension of 0.8 × 0.8 × 0.645 µm³ (Fig. S3A).

Fig. S3.

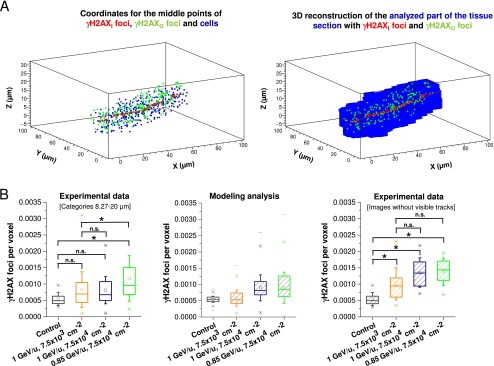
Radial and longitudinal analysis of γH2AX foci induction after particle irradiation. (A) Reconstruction of the analyzed part of the tissue section. (Left) Coordinates for the middle points of all γH2AX_I (red) and γH2AX_O foci (green) and all nuclei (blue) inserted into a 3D-histogram. (Right) The analyzed part of the tissue section (shown in blue) reconstructed from the middle points of the cells at a voxel resolution of 0.8 × 0.8 × 0.645 µm³. (B) Analysis of the fluence dependency of the background dose. (Left) The last six distance categories of Fig. 3A (corresponding to foci with a distance to the ion trajectory between 8.27 and 20 µm) were pooled for each irradiation condition and compared with the distribution of spontaneous foci per voxel. This latter value was obtained from images of unirradiated control retinae from the experiments shown in Fig. 3A by transforming foci per cell into foci per voxel using the conversion factor of 233.4 voxels/cell. All three irradiation conditions show higher foci levels than the control sample, although the differences are statistically significant only for Ti ions with 0.85 GeV/u. Moreover, only one of the two higher fluences shows increased foci levels compared with the low fluence condition. (Center) Modeling analysis for the expected distribution of foci per voxel for the three irradiation conditions in the left panel. The unirradiated control distribution of foci per voxel considered a Poissonian distribution of the counted foci. The distribution of the irradiated samples considered two convoluted distributions, a Poissonian distribution for the foci and a “long-tailed” distribution for the doses in the distance categories used for foci counting. This procedure essentially takes the limited experimental dataset in the left panel into account. Of note, the expected variations in foci level for the different fluences are in reasonable agreement with the experimental data. (Right) To enhance the statistical power of the fluence-dependent analysis of the background dose, images from the three irradiation conditions that did not contain a visible ion trajectory were analyzed. These images provide larger areas and therefore more cells for the analysis of the background dose than the last six categories in the left panel. γH2AX foci were enumerated by eye in at least nine images with ∼2,000 cells from one retina (for 0.85 GeV/u) or two retinae (for 1 GeV/u) for each of the three irradiation conditions. The number of foci per cell was transformed into foci per voxel to allow the comparison with the data in the left panel. The results show a clear dependency of the background dose on particle fluence, although the difference between the high and low fluences was smaller than (but not inconsistent with) the expected value of 10. The whiskers of the box (25–75% of the data points) represent the SD between the foci numbers for each irradiation condition. The ranges between the “x” below and the “x” above the boxes encompass 98% of the data. Statistical significance was tested by ANOVA; *P < 0.05; n.s., not significant.

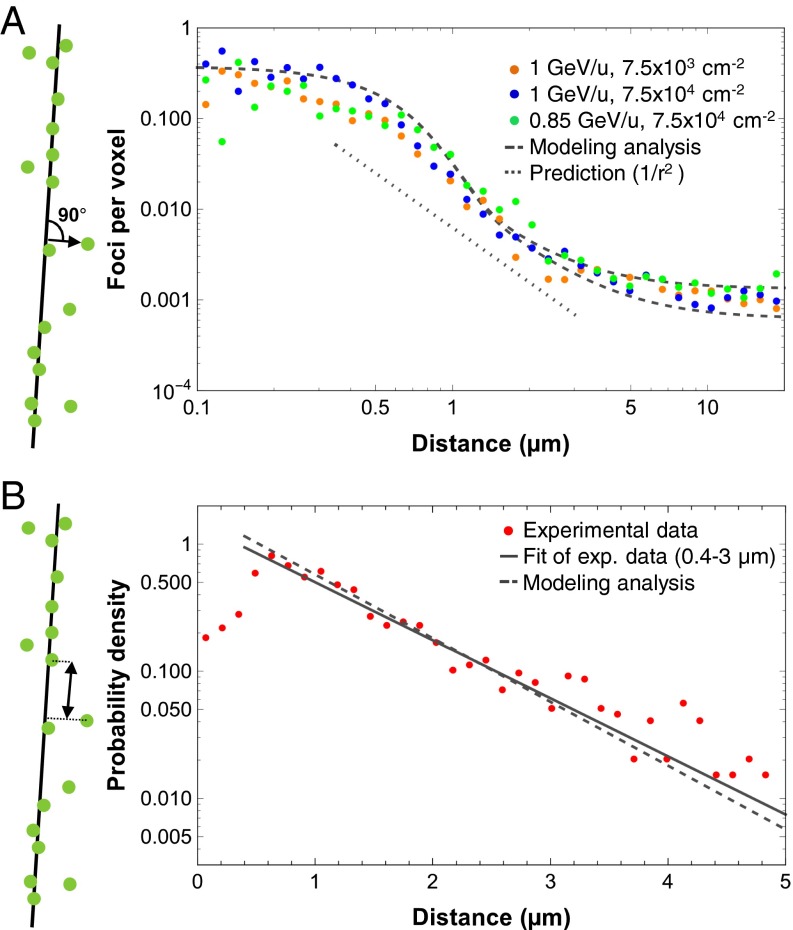
Using the above-described procedures, we determined the number of γH2AX foci per voxel as a function of the logarithm of the distance to the approximated particle trajectory. We also used a logarithmic scale for the vertical axis, given that a double-logarithmic plot allows visualization of the expected 1/r² dependency as a linear function. For the three independent experiments from Fig. 2D, we obtained a plateau for γH2AX foci per voxel in the inner region up to a distance of approximately 0.4 µm, followed by a decrease slightly steeper than a 1/r² dependency between 0.4 and 4 µm and by another plateau region above 4 µm (Fig. 3A). Although the decreasing foci numbers in the middle region roughly follow the theoretical prediction, the plateaus in the smaller and larger categories reflect expected experimental restrictions. The resolution of the focus structure with a typical size of roughly 0.5 µm and slight foci movement processes (37, 38) (Fig. S2E) might contribute to the deviation from the 1/r² dependency below 0.4 µm, and also might give rise to a slightly steeper decrease than expected above 0.4 µm. Moreover, dose depositions from neighboring particles below or above the analyzed tissue slices represent a background dose and contribute to foci numbers in larger categories, which can explain the deviation from the 1/r² dependency above 4 µm.

Fig. 3.

Radial and longitudinal distance analysis of γH2AX foci. (A) Radial distance analysis of γH2AX foci perpendicular to the trajectory. The analyzed part of the tissue was reconstructed using approximately 233 voxels per cell, and the number of γH2AX foci per voxel was determined from the data presented in Fig. 2D. The lower and upper dashed curves represent the results of simulations based on LEM for fluences of 7.5 × 10³ and 7.5 × 10⁴ ions/cm², respectively. The spontaneous number of 0.00054 γH2AX foci per voxel obtained from nonirradiated retinae of the same experiments was added to the simulated curves to allow comparison with the experimental results. The dotted curve representing the theoretical 1/r² dependency is down-shifted for clarity. (B) Longitudinal distance analysis of γH2AX foci along the trajectory. For γH2AX foci closer than 2 µm to the approximated trajectory, the longitudinal distances between next neighboring foci and the resulting probability densities of foci distances were calculated. Data for the three irradiation conditions were pooled. An exponential fit was performed to obtain the average distance between the observed foci (solid line), which is compared with results of a simulation based on LEM (for 0.85 GeV/u Ti ions; dashed line).

We next compared our experimental data with a theoretical model for high-LET radiation that is based on the dose deposition within particle tracks and takes the restrictions of the experimental system into account. We exploited the LEM (14) and considered the track structure description of the local doses deposited around a particle trajectory, as well as the enhanced DSB production for high doses (i.e., close to the trajectory) from the induction of two single-strand breaks from two different δ-electrons. We found that the latter effect played only a marginal role in the particle energies used, however, and had only a slight affect on the simulated focus yields in the inner part of the track. Fig. 3A shows that the simulation reflects the experimental foci distributions. In particular, the dose decrease for intermediate distances was well reproduced and slightly steeper than the expected 1/r² dependency. For small distances (< ∼0.4 µm), the number of foci was slightly higher in the simulation compared with the experiments. For large distances (> ∼4 µm), the data from the three different experiments lie within the predictions for the two different ion fluences used in these experiments.

To evaluate the fluence dependency of the background dose with better statistics, we also analyzed images from irradiated retinae without visible particle tracks. Of note, the two high fluences provided a substantially higher background dose than the low fluence (Fig. S3B).

Along with the shape of the radial dose distribution, the LET is another characteristic parameter of the track structure, describing the amount of energy deposited along the ion track. Thus, we also determined the distance distribution of foci along the particle path, hereinafter called the longitudinal distance distribution. We considered all foci falling within a radial distance of 2 µm to the approximated ion trajectory and calculated the distance of the next neighboring foci by transforming their spatial coordinates to their position along the track. The distribution of distances decreased essentially exponentially above foci distances of 0.4 µm (i.e., along a straight line in a semilogarithmic diagram where the distance between 0 and 5 µm is divided into 35 categories of equal width), indicating that foci induction along the track is random and follows Poissonian statistics (Fig. 3B). This observation confirms a previous study (39) and justifies the random induction distribution of lesions along ion tracks used in almost all model approaches. Deviations from the exponential decrease below 0.4 µm might be explained by limitations in the resolution of foci structure, such that nearby DSBs are monitored as a single γH2AX focus.

DSB clustering in the inner part of the track is also supported by the difference between the simulation and the experimental data describing the radial dose distribution shown in Fig. 3A and by our analysis of foci sizes in Fig. 2B and foci intensities in Fig. S2F. This notion is in line with the observed saturation of foci numbers along tracks of high- and ultrahigh-LET particles (40–42). The slope of the solid curve, which reflects the average distance between observed foci, was calculated as 0.95 µm by a fit of the data between 0.4 and 3 µm. We restricted the fit to 3 µm because the presence of intercellular space might lead to a slight overrepresentation of large foci distances. Similar to the analysis of the radial dose distribution, we modeled the longitudinal distance distribution by implementing the condition that foci closer than 0.4 µm cannot be resolved owing to clustering (Fig. 3B). Using the track structure model of LEM, we obtained an average distance of 0.87 µm between the next neighboring foci, which is in reasonable agreement with the experimentally determined value of 0.95 µm.

Conclusions

Charged particles are generally more effective per unit dose than X-rays in inducing early and late biological effects. This increased effectiveness is exploited in cancer therapy against radioresistant tumors, but carries a higher risk for normal tissues exposed to α-particles on earth or protons and heavy ions during space travel. The ultimate reason for this high effectiveness is the spatial distribution of the induced DNA damage. For many decades, biophysical models were built on track structure models to predict increased effectiveness, yet a direct biological benchmark of these models was hitherto lacking. We applied a biological approach to assess the spatial DNA lesion and dose distribution of single charged particles. Whereas all previous studies used 2D cell culture systems, our biodosimetric study uses the mouse retina as a model tissue and uses 3D microscopic detection of DNA lesions (foci representing DSBs or more complex lesions) that arise in the nuclei of retina cells after irradiation. Calibration studies with X-rays showed that these lesions are induced linearly with dose over a large dosage range, allowing the transformation between the lesion distribution and the corresponding dose distribution. The biologically obtained distributions are in excellent agreement with results from the LEM approach that was carried out independently without any fitting parameters.

Our measurements reveal that cells hit directly by single Ti ions form a chain of foci along their particle trajectory that corresponds to an average dose in the cells of ∼0.5 Gy. In contrast, neighboring cells not hit directly by primary particles but exposed to far- reaching secondary electrons (δ-electrons) show much lower dose depositions, on the order of a few mGy. Strikingly, we were able to assess the radial dose distribution of single particle tracks with sub-micrometer resolution and could confirm the 1/r² dependency of the dose deposition by δ-electrons, which hitherto has been determined only with physical approaches in inorganic material, usually in gases. Moreover, the biological measurements indicate the presence of a background dose at larger distances from primary particles that arises as a result of additive dose contributions from several independent particles.

Along with determining the lateral dose distribution, we were able to assess the induction of foci along the track of single Ti ions. We have shown that this longitudinal energy deposition follows Poissonian statistics, indicating that the lesions are induced independently. This analysis validates the random distribution of lesions induced along ion tracks, an assumption that has been used in almost every model approach but until now has not been clearly verified with a biological model system. Collectively, our results contribute to benchmark the track structure model adopted in the LEM and in LEM-based charged particle treatment planning software. Finally, our comparison of the biological measurements and the theoretical predictions revealed a slight underrepresentation of foci induction close to the inner part of the particle track, which is consistent with the notion that several nearby DSBs in this high-dose region can form a single, microscopically detectable focus. Such DSB clustering was previously observed by others (40, 43–46) and is also evident from our analysis of foci sizes and intensities showing that foci in the inner part of the particle track were on average larger and brighter than foci in the outer part of the track.

Cells hit directly by the track core can have a low probability of survival, but the tissue exposed in the penumbra will almost certainly survive with little damage. Because the extension of the penumbra increases with particle velocity, tissues exposed to very high-energy ions, such as those in space or used in therapy, will experience hotspots of high doses and large volumes with low dose exposure. Controversy surrounding the effects of low doses persists (2, 47, 48), but our results support the view that every exposure to charged particles should be considered a 3D entanglement of high-dose and low-dose DNA damage induction in tissues.

Materials and Methods

All animal experiments were approved by the Regional Board of Darmstadt. Details of the preparation, irradiation, and immunostaining of retina explants; image acquisition and evaluation; and modeling analysis are provided in SI Materials and Methods.

Preparation of Retina Explants.

After the mice were killed, the eyes were removed, and the retinae together with lenses and vitreous bodies were isolated and cultured in medium before irradiation.

Irradiation.

Low-LET irradiation was performed with an X-ray machine at two different settings. High-LET Ti ion irradiation was performed at a synchrotron accelerator of the GSI.

SI Materials and Methods

Preparation and Culturing of Mouse Retina Explants.

Institutional and national guidelines for the care and use of laboratory animals were followed. The eyes were removed after the killing of adult C57BL/6 mice; the retinae together with the lenses and the vitreous bodies were isolated by using a binocular and cultured in medium [DMEM complemented with 10% (vol/vol) FCS, 1% l-glutamine, 1% nonessential amino acids, 100 U/mL penicillin, and 0.1 mg/mL streptomycin] at 37 °C and 5% CO₂ for 30–60 min before irradiation. For the analysis of kidney and brain tissue, mice were irradiated, and organs were removed at 15 min after irradiation.

Irradiation of Mouse Retina Explants with Photons and Ti Ions.

Low-LET irradiation was performed with an X-ray machine (Titan Isovolt 160; GE Healthcare) at 90 kVp, 6 mA, and a dose rate of 83.6 mGy/min (for doses up to 50 mGy) or at 135 kVp, 19 mA, and a dose rate of 1.85 Gy/min (for doses of 1 Gy). High-LET Ti ion irradiation was performed at the SIS18 ring accelerator at the GSI, Darmstadt, Germany. The energies of the Ti ions were 0.85 GeV/u with an LET of 129 keV/µm and 1 GeV/u with an LET of 114 keV/µm. Three retinae each were X-irradiated with 5, 10, 20, 50 or 1,000 mGy. One retina was irradiated with 7.5 × 10⁴ Ti ions/cm² (0.85 GeV/u), two retinae were irradiated with 7.5 × 10³ Ti ions/cm² (1 GeV/u), and two retinae were irradiated with 7.5 × 10⁴ Ti ions/cm² (1 GeV/u).

Fixation and Immunostaining of Tissues.

Tissues were fixed in 4% (vol/vol) neutral buffered formalin for 16 h, dehydrated (with increasing ethanol concentrations followed by xylene treatment), embedded in paraffin, and sectioned at a thickness of 4 µm roughly parallel to the direction of the ion beam (as shown schematically in Fig. S2A). Sections were then dewaxed (using xylene), rehydrated (with decreasing ethanol concentrations), and incubated in citrate buffer (target retrieval solution; Dako) at 99 °C for 1 h. The dehydration procedure reduced the thickness of the tissues, but rehydration reversed this effect, to provide sections with a thickness of ∼12 µm. Control experiments showed that cell dimensions are not altered by this procedure (Fig. S2D). After cooling to room temperature, sections were washed with PBS and incubated with anti-Lamin B antibody (goat; Santa Cruz Biotechnology) at 1:200, with anti-H3K4me3 antibody (rabbit; Cell Signaling Technology) at 1:500, or with anti-γH2AX antibody (mouse; Millipore) at 1:400 in PBS containing 0.2% Triton X100 for 5 h at 37 °C. Sections were washed three times for 10 min each with 0.1% Tween 20 in PBS and then stored overnight in PBS at 4 °C. The next day, sections were incubated with chicken anti-goat, goat anti-rabbit, or goat anti-mouse antibody (Alexa Fluor 488 or 594; Invitrogen) at 1:600 in PBS containing 0.2% Triton X100 for 3 h at room temperature, then washed three times with 0.1% Tween 20 in PBS, incubated with DAPI (0.4 µg/mL), washed again with PBS, and finally mounted with VECTASHIELD mounting medium (Vector Laboratories).

Image Acquisition.

Typically three or four images with a size of 100 × 100 µm² were captured for the analysis of approximately 1,500 cells from unirradiated or X-irradiated retinae. For the Ti ion experiments, one image per track was captured, which showed a single chain of γH2AX foci and no indication of further ion traversals. In addition, five images per irradiated retina without any visible Ti ion tracks were acquired. Although the cells on these images were not located close to any ion track, they were expected to receive dose contributions from far-reaching δ-electrons from all Ti ions traversing the sample.

Z-stacks were obtained with a confocal laser scanning microscope (Leica TCS SP5 II) using a 63× HCX PL APO lambda blue immersion objective (NA 1.4) and a pixel resolution of ∼50 × 50 × 210 nm³ after X-irradiation and 50 × 50 × 130 nm³ after Ti ion exposure. The oversampled pixel resolution was chosen according to the SVI Nyquist calculator (Scientific Volume Imaging). The pinhole was set to 1 Airy unit, and the laser power was set to 6% for the 405-nm diode, to 8% for the 488-nm argon laser (tube current set to 15%) and to 10% for the 561-nm diode-pumped solid-state laser.

Assessment of Foci and Cell Coordinates and Diameters, and Foci Intensities.

For X-irradiated and Ti ion-exposed retinae without any visible trajectory, foci and cell numbers were assessed by eye. For images showing an ion track, the X and Y coordinates for the foci and cells (up to 20 µm around the trajectory) were obtained by selecting the middle points of their fluorescent signal; that is, if the signal extended from pixel X_i to pixel X_j, the coordinate X_(i+j)/2 was taken to represent the focus or the cell. The Z coordinates were obtained accordingly by selecting the middle Z-planes of the foci and cell signals (using ImageJ; National Institutes of Health). The determination of whether a γH2AX focus was located in the inner (γH2AX_I) or outer part of the track (γH2AX_O) was made on an arbitrary basis by eye. The distance analysis for each γH2AX_I/O focus was performed in 3D. After 3D regression analysis of the γH2AX_I foci representing the ion trajectory, lateral distances to the regression line were determined for all foci and cells (see below). Here the Z-distance was corrected for the refractive index mismatch with a correction factor of 0.9474.

For the analysis of foci and cell diameters and foci intensities, the middle Z-plane of each focus and cell was selected, the foci and cell boundaries were visually approximated, and the diameters and mean pixel intensities were obtained (ImageJ).

Principal Component and Distance Analysis.

The coordinates for all γH2AX_I/O foci were transformed such that the origin of the new coordinate system (X', Y', Z') was located in the center of the dataset representing the γH2AX_I foci. A regression line for the γH2AX_I foci was calculated using principal component analysis (OriginPro 9.0; OriginLab). In brief, based on the coordinates of γH2AX_I foci, a 3 × 3 covariance matrix and its three eigenvalues were calculated. The eigenvector corresponding to the highest eigenvalue provided the best fit to the dataset and was used for further calculations.

For determining vertical distances to the regression line, a plane orthogonal to the regression line and containing the focus or cell coordinate was defined. The resulting intersection point of the line and the plane identified the point on the line with the minimal lateral distance to the focus or cell coordinate. Afterward the pixel distance between the intersection point and the focus or cells was calculated and converted into micrometers.

Routine for the Reconstruction of the Cell Volume.

Limitations arise during the calculation of foci per cell at short distances from the trajectory, because cells are reduced to point-like objects (the coordinates) and assigned to only one distance category despite their finite size. To reduce these limitations, all focus and cell coordinates were inserted into a 3D histogram with voxel size of 0.8 × 0.8 × 0.645 µm³, and the analyzed part of the tissue section was reconstructed (Fig. S3A). This reconstruction involved the identification of all voxels containing a cell coordinate and the subsequent filling of the surrounding voxels until the entire cellular and intercellular space was filled. This procedure assigned an average number of 233.4 voxels to a cell with its intercellular space.

Modeling Analysis of the Radial and Longitudinal Dose Distribution Within the Ion Track.

The LEM is usually used to simulate the dose–response of cells and tissue after high-LET irradiation. Here we adopted the model for the description of foci induction patterns. Chromatin is assumed to be homogeneously distributed in the nucleus, which is simulated as a cylinder with its main axis parallel to the ion direction. According to the experimental information, the nucleus is described as a cylinder with a radius of 2.5 µm and a total volume of 65 µm³. The amorphous track structure model of LEM assumes that the energy loss of a particle, parameterized by its LET, decreases laterally with a continuous 1/r² characteristic up to the maximum range of the δ-electrons, whereas the dose profile in the central part is flat up to a threshold radius. The simulation was performed for the two fluences of 7.5 × 10³ and 7.5 × 10⁴ Ti ions per cm² (exemplarily for 0.85 GeV/u ions).

To account for the special constraints of our experimental setup, we empirically applied a Gaussian convolution of the modeled dose distribution to correct for the uncertainties in foci position in the inner region that result from the finite foci sizes, the imaging resolution, chromatin movement, and distortions during tissue processing. For this, we chose a convolution of the Gaussian function with a width of 0.8 µm, in the order of the focus size measured in the inner track. To reconstruct the plateau for very large distances from the inner part of the track, we accounted for the measured spontaneous foci number obtained in control samples and furthermore modeled the contributions of surrounding tracks to the foci distribution with a photon-like background dose, which is homogeneously distributed in the entire volume and reflects the sum of overlapping penumbrae of many tracks. Finally, we converted the dose distribution into a distribution of foci per voxel by considering the experimentally determined DSB yield of 11.8 foci/cell/Gy obtained in the photon experiments and the corresponding ratio between voxels and cells of 233.4.

To predict the longitudinal foci distribution within a corridor of 2 µm around the approximated trajectory of a 0.85 GeV/u Ti ion, we calculated the stored energy and, from thar value, the average dose in the 2-µm corridor around the track length of 1 µm. The number of induced foci in this corridor was obtained from the foci yield of 11.8/cell/Gy multiplied by the average dose in the corridor and by the ratio of the corridor volume to the cell volume. This approach led to a mean focus distance of 0.58 µm. However, considering that the space is not entirely filled with cell nuclei, but also includes cytoplasm and extracellular medium, the fraction of the volume covered by nuclei during the reconstruction process was determined to be 67%, which corrects the average expected distance to 0.87 µm.