Significance
Origami, the ancient art of folding paper, has recently emerged as a method for creating deployable and reconfigurable engineering systems. These systems tend to be flexible because the thin sheets bend and twist easily. We introduce a new method of assembling origami into coupled tubes that can increase the origami stiffness by two orders of magnitude. The new assemblages can deploy through a single flexible motion, but they are substantially stiffer for any other type of bending or twisting movement. This versatility can be used for deployable structures in robotics, aerospace, and architecture. On a smaller scale, assembling thin sheets into these tubular assemblages can create metamaterials that can be deployed, stiffened, and tuned.
Keywords: stiff deployable structures, origami tubes, rigid origami, thin sheet assemblages, reconfigurable metamaterials
Abstract
Thin sheets have long been known to experience an increase in stiffness when they are bent, buckled, or assembled into smaller interlocking structures. We introduce a unique orientation for coupling rigidly foldable origami tubes in a “zipper” fashion that substantially increases the system stiffness and permits only one flexible deformation mode through which the structure can deploy. The flexible deployment of the tubular structures is permitted by localized bending of the origami along prescribed fold lines. All other deformation modes, such as global bending and twisting of the structural system, are substantially stiffer because the tubular assemblages are overconstrained and the thin sheets become engaged in tension and compression. The zipper-coupled tubes yield an unusually large eigenvalue bandgap that represents the unique difference in stiffness between deformation modes. Furthermore, we couple compatible origami tubes into a variety of cellular assemblages that can enhance mechanical characteristics and geometric versatility, leading to a potential design paradigm for structures and metamaterials that can be deployed, stiffened, and tuned. The enhanced mechanical properties, versatility, and adaptivity of these thin sheet systems can provide practical solutions of varying geometric scales in science and engineering.
Introducing folds into a thin sheet can restrict its boundaries, cause self-interaction, and reduce the effective length for bending and buckling of the material (1–4). These phenomena make thin sheets practical for stiff and lightweight corrugated assemblies (5, 6); however, such systems tend to be static, i.e., functional in only one configuration. For creating dynamic structures, origami has emerged as a practical method in which continuous thin sheet panels (facets) are interconnected by prescribed fold lines (creases). Existing origami patterns and assemblages can easily be deployed; however, they tend to be flexible and need to be braced or locked into a fixed configuration for a high stiffness-to-weight ratio to be achieved (7–10). The zipper-coupled system is different because it is stiff throughout its deployment without having to be locked into a particular configuration.
Origami principles have broad and varied applications, from solar arrays (11) and building façades (12) to robotics (13), mechanisms in stent grafts (14), and DNA-sized boxes (15). The materials and methods used for fabricating, actuating, and assembling these systems can vary greatly with length scale. On the microscale, metallic and polymer films or, more often, layered composites consisting of stiff and flexible materials can be folded by inducing current, heat, or a chemical reaction (16, 17). Large-scale origami structures can be constructed from thickened panels connected by hinges and can be actuated with mechanical forces (11, 18, 19). The kinematic motion, functionality, and mechanical properties of the origami are governed largely by the folding pattern geometry. For example, rigid origami systems are defined as those having a kinematic deformation mode in which movement is concentrated along the fold lines, whereas the panels remain flat (20, 21). Among various rigid folding patterns, the Miura-ori has attracted attention for its folding characteristics (22, 23), elastic stiffness properties beyond rigid folding (24, 25), geometric versatility (26, 27), and intrinsic material-like characteristics (28, 29).
The zipper-coupled tubes introduced here are derived from the Miura-ori pattern and can undergo the same type of rigid kinematic deployment. All other deformations are restrained as they require stretching and shear of the thin sheets. Thus, the structure is light and retains a high stiffness throughout its deployment. It has only one flexible degree of freedom and can be actuated by applying a force at any point (Fig. 1 and Movie S1). To explore unique mechanical properties of the zipper tubes, we introduce concepts of eigenvalue bandgaps and cantilever analyses to the field of origami engineering. Zipper assemblages can be fabricated with a variety of materials and methods. We envision applications of these assemblages will range in size from microscale metamaterials that harness the novel mechanical properties to large-scale deployable systems in engineering and architecture (Movies S2–S4).
Fig. 1.
Deployment and retraction sequence of a zipper-coupled tube system. This origami has only one flexible motion through which it can deform, and thus it is deployed by actuating only on the right end. See Movie S1 for complete simulation.
This paper is organized as follows. First, the Miura-ori pattern is introduced, and the geometries of three fundamental coupling orientations are discussed. Next, we demonstrate how the system stiffness changes as we assemble two sheets into a tube and then two tubes into the unique zipper-coupled tubes. The fundamental coupling orientations are then studied as deployable cantilevers that can carry perpendicular loads. Next, we discuss cellular assemblages, geometric variations, and practical applications that can be created from coupled tubes, and we conclude with some final remarks.
Geometric Definitions
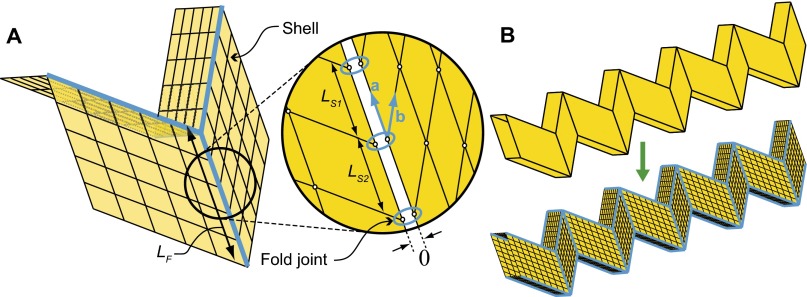
A Miura-ori cell consists of four equivalent panels, defined by a height a, width c, and vertex angle α (Fig. 2A). For our analytical investigation, we use a cell with and as the basis for all structures unless otherwise noted. A sheet is created by repeating this cell times in the X direction (Fig. 2B). We define the configuration of this sheet as a percentage of extension (a percentage of the maximum extended length ). At 0% extension the sheet lies folded on the plane and at 100% extension it lays flat on the plane. The single tube structure (30) is created by combining the single sheet with its mirrored counterpart (Fig. 2C and Movie S5). Previously, Miura-ori sheets and tubes have been coupled (or stacked) to create several different folding assemblages (7, 9, 30, 31). For the zipper orientation of tube coupling, one tube is rotated and connected in a zig-zag (zipper) manner (Fig. 2D and Movie S1). We explore the mechanical properties of this assemblage and compare it with an aligned-coupled system where tubes are only translated (30, 31) and an internally coupled system consisting of two compatible tubes (7) (Fig. 2 E and F). Symmetry in these assemblages permits them to be rigid foldable, meaning that they can fold with no bending of the panels, but only the zipper and aligned systems can reach a flat state when deployed to a 100% extension. The range of extension for internally coupled systems is limited because the internal tube reaches a flat configuration and locks the system in place. Geometric parameters of the compatible internal tube , , and , are discussed in SI Text, section S5.
Fig. 2.
Geometry and assembly of origami tube structures. (A) Miura-ori pattern defined with , and folded into a three-dimensional Miura-ori cell. This cell is used as the basis for all structures unless otherwise noted. (B) A Miura-ori sheet in four configurations defined as a percentage of extension. (C) Two mirror-image sheets shown at 70% extension and combined into a rigid, flat foldable tube. (D) Zipper-coupled tubes. A tube is translated and rotated in the plane until the opposing faces of the two tubes align. For clarity, a different shade is used for one of the zipper tubes, but both tubes are identical to the definitions in A–C. (E) Aligned-coupled tubes. A tube is translated in the plane and coupled with the tube in the initial configuration. (F) Internally coupled tubes, inspired by ref. 7. External tube is the same as in C, and the internal tube is defined to reach a flat configuration when the external tube is at 80% extension.
Eigenvalue Analyses
To model the stiffness and mass of origami, we use a bar and hinge approach that provides insight into the structural behavior of the origami assemblages. It captures three fundamental physical behaviors: bending along fold lines, bending of initially flat panels, and stretching and shearing of panels (SI Text, section S1 and Fig. S1) (24). The simplicity of the bar and hinge model allows for straightforward implementation and versatility where tubes can be coupled and analyzed as more complex assemblages (see SI Text, sections S2 and S5 and Figs. S2 and S3). The model is made scalable and incorporates thickness (), Young’s modulus (), Poisson’s ratio (), and density () of the material (32). A parameter, , relates fold line bending to panel bending stiffness and can vary greatly, depending on the materials, the fabrication technique, and the actuation process (33–36). Using a sensitivity analysis in SI Text, section S3 and Fig. S4, we show that the value of and other parameters do not affect the qualitative results and conclusions presented in this paper. A finite-element (FE) model, where each panel is discretized with shell elements, is used to verify the results and to study local deformations and stress concentrations in the origami (SI Text, section S4; Fig. 3; and Figs. S5–S7). The bar and hinge model cannot capture all localized effects, but it is significantly faster and provides a sufficiently high level of accuracy for global origami behaviors.
Fig. S1.
Schematics and tests of the bar and hinge model. (A) Schematic of indeterminate bar frame for simulating in-plane panel stretching and shearing. (B) Tensile patch test of bar frame exhibiting isotropic behavior. (C) Shear patch test of bar frame. (D) Schematic orientation of rotational hinge simulating panel bending along the diagonal . (E) FE model used to study bending of thin sheet restrained at edges by orthogonally placed thin sheets. (F) Curvature along the diagonals of the FE model for a small displacement () and a large displacement () case. (G) Schematic of the two rotational hinges used to simulate bending along a prescribed fold line of length . (H) The three components of the bar and hinge model shown on the single tube.
Fig. S2.
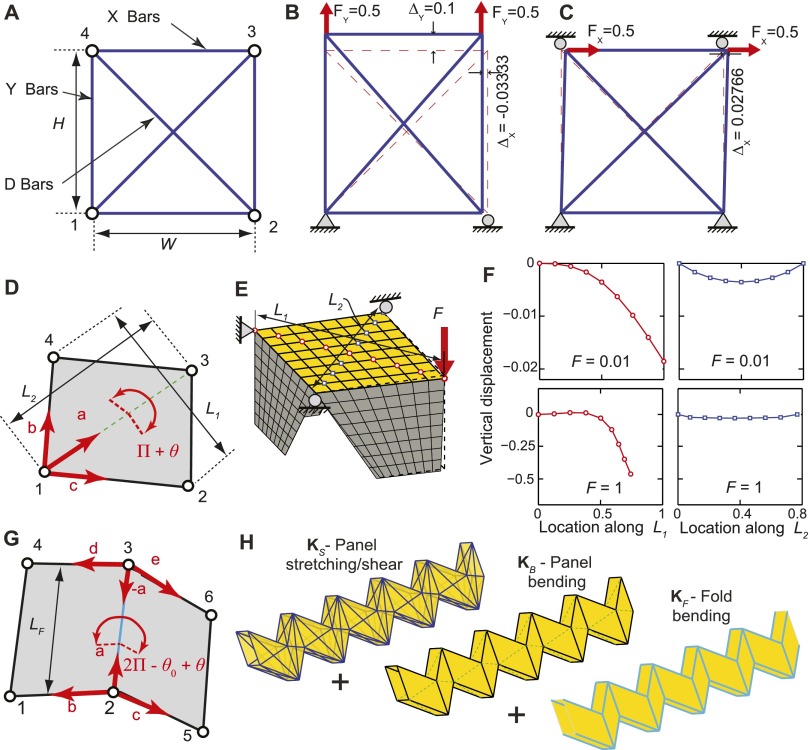
Coupling elements used to connect zipper tubes in the bar and hinge model. (A–C) Configuration of , , and coupling elements, respectively, for a segment of zipper-coupled tubes. The local axes are shown for the leftmost and rightmost panels of A. Only representative coupling elements are shown for the coupling. (D–F) The sensitivity of the system eigenvalues vs. magnitude of each of the coupling coefficients , , and , respectively, when the other coupling coefficients remain at a value of 1.
Fig. S3.
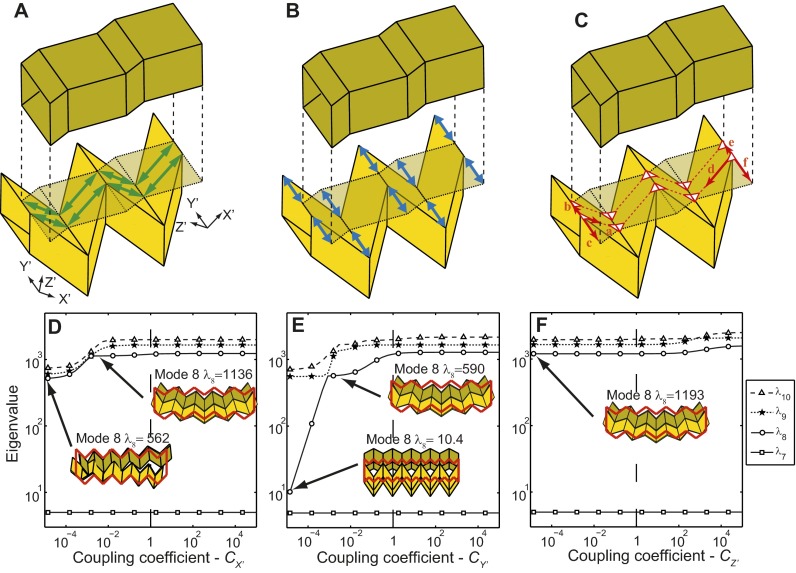
Squeezing deformation of zipper-coupled tubes when the coupling coefficients are reduced to . (A) Top view of only the deformed bottom tube with an outline of its initial configuration. The x marks indicate the panel-edge center points on the side of the tube that is attached. (B) Only the deformed top tube. (C) The squeezing deformation of the zipper-coupled assembly with low coupling. (D) Change in the distance between the panel-edge center points of the two tubes. Initial distance before deformation is 0.7 units for all locations; the squeezing results in separation on the left side and closing on the right side of the coupled tubes.
Fig. S4.
Eigenvalue sensitivity for a single tube and the zipper-coupled tubes. (A–D) Scaling of with respect to E, ρ, t, and . (E–H) Scaling of for the same cases. These relations directly govern the scaling sensitivity of the bandgap.
Fig. 3.
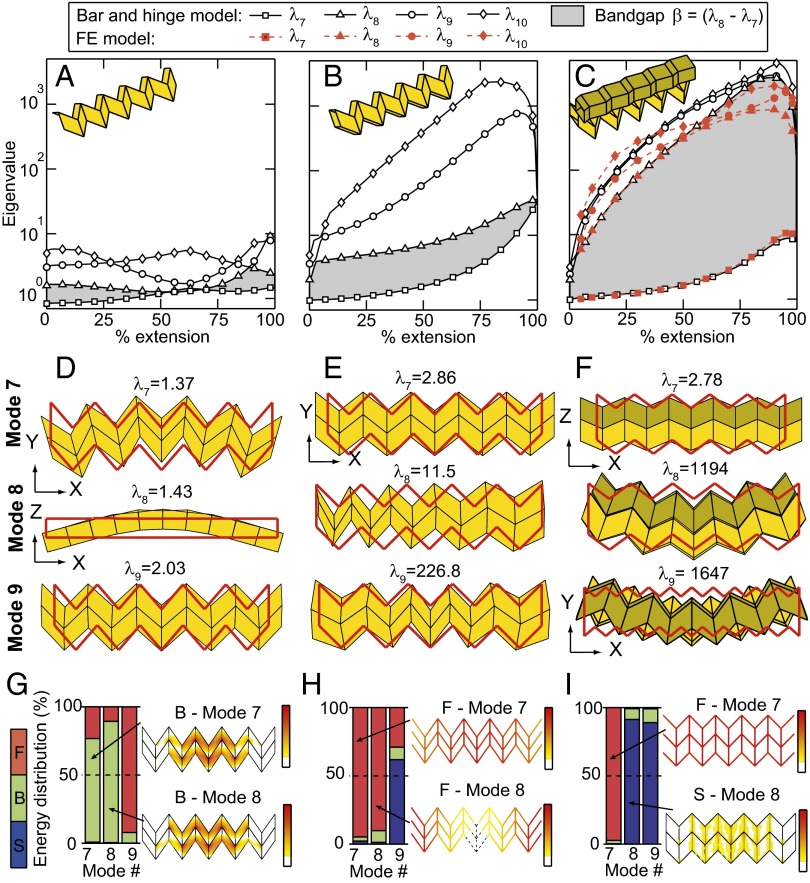
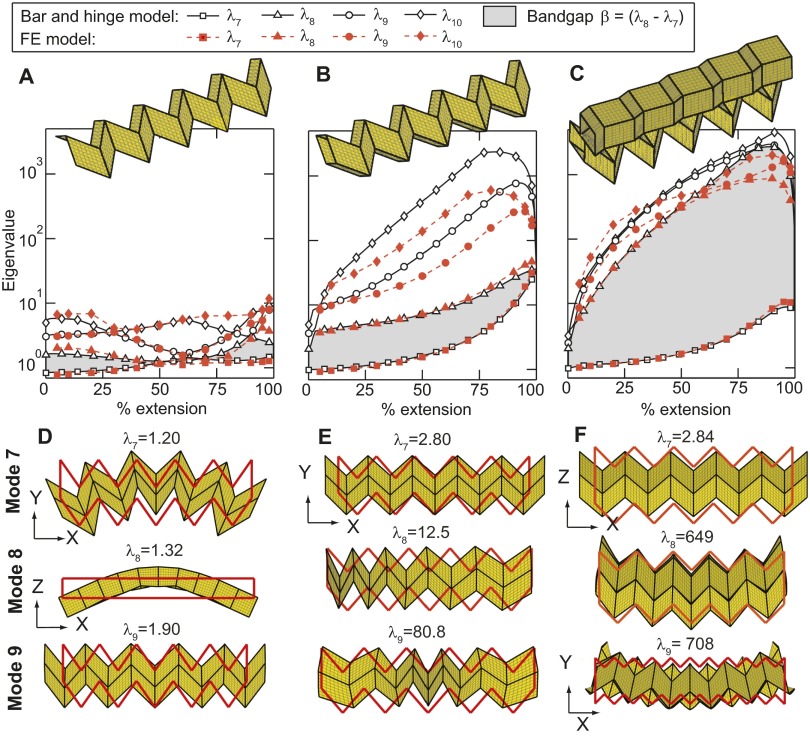
Stiffness characteristics of a sheet, a single tube, and a zipper-coupled tube. (A–C) Eigenvalue vs. configuration (percentage of extension) for the sheet, the single tube, and zipper-coupled tubes, respectively. The large bandgap from the zipper-coupled tubes is also verified with an FE model. (D–F) Seventh, eighth, and ninth deformation eigenmodes when structures are at 70% extension (undeformed outline in red). (G–I) Energy distributions for the sheet, the single tube, and zipper tubes, respectively. The energy distribution is presented as a bar graph indicating the percentage of energy in fold bending (F), panel bending (B), and panel stretching and shearing (S). Representative element energies are shown for modes 7 and 8 of each structure. For detailed energy presentation see SI Text, section S4 and Fig. S7.
Fig. S5.
FE model used for verification. (A) Miura-ori cell discretized with elements for each panel; Inset shows local zero-length connectivity at fold lines. (B) Discretization of single tube with .
Fig. S7.
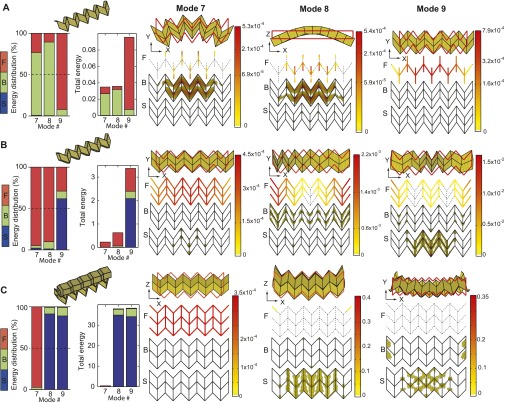
(A–C) Eigenmode energies of the sheet, the single tube, and the zipper-coupled tubes, respectively, using FE analysis. Energy distributions (as a percentage and as a total amount) are presented in stacked bar graphs indicating energy in the different sets of components [i.e., fold bending (F), panel bending (B), and panel stretching (S)]. The energy within the structure is shown by shading of elements to show the concentrations of energy. The color scale indicates the magnitude of energy.
Stiffness (K) and mass matrices (M) are used to construct a linear dynamics system of equations (no sum), where is the ith eigenvalue and is the corresponding eigenmode of the structure. Each eigenmode represents a structural deformation mode of the system, and its corresponding eigenvalue (in units of ) represents an excitation frequency that would result in the given deformation. The eigenvalue is proportional to the total energy in the system (kinetic and elastic strain energy), meaning that a deformation mode with higher energy will require a higher excitation frequency. The structure is analyzed with no boundary constraints, and thus the first six eigenmodes correspond to rigid body motion of the structure in 3D space (three displacement and three rotational modes). We omit these modes from our study, as they require zero energy. The seventh eigenmode and those following represent deformations requiring incremental energy input. The eigenvalues of a single Miura-ori sheet, a single tube, and a zipper-coupled tube are plotted vs. percentage of extension (Fig. 3 A–C), and representative deformation modes are shown for each structure at extension (Fig. 3 D–F). Eigenvalues scale linearly with mass and stiffness and therefore comparisons remain scale independent and highlight the influence of coupling on the global system behaviors. The single sheet can bend and twist globally in several directions with little energy input, resulting in low eigenvalues. The distribution of energy for the seventh and eighth deformation modes (Fig. 3G and Fig. S7) illustrates that bending occurs in the central panels and folds whereas the remainder of the structure remains unstressed. As expected, the bending energy in the panels is highest at the vertices, where the curvature approaches infinity (1, 37). The ninth mode of the sheet and the seventh mode of the tube represent a rigid folding motion where bending is primarily concentrated in the folds and the panels remain essentially flat throughout the deformation (Fig. 3 D and E).
For practical purposes, we prefer that corresponds to rigid folding and that subsequent eigenvalues are higher, creating a bandgap . A structure with a large bandgap has a flexible mode that allows for easy deployment but is stiff for all other types of loading. Mode switching may occur, meaning that the deformed shape corresponding to a given eigenvalue can differ drastically, depending on extension. For example, the seventh and eighth modes switch for the single Miura-ori sheet around 70% extension (Fig. 3A). The single and zipper-coupled tubes display a continuous bandgap and do not experience switching of the rigid folding mode (seventh). The eighth mode of the single tube constitutes a “squeezing” deformation, where one end of the structure is folded and the other end is unfolded (Fig. 3E and Movie S5). This mode requires bending of folds and panels at the ends of the structure; however, the panels do not stretch or shear, and thus is only slightly higher than . The aligned and internally coupled assemblages are also prone to squeezing and the bandgap is not increased (SI Text, section S5 and Fig. S8).
Fig. S8.
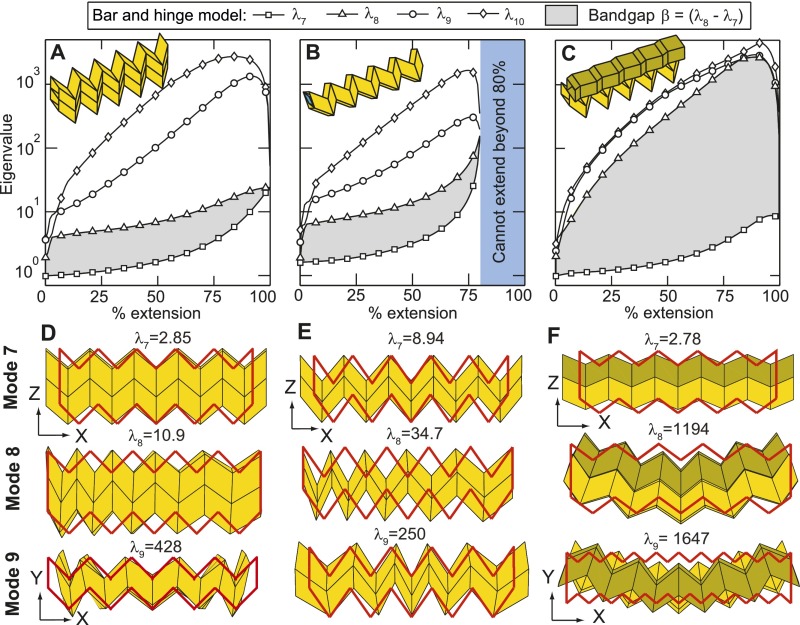
Eigenvalue comparison for the different coupling assemblies. (A–C) Eigenvalue vs. extension for the aligned-, internally, and zipper-coupled structures, respectively. (D–F) Seventh, eighth, and ninth deformation eigenmodes when structures are at 70% of the maximum extension length (undeformed outline in red).
However, when coupling the tubes into a zipper assemblage we observe that the structure has a substantially increased bandgap, where is often two orders of magnitude greater than . The large increase in occurs because all deformation modes except for rigid folding () require stretching and shearing of the thin sheets and thus a substantially higher amount of energy. Deforming the zipper-coupled tubes in a global bending mode (eighth or ninth) requires stretching the structure’s panels (Fig. 3 F and I). When actuated at one end, a single, aligned, or internally coupled tube squeezes (Movie S5 and Fig. S8), whereas zipper-coupled tubes expand and contract in a consistent rigid folding motion (Fig. 1 and Movie S1). The zipper-coupled tubes are not prone to the squeezing-type deformation, as it would require differential movement between the tubes and stretching the thin sheet (SI Text, section S2 and Fig. S3).
Structural Cantilever Analyses
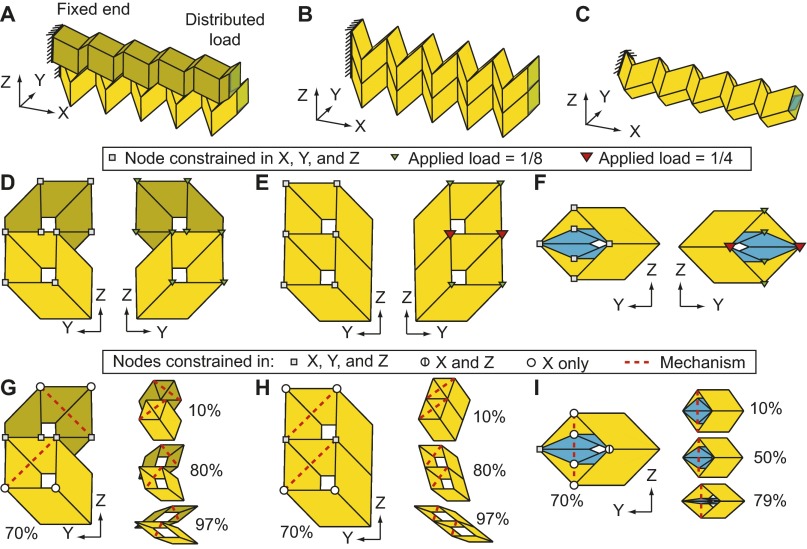
The zipper, aligned, and internally coupled tube systems can be applicable as deployable cantilever structures when restrained on one end (Fig. 4). At the supported end all nodes are fully fixed (X, Y, and Z displacements), whereas a total load of 1 is distributed on the other end of the structure (Fig. S9 D–F). When used as cantilevers, the tubes exhibit behavior similar to that of an I-beam, wherein the second moment of area (or area moment of inertia) is increased by distributing material away from the centroid. The aligned and internally coupled tube systems often experience squeezing-type deformations when loaded on one end, whereas the zipper-coupled tubes experience more uniform bending deformations (Fig. 4A). The stiffness of the structures is calculated for the three Cartesian directions for different extensions (Fig. 4 B–D). The loads are applied for each configuration, and the resultant displacements (, , and ) are calculated from the linear function , where F is a force vector. A quantitative stiffness of the system is then calculated as based on the maximum system displacement (δ). The zipper-coupled tubes tend to be stiffer than the other two systems and have a greater stiffness when closer to full extension. The internally coupled tubes tend to be stiff for Z-direction loading and when locked into a fixed configuration (i.e., 80% extension). The results for stiffness presented here show the general system behavior and are in consistent units of force per length (e.g., newtons per millimeter). A realistic length scale and elastic modulus can be substituted to find quantitative results for the cantilevers.
Fig. 4.
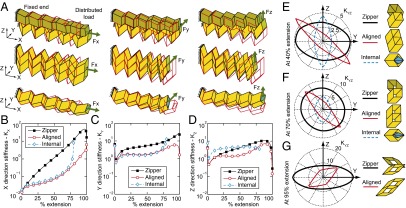
Zipper, aligned, and internally coupled tubes used as cantilevers. (A) Initial (red line) and deformed geometry of the structures at 70% extension when the left end is fixed and a uniform load is applied on the right end. The deformed shapes are scaled so the maximum displacement for each case is equal to the panel height () and do not necessarily represent stiffness. (B–D) The stiffness (force/length) of the cantilevers in the three Cartesian directions. The internally coupled tube cannot extend beyond 80% extension of the external tube. (E–G) The stiffness for loads in the plane represented as a radial plot at extensions of 40%, 70%, and 95%, respectively. Stiffness is shown as distance from the origin.
Fig. S9.
Support and loading conditions of origami cantilever structures. (A–C) Initial configurations for the zipper-, aligned-, and internally coupled structures, respectively. (D–F) Support conditions (Left) and loading conditions (Right) used in the analyses of the three cantilever systems in Fig. 4. The total load of 1 is distributed by placing one-eighth of the load at each of the eight nodes, whereas double the load (one-quarter) is placed on colocated nodes occurring in the aligned- and internally coupled systems. (G–I) Support conditions (Left) for the cantilevers, if a mechanism is installed to deploy the system, and cantilever configurations (Right) for different levels of system extensions/contractions.
The stiffness for different directions of loading, orthogonal to the X axis, is investigated, by rotating the load in the plane. The stiffness for each structure is calculated at extensions of 40%, 70%, and 95% and presented as a radial plot corresponding to the direction of loading (Fig. 4 E–G). The structure is analyzed with the same constraint and load distributions, and only the direction of the load vector (equating to 1) is rotated in the plane. The aligned and internally coupled tube systems demonstrate anisotropic behavior, wherein only one loading direction (in the plane) displays high stiffness. On the other hand, the zipper-coupled tubes tend to be stiff for all directions of loading, as depicted by the more circular profile on the plots (Fig. 4 E–G).
The fixed end of the cantilevers may be constrained in a different fashion, so that a mechanism is installed to fold and deploy the entire structure (Fig. S9 G–I). The mechanism would control the rigid folding mode of the system, thus permitting easy deployment (especially for zipper-coupled tubes—see actuation in Movie S1). When the mechanism is contracted, the structure will deploy, and when it is extended, the structure will fold. When the length of the mechanism is fixed, the cantilever will behave much as if the support is fully fixed.
Cellular Assemblages
Cellular origami can permit self-assembly of engineered hierarchical materials (5, 38), whose mechanical properties depend on the microstructure geometry. The structural stiffness and energy absorption properties of cellular origami can be optimized to complement and improve naturally occurring materials (39). Zipper-coupled tubes can be integrated with aligned or internal coupling to create layered foldable assemblages (Fig. 5 and Movie S3). Structures that incorporate zipper coupling inherit the large bandgap, while also retaining properties from the other coupling techniques (e.g., space filling from aligned or locking from internal coupling). The zipper/aligned metamaterial studied in Fig. 5 B–E has the same parameters as before, except the fold to panel stiffness ratio is set to , to simulate an assemblage constructed by additive manufacturing (Fig. 5 F and G). Origami metamaterials created with 3D printing do not fold like traditional origami, but possess novel characteristics such as the single flexible mode of zipper coupling.
Fig. 5.
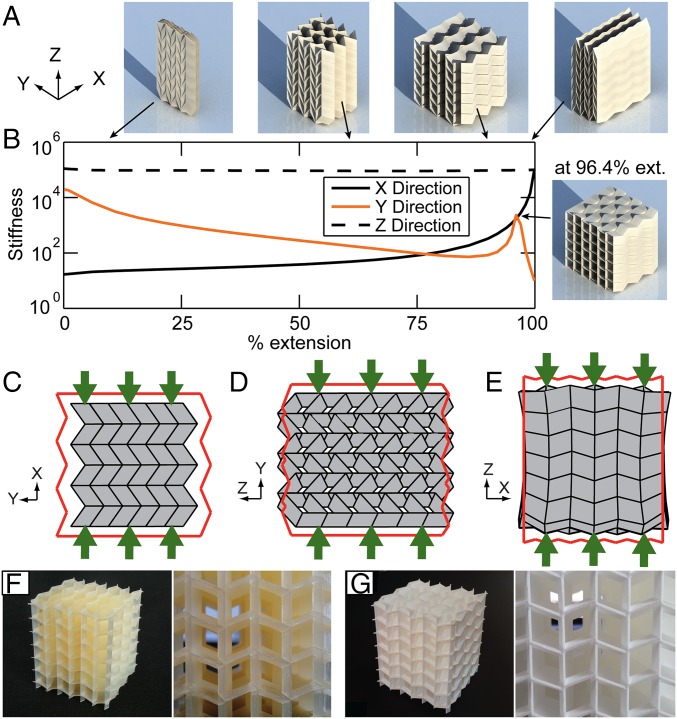
Cellular origami metamaterial consisting of 36 tubes with , arranged as zipper in the horizontal Y direction and as aligned in the vertical Z direction. (A) Kinematic folding sequence of the assemblage (Movie S3). (B) Compression stiffness of the metamaterial in the three Cartesian directions vs. extension. (C–E) Initial (red line) and deformed geometry of the assemblage at 90% extension for uniform compression tests in the X, Y, and Z directions, respectively. The deformed shapes are scaled so the mean displacement of the loaded surfaces is equal to the panel height () and do not represent stiffness. (F and G) Metamaterial prototypes constructed with additive manufacturing cannot undergo the full folding motion in A, but inherit the anisotropic mechanical properties of the cellular zipper assemblages. In F a soft metamaterial from resin with a wall thickness of 0.09 mm can be deformed by hand, whereas the polyamide assemblage in G with a wall thickness of 0.8 mm is substantially stiffer (Materials and Methods).
We analyze the assemblage in Fig. 5 by applying symmetric uniform forces (summing to 1) on opposing faces of the system and calculate the compression stiffness as , where δ is the mean total displacement in the direction of loading. Because of the zipper geometry, the system is primarily flexible in the X direction at lower extensions (0–70%) and in the Y direction at higher extensions (70–100%). The peak in the Y-direction stiffness (at 96.4% extension) corresponds to a bistable state, where the tube cross section is square, and can transition to a different rhombus, depending on the direction of folding (Movie S3). In addition to the stiffness, the deformation characteristics of the material are also anisotropic. The perceived Poisson’s ratio is negative in the Y direction when compressed in X, whereas it is positive in the Z direction when compressed in Y (Fig. 5 C and D). The structure is substantially stiffer in the Z direction, and deformations do not follow the kinematic folding mode.
Geometric Variations
There are numerous other ways in which rigid foldable tubes can be defined, combined, and coupled. For example, a different vertex angle α and panel height a may be used with rigid and flat foldability of the system preserved. Zipper coupling can be continued in one direction to create an easily deployable slab structure resistant to out-of-plane loads; potential applications are architectural canopies (Fig. 6A), bridges (Fig. 6B), solar arrays, or synthetic materials. When the vertex angle is varied for the coupled zipper tubes, we can create arbitrarily curved systems with high out-of-plane stiffness (Fig. 6A and Movie S4). The bridge deck uses tubes with a vertex angle of to provide a more even surface, whereas the bridge parapet tubes have a lower vertex angle to provide stiffness during deployment (Fig. 6B and Movie S2). If the zipper coupling is repeated in more than one direction, the structure will self-interlock during the deployment, creating a stiff array of coupled thin sheets (Fig. 6C and Movie S2). The structure does not necessarily need to have a square final cross section (four segments of zipper-coupled tubes), but can be any radially symmetric shape (SI Text, section S6).
Fig. 6.
Variations of cellular assemblages in different stages of deployment. Approximate percentage of extension is shown. (A) Deployable architectural canopy with high out-of-plane stiffness for transformable building design. (B) Bridge structure from zipper-coupling tubes of different geometries. The structure is flat foldable in two directions and stiff for out-of-plane loading. (C) Structure that interlocks into a fully conforming shape. The structure’s edges are each composed of four tubes coupled in a zipper orientation. For details see Table S1 and Movie S2.
Table S1.
| Structure | Number and geometries of tubes | Coupling orientation and discussion |
| Canopy structure (Fig. 6A) | Thirty-two alternating tubes with α varying between and . All tubes with m and . | All tubes are coupled in the zipper orientation. The vertex angles α are calculated so the overall cross section follows a smooth planar curve (e.g., for the first six tubes). This structure covers an area of m with a 2.6-m rise when deployed to 97% extension and can fold down to a size of 1.3 m at 5% extension. |
| Bridge (Fig. 6B) | Two tubes with (yellow) and six with (green). All tubes with mm and . | Zipper coupling is continued in one direction only, where each tube is coupled on two opposite faces. The system remains rigid and flat foldable in two directions. The structure has a high out-of-plane stiffness. |
| Self-interlocking structure (Fig. 6C) | Twelve tubes with mm, , and (red). | Zipper coupling is continued in one direction for each side of the structure. The tubes at the corners have zipper coupling in orthogonal directions (i.e., on two adjacent faces of the tube). The system is flat foldable in one direction and interlocks into a stiff conforming assembly at an extension of 96.3%. |
| Coupled polygonal tube (Fig. 7A) | Polygonal tube : cross section with four panels of mm, (yellow) and two panels of mm, mm, (blue). One tube has mm, (brown). | Zipper coupling between the polygonal and the regular square tube can be done on any of the polygonal tube faces. The internal (blue) panels of the polygonal tube are defined to reach a flat configuration when external panels (yellow) are at extension. The structure is flat foldable only in one direction, but the internal folds (on blue) can change their polarity and can reconfigure the overall structural shape (Movie S2). |
| Zipper-coupled tubes with thickness (Fig. 7B) | Two tubes with mm, mm, , and . The thickness is mm on the thin part and mm on the thick part of the panels. | A technique of cutting out material (18) is adopted, allowing the structure to fold down completely to the minimal feasible thickness of mm. The structure cannot extend to extension because intersection of the thick material will occur. |
| Actuator (Fig. 7C) | One tube of and one of cells, with mm, (orange). The rigid boundary is a bounded paper box (blue). | Zipper coupling along the middle section of the longer tube, while its ends are adhered to stiff boundaries. The zipper-coupled section prevents local and squeezing-type deformations. At the ends, the longer tube can undergo squeezing, allowing for the rigid attachment. |
The cross section of the tubes is not restricted to a quadrilateral shape (30, 31); any polygon with translational symmetry can be used to extrude a rigid, foldable origami tube. The tubes can have any cross section where each segment of the cross section has an equal-length counterpart (or counterparts) that is (are) translationally symmetric. The internal panels of the six-sided polygonal tube (blue in Fig. 7A and Movie S2) are defined to conform with the flat and rigid foldability of the system. The direction of the folds in these segments can be reversed (e.g., mountain to valley), thus changing the geometry. Polygonal tubes with more sides can be reconfigured in the same way, with many more variable cross sections. In Fig. 7B we show that finite thickness may also be incorporated into the construction of the coupled origami tubes. Using available techniques for thick origami (18, 19), we can create structures of thick panels adjoined with physical hinge elements. With these techniques cost-effective materials (e.g., thin wood panels with metal hinges) can be used to create large structures that can be easily deployed, but possess large global stiffness from the zipper-coupling framework. Finally, the characteristics of origami assemblages can be modified by coupling only specific portions of a tube. The long tube in Fig. 7C has zipper coupling only in the middle portion to restrict the global squeezing and bending of the system. The ends remain uncoupled, allowing for a rigid connection to the outside edge while still permitting the system to fold and unfold.
Fig. 7.
Local variations in coupling origami tubes. Different stages of deployment are shown with approximate percentage of extension. (A) Zipper coupling of a reconfigurable tube with a polygonal cross section. The six-sided polygonal tube has two possible shapes (I and II). (B) Computer visualization of zipper tubes from thick material (thick origami). (C) Actuator system from zipper coupling of two tubes of different length. The edges of the long tube are restrained, but squeezing can occur on the uncoupled sections, allowing the system to fold. For details see Table S1.
Concluding Remarks
This paper introduces an approach for coupling origami tubes in a zipper fashion and explores their unique mechanical characteristics. These assemblages engage the thin sheets in tension, compression, and shear for any deformation mode that does not follow the kinematic deployment sequence. The origami tubes can be stacked and coupled into a variety of cellular assemblages that can further enhance the mechanical characteristics and versatility of the systems. Extensions and refinements of this work may explore geometric arrangements that improve the stiffness-to-weight ratio, and impact energy dissipation and other mechanical properties. Further study of the hierarchical system properties with respect to fabrication, scale, and materials will be needed to inform potential applications. As origami becomes more widely used in science and engineering, the coupled tube assemblages will serve as an important component that allows flexible deployment while simultaneously retaining a high global stiffness.
Materials and Methods
Prototypes of the origami were created for demonstrating the mechanical characteristics and for showing the kinematic folding. The origami assemblages in Movies S1, S2, and S5 and Figs. 1, 6, and 7 are created from perforated paper that is folded and adhered together. The Miura-ori sheets were created from 160-g/m2 paper by perforating along the fold lines with cuts of length 0.5 mm spaced evenly at 1-mm intervals. Because each tube cannot be developed from a single flat piece of paper, it is assembled by connecting two Miura-ori sheets (Fig. 2C and Movie S5). One of the sheets is constructed with perforated tabs at the edge, which can be folded and attached with standard paper adhesive to a mirror-image Miura-ori sheet. When connecting two tubes into either the zipper or the aligned assemblage, the adjacent facets are adhered together (Fig. 2 D and E and Movie S1). For internally coupled tubes, the structure is assembled in sequence (Fig. 2F) by connecting individual Miura-ori sheets with the joining tabs. The numerous variations of the coupling configurations (Figs. 6 and 7) were also assembled using the same techniques. In Fig. 5 F and G, we show how additive manufacturing can be used to create cellular metamaterials with characteristics inherited from the zipper tubes. The model in Fig. 5F was created with a Keyence AGILISTA 3000 3D printer that uses digital light processing (DLP) technology. The model material is an AR-M2 transparent resin and the support material is an AR-S1 water-soluble resin. The cube has dimensions of 68 62 61 mm with wall thickness of 0.09 mm. The model in Fig. 5G was created with an EOS Formiga P 100 selective laser sintering (SLS) system. The model uses a PA 2200 (Polyamide 12) material that is sintered together and does not require support material. This assemblage has dimensions of 102 93 92 mm with wall thickness of 0.8 mm.
SI Text
S1) Stiffness Calculations
For our analyses and discussion in the main text, we examine the thin sheet origami in a consistent fashion to highlight the behaviors, while staying independent of scale (eigenvalue and static analyses). The eigenvalues (λ) have units of and represent the global characteristics of the structure considering both mass and stiffness. The static analyses present the global structural stiffness in the form of force divided by displacement. The two different computational models used herein (bar and hinge model and finite elements) give similar results and correspond well with observations of physical models.
For our analyses we use the following parameters unless otherwise noted. The Miura-ori sheet (Fig. 2B) with unit dimensions , , and is used to define the tubes and coupled tube systems used in the analyses of Figs. 3 and 4 (see SI Text, section S5 for additional details on internally coupled tubes). A Miura-ori sheet with , , and is used for the cellular assemblage in Fig. 5. The thickness is used to simulate a thin sheet that is much thinner than it is long (). A Young’s modulus and material density , both arbitrary but within a realistic range, are selected to scale stiffness and mass linearly and do not affect the global behavior or characteristics of the origami tubes (Fig. S4 and accompanying discussion). The elastic modulus is assumed to be in units of force per length squared (e.g., newtons per square millimeter) and the density as mass per length cubed (e.g., kilograms per cubic millimeter). When appropriate numerical values and length scales are used, the analyses presented here will provide quantitative approximations for stiffness and eigenvalue response. Other parameters used in the modeling are discussed in the text below and are chosen based on existing literature, approximate physical behavior, and type of computation performed (e.g., Poisson’s ratio ).
Here, we describe the simple bar and hinge method for the numerical modeling of thin sheets in origami systems. A previously established model (24) is used as a basis, and several improvements are incorporated to make the model scalable and isotropic and to incorporate material characteristics (32). We make the stiffness dependent on the material’s thickness (t), Young’s modulus (E), and Poisson’s ratio (ν). The stiffness matrix (K) for the origami structure incorporates stiffness parameters for (i) panels stretching and shearing (), (ii) panels bending (), and (iii) bending along prescribed fold lines (). The global stiffness matrix is constructed as
| [S1] |
where the compatibility matrix (C) and Jacobian matrices ( and ) relate the stiffness of the various components to the nodal displacements, as discussed in detail below. Each node has 3 degrees of freedom (DOFs) (X, Y, and Z displacement) and the stiffness matrix is of size (), where represents the total number of DOFs in the system. The mass of each panel is calculated from the panel volume and material density ρ. A mass matrix M for the entire structure is constructed by distributing one-quarter of the mass of each panel to each of its connecting nodes.
S1.1) Panel Stretching and Shearing.
In-plane axial and shear stiffness is simulated using the indeterminate bar frame (Fig. S1A). A general formulation for bar elements is used with an equilibrium matrix (A) relating internal bar forces (t) to nodal forces (f) as , a compatibility matrix (C) relating bar nodal displacements (d) to bar extensions (e) as , and a diagonal matrix () relating bar extensions (e) to local forces (t) as . Using the static-kinematic duality that , the linear system for stretching and shear of the panels (i.e., the bars) is represented as the first row of Eq. S1. The crossed bar frame (Fig. S1A) has six bars connected at the four corner nodes of the origami panel. This crossed bar geometry results in the frame behaving as an isotropic panel. The bar stiffness parameters (i.e., components of ) are defined for each bar as , where is the bar length and is the bar area. To achieve the isotropic behavior for the panel, the bar areas are defined as
| [S2] |
| [S3] |
| [S4] |
for the horizontal (X), vertical (Y), and diagonal (D) bars, respectively. The height (H) and width (W) of the panel are taken as an average for skewed panels. To verify the frame model we define a panel with , , , and and subject it to a tensile (Fig. S1B) and a shear patch test (Fig. S1C). For tensile loading the system always satisfies the patch test, but for shear loading, the behavior of the model is highly dependent on the chosen Poisson’s ratio. From Eq. S4, when a low ν is used, the diagonal bars have a low area, and the frame demonstrates a low shear stiffness. The converse is also true, countering the behavior expected in a truly isotropic material. Alternatively, when ν is set to , the behavior of the frame model in shear is identical to that of a homogeneous, isotropic block of material. Each diagonal bar carries a force of in the X direction, and the top of the frame laterally displaces in the direction of loading. When , the frame displacement matches the lateral displacement of a solid block with dimensions loaded in pure shear, analytically defined as , where is the total shear force and G is the shear modulus, defined as for a homogeneous, isotropic, linear elastic material. With , the frame is scale independent for shear loadings. If the shear patch is remeshed, then the frame model converges to the same solution as any generic finite-element approach. However, because only a single six-bar frame is used to model each panel, the shear stiffness of the panel is overestimated (similarly to any finite-element approach). In reality, the shear stiffness of the panels is lower than a pure shear case because, in addition to the shear deformations, tensile deformations also occur over the width and height of the panel. Using a lower Poisson’s ratio, we artificially reduce the shear stiffness of the frame. To this end, we choose to use . At this value, the single bar frame exhibits approximately the same shear deformation as a patch test performed on a mesh of 2,500 finite elements.
S1.2) Panel Bending.
Out-of-plane bending of the panel is modeled as an angular constraint between two triangular segments of the panel (1–2–3 and 1–3–4 in Fig. S1D). For small displacements, the choice of the diagonal does not affect the kinematics of the system (7). Previous findings (1, 4) show that the bending energy is lower along the shorter length, so we formulate our model assuming that bending occurs along the shorter diagonal (i.e., 1–3 in Fig. S1D). An angular constraint, F, is formulated based on the dihedral bending angle, θ, which can be calculated by using cross and inner products of the vectors a, b, and c from the nodal coordinates of the panel p. This constraint is defined as
| [S5] |
and the corresponding Jacobian for panel bending, , is calculated as
| [S6] |
where d are the displacements of the panel nodes. The second row of Eq. S1 incorporates panel bending stiffness where each element in the diagonal matrix corresponds to the bending stiffness of an individual panel.
We assume that the in-plane stiffness of the thin sheet (e.g., paper) is high enough to prevent bending and buckling at the edge connecting two panels (i.e., at the fold line of a thin sheet). The bending energy of thin sheets increases when the edges of the sheet are restrained. In this case, tensile forces develop over the sheet’s surface, and flexural deformations become restricted to a small area focused at the bending ridge (i.e., the diagonal 1–3 in Fig. S1 D–F) (1, 2, 4). This phenomenon occurs with large displacements and the elastic energy of the panel bending scales approximately as , where k is the bending modulus of the sheet, defined as (1). In our model we define the panel stiffness as
| [S7] |
which incorporates the nonlinear effect of the ratio in the restricted bending of a thin sheet. We use a finite-element model (discussed in detail later) to show thin sheet bending for small and for large displacement cases. We define a thin sheet with a long diagonal and a short diagonal of . The thin panel is restrained at the edges by thin sheets in a perpendicular orientation (similar to typical origami). The structure is restrained in the vertical direction at three corners and is subjected to bending with a downward force F at the fourth corner (Fig. S1E). When a small force is applied (), the structure remains in the small displacement regime and the thin sheet experiences curvature along both diagonals (Fig. S1F, Top). For a larger force () the structure experiences large displacements, and curvature occurs in the center of the diagonal, creating a bending ridge along the diagonal (Fig. S1F, Bottom). As discussed in previous literature (1, 4) the large displacement case has a higher stiffness and the rotational hinge formulation in Eq. S7 would give a realistic result with a factor of . Here we restrict ourselves to small displacements, and so we use for all analyses. The stiffness coefficient has not been investigated in detail yet. A more comprehensive formulation would incorporate a nonlinear scaling associated with the dihedral bending angle θ into Eq. S7 that would scale stiffness between small and large displacement cases. For example, ref. 1 suggests that the total bending energy (and thus stiffness) of the restricted sheet should scale with vs. for a linear rotational hinge.
S1.3) Folds Bending.
Folds are modeled in a similar fashion to the bending of panels. Realistic origami behavior does not allow for out-of-plane displacements along fold lines due to the restrictive nature of the perpendicularly oriented sheets. Thus, it is sufficient to use a simplified approach: modeling the origami fold as a rotational hinge along an edge. A schematic of the fold model contains a fold spanning nodes 2 and 3 connecting two panels (1–2–3–4 and 2–5–6–3) (Fig. S1G). The length of the fold is , and the stiffness is expected to scale linearly with this length, because curvature and bending energy are expected to exist only on the infinitesimally small width of the fold. The same constraint formulation presented for the panel bending is used to formulate two independent fold elements from the two vector sets: (i) a, b, and c and (ii) −a, d, and e. This approach distributes the stiffness of the fold to all relevant nodes on the two adjacent panel elements. The initial fold angle, , is different for different folds on the Miura-ori sheet and tube and can be calculated using basic geometric relations (7, 25, 27) for each chosen configuration (percentage of extension). Here, the angle θ represents a rotation away from the initial folded configuration.
We introduce a parameter to relate the stiffness between the bending of a fold with length and the bending of a panel with a diagonal of . Structures consisting of thick panels with near frictionless hinges (18, 19) could have a low (e.g., ); structures where perforation or plastic deformation is used to facilitate creasing (34, 35) could have a medium (e.g., 0.1); whereas origami created with additive manufacturing (40), or where creasing is near elastic (36), could have a and perhaps higher if movement at folds is intentionally restricted. The interaction between bending of flat material and folding at fold lines as well as highly nonlinear folding behaviors of origami are currently being studied (33–36). Our simplifications assume that only linear elastic deformations occur at the folds. For the analyses in Figs. 3 and 4 and SI Text, we assume that the folds are less stiff than the panels, and we use an arbitrary choice of based on visual observations of our physical models. For the cellular assemblage in Fig. 5, we use to simulate folds that are as stiff as the panels, because this is likely the case for continuous 3D printed structures. In SI Text, section S3 we show that influences the magnitude of eigenvalues associated with fold bending; however, it does not influence the overall behavior and the qualitative results presented in this paper. For our implementation, the stiffness for each of the twofold elements (i.e., a, b, c and −a, d, e) is calculated similarly to Eq. S7, as
| [S8] |
except here the function scales linearly with the length . More comprehensive future formulations may incorporate nonlinear scaling associated with material properties, the angle θ, the angle , and other fold-related variables (33–36).
S2) Coupling of Zipper Tube Structures
In the computer model, the coupling of the zipper structures is performed by inserting coupling elements that restrict relative movement between the adjacent panels of the two tubes. These coupling elements can be thought of as an adhesive joint between the adjacent faces of the tube. The relative local coordinates ( and ) are different for the odd and even panels of the structure (Fig. S2). The coupling elements restrain relative movement between panels along the length of the tube (relative to the local axes), and the coupling elements restrain differential orthogonal movement in the () axis. The and coupling elements are formulated using a compatibility relation where bar elements are used to restrain relative movement between two nodes. The stiffness for the coupling elements is defined as
| [S9] |
and
| [S10] |
where E is Young’s modulus, t is the thickness of the thin sheet, and the coupling coefficients ( and ) can be used to vary the stiffness of the coupling elements. When these coupling coefficients are set to 1, each coupling element has the same axial stiffness as a 0.5-unit-wide, 1-unit-long, and t-thick piece of panel material. Finally, coupling elements are used to prevent nodes lying on the same plane (on a panel) from moving out-of-plane (in the relative direction). The coupling elements are defined in the same fashion as the out-of-plane rotational hinges for panel and fold bending. Here, we consider a node on one of the zipper tubes that overlaps a panel on the opposite tube, indicated as a red/white triangle in Fig. S2C. A rotational hinge element is constructed that restricts out-of-plane movement between each of the overlapping nodes and the three corresponding nodes on the opposing tube. For clarity, only two sample corresponding node sets are illustrated in Fig. S2C. The vectors groups (a, b, and c) and (d, e, and f) can be used to define the rotational hinge for each set. The stiffness for each of these rotational hinges is defined as
| [S11] |
where the parameters are the same as the panel definition in Eq. S7, and the coupling coefficient can be used to vary the stiffness of the coupling elements. With this formulation, the stiffness of each coupling element is equal to the bending stiffness of a panel element with a diagonal length, . Because the equation for is based on bending of the thin sheet, the value of this stiffness is substantially lower than that of the and coupling elements.
The sensitivity of the model eigenvalues vs. the magnitude of each of the coupling coefficients is explored for the zipper-coupled tubes deployed to 70% extension (Fig. S2). The rigid folding mode () of the coupled tube is not affected by any of the coupling elements; i.e., it is neither easier nor harder to fold and unfold the structure due to the coupling. When the coupling coefficient is substantially reduced (lower than ), the eighth and subsequent eigenvalues experience a drop in magnitude from ∼1,200 to ∼500. This drop occurs because the tubes are not restrained in the relative direction, and thus the eighth mode switches to a deformation mode in which the tubes begin to separate. Due to the presence of the coupling elements, the magnitude of this eigenvalue remains relatively high even when ( vs. for a single tube). When decreasing the value of the coupling coefficient, there is a more significant effect on and the subsequent eigenvalues. The eigenvalue corresponding to bending reduces to , when , and experiences a mode switch for lower coupling coefficients. When is substantially reduced, the tubes are free to slide apart in the Y direction. The coupling coefficients, on the other hand, have no influence on any of the eigenvalues. This is due to the zig-zag geometry of the tubes, which causes the axial members to restrain global out-of-plane movement between the two tubes. When any of the coupling coefficients are increased past a value of 1, there is negligible increase in the eighth and subsequent eigenvalues of the structure.
When changing the value of the vertex angle α or the extended configuration of the zipper-coupled tubes, there is little change in the sensitivity of the different coupling elements, and the general trends remain. The tubes are effectively coupled when the coupling coefficients are about equal to 1. The and coupling elements have a higher influence on the coupling and on maintaining the relatively large bandgap (), whereas the coupling elements have little influence on the eigenvalues.
To better understand why the zipper coupling results in the large bandgap increase, we investigate how the squeezing deformation mode is restrained by the new geometry. We perform an eigenvalue analysis on two tubes arranged in a zipper-coupling fashion, when the stiffness of all coupling elements is substantially reduced (). In this scenario the tubes can simultaneously undergo the squeezing deformation mode, where the tubes fold on the left side and unfold on the right (Fig. S3 A–C). However, this motion is incompatible for an effectively coupled zipper system. On the left side, the first vertex of the bottom tube moves downward (point I in Fig. S3A), whereas the first vertex on the top tube moves upward (point II in Fig. S3B) and vice versa on the right side. This transverse motion between the two tubes can be quantified by tracking the distance between adjacent panel-edge center points on the two tubes (Fig. S3D). In an undeformed (or effectively coupled) system the distance between adjacent edge center points is uniform at 0.7 units. The squeezing of the loosely coupled system results in separation on the left side (distance increases up to 0.9 units) and a closing on the right side (distance decrease down to 0.5 units). In an effectively coupled zipper system these in-plane motions are restrained, and it would be necessary to stretch and shear the thin sheet to achieve a squeezing-type deformation.
S3) Sensitivity of Model and Analysis
In Fig. S4 we show differences in scaling of eigenvalues, for the tube and zipper-coupled tubes, with respect to different model parameters. The seventh eigenvalue for both the single tube and the zipper-coupled tubes corresponds to the rigid folding mode, in which deformation primarily occurs as bending of the prescribed folds (Fig. 3 and Fig. S7). The eighth mode for the single tube corresponds to squeezing, in which bending occurs in the fold and panel elements. However, the eighth mode for the zipper-coupled tubes requires stretching and shearing of the thin sheet, which require much more energy than bending and result in drastic differences for the scaling of eigenvalues.
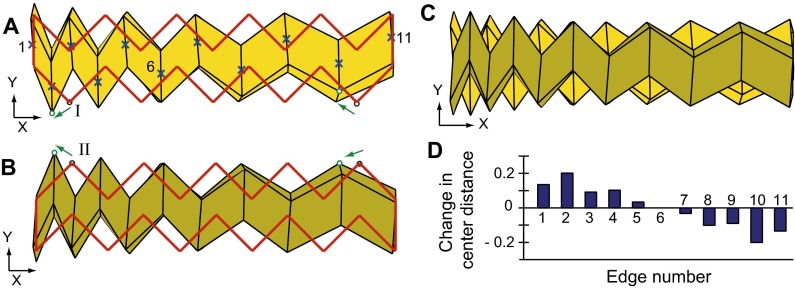
All eigenvalues ( and for both systems) scale proportionally with Young’s modulus E (i.e., doubling E doubles the eigenvalue) and inversely proportionally with the material density ρ (Fig. S4 A, B, E, and F). This is expected because E scales the stiffness proportionally, and ρ scales the mass proportionally in equation . Scaling of other parameters, however, does not necessarily influence all eigenvalues proportionally. When changing the sheet’s thickness, t, its stretching/shearing stiffness and the system’s mass scale proportionally. On the other hand, the bending stiffness for both the panels and the folds scales as based on Eqs. S7 and S8. Therefore, when scaling the thickness, the eigenvalues scale as for the rigid folding modes () of both tubes, and the squeezing mode () of the single tube (Fig. S4 C and G). The eighth eigenvalue for the zipper-coupled tubes does not change because both mass and stretching/shear stiffness scale proportionally (both are defined by t). When scaling the fold stiffness ratio, , scales proportionally for both structures, scales as 0.8 for the single tube, and remains constant for the zipper tubes (Fig. S4 D and H). The system behaviors that lead to these scaling relations are complemented by the energy distributions shown in Fig. S7.
In summary, Young’s Modulus E and material density ρ directly scale all system eigenvalues, whereas the material thickness t and fold stiffness ratio scale eigenvalues influenced by panel and fold bending. The scaling of different parameters does not cause mode switching and the order of eigenmodes remains the same as shown in Fig. 3. Scaling different parameters can change the quantitative results (e.g., magnitude of ); however, it does not influence the qualitative results presented here. The eighth eigenvalue for the zipper-coupled tubes remains substantially higher than the seventh, ensuring a large bandgap () regardless of the parameter values used. The results presented in this paper are independent of length scale, making the zipper-coupled tubes applicable across scales.
S4) Model Verification with Finite-Element Analysis
In this section, we verify and explore the accuracy of the bar and hinge model by comparing the results from the bar and hinge model to those of a shell model created using the commercial finite-element (FE) analysis software ABAQUS (41). Details of the FE implementation are shown in Fig. S5A for a single Miura-ori cell. For the FE model, we discretize each panel into D segments in each direction, such that each panel will now be modeled using shell elements ( for Fig. S5B and for all FE analyses herein). General purpose, four-node shell elements with finite membrane strains are used (S4 elements) and are connected with one node at each corner. The fully 3D FE model contains 6 DOFs at each node (3 displacements and 3 rotations). Mass in the model is distributed based on the volume and the density, ρ, of the shell elements. All model parameters are defined to be the same as those for the bar and hinge model.
At the fold lines, collocated (overlapping) nodes are placed with one node connected to the shell elements of each adjoining panel. Each set of collocated nodes, shown in Fig. S5A, Inset, is connected with an element that restricts the nodes to the same coordinates throughout the analysis. At the same location, the fold stiffness is modeled as an elastic rotational spring that resists rotation between the adjacent panels. The spring is placed locally on each pair of collocated nodes and resists rotations about the local a vector shown in Fig. S5A, Inset. The stiffness of the fold is based on the dimensions of connected shell elements and is defined as
| [S12] |
where and are the lengths of the connected shell element parallel to the fold line. The parameter denotes the length of the entire fold, and the equation is a function of stiffness (i.e., Eq. S8) based on the fold length and the same material properties as before. Eq. S12 distributes the stiffness of the fold (as calculated for the bar and hinge model) based on the tributary length of the shell elements used. Collocated nodes that are at the end of a fold (i.e., at a vertex) will have only one adjacent shell element and thus the stiffness will be based only on or on .
Discretized FE models of the sheet, the single tube, and zipper-coupled tubes are created with and a natural eigenvalue extraction is performed. The eigenvalue spectra calculated with the FE model and the bar and hinge model are presented in Fig. S6. The seventh through ninth eigenmodes for the FE model match those of the bar and hinge model when considering the global deformation of the structure (Fig. 3 D–F and Fig. S6 D–F), which we expect because these deformation modes correspond to global behaviors of the structure such as bending and rigid folding. The magnitudes of the eigenvalues follow similar trends between the two models but do not always match exactly. For example, with the single tube, and match well because the fold stiffness between the two models is the same (i.e., Eqs. S8 and S12), and in the FE model, panel bending occurs globally on the diagonal (as predicted for Eq. S7). However, the magnitude of the eigenvalues and for the tube is lower with the FE model. The difference in magnitude can be attributed to the localized deformations and stress concentrations that can be captured with the FE discretization, but cannot be captured using the bar and hinge model. For example, in the ninth mode the Miura-ori cell in the middle of the tube experiences bending, stretching, and shear localized at the vertex. The FE model can capture localized effects and individual shell elements can deform more than others. On the other hand, in the bar and hinge model stretching, shear, and bending can be captured globally only over the entire panel.
Fig. S6.
Eigenvalue analyses of a sheet, a single tube, and a zipper-coupled tube performed with the FE model. (A–C) Eigenvalue vs. extension for the three structures, performed with both the FE and the bar and hinge models. (D–F) Seventh, eighth, and ninth deformation eigenmodes when structures are at 70% extension (undeformed outline in red).
We also use the FE model to perform energy analyses for the Miura-ori sheet, the single tube, and the zipper-coupled tubes (Fig. S7). The energies are calculated based on the structural deformation for the normalized mode shapes (Fig. S6 D–F). The percentage of distribution between the different sets of element deformations (i.e., fold bending, panel bending, and panel stretching/shear) and the total energy for each mode are shown. The total energy for eigenvalues of the single sheet is relatively low, because deformations consist of localized bending in panels and folds. On the other hand, the eighth and ninth modes of the zipper-coupled tubes require much more energy, because the thin sheets are engaged in stretching and shearing. The rigid folding modes, ninth for the sheet and seventh for the tube structures, primarily engage the fold lines in bending as previously expected.
S5) Aligned and Internally Coupled Tubes
The eigenvalue vs. configuration plots and representative eigenmodes at extension are illustrated for the aligned-, internally, and zipper-coupled tubes in Fig. S8. The aligned-coupled tubes are constructed by translating a tube and attaching it to the initial tube without rotation (Fig. 2E). The tube could be a copy of the original geometry or could have different parameters a and/or α. For internally coupled tubes, the geometries of the internal and external tubes have to conform to preserve flat and rigid foldability as discussed in ref. 7. Here, we define the internal tube geometry, using a parameter that describes the maximum extension of the internal tube with respect to the external tube. For example, if we take an internal tube defined with , then the internal tube will reach extension (lie flat in the ) plane, when the external tube reaches of its maximum extension. The internal tube geometry (, , and ) is calculated from
| [S13] |
and
| [S14] |
where a, c, and α define the external tube geometry. The internally coupled tubes discussed in this paper (Figs. 2F and 4 and Figs. S8 and S9) use and the conforming Miura-ori cell geometry is therefore , , and . Computational modeling of the connectivity required to create aligned and internally coupled tubes is much simpler to formulate than that of the zipper-coupled tubes. Nodes on adjacent faces and edges of each tube are conveniently located at the same coordinates; therefore, the same DOFs are used for both tubes, and only one of the colocated nodes is used in the model. This modeling approach effectively connects the two systems but provides more stiffness than the coupling element approach used for the zipper-coupled tubes.
The eigenvalues and for the aligned-coupled tubes (Fig. S8A) are almost identical to those of the single tube (Fig. 3B), because coupling tubes in this fashion doubles the system’s mass, and simultaneously adding an identical set of elements to the system doubles the stiffness. The seventh and eighth mode shapes are identical to the single tube and are not restricted by this form of coupling (Fig. 3E and Fig. S8D). The magnitude of the ninth eigenvalue increases slightly, which can be attributed to the aligned coupling.
Coupling tubes internally (Fig. 2F) has more of an effect on their behavior; however, and still correspond to the rigid folding and squeezing modes, respectively, and the bandgap is not substantially increased (Fig. S8 B and E). When approaching an extension of (with respect to the external tube), the internal tube becomes flat, and the system essentially locks. At these larger extensions (60–), the eigenvalues and increase significantly, meaning that the system is substantially stiffer. When the internal tube is flattened, folding the structure (rigid folding mode) or deforming it in any other mode becomes more difficult. With other coupling orientations (i.e., zipper or aligned), the eigenvalues drop rapidly at large extensions. In those cases, the entire structure becomes essentially flat (in the plane), and it becomes easy to bend the system out-of-plane. In contrast to the zipper-coupled tubes, neither the aligned-coupled tubes nor the internally coupled tubes show a substantial increase in the bandgap () (Fig. S8 A–C). However, multiple coupling orientations can be integrated into a single system to take advantage of the different behaviors. For example, a combined zipper-coupled and internally coupled system would not experience squeezing and it would lock at a specified configuration.
S6) Self-Interlocking Structure
Each side of the self-interlocking structure (Fig. 6C) can be composed of any number of zipper-coupled tubes together (of same α). The structure can be any radially symmetric shape with n sides, as long as there is no self-intersection. The structure will interlock when an angle (γ) between the two faces on the cross section of the Miura-ori cell is at . Thus, the structure will interlock at an extension of
| [S15] |
Supplementary Material
Acknowledgments
This work was partially funded by the National Science Foundation (NSF) through Grant CMMI 1538830. E.T.F. is grateful for support from the NSF Graduate Research Fellowship and the Japan Society for the Promotion of Science Fellowship. The authors also acknowledge support from the Japan Science and Technology Agency Presto program and the Raymond Allen Jones Chair at the Georgia Institute of Technology.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
See Commentary on page 12234.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1509465112/-/DCSupplemental.
References
- 1.Lobkovsky AE, Gentges S, Li H, Morse D, Witten TA. Scaling properties of stretching ridges in a crumpled elastic sheet. Science. 1995;270(5241):1482–1485. [Google Scholar]
- 2.Vliegenthart GA, Gompper G. Forced crumpling of self-avoiding elastic sheets. Nat Mater. 2006;5(3):216–221. doi: 10.1038/nmat1581. [DOI] [PubMed] [Google Scholar]
- 3.Cambou AD, Menon N. Three-dimensional structure of a sheet crumpled into a ball. Proc Natl Acad Sci USA. 2011;108(36):14741–14745. doi: 10.1073/pnas.1019192108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Witten TA. Stress focusing in elastic sheets. Rev Mod Phys. 2007;79(2):643–675. [Google Scholar]
- 5.Côté F, Deshpande VS, Fleck NA, Evans AG. The compressive and shear responses of corrugated and diamond lattice materials. Int J Solids Struct. 2006;43(20):6220–6242. [Google Scholar]
- 6.Yokozeki T, Takeda S, Ogasawara T, Ishikawa T. Mechanical properties of corrugated composites for candidate materials of flexible wing structures. Compos Part A Appl Sci Manuf. 2006;37(10):1578–1586. [Google Scholar]
- 7.Schenk M, Guest SD. Geometry of Miura-folded metamaterials. Proc Natl Acad Sci USA. 2013;110(9):3276–3281. doi: 10.1073/pnas.1217998110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Heimbs S. Foldcore sandwich structures and their impact behaviour: An overview. In: Abrate S, Castanié B, Rajapakse YDS, editors. Dynamic Failure of Composite and Sandwich Structures. Vol 192. Springer; Dordrecht, The Netherlands: 2013. pp. 491–544. [Google Scholar]
- 9.Cheung KC, Tachi T, Calisch S, Miura K. Origami interleaved tube cellular materials. Smart Mater Struct. 2014;23(9):094012. [Google Scholar]
- 10.Gattas JM, You Z. Geometric assembly of rigid-foldable morphing sandwich structures. Eng Struct. 2015;94:149–159. [Google Scholar]
- 11.Zirbel SA, et al. Accommodating thickness in origami-based deployable arrays. J Mech Des. 2013;135(11):111005. [Google Scholar]
- 12.Del Grosso AE, Basso P. Adaptive building skin structures. Smart Mater Struct. 2010;19(12):124011. [Google Scholar]
- 13.Felton S, Tolley M, Demaine E, Rus D, Wood R. Applied origami. A method for building self-folding machines. Science. 2014;345(6197):644–646. doi: 10.1126/science.1252610. [DOI] [PubMed] [Google Scholar]
- 14.Kuribayashi K, et al. Self-deployable origami stent grafts as a biomedical application of Ni-rich TiNi shape memory alloy foil. Mater Sci Eng A. 2006;419(1–2):131–137. [Google Scholar]
- 15.Andersen ES, et al. Self-assembly of a nanoscale DNA box with a controllable lid. Nature. 2009;459(7243):73–76. doi: 10.1038/nature07971. [DOI] [PubMed] [Google Scholar]
- 16.Gracias DH, Kavthekar V, Love JC, Paul KE, Whiteside GM. Fabrication of micrometer-scale, patterned polyhedra by self-assembly. Adv Mater. 2002;14(3):235–238. [Google Scholar]
- 17.Peraza-Hernandez EA, Hartl DJ, Malak RJ, Jr, Lagoudas DC. Origami-inspired active structures: A synthesis and review. Smart Mater Struct. 2014;23(9):094001. [Google Scholar]
- 18.Hoberman C. 2010. Folding structures made of thick hinged sheets. US Patent 7,794,019 B2,14.
- 19.Tachi T. Rigid-foldable thick origami. In: Wang-Iverson P, Lang RJ, Yim M, editors. Origami 5. CRC; Boca Raton, FL: 2011. pp. 253–263. [Google Scholar]
- 20.Huffman DA. Curvature and creases: A primer on paper. IEEE Trans Comput. 1976;C-25(10):1010–1019. [Google Scholar]
- 21.Hull TC. Project Origami: Activities for Exploring Mathematics. 2nd Ed CRC; Boca Raton, FL: 2012. [Google Scholar]
- 22.Mahadevan L, Rica S. Self-organized origami. Science. 2005;307(5716):1740. doi: 10.1126/science.1105169. [DOI] [PubMed] [Google Scholar]
- 23.Miura K. The science of Miura-ori: A review. In: Lang RJ, editor. Origami 4. AK Peters; Natick, MA: 2009. pp. 87–99. [Google Scholar]
- 24.Schenk M, Guest SD. 2011. Origami folding: A structural engineering approach. Origami 5, Wang-Iverson P, Lang RJ, Yim M (CRC, Boca Raton, FL) pp 293–305.
- 25.Wei ZY, Guo ZV, Dudte L, Liang HY, Mahadevan L. Geometric mechanics of periodic pleated origami. Phys Rev Lett. 2013;110(21):215501. doi: 10.1103/PhysRevLett.110.215501. [DOI] [PubMed] [Google Scholar]
- 26.Tachi T. Proceedings of the International Association for Shell and Spatial Structures. 2009. Generalization of rigid foldable quadrilateral mesh origami. , eds Domingo A, Lazaro C (Universidad Politecnica de Valencia, Valencia, Spain), pp 2287–2294. [Google Scholar]
- 27.Gattas JM, Wu W, You Z. Miura-base rigid origami: Parameterizations of first-level derivative and piecewise geometries. J Mech Des. 2013;135(11):111011. [Google Scholar]
- 28.Silverberg JL, et al. Applied origami. Using origami design principles to fold reprogrammable mechanical metamaterials. Science. 2014;345(6197):647–650. doi: 10.1126/science.1252876. [DOI] [PubMed] [Google Scholar]
- 29.Lv C, Krishnaraju D, Konjevod G, Yu H, Jiang H. Origami based mechanical metamaterials. Sci Rep. 2014;4:5979–5981. doi: 10.1038/srep05979. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Tachi T. Proceedings of the International Association for Shell and Spatial Structures. 2009. One-Dof cylindrical deployable structures with rigid quadrilateral panels. , eds Domingo A, Lazaro C (Universidad Politecnica de Valencia, Valencia, Spain), pp 2295–2305. [Google Scholar]
- 31.Tachi T, Miura K. Rigid-foldable cylinders and cells. J Int Assoc Shell and Spatial Structures. 2012;53(4):217–226. [Google Scholar]
- 32.Filipov ET, Tachi T, Paulino GH. 2015. Toward optimization of stiffness and flexibility of rigid, flat-foldable origami structures. The 6th International Meeting on Origami in Science, Mathematics and Education, eds Kawasaki T, Uehara R, Tachi T, Maekawa J (University of Tokyo, Tokyo), p 121.
- 33.Lauff C, et al. 2014. Differentiating bending from folding in origami engineering using active materials. Proceedings of the ASME 2014 International Design Engineering Technical Conferences & Computers and Information Engineering Conference (ASME, Buffalo, NY), p V05BT08A040.
- 34.Giampieri A, Perego U, Borsari R. A constitutive model for the mechanical response of the folding of creased paperboard. Int J Solids Struct. 2011;48(16–17):2275–2287. [Google Scholar]
- 35.Mentrasti L, Cannella F, Pupilli M, Dai JS. Large bending behavior of creased paperboard. I. Experimental investigations. Int J Solids Struct. 2013;50(20–21):3089–3096. [Google Scholar]
- 36.Lechenault F, Thiria B, Adda-Bedia M. Mechanical response of a creased sheet. Phys Rev Lett. 2014;112(24):244301. doi: 10.1103/PhysRevLett.112.244301. [DOI] [PubMed] [Google Scholar]
- 37.Cerda E, Chaieb S, Melo F, Mahadevan L. Conical dislocations in crumpling. Nature. 1999;401(6748):46–49. [Google Scholar]
- 38.Fratzl P, Weinkamer R. Natures hierarchical materials. Prog Mater Sci. 2007;52(8):1263–1334. [Google Scholar]
- 39.Gibson LJ, Ashby MF, Harley BA. Cellular Materials in Nature and Medicine. Cambridge Univ Press; Cambridge, UK: 2010. [Google Scholar]
- 40.Ahn BY, et al. Printed origami structures. Adv Mater. 2010;22(20):2251–2254. doi: 10.1002/adma.200904232. [DOI] [PubMed] [Google Scholar]
- 41.Hibbitt D, Karlsson B, Sorensen P. 2010. ABAQUS FEA Version 6.10 (Dassault Systemes, Vélizy-Villacoublay, France)
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.