Implications of simplified linkage equilibrium SNP simulation

Golan et al. (1) report that restricted maximum likelihood (REML) seriously underestimates SNP heritability when using a case–control design. Their conclusions are based on results from simplified linkage equilibrium SNP simulation (SLES), which the authors acknowledge may be unrealistic.

We simulated case–control data using the liability threshold model (1, 2), based on a real genome-wide association study (GWAS) of 800,000 SNPs from 64,000 samples, i.e., a genome-wide linkage disequilibrium SNP simulation (GLDS). Our simulation used a population disease risk of K = 0.01 and proportion of cases in the sample of P = 0.5 (therefore, there were 640 cases and 640 controls in the estimation analyses). A random 10,000, 1,000, or 100 SNPs across the genome were selected as risk loci. The genomic relationship matrix (GRM) was based on all of the SNPs. For comparison, the SLES (without real GWAS data) was used, following Golan et al. (1) where the GRM was calculated only from the risk SNPs that are independent from each other.

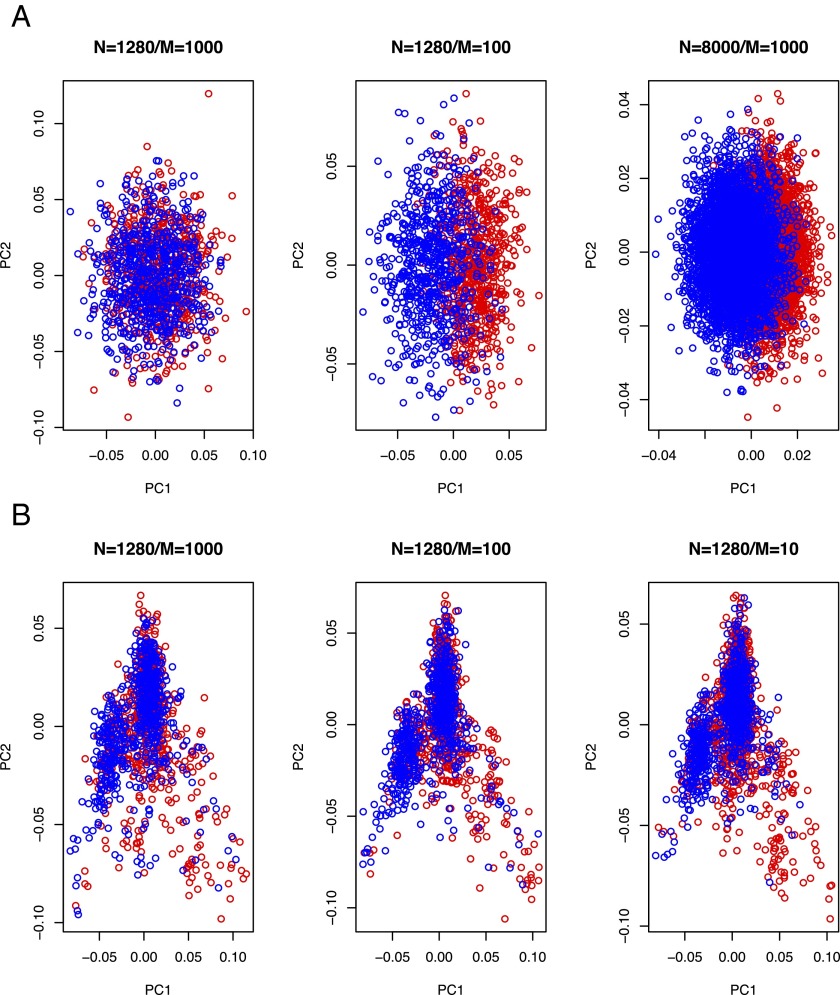
In Fig. 1A, we show that SLES unrealistically inflates the correlation between the eigenvectors of the GRM and disease status compared with GLDS (Fig. 1B) or that inferred from real data [e.g., figure S1 in the study by Gusev et al. (3)]. The artifactual correlation between the eigenvectors and disease status caused the inaccuracy of the REML estimates. The bias depends on the ratio of the number of individuals (N) to the number of risk SNPs (M) (Fig. 1). Unlike REML, a sophisticated approach, Haseman–Elston regression [referred to as phenotype correlation–genotype correlation (PCGC) by Golan et al. (1)] does not use the eigensystem of covariance structure; therefore, SLES does not affect the PCGC estimate (1). With GLDS, the REML estimates were stable and close to the true value regardless of the value of N/M (Fig. 2A). With SLES, the REML estimates were severely biased with increasing value of N/M (Fig. 2A).

Fig. 1.

Artifactual correlation between the eigenvectors of the GRM and disease status generated from the SLES simulation. (A) With the SLES simulation, the association between the eigenvectors and case–control status is unrealistically inflated when the value for N (# individuals)/M (# SNPs) increases. The correlation between the first principal component and disease status is 0.14, 0.70, and 0.63 with the value for N/M = 1.3, 13, and 8, respectively. Population disease risk of K = 0.01 and proportion of cases in the sample of P = 0.5 were used. Red represents cases, and blue represents controls. (B) With the GLDS simulation, the association between the eigenvectors and case–control status is negligible, regardless of the values for N/M, i.e., more realistic compared with the SLES. The correlation between the first principal component and disease status is 0.04, 0.03, and 0.06, with the value for N/M = 1.3, 13, and 130, respectively (GLDS could not simulate n = 8,000, because a GWAS data set of ∼400,000 individuals would be needed; instead, we tested it with an extreme with M = 10, i.e., N/M = 130). Population disease risk of K = 0.01 and proportion of cases in the sample of P = 0.5 were used. Red represents cases, and blue represents controls.

Fig. 2.

REML bias is negligible with a more realistic simulation and real data. (A) The average of estimated SNP heritability and empirical SE bar of the mean estimate from REML with GLDS simulation (blue line) and SLES simulation (red line) over 50 replicates. The true simulated SNP heritability is 0.5. (B) Estimated SNP heritability from REML and PCGC with real data analyses [to be compared with figure 2B in Golan et al. (1)]. We excluded two diseases that had highly confounded population structure [figure S1 in Gusev et al. (3)]. HE, Haseman–Elston regression. (C) Estimation error assuming that PCGC estimate is true value [to be compared with figure S4 in Golan et al. (1)].

We considered results from real data analyses (3) and plotted published SNP heritability estimates against the sample size for nine diseases (Fig. 2B). There was no difference between REML and PCGC, regardless of sample size, which was strikingly different from figure 2B in the study by Golan et al. (1). We also show estimation errors for the nine diseases assuming that the PCGC estimates are the true values (Fig. 2C), which were again dramatically different from results in figure S4 from Golan et al.

In derivation of the correction factor for case–control ascertainment bias, Lee et al. (2) used a simulation from a multivariate normal distribution based on a predefined relationship matrix. In real data analyses, the true relationship matrix is not known but can be approximated from genotypes, i.e., GRM pairwise estimator is unbiased under linkage disequilibrium; that is, the expectation of the estimator for each SNP is the kinship in the identical-by-descent (IBD) fraction sense (4), and therefore so is the estimate averaged over multiple SNPs. SLES ignores the concept of linkage disequilibrium, IBD, and coalescence. We urge researchers to use a more realistic genetic model (e.g., GLDS at least) in their simulation strategies and to be cautious of results drawn from SLES (1, 5).