The use of restricted maximum likelihood (REML) to estimate the heritability explained by common SNPs in a genome-wide association study (GWAS) of quantitative traits was proposed by Yang et al. (1) and implemented in the widely used GCTA software. Lee et al. (reference 2 in ref. 2) tries to extend REML to estimate heritability in case–control GWAS of disease.
Our paper (3) demonstrates that Lee et al.’s method suffers from consistent downward bias. Most importantly—and contrary to the behavior of any reasonable estimator—the bias increases with study size. To alleviate these problems, we developed an alternative approach—phenotype correlation–genotype correlation (PCGC) regression.
The flaws with Lee et al.’s method have been confirmed by others (4–6). They do not affect REML in general, but only the extension to case–control studies.
Dr. S. H. Lee (2) claims our paper exaggerates the downward bias in his method because our simulations use SNPs with simplified linkage disequilibrium (SLD) rather than actual linkage disequilibrium (ALD) patterns. He asserts that SNPs with SLD create an unrealistic correlation between the phenotype and the top principal component of the genetic-relationship matrix, and that this correlation causes the observed bias. To support his claim, he compares simulations with SLD vs. ALD.
However, Dr. S. H. Lee compares apples to oranges. Although both simulations use 1,280 individuals, his SLD simulation uses only few SNPs (100–1,000), whereas the ALD simulation uses many SNPs (800,000, with only 100–1,000 being causal). According to random-matrix theory, the behavior of the top principal component depends on N/M, where N is the number of individuals studied, and M is the “effective” number of SNPs (after accounting for ALD patterns; see reference 22 in ref. 3). It is thus pointless to compare simulations with radical differences in the effective number of SNPs.
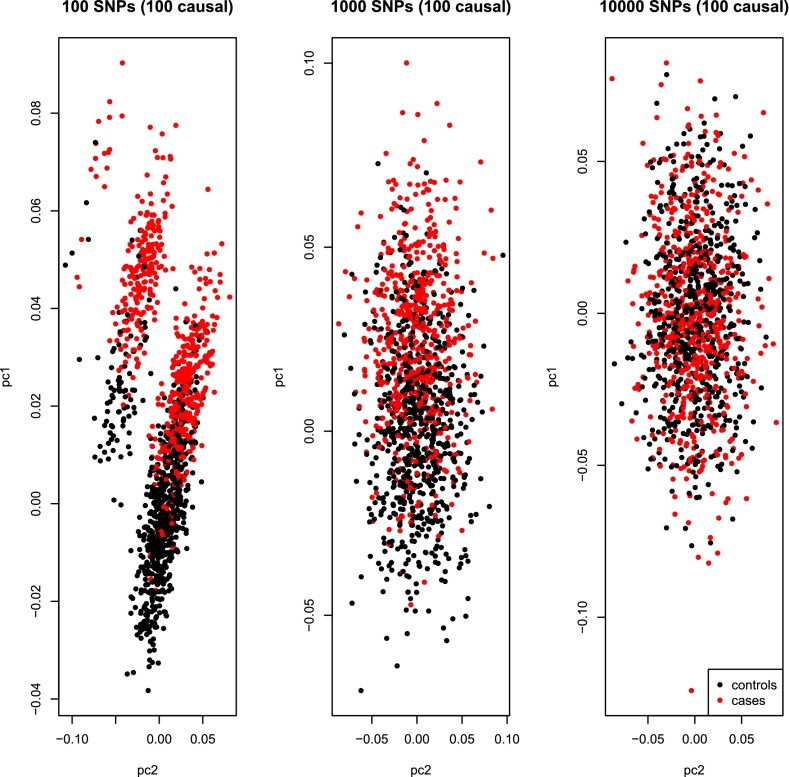
To demonstrate this point, we reran our simulations, fixing the number of causal SNPs to 100, but changing the overall number of SNPs from 100 (as in Dr. S. H. Lee’s simulations), to 1,000 or 10,000 (the latter used in our simulations). As expected, once the ratio N/M returns to the realm of reasonable values, the unrealistic correlation between the top principal component and the phenotype disappears (Fig. 1).
Fig. 1.
The correlation between the top principal component and the phenotype depends on the number of genotyped SNPs and not only on the number of causal SNPs. We used our method (3) to simulate GWAS of 1,280 individuals as in Dr. S. H. Lee’s letter (2), fixing the number of causal SNPs to 100, but changing the overall number of SNPs from 100 to 1,000–10,000. It is apparent that, as expected according to random matrix theory, as the number of genotyped SNPs increases, the correlation between the top PC and the phenotype diminishes. Importantly, because we simulate 10,000 “effective” SNPs, these simulations are equivalent to simulating roughly 100,000 SNPs with realistic linkage disequilibrium. In our paper, we used simulations with 10,000 SNPs, which do not present the unrealistic eigenstructure observed by Dr. S. H. Lee.
Thus, the phenomenon seen by Dr. S. H. Lee is not due to the use of SLD vs. ALD data, but to different numbers of SNPs in his simulations.
Finally, Dr. S. H. Lee cites a paper he claims shows (reference 3 in ref. 2, supplementary table S32) no downward bias relative to PCGC regression for several diseases. In fact, the bias is clear in columns 3 and 4 of the table; it disappears in columns 5 and 6 only because correction for population structure was not handled correctly.
Because bias should increase with size, a recent huge GWAS of schizophrenia (6) is particularly informative. Applying Lee et al.’s method to subsamples of varying sizes, the authors report that estimated heritability decreases sharply with sample size. Notably, Dr. S. H. Lee is a coauthor of ref. 6.
To conclude, papers by multiple authors—including Dr. S. H. Lee himself—show (3–6) that Lee et al.’s method is biased downward, with bias growing with sample size.
Footnotes
The authors declare no conflict of interest.
References
- 1.Yang J, et al. Common SNPs explain a large proportion of the heritability for human height. Nat Genet. 2010;42(7):565–569. doi: 10.1038/ng.608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Lee SH. Implications of simplified linkage equilibrium SNP simulation. 2015;112:E5449–E5451. doi: 10.1073/pnas.1502868112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Golan D, Lander ES, Rosset S. Measuring missing heritability: Inferring the contribution of common variants. Proc Natl Acad Sci USA. 2014;111(49):E5272–E5281. doi: 10.1073/pnas.1419064111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Yang J, Zaitlen NA, Goddard ME, Visscher PM, Price AL. Advantages and pitfalls in the application of mixed-model association methods. Nat Genet. 2014;46(2):100–106. doi: 10.1038/ng.2876. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Chen G-B. Estimating heritability of complex traits from genome-wide association studies using IBS-based Haseman–Elston regression. Front Genet. 2014;5:107. doi: 10.3389/fgene.2014.00107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Loh P-R, et al. 2015. Contrasting regional architectures of schizophrenia and other complex diseases using fast variance components analysis. bioRxiv: dx.doi.org/10.1101/016527.