Core formation and core composition from coupled geochemical and geophysical constraints

Significance

We combine, for the first time to our knowledge, two approaches to study Earth’s core composition: a geochemical approach based on trace element depletion in the mantle and a geophysical approach based on a seismically lighter and faster (than pure iron−nickel) core. The joint approach allows making strong statements; first of all, as opposed to the current belief, Earth must have accreted material that is more oxidized than the present-day mantle, similar to that of planetesimals such as 4-Vesta, and got reduced to its present state during core formation. Secondly, core light-element concentrations in those conditions are 2.7% to 5% oxygen alongside 2% to 3.6% silicon; the oxygen concentrations in the core are higher than previously thought, and, conversely, silicon concentrations are lower than previous estimates.

Abstract

The formation of Earth’s core left behind geophysical and geochemical signatures in both the core and mantle that remain to this day. Seismology requires that the core be lighter than pure iron and therefore must contain light elements, and the geochemistry of mantle-derived rocks reveals extensive siderophile element depletion and fractionation. Both features are inherited from metal−silicate differentiation in primitive Earth and depend upon the nature of physiochemical conditions that prevailed during core formation. To date, core formation models have only attempted to address the evolution of core and mantle compositional signatures separately, rather than seeking a joint solution. Here we combine experimental petrology, geochemistry, mineral physics and seismology to constrain a range of core formation conditions that satisfy both constraints. We find that core formation occurred in a hot (liquidus) yet moderately deep magma ocean not exceeding 1,800 km depth, under redox conditions more oxidized than present-day Earth. This new scenario, at odds with the current belief that core formation occurred under reducing conditions, proposes that Earth’s magma ocean started oxidized and has become reduced through time, by oxygen incorporation into the core. This core formation model produces a core that contains 2.7–5% oxygen along with 2–3.6% silicon, with densities and velocities in accord with radial seismic models, and leaves behind a silicate mantle that matches the observed mantle abundances of nickel, cobalt, chromium, and vanadium.

Earth formed ∼4.56 billion years ago (1–3), over a period of several tens of millions of years, through the accretion of planetary embryos and planetesimals (4). The energy delivered by progressively larger impactors maintained Earth’s outer layer as an extensively molten (4) magma ocean. Gravitational segregation of metal and silicate within the magma ocean resulted in the primary differentiation of the planet characterized by a metallic core and silicate mantle. Although numerous accretion/core formation models have been proposed (5, 6), perhaps the simplest in terms of quantitative testability postulates that the molten metal and silicate maintained chemical equilibrium (7–11), allowing phase relations and partitioning constraints to be applied in modeling their chemical evolution. This scenario couples the chemical evolution of the mantle and core with the evolving conditions (depth, pressure, temperature, composition) in the magma ocean that directly influence partitioning behavior and the resulting composition of metal and silicate.

The primary observations that constrain core formation models are (i) siderophile abundance patterns in the silicate mantle, (ii) the geophysically inferred requirement that the core contains elements lighter than iron (12), and (iii) the concentration of FeO (e.g., redox) in the primitive upper mantle. Assuming that core formation proceeds under conditions where metal−silicate equilibrium is maintained, it should be possible (13, 14) to invert for the pressure (P), temperature (T), composition (X), and oxygen fugacity (fO₂) conditions of core formation that satisfy all of these constraints.

Depletion of siderophile elements in the present-day mantle (relative to chondrites) is the direct result of metal−silicate equilibration and core formation (5, 7–9, 11) during which these elements were scavenged from the silicate and sequestered in the core. Numerous experiments (5, 7–11, 14–18) have been performed to determine the metal−silicate partitioning of siderophile elements, parameterizing these results as a function of thermodynamic variables. Here we consider four siderophile elements: nickel, cobalt, chromium, and vanadium. These are the only elements whose metal−silicate partitioning has been studied under the broadest range of P–T conditions, thanks to recent experimental advances with the laser-heated diamond anvil cell (16, 17, 19); therefore, we expect the most-accurate predictions with no recourse to extrapolation. These partition coefficients have then been extensively used to model diverse core formation scenarios, characterized by various P–T–X–fO₂ paths, to determine conditions that produce a model silicate mantle that has the same siderophile element patterns as Earth’s mantle for all four elements. As illustrated below, many P–T–X–fO₂ paths yield satisfactory agreement, but no unique solution has been identified.

Additional constraints arise from consideration of the composition of the core, which can be constrained through geophysical inference. If metal−silicate equilibrium was maintained along a particular P–T–X–fO₂ path, then the composition of the core is thermodynamically linked to that of the silicate magma ocean, and numerous metal−silicate partitioning experiments have shown that two of silicate mantle’s major elements, silicon and oxygen, can partition into the metallic liquid. As is the case for trace elements, the amount of Si and O dissolved in the core is directly linked to the conditions of equilibrium prevailing during differentiation in the magma ocean. Core composition (in terms of light elements) produced from a particular core formation model must satisfy the geophysically observed seismic velocities and density of the core, and more specifically of the outer core; because the inner core represents only 5% of the core’s mass, its crystallization barely changes the composition of the outer core in terms of light elements, and this minor adjustment is much smaller than the uncertainties on the compositional models.

Methods

To produce a geochemically and geophysically consistent model of the terrestrial core formation, we use the following procedure (details described below and in SI Appendix). First, core and mantle compositions resulting from the various core formation models are calculated using a broad range of model parameters. A geochemical filter is applied eliminating models that fail to satisfy the present-day mantle concentrations of Ni, Co, Cr, V, and FeO (20). The geophysical constraints are then applied to the remaining models to eliminate those with core Si and O concentrations that do not yield seismic parameters consistent with the AK135 (21) radial seismological model. The resulting models define a set of allowable P−T−X−fO₂ paths that, for the first time to our knowledge, agree with both the existing mantle siderophile abundance patterns and geophysically inferred core compositions.

The standard model of core formation stipulates that the core formed in ∼30 Ma (22, 23) and therefore took place during Earth’s accretion. As accretionary material was added to the proto-Earth, the metal separated from the silicate and equilibrated in the magma ocean, and was then transported to the core without further equilibration with the solid silicate mantle (5, 24). This evolutionary process, known as multistage core formation, was used here and discretized here in 1,000 steps. At each stage (or accretion step), the pressure at the base of the magma ocean is calculated as a function of total accreted mass and magma ocean depth, which is a free parameter. The temperature at the base of the magma ocean is then calculated using mantle geotherms described below; the choice of mantle geotherm is another free parameter. Finally, the FeO content (oxygen fugacity, or composition) of the magma ocean is calculated at each step to follow a given redox path, which is the last free parameter of the model. At each accretion step, P, T, and X_FeO are used to calculate the composition (Ni, Co, V, Cr, O, and Si) of the metal equilibrated at the base of the magma ocean as well as that of the coexisting magma ocean, using Monte Carlo simulations (see SI Appendix) to fully propagate all uncertainties (SI Appendix, Table S1). Finally, the metal is extracted to the core. The process is repeated (1,000 times) until Earth is fully accreted, and the core is fully formed. At the end of accretion, the mantle and core reach their final composition for the six aforementioned elements. This can be conveniently expressed as either concentrations (in the case of Si and O) in the metal, or as a metal–silicate concentration ratio (i.e., an effective core−mantle partition coefficient) in the case of Ni, Co, V, and Cr. The final composition is the path integral of the entire process, and is solely determined by the input parameters of the model.

Results and Discussion

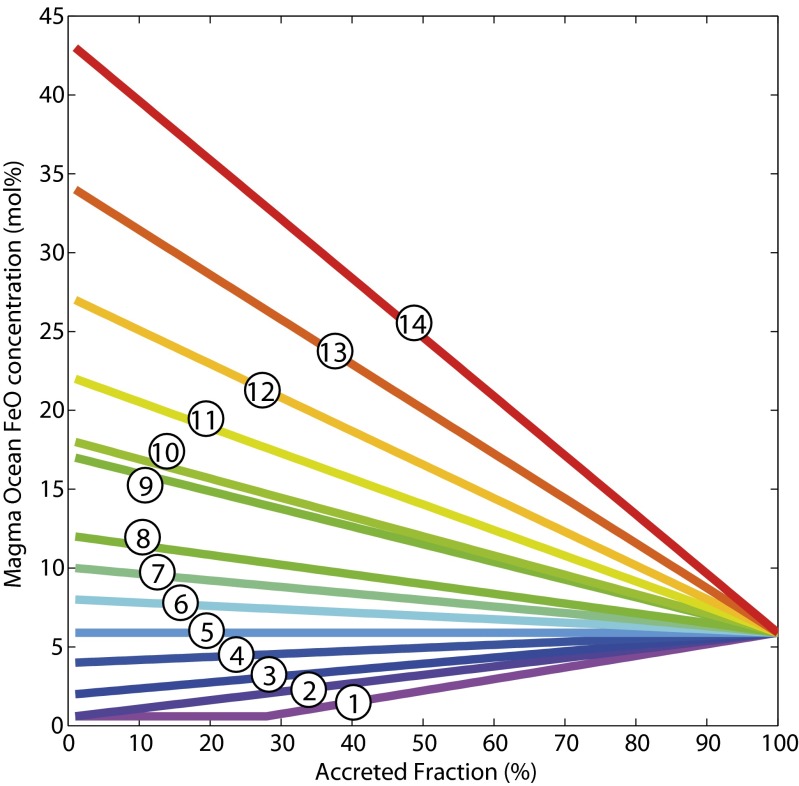
The main parameters of the model (magma ocean depth, geotherm, and redox path) were tested over the broadest possible range. The final depth of the magma ocean was varied from 0 km to 2,900 km: in other words, from an evanescent thin magma ocean to a fully molten mantle, respectively. Four magma ocean geotherms spanning the whole plausible temperature range were used: peridotite solidus (25), two (cool and hot) peridotite liquidus (25, 26), and an intermediate average liquidus. Last, 14 magma ocean redox paths, equating to the variation in the magma ocean FeO content during accretion, were tested (Fig. 1) with initial conditions spanning 4 log units of fO₂ and ranging from very reduced conditions (below those existing in enstatite chondrites) to very oxidizing conditions (those observed in CI carbonaceous chondrites). The final redox condition for each model is required to yield the present-day value for the mantle (5.9 mol% FeO). All details are in SI Appendix.

Fig. 1.

The evolution of FeO concentration in the magma ocean, over the course of accretion, for 14 redox models. The final FeO content is fixed at the present-day value for the primitive upper mantle, 5.9% FeO (all fractions in mol%). Path 5 is the constant redox path, where FeO concentration is maintained at 5.9% throughout accretion. Paths 1–4 start more reduced than the present-day mantle, and the magma ocean oxidizes throughout accretion. Paths 6–14 all start more oxidized than the present-day mantle, and the magma ocean becomes more reduced over the course of accretion. Some paths have initial FeO concentrations similar to the silicate fractions of common meteorite groups: paths 1 and 2 are similar to that of EH chondrites, but path 1 has a constant low fO₂ until 28% accretion as proposed in ref. 15; path 9 is similar to that of H chondrites; path 10 is similar to that of HED meteorites; paths 11 through 14 are similar to that of L, LL, CV, and CI chondrites, respectively. The paths span four orders of magnitude in initial fO₂ ranging from IW-4.5 (paths 1 and 2) to IW-0.6 (path 14), so as to cover the entire plausible range of redox conditions found in Earth’s accretionary building blocks.

The metal−silicate partition coefficients (SI Appendix, Figs. S1 and S2) vary as a function of final magma ocean pressure for the whole range of model parameters (geotherm and redox). In addition, siderophile element activity coefficients in the metallic phase are also dependent upon the concentrations of Si and O in the metallic melt (16, 18, 27, 28). Geochemically consistent models are those for which the mantle abundances for Ni, Co, Cr, and V are simultaneously satisfied, within uncertainties. As most recent findings (16, 17, 29) show, this analysis does not yield a unique solution to the problem, especially when properly propagating all uncertainties (29) on the thermodynamic parameters. Here we find solutions for all geotherms and all redox paths, meaning that there is always a range of magma ocean depths where core formation leaves behind a geochemically consistent mantle, regardless of temperature and redox. The allowable depth range is fairly narrow, however, and spans the 42- to 75-GPa range for reducing conditions to 50–63 GPa for oxidizing conditions (Table 1 and SI Appendix, Table S2), limiting the magma ocean to midmantle depths.

Table 1.

Model outputs of multistage core formation model for which Ni, Co, V, and Cr concentrations in the mantle match the present-day geochemical observables

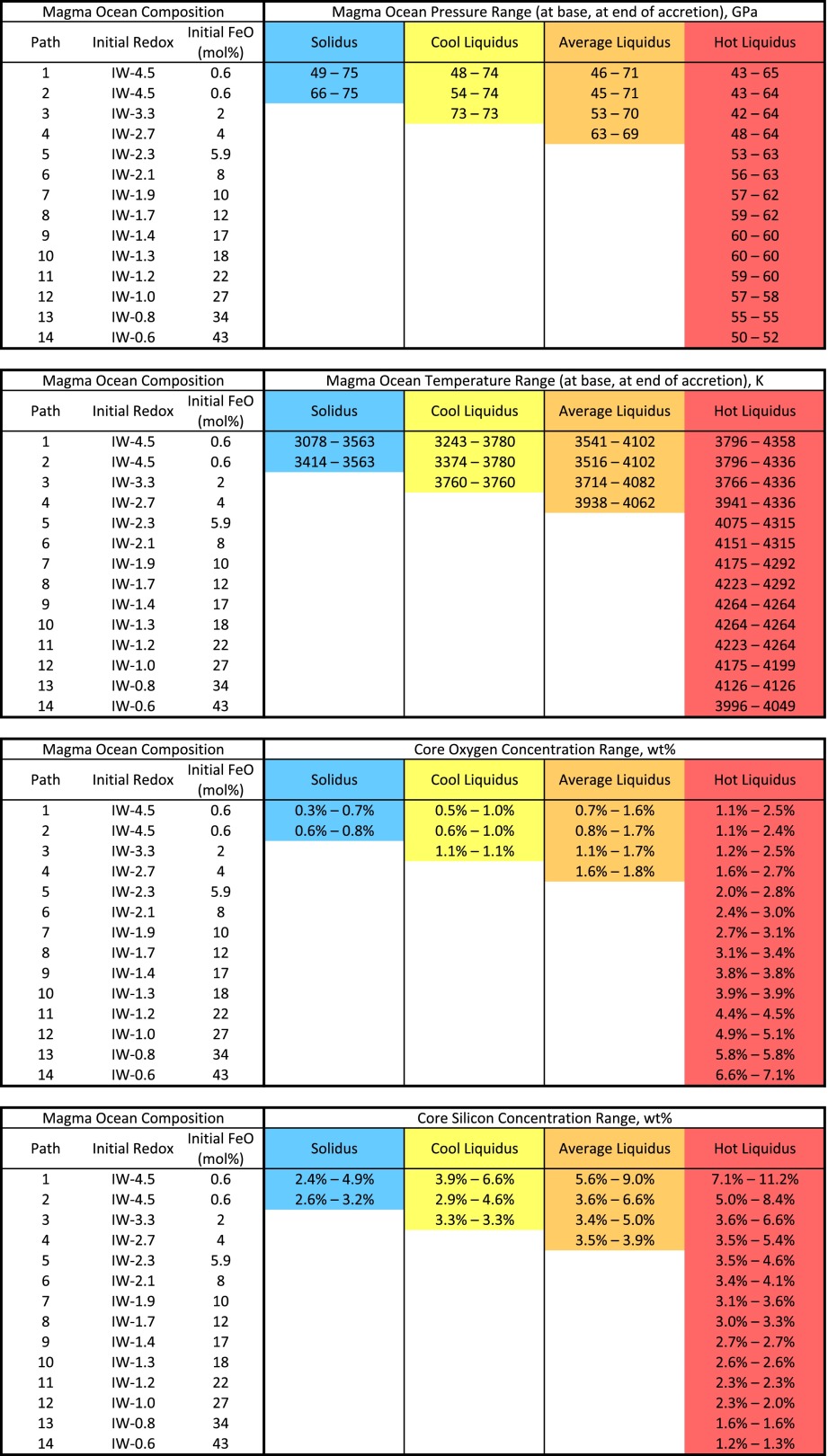The four sections represent, from top to bottom, (i) final magma ocean pressure range, (ii) final magma ocean temperature range, (iii) final oxygen core concentration, and (iv) final silicon core concentrations; these are given for each redox path (Fig. 1) and each geotherm (solidus in blue, cool liquidus in yellow, average liquidus in orange, hot liquidus in red). When no solution for the relevant redox/geotherm pair is found, no numbers were reported (empty cells). It noteworthy that low fO₂ models have solutions for all geotherms from cold to hot. Thus, the combined pressure and temperature range where solutions can be found is large, and so are the Si and O concentration ranges in the core. A natural result is the breadth of the solutions for those models in Fig. 2. Conversely, high fO₂ models have solutions only with the hottest geotherm, yielding narrow pressure and temperature ranges, and therefore narrow Si and O concentration ranges in the core. A more detailed table can be found in SI Appendix, Table S2, containing additional information such as average pressure and temperature, depth, and total light-element content for each model.

The low-fO₂ models (Fig. 1: blue curves, paths 1–4) have solutions over a large range of temperature and pressure conditions, whereas the higher fO₂ models (Fig. 1: greens to reds, paths 6–14) have solutions in a smaller range of magma ocean pressures and are restricted to warmer geotherms. This is because core formation models at low fO₂ can occur over a much larger P and T range than at higher fO₂; this is seen in Table 1, where the most-reducing models have solutions for all geotherms and for a pressure range spanning more than 30 GPa (42–75 GPa) and a temperature range spanning 1,300 K. This is a consequence of the partitioning behavior of V and Cr; they have a natural tendency to be fairly lithophile. Low fO₂ makes them more siderophile (SI Appendix, Eq. 2) across the board, irrespective of P–T conditions, and therefore their concentration in the mantle after core formation can be satisfied for a large P–T range of metal−silicate equilibration. High fO₂, on the other hand, makes them even more lithophile, and it is rather the incorporation of Si and O in the metal that increases their siderophile character, tipping the balance in the right way. To be effective and have a strong quantitative effect, this process requires a significant amount of Si and especially O to be present in the metal, which in turn requires high equilibration temperatures. Therefore, as seen in Table 1, the oxidizing models are restricted to the single hottest geotherm, naturally yielding a narrower P–T range where core formation could have taken place. In turn, this narrow P–T range is characterized by a narrow Si–O range for core composition, as can be seen in Fig. 2.

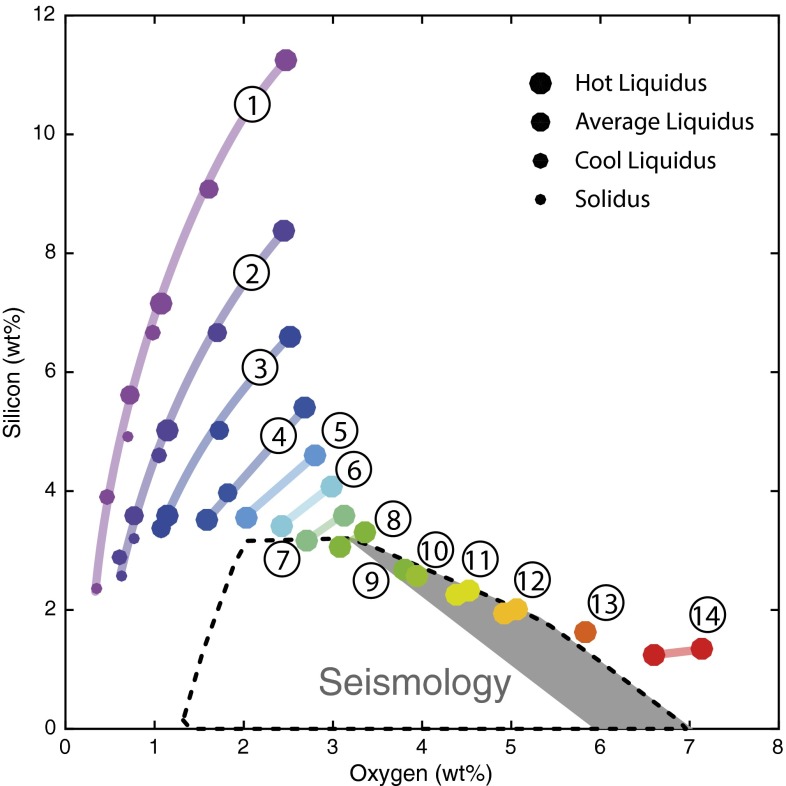
Fig. 2.

Core light-element (Si and O) composition that satisfies geochemistry (colored bands and symbols) and seismology (black dashed line and gray background). The geochemically consistent cores are generated from multistage core formation models, for all geotherms, all magma ocean depths, and all 14 redox conditions in Fig. 1 and Table 1 (this plot uses the same color code and numbering scheme). The points underlying the curves correspond to the lower and upper bounds on solutions for each geotherm in Table 1. The curves show the spread of possible core compositions for each redox model calculated by fully propagating all uncertainties and keeping the ones whose final silicate concentrations of siderophile elements (Ni, Co, V, Cr) match geochemistry within 1-σ uncertainty propagation (solutions with 2-σ uncertainty propagation can be found in SI Appendix). The spread of each curve reflects the range of depths and temperatures in the magma ocean where geochemically consistent models can be found (see Table 1 and SI Appendix, Table S2). The seismologically consistent composition space consists of the area delimited by the black dashed line; the grayed subarea corresponds to O–Si concentrations if the core contains no C and no S, and the rest of the polygon corresponds to O–Si concentrations if the core contains S and C (see SI Appendix): any core with an O–Si composition falling outside the black dashed line is not consistent with the AK135 radial seismic model. To satisfy both the geochemical constraint and the geophysical constraint simultaneously, geochemically consistent core compositions have to overlap with the area defined by the dashed black line. Only cores produced along redox paths 7–12, all strictly more oxidizing than present-day Earth, can satisfy this requirement. A larger tolerance on uncertainties (2-σ solution; see SI Appendix) extends possible solutions from path 6 to path 14, still strictly more oxidizing conditions than present-day Earth.

Core Si and O concentrations of these geochemically consistent models are plotted in Fig. 2, and grouped by redox condition (the numbers and colors matching the redox paths in Fig. 1 and Table 1). As expected, highly reducing conditions in the magma ocean produce cores that have high silicon and low oxygen contents, whereas oxidized magma oceans show the opposite behavior. Also, the larger P–T solution range for the low-fO₂ models translates into a broad range in Si and O concentrations in the core, and, conversely, high-fO₂ models with a smaller P–T solution range generate a more compact Si–O band.

To eliminate geophysically unacceptable models, we use recent results from ab initio molecular dynamics simulations to calculate the density and bulk sound velocity of liquid alloys in the (Fe,Ni)–O–Si–S–C system at core−mantle boundary (CMB) and inner-core boundary (ICB) pressure and temperature conditions (30). The details of the calculations can be found in SI Appendix. We fixed the core’s Fe/Ni ratio to 16, and let S and C concentration fluctuate anywhere in their plausible concentration range: 0–2% for S, and 0% to no upper limit on C. We then searched for all of the oxygen and silicon concentrations that matched the density and bulk sound velocity in the core, determined with the AK135 radial velocity model (at the CMB and ICB simultaneously). The O–Si solution space is plotted in Fig. 2, and is an area bounded by the dashed black line: O and Si compositions that lie outside of this area cannot fit the seismic constraints, meaning that a core with such a composition would not be consistent the AK135 radial seismic model. The gray shaded area inside the solution space corresponds to the subset of solutions for a C/S-free core (i.e., where C and S concentration is 0%). A more granular depiction of the solution space and O–Si boundaries can be found in SI Appendix, for various S and C contents. However, the polygon defined by the gray dashed line encompasses all possible oxygen and silicon concentrations that fit the seismological data, for any plausible carbon and sulfur concentration; it therefore defines the broadest possible oxygen and silicon concentration range that can produce a seismologically consistent core. It is clear from Fig. 2 that the cores produced under highly reducing conditions have O–Si concentrations outside of that range (Si too high, or O too low) and are therefore not geophysically consistent. The same applies for cores produced in the most-oxidizing conditions, which have O concentrations higher than geophysically allowable. Only geochemically consistent cores with initial magma ocean FeO content ranging between 10 mol% (path 7) and 26 mol% (path 12) have Si–O contents that match seismology. These models define a very narrow pressure range, 57–62 GPa, corresponding to a final magma ocean depth of 1,400–1,500 km, roughly the midmantle. This has strong implications for core composition: Combining the O and Si contents for all redox paths from 7 to 12 that are compatible with the seismic data yields a rather tightly constrained core composition of 2.7–5% oxygen and 2–3.6% silicon.

Our range of silicon concentrations is in agreement with inner core compositional models. Inner core light-element concentration derives from that of the outer core and is dependent on liquid–solid phase equilibrium (31, 32) in the metal. In a silicon- and oxygen-bearing outer core, only silicon is compatible in the solid phase and can enter the inner core, whereas oxygen is substantially incompatible and can only exist as trace amounts in the inner core (33). Hence, silicon represents the only light-element candidate for the inner core (34), and recent models have constrained the maximum amount to be 1–2% silicon (35). Assuming a solid/melt partition coefficient for Si in iron (33) around 1.2 ± 0.5, this implies that the outer core must contain between 0.7% and 3.5% silicon, hence entirely consistent with our range of 2–3.6%.

On the other hand, the high oxygen concentration in the outer core elegantly solves for one of the core’s most perplexing observations: that of the very strong density jump (4.8–7.4%) at the ICB (36, 37), between the liquid outer core and solid inner core. The density change due to melting is on the order of 1.7% (38), and the observation naturally calls for strong chemical buoyancy and a stark chemical contrast between the inner core and outer core; this can only be achieved by the presence of a very incompatible light element in the outer core. Oxygen is the only candidate among the four (C, O, Si, S) to exhibit that behavior (33), and concentrations between 2% and 5% at the ICB produce a 2.5–5.3% density contrast with respect to the oxygen-free composition (all other things being equal) assumed for the inner core. Adding the density change due to melting, the density contrast between our oxygen-rich outer core (4.2–7%) and an oxygen-free inner core is consistent with seismology.

Accretion under higher fO₂ requires higher FeO concentrations than that of the present-day mantle. The core is an obvious sink for that excess FeO, because its incorporation increases the oxygen content of the core. Using simple mass balance constraints, we can calculate the amount of oxygen added to the core by assuming that all of the excess FeO in the mantle (in excess of the 5.9 mol% in the present-day mantle) was added to the core during the differentiation process. At constant redox (Fig. 1: path 5), there is no excess FeO to add to the core. A redox path starting with 8 mol% FeO, path 6, produces a total of 0.7% O in the core, less than that obtained from the equilibrium conditions (Fig. 2: curve 6). On the other hand, path 10 yields a total of 4.5% O in the core, more than that required by equilibrium metal−silicate partitioning (Fig. 2: curve 10). Path 9 yields good agreement between the calculated equilibrium oxygen content of the core and mass balance, yielding 2.3% O in the core. Of course, this argument neither rules out the possibility of FeO enrichment in the lower mantle (39) nor the simultaneous dissolution of Si and O in the core from the SiO₂ component of the mantle (40). Rather, it demonstrates that accretion, initiated under conditions more oxidizing than the present-day mantle, provides a necessary mechanism for an oxygen-rich core, and that the core can be the natural sink for the excess FeO supplied during accretion.

We have shown that geochemistry can constrain a range of conditions of core formation based on compatibility of Ni, Co, V, and Cr concentrations in present-day bulk silicate Earth, and that only a subset of these geochemically consistent models satisfies the present-day seismic density and bulk sound velocity of the core, constraining the Si–O concentration in the core. These geophysically consistent models are limited to those for which accretion proceeds from a redox state more oxidized than the present-day mantle. Accretion of objects with a high bulk FeO content, such as asteroids like 4-Vesta, is at odds with the standing paradigm that the core formed in reducing conditions, and constrains the light-element composition of the core to 2.7–5% oxygen and 2–3.6% silicon.