MCAT to XCAT: The Evolution of 4-D Computerized Phantoms for Imaging Research

Abstract

Recent work in the development of computerized phantoms has focused on the creation of ideal “hybrid” models that seek to combine the realism of a patient-based voxelized phantom with the flexibility of a mathematical or stylized phantom. We have been leading the development of such computerized phantoms for use in medical imaging research. This paper will summarize our developments dating from the original four-dimensional (4-D) Mathematical Cardiac-Torso (MCAT) phantom, a stylized model based on geometric primitives, to the current 4-D extended Cardiac-Torso (XCAT) and Mouse Whole-Body (MOBY) phantoms, hybrid models of the human and laboratory mouse based on state-of-the-art computer graphics techniques. This paper illustrates the evolution of computerized phantoms toward more accurate models of anatomy and physiology. This evolution was catalyzed through the introduction of nonuniform rational b-spline (NURBS) and subdivision (SD) surfaces, tools widely used in computer graphics, as modeling primitives to define a more ideal hybrid phantom. With NURBS and SD surfaces as a basis, we progressed from a simple geometrically based model of the male torso (MCAT) containing only a handful of structures to detailed, whole-body models of the male and female (XCAT) anatomies (at different ages from newborn to adult), each containing more than 9000 structures. The techniques we applied for modeling the human body were similarly used in the creation of the 4-D MOBY phantom, a whole-body model for the mouse designed for small animal imaging research. From our work, we have found the NURBS and SD surface modeling techniques to be an efficient and flexible way to describe the anatomy and physiology for realistic phantoms. Based on imaging data, the surfaces can accurately model the complex organs and structures in the body, providing a level of realism comparable to that of a voxelized phantom. In addition, they are very flexible. Like stylized models, they can easily be manipulated to model anatomical variations and patient motion. With the vast improvement in realism, the phantoms developed in our lab can be combined with accurate models of the imaging process (SPECT, PET, CT, magnetic resonance imaging, and ultrasound) to generate simulated imaging data close to that from actual human or animal subjects. As such, they can provide vital tools to generate predictive imaging data from many different subjects under various scanning parameters from which to quantitatively evaluate and improve imaging devices and techniques. From the MCAT to XCAT, we will demonstrate how NURBS and SD surface modeling have resulted in a major evolutionary advance in the development of computerized phantoms for imaging research.

I. INTRODUCTION

Computerized phantoms are finding an increasingly important role in medical imaging research. With the ability to simulate an unlimited number of known patient anatomies, they offer a practical means with which to quantitatively evaluate, compare, and improve medical imaging devices and techniques. In order for computerized phantoms to reach their full potential as a research tool, however, it is vital for them to be as anatomically realistic as possible. Otherwise, studies using them would not be indicative of what would occur in live patients.

Computerized phantoms generally fall into one of two categories: 1) voxelized or 2) mathematical phantoms. Based on segmented patient data, voxelized phantoms [1]–[8] are very realistic, but they are limited in their abilities to model anatomical variations and patient motion. They are essentially fixed to the patient data upon which they are based. To model a patient population, one would have to assemble voxelized models based on many different patient datasets. This would take a great amount of work and a long time to achieve since every structure in the body would have to be segmented for every phantom, most manually. As a result, voxelized phantoms have been limited to only a handful of models. Mathematical or stylized phantoms [9]–[13], on the other hand, are mathematically defined (typically using simple geometric primitives), so they can be easily manipulated to model anatomical variations and patient motion, but they are not very realistic due to the simplicity of the mathematical equations upon which they are based.

Current work in phantom development has focused on the development of “hybrid” phantoms that seek to combine the realism of a patient-based voxelized phantom with the flexibility of an equation-based mathematical phantom [14]. We have been leading the development of such phantoms for use in medical imaging research. Foremost among these are the four-dimensional (4-D) Mathematical Cardiac-Torso (MCAT), the 4-D NURBS-based Cardiac-Torso (NCAT), the 4-D extended Cardiac-Torso (XCAT), and the Mouse Whole-Body (MOBY) phantoms. The work we have done in creating these phantoms is representative of the evolution of computerized models toward more realistic hybrid models. In this paper, we will discuss each of these phantoms in detail, showing our progression from a simple geometrically based phantom to an ultrarealistic phantom based on state-of-the-art computer graphics techniques.

II. THE 4-D MATHEMATICAL CARDIAC-TORSO (MCAT) PHANTOM

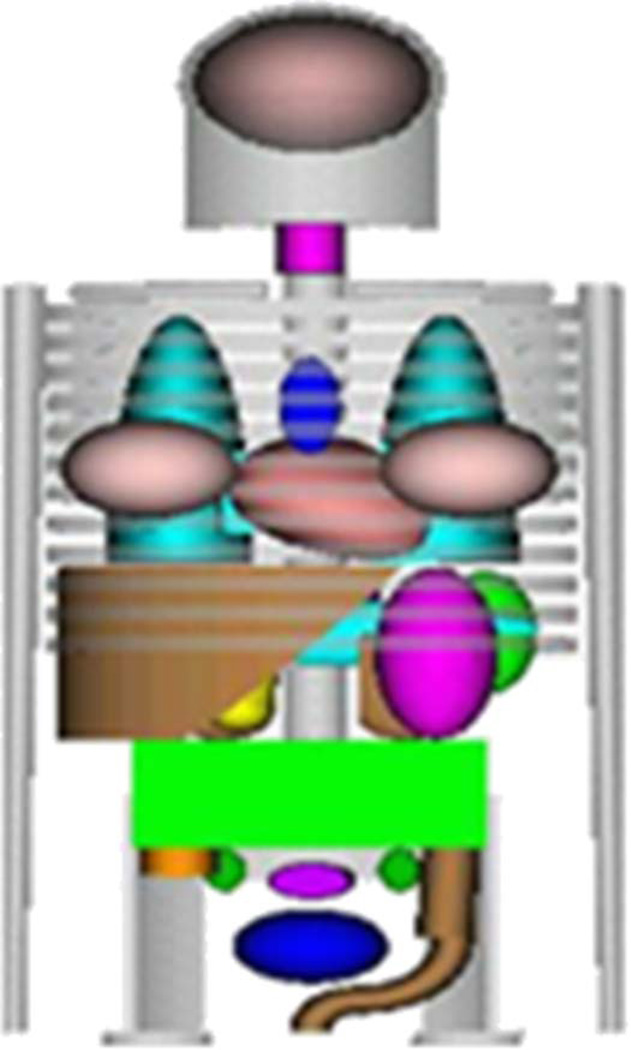
The 4-D MCAT phantom was first developed in our laboratory about 15 years ago as an improvement upon the original MIRD-5 stylized model [15] used for radiation dosimetry, Fig. 1. Since it was based on simple geometric primitives, the MIRD model was severely limited in its level of realism. To achieve a higher level of realism without sacrificing the flexibility of the mathematical basis, the MCAT anatomy was constructed using similar geometric primitives but used overlap, cut planes, and intersections of the geometric objects to form more realistic organ shapes for the human torso Fig. 2. The 4-D MCAT was developed for nuclear medicine imaging research, specifically, single-photon emission computed tomography (SPECT) and positron emission tomography (PET).

Fig. 1.

Original MIRD phantom [15] based on geometric primitives.

Fig. 2.

(a) Anterior and (b) posterior views of the 4-D MCAT phantom.

Like all computer-based phantoms, the 4-D MCAT can be used in conjunction with models of the imaging process [e.g., SPECT, PET, magnetic resonance imaging (MRI), and computed tomography (CT)]. These models include an accurate simulation of the physics and instrumentation of the imaging procedure. Many different methods have been developed and validated using comparisons to physical experiments [16]–[60]. To combine the MCAT with these simulators, the phantom software was set up so that it could generate voxelized representations of the anatomy at any user-defined resolution. Since the phantom is mathematically defined, there are no errors associated with generating the phantom at different resolutions. Depending on the modality, organs in the voxelized phantom can be set to different tissue properties. These voxelized representations can be used as input to any analytical or Monte Carlo based models of the imaging process to simulate multimodality imaging data. The top of Fig. 3 illustrates the use of the 4-D MCAT as a transmission phantom for the 72 keV radionuclide Thallium-201. The organs were set with their individual attenuation coefficients defined at 72 keV. Projection images, similar to those acquired from a patient during transmission imaging, were simulated from the voxelized attenuation coefficient phantom using a model of the projection process. The bottom of Fig. 3 shows the use of the 4-D MCAT as a radiopharmaceutical uptake phantom for Thallium-201. The intensity values of the organs in this case were set to their individual uptake ratios for the desired radiopharmaceutical. The projection images simulated from the uptake phantom emulate those that would be acquired during an emission-imaging scan. Areas of higher uptake are indicated by the brighter intensities, whereas areas of lower uptake are indicated by darker intensities.

Fig. 3.

Transmission and emission simulations using the 4-D MCAT.

In order to study the effects of patient involuntary motion on SPECT and PET imaging, models for the beating heart [13] and respiration [61] were developed for the MCAT. These models extended the phantom to a fourth dimension: time. Both models were parameterized so that a user can alter the magnitude or rates of each motion to simulate many different variations (normal and abnormal). The motions could be simulated separately (holding one constant at a given phase) or simultaneously. The MCAT simulates motion by outputting a series of three-dimensional (3-D) voxelized phantoms over a given time period, with each phantom representing a snapshot of the body as it moves. The time period, number of phantoms output, and type of motion are all determined by user-defined parameters.

The MCAT cardiac model was based on ellipsoids and was set up to emulate the changes in chamber volume, left ventricular wall thickness, and heart rotation [62]–[64] that occur throughout the cardiac cycle, as seen in Fig. 4. The changes and motion of the beating heart were simulated by altering the parameters that define the ellipsoid models. The ellipsoids were altered so that the heart mass and volume remained constant throughout the cardiac cycle and equal to that of an average male [65].

Fig. 4.

(a) 4-D MCAT cardiac model based on ellipsoids. The ventricles and atria are each defined by two ellipsoids, one for the inner and one for the outer boundary. (b) Single long-axis slices of the beating heart during end-diastole and end-systole. (c) Left ventricle chamber volume of the MCAT as compared to a normal curve for an adult male [66].

The respiratory model of the 4-D MCAT was based on known respiratory mechanics [61]. In order to simulate respiratory motion, we altered the geometric solids for the diaphragm, heart, ribs, and lungs through the manipulation of parameters defining them. To do this, we simulated the movement of the diaphragm during respiration by altering the parameters that define the height of the left and right diaphragm sections. The heart, liver, stomach, spleen, and kidneys were rigidly translated with the motion of the diaphragm. Tiled cut planes through the cylinder define the positions of the ribs in the MCAT (Fig. 2). The rib rotation and expansion/contraction that occur during respiration were simulated by altering the tilt angle of the ribs and modifying the anterior–posterior (AP) length of the rib cage. Fig. 5 shows coronal cut slices of the 4-D MCAT at end-inspiration and end-expiration. The time-varying parameters for the organs and structures were chosen to fit a volume curve for normal respiration [66]. Time curves were derived for both the diaphragm motion and the AP expansion of the chest.

Fig. 5.

(Top) Normal respiratory curve (from [67]). (Middle and bottom) 3-D and 2-D views of the MCAT at (left) end-inspiration and (right) end-expiration.

In addition to motion, the MCAT has the ability to model male and female anatomical variations. Female subjects are modeled in a limited fashion by simply adding breast extensions onto the male chest anatomy. Fig. 6 shows examples that demonstrate the ability of the phantom to vary patient anatomy. In each case, the phantom is altered to match the anatomy of the patient as determined by the patient’s PET scan [67], [68]. With this ability to modify the anatomy, the MCAT can be used to simulate a patient population involved in patient studies.

Fig. 6.

MCAT phantoms created with varying anatomies. In each case, the phantom was altered through the parameters that define the different structures to match the anatomy of the patient as determined by the patient’s PET scan [68], [69].

The 4-D MCAT represents a small improvement over the typical stylized phantom. It provides a better representation of the anatomy while maintaining the flexibility to model anatomical variations and patient motion. With its capabilities, the 4-D MCAT has been applied to many studies in emission imaging that seek to improve the quality of medical images. It has been used to research new image acquisition strategies and reconstruction algorithms; to investigate the effects of physical factors, anatomy, and motion on medical images; and to develop compensation methods for these effects. Despite its success, however, the MCAT is still limited in its ability to realistically model the human anatomy due to its geometrical design.

III. THE 4-D NURBS-BASED CARDIAC-TORSO (NCAT) PHANTOM

In order to create a better computational phantom for imaging research, we sought a new basis that would afford us the same capabilities as the 4-D MCAT but allow for much more realistic modeling of the human anatomy. Within the field of computer graphics, we found such a primitive in nonuniform rational B-splines (NURBS) [69], [70].

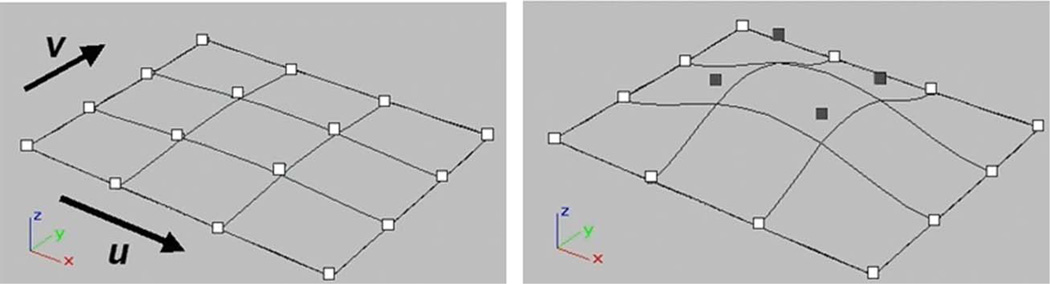
NURBS are widely used in computer graphics, animation, and computer-aided design to accurately model complex curves and three-dimensional surfaces. As such, they can accurately model the complex anatomical shapes of the body, providing a level of realism comparable to a voxelized phantom. In addition, NURBS are a very flexible, mathematical representation. Their shape can be altered easily via affine and other transformations. The shape is defined by a set of control points which form a convex hull around the surface. To alter the surface, one only has to apply transformations to these control points [69], [70], Fig. 7. With this flexibility, NURBS have the same ability to model anatomical variations and patient motion as a mathematical phantom. With these abilities, NURBS provide an excellent basis for a hybrid computerized phantom.

Fig. 7.

The shape of the NURBS surface is modified by manipulating its control points. In the above example, the shaded control points are translated upward, altering the shape of the surface.

The 4-D NCAT phantom [71]–[73] was thus developed as the next-generation MCAT phantom (Fig. 8). NURBS surfaces were used to construct the organ shapes using the 3-D Visible Human CT dataset¹ as their basis. The CT data consisted of 512 × 512 axial CT scans covering the entire body taken at 1 mm slice intervals with a pixel width of 0.898 mm per pixel. The CT data slices were manually segmented, and 3-D NURBS surfaces were fit to each segmented structure using the Rhinoceros NURBS modeling software [74]. Since it was based on imaging data, the anatomy of the NCAT is much more realistic than that of the MCAT.

Fig. 8.

(a) Anterior view of the 4-D NCAT. (b) Combined with models of imaging process, the phantom can simulate emission and transmission imaging data.

The NCAT was set up to have the same capabilities as its MCAT predecessor. It was extended into four dimensions to model the cardiac and respiratory motions using actual gated patient data as the basis. The cardiac motion [75] was based on 4-D tagged MRI data obtained from Ozturk of The Johns Hopkins University (JHU) and McVeigh of the National Institutes of Health and JHU. Three sets of tagged MR images from a normal subject were obtained and used to analyze the motion. The data were acquired for 26 time-frames over the cardiac cycle and included two sets of parallel, short-axis images and one set of long-axis images to analyze the x, y, and z deformation of the heart, respectively. From the motion of the tag lines in the data, the full 3-D motion of the heart over the cardiac cycle was analyzed and used to create time-dependent 3-D NURBS surfaces for each of the four chambers of the heart. A 4-D NURBS surface was then fit to the 3-D surfaces, creating a time-continuous 4-D NURBS cardiac model (Fig. 9). With its basis on patient-tagged MRI data, the NCAT heart illustrates the realistic contracting and twisting motion of the normal heart. The heart model was parameterized, including variables for ejection fraction, contraction, cardiac twist, heart rate, etc., so that it could model a wide variety of beating heart motions, normal and abnormal [75], [76].

Fig. 9.

Cardiac model of the 4-D NCAT. The model illustrates the contracting, twisting motion of a normal heart. Plots of the volume change in the chambers over time are shown at the right.

The NCAT respiratory motion was based on a set of respiratory-gated CT data from the University of Iowa taken of a normal volunteer at 5%, 40%, 75%, and 100% of his/her total lung capacity. By tracking landmark points on and within the respiratory structures, a general motion model for each organ and different regions inside the lungs was formulated. The motions were scaled down to correspond to normal tidal breathing (diaphragm motion ~1 cm) and incorporated into the phantom. We simulated the motion by applying transformations to the control points defining the respiratory structures. The motion the diaphragm was modeled by translating control points that define the left and right diaphragm surfaces. The heart, the stomach, and the spleen were translated rigidly up, down, backward, and forward with the movement of the diaphragm. The ribs were rotated about the axis through their costal necks to simulate their motion to expand and contract the chest. Control points defining the lungs and body surfaces were altered, expanding or contracting them, depending on the rib and diaphragm motion. Time curves were fit to the two time-varying parameters for the diaphragm motion and the AP expansion in the chest. These motions were set up to work in concert to produce a normal respiratory volume curve [75]. Fig. 10 shows two-dimensional (2-D) and 3-D views of the NCAT defined at end-inspiration and end-expiration. The respiratory motion is much more realistic than that of the 4-D MCAT. Similar to the beating heart, the respiratory model was parameterized in terms of chest and diaphragm breathing so as to model different types of respiratory motions. With its realism and flexibility, the 4-D NCAT cardiac and respiratory models provide useful tools to study the effects of motion and investigate 4-D imaging techniques.

Fig. 10.

(Top) Normal respiratory curve (from [67]). (Middle and bottom) 3-D and 2-D views of the NCAT at (left) end-inspiration and (right) end-expiration.

In addition to motion, the flexibility of the NURBS surfaces allows for modeling of anatomical variations. As mentioned above, the organs and structures of the NCAT can be altered by applying transformations to the control points that define them [77], [78]. The NCAT includes many parameters (height, chest, and rib cage measurements; heart size, position, and orientation; diaphragm position; etc.) that can be used to produce anatomical variations. Modifications of these parameters can be based on statistics from available imaging databases. For example, anatomical parameters randomly sampled from distributions obtained from the Emory PET Torso Model Database [79] were used to create different anatomies for male and female adults to perform a study of compensation methods in myocardial SPECT [80] (Fig. 11).

Fig. 11.

(Top) One slice from six different models. (Bottom) Corresponding attenuation maps.

As can be seen above, the 4-D NCAT offered a vast improvement over the geometry-based MCAT by providing a more realistic model of the human anatomy and physiology. As such, the NCAT has gained a widespread use in nuclear medicine imaging research, especially for evaluating and improving imaging instrumentation, data acquisition techniques, and image processing and reconstruction methods. Despite this success, the NCAT still has its limitations. The anatomy was based solely on the Visible Male CT dataset from the National Library of Medicine and was restricted to just the region of the torso. Also, as was the case with the MCAT, female subjects were modeled with the addition of user-defined breast extensions onto the male anatomy. Another limitation is that the phantom, although capable of being far more realistic, was originally designed for low-resolution imaging research and lacks the anatomical details for application to high-resolution imaging such as X-ray CT and MRI.

IV. THE 4-D EXTENDED CARDIAC-TORSO (XCAT) PHANTOM

To expand the applications of the NCAT beyond that of nuclear medicine, we greatly enhanced its ability to represent the human anatomy and physiology. This work resulted in the development of the new 4-D XCAT phantom for high-resolution imaging research based on a combination of NURBS and SD surfaces.

The XCAT phantom includes highly detailed whole-body anatomies for the adult male and female based on the high-resolution Visible Male and Female anatomical datasets from the National Library of Medicine (NLM). The NLM anatomical images are much more detailed than those of the CT used to create the original NCAT. The Visible Male dataset consisted of 1878 anatomical slices over the body with a resolution of 1760 × 1024 and a pixel size and slice width of 0.33 and 1 mm, respectively. The female dataset was defined similarly except the slices were obtained at 0.33 mm intervals, resulting in more than 5000 anatomical images over the body. Similar techniques as those used to create the NCAT organ models were used to create the detailed male and female anatomies for the XCAT. Fig. 12 shows different levels of detail for both genders. The anatomy of the XCAT phantom is much more detailed than that of the NCAT. The NCAT was originally developed for low-resolution nuclear medicine imaging research, and, as such, only included a limited number of structures restricted to the region of the torso (Fig. 8). Based on segmentation of the NLM anatomical datasets, the XCAT includes more than 9000 anatomical objects over the entire human body. With the improved anatomical detail and the extension to new areas, the new 4-D XCAT is applicable to more medical imaging applications using nuclear medicine or high-resolution techniques such as CT or MRI.

Fig. 12.

(a) Male and (b) female anatomies of the extended NCAT or XCAT phantom. Different levels of detail are shown, building up to the whole model for each, shown with transparency. The circulatory system, organs and glands, skeleton, and muscles are shown for both male and female.

Unlike the NCAT, the XCAT phantom is not solely based on NURBS surfaces. It is defined using a combination of NURBS and SD surfaces. Subdivision surfaces [81] are used to model structures with an arbitrary topological type, such as the structures in the brain and the interior structure of the breast. NURBS surfaces can only model such structures by partitioning the model into a collection of individual NURBS surfaces, which introduces a large number of parameters to define the model. Subdivision surfaces are capable of modeling smooth surfaces of arbitrary topological type more efficiently. A subdivision surface represents an object initially as a coarse polygon mesh. This mesh can be iteratively subdivided and smoothed using a refinement scheme to produce a smooth surface (Fig. 13). For our purposes, we used the Loop [82] subdivision scheme to refine our surfaces, within the phantom software, since our initial meshes were defined using triangles. Typically, only two to three subdivisions are necessary to produce smooth surfaces. Fig. 14 shows the detailed XCAT brain model, including more than a hundred structures defined using SD surfaces based on the segmentation of patient MRI data.

Fig. 13.

Subdivision surface modeling a human hand. (a) The model is initially defined as a simple polygon mesh. (b) A refinement scheme is used to subdivide and smooth the mesh to produce a smooth surface representation of the object.

Fig. 14.

(a) Structures and (b) vessels of the XCAT brain model.

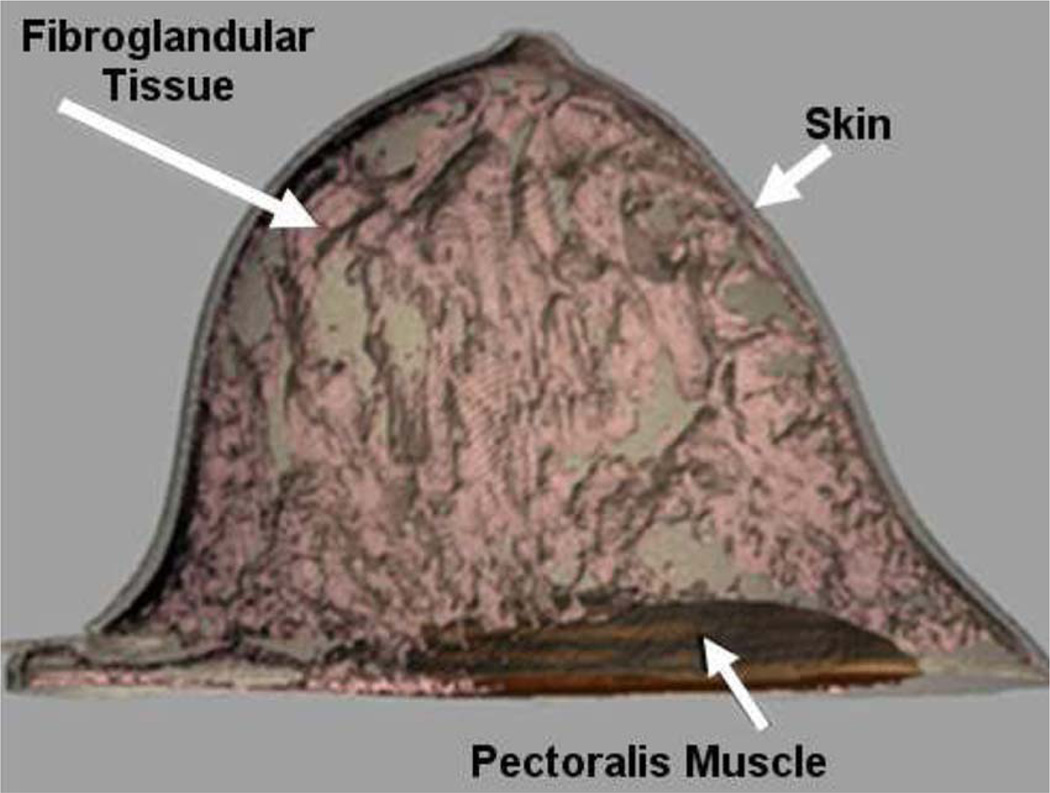
As seen in Fig. 12, the XCAT phantom does provide a separate anatomy for the female body. Females were modeled in the NCAT by adding breast models to the male anatomy. The breast models were simple surfaces and did not include any interior anatomical detail. This hindered the NCAT from finding widespread use in breast imaging research, an area where it could have a profound impact. We are currently developing a series of detailed 3-D computational breast models to incorporate into the female XCAT for breast imaging research [83] based on high-resolution dedicated breast CT data obtained from Boone at the University of California Davis. Models for segmented structures from the CT data are created using subdivision surfaces. When complete, the models will be capable of realistically simulating a wide range of anatomical variations in health and disease and will include finite-element based techniques to simulate different compression states of the breast for various imaging modalities. Figs. 15 and 16 show an initial model we have created along with simulated multimodality imaging data generated from it as compared to actual patient data.

Fig. 15.

3-D renderings of the initial breast model with the skin surface, pectoral muscle, and fibroglandular tissue.

Fig. 16.

(a) Mammogram, (b) tomosynthesis, and (c) positron emission mammography images simulated from the compressed breast phantom as compared to patient images.

In addition to the basic anatomy, the XCAT also includes updated cardiac and respiratory models. A more detailed cardiac model was developed based on state-of-the-art high-resolution cardiac gated data from multi-detector CT (MDCT) scanners [84], [85]. A male version of the heart was created using a CT dataset of a normal male subject that included 100 time-frames over the cardiac cycle with a pixel size of 0.32 mm and a slice thickness of 0.4 mm. With the increased spatial and temporal resolution offered by this dataset, a more accurate model for the cardiac motion was created (Fig. 17). A female version for the heart was similarly created based on MDCT data from a normal female subject. This dataset consisted of only 12 time frames, however. In this case, the motion of the male heart (based on 100 frames) was used as a guide to better interpolate the motion between the 12 frames. As before, the new heart models were parameterized, giving them the ability to model different normal and abnormal motion variations. By including more anatomical detail (coronary vessels, valves, papillary muscles), the improved cardiac phantom can produce more realistic simulated cardiac imaging data and is already being applied in our research in 4-D cardiac CT [84], [86]–[88].

Fig. 17.

Enhanced cardiac model of the 4-D XCAT based on MDCT. Plots of the volume change in the cardiac chambers are shown to the right. Beating heart of the male XCAT is shown. A similar model was created for the female.

The respiratory model for the XCAT was updated based on current state-of-the-art respiratory gated CT data. The previous NCAT model was limited in that it was based on only one realization of the normal respiratory motion. Also, the data upon which it was based had a resolution lower than that offered by more advanced CT scanners and consisted of only four time-frames that did not adequately cover normal tidal breathing. We better characterized the respiratory motion and its variations in the XCAT through an analysis of several sets of respiratory-gated CT image data obtained from Chen of the Massachusetts General Hospital [89]. More than 30 sets of data were used, with each dataset containing 20 time-frames over the respiratory cycle with the patient breathing normally. From an analysis of the patient datasets, we determined the range of motion of all the respiratory structures and altered the respiratory model of the XCAT to reflect the general trends we observed in the data. The new respiratory model was also set up to work with the enhanced anatomical detail now included in the phantom (Fig. 18).

Fig. 18.

Respiratory motion of the enhanced 4-D XCAT. Plots of the volume change in the lungs are shown to the right.

The XCAT phantom was parameterized in the same manner as the NCAT so as to create different patient anatomies. However, to more fully expand the XCAT library of anatomies beyond the Visible Human–based adults, we developed an initial series of realistic and anatomically detailed computational phantoms with ages ranging from newborn to adult [90], [91]. Several MDCT datasets of normal subjects were obtained from Frush from the CT database at the Duke University Medical Center. The imaging datasets consisted of chest, abdomen, or chest/abdomen/pelvis scans. The initial anatomy of each phantom was developed based on manual segmentation of the MDCT data and using 3-D NURBS and SD surfaces to define the organs and structures (e.g., backbone, ribcage, lungs, liver, heart, stomach, and spleen) visible in the field of view. Each phantom was extended to include a more detailed whole-body anatomy based on transforming the XCAT full-body adult phantom (male or female) to match the limited framework (based on segmentation) defined for the pediatric model.

For the work reported in this paper, the transformation of the adult to the patient was performed manually using the Rhinoceros software [74]. Rhinoceros was used to display the adult and patient models in several 2-D and 3-D views. With this visualization, transformations were applied to match the adult template model to the patient framework. The volumes of the organs defined in this manner for each model were checked and scaled, if necessary, to match age-interpolated organ volume data in ICRP Publication 89 [92]. Body measurements (head circumference, chest diameter, arm/leg lengths, and widths) were also adjusted to match anthropometry data defined for each particular age. By morphing a full-body template anatomy to match the patient data, it was possible to create a patient specific phantom with many anatomical structures, some not even visible in the CT data.

We created 47 (25 male and 22 female) phantoms in total (Fig. 19). A limitation to these phantoms is that they do not contain the same level of detail as the XCAT adult models. They only contain ~30 organs and do not include the muscle tissue or blood vessels. Manual transformation of just these basic structures took a great deal of time—a matter of days for each phantom. To define all the structures manually would require even more time, on the order of 1–2 weeks per phantom. Plus nonrigid transformations are needed to better match the patient anatomy. These were difficult to carry out in Rhinoceros given the number of structures in the XCAT. We are now applying methods from computational anatomy that can perform high-level nonrigid transformations automatically, allowing the definition of all 9000 structures in each phantom.

Fig. 19.

Whole-body phantoms created based on patient CT data. Ages from left to right are 2 months, 16 months, 4 years, 6 years, 8 years, 10 years, and 12 years.

We are currently using the Large Deformation Diffeomorphic Metric Mapping (LDDMM) framework [93], developed by Miller’s group in the Center for Imaging Science, JHU, to fill in the rest of the anatomy for these phantoms by nonrigidly transforming a selected XCAT phantom (male or female) to match the limited framework defined for the patient model [94]. The LDDMM algorithm was developed as a computational anatomy tool from which to study populations of anatomies by mapping them to a common template. It is used to compute a nonrigid high-dimensional transformation from a template image to a target and vice versa. The transformations are constrained to be diffeomorphic—one to one (invertible) and smooth. Information for computing the transformation comes from specification of point-to-point correspondences and image intensity, where the optimal transformation minimizes the error in overlap of these features and follows imposed smoothness constraints to ensure consistent transformation of the relationship among the structures observed in the image.

The LDDMM algorithm requires a template and a target image to calculate the transform. The target image is created by voxelizing the initial patient model, with each segmented structure assigned a unique integer ID. The template image is created by voxelizing the selected XCAT phantom (male or female), modeling the same structures as those in the patient. Given the two images, the LDDMM method finds the optimal high-level transform to map the whole-body template to the target. This transformation is based solely on those structures segmented from the CT data. Once the transform is determined, it can be applied to the NURBS and SD surfaces of the XCAT to create the patient-specific phantom, filling in the detailed anatomy that could not be segmented. Fig. 20 shows the results of mapping a male XCAT anatomy to the segmented framework of a 16-month-old boy. This process is very efficient. Using the LDDMM algorithm, it was possible to create, within a matter of hours, a detailed computational phantom for a patient containing all 9000 structures defined in the XCAT. We are currently investigating automating this process so as to create hundreds of anatomically variable 4-D XCAT phantoms for imaging research.

Fig. 20.

Result of mapping a male XCAT anatomy to match the anatomy of a 16-month-old boy. The initial anatomy of the pediatric phantom was based on segmentation of the patient CT data. The rest of the anatomy was defined through the LDDMM mapping.

With the above enhancements, the new 4-D XCAT approaches that of an ideal phantom, with its basis upon human data and the inherent flexibility of the NURBS and subdivision surface primitives. Combined with accurate models for the imaging process, the XCAT can provide a wealth of simulated image data that are far more consistent with those of actual patients, as seen in Fig. 21. There is essentially no limitation. Any number of different anatomies, cardiac or respiratory motions or patterns, and spatial resolutions can be simulated to perform research.

Fig. 21.

Imaging simulations performed using the XCAT phantom.

V. THE 4-D MOUSE WHOLE-BODY (MOBY) PHANTOM

Using the same techniques as those for the NCAT and XCAT, the 4-D MOBY phantom [95] (Fig. 22) was developed as a tool for use in small-animal imaging research to investigate new instrumentation, data-acquisition strategies, and image-processing and reconstruction techniques. The MOBY phantom was based on a 256 × 256 × 1024 3-D magnetic resonance microscopy dataset of a normal 16-week-old male C57BL/6 mouse obtained from Johnson of the Duke Center for In Vivo Microscopy, a National Institutes of Health resource (P41 05959/R24 CA 92656). The dataset with an isotropic resolution of 110 µm was extremely detailed, allowing the creation of realistic models for several different anatomical structures.

Fig. 22.

4-D MOBY phantom and its model for motion

Cardiac and respiratory models were also included within the phantom. The beating heart model was based on a gated black-blood MRI (bb-MRI) [96] cardiac data set of a normal 15-week-old male C57BL/6 mouse. The respiratory motion was based on similar respiratory mechanics observed when creating the human NCAT and XCAT phantoms [61], [75].

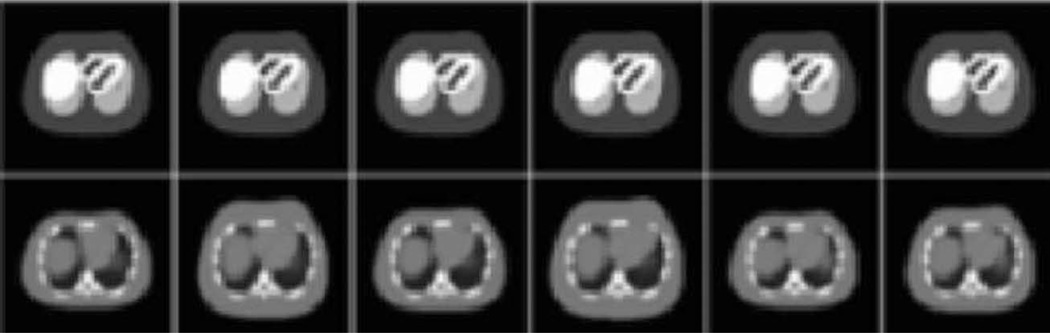
Used in combination with accurate models of the imaging process, the 4-D MOBY phantom can produce realistic imaging data to serve as a standard from which other molecular imaging devices and techniques can be evaluated and improved. The top of Fig. 23 shows reconstructed SPECT images generated from the phantom simulating the uptake of Tc-99m MDP in a normal mouse without respiratory motion. The bottom of Fig. 23 shows similar images obtained from imaging a mouse with the same radiopharmaceutical in our laboratory. Coronal image slices are shown. The top of Fig. 24 shows reconstructed X-ray CT transaxial images simulated using the mouse phantom, while the bottom of Fig. 24 shows similar CT images obtained from a live mouse using a microCT system built in our laboratory. In both cases, the simulated images are comparable to those obtained experimentally.

Fig. 23.

(Top) Reconstructed SPECT coronal images generated from the mouse phantom simulating the uptake of Tc-99 m MDP. (Bottom) Coronal SPECT images obtained experimentally from an actual mouse.

Fig. 24.

(Top) Reconstructed cone-beam x-ray CT images generated from the mouse phantom. (Bottom) Reconstructed cone-beam X-ray CT images obtained from a live mouse using a microCT system developed in our laboratory.

Like its human phantom counterparts, the MOBY phantom also has the ability to simulate different anatomies. Current work is under way to create anatomically variable models of the MOBY phantom as well as to create a model for the laboratory rat.

VI. DISCUSSION AND CONCLUSIONS

The above presents our developments toward ideal hybrid computational phantoms for use in medical and small-animal imaging research. The use of state-of-the-art computer graphics techniques has allowed us to move far beyond simple geometrically based phantoms toward a more ideal phantom combining the advantages of voxelized and mathematical models. Based on actual imaging data, NURBS and subdivision surfaces can accurately model the complex anatomical structures of the body, providing a level of realism comparable to that of a voxelized phantom. With their inherent flexibility, they can also accurately model motion and anatomical variations as well as a mathematical phantom. With this ability, the surface-based phantoms have offered a major evolutionary advance in the development of computerized models. Previously, the most realistic phantoms were of the voxelized variety based on segmented patient data. Due to the time required to segment whole-body datasets, only a handful of these models existed, and these were strictly 3-D and did not include motion. Now, NURBS and SD surface modeling combined with the computational anatomy methods presented above have the potential to open the door to the rapid development of hundreds of realistic patient-specific 4-D computational models. As is the case with the phantoms developed in our laboratory, such a library of computational models will have widespread use in imaging research to develop, evaluate, and improve imaging devices and techniques and to investigate the effects of anatomy and motion. They will also provide vital tools in radiation dosimetry to estimate patient-specific dose and radiation risk and optimize dose-reduction strategies, an important area of research given the high amounts of radiation exposure attributed to medical imaging procedures.

Biographies

W. Paul Segars received the Ph.D. degree in biomedical engineering from the University of North Carolina, Chapel Hill, in 2001.

He is an Assistant Professor of radiology and biomedical engineering and a member of the Carl E. Ravin Advanced Imaging Laboratories (RAILabs) at Duke University, Durham, North Carolina. He is among the leaders in the development of simulation tools for medical imaging research where he has applied state-of-the-art computer graphics techniques to develop realistic anatomical and physiological models. Foremost among these are the extended 4D NURBS-based Cardiac-Torso (XCAT) phantom, a computational model for the human body, and the 4D Mouse Whole-Body (MOBY) phantom, a model for the laboratory mouse. These phantoms are widely used to evaluate and improve imaging devices and techniques.

Benjamin M. W. Tsui (Member, IEEE) received the B.S. degree in physics from the Chinese University of Hong Kong in 1970, the A.M. degree in physics from Dartmouth College, Hanover, NH, in 1972, and the Ph.D. degree in medical physics from the University of Chicago in 1977.

After graduation, he continued to work at the University of Chicago as a Postdoctoral Fellow and became an Assistant Professor of Radiology in 1979. He joined the University of North Carolina, Chapel Hill, in 1982 as a Research Associate Professor of Radiology and Biomedical Engineering (BME) and was promoted to tenured Professor and became the Director of the Medical Imaging Research Laboratory and the Associate Chair of the Department of BME in 1991. He joined the Johns Hopkins University, Baltimore, MD, in 2002 as a Professor of Radiology, Electrical and Computer Engineering, Environmental Health Sciences and Biomedical Engineering and as the Director of the Division of Medical Imaging Physics in the Department of Radiology. His research interests include imaging physics of SPECT, PET and CT, 4-D computer generated phantoms that realistically mimic human anatomy and physiology, computer simulation techniques including the use of Monte Carlo methods, statistical and quantitative image reconstruction methods, image quality evaluation using model and human observers, 4-D cardiac and respiratory motion compensation, and preclinical small animal imaging instrumentation and techniques.