Predicting Cognitive Data from Medical Images Using Sparse Linear Regression

Abstract

We present a new framework for predicting cognitive or other continuous-variable data from medical images. Current methods of probing the connection between medical images and other clinical data typically use voxel-based mass univariate approaches. These approaches do not take into account the multivariate, network-based interactions between the various areas of the brain and do not give readily interpretable metrics that describe how strongly cognitive function is related to neuroanatomical structure. On the other hand, high-dimensional machine learning techniques do not typically provide a direct method for discovering which parts of the brain are used for making predictions. We present a framework, based on recent work in sparse linear regression, that addresses both drawbacks of mass univariate approaches, while preserving the direct spatial interpretability that they provide. In addition, we present a novel optimization algorithm that adapts the conjugate gradient method for sparse regression on medical imaging data. This algorithm produces coefficients that are more interpretable than existing sparse regression techniques.

1 Introduction

The advent of large population databases that seek to establish imaging-based biomarkers has spurred a need for generalizable prediction models in imaging. To serve this need, we seek to develop new statistical standards wherein models are trained on input data, the parameters of the model are fixed, and the model is then evaluated on unseen test datasets. This system of analysis both provides a validation of its accuracy in terms of the units of the dependent variable, as opposed to p-values, and also mimics the realistic restrictions of translational applications.

Despite this need, the large majority of medical imaging research uses traditional voxel-based morphometry (VBM) [1] which employs mass univariate testing. VBM generates statistical maps that display the correlation coefficient between a given voxel and an outcome or variable of interest and gives no indication of how these models will generalize. In contrast to VBM, several recent approaches [22] may be used to combine voxels across the brain to explicitly optimize prediction, rather than to test for an association or correlation. The distinction is important, as the p-value is not intended as a goodness-of-fit metric and does not guarantee accurate prediction estimates. Multivariate prediction approaches instead seek the best combination of voxels for predicting a given outcome, rather than testing for associations one voxel at a time. This provides a second motivation for multivariate voxel-driven prediction: they implement a network-like model which fits naturally with the neural network basis of cognition.

Toward this end, much effort has recently been invested in developing prediction-based methods of analyzing medical images. Such techniques have included efforts to diagnose Alzheimer’s Disease from medical images [8], among many other applications. One drawback that many of these methods share, however, is that they do not directly produce anatomically informative results. This drawback is inherent to the high-dimensional and non-linear nature of the algorithms used to analyze the data [9]. On the other hand, these methods do not have the drawbacks that mass-univariate methods such as VBM have.

We present here a method that combines advantages of traditional linear regression and high-dimensional machine learning approaches to analyzing medical image data. Our method leverages the inherently multivariate nature of imaging information to produce a sparse and anatomical prediction model for a univariate response. We demonstrate how careful use of cross-validation can provide assurance that results obtained from a sample population can be confidently applied to another population. Underlying our method is an adaptation of sparse linear regression. Drawing on recent advances in sparse regression and optimization techniques for sparsity-constrained problems, we show that sparse regression can both produce anatomically meaningful results and also give good prediction accuracy for a variety of psychometric and other clinical data. In addition, by using the framework of linear regression, we maintain the applicability of the mature analytical tools that have been developed for linear regression, including confidence intervals and significance metrics.

In sum, our contributions are: 1) An imaging-specific implementation of penalized regression; 2) Evaluation on a range of distinct response variables; 3) A cross-validation paradigm that completely separates training and testing; 4) A fully specified method of setting parameters; 5) Empirical demonstration that the models produced by our method are more accurate and generalizable than a state-of-the-art algorithm, elastic net; and 6) Establishing contrasting biologically plausible substrates for distinctive cognitive domains and aging.

2 Methods

2.1 Sparse Regression Background

Linear regression finds a linear transformation x that minimizes the error between an observed outcome variable b and the observed data A:

$$\underset{x}{argmin}{\Vert Ax-b\Vert }_2^2.$$ (2.1)

In the context of medical imaging as considered in this work, A is an n × p matrix of n vectorized images, each with p voxels; x is a p × 1 transformation matrix to be solved for; and b is the known n × 1 response variable, such as a psychometric score. Because A is “fat”, i.e. p ≫ n, it is not invertible and some form of regularization is necessary to solve for x.

Recently, much effort has been invested in finding sparse solutions to linear least squares problems, that is, solutions that have only a few non-zero components [6]. In the context of predicting clinical or cognitive data from medical images, sparse solutions include only a few anatomical regions of interest to predict a given outcome [15,17]. Sparsity is crucial for generating clinically and neurobiologically meaningful predictive results for two reasons. First, we can validate a proposed approach by verifying that the anatomical regions associated with a given clinical outcome are consonant with existing neuroanatomical knowledge. Second, by highlighting the effect of a given anatomical region, sparse regression techniques can discover novel brain-behavior associations by selecting specific brain regions that are predictive of a given clinical result.

The most direct way of enforcing sparsity constraints on solutions to linear regression problems of the form 2.1 is to restrict the number of non-zero entries in x using a metric known as the ℓ₀ “norm” which returns the number of non-zero entries in its argument. This modifies Equation 2.1 by restricting the number of non-zero entries in x to be less than a given level of sparsity s, as follows:

$$\begin{array}{ll}\underset{x}{argmin}\hfill & {\Vert Ax-b\Vert }_2^2,\hfill \\ \text{subject}\text{to}\hfill & {\Vert x\Vert }_0\le s.\hfill \end{array}$$ (2.2)

Solving this problem is known to be NP-hard, so a wide variety of approaches have been proposed to solve the problem [25]. One method for finding a solution to Equation 2.2 that has attracted much attention in recent years is replacing the ℓ₀ penalty with the convex ℓ₁ penalty [22], as the two penalties give identical solutions for many problems [11].

Incorporating feasibility constraints into optimization techniques has been a subject of research for over 50 years, and optimization methods dealing with feasibility constraints are mature and perform well. One of the most widely-used methods for incorporating hard feasibility constraints is known as projected gradient descent [5]. In this method, the solution is constructed by following a gradient descent algorithm, with the modification that if the gradient descent takes the solution out of the feasible set, the projection operator returns the solution to the point in the feasible set that is closest (in Euclidean distance) to the optimal, but infeasible, solution. Mathematically, if x_i is the estimate of the minimum of function f(x) at the i’th iteration, the estimate at iteration i+1 is given as

$$x_{i+1}=P_F(x_i-\alpha \nabla f(x)),$$ (2.3)

where P_F(·) is the projection (or “proximal”) operator that finds the point within the feasible set F that is closest to the operand and α is the step size.

For ℓ₁ norms, the projection operator is known as a “soft-thresholding” or “shrinkage” operator, and has a simple closed-form expression [10]:

$$\underset{v}{argmin}{\Vert u-v\Vert }_2^2+\gamma {\Vert v\Vert }_1=S(u,\gamma ),$$ (2.4)

where the soft-thresholding operator S (u, γ) is evaluated entry-wise and is defined as

$$S(u_i,\gamma )=\{\begin{array}{ll}{u}_i-\gamma ,\hfill & u_i>\gamma \hfill \\ 0,\hfill & -\gamma \ge u_i\le \gamma \hfill \\ u_i+\gamma ,\hfill & u_i<-\gamma \hfill \end{array}.$$ (2.5)

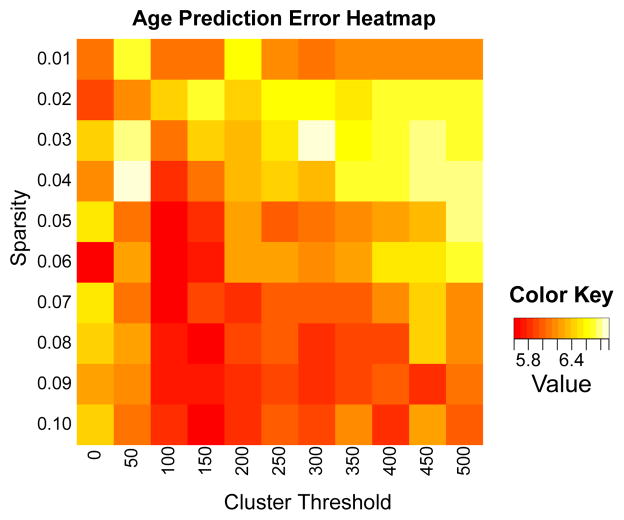
Although the shrinkage operator does not explicitly define a feasible set with a desired amount of sparsity, it is simple to run a search over possible values of γ to obtain the value of γ that will return a solution with the desired amount of sparsity, as in [27]. We denote the operator that finds the appropriate level of γ for achieving sparsity s as G(u, s). Requiring only the desired level of sparsity as an input to the algorithm as opposed to a penalty value avoids the well-documented [12] instability of solutions of ℓ₁-constrained solutions with regard to choice of penalty on the ℓ₁ norm. In addition to the sparsity penalty, we also include in the projection operator an optional minimum cluster size threshold, as is commonly performed in VBM-type analyses. We have found that including a (optional) minimum cluster threshold size generally improves robustness of results (see Figure 1) and, critically, helps prevent overfitting.

Fig. 1.

Heat map of errors for age prediction (lower is better), used to tune parameters. Units are in years. We found that for most tests, a sparsity of 0.04–0.05 and a cluster threshold of 100–250 generally provided the most stable results.

The fundamental difference between imaging data and other types of data is that in imaging data, the spatial information contained in the data is important. Because we are interested in obtaining neuroanatomically interpretable solutions, we wish to constrain our sparse solutions to be coherent and smooth, as in [4]. A few scattered non-zero voxels throughout the brain do not give rise to meaningful anatomical conclusions and these voxels will be difficult to locate in new datasets. That is, searching for individual voxels in the brain, as opposed to regions, is likely to give rise to spurious regression curves that cause overfitting on the data. Instead, we aim to recover coherent regions in the brain that are large enough and smooth enough to correspond to anatomically meaningful regions. To achieve anatomical coherence, we add a penalty to the norm of the gradient of the coefficient vector to our objective function:

$$\begin{array}{ll}\underset{x}{argmin}\hfill & \frac{1}{2}{\Vert Ax-b\Vert }_2^2+\frac{{\lambda }_1}{2}{\Vert x\Vert }_2^2+\frac{{\lambda }_2}{2}{\Vert \nabla x\Vert }_2^2,\hfill \\ \text{subject}\text{to}\hfill & {\Vert x\Vert }_1\le s.\hfill \end{array}$$ (2.6)

λ₁ is the value of the ridge penalty, commonly used to regularize least-squares solutions to linear equations, and λ₂ is the value of the smoothing penalty applied to the coefficient vector x. Taking the derivative, we get

$$A^{\mathrm{T}}(Ax-b)+{\lambda }_{1}x+{\lambda }_2\mathrm{\Delta }x,$$ (2.7)

which gives us our update step for projected gradient descent (Equation 2.3).

Instead of the classical gradient descent, we used a projected conjugate gradient algorithm. Optimization algorithms of this type have been proposed before [20], but to the best of our knowledge the formulation of the projected conjugate gradient algorithm in this context is novel. Pseudocode for the projected conjugate gradient algorithm we used is given in Algorithm 1. For extracting multiple areas in the brain that contribute independently to the outcome variable of interest, we used a variant of Orthogonal Matching Pursuit [24]. After using Algorithm 1 for determining the solution to the problem Ax = b, we subtracted the component of b that is not orthogonal to x₀ (b₁ = b−Ax₀), and then used the component of b that is orthogonal to x₀ for the next round of sparse predictions. In this way, we retrieve multiple areas of the brain that contribute to different components of cognitive ability.

Algorithm 1.

Algorithm for optimizing sparse regression vector

Input: A, b, s, α.	▷ Input data A, predicted data b, sparseness level s, step size α.
x0 ← random seed.	▷ Initialize regression vector.
p0 ← AT (b − Ax) − λ1x − λ2Δx	▷ Initialize direction with negative of gradient.
r0 ← p0	▷ Initialize residual.
k ← 0	▷ Initialize iterator.
while not converged do
xk+1 ← xk + αpk	▷ Update solution.
γopt ← G(xk+1, s)	▷ Find appropriate value of γ for desired sparsity.
xk+1 ← S(xk+1, γopt)	▷ Project solution to entry in sparse feasible set.
rk+1 ← AT (b − Axk+1) − λ1xk+1 + λ2Δxk+1	▷ Update residual.
$\beta \leftarrow \frac{r_k^{\mathrm{T}}{r}_k}{r_{k-1}^{\mathrm{T}}{r}_{k-1}}$
pk ← rk + βpk−1	▷ Update direction.
k ← k +1.
end while
Output: xk.

2.2 Prediction Methodology

One of the motivations for moving from a correlation-based statistical approach to a prediction-based approach is that a prediction-based approach provides falsifiable hypotheses. These can be tested using the model that is an output of the sparse regression algorithm within cross-validation. To provide more rigorous and generalizable results, we use a two-step cross-validation approach. In the first step, we use cross-validation within the training data to tune sparsity and cluster threshold parameters (Figure 1). Using cross-validation in the training data also enables us to average the coefficient vector over several trials, which helps minimize the dependence on initialization of the algorithm. The coefficient vectors returned from each fold are then averaged to return a final result for use on the test data. Thus, the model parameters are selected and fixed via exploration of the training data and applied, with set coefficients, to evaluate prediction accuracy in unseen datasets.

In the second step of cross-validation, stepwise forward regression using the Bayesian Information Criterion (BIC) [21] was used to select the coefficient vectors necessary for constructing an optimal linear model predicting the outcome of interest from the training imaging data. The optimal linear model was then trained on the training data and used to predict the outcome variable in the test data. Two-thirds of the data was used for training, and the other one-third was used for testing.

2.3 Clinical Data

Test data for the study consisted of 216 scans of patients collected in the course of the Penn Memory Center/Alzheimer’s Disease Center longitudinal cohort. Subjects were scanned on Siemens Sonata, Espree, Verio, or Trio Tim scanners using an MPRAGE T1 sequence. All scans were resampled to 2×2×2 mm isotropic resolution for analysis. The patient population had a mean age of 71.8 with standard deviation of 8.41. Of the 216 subjects, a definitive diagnosis was available for 191. There were 36 normal controls, 59 mild cognitive impairment (MCI) patients, 71 patients with Alzheimer’s Disease, and 25 with a variety of other conditions.

For analysis, we employed a standard pipeline wherein all images were diffeomorphically registered to a common template using ANTs [3] and cortical thickness measurements were computed using DiReCT [7].

2.4 Predictions

To evaluate the accuracy of our sparse linear prediction method for predicting a variable of interest, we began by predicting age because of the unambiguous ground truth measurement and because of the availability of comparison results. Competing methods have reported accuracies of mean absolute errors ranging from 5 to 6.5 years [26,13,2]. In addition to age, we predict a set of cognitive scans that correspond to distinct cognitive and neuroanatomical domans: The Boston Naming Test, which tests language ability; Consortium to Establish a Registry for Alzheimer’s Disease (CERAD) word list memory test (“Word List-Trial1”), which tests working memory; and the CERAD 5-minute delayed recall test (“Word List-Total”), which tests memory encoding and longer-term memory [18]. Age was predicted using only the scans, without any clinical data, as the ages of the control and diseased population was matched. All subjects were used in the age prediction. To avoid group effects, prediction of cognitive scores was done by grouping the patients into normals and patients with dementia. Only subjects with a definitive diagnosis were used for prediction of cognitive scores.

As a comparison to state-of-the-art results, we used the popular “elastic net” model [14], which combines the ℓ₂ ridge penalty with an ℓ₁ “Lasso” penalty on the coefficient vector. We used the implementation in the R glmnet package. In a similar manner to our method of parameter tuning on training data, we used the cv.glmnet function to find optimal parameters in the training data and the predict.cv.glmnet function to predict the outcome variables in the test data. The elastic net optimization algorithm uses a version of Least Angle Regression [12], which is similar to the variant of Orthogonal Matching Pursuit we used to create successive coefficient vectors using our sparse regression algorithm, so we did not generate more than one coefficient vector using elastic net.

A smoothed version of Lasso algorithm, called the “fused Lasso” algorithm [23], has been proposed. We were not able to run the optimization algorithm on problems of the magnitude considered here, as the time necessary for computing the fused Lasso increases significantly with the number of predictors and exponentially with the dimensionality of the problem. We typically deal with tens or hundreds of thousands of predictors and three-dimensional arrays, making the resulting optimization problem infeasible for fused Lasso.

Our algorithm implementation is open-source, and detailed instructions for replicating the results found here, including input data, are available from https://github.com/bkandel/KandelSparseRegressionIPMI.git.

3 Results

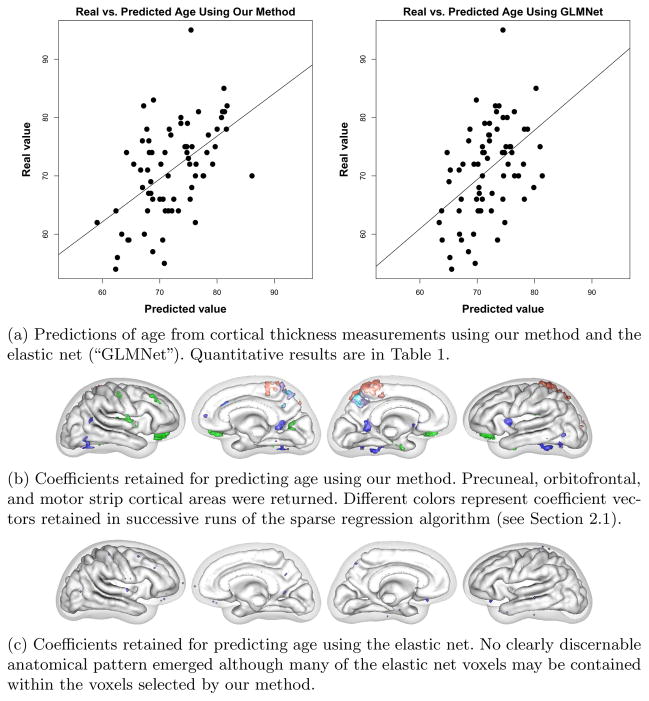
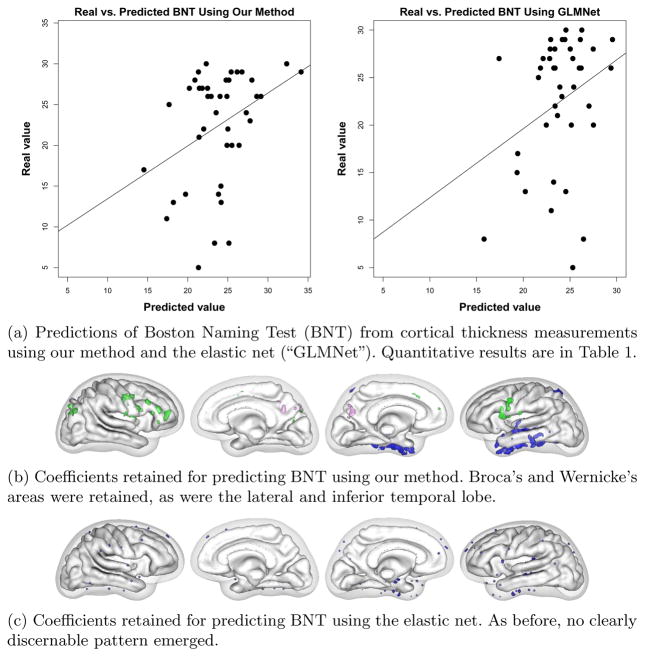
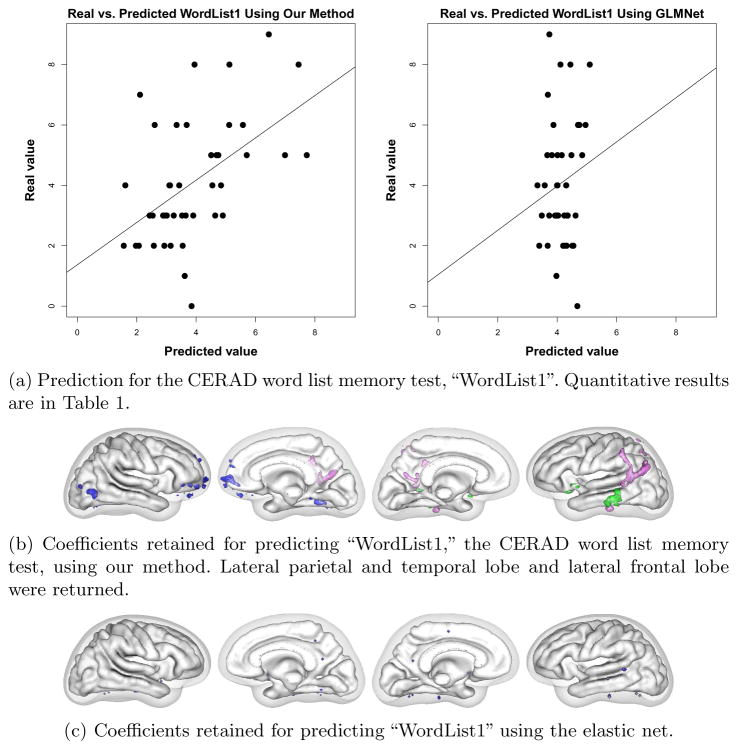
We used cortical thickness measurements to predict age and three cognitive tests with different neurobiological substrates to demonstrate that our algorithm achieves state-of-the-art prediction results while obtaining anatomically interpretable prediction coefficients. Numerical results for all trials are presented in Table 1. Our results for predicting age compare favorably with the errors of 5–6.5 years reported in the literature. The linear models produced by our method achieved higher significance (lower p-value) and higher correlation with test data than the model from the elastic net in every case. In addition, our models achieved higher generalizability (training / testing error) for every case except Word List 1, where the elastic net failed to discover a significant correlation at all.

Table 1.

Table of p-value, correlation coefficient (“Co. Coef.”), average training and testing errors, and generalizability (Gen.), defined as training error / testing error, for our sparse regression method and the elastic net. Our method produced more significant models with higher correlation in every case.

	Our method					Elastic net
	p-value	Cor. Coeff.	Train Error	Test Error	Generalizability	p-value	Cor. Coeff.	Train Error	Test Error	Generalizability
Age	3.25e-06	0.521	3.7	5.58	0.663	4.74e-05	0.463	3.12	5.86	0.533
BNT	0.0211	0.359	2.44	5.29	0.46	0.0599	0.296	1.6	5.06	0.316
Word List 1	0.000508	0.513	0.813	1.32	0.616	0.331	0.154	1.31	1.59	0.823
Word List Total	1.44e-06	0.673	1.2	2.01	0.599	0.0015	0.48	0.612	2.47	0.248

In addition to achieving greater generalizability, our method produced more interpretable coefficient vectors than the elastic net. For predicting age, our method found that the precuneal, or bitofrontal, and motor strip cortical regions were important (Figure 2). For BNT, we found that Broca’s and Wernicke’s areas were retained, as were the lateral and inferior temporal lobe (Figure 3). For WordList1, the word list memory CERAD test, we found that lateral parietal and temporal lobe and lateral frontal lobe were returned (Figure 4). Word List Total, the delayed recall CERAD test, returned left medial temporal lobe and precuneus (figure omitted due to space restrictions). A detailed clinical explanation of these areas is beyond the scope of this brief paper, but the areas found to predict the cognitive tests show dissociation for each test and match well with each test’s known neurological substrate. The elastic net found scattered non-zero coefficients, but they did not form a recognizable anatomical pattern for each test and did not dissociate the different cognitive tests.

Fig. 2.

Age results

Fig. 3.

BNT results.

Fig. 4.

WordList1 results

4 Discussion and Conclusion

We have presented a method that both provides neuroanatomically meaningful information about a population and also uses learning techniques to predict the results of psychometric tests. Our prediction method maintains the direct anatomical interpretability of VBM-type studies, but incorporates a multivariate learning approach that incorporates the networked nature of neurological function. The method has prediction accuracy that is competitive with the state of the art. In addition, the anatomical regions associated with cognitive scores match closely with current understanding of neuroanatomical specificity. These results provide confidence that the method is capable of producing anatomically and neurobiologically meaningful and accurate results.