Abstract
Combining accurate bone kinematics data from biplane radiography with cartilage models from magnetic resonance imaging, it is possible to estimate tibiofemoral cartilage contact area and centroid location. Proper validation of such estimates, however, has not been performed under loading conditions approximating functional tasks, such as gait, squatting, and stair descent. The goal of this study was to perform an in vitro validation to resolve the accuracy of cartilage contact estimations in comparison to a laser scanning gold standard. Results demonstrated acceptable reliability and accuracy for both contact area and centroid location estimates. Root mean square errors in contact area averaged 8.4% and 4.4% of the medial and lateral compartmental areas, respectively. Modified Sorensen-Dice agreement scores of contact regions averaged 0.81 ± 0.07 for medial and 0.83 ± 0.07 for lateral compartments. These validated methods have applications for in vivo assessment of a variety of patient populations and physical activities, and may lead to greater understanding of the relationships between knee cartilage function, effects of joint injury and treatment, and the development of osteoarthritis.
Keywords: knee biomechanics, cartilage contact, biplane radiography, validation
INTRODUCTION
Estimation of in vivo knee joint contact is technically challenging, particularly during functionally relevant loading. Understanding the location and area of contact between the articulating joint surfaces can provide essential and clinically relevant insight into joint function of normal, injured, and surgically operative or rehabilitated knees. Articular cartilage contact has been assessed in the knee [1–9]. Methods for analyzing knee contact have typically utilized magnetic resonance imaging (MRI) to directly assess opposing cartilage and meniscal tissues in both unloaded supine conditions and simulated loading during low load static and dynamic flexion activities [2, 8, 10, 11]. The low temporal sampling rates and physically restrictive environment of the MRI magnet, however, limit testing to loading magnitudes and ambulatory speeds that are far below those typically encountered during activities of daily living. Data of cartilage contact behavior during activities such as gait, stair climbing, hopping, and running is essential for a more complete understanding of the behavior of healthy and unhealthy joints [12].
Dynamic assessments of knee kinematics have been performed using motion capture, single-plane or biplane fluoroscopy or radiography [3, 5–7, 9, 13–20]. Biplane radiographic and fluoroscopic systems have precisely quantified bone motion during functional activities [3, 9, 13, 21, 22]. These systems cannot directly assess cartilage contact within joints (because soft tissues do not appear on x-ray images), but simple approximations of articular surface interactions have been performed using three-dimensional (3D) bone models derived from computed-tomography (CT) scans while assuming uniform cartilage thickness [21, 23, 24]. For joint surfaces with varying cartilage thickness (such as the tibial plateau), cartilage contact estimations can be improved by combining kinematic data of bones with subject-specific cartilage models generated from MRI. This approach has been used to assess in vivo ankle and knee contact during squatting, quasi-static lunging, and low-speed gait [5, 6, 9, 25, 26]. These studies were performed using commercially available “C-arm” fluoroscopy systems, which are suitable only for relatively low-speed movements due to limitations in maximum frame rate and image acquisition time [27]. The authors modeled bones from MRI images and derived joint kinematics by matching the projected external bony contours of the models onto the stereo fluoroscopic images. While both cartilage and bone can be modeled using MRI without ionizing radiation, MRI-derived bone models are subject to geometric distortion which has been previously reported to decrease kinematic accuracy [28] compared to models produced from CT that have low distortion and utilize full volumetric radiodensity information for the matching process [29].
High-speed biplane radiography systems [13, 14, 22] are designed specifically for dynamic imaging and are capable of the sampling rates (up to 250 frames/s of pulsed x-rays) and short exposure times (down to 1 ms) necessary for blur-free imaging of dynamic, functional activities such as gait, running, and hopping. When used with volumetric model-based tracking methods utilizing digitally reconstructed radiographic projections of CT bone models [29, 30], high-speed biplane radiographic systems can accurately reproduce knee kinematics during such activities. With these systems, however, estimating cartilage contact requires the additional step of mapping cartilage surface models generated from MRI onto the CT bone models. The errors introduced by combining the MRI and CT modalities and the repeatability of multiple MRI segmentation operators and their cumulative effect on articular contact estimation error has not been assessed.
The purpose of this study was therefore to evaluate the accuracy of estimations of area, shape, and centroid of cartilage contact determined by combining subject-specific articular knee cartilage models from MRI with a previously validated CT model-based method of determining tibiofemoral kinematics using biplane radiography. This validation was performed using a load-bearing human cadaveric knee model with laser scan data of joint contact as a gold standard. Laser scanning has been established as an acceptable gold standard method for assessing cartilage geometry [31, 32]. Repeatability analysis of contact estimation from multiple operators performing the cartilage modeling was performed to quantify the sensitivity to error of multiple technicians working cooperatively with a given dataset as would be required for large studies.
METHODS
Specimen Preparation
Three fresh-frozen knee cadaver specimens (3 males, ages 54–61) were obtained after approval of the institution’s Office for Oversight of Anatomic Specimens. Specimens were screened using MRI and fluoroscopy for evidence of osteophytes, ligamentous injuries, osteoarthritis, or defects in articular cartilage and stored at −20°C prior to use. Three poly-ether-ether-ketone screws were bi-cortically fixed in each specimen’s femur and tibia 35 mm distal and 50 mm proximal relative to the joint line to avoid damaging the articular cartilage. Plastic fiducial marker spheres (8 mm inner diameter, 10 mm outer diameter) were printed on a stereo lithography machine. The spheres were filled with multi-modality radiographic contrast fluid (Beekley Medical, Bristol CT), sealed with septum rubber, and rigidly attached to each screw head. Bone and cartilage volumetric data were acquired via CT scanning (GE LightSpeed Pro 16, voxel size: 0.589 x 0.589 x 1.25 mm, manufacturer’s “bone” convolution kernel) and MRI scanning (Siemens 3T Magnetom Trio, near-isotropic 3D Dual Echo Steady State (DESS) with water suppression, CP Extremity knee coil, voxel size: 0.45 x 0.45 x 0.70 mm, TR: 16.32 ms, TE: 4.71 ms, Flip Angle= 25°, 140 x 140 mm matrix). These CT scanning parameters are identical to those used for in vivo studies assessing dynamic knee function with the biplanar radiography system and balance bone model accuracy and subject radiation exposure [29]. The 3D DESS MRI sequence provides enhanced contrast between cartilage tissue and bone, meniscus, and synovial fluid and permits accurate quantification of articular cartilage morphology [33, 34]. Knees were held in position during scanning by use of a braided suture (#2 Ti-Cron, Covidien, Dublin, Ireland) whipstitched into the quadriceps tendon, passed through a 3 mm bicortical hole drilled into the femur bone shaft 15 cm proximal to the knee joint line, and knotted after the knee was placed into a normal extension position. During MRI scanning, knees were aligned near the magnet isocenter to reduce geometric distortions of the specimen tissues and fiducial spheres.
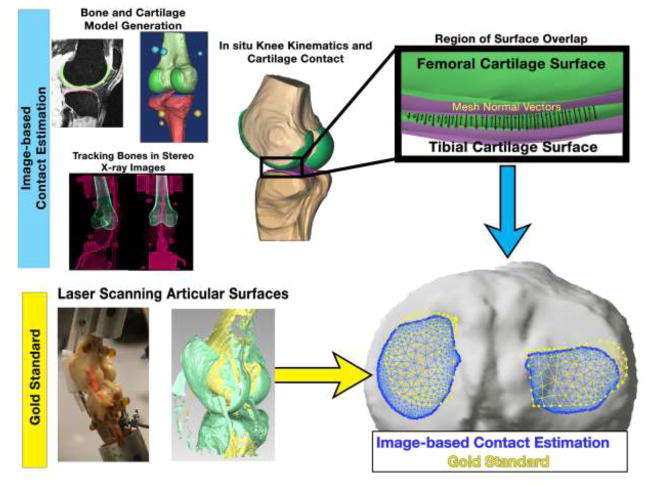
Skin and muscle tissues were carefully stripped from the knee specimens to expose the joint capsule. The capsule was dissected and the menisci and patella-quadriceps-tendon construct removed to facilitate direct visualization and laser scanning of tibiofemoral cartilage-cartilage contact during testing (Figure 1). Caution was exercised to avoid disruption of the cruciate and collateral ligaments and damage to the articular cartilage. Femoral and tibial bone shafts were cut 15 cm from the joint line and potted in fiberglass resin cylinders aligned to the native anatomical axes.
Figure 1.

Knees were posed in a weight-bearing flexion test rig with quadriceps loading within the capture volume of a biplane radiography system. Specimen menisci and patellae were removed to permit laser scanning and probing of the contacting cartilage regions. Quadriceps loading was applied through a stainless steel cable tendon and Teflon patella using a mechanical actuator.
Simulated quadriceps loading was applied through a stainless steel aircraft cable covered with polyethylene tubing. The cable acted as both the patella tendon and quadriceps tendon. The proximal cable end was routed over a pulley mounted to the testing frame and connected to the quadriceps mechanical actuator. The quadriceps angle was tailored for each specimen by adjusting the medial-lateral pulley position. The distal end of the cable was passed through a 5 mm hole drilled posteriorly through the tibial tubercle (anatomical patella tendon insertion site) and fixed with cable locks on the posterior aspect of the tibia (Figure 1). The patellar fulcrum mechanism was simulated using an artificial patella made from a short section of 25 mm diameter Teflon pipe that fit inside the trochlear groove (Figure 1). Friction between the Teflon tubing and femur was negligible, and the simulated patella allowed for fluid knee flexion and extension.
Load Bearing Cadaveric Model
A custom-made knee loading rig inspired by the Oxford Knee Rig [35] was designed and fabricated to apply controlled amounts of bodyweight proximally while controlling flexion angle with mechanically actuated quadriceps extension loading. A range of knee loading combinations was selected to approximate those occurring during in vivo squatting, stair descent, and stance-phase of gait.
The specimens were loaded into the rig, which was positioned in the capture volume of a biplane radiographic system (Figure 1). The system was configured as previously described for in vivo assessment of knee joint behavior during gait [29]. One of the pairs of x-ray sources and image intensifiers was aligned to provide an anterior-posterior radiograph, and the other was offset medially 50° from the anterior-posterior direction.
A coordinate measurement machine with probing and laser scanning head (FARO Arm Platinum FARO, Durham, NC) was rigidly bolted to the testing rig. The articulating arm of this scanner allowed easy scanning about 360° of the knee specimen. A 0.5 mm spherical tip was used for contact probing with a calibrated accuracy of 0.09 mm. The laser scanner was calibrated prior to testing to an accuracy of 0.10 mm for cartilage. Laser exposure settings were empirically optimized and ambient laboratory lighting was kept to a minimum to provide reliable scans from moistened cartilage surfaces.
Knees were positioned in static poses in 5° increments from full extension to 35° of flexion, measured with a goniometer, by adjusting quadriceps tension force. Testing was repeated with 1-, 2-, and 3-times typical bodyweight (70 kg) axial loading. Laser scanning of the medial and lateral knee compartment articular cartilage was performed with multiple passes of the FARO arm for each pose to fully assess the contacting regions. The contact probe tip was inserted into the tibiofemoral contacting regions that were not directly accessible with the laser beam (close to the tibial spine and behind the collateral ligaments) and the contact boundary was probed every 1 mm. Total scanning and probing time for each pose was less than 60 seconds. Immediately after scanning and probing, biplane radiographic images were acquired of the knee. The specimen was then unloaded, returned to extension, and the articular cartilage soaked with saline solution and allowed to rest for 15 minutes before the next trial. At the conclusion of testing, radiographic images and laser scans of a calibration cube were acquired to generate a transformation matrix between the biplane radiography system and probe/scanner coordinate systems. The co-registration error between the FARO arm and the biplane radiography system was 0.19 ± 0.07 mm.
All probe and laser scan data were collected via the FARO arm into the Geomagic Studio (Geomagic, Lake Mary, FL) software environment. For each trial, overlap error from the multiple scans (average 0.04 mm) and noise of merged laser scan point clouds was minimized using the global registration optimization and filtering pipelines in Geomagic, and point clouds were wrapped as triangular mesh surface models. The intersection of the femoral and tibial laser scan surfaces, determined via local mesh crease angle in Geomagic and refined with manual adjustment, was used in conjunction with probe data to determine the contacting region boundaries within each compartment.
Image-based Estimation of Cartilage Contact
Volumetric models of femurs and tibias were segmented from the CT scans using grayscale (Hounsfield units) thresholding and rendered into triangular mesh surface models (average element side length: 0.7 mm) using Mimics software (v17, Materialise, Leuven, Belgium). These bone surface models were smoothed in custom MATLAB (Mathworks, Natick, MA) software using a volume-preserving low-pass filter method [36] (smoothing iterations: 15, scale factor: 0.3). The volumetric bone models were used to create digitally reconstructed radiographs that were optimally matched to the collected radiographic image pairs in a virtual computer environment to accurately reproduce tibiofemoral kinematics in a manner previously described [29]. Automated methods for determining anatomical femoral and tibial coordinate systems were applied to the bone models [37].
MRI sequences were segmented in Mimics software (using the LiveWire function) to produce surface models of femur and tibia articular cartilage and bones [38]. Boolean operations were performed between tibia and femur cartilage segmentation masks to ensure no overlap occurred between models. Three independent operators with between 1 month and 6 years of experience segmented each knee dataset independently. Triangulated mesh surface models were decimated until mean element side length was 0.5 mm, and any spikes or holes in the mesh were repaired in Geomagic. Models were then smoothed in MATLAB with an implementation of an algorithm [39] not permitting more than 0.05 mm displacement of the mesh nodes along vertex normal vectors. MRI-derived bone surface models were co-registered to CT-based models using an iterative closest-point (ICP) method (point matching within 45° angle of source normal vector [40] and point-to-plane error metric [41] accelerated with a k-d tree search method [42]) implemented in MATLAB, and the resulting transforms were applied to cartilage models. As a result, the cartilage models resided on the articular ends of their respective CT-derived bone models. ICP co-registration was typically achieved within 15 iterations and resulted in an average deviation between MRI and CT bone surfaces of 0.41 ± 0.36 mm. Following the ICP alignment of the bones, the root mean square error between the centers of the MRI and CT fiducial sphere pairs was 0.63 mm. These alignment errors were due to factors such as image segmentation error and geometric distortion in the MRI volume. When the MRI-to-CT bone transformation matrices were applied to the cartilage models to map them onto the ends of the CT bones, regions of false contact between femoral and tibial cartilage models in the non-weight bearing extension position resulted. The average false contact areas were 248.6 ± 172.3 mm2 for medial compartments and 246.5 ± 59.7 mm2 for lateral compartments. The root mean square depth of overlap of opposing cartilage models in the false contact regions was 0.37 ± 0.17 mm.
For each trial, tibiofemoral positions and orientations were recreated by combining the bone/cartilage models from CT/MRI with tibiofemoral kinematics from biplane radiographs, resulting in overlap of the undeformed cartilage surface models in areas of articular contact (Figure 2). These overlapping mesh regions were detected via an algorithm implemented in custom MATLAB software that searched along the normal vectors of the outer cartilage surface until the opposing cartilage model’s outer surface was penetrated (Figure 2) [43, 44]. Intersecting regions were projected upon the tibial plateau and the outer-most vertices of overlapping mesh elements defined the contact patch boundary (Figure 2). Cartilage contact data was generated for each loading condition of each specimen and repeated by each operator using his or her respective anatomical models created from MRI.
Figure 2.
At each pose, laser scans of the articular surface and radiographs of the knee were acquired. Specimen-specific anatomical models of bones and cartilage were derived from CT and MRI scans. Tibiofemoral kinematics were derived by tracking bone positions in the stereo radiographic images. Cartilage models were mapped onto the ends of the tracked bone models and their subsequent overlap estimated tibiofemoral cartilage contact. The area, centroid, and agreement of the contacting regions between the image-based estimation and gold standard were assessed within each compartment of the tibia.
Validation of MRI-based Cartilage Model Accuracy
At the conclusion of specimen testing, knees were removed from the testing jig, rehydrated with saline, and allowed to rest for 30 minutes. The joints were disarticulated carefully to avoid cartilage damage. The femurs and tibias were rigidly clamped into place and the fiducial spheres and cartilage surfaces were laser scanned. The specimens were exposed to the lab environment (21° C, 41% humidity) for one hour, at which time laser scanning was repeated to estimate thickness changes due to dehydration. Cartilage was then removed from specimens by soaking the articular surfaces in a 6% bleach solution for 90 minutes. Remaining cartilage was manually removed by scraping gently with a scalpel. The bare bones were clamped into place and laser scanned again. 3D cartilage models were generated using the cartilage scans as the outer border and the bone scans as the inner border. These reference laser scan models were co-registered with the MRI-derived cartilage models using the centers of the fiducial spheres (visible in both laser scans and MRI) as reference points. This enabled direct comparison of cartilage thickness maps between the gold-standard laser scan and the MRI-segmented cartilage models. Average cartilage thickness errors across three operators between MRI-models and laser scans were 0.09 ± 0.27 mm for femurs and 0.05 ± 0.19 mm for tibias.
Comparison of Contact Regions Between Estimation and Gold Standard
Overlapping mesh regions and contact boundaries from laser scanning and probing were projected into the tibial transverse anatomical plane for comparison to the contact estimates from biplane radiography. The projected boundary regions were closed and meshed using a refined Delaunay method [45, 46]. The pure centroids and areas of the contacting regions from each modality were calculated. Contact area error was expressed as a percentage of the total area for each tibia compartment. Centroid location error in the anterior-posterior and medial-lateral directions was expressed in millimeters. Quantification of agreement in contacting region shapes between the two modalities was performed using the Agreement Scoring method, a modified version of the Sorensen-Dice coefficient, described by Willing [47]. The agreement score ranges between 0 (no agreement) and 1 (perfect agreement) and accounts for the disagreement between the gold standard (laser scanned/probed) and image-based estimations.
Statistical Analysis
For each loading condition (applied bodyweight/flexion angle), the cartilage models generated by each of the three MRI segmentation operators were used to generate separate estimations of joint contact from the biplane radiography system. The estimation errors of area, centroid, and agreement scores at each loading condition were averaged between-operators and between-specimens. Intra-class correlations (ICC) were calculated using two-way mixed models of absolute agreement to compare repeatability between operators and reliability between image-based estimation and gold standard for contact area and centroid locations within each compartment. Pearson correlations were used to test for relationships between error and flexion angle. All statistical analyses were performed in SPSS statistical software (v22, IBM) with α=0.05.
RESULTS
Contact Area
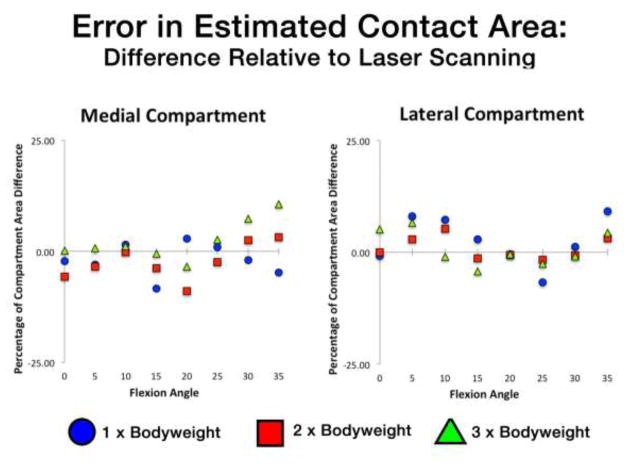
Medial and lateral compartment contact area errors for each specimen across all flexion angles and loading conditions are reported in Table 1. Medial compartment errors were typically higher than lateral compartment error for a given flexion angle/applied load. In the medial compartment, there was a general trend of area underestimation at low flexion angles and overestimation at flexion angles greater than 25° (Table 1). Medial compartment contact area error was correlated with flexion angle (R=0.65, p=0.001). Across-specimens compartmental averages in contact area errors for all loading conditions as a function of flexion angle are illustrated in Figure 3. RMS differences in contact area across all loading conditions and flexion angles between the image-based estimation and gold standard were 8.4% and 4.4% of the medial and lateral compartmental areas, respectively. Error in contact area increased with applied loading in the medial compartment (Table 1) but not for the lateral compartment. Overall intra-class correlation coefficients for medial contact area and lateral contact area reliability were 0.68 and 0.88, respectively (Table 2). Repeatability between operators for medial contact area was lower than lateral (Table 2).
Table 1.
Compartmental contact area error (% compartmental area) for each specimen at each loading condition and flexion angle.
| 1 X Bodyweight Loading | 2 X Bodyweight Loading | 3 X Bodyweight Loading | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Flexion Angle (°) | Specimen 1 | Specimen 2 | Specimen 3 | Average | Standard Deviation |
Specimen 1 | Specimen 2 | Specimen 3 | Average | Standard Deviation |
Specimen 1 | Specimen 2 | Specimen 3 | Average | Standard Deviation |
|
| Medial | 0 | −2.3 | −2.7 | −5.7 | −3.5 | 1.9 | −5.8 | −6.4 | −11.9 | −8.0 | 3.4 | 0.1 | −1.2 | −1.5 | −0.8 | 0.9 |
| 5 | −3.0 | −4.9 | −6.8 | −4.9 | 1.9 | −3.5 | −4.8 | −5.7 | −4.7 | 1.1 | 0.7 | −0.8 | −1.4 | −0.5 | 1.1 | |
| 10 | 1.4 | 0.0 | −1.5 | 0.0 | 1.5 | −0.3 | −1.5 | −2.6 | −1.5 | 1.2 | 1.1 | 12.1 | 10.4 | 7.9 | 5.9 | |
| 15 | −8.4 | −9.3 | −10.7 | −9.5 | 1.1 | −3.8 | 1.6 | −1.0 | −1.1 | 2.7 | −0.5 | 11.4 | 9.9 | 6.9 | 6.5 | |
| 20 | 2.8 | 15.3 | 12.9 | 10.4 | 6.7 | −8.9 | −5.7 | −7.6 | −7.4 | 1.6 | −3.5 | −3.9 | −3.9 | −3.8 | 0.2 | |
| 25 | 0.9 | 18.0 | 13.0 | 10.6 | 8.8 | −2.4 | 8.6 | 5.4 | 3.8 | 5.7 | 2.6 | 13.1 | 10.6 | 8.8 | 5.5 | |
| 30 | −1.9 | 16.7 | 12.1 | 9.0 | 9.7 | 2.5 | 18.2 | 14.5 | 11.8 | 8.2 | 7.3 | 21.8 | 18.5 | 15.9 | 7.6 | |
| 35 | −4.8 | 15.5 | 11.2 | 7.3 | 10.7 | 3.2 | 18.2 | 14.8 | 12.0 | 7.9 | 10.6 | 22.3 | 19.8 | 17.6 | 6.1 | |
| 1 X Bodyweight Loading | 2 X Bodyweight Loading | 3 X Bodyweight Loading | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Flexion Angle (°) | Specimen 1 | Specimen 2 | Specimen 3 | Average | Standard Deviation |
Specimen 1 | Specimen 2 | Specimen 3 | Average | Standard Deviation |
Specimen 1 | Specimen 2 | Specimen 3 | Average | Standard Deviation |
|
| Lateral | 0 | −0.8 | −1.3 | −1.9 | −1.3 | 0.5 | 0.0 | 1.0 | −0.8 | 0.1 | 0.9 | 5.1 | 6.1 | 3.8 | 5.0 | 1.1 |
| 5 | 8.0 | 7.4 | 7.0 | 7.5 | 0.5 | 2.9 | 2.7 | 2.1 | 2.6 | 0.4 | 6.6 | 6.9 | 5.7 | 6.4 | 0.6 | |
| 10 | 7.3 | 6.0 | 6.2 | 6.5 | 0.7 | 5.3 | 4.2 | 4.5 | 4.6 | 0.6 | −1.0 | 1.3 | −0.3 | 0.0 | 1.2 | |
| 15 | 2.9 | 0.8 | 2.0 | 1.9 | 1.1 | −1.3 | −0.8 | −0.8 | −0.9 | 0.3 | −4.2 | −2.4 | −3.8 | −3.5 | 0.9 | |
| 20 | −0.4 | 3.4 | 2.3 | 1.8 | 2.0 | −0.6 | −1.2 | −0.8 | −0.9 | 0.3 | −0.5 | −2.0 | −2.0 | −1.5 | 0.9 | |
| 25 | −6.7 | 0.6 | −1.9 | −2.7 | 3.7 | −1.7 | 1.5 | −0.2 | −0.1 | 1.6 | −2.6 | 1.3 | 0.8 | −0.1 | 2.1 | |
| 30 | 1.2 | 5.9 | 3.7 | 3.6 | 2.3 | −0.7 | 4.7 | 2.0 | 2.0 | 2.7 | −1.0 | 5.8 | 4.7 | 3.2 | 3.6 | |
| 35 | 9.1 | 11.1 | 9.4 | 9.9 | 1.1 | 3.1 | 8.2 | 5.9 | 5.7 | 2.5 | 4.4 | 11.3 | 9.8 | 8.5 | 3.7 | |
Figure 3.
Percentage of the compartmental area over- or under-estimated using combined biplane radiographic and MRI methods (relative to laser scan). Medial compartment (left) and lateral compartment (right) errors shown as a function of flexion angle for each applied bodyweight loading condition. Data points are the averages between three specimens at each position.
Table 2.
Intra-class correlation coefficients (ICC) across all flexion angles and specimens indicating reliability of image-based contact area and centroid location estimation relative to gold standard for the medial and lateral compartments at each applied bodyweight. Reliability was lowest at three times bodyweight loading, and medial compartment was lower than lateral compartment. Anterior-posterior centroid locations had consistent reliability across all loading conditions. Repeatability between the three operators was acceptable for centroid location and contact area estimations.
| Contact Area | Medial-Lateral Centroid Location | Anterior-Posterior Centroid Location | |||||
|---|---|---|---|---|---|---|---|
| Loading Condition | Medial | Lateral | Medial | Lateral | Medial | Lateral | |
| Reliability | 1X Bodyweight | 0.76 | 0.81 | 0.76 | 0.88 | 0.86 | 0.98 |
| 2X Bodyweight | 0.74 | 0.85 | 0.64 | 0.86 | 0.96 | 0.95 | |
| 3X BodyWeight | 0.52 | 0.59 | 0.41 | 0.56 | 0.82 | 0.98 | |
| Overall Conditions | 0.68 | 0.88 | 0.71 | 0.77 | 0.90 | 0.98 | |
|
| |||||||
| Repeatability | Overall Between-Operators | 0.80 | 0.95 | 0.95 | 0.95 | 0.99 | 0.99 |
Contact Centroid
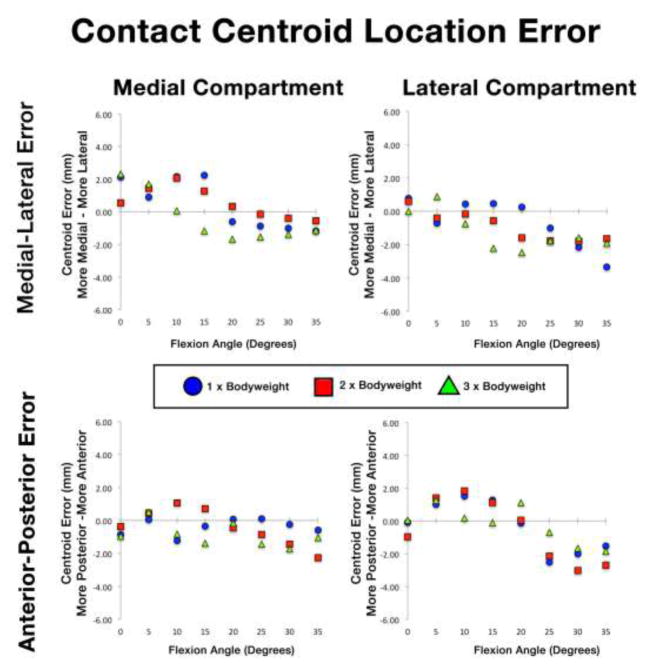
The across-specimens average locations of contact centroids on the tibial plateau are depicted in Figure 4 for each bodyweight loading condition. Contact centroids moved posteriorly on the tibial plateau with increasing flexion. Medial and lateral compartment contact centroid errors for each specimen across all flexion angles and loading conditions are reported along the anterior-posterior direction in Table 3 and the along the medial-lateral direction in Table 4. Anterior-posterior direction centroid errors were larger in the lateral compartment than the medial compartment (Table 3). Medial-lateral direction errors were consistent across specimens (Table 4). Across-specimens average errors in estimated contact centroid location as a function of flexion angle are depicted in Figure 5 for each loading condition. Centroid error did not change consistently with increasing load. Centroids were biased posteriorly and medially in both compartments for flexion angles greater than 20° (Figure 5). Overall ICC values for medial-lateral direction centroid locations were 0.71 and 0.77 in the medial and lateral compartments, respectively (Table 2). Overall ICC values for anterior-posterior centroid location were 0.90 (medial) and 0.98 (lateral). Repeatability ICC between operators for centroid location was 0.95 for medial-lateral direction in both compartments and 0.99 for anterior-posterior direction in both compartments (Table 2).
Figure 4.
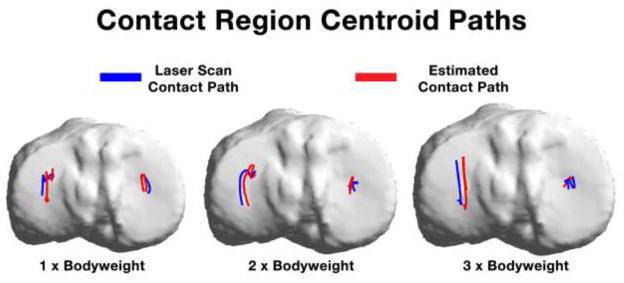
Between-specimens average contact region centroid paths through the range of flexion upon the tibial plateau for each applied bodyweight loading. Contact paths were similar in the medial compartment. A medial bias in the estimation was present in the lateral compartment.
Table 3.
Compartmental contact centroid error (mm) in the anterior-posterior direction for each specimen at each loading condition and flexion angle.
| 1 X Bodyweight Loading | 2 X Bodyweight Loading | 3 X Bodyweight Loading | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Flexion Angle (°) | Specimen 1 | Specimen 2 | Specimen 3 | Average | Standard Deviation |
Specimen 1 | Specimen 2 | Specimen 3 | Average | Standard Deviation |
Specimen 1 | Specimen 2 | Specimen 3 | Average | Standard Deviation |
|
| Medial | 0 | −0.9 | −1.6 | −0.6 | −1.0 | 0.5 | −0.4 | −1.1 | 0.0 | −0.5 | 0.6 | −1.0 | −1.6 | −1.0 | −1.2 | 0.3 |
| 5 | 0.1 | −0.3 | 0.4 | 0.1 | 0.4 | 0.5 | −0.1 | 0.4 | 0.2 | 0.3 | 0.5 | 0.1 | 0.5 | 0.4 | 0.2 | |
| 10 | −1.2 | −1.6 | −1.1 | −1.3 | 0.3 | 1.1 | 0.7 | 1.0 | 0.9 | 0.2 | −0.8 | 1.0 | 0.9 | 0.4 | 1.0 | |
| 15 | −0.3 | −0.4 | −0.4 | −0.4 | 0.0 | 0.7 | 1.6 | 1.8 | 1.4 | 0.6 | −1.4 | 0.7 | 0.5 | −0.1 | 1.1 | |
| 20 | 0.1 | 2.0 | 1.9 | 1.3 | 1.1 | −0.4 | 0.3 | 0.1 | 0.0 | 0.4 | −0.2 | −0.1 | −0.1 | −0.1 | 0.0 | |
| 25 | 0.1 | 2.8 | 2.6 | 1.8 | 1.5 | −0.9 | 0.7 | 0.7 | 0.2 | 0.9 | −1.4 | 0.0 | −0.2 | −0.5 | 0.8 | |
| 30 | −0.2 | 2.3 | 2.4 | 1.5 | 1.5 | −1.4 | 0.7 | 0.7 | 0.0 | 1.2 | −1.7 | 0.3 | 0.0 | −0.5 | 1.1 | |
| 35 | −0.6 | 1.8 | 2.2 | 1.1 | 1.5 | −2.3 | −0.1 | −0.2 | −0.9 | 1.2 | −1.0 | 0.9 | 0.6 | 0.1 | 1.0 | |
| 1 X Bodyweight Loading | 2 X Bodyweight Loading | 3 X Bodyweight Loading | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Flexion Angle (°) | Specimen 1 | Specimen 2 | Specimen 3 | Average | Standard Deviation |
Specimen 1 | Specimen 2 | Specimen 3 | Average | Standard Deviation |
Specimen 1 | Specimen 2 | Specimen 3 | Average | Standard Deviation |
|
| Lateral | 0 | −0.2 | 0.3 | −0.4 | −0.1 | 0.3 | −1.1 | −0.7 | −1.2 | −1.0 | 0.2 | 0.0 | 0.3 | −0.1 | 0.1 | 0.2 |
| 5 | 0.9 | 1.3 | 0.8 | 1.0 | 0.3 | 1.3 | 1.7 | 1.2 | 1.4 | 0.3 | 1.2 | 1.5 | 1.1 | 1.2 | 0.2 | |
| 10 | 1.3 | 2.0 | 1.2 | 1.5 | 0.4 | 1.7 | 2.3 | 1.6 | 1.8 | 0.4 | 0.1 | 0.3 | 0.2 | 0.2 | 0.1 | |
| 15 | 1.2 | 1.7 | 0.9 | 1.3 | 0.4 | 1.0 | 1.4 | 0.9 | 1.1 | 0.3 | −0.3 | 0.0 | 0.0 | −0.1 | 0.2 | |
| 20 | −0.2 | 0.0 | −0.2 | −0.1 | 0.1 | −0.1 | 0.4 | −0.1 | 0.0 | 0.3 | 0.8 | 1.3 | 1.3 | 1.1 | 0.3 | |
| 25 | −2.5 | −2.5 | −2.5 | −2.5 | 0.0 | −2.2 | −2.0 | −2.2 | −2.1 | 0.1 | −0.6 | −0.7 | −0.8 | −0.7 | 0.1 | |
| 30 | −1.9 | −2.1 | −2.0 | −2.0 | 0.1 | −3.1 | −3.0 | −3.0 | −3.0 | 0.1 | −1.3 | −1.8 | −1.9 | −1.7 | 0.3 | |
| 35 | −1.4 | −1.6 | −1.6 | −1.5 | 0.1 | −2.8 | −2.7 | −2.6 | −2.7 | 0.1 | −1.4 | −2.0 | −2.1 | −1.8 | 0.4 | |
Table 4.
Compartmental contact centroid error (mm) in the medial-lateral direction for each specimen at each loading condition and flexion angle.
| 1 X Bodyweight Loading | 2 X Bodyweight Loading | 3 X Bodyweight Loading | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Flexion Angle (°) | Specimen 1 | Specimen 2 | Specimen 3 | Average | Standard Deviation |
Specimen 1 | Specimen 2 | Specimen 3 | Average | Standard Deviation |
Specimen 1 | Specimen 2 | Specimen 3 | Average | Standard Deviation |
|
| Medial | 0 | 2.1 | 2.0 | 2.3 | 2.1 | 0.1 | 0.7 | 0.3 | 0.6 | 0.6 | 0.2 | 2.4 | 2.2 | 2.4 | 2.3 | 0.1 |
| 5 | 1.0 | 0.7 | 1.0 | 0.9 | 0.2 | 1.5 | 1.2 | 1.5 | 1.4 | 0.2 | 1.8 | 1.5 | 1.8 | 1.7 | 0.2 | |
| 10 | 2.2 | 1.9 | 2.3 | 2.2 | 0.2 | 2.2 | 1.8 | 2.2 | 2.1 | 0.2 | −0.2 | 0.2 | 0.2 | 0.1 | 0.2 | |
| 15 | 2.3 | 2.0 | 2.4 | 2.2 | 0.2 | 1.2 | 1.1 | 1.5 | 1.3 | 0.2 | −1.4 | −1.0 | −1.1 | −1.2 | 0.2 | |
| 20 | −0.8 | −0.6 | −0.4 | −0.6 | 0.2 | 0.2 | 0.2 | 0.5 | 0.3 | 0.1 | −1.5 | −1.8 | −1.8 | −1.7 | 0.2 | |
| 25 | −0.2 | −1.2 | −1.3 | −0.9 | 0.6 | 0.1 | −0.3 | −0.3 | −0.2 | 0.2 | −1.6 | −1.5 | −1.6 | −1.5 | 0.1 | |
| 30 | −0.5 | −1.3 | −1.2 | −1.0 | 0.4 | −0.1 | −0.5 | −0.6 | −0.4 | 0.3 | −1.5 | −1.2 | −1.4 | −1.4 | 0.1 | |
| 35 | −0.9 | −1.5 | −1.1 | −1.2 | 0.3 | −0.3 | −0.6 | −0.7 | −0.5 | 0.2 | −1.2 | −1.1 | −1.1 | −1.2 | 0.1 | |
| 1 X Bodyweight Loading | 2 X Bodyweight Loading | 3 X Bodyweight Loading | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Flexion Angle (°) | Specimen 1 | Specimen 2 | Specimen 3 | Average | Standard Deviation |
Specimen 1 | Specimen 2 | Specimen 3 | Average | Standard Deviation |
Specimen 1 | Specimen 2 | Specimen 3 | Average | Standard Deviation |
|
| Lateral | 0 | 0.7 | 0.9 | 0.7 | 0.8 | 0.1 | 0.6 | 0.6 | 0.6 | 0.6 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 |
| 5 | −0.8 | −0.6 | −0.8 | −0.7 | 0.1 | −0.4 | − −0.4 | −0.4 | −0.4 | 0.0 | 0.9 | 0.9 | 0.9 | 0.9 | 0.0 | |
| 10 | 0.4 | 0.5 | 0.4 | 0.4 | 0.1 | −0.2 | −0.1 | −0.2 | −0.2 | 0.1 | −0.7 | −0.7 | −0.8 | −0.7 | 0.1 | |
| 15 | 0.3 | 0.7 | 0.4 | 0.5 | 0.2 | −0.5 | −0.5 | −0.7 | −0.6 | 0.1 | −2.2 | −2.2 | −2.3 | −2.2 | 0.0 | |
| 20 | 0.7 | 0.1 | −0.1 | 0.3 | 0.4 | −1.6 | −1.4 | −1.7 | −1.6 | 0.1 | −2.7 | −2.4 | −2.4 | −2.5 | 0.1 | |
| 25 | 0.0 | −1.4 | −1.6 | −1.0 | 0.9 | −1.4 | −1.9 | −2.0 | −1.8 | 0.4 | −1.7 | −1.8 | −1.9 | −1.8 | 0.1 | |
| 30 | −1.8 | −2.4 | −2.3 | −2.2 | 0.3 | −1.3 | −2.1 | −2.0 | −1.8 | 0.5 | −1.4 | −1.6 | −1.7 | −1.6 | 0.1 | |
| 35 | −3.6 | −3.3 | −3.1 | −3.3 | 0.2 | −1.3 | −1.8 | −1.8 | −1.6 | 0.3 | −1.9 | −1.9 | −1.9 | −1.9 | 0.0 | |
Figure 5.
Contact region centroid error as a function of flexion angle. Medial compartment (left) and lateral compartment (right) errors are depicted along the medial-lateral (top) and anterior-posterior (bottom) anatomical directions.
Contact Region Agreement
Agreement scores (average ± standard deviation) of contact regions between modalities were 0.81 ± 0.07 for the medial side and 0.83 ± 0.07 for the lateral side. Agreement scores did not change with increased loading. As flexion increased, agreement scores decreased from 0.93 to 0.76 on average.
DISCUSSION
We have developed a method that allows for assessment of subject-specific cartilage contact in a range of knee poses commonly occurring during functional activities of daily living such as walking, running, squatting, and stair gait. This study demonstrated reliable and repeatable subject-specific tibiofemoral cartilage contact estimation during simulated physiologic loading conditions using a combination of biplane radiography, computed tomography and magnetic resonance imaging. The bias errors reported include the cumulative errors of our processing pipeline (Figure 6): the tracking of CT bone models on radiographic images, segmentation and modeling of tibiofemoral cartilage from MRI from multiple operators, the coregistration of CT and MRI modalities, and the cartilage contact algorithm itself. These multiple sources of error necessitated this cadaveric validation of three specimens that, while certainly not a complete representation of possible variations in knee anatomy, is a sample size on par with previous in vitro validations of joint contact [1, 48, 49].
Figure 6.
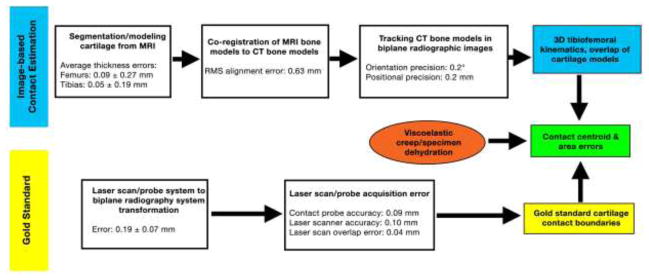
Processing pipeline errors for the image-based estimation of contact (top) and gold standard (bottom).
Only one previous validation of knee cartilage contact using a system similar to that of the present study has been reported [1]. This study evaluated three specimens at half bodyweight in a single extension position using biplanar fluoroscopy and MRI bone/cartilage models with an average error in contact area of 14±11% of compartmental area. These data are similar to the values reported in this manuscript at similar loading conditions. However, our results indicate the importance of validation at multiple loading and flexion conditions. Increasing flexion resulted in overestimation of contact area in the medial but not the lateral compartment. While previous analyses of sagittal plane distal femur condyle radii have indicated no significant differences between compartments [50, 51], the combination of the cam-like distal femur morphology and the respective medial concavities and lateral convexities [52] of the tibial plateau may provide a possible explanation. Further investigation into the geometric factors of the trend in medial compartment error may yield an algorithm for correcting the linearly increasing bias. Maximum observed centroid location bias error was about 3 mm for either anatomical direction of either compartment (Tables 3 & 4). In the context of the average size of the two tibiofemoral compartments [53], these peak errors correspond to 6.6–10% of the anterior-posterior and medial-lateral dimensions. Contact region agreement scores generally exceeded those reported and described by Willing [47], although those were in reference to the elbow joint.
Extra care was taken in the current study to position and load the specimens in a manner that approximated natural contact and motion behavior. Bodyweight loads applied in this cadaveric simulation were in the same range as tibiofemoral knee loads assessed in vivo in instrumented knee replacements and in computational models during gait and stair activities [54-57]. Contact centroid paths followed trajectories similar to those previously reported in vivo during gait [58]. It is impossible in any cadaver study to completely reproduce the complex muscle and external forces that occur in vivo, and the single-muscle model employed for this study is a considerable simplification. However, allowing for free knee motion while utilizing quadriceps loading to offset the gravitational effects of bodyweight loading simulated in vivo knee behavior as well as or better than previous cadaveric validation of knee contact, which primarily relied upon simple axial loading with the tibia and femur held fixed [1].
Since cartilage deforms under load, Wan stated that use of overlapping rigid cartilage models might underestimate contact area [49]. In the present study however, for flexion angles greater than 25°, contact area was consistently overestimated in both compartments. The causes for overestimation are most likely a combination of the false contact regions introduced by MRI-to-CT bone model co-registration error, cartilage segmentation error, specimen dehydration, and viscoelastic creep. Larger medial-lateral centroid position and medial contact area errors with increasing flexion angles may also be due to regional MRI cartilage segmentation errors. Because the LiveWire tool operates by fitting region of interest contours along the image gradients, the segmentation boundary can be attracted towards the meniscal boundaries or areas of high contrast with synovium. This, in effect, would tend to locally overestimate cartilage thickness. These regions occur in the posterior portions of the joint, which are in contact with increasing flexion. This also provides a possible explanation for the posterior bias of centroid location with increasing flexion (Figure 5). Errors in contact area (Figure 3) and centroid location were not affected by the magnitude of applied load (Figure 5). Between-operators repeatability and reliability of the contact variables was lower in the medial compartment than the lateral compartment. Relatively small additions or omissions about the border of the contact regions would not shift the centroid of contact greatly, while almost certainly influencing the area estimation. The higher repeatability and reliability scores for centroid location than contact area suggest that discrepancies between the estimation and gold standard are the result of over or under estimation errors at the periphery of a given contacting region.
Previous assessments of joint contact have used silicone casting [1, 59, 60] or dye staining [61, 62], both of which require complete disarticulation of the joint after each trial to quantify contacting regions via digitization stylus or photography, thus limiting validation to a single load/flexion angle configuration for each specimen. Other authors have utilized pressure sensitive film [63, 64], or digital pressure measurement sensors [65, 66]. However, these methods introduce an artificial body into the articular contacting space (altering the nature of joint contact) and introduce an additional registration error (especially if they slip relative to the joint surface). While the newest digital pressure sensors permit dynamic measurement, they may overestimate contact area if any portion of a given sensing element (sensel) is under load. The sensels are prone to damage or biases with shear forces or during loads exceeding 1500 N [67], and the current study examined knees under axial loads up to 2060 N. Additionally, sensor bias is sensitive to calibration method [68] and fluid inhabiting the joint [69]. Non-invasive laser scanning has been previously established as a gold standard for quantifying cartilage geometry with high accuracy [31, 32], and enables assessment of cartilage-to-cartilage contact without interfering with the interactions of the articular surfaces. While providing similar information as the previously employed silicone and dye methods, laser scanning also enables multiple tests per specimen.
The greatest limitation of the laser scan methodology is that it is not possible to obtain complete laser scans instantaneously or during movement, restricting validation results to a series of static positions. Thus, it is possible that errors during movement could be higher than reported here. However, since the radiographic imaging protocol employed short-duration (1 ms), low-dose pulsed imaging (identical to the protocol typically used for dynamic, in vivo testing), decreases in kinematic measurement accuracy with dynamic motion would be small. Any increases in contact measurement errors for dynamic studies would most likely be due to viscoelastic effects in cartilage; these would probably be small for healthy cartilage (as suggested by the insensitivity of errors to loading magnitude found during the present study), but might increase for damaged/softened cartilage. The static loading may also have led to viscoelastic creep occurring during the short delay between radiographic imaging and laser scan completion, contributing to observed overestimation errors in the contact data. Degraded/softened cartilage may also increase this effect. Further studies (and perhaps the development of novel methodologies) are warranted to evaluate the effects of cartilage condition and joint motion speed on contact area measurements.
This study has several additional limitations. The small sample of specimens came from older donors that, while free from degeneration (assessed with x-ray, MRI, and direct visualization of cartilage), may have different cartilage characteristics than younger specimens. Menisci were removed from the specimens prior to testing in order to directly laser scan the contacting cartilage regions (a limitation also present for the silicone and dye methodologies), which almost certainly altered tibiofemoral load distribution and contact areas. Note that this is a limitation of only the laser scan methodology; the biplane imaging method described can be (and has been) used for assessing tibiofemoral cartilage contact during a variety of dynamic, functional activities. MRI enables direct measurement of meniscal position and function as well as cartilage contact, but only under slow-moving or static, simulated loading conditions [11, 70]). Both the imaging speed and the space constraints of the MRI magnet proscribe use of MRI for joint function assessment during dynamic, functional tasks such as normal-speed walking or running.
In summary, a method for the estimation of in situ knee cartilage contact combining biplane radiography and MRI has been validated under multiple bodyweight loading and over a range of knee flexion angles. This is the most comprehensive validation to date combining biplane radiographic imaging and MRI to assess cartilage contact. Some limitations associated with modifications to the anatomy and loading of cadaveric specimens are acknowledged; however the goal of the experimental design was not to assess physiological joint contact, but rather to employ a range of joint loads and positions sufficiently similar to those encountered in vivo to assess measurement system function. Future applications of this method include assessing knee cartilage contact in healthy, injured, surgically reconstructed, and osteoarthritic knees, as well as in obese populations.
Highlights.
We validate knee cartilage contact estimation from biplane radiography, CT, and MRI
We compare a physiologic cadaveric model to laser scanning gold standard
Errors in contact area averaged 8.4% for medial and 4.4% for lateral compartment
Amount of applied load did not affect errors
Errors increased with increasing knee flexion angle
Acknowledgments
This study was not possible without the expertise of Andrew Holmes and Thorin Tobiassen of the University of Pittsburgh Swanson Center for Product Innovation. Greta Brecheisen of the University of Pittsburgh and Dr. Yong Ma of the Peking University Third Hospital assisted in data processing.
Funding
Study was partially funded by NIH/NIAMS grant R01 AR056630.
Footnotes
Conflicts of Interest
None
Ethical Approval
The study was approved by the University of Pittsburgh Office for Oversight of Anatomical Specimens.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Bingham JT, Papannagari R, Van de Velde SK, Gross C, Gill TJ, Felson DT, Rubash HE, Li G. In vivo cartilage contact deformation in the healthy human tibiofemoral joint. Rheumatology (Oxford, England) 2008;47:1622–1627. doi: 10.1093/rheumatology/ken345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Cohen ZA, McCarthy DM, Kwak SD, Legrand P, Fogarasi F, Ciaccio EJ, Ateshian GA. Knee cartilage topography, thickness, and contact areas from MRI: in-vitro calibration and in-vivo measurements. Osteoarthritis and cartilage/OARS, Osteoarthritis Research Society. 1999;7(1):95–109. doi: 10.1053/joca.1998.0165. [DOI] [PubMed] [Google Scholar]
- 3.DeFrate LE, Sun H, Gill TJ, Rubash HE, Li G. In vivo tibiofemoral contact analysis using 3D MRI-based knee models. Journal of biomechanics. 2004;37(10):1499–1504. doi: 10.1016/j.jbiomech.2004.01.012. [DOI] [PubMed] [Google Scholar]
- 4.Gold GE, Besier TF, Draper CE, Asakawa DS, Delp SL, Beaupre GS. Weight-bearing MRI of patellofemoral joint cartilage contact area. Journal of magnetic resonance imaging : JMRI. 2004;20(3):526–530. doi: 10.1002/jmri.20146. [DOI] [PubMed] [Google Scholar]
- 5.Hosseini A, Velde SVD, Gill TJ, Li G. Tibiofemoral Cartilage Contact Biomechanics in Patients after Reconstruction of a Ruptured Anterior Cruciate Ligament Location of Cartilage Contact. 2012:1–8. doi: 10.1002/jor.22122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Hosseini A, Van de Velde SK, Kozanek M, Gill TJ, Grodzinsky AJ, Rubash HE, Li G. In-vivo time-dependent articular cartilage contact behavior of the tibiofemoral joint. Osteoarthritis and cartilage/OARS, Osteoarthritis Research Society. 2010;18(7):909–916. doi: 10.1016/j.joca.2010.04.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Li G, DeFrate LE, Park SE, Gill TJ, Rubash HE. In vivo articular cartilage contact kinematics of the knee: an investigation using dual-orthogonal fluoroscopy and magnetic resonance image-based computer models. The American journal of sports medicine. 2005;33(1):102–107. doi: 10.1177/0363546504265577. [DOI] [PubMed] [Google Scholar]
- 8.Shin CS, Souza RB, Kumar D, Link TM, Wyman BT, Majumdar S. In vivo tibiofemoral cartilage-to-cartilage contact area of females with medial osteoarthritis under acute loading using MRI. Journal of magnetic resonance imaging : JMRI. 2011;34(6):1405–1413. doi: 10.1002/jmri.22796. [DOI] [PubMed] [Google Scholar]
- 9.Van de Velde SK, Bingham JT, Hosseini A, Kozanek M, DeFrate LE, Gill TJ, Li G. Increased tibiofemoral cartilage contact deformation in patients with anterior cruciate ligament deficiency. Arthritis and rheumatism. 2009;60(12):3693–3702. doi: 10.1002/art.24965. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Chen B, Lambrou T, Offiah A, Fry M, Todd-Pokropek A. Combined MR imaging towards subject-specific knee contact analysis. The Visual Computer. 2010;27:121–128. [Google Scholar]
- 11.Vedi V, Williams A, Tennant SJ, Spouse E, Hunt DM, Gedroyc WMW. Meniscal movement. 1999:37–41. doi: 10.1302/0301-620x.81b1.8928. [DOI] [PubMed] [Google Scholar]
- 12.Andriacchi TP, Mundermann A, Smith RL, Alexander EJ, Dyrby CO, Koo S. A framework for the in vivo pathomechanics of osteoarthritis at the knee. Annals of biomedical engineering. 2004;32(3):447–457. doi: 10.1023/b:abme.0000017541.82498.37. [DOI] [PubMed] [Google Scholar]
- 13.Deneweth JM, Bey MJ, McLean SG, Lock TR, Kolowich PA, Tashman S. Tibiofemoral joint kinematics of the anterior cruciate ligament-reconstructed knee during a single-legged hop landing. The American journal of sports medicine. 2010;38(9):1820–1828. doi: 10.1177/0363546510365531. [DOI] [PubMed] [Google Scholar]
- 14.Tashman S, Kolowich P, Collon D, Anderson K, Anderst W. Dynamic function of the ACL-reconstructed knee during running. Clinical orthopaedics and related research. 2007;454:66–73. doi: 10.1097/BLO.0b013e31802bab3e. [DOI] [PubMed] [Google Scholar]
- 15.Tashman S, Araki D. Effects of anterior cruciate ligament reconstruction on in vivo, dynamic knee function. Clinics in sports medicine. 2013;32(1):47–59. doi: 10.1016/j.csm.2012.08.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Tashman S, Anderst W. In-vivo measurement of dynamic joint motion using high speed biplane radiography and CT: application to canine ACL deficiency. Journal of biomechanical engineering. 2003;125(2):238–245. doi: 10.1115/1.1559896. [DOI] [PubMed] [Google Scholar]
- 17.Chaudhari AM, Briant PL, Bevill SL, Koo S, Andriacchi TP. Knee kinematics, cartilage morphology, and osteoarthritis after ACL injury. Medicine and science in sports and exercise. 2008;40(2):215–222. doi: 10.1249/mss.0b013e31815cbb0e. [DOI] [PubMed] [Google Scholar]
- 18.Moro-oka TA, Muenchinger M, Canciani JP, Banks SA. Comparing in vivo kinematics of anterior cruciate-retaining and posterior cruciate-retaining total knee arthroplasty. Knee surgery, sports traumatology, arthroscopy : official journal of the ESSKA. 2007;15(1):93–99. doi: 10.1007/s00167-006-0134-6. [DOI] [PubMed] [Google Scholar]
- 19.Moro-oka TA, Hamai S, Miura H, Shimoto T, Higaki H, Fregly BJ, Iwamoto Y, Banks SA. Dynamic activity dependence of in vivo normal knee kinematics. Journal of orthopaedic research : official publication of the Orthopaedic Research Society. 2008;26(4):428–434. doi: 10.1002/jor.20488. [DOI] [PubMed] [Google Scholar]
- 20.Taylor KA, Cutcliffe HC, Queen RM, Utturkar GM, Spritzer CE, Garrett WE, DeFrate LE. In vivo measurement of ACL length and relative strain during walking. Journal of biomechanics. 2013;46(3):478–483. doi: 10.1016/j.jbiomech.2012.10.031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Anderst WJ, Les C, Tashman S. In vivo serial joint space measurements during dynamic loading in a canine model of osteoarthritis. Osteoarthritis and cartilage/OARS, Osteoarthritis Research Society. 2005;13(9):808–816. doi: 10.1016/j.joca.2005.04.019. [DOI] [PubMed] [Google Scholar]
- 22.Miranda DL, Fadale PD, Hulstyn MJ, Shalvoy RM, Machan JT, Fleming BC. Knee biomechanics during a jump-cut maneuver: effects of sex and ACL surgery. Medicine and science in sports and exercise. 2013;45(5):942–951. doi: 10.1249/MSS.0b013e31827bf0e4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Anderst WJ, Tashman S. The association between velocity of the center of closest proximity on subchondral bones and osteoarthritis progression. Journal of orthopaedic research : official publication of the Orthopaedic Research Society. 2009;27(1):71–77. doi: 10.1002/jor.20702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Anderst WJ, Tashman S. A method to estimate in vivo dynamic articular surface interaction. Journal of biomechanics. 2003;36(9):1291–1299. doi: 10.1016/s0021-9290(03)00157-x. [DOI] [PubMed] [Google Scholar]
- 25.Qi W, Hosseini A, Tsai T-Y, Li J-S, Rubash HE, Li G. In vivo kinematics of the knee during weight bearing high flexion. Journal of biomechanics. 2013;46:1576–1582. doi: 10.1016/j.jbiomech.2013.03.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Liu F, Kozanek M, Hosseini A, Van de Velde SK, Gill TJ, Rubash HE, Li G. In vivo tibiofemoral cartilage deformation during the stance phase of gait. Journal of biomechanics. 2010;43:658–665. doi: 10.1016/j.jbiomech.2009.10.028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Tashman S. Comments on “validation of a non-invasive fluoroscopic imaging technique for the measurement of dynamic knee joint motion”. Journal of biomechanics. 2008;41(15):3290–3291. doi: 10.1016/j.jbiomech.2008.07.038. author reply 3292–3293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Moro-oka TA, Hamai S, Miura H, Shimoto T, Higaki H, Fregly BJ, Iwamoto Y, Banks SA. Can magnetic resonance imaging-derived bone models be used for accurate motion measurement with single-plane three-dimensional shape registration? Journal of orthopaedic research : official publication of the Orthopaedic Research Society. 2007;25(7):867–872. doi: 10.1002/jor.20355. [DOI] [PubMed] [Google Scholar]
- 29.Anderst W, Zauel R, Bishop J, Demps E, Tashman S. Validation of three-dimensional model-based tibio-femoral tracking during running. Medical engineering & physics. 2009;31(1):10–16. doi: 10.1016/j.medengphy.2008.03.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Miranda DL, Schwartz JB, Loomis AC, Brainerd EL, Fleming BC, Crisco JJ. Static and dynamic error of a biplanar videoradiography system using marker-based and markerless tracking techniques. Journal of biomechanical engineering. 2011;133(12):121002. doi: 10.1115/1.4005471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Trinh NMS, Lester J, Fleming BC, Tung GAMD, Kimia BB. Lecture Notes in Computer Science. Springer-Verlag GmbH; Berlin Heidelberg: 2006. Computer Vision Approaches to Medical Image Analysis Second International ECCV Workshop, CVAMIA 2006, Graz, Austria, May 12, 2006, Revised Papers; pp. 37–48. [Google Scholar]
- 32.Koo S, Giori NJ, Gold GE, Dyrby CO, Andriacchi TP. Accuracy of 3D cartilage models generated from MR images is dependent on cartilage thickness: laser scanner based validation of in vivo cartilage. Journal of biomechanical engineering. 2009;131(12):121004. doi: 10.1115/1.4000087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Moriya S, Miki Y, Matsuno Y, Okada M. Three-dimensional double-echo steady-state (3D-DESS) magnetic resonance imaging of the knee: establishment of flip angles for evaluation of cartilage at 1.5 T and 3.0 T. Acta radiologica. 2012;53(7):790–794. doi: 10.1258/ar.2012.110532. [DOI] [PubMed] [Google Scholar]
- 34.Eckstein F, Hudelmaier M, Wirth W, Kiefer B, Jackson R, Yu J, Eaton CB, Schneider E. Double echo steady state magnetic resonance imaging of knee articular cartilage at 3 Tesla: a pilot study for the Osteoarthritis Initiative. Annals of the rheumatic diseases. 2006;65(4):433–441. doi: 10.1136/ard.2005.039370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Zavatsky AB. A kinematic-freedom analysis of a flexed-knee-stance testing rig. Journal of biomechanics. 1997;30(3):277–280. doi: 10.1016/s0021-9290(96)00142-x. [DOI] [PubMed] [Google Scholar]
- 36.Taubin G. A signal processing approach to fair surface design. Proceedings of the 22nd annual conference on Computer graphics and interactive techniques; ACM; 1995. pp. 351–358. [Google Scholar]
- 37.Miranda DL, Rainbow MJ, Leventhal EL, Crisco JJ, Fleming BC. Automatic determination of anatomical coordinate systems for three-dimensional bone models of the isolated human knee. Journal of biomechanics. 2010;43(8):1623–1626. doi: 10.1016/j.jbiomech.2010.01.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Bowers ME, Trinh N, Tung GA, Crisco JJ, Kimia BB, Fleming BC. Quantitative MR imaging using “LiveWire” to measure tibiofemoral articular cartilage thickness. Osteoarthritis and cartilage/OARS, Osteoarthritis Research Society. 2008;16(10):1167–1173. doi: 10.1016/j.joca.2008.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Desbrun M, Meyer M, Schröder P, Barr AH. Implicit fairing of irregular meshes using diffusion and curvature flow. Proceedings of the 26th annual conference on Computer graphics and interactive techniques; ACM Press/Addison-Wesley Publishing Co; 1999. pp. 317–324. [Google Scholar]
- 40.Pulli K. Multiview registration for large data sets. 3-D Digital Imaging and Modeling, 1999. Proceedings. Second International Conference on; 1999. pp. 160–168. [Google Scholar]
- 41.Chen Y, Medioni G. Object modeling by registration of multiple range images. Robotics and Automation, 1991. Proceedings., 1991 IEEE International Conference on; 1991. pp. 2724–2729. [Google Scholar]
- 42.Simon DA. Fast and accurate shape-based registration. Carnegie Mellon University; 1996. [Google Scholar]
- 43.Mo3ller T. A Fast Triangle-Triangle Intersection Test. Journal of Graphics Tools. 1997;2(2):25–30. [Google Scholar]
- 44.van den Bergen G. Efficient Collision Detection of Complex Deformable Models Using AABB Trees. Journal of Graphics Tools. 1997;2(4) [Google Scholar]
- 45.Ruppert J. A Delaunay Refinement Algorithm for Quality 2-Dimensional Mesh Generation. Journal of Algorithms. 1995;18(3):548–585. [Google Scholar]
- 46.Chew LP. Guaranteed-Quality Mesh Generation for Curved Surfaces. Ninth Annual Symposium on Computational Geometry; San Diego: Association for Computing Machinery; 1993. pp. 274–280. [Google Scholar]
- 47.Willing RT, Lalone EA, Shannon H, Johnson JA, King GJ. Validation of a finite element model of the human elbow for determining cartilage contact mechanics. Journal of biomechanics. 2013;46(10):1767–1771. doi: 10.1016/j.jbiomech.2013.04.001. [DOI] [PubMed] [Google Scholar]
- 48.McWalter EJ, O’Kane CM, Fitzpatrick DP, Wilson DR. Validation of an MRI-based method to assess patellofemoral joint contact areas in loaded knee flexion in vivo. Journal of magnetic resonance imaging : JMRI. 2014;39:978–987. doi: 10.1002/jmri.24240. [DOI] [PubMed] [Google Scholar]
- 49.Wan L, de Asla RJ, Rubash HE, Li G. Determination of in-vivo articular cartilage contact areas of human talocrural joint under weightbearing conditions. Osteoarthritis and cartilage/OARS, Osteoarthritis Research Society. 2006;14:1294–1301. doi: 10.1016/j.joca.2006.05.012. [DOI] [PubMed] [Google Scholar]
- 50.Siebold R, Axe J, Irrgang JJ, Li K, Tashman S, Fu FH. A computerized analysis of femoral condyle radii in ACL intact and contralateral ACL reconstructed knees using 3D CT. Knee surgery, sports traumatology, arthroscopy : official journal of the ESSKA. 2010;18(1):26–31. doi: 10.1007/s00167-009-0969-8. [DOI] [PubMed] [Google Scholar]
- 51.Li K, Langdale E, Tashman S, Harner C, Zhang X. Gender and condylar differences in distal femur morphometry clarified by automated computer analyses. Journal of orthopaedic research : official publication of the Orthopaedic Research Society. 2012;30(5):686–692. doi: 10.1002/jor.21575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Hashemi J, Chandrashekar N, Gill B, Beynnon BD, Slauterbeck JR, Schutt RC, Jr, Mansouri H, Dabezies E. The geometry of the tibial plateau and its influence on the biomechanics of the tibiofemoral joint. The Journal of bone and joint surgery. American volume. 2008;90(12):2724–2734. doi: 10.2106/JBJS.G.01358. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Iriuchishima T, Ryu K, Aizawa S, Fu FH. Size correlation between the tibial anterior cruciate ligament footprint and the tibia plateau. Knee surgery, sports traumatology, arthroscopy : official journal of the ESSKA. 2014 doi: 10.1007/s00167-014-2927-3. [DOI] [PubMed] [Google Scholar]
- 54.Kutzner I, Heinlein B, Graichen F, Bender A, Rohlmann A, Halder A, Beier A, Bergmann G. Loading of the knee joint during activities of daily living measured in vivo in five subjects. Journal of biomechanics. 2010;43(11):2164–2173. doi: 10.1016/j.jbiomech.2010.03.046. [DOI] [PubMed] [Google Scholar]
- 55.Kutzner I, Stephan D, Dymke J, Bender A, Graichen F, Bergmann G. The influence of footwear on knee joint loading during walking--in vivo load measurements with instrumented knee implants. Journal of biomechanics. 2013;46(4):796–800. doi: 10.1016/j.jbiomech.2012.11.020. [DOI] [PubMed] [Google Scholar]
- 56.Winby CR, Lloyd DG, Besier TF, Kirk TB. Muscle and external load contribution to knee joint contact loads during normal gait. Journal of biomechanics. 2009;42(14):2294–2300. doi: 10.1016/j.jbiomech.2009.06.019. [DOI] [PubMed] [Google Scholar]
- 57.D’Lima DD, Patil S, Steklov N, Slamin JE, Colwell CW., Jr Tibial forces measured in vivo after total knee arthroplasty. The Journal of arthroplasty. 2006;21(2):255–262. doi: 10.1016/j.arth.2005.07.011. [DOI] [PubMed] [Google Scholar]
- 58.Koo S, Rylander JH, Andriacchi TP. Knee joint kinematics during walking influences the spatial cartilage thickness distribution in the knee. Journal of biomechanics. 2011;44(7):1405–1409. doi: 10.1016/j.jbiomech.2010.11.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Seedhom BB, Tsubuku M. A technique for the study of contact between visco-elastic bodies with special reference to the patello-femoral joint. Journal of biomechanics. 1977;10(4):253–260. doi: 10.1016/0021-9290(77)90048-3. [DOI] [PubMed] [Google Scholar]
- 60.Fujikawa K, Seedhom BB, Wright V. Biomechanics of the patello-femoral joint. Part I: A study of the contact and the congruity of the patello-femoral compartment and movement of the patella. Engineering in medicine. 1983;12(1):3–11. doi: 10.1243/emed_jour_1983_012_004_02. [DOI] [PubMed] [Google Scholar]
- 61.Yao JQ, Seedhom BB. A new technique for measuring contact areas in human joints--the ‘3S technique’. Proceedings of the Institution of Mechanical Engineers. Part H, Journal of engineering in medicine. 1991;205(2):69–72. doi: 10.1243/PIME_PROC_1991_205_270_02. [DOI] [PubMed] [Google Scholar]
- 62.Black JD, Matejczyk MB, Greenwald AS. Reversible cartilage staining technique for defining articular weight-bearing surfaces. Clinical orthopaedics and related research. 1981;(159):265–267. [PubMed] [Google Scholar]
- 63.Liau JJ, Cheng CK, Huang CH, Lo WH. Effect of Fuji pressure sensitive film on actual contact characteristics of artificial tibiofemoral joint. Clinical biomechanics. 2002;17(9–10):698–704. doi: 10.1016/s0268-0033(02)00102-x. [DOI] [PubMed] [Google Scholar]
- 64.Hille E, Schulitz KP, Henrichs C, Schneider T. Pressure and contract-surface measurements within the femoropatellar joint and their variations following lateral release. Archives of orthopaedic and traumatic surgery. Archiv fur orthopadische und Unfall-Chirurgie. 1985;104(5):275–282. doi: 10.1007/BF00435942. [DOI] [PubMed] [Google Scholar]
- 65.Lee SJ, Aadalen KJ, Malaviya P, Lorenz EP, Hayden JK, Farr J, Kang RW, Cole BJ. Tibiofemoral contact mechanics after serial medial meniscectomies in the human cadaveric knee. The American journal of sports medicine. 2006;34(8):1334–1344. doi: 10.1177/0363546506286786. [DOI] [PubMed] [Google Scholar]
- 66.Becker R, Wirz D, Wolf C, Gopfert B, Nebelung W, Friederich N. Measurement of meniscofemoral contact pressure after repair of bucket-handle tears with biodegradable implants. Archives of orthopaedic and traumatic surgery. Archiv fur orthopadische und Unfall-Chirurgie. 2005;125(4):254–260. doi: 10.1007/s00402-004-0739-5. [DOI] [PubMed] [Google Scholar]
- 67.Wirz D, Becker R, Li SF, Friederich NF, Muller W. Validation of the Tekscan system for statistic and dynamic pressure measurements of the human femorotibial joint. Biomedizinische Technik. Biomedical engineering. 2002;47(7–8):195–201. doi: 10.1515/bmte.2002.47.7-8.195. [DOI] [PubMed] [Google Scholar]
- 68.Brimacombe JM, Wilson DR, Hodgson AJ, Ho KC, Anglin C. Effect of calibration method on Tekscan sensor accuracy. Journal of biomechanical engineering. 2009;131(3):034503. doi: 10.1115/1.3005165. [DOI] [PubMed] [Google Scholar]
- 69.Jansson KS, Michalski MP, Smith SD, LaPrade RF, Wijdicks CA. Tekscan pressure sensor output changes in the presence of liquid exposure. Journal of biomechanics. 2013;46(3):612–614. doi: 10.1016/j.jbiomech.2012.09.033. [DOI] [PubMed] [Google Scholar]
- 70.Shefelbine SJ, Ma CB, Lee KY, Schrumpf MA, Patel P, Safran MR, Slavinsky JP, Majumdar S. MRI analysis of in vivo meniscal and tibiofemoral kinematics in ACL-deficient and normal knees. Journal of orthopaedic research : official publication of the Orthopaedic Research Society. 2006;24(6):1208–1217. doi: 10.1002/jor.20139. [DOI] [PubMed] [Google Scholar]