Proximal arm kinematics affect grip force-load force coordination

Abstract

During object manipulation, grip force is coordinated with load force, which is primarily determined by object kinematics. Proximal arm kinematics may affect grip force control, as proximal segment motion could affect control of distal hand muscles via biomechanical and/or neural pathways. The aim of this study was to investigate the impact of proximal kinematics on grip force modulation during object manipulation. Fifteen subjects performed three vertical lifting tasks that involved distinct proximal kinematics (elbow/shoulder), but resulted in similar end-point (hand) trajectories. While temporal coordination of grip and load forces remained similar across the tasks, proximal kinematics significantly affected the grip force-to-load force ratio (P = 0.042), intrinsic finger muscle activation (P = 0.045), and flexor-extensor ratio (P < 0.001). Biomechanical coupling between extrinsic hand muscles and the elbow joint cannot fully explain the observed changes, as task-related changes in intrinsic hand muscle activation were greater than in extrinsic hand muscles. Rather, between-task variation in grip force (highest during task 3) appears to contrast to that in shoulder joint velocity/acceleration (lowest during task 3). These results suggest that complex neural coupling between the distal and proximal upper extremity musculature may affect grip force control during movements, also indicated by task-related changes in intermuscular coherence of muscle pairs, including intrinsic finger muscles. Furthermore, examination of the fingertip force showed that the human motor system may attempt to reduce variability in task-relevant motor output (grip force-to-load force ratio), while allowing larger fluctuations in output less relevant to task goal (shear force-to-grip force ratio).

proper grip force modulation during object transport is necessary to counteract the time-varying load force caused by object inertia and is an essential aspect of human motor control required for successful completion of object manipulation tasks, i.e., preventing an object from slipping (Flanagan and Wing 1993). Different control mechanisms, utilizing somatosensory feedback (Johansson and Westling 1984) and anticipatory feedforward control (Forssberg et al. 1991), are employed in the grip force modulation (for review, see Flanagan et al. 2006). Specifically, “internal models” within the central nervous system, presumably located in the cerebellum (Kawato et al. 2003; Rost et al. 2005), are thought to take part in control processes that integrate multimodal sensory information and generate proper motor commands to control grip force accordingly (Johansson and Cole 1992; Kawato 1999). Grip force control, however, can be significantly affected when performance of any component of the sensorimotor system involved in the control is disrupted. For example, erroneous visual size cues (Gordon et al. 1991), impairments in tactile/cutaneous afferents (Nowak et al. 2004), and/or abnormalities in the cerebellum (Muller and Dichgans 1994; Nowak et al. 2005; Nowak et al. 2009; Rost et al. 2005).

Another aspect of object transportation that could affect grip force control is variations in proximal kinematics during object transport. Due to the large number of degrees of freedom (DOF) in the upper extremity (UE), similar end-point trajectories can be achieved via different elbow and shoulder movements, which could affect distal hand muscles via several biomechanical or neurological pathways; many extrinsic hand muscle tendons cross the elbow joint; thus elbow flexion during movements could biomechanically alter the force-generating capacity of hand muscles (An et al. 1981). Different arm configurations involve different levels of energy expenditure, which may affect motor planning of the UE dynamics (Soechting and Flanders 1998), including grip force production. Change in the proximal joint use may differently excite/inhibit multijoint spinal/subcortical pathways used during voluntary arm movements (e.g., Bullock et al. 1988) that could also affect hand muscle use (Baker 2011). Alternatively, grip force production may be affected by involuntary coupling between distal and proximal UE muscles during planning (d'Avella et al. 2006; Santello et al. 1998) or execution (Lee et al. 2014).

Despite the importance, the effects of proximal kinematics on grip force control remain mostly unexplored. The purpose of this study was to clarify the effects of varying kinematics of the proximal arm joints on grip force modulation during object manipulation. Subjects were asked to perform three lifting tasks that involved distinct elbow and shoulder joint movements but resulted in similar vertical movements of the hand (end-point). Our hypothesis was that, despite similar end-point trajectories, differences in proximal arm joint kinematics across these tasks would significantly affect the grip force-to-load force coordination. Comparison of grip force-load force characteristics between tasks will help clarify mechanisms of potential correlation between proximal kinematics and grip force control. We also hypothesize that, during each lifting movement, some hand muscles would be more affected by the change in the proximal muscle activation, similar to the observation made in our laboratory's previous study during static task condition (Lee et al. 2014), and such distal-proximal coupling in a subset of hand muscles would result in changes in the fingertip force direction. Therefore, we examined two force components, grip force (normal force) and shear force at the fingertip, and their correlation with the load force during the movement. The fingertip force direction would remain relatively unchanged, if the grip force is controlled voluntarily by a forward model that scales muscle activation patterns with increasing grip force (Valero-Cuevas 2000), while an involuntary coupling between proximal UE muscles and certain hand muscles could result in changes in fingertip force direction during lifting movements.

MATERIALS AND METHODS

Subjects

Fifteen young adults with no known history of neurological or musculoskeletal disorders (11 men, 4 women; mean ± SD age = 24 ± 2 yr; 13 right-handed) participated in the study. The experimental protocol was approved by both the MedStar Health institutional review board and the institutional review board at the Catholic University of America, and written, informed consent was obtained from each subject prior to participation.

Instrumentation

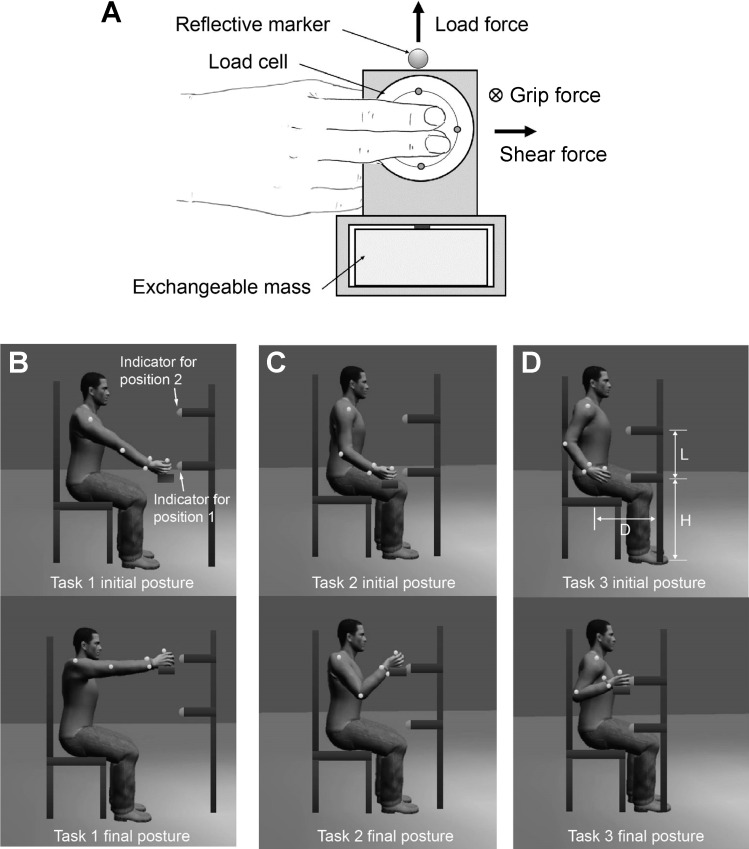
During experiments, subjects held an instrumented object, on which a 6-DOF load cell (Mini40; ATI Industrial Automation, Apex, NC) was mounted, with their dominant hand. The contact surface of the object was covered with sandpaper (320 grit), and an exchangeable mass was placed in the base (Fig. 1A). The object weight was scaled to subjects' grip capacity; for subjects whose maximum force produced during three-digit palmar pinch (see Target Tasks section for the description of the grip task) exceeded 15 N, a steel block of 500 g was placed in the base (Fig. 1A). For all other subjects, a 300-g mass was used. The load cell recorded grip force (normal to the surface), load force (vertical), and shear force (horizontal) during task performance. Given the experimental setup, the vertical force (y-direction) reflects the sum of the gravitational and inertial forces, the normal force (z-direction) corresponds to grip force normal to the object surface, and the shear force (horizontal; x-direction) denotes distal shear force produced at the fingertip, which represents force components that deviate from the task-relevant direction (i.e., normal force) (e.g., Seo et al. 2010). Fingertip force direction, i.e., grip (normal) force-to-shear force ratio, is indicative of coordination pattern of the hand muscles, as each finger muscle produces a unique fingertip force direction (i.e., normal-to-shear force ratio) (Lee et al. 2008; Milner and Dhaliwal 2002; Valero-Cuevas et al. 1998).

Fig. 1.

Experimental setup and target tasks. A: instrumented object used in the experiment. B–D: lifting tasks performed by subjects. A 6-degrees-of-freedom load cell recorded fingertip forces in three directions: grip force (normal to the surface), load force (vertical), and shear force (horizontal). During the experiment, the horizontal distance from the body to the target (D) was changed for each task so that distinct types of shoulder and elbow joint movements were used for the three tasks. For example, the lifting movement was performed primarily through shoulder flexion in task 1, while elbow flexion primarily contributed to the lifting movement in task 3. While the vertical locations of these indicators (H) were adjusted across the tasks, the distance between the two indicators (L) remained unchanged (so that the end-point trajectories of the three tasks were similar).

An eight-camera motion capture system (Osprey Digital RealTime System; Motion Analysis, Santa Rosa, CA) recorded the joint angles of the UE during experiments. For each subject, seven reflective markers were placed on the wrist (2), elbow (1), shoulder (1), and torso (3). One additional marker was also placed on the object to record its trajectory during movements (Fig. 1). Marker locations were recorded at 60 Hz for each trial.

Eight pairs of disposable, self-adhesive silver/silver chloride surface electrodes (diameter 15 mm, center spacing 20 mm; Noraxon, Scottsdale, AZ) were used for surface EMG recordings. Two pairs were placed on the hand to record the activities of intrinsic hand muscles [flexor pollicis brevis (FPB) and first dorsal interosseous (FDI)], two pairs on the forearm to record extrinsic hand muscle activities [1st and 2nd compartments of the flexor digitorum superficialis (FDS) and extensor digitorum communis (EDC)], two pairs on the upper arm to record the activity of elbow flexor and extensor muscles [short head of biceps brachii (BB) and lateral head of triceps brachii (TB)], and two pairs on the shoulder to record shoulder flexor and abductor activities [anterior deltoid (AD) and lateral deltoid (LD)]. To ensure accurate placement of each electrode, EMG signals from the electrodes were inspected while subjects performed several thumb and finger movements associated with the target muscle and adjacent muscles. The electrode location was adjusted if the EMG signal changed during isolated contraction of any neighboring muscle.

Target Tasks

Subjects were instructed to perform one of the three lifting tasks (tasks 1–3; Fig. 1, B–D), during which they transported/lifted the instrumented object from a lower position (position 1) to a higher position (position 2). The locations of the initial and final hand positions were specified by two indicators mounted on a vertical rod (Fig. 1, B–D). Subjects were simply asked to move (or lift) the object from position 1 to position 2. As shown in Fig. 1, the horizontal distance from the body to the rod (D in Fig. 1) was adjusted for each task so that each of the three tasks required distinct combinations of shoulder and elbow joint flexion movements. However, the distance between the two indicators (L in Fig. 1) was kept constant across the tasks to maintain a similar end-point (hand) trajectory between tasks.

For each task, subjects were asked to move the object on a straight, vertical line (defined by the two indicators; Fig. 1) and to keep object orientation constant during movement. Subjects were also instructed to grasp the object with three digits, the index and middle fingers and the thumb, using opposing thumb pad and finger pads (i.e., three-digit palmar pinch; Fig. 1A). As the FDS produces a proximal interphalangeal joint flexion moment (An et al. 1983; Valero-Cuevas et al. 1998) and its involvement in grip increases as the distal interphalangeal (DIP) joint extends (Vigouroux et al. 2006), subjects were asked to keep their proximal interphalangeal joints flexed while maintaining extension of their DIP joints to maximize the contribution of the FDS during the grip task.

Experimental Protocol

Prior to the experimental session, maximum EMG activity was recorded for each muscle. Subjects performed maximal isometric contractions of the eight muscles by performing each of the following tasks for approximately 2 s: maximum finger extension (EDC), maximum index finger flexion with the DIP joint extended (FDS), maximum thumb interphalangeal joint flexion (FPB), maximum index finger abduction (FDI), maximum elbow flexion (BB), maximum elbow extension (TB), maximum shoulder flexion (AD), and maximum shoulder abduction (LD). During maximal contraction, EMG data were recorded for 4 s. During the first second, subjects increased muscle activation to the maximum level (ramp-up phase), then subjects sustained maximum contraction for the next 3 s. Only data recorded during the middle 2 s of the contraction were used to calculate the maximum EMG level.

Each subject was instructed to perform each of the three target tasks (tasks 1–3) eight times (trials 1–8) in random order. Subjects were instructed to initially hold the object at the lower position (position 1), and lift it to the higher position (position 2) upon a sound queue (beep). The following verbal instructions were given: “Lift the object from the lower position to the higher position marked by the indicators. Do it at your own pace.” To prevent fatigue, subjects were asked to take a 30-s break after each trial. In addition, a 3-min rest period was administered after every five trials. The force data, including grip force, load force, shear force, and EMG signals from the eight muscles, were recorded during task performance. Typical force and kinematics data during lifting movements are depicted in Fig. 2.

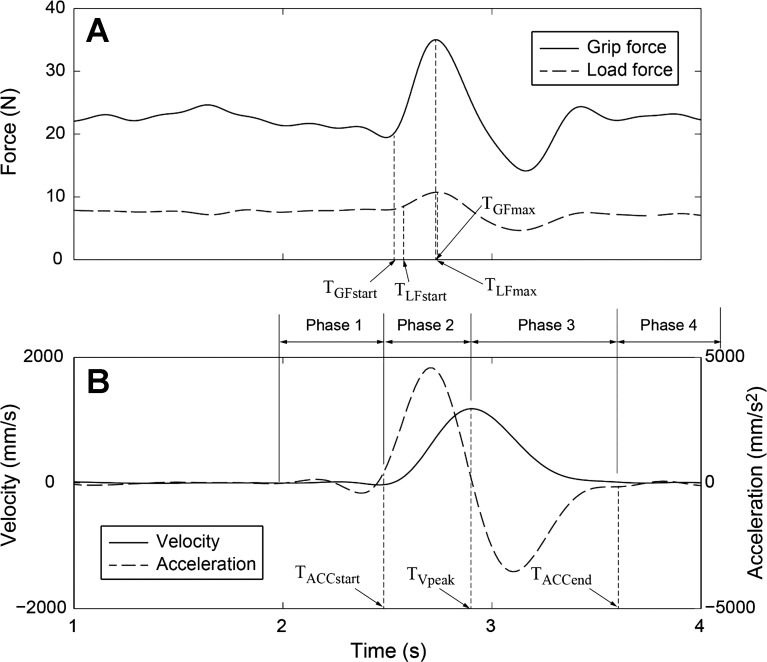
Fig. 2.

Representative force (A) and kinematics (B) data (subject 3, task 1, trial 2). Seven time points [grip force onset (T_GFstart), load force onset (T_LFstart), maximum grip force (T_GFmax), maximum load force (T_LFmax), movement start time (T_ACCstart), peak velocity time (T_Vpeak), movement termination time (T_ACCend)] were determined from the temporal trajectories of the marker placed on the instrumented object and force profiles, and four movement phases (phases 1–4) were consequently defined by these time points.

Data Analysis

Movement kinematics.

The temporal trajectory of each reflective marker was digitally filtered forward and backward by a third-order low-pass Butterworth filter (cutoff frequency: 5 Hz) using MATLAB (The MathWorks, Natick, MA). Angular displacements of the following joint DOF were computed using the law of cosines from the spatial trajectories of the markers: shoulder flexion/extension, elbow flexion/extension, wrist flexion/extension, wrist abduction/adduction.

For each lifting movement, three time points were determined: 1) movement start time (T_ACCstart); 2) movement termination time (T_ACCend); and 3) peak velocity time (T_Vpeak). T_ACCstart was identified during the initiation of movement as the time at which the magnitude of vertical acceleration of the marker attached to the object exceeded 2% of its maximum acceleration. Similarly, T_ACCend was identified during the conclusion of the movement as the time at which the magnitude of vertical acceleration decreased and returned to within 2% of the maximum acceleration. Finally, T_Vpeak was identified as the time at which the velocity was the largest and vertical acceleration was zero. From these time points, the following four periods (movement phases) were defined (Fig. 2):

1) Phase 1 (Hold at position 1): 500 ms before movement initiation–movement initiation (T_ACCstart − 500 ms < t < T_ACCstart).

2) Phase 2 (Acceleration): movement initiation-peak velocity (T_ACCstart < t < T_Vpeak).

3) Phase 3 (Deceleration): peak velocity-movement termination (T_Vpeak < t < T_ACCend).

4) Phase 4 (Hold at position 2): movement termination-500 ms after movement termination (T_ACCend < t < T_ACCend + 500 ms).

Similarly, from the grip force and load force data, two other sets of time points were determined: for grip force, 1) grip force onset (T_GFstart) defined as the time point when the grip force reached and surpassed 2% of its maximum value, and 2) maximum grip force (T_GFmax); similarly, for load force, 1) load force onset (T_LFstart), 2) load force termination time (T_LFend), and 3) maximum load force (T_LFmax) (Fig. 2).

Spatial coordination of grip force.

First, the ratio of grip force and load force magnitudes during the lifting movements was computed. Then, the values of time-averaged grip force-to-load force ratio (GLR) were computed by averaging the ratio values within each of the four phases of movement:

$$\text{GLR}\left(p\right)=\frac{1}{N_{fp}-N_{ip}}{\displaystyle \sum _{k=N_{ip}}^{N_{fp}}\frac{F_G\left(k\right)}{F_L\left(k\right)}}\left(p=1,\dots ,4\right)$$ (1)

where p denotes the movement phase, F_G(k) is the measured grip force at a discrete time point k, F_L(k) the load force, and N_ip and N_fp indicate the discrete time points that correspond to the initial and final times of phase p, respectively.

Similarly, the ratio of shear force and grip force was computed. Activation of hand muscles creates different fingertip force vectors with distinct normal-to-shear force ratios (i.e., distinct fingertip force directions) (Valero-Cuevas 2000; Valero-Cuevas et al. 1998), and different muscle activation patterns can create different fingertip normal-to-shear force ratios (Lee et al. 2008; Seo et al. 2010). This ratio indicates how much of the fingertip force was directed in the shear direction. The averaged shear force-to-grip force ratio (SGR) was then computed by averaging

$$\text{SGR}\left(p\right)=\frac{1}{N_{fp}-N_{ip}}{\displaystyle \sum _{k=N_{ip}}^{N_{fp}}\frac{F_S\left(k\right)}{F_G\left(k\right)}}\left(p=1,\dots ,4\right)$$ (2)

where F_S(k) denotes the measured shear force at time k.

GLR is a parameter that is critically controlled during movements and should be maintained above a “safety margin” to prevent slip of the object during movements (Westling and Johansson 1984). In contrast, SGR represents a motor variable that is irrelevant to the task, as the shear force at the fingertip is not required to prevent slip.

Temporal coordination.

Two types of temporal coordination characteristics were examined. First, we examined how the measured forces (i.e., grip force, load force, and shear force) were correlated with each other within each trial. Correlation coefficients were estimated and compared between the three tasks (task 1--task 3). Resulting correlation coefficients between grip force and load force can be used to gauge whether changes in the load force were anticipated and reflected in grip force modulation (e.g., Nowak et al. 2004). On the other hand, correlation between grip force and shear force indicates change in the coordination of hand muscles. High correlation between grip and shear forces would suggest that the fingertip force direction did not change significantly during the lifting movement, thereby hand muscle coordination pattern was maintained during the movement, while low correlation would indicate that the coordination of the extrinsic and intrinsic hand muscles have changed during the course of lifting movement.

The time lags between different onset time points, specifically, two time lag values, were estimated from the force and kinematic data: 1) the time lag between T_ACCstart and T_GFstart; and 2) the time lag between peak grip force (T_GFpeak) and peak load force (T_LFpeak). These time lag values may also indicate the degree to which changes in load force were anticipated and reflected in grip force modulation.

Muscle activation levels.

For each trial, the activation levels of the four hand muscles (associated with the grip task) were estimated from the recorded EMG signals by calculating root-mean-square (RMS) values of the EMG signals. The activation levels were then averaged within each of the four periods (phases 1–4). We also computed relative magnitude of the flexor (FDS) and extensor (EDC) muscle activities, and flexor-extensor ratio (FER), which would better correlate to the grip force than individual muscle activities. Here, to account for between-subject variability of FER values, FER values were normalized to the FER value obtained during task 2 for each subject:

$$\text{FER}\left(p,k\right)=\frac{RM{S}_{FDS}\left(p,k\right)}{RM{S}_{EDC}\left(p,k\right)}/\frac{RM{S}_{FDS}\left(1,1\right)}{RM{S}_{EDC}\left(1,1\right)}\left(p=1,2,3,4;k=1,2,3\right)$$ (3)

where p denotes phase, and k task.

Intermuscular coherence.

The coherence between two EMG signals was computed to quantify correlations between muscle activations in the time and frequency domains. Intermuscular coherence estimates can quantify an oscillatory synchrony between pairs of muscles, providing an objective measure of common synaptic drive shared between motoneurons controlling the muscles of interest (Farmer et al. 1998; Gibbs et al. 1997; Grosse et al. 2003; Perez et al. 2006). Therefore, EMG-EMG coherence was calculated between distal hand muscles.

EMG-EMG coherence between six pairs of hand muscles (EDC-FDS, EDC-FPB, EDC-FDI, FDS-FPB, FDS-FDI, FPB-FDI) was estimated for each trial. The coherence values between muscle-pairs were estimated using non-overlapping segments (rectangular window) that resulted in a frequency resolution of 2 Hz. Calculations were performed within the MATLAB environment, employing a script developed by Neurospec (http://www.neurospec.org; Halliday et al. 1995). The time frequency analysis was done by moving a sliding window of duration 500 samples (500 ms) across each trial with offset values ranging from 0 to 750 samples. The 95% confidence limits of the coherence estimates were also calculated by Neurospec, and only the coherence values above this limit were considered throughout the analysis.

Briefly, given two EMG signals x and y, let the power spectra of the two signals be denoted as f_xx(λ) and f_yy(λ), and their cross-spectrum as f_xy(λ). The coherence between two signals at frequency λ, R_xy(λ), is defined as (Halliday et al. 1995):

$$\left|R_{xy}\left(\lambda \right)\right|=\frac{{\left|f_{xy}\left(\lambda \right)\right|}^2}{f_{xx}\left(\lambda \right)f_{yy}\left(\lambda \right)}$$ (4)

The cumulant density function in the time domain q_xy(t) is defined as the inverse Fourier transform of the cross spectrum f_xy(λ):

$$q_{xy}\left(t\right)={\displaystyle {\int }_{-\pi }^{\pi }{f}_{xy}\left(\lambda \right)e^{j\lambda t}d\lambda }$$ (5)

The EMG-EMG coherence was estimated in the following four frequency bands: δ/θ (0–5 Hz), α (6–15 Hz), β (16–35 Hz), and γ (36–55 Hz), but analyses were focused on the α-, β-, and γ-bands. The coherence values at the lowest frequency band [i.e., δ- and θ-bands (0–5 Hz)] were not examined in detail, since the coherence in this frequency band is not thought to originate from the corticospinal system (Farmer et al. 1993). Then, the coherence estimates were z-transformed as follows,

$$z\left(\lambda \right)=\frac{1}{2}\log \frac{1+R_{xy}\left(\lambda \right)}{1-R_{xy}\left(\lambda \right)}$$ (6)

as the “z-transformed” coherence values will be normally distributed with a standard deviation of ∼1 (Rosenberg et al. 1989). Then, the integral of z-transformed coherence was estimated within three frequency bands.

Statistical analysis.

For the following independent variables, kinematic variables [range of motion (ROM), peak velocity, peak acceleration], GLR, SGR, time lag (T_GFstart − T_ACCstart and T_GFmax − T_LFmax), and coherence values, an analysis-of-variance (ANOVA) was implemented to determine the effects of proximal kinematics (i.e., task) and movement phase (IBM SPSS Statistics version 20; IBM, Armonk, NY). For the activation pattern of the muscles, a multivariate analysis of variance (MANOVA) was implemented. Additionally, a post hoc univariate ANOVA was implemented to the activation of each muscle to avoid potential type I error (Wetcher-Hendricks 2011). Significance was set to 0.05. Pairwise comparisons between the proximal kinematics and movement phases were also made with Bonferroni's adjustment for multiple comparisons.

RESULTS

Despite differences in proximal kinematics among tasks 1–3, the end-point trajectories of all three lifting movements were similar and were primarily in the vertical direction. For all three tasks, grip force and load force were temporally coordinated with each other during movements, while shear force did not temporally correlate with either grip force or load force, indicating that shear force was modulated independently. While the proximal kinematics did not have a significant effect on temporal coupling of grip force and load force, there was a significant effect of proximal kinematics on the modulation of grip force magnitude (GLR).

Movement Characteristics

The kinematic characteristics of the end-point trajectories of the three movements indicated that the primary movement direction for all three movements was vertical, signified by high vertical-to-horizontal ROM ratios (10.2:1, 8.6:1, and 5.5:1 for tasks 1, 2, and 3, respectively) and by high vertical-to-horizontal peak acceleration ratios (4.4:1, 4.73:1, and 6.32:1 for tasks 1, 2, and 3, respectively). These results indicate that the magnitude of horizontal inertial force produced during these movements was relatively small (Table 1).

Table 1.

Mean values of kinematic parameters of the three movements (tasks)

	Task 1 (Distant)	Task 2 (Middle)	Task 3 (Close)
End-point kinematics
ROM, cm
Vertical	49.0 (6.0)	46.5 (5.3)	41.6 (9.1)
Horizontal	4.8 (3.6)	5.4 (3.5)	7.5 (4.7)
Peak velocity, cm/s
Vertical	91.6 (6.8)	121.6 (12.5)	120.4 (4.6)
Horizontal	16.3 (2.7)	17.0 (1.9)	11.8 (4.6)
Peak acceleration, cm/s2
Vertical	393.9 (38.5)	485.0 (63.9)	477.2 (34.7)
Horizontal	89.8 (12.5)	102.5 (19.1)	75.5 (25.0)
Joint kinematics
ROM, cm
Shoulder	47.8 (8.1)	39.7 (10.6)	13.8 (17.6)
Elbow	14.2 (13.3)	39.3 (14.4)	80.6 (18.8)
Peak velocity, cm/s
Shoulder	123.1 (18.8)	120.1 (22.5)	43.6 (19.4)
Elbow	51.6 (23.8)	133.6 (30.6)	205.9 (29.7)
Peak acceleration, cm/s2
Shoulder	560.9 (100.5)	615.2 (116.6)	250.9 (104.8)
Elbow	341.4 (128.7)	796.4 (180.5)	1,010.7 (236.5)

Values are means (SD). ROM, range of motion.

While the end-point kinematics of the three movements were similar, the joint kinematics employed during these movements were substantially different, indicated by distinct shoulder and elbow joint ROM values for each task (Table 1). Between-task difference in ROM values of both shoulder and elbow joints were significant between all task pairs (P < 0.001). For the elbow joint, both peak velocity and peak acceleration values were significantly different between all task pairs (P < 0.001). For the shoulder joint, both peak velocity and peak acceleration values of task 3 were different from those of task 1 and task 2 (P < 0.001 for task 1–task 3 pair and for task 2–task 3 pair), but there was no task difference in these values between task 1 and task 2 (P = 0.55 for peak velocity; P = 0.11 for peak acceleration).

Changes in the wrist flexion angle (flexion ROM) during these movements were relatively small (mean ROM = 19.2°), which were also not different across the three tasks (task 1–task 3) (P = 0.43). The wrist abduction/adduction ROM values (mean ROM = 40.5°) were found to be greater than the flexion ROM.

GLR and SGR

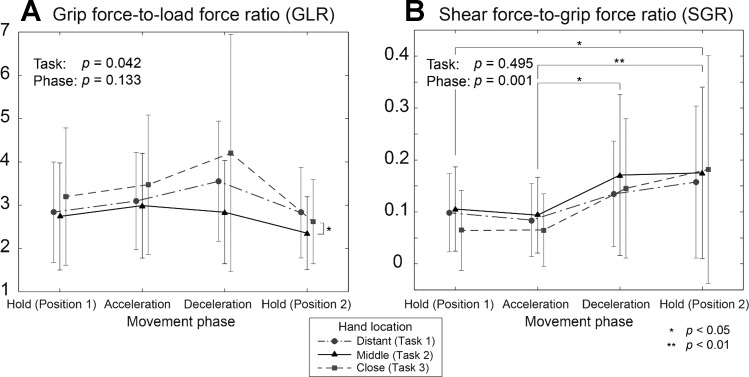
There was a significant effect of proximal kinematics on the GLR (Fig. 3A). Differences in the GLR between tasks were statistically significant [task: F_(2,168) = 3.23; P = 0.042], indicating the effects of proximal kinematics on grip force control. Specifically, the GLR for task 2 was smaller than for task 3 (P = 0.040). The GLR value was not significantly different between movement phases [phase: F_(3,168) = 1.894; P = 0.133].

Fig. 3.

Mean (SD) grip force-to-load force ratio (GLR; A) and shear force-to-grip force ratio (SGR; B) for the three tasks. Overall, the GLR values were significantly higher during task 3 (P < 0.001). Specifically, for the second half of the movements (deceleration and hold in position 2), GLR for task 3 (close hand locations) were significantly greater than for task 2 (middle location) (P < 0.05). In contrast, no difference between tasks were found in SGR values (P = 0.930). Overall, the SGR values were significantly higher during the second half of the movement (phases 3 and 4; P = 0.001). Significant differences: *P < 0.05, **P < 0.01.

SGR exhibited different between-task variability compared with GLR. Unlike GLR, the SGR did not differ significantly across the three tasks [task: F_(2,168) = 0.705; P = 0.495]. However, SGR did significantly vary during movement phases [phase: F_(3,168) = 5.792; P = 0.001]. SGR during the second half of the movement (phases 3 and 4) were relatively larger than those during the first half (phases 1 and 2) (Fig. 3B).

Temporal Coupling: Time Lag Values

There was no significant difference across the three tasks in either time lag value [time lag between the start of grip force change and onset of acceleration (T_GFstart − T_ACCstart; P = 0.333; Table 2) and time lag between the maximum grip force and maximum load force (T_GFmax − T_LFmax; P = 0.682; Table 2)]. Positive time lag values between T_GFstart − T_ACCstart (mean = 0.252 s) indicate that the grip force started to increase before the arm movements began for all tasks. T_GFmax also preceded T_LFmax, but the time lag values were very small (mean = 0.008 s).

Table 2.

Mean values of time lag across kinematics (all subjects)

	Task/Proximal Kinematics
Time Lag	Task 1 (Distant)	Task 2 (Middle)	Task 3 (Close)
TGFstart − TACCstart, s	0.259 (0.007)	0.255 (0.009)	0.243 (0.011)
TGFmax − TLFmax, s	0.008 (0.033)	0.002 (0.044)	0.013 (0.075)

Values are means (SD). T_GFstart, grip force onset time point; T_ACCstart, movement start time; T_GFmax, maximum grip force time point; T_LFmax, maximum load force time point.

Temporal Coupling: Correlation between Grip Force and Load Force vs. between Shear Force and Grip Force

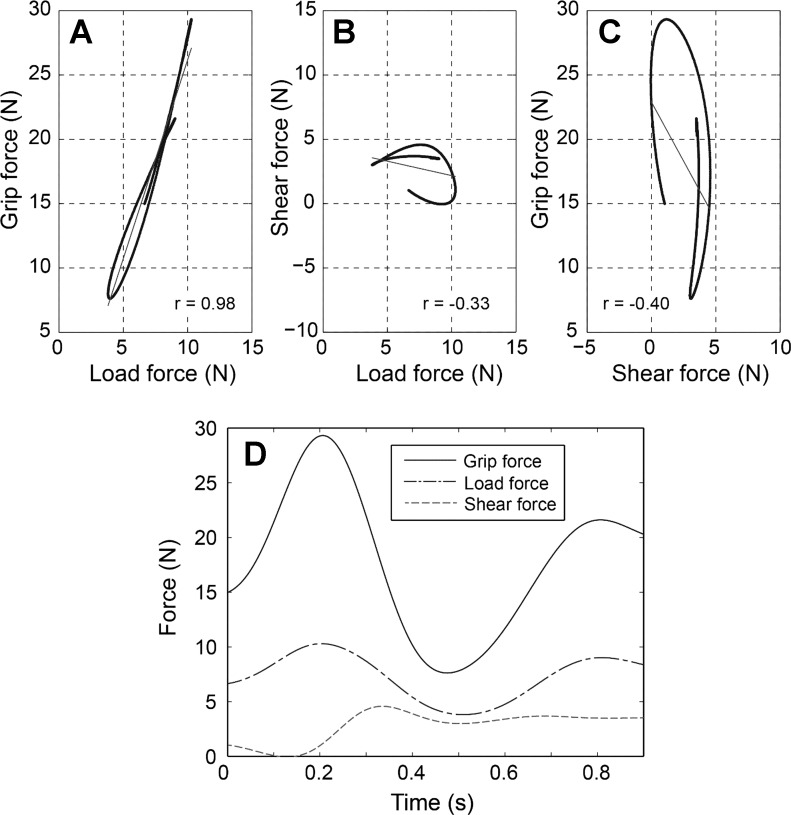
Correlation analyses, which examined temporal coordination of different force pairs (e.g., grip force-load force and grip force-shear force) within each trial, showed that grip force and load force were highly coordinated with each other during movements, while shear force was modulated independently. In general, while the grip force and load force covaried within each trial (mean r value = 0.71, Table 3; Fig. 4A), shear force was not correlated with either load force (Fig. 4B) or grip force (mean r value = 0.02, Table 3; Fig. 4C). Note that low correlation between shear and grip forces is also signified by the significant phase effect on SGR value (Fig. 3B). While the ratio between grip force and load force (i.e., GLR) remained relatively constant throughout the movement (no phase effect; P = 0.133), the ratio between shear force and grip force (i.e., SGR) was significantly affected by the movement phase (P = 0.001), indicating that these two forces were not correlated to each other. During the movement, while grip force generally covaried with load force, shear force increased primarily during the acceleration phase and then remained at the increased force level until the movement was completed (Fig. 4D). This trend was also seen in the group-averaged SGR data (Fig. 3B).

Table 3.

Mean correlation coefficient (r) across kinematics (all subjects)

	Task (Proximal Kinematics)
Correlation Coefficient Between	Distant (Task 1)	Middle (Task 2)	Close (Task 3)
Grip force-load force	0.75 (0.39)	0.71 (0.32)	0.66 (0.34)
Shear force-load force	0.21 (0.59)	0.04 (0.51)	0.12 (0.48)
Shear force-grip force	0.05 (0.62)	−0.06 (0.42)	0.06 (0.45)

Values are means (SD).

Fig. 4.

Representative plot of grip force-load force coordination (A), shear force-load force coordination (B), grip force-shear force coordination (C), and temporal trajectories (D) of the three forces during the acceleration and deceleration phases (subject 6, task 2, trial 1). Overall, grip force was highly correlated with load force, while the shear force was not correlated with either grip force or load force.

Muscle Coordination

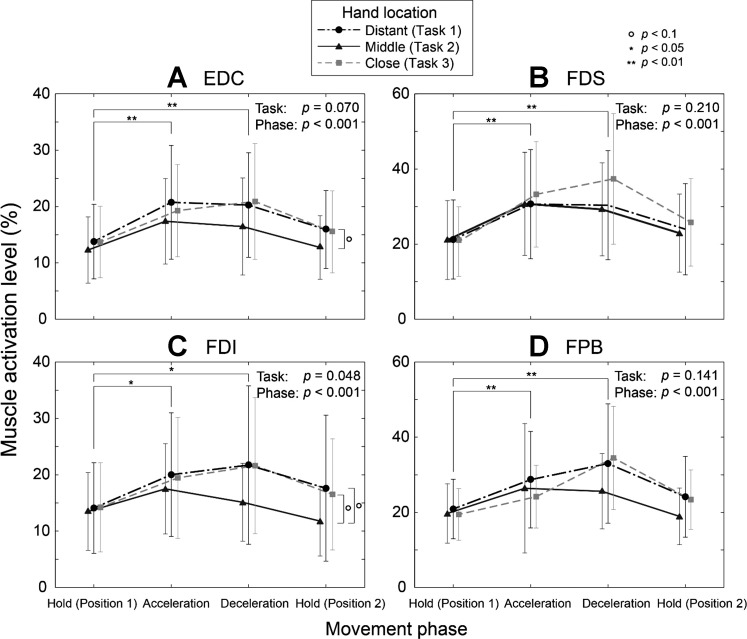
Movement phase was found to have a significant impact on the coordination of hand muscles (relative muscle activities; P < 0.001; also see Fig. 5), but the between-task difference in the hand muscle coordination (relative muscle activities or ratio) was not found to be statistically significant [P = 0.070; F_(8,332) = 1.83; 95% confidence interval: 0.34 < F_(8,332) < 1.97]. Post hoc univariate ANOVAs revealed that the task-related changes in the activation level of most hand muscles were indeed small (P = 0.070 for EDC; P = 0.210 for FDS; P = 0.141 for FPB), but that the activation level of the intrinsic finger muscle (FDI) was found to be significantly affected by the proximal kinematics (P = 0.048; Fig. 5C).

Fig. 5.

Mean (SD) activation level of the hand muscles across the three tasks: extensor digitorum communis (EDC; A), flexor digitorum superficialis (FDS; B), first dorsal interosseous (FDI; C), and flexor pollicis brevis (FPB; D). Movement phase was found to have a significant impact on all hand muscles (P < 0.001), but the between-task difference was not statistically significant (P = 0.070). Post hoc univariate ANOVA showed that only FDI muscle activation was found to be significantly affected by the proximal kinematics (task; P = 0.048). Significant differences: ^o|P < 0.1, *P < 0.05, **P < 0.01.

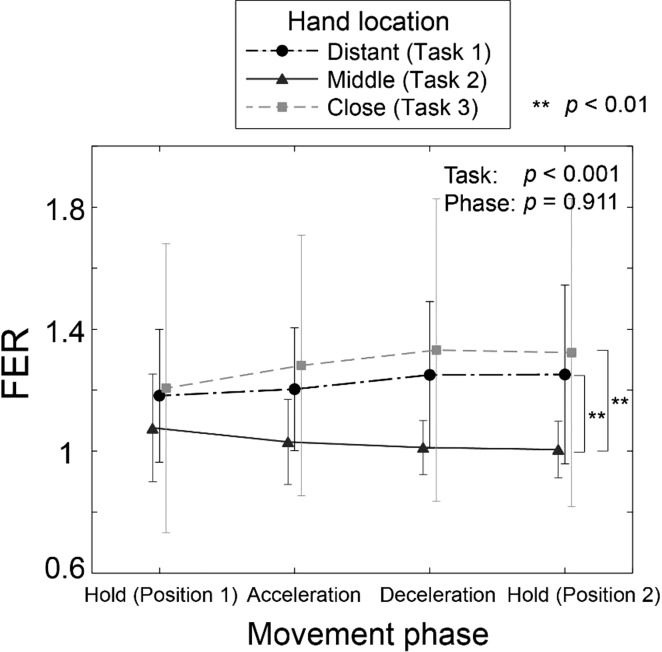
While the activation level of the individual finger flexor (FDS) and extensor (EDC) was not affected by task, the relative FER was found to be significantly affected by task (P < 0.001), but not by phase (P = 0.495) (Fig. 6). FER values during task 2 were significantly smaller than those of task 1 (P = 0.002) and task 2 (P = 0.001).

Fig. 6.

Mean (SD) flexor-extensor ratio (FER). There was a significant task effect on FER values (P = 0.001); however, FER values did not change significantly during the movement (no phase effect; P = 0.495). Significant differences: **P < 0.01.

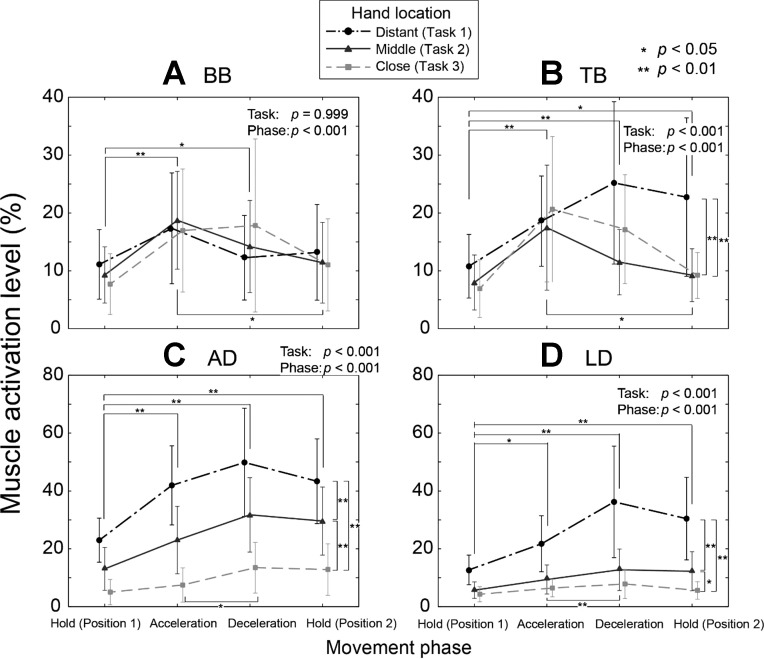
Both task (P < 0.001) and phase (P < 0.001) have significant effects on the activation patterns of both elbow muscles and shoulder muscles (Fig. 7). While no task effect was found in BB, TB activation was found to be higher during task 1 than task 2 (P < 0.001) or task 3 (P = 0.001). For both shoulder muscles (AD and LD), their activation levels during task 3 were higher than during task 2 (P < 0.001), and those during task 2 were higher than during task 1 (P < 0.001).

Fig. 7.

Mean (SD) activation level of the proximal arm muscles across the three tasks: short head of biceps brachii (BB; A), lateral head of triceps brachii (TB; B), anterior deltoid (AD; C), and lateral deltoid (LD; D). Both movement phase (P < 0.001) and proximal kinematics (task; P < 0.001) were found to have significant impact on all proximal arm muscles except BB. For BB, proximal kinematics did not have a significant effect (task; P = 0.999), while movement phase significantly affected its activation level (P < 0.001). Significant differences: *P < 0.05, **P < 0.01.

Intermuscular Coherence

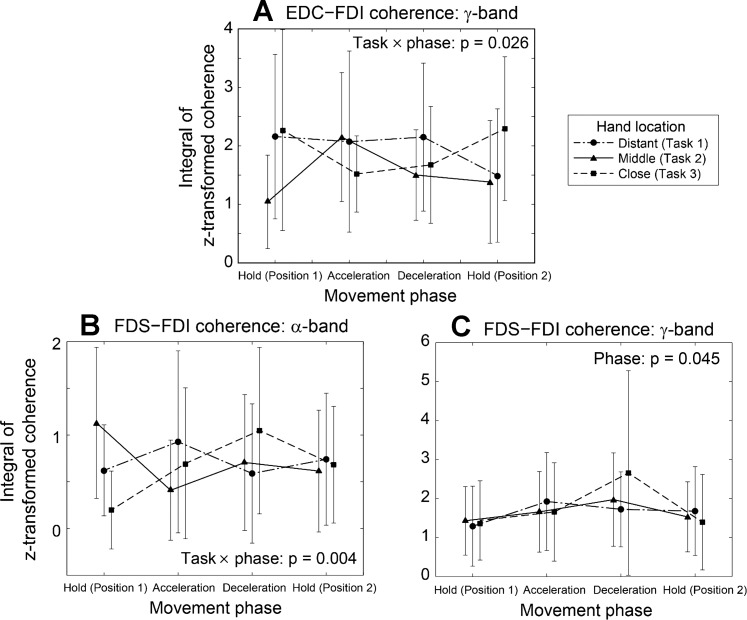
Task-related changes in the intermuscular coherence values support the finding that change in the proximal kinematics (task) affected common neural inputs to the hand muscles. Of all the hand muscle pairs examined, the task-related effects were most significant in the following two muscle pairs: 1) EDC-FDI, which represents the agonist-antagonist muscles of the index finger, and 2) FDS-FDI, which corresponds to the synergist muscles of the index finger for the grip task. Note that both muscle pairs include FDI muscle, whose activation level was affected by the proximal kinematics, as shown above (P = 0.048).

Two different types of task-related changes were observed in these two muscle pairs. For the EDC-FDI pair, a significant interaction between task and phase was found in the γ-band (P = 0.026); for the tasks 1 and 2, the γ-band coherence values were higher during the movements (phases 2 and 3) compared with the other phases (phases 1 and 4); for the task 3, however, the γ-band coherence values decreased during the movements (phases 2 and 3) (Fig. 8A). For the FDS-FDI pair, a significant interaction between task and phase was found in coherence values in the α-band (P = 0.004). But for the task 3, in contrast to what was observed in the γ-band coherence of the EDC-FDI pair, α-band coherence of the FDS-FDI muscle pair increased during the movements (phases 2 and 3; Fig. 8B). Additionally, for this muscle pair, phase had a significant impact on the coherence values in the γ-band (P = 0.045; Fig. 8C); for all tasks, the γ-band coherence values increased during later phase.

Fig. 8.

Pooled coherence values of the three muscle pairs that showed significant task effects: EDC-FDI, γ-band (A); FDS-FDI, α-band (B); and FDS-FDI, γ-band (C). For the EDC-FDI pair, a significant interaction between task and phase was found in the γ-band (P = 0.026). For the FDS-FDI pair, a significant task-phase interaction was found in the α-band (P = 0.004), while phase had a significant effect on the γ-band coherence (P = 0.045).

For both muscle pairs, the task effects on intermuscular coherence were mainly observed outside the β-band: for the EDC-FDI pair, a significant task-phase interactions was found in the γ-band coherence. For the FDS-FDI pair, a significant task-phase interaction was found in the α-band, and a significant task effect was found in the γ-band coherence (e.g., see Fig. 9).

Fig. 9.

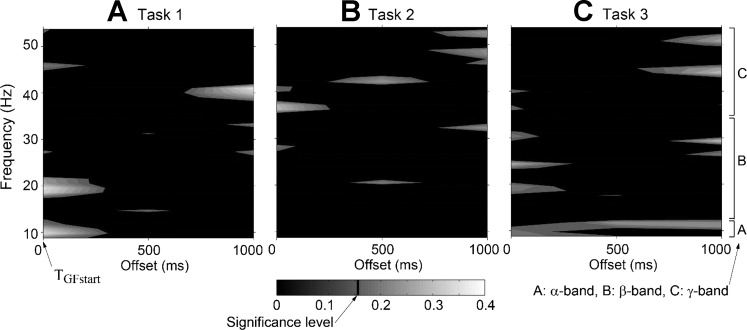
A representative time-dependent coherence estimate for the FDS-FDI muscle pair (subject 10). Analysis (type 2; sp2a2_m1.m function in Neurospec) was done using 10 offset values from 0 to 1,000 ms in 100-ms increments. For this subject, increased coherence in α-band was observed in task 3 (and earlier phase in task 1), but not in task 2 (task × phase interaction). Also for all three tasks, γ-band coherence increased during later phase (>500 ms) (phase effect).

DISCUSSION

Our results showed that proximal arm kinematics affect the coordination of grip force magnitude, primarily in the later phases of lifting movements, while the temporal coordination of grip force and load force remains relatively unaffected. Grip force and load force were well correlated during all three movements, while shear force at the fingertip did not correlate with either grip force or load force.

Impact of Proximal Arm Kinematics on Spatial Coordination of Grip Force and Load Force

Previous work has demonstrated coordinated activation of proximal and distal muscles during object transport. A large number of studies have demonstrated the tight coupling of grip and load forces when object transport is vertical and grip force direction is horizontal (for review, see Flanagan et al. 2006). However, when the transport direction is also horizontal, peak grip force occurs at peak velocity, not peak acceleration, and opposing digits work out of phase, such that increased contact force in one digit is synchronous with decreased force in opposing digits (Gao et al. 2005). When multiple horizontal movement directions were tested during a tripod grasp, grip force changes during transport were directionally tuned, but in a subject-specific manner (Smith and Soechting 2005). Authors suggested that coupling between proximal and distal muscles played a role in this directional tuning. Subsequent EMG studies showed that horizontal transport was achieved by feedforward stiffness modulation (Winges et al. 2007a), which was potentially mediated by coupling between proximal arm muscles and intrinsic hand muscles (Winges et al. 2007b). These coordination patterns extend to more complex circular movements, where grip force reflects the additive effects of the vertical and horizontal movement components (Slota et al. 2011). While all of these studies emphasize the importance of object kinematics on grip force, our study contributes to this line of work by demonstrating the influence of proximal arm joint kinematics. Note that our study also differs from these previous studies that examined horizontal transport, since the movement direction of the object was mainly vertical.

Observed increase in the GLR magnitude can be biomechanically explained by the increase in the FDI muscle activation (Fig. 5C). While patterns of the task-dependent change in the activation levels appeared to be similar across all of the hand muscles, only the changes in the FDI muscle activation levels were found to be significant (P = 0.048), which would explain the observed differences in grip force magnitudes and GLR values across tasks. Note that, in our study design, between-task variability in the FDI muscle activation also represents that of other finger intrinsic muscles involved in the target task (i.e., three-digit grip), which are first palmar interosseous, second dorsal interosseous, and third dorsal interosseous muscles, as previous studies have shown that all intrinsic muscles that control index and long fingers (i.e., four interosseous muscles) are “coordinated in a fairly uniform fashion” (or scaled) during three-digit grip over a wide range of grip force (Poston et al. 2010).

In addition to the significant task-effect on the FDI muscle, co-contraction of the extrinsic finger muscles may have contributed to the observed between-task difference in grip force. While activation level of individual extrinsic finger muscles (i.e., EDC and FDS) was not affected by the task, the FER (or agonist-to-antagonist co-contraction ratio) was found to be significantly affected by task (P < 0.001); as the degree of agonist-antagonist co-contraction would correlate to the grip force better than individual muscle activities, observed increase in FER may have contributed to the observed task difference in GLR values.

It should be acknowledged that some hand muscles, such as the extrinsic hand muscles, cross the elbow joint; thus the multiarticular nature of these muscles may have affected the coordination patterns observed during concurrent elbow movement. However, these muscles have relatively small moment arms around the elbow joint (An et al. 1981) and usually act at the elbow only when the finger and wrist joints are fully extended or fully flexed (Standring 2009). Furthermore, such biomechanical coupling would not be able to explain the similar patterns of task-related changes observed in the intrinsic hand muscle (FDI), which does not cross the elbow joint and had greater variations in activation across tasks than the extrinsic muscles (Fig. 5). In addition, as the wrist flexion ROM was similar across the tasks, the effects of wrist posture on the force-generating capacity of hand muscles (Li 2002; Mogk and Keir 2003; Werremeyer and Cole 1997) would not account for the observed between-task difference in the grip force production. Thus a neural coupling between the entire UE musculature is likely, with intrinsic and extrinsic hand muscles controlled in synchrony with proximal muscles.

Temporal Coordination of Grip Force: Load Force Across Different Proximal Kinematics

In contrast to the small but significant effects of proximal kinematics on the spatial coordination of grip force and load force (GLR), temporal coordination of these two forces was not affected by proximal kinematics, as indicated by both similar time lag values (T_GFmax − T_LFmax; Table 2), correlation coefficients between grip force and load force (Table 3), and time delay values between movement initiation and grip force production (T_GFstart − T_ACCstart; Table 2) across the three tasks. Also note that no phase effect on GLR values was observed (P = 0.133). Previous studies showed that temporal coordination of grip force can be affected by different task-related factors, such as rates of load force (Johansson and Cole 1992) and sensory (tactile/visual) information (Jenmalm et al. 2000). Temporal coordination of the grip force and load force can also be affected by neurological abnormalities of the subjects (Hermsdörfer et al. 2003; Rost et al. 2005). While changes in the proximal kinematics may provide different visuomotor feedback (Jeannerod 1981) and/or alter energy expenditure (e.g., Soechting and Flanders 1998), such changes did not affect the planning (i.e., movement initiation) and/or temporal coordination of the grip force during movements (i.e., timing of peak forces).

Coordination of Grip Force and Shear Force: Change in Fingertip Force Direction

In addition to the motor outputs more relevant to the task (grip force and load force), examination of the temporal coordination of other force outputs during the lifting movements could allow us to examine how the human sensorimotor system controls multimuscle systems to produce multidimensional motor outputs (i.e., multidirectional forces) during functional tasks. The number of muscles involved in fingertip force production is much greater than the dimension of motor outcome (i.e., dimension of the fingertip force vector) (e.g., Kutch and Valero-Cuevas 2011; Valero-Cuevas 2000), which makes muscle coordination of the fingertip force production a “redundant” task (Bernstein 1967). Previous studies on grip force-load force coordination generally examined fingertip force components directed toward the main movement direction of an object, responding to tangential load and frictional status at the digit-object interface (see Flanagan et al. 2006 for review), but other components of the fingertip force, such as horizontal fingertip force components during vertical object movements, were typically not examined in detail. Examination of other fingertip force components could allow us to examine in more detail how motor control of multidimensional fingertip force is performed in accordance with proximal arm movements. Various studies have shown that human neural control strategies do allow variability in redundant (or task-irrelevant) dimensions, while minimizing errors/deviations that interfere with task goals (minimal intervention principle: Todorov 2004; Valero-Cuevas et al. 2009; uncontrolled manifold hypothesis: Latash et al. 2002).

Our analysis showed that, despite the significant effect of movement phase on the muscle coordination (P < 0.001), the GLR remained unchanged during movement (no phase effect: P = 0.133). In contrast, the SGR was found to be significantly affected by the movement phase (P = 0.001). This significant phase effects on the SGR indicate that the fingertip force direction had changed during movements, which could have resulted from the change in the muscle coordination (significant phase effect; P < 0.001). Note that, however, the GLR values remained unaffected during lifting movements, despite the changes in the muscle coordination, while SGR fluctuated significantly. The FER value, a parameter that is more relevant to the grip force magnitude, also did not change during movement (no phase effect; P = 0.911).

While it is certainly possible that the shear force at the fingertip had been produced to counteract horizontal load force caused by the object movement (i.e., horizontal acceleration), the observed patterns of the shear force change during the movement indicate that the change in the SGR was not likely due to the task requirement (counteracting horizontal load force). Although the shear force magnitude increased significantly during the later phase of the movement (phases 3 and 4; see Fig. 3B), a post hoc analysis on the object kinematics showed that the peak horizontal acceleration of the object actually occurred mostly during phase 2; most of the times, peak horizontal acceleration of the object (T_hACCpeak) even preceded peak vertical acceleration (T_vACCpeak), as the time difference between peak horizontal acceleration and peak vertical acceleration (T_hACCpeak − T_vACCpeak) was smaller than 0 (mean ± SD = −0.17 ± 0.16 s). Additionally, while object acceleration in the vertical direction was moderately correlated with both FDS and FDI muscle activities (mean r = 0.34), no correlation between horizontal acceleration and the activation levels of these two muscles was found (mean r = −0.06).

Therefore, our results suggest that fingertip force direction did change during lifting movements, which was not likely mediated by task requirements (e.g., counteracting object inertia in horizontal direction). Since the FER value, co-contraction ratio of the extrinsic finger flexor-extensor muscles, did not change during movements, the observed phase-dependent change in the muscle coordination, indicated by MANOVA, could mainly reflect the change in the coordination between intrinsic muscles (e.g., FDI) and extrinsic muscles (e.g., FDS) during movements. It should be acknowledged that, while such changes in the coordination between intrinsic and extrinsic finger muscles during lifting movements affected SGR (increased during later phases; phase, P = 0.001), these changes did not affect GLR values, which was more relevant to the task goal (i.e., preventing vertical slip) (no phase effect; P = 0.133).

Proximal: Distal Neural Coupling

The observed pattern of the between-task difference in the GLR (higher during task 3 than tasks 1 and 2, but no difference between tasks 1 and 2) is different from the between-task difference in elbow joint kinematic variables, which showed significant differences between all task pairs (i.e., P < 0.01 for all task pairs, i.e., task 1–task 2, task 1–task 3, task 2–3; Table 1).

Instead, the pattern of between-task difference in the hand muscle activation levels and GLR (highest during task 3; no significant difference between tasks 1 and 2) contrasts to that of the shoulder joint kinematics (peak velocity and peak acceleration; smallest during task 3; no significant difference between tasks 1 and 2). The observed task-related changes in grip force control, therefore, may have been affected by the proximal joint dynamics (shoulder). Here, it should be acknowledged that our results may not be explained well by previous theories that explain control of distal joints (hand) as an attempt to regulate the “dynamic” consequence of the proximal joint movements (e.g., leading joint hypothesis; Dounskaia 2005). While increase in the grip force was observed during task 3, joint torque at the most proximal joint (shoulder) was the smallest during task 3, indicating that dynamic effects of the shoulder joint movements would also have been the smallest.

Also note that, although task 1 was designed to involve only the shoulder joint, the elbow muscles were also highly activated (Fig. 7, A and B), which could be partially contributed to the mechanical disadvantage of the task. The angle between the forearm and the ground for task 1 was found to be significantly smaller than that of tasks 2 and 3 (task 1: 32.1 ± 6.7°; task 2: 51.3 ± 4.4°; task 3: 52.2 ± 7.8°) (P < 0.001), denoting that the moment arm of the object weight with respect to the elbow joint during task 1 was the largest among the three tasks.

The task-related changes in the grip force may have been caused by increased/decreased neural coupling between the extrinsic and intrinsic finger muscles (FDS/EDC and FDI). Note that shoulder joint dynamics were found to have significant effects on hand muscle coordination after neurological injuries (Miller and Dewald 2012). Changes in proximal joint kinematics/dynamics (i.e., shoulder) may have affected the intermuscular coherence between these muscles, albeit to a lesser degree than in patients. Note that the α-band coherence between FDS and FDI muscles was higher in task 3 than in task 2 during later phases (task × phase: P = 0.004), while the γ-band coherence between EDC and FDI muscles was lower in task 3 than in task 2 during these phases (task × phase: P = 0.026) (Fig. 8). Intermuscular coherence analysis can provide information regarding the origin of common oscillatory drive to different motor units and can also assess their degree of synchrony (Farmer et al. 1998; Lowery et al. 2007); thus various studies examined EMG-EMG coherence of the hand muscles to examine different neurological factors affecting human grip (Keenan et al. 2012; Kilner et al. 2004; Perez et al. 2006; Poston et al. 2010). Previous studies on spinal cord injury patients found that intermuscular coherence in α-band may be spinal in origin (Norton et al., 2003, 2004). On the other hand, a recent study suggested that γ-band coherence may represent inputs from subcortical pathways, such as the reticulospinal and/or rubrospinal tracts (Nishimura et al. 2009), which play an important role in motor control of various functional hand movements (Baker 2011). γ-Band corticomuscular coherence was also found to increase specifically during strong isometric grip exertions (Brown 2000). Therefore, during the tasks that involved the smallest shoulder joint velocity/acceleration (task 3), it appears that the common neural input to the intrinsic and extrinsic finger muscles via subcortical or spinal pathways was modulated, which may be related to the observed change in grip force.

It should be acknowledged that some limitations of our analysis on the muscle activation may have affected the results of the statistical tests. First, in the muscle coordination analysis, the “selection” of the hand muscles to be examined in this study may have affected the statistical analysis. As all hand muscles may not be equally affected by the proximal muscle activation (e.g., see Lee et al. 2014), it is possible that the effects of the task on the muscle coordination could have been found significant if another set of hand muscles had been selected. Second, the sample size was relatively small (n = 15), which has limited the statistical power of our analyses.

Conclusion

In summary, changes in proximal kinematics primarily affected the spatial aspects of grip force-load force coordination, while temporal coordination of these forces relatively remained unaffected across different arm movements, despite a large kinematic difference between the movements. The impact of proximal kinematics is signified in the task-related change in the extrinsic finger extensor-to-flexor co-contraction ratio (i.e., FER) and activation level of intrinsic finger muscle (FDI). Simple biomechanical coupling could not explain the changes in intrinsic hand muscle activation across tasks, which suggests that more complex neural couplings in the distal-proximal UE musculature may be involved. In addition, examination of the fingertip force in the shear direction (task-irrelevant dimension) provided insights into a human motor control strategy that controls motor parameters with a large DOF, so that the variability in the task-relevant motor output (GLR) is minimized (between-phase variability: P = 0.133), while motor output less relevant to the task goal (SGR) is allowed to fluctuate to a larger degree (between-phase variability: P = 0.001).

GRANTS

This work was partially supported by US Army Medical Research and Materiel Command Grant W81XWH-11-1-0632 and National Institute of Child Health and Human Development Grant 1R03-HD-74870-01A1.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: B.C.V. and S.W.L. performed experiments; B.C.V. and S.W.L. analyzed data; B.C.V., P.S.L., and S.W.L. edited and revised manuscript; B.C.V., P.S.L., and S.W.L. approved final version of manuscript; P.S.L. and S.W.L. conception and design of research; P.S.L. and S.W.L. interpreted results of experiments; S.W.L. prepared figures; S.W.L. drafted manuscript.