Development of a Virtual Spectrometer for Chiroptical Spectroscopies: The Case of Nicotine

Abstract

The impressive advances of computational spectroscopy in most recent years are providing robust and user-friendly multifrequency virtual spectrometers, which can be used also by non specialists to complement experimental studies. At the heart of these developments there are latest-generation models based on density functional theory for the proper treatment of stereo-electronic effects, coupled to the polarizable continuum model to deal with bulk solvent effects, and low-order perturbative treatments of anharmonic effects. Continuing our efforts to increase the range of application of virtual spectrometers, we will report here about chiroptical spectroscopies with special reference to optical rotation and vibrational circular dichroism. The capabilities and possible limitations of our latest tool will be analyzed for the specific case of (S)-nicotine in vacuo and in different solvents.

INTRODUCTION

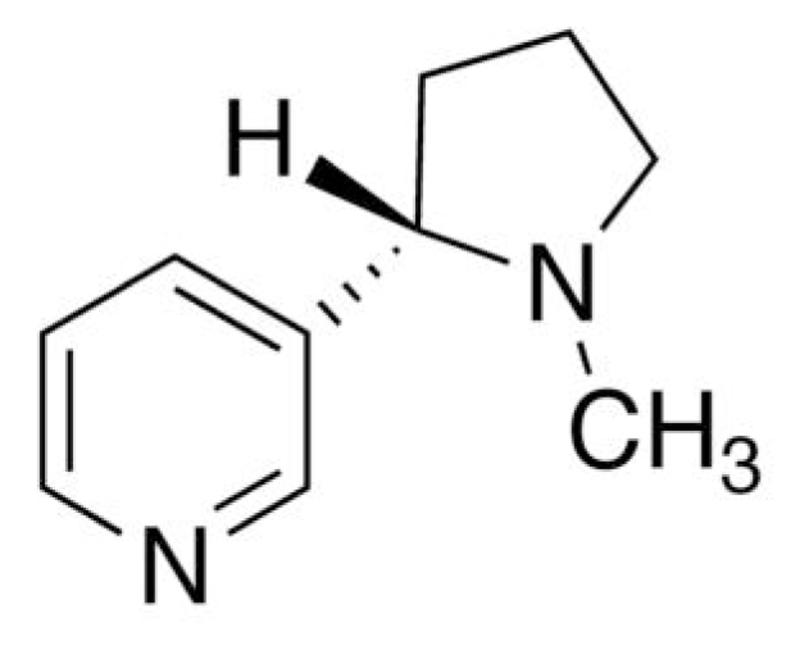
The space and time scales for systems and processes of current biological and/or technological interest (e.g. nanotechnologies, nanobiomedicine, etc.) are approaching more and more the molecular level, and can be most effectively probed by techniques related to molecular spectroscopy. The diverse spectroscopic techniques available today provide a wealth of information about widely different aspects of the molecular systems for strongly different environments. The most powerful approaches involve the integration of several spectroscopic techniques combined together and further supported by reliable computational tools. As a matter of fact, spectroscopic features are only indirectly related to structural and dynamical characteristics of the systems under study, so that interpretation of the experimental outcome in terms of stereo-electronic effects and of their tuning by dynamics and changing environment is seldom straightforward. In this context, computational spectroscopy represents an increasingly indispensable aid for unraveling the various contributions to the spectroscopic signal, allowing a deeper understanding of the underlying elementary effects.^1-3 The predictive and interpretative power of computational spectroscopy is ever increasing from small rigid molecules in gas phase to large flexible systems in condensed phases also thanks to the development of so-called virtual spectrometers, which make this kind of studies accessible to non-specialists via their inclusion on robust and user-friendly computational packages.⁴ In recent years, we have been deeply involved in the development of a multifrequency virtual spectrometer, which can be tuned to provide more and more reliable vibrational, electronic and magnetic spectra.^5-7 Here we will be concerned with our recent activity regarding the support of chiroptical spectroscopies, which are becoming the methods of choice for studying, inter alia, biomolecules. Rather than providing a lengthy theoretical development and a number of more or less interesting applications, we have decided to concentrate on a multispectroscopic approach to a single prototypical molecule, namely (S)-nicotine (see figure 1). Starting from the infra-red (IR) spectrum (both peak positions and intensities) we have computed the optical rotation (OR) at the sodium D-line wavelength, together with vibrational circular dichroism (VCD). Because of its well-known biological activity, (S)-nicotine has been the subject of several studies aimed at providing better insights into its structure and properties.^8-11 To the best of our knowledge, however, nicotine lacks a thorough computational study in spite of the availability of nuclear magnetic resonance (NMR)¹², circular dichroism (CD),^13,14 Raman and ROA spectra.¹⁵ Taking also into account that nicotine is a medium-size semirigid molecule, soluble in a variety of environments, it represents indeed an ideal benchmark for our developments. As mentioned above, we will focus our study on the general aspects of the new chiroptical spectrometer and on its application to (S)-nicotine rather than on a more detailed analysis of methodological aspects.

Figure 1.

Structure of (S)-nicotine.

SPECTROSCOPIC PROPERTIES OF SOLVATED SYSTEMS

In this work we used the Polarizable Continuum Model (PCM)^16,17 to couple solvent effects to the quantum mechanical (QM) description of the spectroscopic properties of nicotine both at the purely electronic and vibrational levels. The PCM approach gives an accurate description of the electrostatic component of solvation at a very low computational cost, and can be coupled to a variety of QM methods, extended to treat spectroscopic and response properties¹⁸ and to surfaces,¹⁹ interfaces,²⁰ metal nanoparticles,²¹ and polymeric materials.²² In PCM, the molecule is placed in a cavity carved within a dielectric continuum representing the solvent. The dielectric properties of the polarizable continuum, i.e. its static and optical dielectric constants, are set equal to those of the chosen solvent. The presence of the solute induces a charge density on the cavity surface, which is modeled using a set of point charges. The latter generate a “reaction field” which acts on the solute, modifying its charge density, therefore the surface charges must be calculated self-consistently.¹⁶ Thus, the presence of the solvent has a direct effect on the electron density of the solute, but also an indirect effect on its molecular geometry, and all molecular geometries must be re-optimized when going from the gas phase to the solvated phase.

Inclusion of solvent contributions on spectroscopic properties calls for additional care because the solvent has a direct interaction with the electromagnetic radiation, in addition to the one mediated by the solute, and because of the dynamical nature of spectroscopic phenomena. The presence of the solvent changes the electromagnetic field that stimulates the spectroscopic response within the molecule, therefore the “local field” acting on the molecule will not be the same as the external field physically imposed on the system. Classically, this problem is solved via the Onsager-Lorentz model,²³ which approximates the molecule as a point-like electric dipole, while the solvent is modeled with a polarizable continuum. If the dipole is placed at the center of a spherical cavity within the polarizable continuum the local field can be related to the external field through a multiplicative factor which depends on the solvent static dielectric constant for static fields (${\overrightarrow{E}}^{\mathrm{loc}}$), and on the solvent optical dielectric constant for dynamic fields (${\overrightarrow{E}}_{\omega }^{\mathrm{loc}}$):

$${\overrightarrow{E}}^{\mathrm{loc}}=\frac{\epsilon +2}{3}{\overrightarrow{E}}^{\mathrm{ext}};{\overrightarrow{E}}_{\omega }^{\mathrm{loc}}=\frac{{\epsilon }_{\mathrm{opt}}+2}{3}{\overrightarrow{E}}_{\omega }^{\mathrm{ext}}$$ (1)

this rather crude approximation for the local field effect does not substantially improve the quality of the results with respect to the experimental values,²⁴ because it acts as a simple scaling factor that only depends on the solvent and therefore it is the same for any molecule and any type of spectroscopy. In PCM the molecule is described using the whole electronic density calculated quantum-mechanically, and not just the dipole term, and the cavity is molecule-shaped rather than spherical. The electric field experienced by the molecule is then the sum of the reaction field and the local field. Consequently, rather than modifying the electric field itself, the attention is equivalently switched to the electric dipole of the system, which is written as the sum of the molecule dipole moment and the dipole moment arising from the molecule-induced dielectric polarization (denoted by $\tilde{\mu }$):²⁵

$${\overrightarrow{\mu }}^{\mathrm{eff}}={\overrightarrow{\mu }}^{\mathrm{mol}}+\tilde{\mu }$$ (2)

In the case of IR and VCD, ${\overrightarrow{\mu }}^{\mathrm{eff}}$ denotes the transition dipole moment between two vibrational states, while in the case of optical rotation it denotes the oscillating dipole moment of the system.

Another aspect that should be taken into account by the model is the so-called non-equilibrium regime which pertains to the dynamical aspects of solvation. The electromagnetic field acting on the system causes the electronic density of the solute, and solute-induced solvent polarization, to oscillate. Depending on the time scale of the phenomenon, not all degrees of freedom of the solvent can remain at equilibrium with the solute. This effect is treated within PCM by splitting the solvent polarization in two contributions, a “fast” polarization attributed to the degrees of freedom of the solvent that remain at equilibrium with the solute, and a “slow” component which accounts for the degrees of freedom that remain static. The partition of the different degrees of freedom of the solvent into the two contributions depend on the property under study.

Optical rotation is usually measured using light in the visible range of the electromagnetic spectrum, and can be seen as a consequence of the interference between the incident radiation and the radiation generated by the molecule’s oscillating electronic density.²⁶ The electronic degrees of freedom of the solvent are able to follow the time evolution of the electronic density of the solute maintaining an equilibrium configuration, whereas the vibrational, rotational, and translational degrees of freedom, whose characteristic timescales are much lower than the period of oscillation of visible radiation, will remain static, so they account for the “slow” component of the solvent polarization. If vibrational corrections to the OR are also to be computed, an additional non-equilibrium contribution arises, which stems from a different partition of the solvent polarization. In this case the electronic and vibrational degrees of freedom are related to the “fast” component, while the “slow” component arises from the translational and rotational degrees of freedom.^27,28

The vibrational non-equilibrium solvation regime also affects the calculation of IR and VCD spectra, both at the level of the vibrational analysis (normal modes and normal mode frequencies) and the spectroscopic IR and VCD intensities. It is therefore crucial to include non-equilibrium effects while performing the harmonic vibrational analysis and the subsequent calculation of the anharmonic contributions, in order to compute all terms constituting the observables in a consistent manner.²⁹

Vibrational averaging of electronic properties

From a theoretical point of view, the optical rotation of a molecular system can be calculated from the isotropic average of the electric dipole-magnetic dipole dynamic polarizability tensor²⁶ $G_{ab}^{\prime }$:

$$\left[\alpha \right]=-\frac{4\pi }{3}\frac{\omega }{c}\frac{N_{\mathrm{A}}}{M_{\mathrm{w}}}\sum _a{G}_{aa}^{\prime }$$ (3)

where ω is the angular frequency of the incident radiation, N_A is Avogadro’s number, and M_w is the molar mass of the chiral substance. To compute the optical rotation of isotropic media the isotropic average of the G′ tensor (i.e. the trace) is calculated. Optical rotation is a mixed electric-magnetic property and, because of the fact that in all ab initio calculations only a finite and therefore not complete basis set is used, it suffers from the so-called gauge problem, which causes the calculated values to depend on the origin of the chosen reference frame.³⁰ This origin-dependence is, of course, unphysical and must be corrected. To circumvent this problem a number of techniques have been developed, and in this work origin independence was ensured by employing Gauge Including Atomic Orbitals (GIAOs).^31,32 In the particular case of PCM calculations of magnetic (or mixed electric-magnetic) properties, an additional PCM term is to be included in the Fock operator.^33,34

Previous studies^35-40 have pointed out the need to include vibrational contributions in the calculation of molecular properties. In this work we have included vibrational effects by performing a vibrational averaging⁴¹ of the molecular property P using an anharmonic vibrational nuclear wavefunction described by means of second order perturbation theory (VPT2).^42,43 In this framework the averaged property is expressed as the sum of the purely electronic property calculated at the equilibrium geometry and a temperature-dependent anharmonic vibrational correction given by:^7,41,44

$${\Delta }_{\mathrm{VC}}P=-\frac{ħ}{4}\sum _a\frac{1}{{\omega }_a^2}{\left({\frac{\partial P}{\partial Q}}_a\right)}_0\sum _b\frac{K_{abb}}{{\omega }_b}\text{coth}\frac{ħ{\omega }_b}{2k_{\mathrm{B}}T}+\frac{ħ}{4}\sum _a\frac{1}{{\omega }_a}{\left(\frac{{\partial }^{2}P}{\partial Q_a^2}\right)}_0\text{coth}\frac{ħ{\omega }_a}{2k_{\mathrm{B}}T}$$ (4)

Equation (4) depends explicitly on the temperature T and contains the first and diagonal second derivatives of the molecular property P (i.e. the OR) calculated with respect to the mass-weighted normal modes and evaluated at the equilibrium geometry of the molecule, the angular frequencies of the normal modes ω_a, the anharmonic semi-diagonal third derivatives of the electronic energy K_abb. The first term in the expression is a consequence of the anharmonicity of the potential energy surface (PES) while the second term would be present even at the harmonic level of the PES, and both terms are sums that run over all normal modes of vibration. Note that, because of the anharmonicity of the PES, increasing the temperature changes the vibrational corrections of all modes, not just the low energy ones, which become more populated. For a mode a with high energy (compared to k_BT ) the first term of the vibrational corrections can change significantly provided the mode is strongly coupled to a low energy mode b through the anharmonic cubic constant K_abb, while the second term will be practically temperature-independent. For low energy modes the same reasoning applies for the first term, but there will also be a significant temperature-dependence in the second term. As temperature increases, the single terms of the vibrational correction tend to increase, but since they may have different signs the total correction may increase or decrease. In this work, anharmonic terms and property derivatives are calculated numerically by automatically displacing the molecular geometry along each normal mode by a fixed amount, and computing the property and force constants matrix at each geometry. The above expression is valid for a molecule in the gas phase, and needs to be re-adapted in the case where solvent effects are included in the model. The presence of the solvent, treated in this work using PCM, alters both the electronic density and the PES of the molecular system. Therefore the vibrational analysis, which yields the normal modes of vibration, must be repeated for all solvents considered, as the normal modes and their frequencies will be affected. As pointed out in the Introduction, when computing spectroscopic properties in solution additional solvent effects should be included in the model, namely those arising from the local field and non-equilibrium effects.⁴⁵ These effects are included in the model at all stages of the calculation, therefore both the electronic property and the anharmonic vibrational correction are calculated in the presence of the solvent.

Anharmonic VCD calculations with the inclusion of solvent effects

The IR and VCD intensities corresponding to a vibrational transition from the ground state to an excited vibrational state are proportional respectively to the dipole strength and rotational strength of the transition, which are defined as:²⁶

$$D_{0e}={\mid {\langle \mu \rangle }_{0e}\mid }^2;R_{0e}=\Im {\langle \mu \rangle }_{0e}\cdot {\langle \mathit{m}\rangle }_{0e})$$ (5)

The peak positions are equal to the energy difference between the ground and excited states, which can be computed from the vibrational analysis of the system. Usually these quantities are calculated by employing a harmonic description for the nuclear wavefunction, while the electric and magnetic dipole moments are expanded in a Taylor series about the equilibrium geometry, and the second or higher order terms are neglected. The combination of these two methods to treat the PES and the dipole moments is often referred to as the double harmonic approximation.

It has been pointed out in previous works^7,46,47 that neglecting the effects due to the anharmonicity of the PES and the higher order terms in the expansion of the dipole moments may yield substantial errors in the calculation of vibrational energies and peak intensities. Another drawback of the harmonic approximation is that all overtones and combination bands have vanishing intensity, giving rise to a much less detailed spectrum, with the exploration of some frequency ranges entirely precluded. In this work we treated this problem using VPT2^{7,42,43,48,49} which allows to compute anharmonic corrections to both vibrational energies and spectroscopic intensities. In addition to the anharmonicity of the PES, the method extends the Taylor expansion of the electric and magnetic dipole moments up to third order, and by combining it with the anharmonic vibrational wavefunction yields the anharmonic dipole strength and rotational strength, which will be non-zero for single overtones and combination bands of two different normal modes, producing a much more realistic and detailed spectrum with respect to the one obtained by means of the double harmonic approximation. Recent works^29,45,47 have pointed out the need to include environment effects in the calculation of IR and VCD spectra in order to obtain results directly comparable to experiment. Also in this case the solvent was treated by means of the PCM method.

COMPUTATIONAL DETAILS

All DFT calculations were performed with a locally modified version of the Gaussian 09 development version⁵⁰ program using the popular B3LYP^51,52 exchange-correlation functional. The equilibrium geometries of (S)-nicotine in the two conformations considered were optimized using the aug-N07D⁵³ basis set. For optical rotation we used the aug-cc-pVTZ basis set to compute the electronic part of the property, and the aug-N07D basis set for the vibrational corrections, to reduce their computational cost. The use of a smaller basis set for the vibrational corrections than the one used for the electronic property is justified by the fact that the former are expected to be small compared to the latter, therefore the relative error due to the incompleteness of the basis set will have a smaller impact on the final calculated value. The use of different levels of theory in the calculation of the various contributions to a molecular property has been shown to be a reliable method by Puzzarini et al.⁵⁴ The aug-N07D basis set was also used to calculate the anharmonic IR and VCD spectra. Origin independence was ensured by using Gauge Including Atomic Orbitals (GIAOs).³¹

The optical rotation of (S)-nicotine was calculated for the system in vacuo and 2-propanol solution. The solvents were chosen because of the availability of experimental values to compare to our results. The vibrational corrections to both properties were calculated at 0 K and 298 K, the latter temperature chosen to reflect the experimental conditions. Optical rotations were evaluated at the wavelength of the sodium D line (589.3nm). The IR and VCD spectra were computed for the molecule in chloroform solution. Solvent effects were included in the calculations by means of the Polarizable Continuum Model (PCM)^16,17, with local field effects^25,44,55 and within the electronic⁵⁶ and vibrational^27,29 non-equilibrium regimes. The PCM cavity was built using a set of interlocking spheres centered on the atoms and with the following radii (in Ångstroms): 1.443 for hydrogen, 1.926 for carbon, and 1.830 for nitrogen, each multiplied by a factor of 1.1. The solvents’ static and optical dielectric constants (the latter used for the non-equilibrium and local field calculations) used are ε = 19.3 and ε_opt = 1.9 for 2-propanol, and ε = 4.7 and ε_opt = 2.1 for chloroform. Gauge invariance in PCM calculations was assured by exploiting the method developed by Cammi.³³

RESULTS AND DISCUSSION

Nicotine conformations

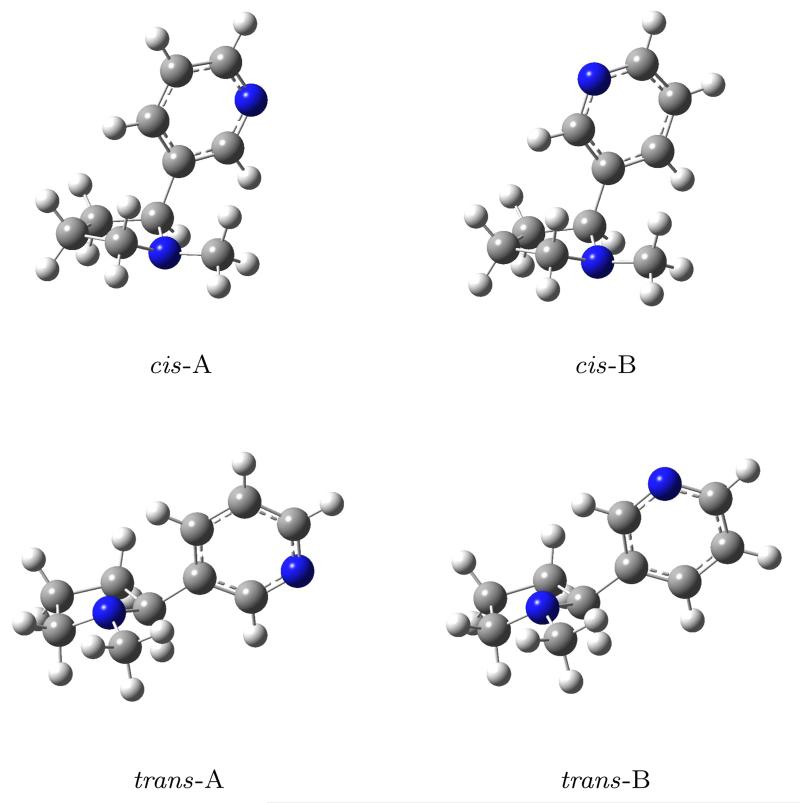
The conformational distribution of nicotine in vacuo and in solution has been previously studied both theoretically and experimentally.^8-11 As a result, it has been established that both in the gas phase and in solution nicotine can assume any of four conformations (figure 2), whose relative populations depend on the solvent. Elmore and Dougherty⁸ have also computed the potential energy barriers separating the conformers, verifying the assumption that the different conformers may be treated as individual molecular species, each with its own equilibrium geometry and normal modes of vibration. In all conformations the pyrrolidinic ring assumes an envelope conformation while the pyridinic ring lies perpendicular to it. The pyridinic ring and the methyl group can be either cis or trans with respect to each other (hence the names of the conformations in figure 2) and the rotation of the pyridinic ring about the bond connecting the two rings gives the molecule additional conformational freedom which allows to distinguish the four different conformations. We calculated the population of the four nicotine conformers in each solvent taken into consideration in this work, i.e. chloroform and 2-propanol. The Boltzmann populations depend upon the relative free energies of the conformers, which were computed with the inclusion of solvent, vibrational, and thermal effects. Note that by employing PCM the computed electronic energy actually has the status of a free energy.^16,57 We also included non-electrostatic contributions calculated using the SMD molecular cavity,⁵⁸ which was specifically designed to estimate energies of solvated systems. The resulting populations of the cis conformers were below 1%, therefore in the following only the trans conformations were considered. Table 1 shows the relative Boltzmann populations of the nicotine conformers in the solvents considered in this work. The population of the trans-B conformer increases with increasing solvent polarity, and this is consistent with the fact that the dipole moment of the molecule in the trans-B conformation (2.88 Debye) is larger than that of the trans-A conformation (2.58 Debye).

Figure 2.

The four main conformations of nicotine.

Table 1.

Boltzmann populations (in %) of the nicotine conformers in chloroform and 2-propanol.

	trans-A	trans-B
Vacuo	69	31
CHCl3	65	35
2-PrOH	62	38

Optical rotation

Table 2 shows the electronic component (${\left[\alpha \right]}_{\mathrm{D}}^{\mathrm{el}}$) and the vibrational corrections to the specific rotation of (S)-nicotine in vacuo and in 2-propanol solution at two different temperatures (${{\Delta }_{\mathrm{VC}}\left[\alpha \right]}_{\mathrm{D}}$), as well as the total calculated specific rotation obtained by summing the electronic component and the 298K vibrational correction for each conformer and by averaging the results according to Boltzmann populations (${\left[\alpha \right]}_{\mathrm{D}}^{\mathrm{T}\mathrm{tot}}$). The experimental value (${\left[\alpha \right]}_{\mathrm{D}}^{\exp }$) for the optical rotation in 2-propanol is also reported. The purely electronic values calculated at the B3LYP/aug-N07D level of theory only differ from the B3LYP/aug-cc-pVTZ ones by about 2% both in vacuo and in solution, therefore the use of the smaller basis set in the vibrational corrections calculations is justified. At the electronic level the solvent causes the optical rotation to increase for both conformers, and a much more pronounced effect can be seen for the zero-point vibrational corrections which significantly decrease in magnitude when solvent effects are added. Temperature has a huge impact on the vibrational corrections, both in vacuo and in solution. Vibrational corrections are obtained by summing the contributions from all normal modes (see equation 4). The gas-phase vibrational correction at 298K increases greatly in magnitude for the trans-A conformer, while it decreases for the trans-B conformer, but the overall effect to the Boltzmann-weighted value is to increase the amount of the correction. The vibrational corrections calculated in 2-propanol increase in magnitude for both conformations and even change sign, demonstrating the importance of including solvent effects into the vibrational component, as well as the electronic value. We also computed the specfic rotation of the two cis conformers to ensure that their contribution can indeed be discarded; we obtained a value of about +180 for both conformers which, because of their very low Boltzmann population, would not give a significant contribution to the average value.

Table 2.

Calculated and experimental¹³ specific rotation of (S)-nicotine in deg dm⁻¹ g⁻¹ cm³.

	2-PrOH		vacuo
	trans-A	trans-B	trans-A	trans-B
${\left[\alpha \right]}_{\mathrm{D}}^{\mathrm{el}}$	−233.95	−227.59	−229.76	−210.31
${{\Delta }_{\mathrm{VC}}\left[\alpha \right]}_{\mathrm{D}}^{0\mathrm{K}}$	−0.60	−1.73	−4.48	−3.03
${{\Delta }_{\mathrm{VC}}\left[\alpha \right]}_{\mathrm{D}}^{298\mathrm{K}}$	7.22	6.24	−16.58	−1.38
${\left[\alpha \right]}_{\mathrm{D}}^{298\mathrm{k}\mathrm{tot}}$	−224.69		−235.58
${\left[\alpha \right]}_{\mathrm{D}}^{\exp }$	−250		-

The sign of the calculated specific rotation in 2-propanol is in agreement with the experimental value, and the relative error of the calculated value with respect to the experimental one is about −10%. While vibrational corrections do not improve the agreement, this might be due to explicit solvent effects originating from the directional nature of the hydrogen bonds that may be present in the nicotine/propanol system. Explicit solvent effects may be treated using hybrid QM/MM/PCM methods⁵⁹ and their application to nicotine is reserved for future work.

IR and VCD spectroscopy

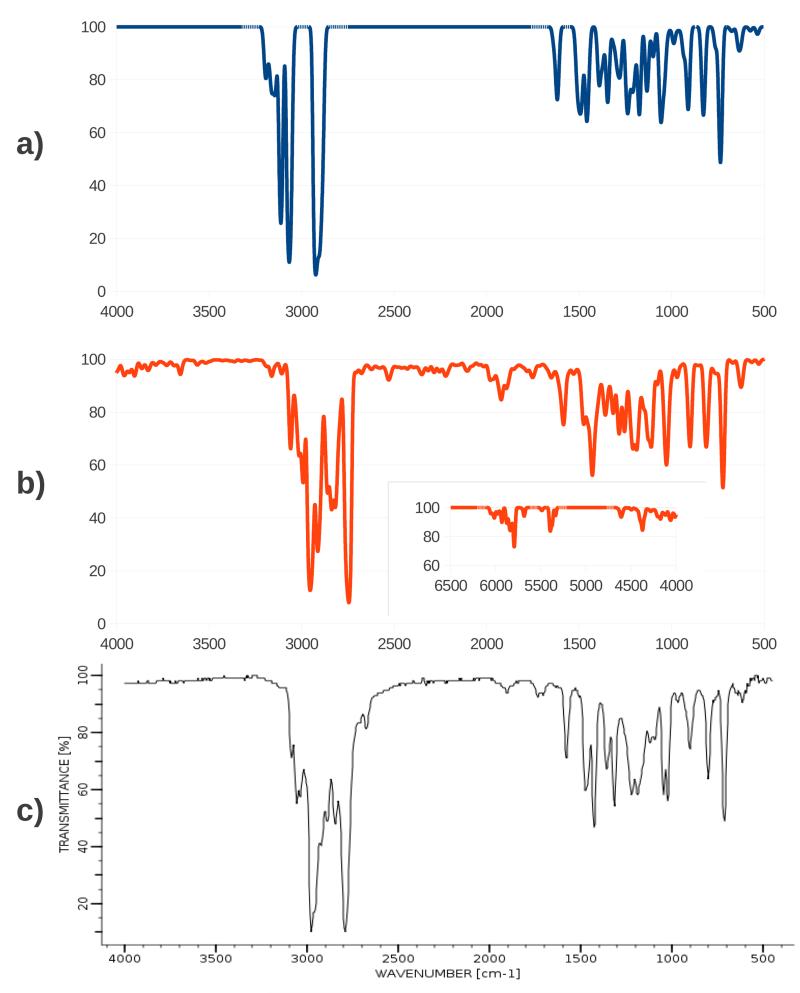
In order to compare our results with the experimental values, the calculated intensities were used to plot the IR spectra by convoluting the stick spectrum with Gaussian functions with an half-width at half-maximum chosen to be 10 cm⁻¹ to match experimental data, and by assuming that the highest band in the spectrum corresponds to a 90% transmittance. The harmonic and anharmonic IR spectra of nicotine in chloroform are shown in figure 3a and 3b. The harmonic spectrum is manifestly separated in two different zones pertaining to different molecular vibrations: all C-C and C-N stretching and all bending motions appear in the 0-1650 cm⁻¹ zone (modes 1-58), while C-H stretching motions emerge in the 2800-3200 cm⁻¹ zone (modes 59-72), the rest of the spectrum appearing featureless due to the fact that the harmonic spectrum only shows fundamental bands. The modes are numbered by increasing harmonic frequency (see the Supplementary Material for a pictorial representation of the normal modes of vibration mentioned throughout the paper).

Figure 3.

IR spectra of Nicotine. a) Harmonic spectrum. b) Anharmonic spectrum, the inset shows the 4000-6500 cm⁻¹ region. c) Experimental spectrum.⁶⁰ Wavenumbers are reported in cm⁻¹ and intensities % Transmittance.

All the bands in the anharmonic spectrum appear red-shifted with respect to the harmonic one; the tendency of the anharmonic frequencies to be lower than the harmonic ones is general, and is particularly significant for the C-H stretching modes, whose anharmonic frequency is on average 145 cm⁻¹ lower in with respect to the harmonic one, whereas the frequency of the other modes is on average 22 cm⁻¹ lower. Furthermore anharmonic corrections change the ordering of some modes, so that wrong assignments would result from direct comparison between the experimental spectrum and its computed counterpart employing the harmonic approximation.

The anharmonic spectrum also shows a more complex structure due to the presence of the overtone and combination bands of two normal modes of vibration. This effect is especially noticeable in the 1600-2700 cm⁻¹ region of the spectrum, which shows a large number of bands with small intensity. In the C-H stretching region the spectrum shows additional peaks with high intensity that are not present in the harmonic spectrum and arise from the combinations of modes 52 and 50, 54 and 48, and 56 and 47. Finally in the 4000-6500 cm⁻¹ region (inset of figure 3b) overtone and combination bands of the higher energy modes can be seen. Around 5800 cm⁻¹ there is a band which arises from the combinations of modes 66 and 62, 65 and 63, and 67 and 64, which are all C-H stretching localized on the pyrrolidinic ring. In the 5400 cm⁻¹ region there is a band which is the superposition of the first overtones of mode 59 and mode 60, which are again C-H stretchings on the pyrrolidinic ring. Finally there is a band at 4380 cm⁻¹, which is mainly a combination band of modes 66 and 51.

The inclusion of the anharmonicity into the model also has a visible effect on the relative intensity of the fundamental bands. To give one example, a close inspection of the bands in the 0-1650 cm⁻¹ zone reveals that the two peaks arising from the excitation of modes 50 and 55, which appear at 1460 cm⁻¹ and 1510 cm⁻¹ in the harmonic spectrum and at 1427 cm⁻¹ and 1476 cm⁻¹ in the anharmonic spectrum, have an almost identical intensity in the harmonic spectrum, while in the anharmonic spectrum the excitation of mode 50 is enhanced and that of mode 55 is quenched.

The experimental spectrum⁶⁰ is reported in figure 3c. The resemblance between the experimental spectrum and the calculated anharmonic one is remarkable: the positions of the peaks are in excellent agreement, whereas the harmonic spectrum fails dramatically to reproduce them, especially in the C-H stretching region. The calculation allows for a ready assignment of the spectral bands that can be seen in the experimental spectrum: the two highest peaks which appear at about 2980 cm⁻¹ and 2785 cm⁻¹ in the experimental spectrum can be respectively assigned to the fundamental bands of modes 65 and 60 respectively. As suggested by further inspection of the anharmonic and experimental spectra, the overtone and combination bands contribute heavily in delineating the band shape, and some combination bands are also separately identifiable, for example the two small bands near 1990 cm⁻¹ and 1720 cm⁻¹ that appear beyond the region where all bendings and heavy atom stretchings fall. Some of the bands in the 4000-6500 cm⁻¹ region of the anharmonic spectrum have an intensity that is comparable to that of some bands that are clearly visible in the bending region, therefore it can be safely assumed that they would have also been visible in the experimental spectrum had it been recorded beyond 4000 cm⁻¹. Overall the inclusion of anharmonic effects in the calculation greatly increases the quality of the calculation with respect to the experimental data.

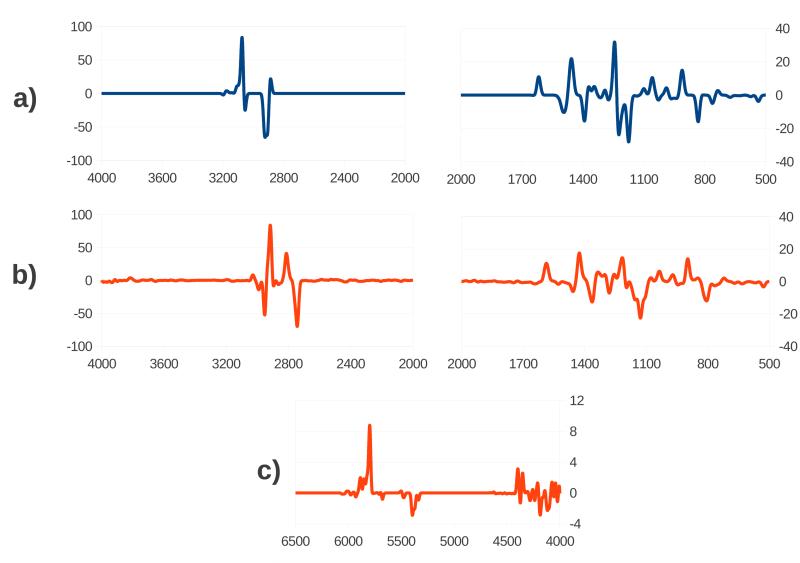
The calculated VCD intensities were convoluted with non-normalized Gaussian functions with half-width at half-maximum arbitrarily chosen to be 10 cm⁻¹. The calculated VCD spectra are shown in figure 4. To improve clarity, the spectra have been split into different zones with a different scale. Figure 4a shows the harmonic spectrum, figure 4b the anharmonic spectrum, and figure 4c shows the 4000-6500 cm⁻¹ zone of the anharmonic spectrum. Both the harmonic and anharmonic VCD spectra appear much less detailed than the corresponding IR spectra, though VCD is a chiral method so the spectrum carries information about the absolute configuration of the system. The difference between the harmonic and anharmonic frequencies discussed for the IR spectra also applies in the case of the VCD spectra in exactly the same way. Frequency shift aside, the two spectra appear similar in the 500-2000 cm⁻¹ zone. A noticeable difference can still be observed, mainly due to two combination bands which have a substantial intensity, i.e. the combination of modes 22 and 7 found at 1130 cm⁻¹, and the combination of modes 19 and 11 found at 1215 cm⁻¹, and due to the quenching of the two negative fundamental bands of modes 35 and 38, and of the positive fundamental band of mode 39, found at 1175 cm⁻¹, 1230 cm⁻¹, and 1240 cm⁻¹ respectively, in the harmonic spectrum.

Figure 4.

Calculated VCD spectra of Nicotine. a) Harmonic spectrum. b) Anharmonic spectrum. c) Anharmonic spectrum, overtones region. Wavenumbers are reported in cm⁻¹ and intensities in arbitrary units.

A much more pronounced difference between the harmonic and anharmonic spectra can be appreciated in the C-H stretching region, where the presence of the high intensity combinations of modes 56 and 47 and modes 54 and 48 produce an additional positive band, and the combination of modes 57 and 49 gives rise to a visible negative band, all of which are not present in the harmonic spectrum. Unfortunately, to the best of our knowledge, experimental VCD spectra have never been reported in the literature for this system, so that a direct comparison with experiment is not possible. The conformer-specific VCD spectra are available in the Supplementary Material.

CONCLUSIONS AND PERSPECTIVES

In the present paper we have shortly reported on the latest developments of our virtual chiroptical spectrometer to effectively deal with the tuning of the spectroscopic outcome by stereo-electronic, vibrational, and environmental effects. After a short sketch of the most important building blocks we analyzed in detail several kinds of spectra of nicotine in different solvents. Our results show that anharmonicity (for both frequencies and intensities) and subtle solvent effects (e.g. non-equilibrium and local fields) cannot be neglected when making a direct comparison with experiment. Thanks to software and hardware developments, all these effects can now be effectively taken into account also for quite large molecules, thus allowing proper assignment of spectra and correct disentanglement of the role played by the different effects in tuning the overall experimental outcome. Together with the specific interest of the system at hand, in our opinion our results show that, though further developments are necessary and undergoing, we already dispose of a robust, powerful and user-friendly tool easily accessible also to non-specialists.