Cerebral metabolic rate of oxygen (CMRO₂) assessed by combined Doppler and spectroscopic OCT

Abstract

A method of measuring cortical oxygen metabolism in the mouse brain that uses independent quantitative measurements of three key parameters: cerebral blood flow (CBF), arteriovenous oxygen extraction (OE), and hemoglobin concentration ([HbT]) is presented. Measurements were performed using a single visible light spectral/Fourier domain OCT microscope, with Doppler and spectroscopic capabilities, through a thinned-skull cranial window in the mouse brain. Baseline metabolic measurements in mice are shown to be consistent with literature values. Oxygen consumption, as measured by this method, did not change substantially during minor changes either in the fraction of inspired oxygen (FiO₂) or in the fraction of inspired carbon dioxide (FiCO₂), in spite of larger variations in oxygen saturations. This set of experiments supports, but does not prove, the validity of the proposed method of measuring brain oxygen metabolism.

1. Introduction

Oxygen is required to support the energetic needs of the brain, which relies primarily on oxidative metabolism to support neuronal activity [1]. Oxygen metabolism may also be impaired or altered in a number of diseases, among them traumatic brain injury [2], Alzheimer’s disease [3], stroke [4, 5], and retinal pathologies such as diabetic retinopathy [6, 7] and glaucoma [8]. The interplay of cerebral blood flow (CBF), cerebral blood volume (CBV), and cerebral metabolic rate of oxygen (CMRO₂) underlie blood oxygenation level dependent (BOLD) functional magnetic resonance imaging (fMRI) [9–11], the basis of which remains poorly understood. Imaging methods that quantify oxygen consumption in vivo therefore have the potential to enable new clinical diagnostics based on metabolism, novel tools for metabolic imaging in preclinical research, and better understanding of the mechanisms of functional neuroimaging methods.

Conventionally, tissue oxygenation has been measured invasively in the brain by Clark-type electrodes [12], however these are invasive and significantly perturb cortical physiology by damaging cells and compressing microvasculature. Quantification of intra- and extra-vascular oxygenation in 3D has been performed by two-photon microscopy combined with phosphorescence quenching [13, 14]. This method can provide micron-scale spatial resolution but requires the use of phosphorescent dyes, raising the prospect of photodamage due to products of the quenching reaction, which include singlet oxygen and other reactive oxygen species. Photoacoustic microscopy has also been demonstrated for quantifying the metabolic rate of oxygen and even imaging oxygen delivery from single red blood cells (RBCs) [15, 16], but requires pulsed lasers and direct acoustic impedance matching between the sample and ultrasonic transducer. Furthermore, quantifying the bulk CBF using either photoacoustic microscopy or two-photon microscopy over a physiologically-relevant large field of view (FOV) is still challenging.

Positron emission tomography (PET) with the ¹⁵O labeled gas tracer O¹⁵O, while technically complex, remains the closest to a gold standard measure of oxygen consumption in human subjects [17]. As frequent arterial blood sampling is typically required, this approach was not feasible in animal models until recent developments in microPET that enabled simultaneous scanning of the heart to derive the arterial input functions [18]. However, microPET technology is expensive and not widely available. Moreover, PET cannot achieve the fine resolution of optical methods, and therefore its usage remains limited to comparison between brain regions [19]. Ultra-high field magnetic resonance spectroscopy (MRS) using ¹⁷O₂ as a gas tracer has been shown to measure CMRO₂ in the mouse brain with high repeatability [20]. Nevertheless, similar to PET, it is expensive, complex, and possesses relatively poor spatial resolution.

Multimodal diffuse optical methods have been investigated to study oxygen metabolism using independent measurements of flow and oxygenation. However, ambiguities inherent to multiply scattered light limit the quantitative capabilities of these techniques. Laser Doppler flowmetry [21], diffuse correlation spectroscopy [22], and laser speckle flowmetry [23] are sensitive to the motion of scattering cells, especially RBCs in blood vessels. However, although relative flow changes may be quantifiable, the variable and unknown scattering properties of biological tissue (and consequently the number of dynamic vs. static scattering events) make absolute measurements challenging. Moreover, near-infrared spectroscopy (NIRS) [24] and Optical Intrinsic Signal Imaging (OISI) [25] are known to be sensitive to hemoglobin absorption changes, and provide absolute changes in chromophore concentrations if a path length is assumed. However, baseline values are not readily obtained using conventional continuous-wave NIRS techniques, and require specialized and expensive time domain [26–28] or frequency domain [29, 30] methods. Simultaneous measures of flow and oxygenation have been combined to yield relative changes in CMRO₂ [31, 32]. However, absolute units (μmol/100g/min for CMRO₂ and ml/100g/min for CBF) are essential to perform comparisons across subjects, across brain regions, and over time. Conventional diffuse optical methods are low resolution, do not estimate baseline consumption, and require numerous assumptions even to estimate relative changes. Thus, all-optical measures of metabolism remain challenging.

Microscopic methods of measuring retinal oxygen metabolism, which use different modalities to measure flow and oxygenation, have been presented [33–35]. However, multimodality imaging systems present challenges, including the need for co-registration, increased complexity and cost, and, in some cases, increased exposure levels.

Recent advances in Doppler OCT [36, 37] have enabled quantitative flow measurements through either explicit [38] or implicit [39] calculation of the Doppler angle. More recently, quantitative hematocrit [40] and saturation [40–42] measurements were demonstrated and validated using visible light spectroscopic OCT. Here, we present a method of quantifying oxygen metabolism that combines quantitative Doppler flowmetry with oxygen saturation and hematocrit mapping, using a single visible light spectral/Fourier domain OCT microscope. As the cortex is supplied and drained primarily via superficial pial arteries and veins, oxygen metabolism in cortical tissue beneath the imaged FOV can be estimated from measurements near the cortical surface and the Fick principle. Measurements of baseline oxygen metabolism in anesthetized mice are presented and shown to be consistent with literature. We verify two negative control cases for oxygen metabolism. Firstly, we show that during slight modulation of FiO₂, changes in arterial O₂ saturation (sO_2,a) and venous O₂ saturation (sO_2,v) compensate each other to keep oxygen metabolism roughly constant. Secondly, we show that during slight modulation of FiCO₂, changes in flow and venous oxygen saturation compensate each other to keep oxygen metabolism roughly constant. While the results of these validation experiments do not prove the validity of the proposed oxygen consumption method, a different set of results could have invalidated the method.

2. Methods

2.1 Visible light OCT system

A visible light spectral/Fourier-domain OCT system [40] was used in this study. Briefly, the system used a supercontinuum light source (SuperK EXW-12, NKT Photonics), filtered to achieve a spectrum centered at 575 nm, and a free-space Michelson interferometer in which the sample arm consisted of a 2D galvanometer scanner (6210H, Cambridge Technology) and an achromatic doublet with focal length of 30 mm. The full-width-half-maximum (FWHM) lateral resolution was 21.6 μm, while the axial resolution enabled by the spectrum was 1.05 μm in air. The lateral resolution was chosen to approximately agree with the spectroscopic OCT axial resolution, discussed further in Section 2.5. The output of the interferometer was directed to a custom-built spectrometer, with a spectral sampling interval of 0.061 nm. The full imaging depth was 1.35 mm in air. Each A-scan (axial scan) had 1280 unique pixels after Fourier transformation (2560 points in the raw spectrum) and the line-rate was set to 90 kHz. The acquisition was controlled by a custom LabVIEW program. The average power at the sample for imaging was ~1 mW.

For OCT angiography and spectroscopic fitting, the scanning protocol sampled each y-location with 100 repeated B-scans, each consisting of 512 A-scans. This was repeated at 256 y-locations, yielding a 4D data set with dimensions of 512 × 256 × 2560 × 100 (x × y × z × repetition number). For Doppler OCT, the scanning protocol acquired B-scans consisting of 4096 A-scans. This was repeated at 256 y-locations, yielding a 3D data set with dimensions of 4096 × 256 × 2560 (x × y × z). The imaged FOV was 3.2 mm (x) by 1.6 mm (y). The data was post-processed using Matlab to obtain CBF, total hemoglobin concentration (C_HbT), and arteriovenous oxygen saturation difference (OE). A more detailed description of the data processing methods can be found in our previous publications [39, 40].

2.2 Animal preparation

For mouse brain imaging, wild-type mice (C57BL/6, N = 3, male, 24-29 g, age 5-7 weeks, Charles River Lab, MA; Crl:SKH1-Hr^hr, N = 1, male, 18-25 g, age 3-5 weeks, Charles River Lab, MA) were used. During the experiment, the mouse was supplied a mixture of isoflurane, medical air, and oxygen through a flow meter and vaporizer (VetEquip. Inc, Pleasanton, CA). The mouse was first anesthetized in an induction chamber with 1.25-1.5% v/v isoflurane in a gas mixture of 80% air and 20% oxygen. After the mouse was anesthetized, it was immobilized on a stereotaxis (Stoelting Co., IL) or a custom-made head mount during both preparation and imaging in order to reduce the motion artifacts caused by breathing. Artificial teardrops were applied to the eyes to prevent corneal dehydration. Then, a round coverslip-reinforced, thinned-skull cranial window of about 3 mm diameter was created over the parietal cortex [43] for imaging. Variability in depth of anesthesia is a factor that can potentially affect neuronal activity and CMRO₂. Thus, anesthesia was titrated by an investigator, through monitoring the breathing rate and pattern to maintain optimal anesthetic depth during imaging. All the experiment procedures and protocols were reviewed and approved by UC Davis Institutional Animal Care and Use Committee (IACUC).

2.3 Physiological manipulations

Graded hypoxia, achieved by decreasing arterial saturation acutely, is commonly used for validation of sensors of tissue ischemia [34, 44]. During severe hypoxia, oxygen supply from arteries is insufficient to meet metabolic demand, resulting in decreased oxygen consumption. However, during mild hypoxia, metabolic demand can still be met by increased oxygen extraction fraction (reduced venous saturation) or increased blood flow. For this study, mild hypoxia was induced to avoid drops in oxygen consumption due to insufficient supply.

Hypercapnia is commonly used as a negative control, as CMRO₂ does not change in response to a mild hypercapnic challenge (~5% FiCO₂) that does not cause metabolic acidosis [45]. For a mild hypercapnic challenge, flow is expected to increase, while oxygen extraction is expected to decrease through increased venous saturation, leaving CMRO₂ constant.

2.4 Cerebral blood flow (CBF) using Doppler OCT

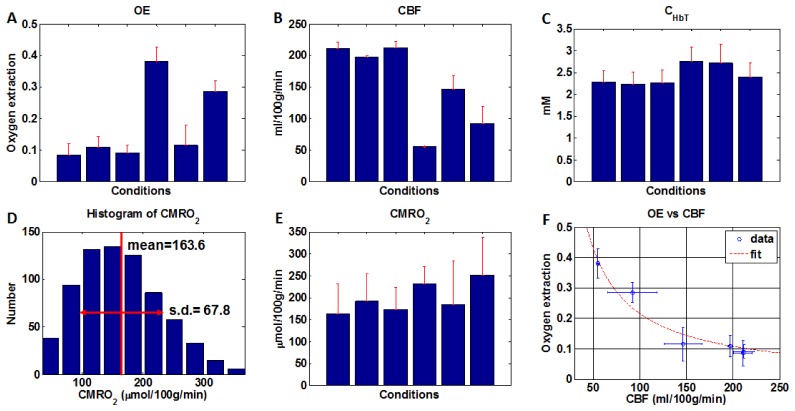
Using the method described in [39], the absolute flow (ml/100g/min) in each individual vessel (arteriole or venule) was obtained by integrating the velocity axial (z) projection over the area of the vessel in the en face (xy) plane before normalizing to the estimated cortical mass corresponding to the imaged FOV. Flows were summed separately over all arterioles and all venules. The two summed flow values (arteriolar and venular) were used to estimate the mean CBF and the standard deviation. Aliasing or phase wrapping of velocity axial projections greater in magnitude than 9.6 mm/s occurred. Hence, for each vessel, an en face plane with a detectable Doppler shift, but without aliasing, was chosen for the flux measurement, as shown in Fig. 1.

Fig. 1.

Absolute CBF measurements were obtained from a volumetric Doppler OCT data set acquired from the mouse (C57BL/6) neocortex through a thinned-skull cranial window. (A) OCT angiogram showing vasculature and numbered transverse locations of vessels designated for absolute flow measurements. (B) Synthesized Doppler OCT image showing axial velocity profiles (in mm/s) at all designated transverse locations (obtained at different depths). Flux (F) was determined based on the product of the area in the en face plane (A_xy) and average axial velocity (v_z) over this area for a particular ascending venule numbered 16 (white arrow). (C) Bar graph shows the flow contributions of individual vessels, at the corresponding numbered locations shown in (A) to the total flow over the field of view (ml/100g/min). Absolute flow was calculated from the flux magnitude assuming a cortical thickness of 1.5 mm and a tissue density of 1.05 g/ml [46]. CBF was estimated as the average of the summed arteriolar flow and summed venular flow.

2.5 Oxygen extraction (OE) and hemoglobin ([HbT]) using spectroscopic OCT

Using the spectroscopic fitting method described in [40], equivalent concentrations of oxyhemoglobin ([HbO₂]) and deoxyhemoglobin ([Hb]) in microvasculature were estimated. Briefly, a noise bias-corrected absorbance spectrum was estimated using a short-time Fourier transform (STFT) of the dynamic scattering signal at each location. The STFT axial resolution was 22 μm, corresponding to a 7 nm spectral resolution. The absorbance spectrum was fit at each axial position using a model that incorporated the effects of scattering and hemoglobin absorption, yielding LC_HbO2 and LC_Hb (L is the single-pass optical path length through the vessel) [40]. Noting that LC_HbT = LC_HbO2 + LC_Hb, and using knowledge of the optical path length, the molar concentration C_HbT was determined (both C_HbO2 and C_Hb can be determined similarly). Oxygen saturation (sO₂) was determined as sO₂ = LC_HbO2 / LC_HbT. In order to determine oxygen metabolism, concentrations were expressed in units of equivalents ([HbT] = 4 C_HbT, [HbO₂] = 4 C_HbO2, and [Hb] = 4 C_Hb). Importantly, all concentrations ([HbT], [HbO₂], and [Hb]) represent intravascular concentrations per unit blood volume, and not per unit brain volume. Thus, our concentrations are more than one order of magnitude higher than those typically associated with diffuse optical imaging, where concentrations per unit brain volume are used. For these reasons [40], our [HbT] measurements are more directly related to hematocrit (intravascular hemoglobin concentration), rather than cerebral blood volume.

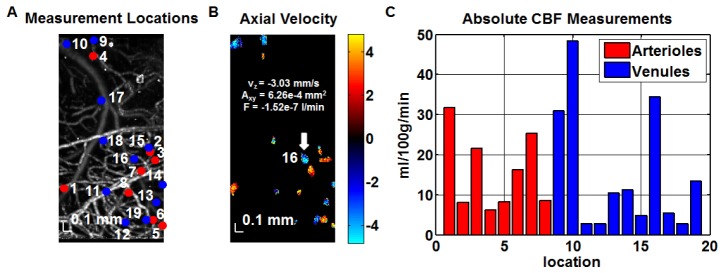
The spectroscopic fitting procedure estimated LC_HbT at each intravascular location, forming a three-dimensional data set which could then be displayed as a projection image in two dimensions (Fig. 2(A)). Based on this image, regions of interest (ROIs) were chosen in both arteries and veins, and the slope of LC_HbT versus depth was determined (Fig. 2(B)). The slope at the vessel center was found to provide the most robust estimation of C_HbT. In Fig. 2(C), estimated C_HbT values in the 5 ROIs circled in Fig. 2(A) are shown. The numbers are consistent with typical hematocrit values of 12-16 g/dl [47] in C57BL/6 mice.

Fig. 2.

Absolute measurements of total intravascular hemoglobin concentration (C_HbT) in the mouse (C57BL/6) neocortex through a thinned-skull cranial window. (A) Locations for C_HbT measurements. (B) Absolute C_HbT values were obtained from the slope of LC_HbT versus depth, where LC_HbT was obtained by spectroscopic fitting at each depth [40]; the vertical red dotted-lines represent the approximate vessel boundaries. (C) Absolute C_HbT measurements at the numbered locations in (A).

Next, sO₂ values in arteries and veins were obtained, from which the arteriovenous oxygen saturation difference was determined. Arteries and veins were readily distinguishable based on their oxygen saturation profiles and morphology. In particular, sO₂ values in arteries and veins (6 ROIs each) were averaged separately to obtain the mean arterial sO₂ and the mean venous sO₂, respectively. The oxygen extraction (OE) estimate was the arteriovenous sO₂ difference (OE = sO_2,a - sO_2,v), while the OE standard deviation estimate was the square root of the sum of the arterial and venous sO₂ variance estimates.

2.6 Cerebral metabolic rate of oxygen (CMRO₂) estimation

The following expression was used to estimate the cerebral metabolic rate of oxygen (CMRO₂):

$$CMR{O}_2=OE\times CBF\times [HbT]=\left(s{O}_{2,a}-s{O}_{2,v}\right)\times CBF\times [HbT]$$ (1)

We note that other CMRO₂ studies typically assume that [HbT] = Hct / (3.0 mL / g × 0.01625 g / μmol) [48], where Hct ~45% is an assumed or measured systemic hematocrit. For this study, we directly determined [HbT] based on local spectroscopic OCT imaging of the cortex. By employing this additional measurement, our method obviates an additional assumption implicit in many CMRO₂ estimation methods.

We constructed a histogram of CMRO₂ values by applying Eq. (1) to all combinations of the four parameters measured in our experiment; sO_2,a, sO_2,v, CBF, and [HbT]. Specifically, we combined 6 sO₂ measurements from arteries, 6 sO₂ measurements from veins, 2 CBF measurements (arterioles and venules), and 10 [HbT] measurements, resulting in 720 CMRO₂ values in the histogram. We used the histogram mean and standard deviation (s.d.) for CMRO₂ estimation. Alternatively, according to the theory of propagation of error [49], the standard deviation of CMRO₂ can be estimated via the relation

$${\widehat{\sigma }}_{CMR{O}_2}=\sqrt{{\left(m_{CBF}{m}_{\left[HbT\right]}{\sigma }_{OE}\right)}^2+{\left(m_{OE}{m}_{\left[HbT\right]}{\sigma }_{CBF}\right)}^2+{\left(m_{CBF}{m}_{OE}{\sigma }_{\left[HbT\right]}\right)}^2}$$ (2)

where m and σ denote the observed mean and standard deviation, respectively, of the subscripted quantities. The two methods yielded similar estimates for the standard deviation of CMRO₂.

3. Results

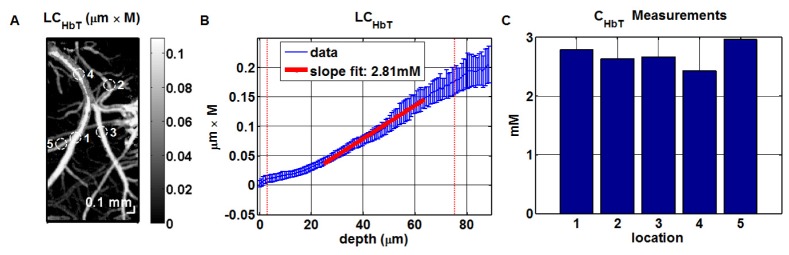
Figure 3 shows imaging of oxygen saturation in the mouse brain during modulation of FiO₂. Microvascular oxygen saturation was mapped using visible light spectroscopic OCT and displayed on a false-color scale (Fig. 3). A uniform reduction in both arterial and venous saturations was observed during mild hypoxia caused by reduction of FiO₂ (Fig. 3(B)). As both arterial and venous saturation decreased by the same amount (~7% sO₂) during mild hypoxia, oxygen extraction remained unchanged. Moreover, as CBF and C_HbT, related to hematocrit, did not change, CMRO₂ did not change appreciably during the oxygen modulation experiment.

Fig. 3.

Imaging of oxygen saturation changes during modulation of FiO₂ in the mouse (Crl:SKH1-Hr^hr) neocortex through a thinned-skull cranial window. Microvascular oxygen saturation was mapped using visible light spectroscopic OCT and displayed on a false-color scale during (A) 36% FiO₂, (B) 16% FiO₂. Since arterial and venous oxygen saturation decreased by equal amounts as FiO₂ was decreased, oxygen extraction remained approximately constant for this experiment. An artery and vein are labelled as “a” and “v” respectively.

Figure 4 shows imaging of oxygen saturation in the mouse brain during modulation of FiCO₂. During hypercapnia (5% FiCO₂), venous saturation increased by more than 25% while arterial saturation remained relatively unchanged, reducing oxygen extraction by ~3.3 × relative to baseline (0% FiCO₂). Moreover CBF increased by ~2.7 × relative to baseline while C_HbT, and thus hematocrit, remained unchanged relative to baseline. Thus, CMRO₂ did not change appreciably during the hypercapnia experiment.

Fig. 4.

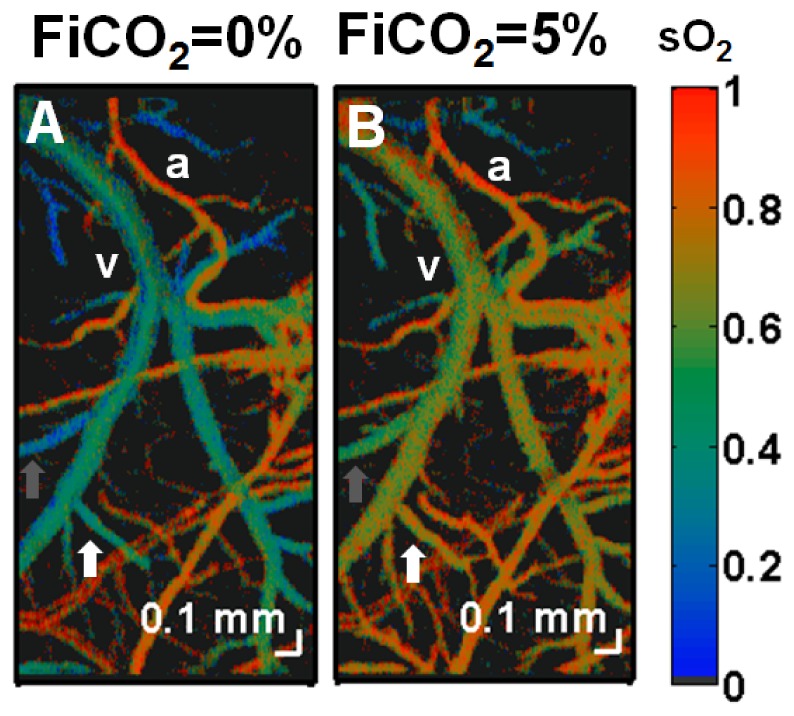
Imaging of oxygen saturation changes during modulation of FiCO₂ in the mouse (C57BL/6) neocortex through a thinned-skull cranial window. Microvascular oxygen saturation was mapped using visible light spectroscopic OCT and displayed on a false-color scale during (A) 0% FiCO₂, (B) 5% FiCO₂. A large increase in oxygen saturation was observed in veins, while the sO₂ in arteries remained unchanged. The reduced oxygen extraction is a consequence of arterial and arteriolar dilation and subsequently, increased CBF during hypercapnia. Note the heterogeneity of oxygen extraction, as evidenced by regionally varying venous sO₂ values both before and after hypercapnia (white and gray arrows). An artery and vein are labeled as “a” and “v” respectively.

Finally, a range of states were achieved in N = 3 C57BL/6 mice through mild modulation of FiO₂ and FiCO₂. Due to the fact that manipulations were not severe, CMRO₂ was not expected to change for any of these states. OE, CBF and C_HbT are shown in Fig. 5(A)-5(C), respectively. Notably, variability in C_HbT (Fig. 5(C)) was lower than variability in either OE (Fig. 5(A)) or CBF (Fig. 5(B)). The coefficients of variation for OE, CBF and C_HbT were 0.70, 0.44, and 0.10, respectively. In Fig. 5(D), a histogram of CMRO₂ values for a single state, calculated from all 720 possible combinations of arterial saturations (different locations), venous saturations (different locations), CBF values (arteriolar and venular), and C_HbT values (different locations) is shown. The mean and standard deviation for a given state were determined from this histogram. Based on this procedure, which incorporates biological heterogeneity in the standard deviation estimate, CMRO₂ for the example in Fig. 5(D) was determined to be 163.6 ± 67.8 μmol/100g/min (mean ± s.d.). In spite of large variability in OE (Fig. 5(A)), CMRO₂ varied less across the investigated states (Fig. 5(E)). This is explained by the observation that OE varied inversely with CBF (Fig. 5(F)), such that a higher CBF is compensated by a lower OE, and vice versa (R² = 0.95 for OE~1/CBF fit). Therefore, as expected based on Eq. (1), the coefficient of variation for CMRO₂ (0.17) was lower than the coefficients of variation for OE (0.70) and CBF (0.44). The lower coefficient of variation of CMRO₂ across animals and states, in spite of its higher relative error (Eq. (2)), is notable.

Fig. 5.

(A-C) Oxygen extraction (OE), cerebral blood flow (CBF), and hemoglobin concentration (C_HbT) were measured in a range of states (achieved by mild modulation of FiO₂ and FiCO₂) and mice (C57BL/6, N = 3). The OE standard deviation estimate (A) was determined as the square root of the sum of the arterial and venous sO₂ variance estimates, obtained from measurements at different locations. The CBF standard deviation estimate (B) was obtained from the summed arteriolar flow and summed venular flow values. (C) The C_HbT standard deviation estimate was obtained from measurements at multiple locations. (D) A CMRO₂ histogram was generated for each animal and state based on applying Eq. (1) to all possible combinations of arterial saturations (different locations), venous saturations (different locations), CBF values (arteriolar and venular), and C_HbT values (different locations). (E) CMRO₂ means and standard deviations were estimated from this histogram and shown across states and mice. (F) OE varied inversely with CBF, leading to a lower coefficient of variation for CMRO₂ (0.17) as compared with OE (0.70). Error bars in (A-F) are standard deviations.

4. Discussion

The current manuscript describes and demonstrates the estimation of CMRO₂ in the mouse brain in vivo through separate quantification of CBF, OE and [HbT]. As CMRO₂ is the product of these three quantities, relative error in CMRO₂ was larger than relative error in the individual measurements of CBF, OE, and [HbT] (Fig. 5(D)). However, Fig. 4 suggests that some of this variability may be due to real biological heterogeneity in oxygen saturation in different veins that serve different cortical regions (denoted by arrows). We anticipate that a flow-weighting of the saturation in each venule (as would be required to calculate the oxygen efflux from cortical tissue) might be a more appropriate way to account for this heterogeneity than to merely average the saturations. We will explore flow-weighting of saturations in future work, using a higher optical resolution to quantify oxygen saturation in every venule where flow is measured.

Since CMRO₂ values were derived from measurements in supplying and draining vessels at the cortical surface, CMRO₂ was not depth-resolved. It is well-known that glucose metabolism in gray matter is 3-fold higher than in white matter [50], and that glucose metabolism varies across different cortical layers [51]. Since oxygen metabolism is expected to parallel glucose metabolism, some of the heterogeneity in venous saturation (Fig. 4) may relate to layer-dependencies in oxygen extraction. Verification of this conjecture would require a vascular graph [52] to ascertain the precise cortical layers drained by each surface venule.

Though CMRO₂ estimates in this study (199 ± 35 μmol/100g/min) are physiologically plausible, they are somewhat lower than previous literature values [20, 53]. A recent study using ultrahigh-field 16.4 Tesla ¹⁷O MR spectroscopy on mice (FVB, N = 2, male, 35-40 g body weight, age 20-25 weeks; C57B6/CBA, N = 3, male, 27-30 g, age 7-10 weeks) anesthetized with 1.2-2% isoflurane [20] reported an average striatal oxygen consumption rate of 2.6 ± 0.4 μmol/g/min. In another study, 11.7 Tesla ¹⁷O MR spectroscopy was applied to measure OEF, CBF, and CMRO₂ in stroke mice (C57BL/6, N = 4, male, 18-30 g) anesthetized by intraperitoneal injection of ketamine/xylazine [53]. In this study, the mean CMRO₂ value was 2.63 ± 0.16 μmol/g/min in the contralateral hemisphere to the stroke. Comparisons between studies should be performed with caution since metabolic rate varies across brain regions [54], with age [51, 55], and with depth of anesthesia [56].

Several limitations of our methodology may also contribute to these discrepancies. First, though almost all of the oxygen carried by blood (> 98%) is bound to hemoglobin under normal physiological conditions [57], oxygen dissolved in plasma may contribute significantly to total blood oxygen content at very high or very low oxygen tensions. Dissolved oxygen may be important in calculating OE, which is an arteriovenous difference. In the future, the CMRO₂ calculation in Eq. (1), currently based on the assumption of oxygen transport solely by hemoglobin, could, in principle, be corrected to account for dissolved oxygen in the calculation of OE. Second, fringe washout occurs when particles move axially on the order of a wavelength over the exposure time, leading to averaging of the spectral interference fringes in spectral/Fourier domain OCT. On average, fringe washout is more severe at the short wavelength end of the broad spectrum, potentially leading to an artifactually higher absorbance at shorter wavelengths. Nevertheless, in the present study, spectra were measured at the center of vessels that were almost perpendicular to the probe beam, meaning the axial velocities and Doppler shifts were small. Third, the scattering coefficient is known to decrease with wavelength, leading to a higher absorbance at shorter wavelengths, particularly at greater depths. The effects of attenuation due to scattering were mitigated in the present study by selecting superficial ROIs for spectroscopic analysis. Other potential solutions to account for wavelength-dependent scattering include a depth-dependent normalization procedure [40] or employing a model that explicitly includes the wavelength-dependence of scattering [42]. Fourth, both thermal damage thresholds and the maximum permissible exposure (MPE) limit are lower at visible wavelengths than at near-infrared wavelengths. In the present study, the power delivered to the sample was maintained at ~1 mW, and pulses at the sample were too broad and low energy to observe saturation effects. No changes in the brain tissue before were noted during and after the imaging session.

Finally, a cortical thickness was assumed in the present study to achieve absolute cortical CBF and CMRO₂ (units of ml/100g/min and μmol/100g/min, respectively). While a cortical thickness of 1.5 mm was used here for consistency with previous studies [39], we have recently observed that the cortical thickness in mice may approach ~1 mm at some locations. The substitution of a smaller cortical thickness, perhaps measured experimentally, would bring our CMRO₂ estimates more in line with literature values [20, 53]. Lastly, isoflurane is known to cause reduction of cerebral metabolism and suppression of neural activity [56] at high doses; thus, uncontrolled variability in anesthesia depth may explain some of the variability in our results. Future experiments will therefore employ simultaneous cortical electrophysiology as a more direct correlate of CMRO₂.

5. Conclusion

A method of quantifying brain oxygen consumption using three independent optical measurements of cortical blood flow, arteriovenous oxygen saturation difference, and hematocrit, using a single OCT microscope, was presented. Physiologically plausible CMRO₂ values were demonstrated, and negative control experiments were performed. While the results of these validation experiments do not prove the accuracy of the CMRO₂ measurements, a different set of results could have invalidated the method. To provide more complete validation, these methods will be compared against gold standards such as PET in the future.