Abstract
Optogenetic approaches to manipulate neural activity have revolutionized the ability of neuroscientists to uncover the functional connectivity underlying brain function. At the same time, the increasing complexity of in vivo optogenetic experiments has increased the demand for new techniques to precisely deliver light into the brain, in particular to illuminate selected portions of the neural tissue. Tapered and nanopatterned gold-coated optical fibers were recently proposed as minimally invasive multipoint light delivery devices, allowing for site-selective optogenetic stimulation in the mammalian brain [Pisanello , et al. , Neuron 82, 1245 (2014)]. Here we demonstrate that the working principle behind these devices is based on the mode-selective photonic properties of the fiber taper. Using analytical and ray tracing models we model the finite conductance of the metal coating, and show that single or multiple optical windows located at specific taper sections can outcouple only specific subsets of guided modes injected into the fiber.
OCIS codes: (220.0220) Optical design and fabrication, (170.0170) Medical optics and biotechnology
1. Introduction
In recent years neuroscientists have made extensive use of optogenetics, a powerful set of tools to stimulate or silence activity of neurons expressing light-gated ion channels or transporters [1, 2]. This approach has made possible an unprecedented investigation of functional connectivity within the living mammalian brain, by virtue of a straightforward combination of new proteins for modulation of neural activity and new techniques to deliver light into the brain tissue [3]. These latter technologies have the main purpose of improving the matching between light-delivery geometries and the very heterogeneous structure of the brain in terms of cellular architecture and their spatial organization in functional sub-regions. Indeed, the requirements for spatial light distribution and light power vary ad hoc with the experiment, and the tools used to guide light inside the brain should be designed accordingly [4]. For example, the cerebral cortex, a region playing a key role in sensation, cognition and behavior, is a layered structure with layer-by-layer differentiation in terms of cellular classes and connectivity [5]. Therefore, tools are needed to dynamically elicit or inhibit cortical activity with layer selectivity in order to study neuronal circuits of the neocortex and to dissect the relationship between circuitry and function [6].
However, in typical in vivo optogenetic experiments light is carried to the target brain region using a short, cleaved optical fiber implanted in the animal’s head and supplied by an extension fiber coupled to a light source [7]. This approach shows two major limitations: (i) the size of the implanted waveguide significantly damages the brain tissue, and (ii) it is not possible to redirect light in a different zone of the brain. Several alternative technological solutions have been developed recently to dynamically redirect light towards different locations of the brain tissue [8–11], including µ-Light Emitting Diodes [6, 12, 13], array of waveguides [14–17], bundle of optical fibers [18, 19] or patterned illumination techniques [4, 20, 21].
A promising approach consists in using multipoint-emitting tapered optical fibers (MPEFs), which are effective as minimally invasive, single waveguides for dynamic and spatial selective in vivo stimulation of neo-cortex and striatum in mice [22]. These devices are composed of a single core optical fiber with the end segment tapered and coated with gold. Light is allowed to outcouple into the brain through multiple optical small apertures in the metal coating, resulting in out-of-axis light delivery points. By changing the coupling angle of the light launched into the fiber, it is possible to selectively activate each individual window, thus allowing for a spatial-selective optogenetic control of neural activity with a minimally invasive and single waveguide [22].
Here we show that the working principle of MPEFs is based on the modal-dependent optical properties of the gold-coated fiber taper, which allows defined modal subsets to propagate at a defined section of the taper, acting as a modal demultiplexer. We used an analytical method coupled with a ray tracing model to evaluate modal propagation length within the gold-coated taper, with the goal of defining the position of the outcoupling windows for light delivery in two different layers of the primary motor cortex. By opening a single optical window at certain sections of the taper, we experimentally observe that the modal subset that allows outcoupling to the surrounding medium depends on the section at which the aperture is realized. In the final device configuration we find that the presence of two windows only slightly alters the modal content emitted from a single aperture, thus resulting in a viable strategy for delivering light in superficial and deep regions of mouse motor cortex.
2. Materials and methods
2.1 Device structure and fabrication process
The devices used for the experiments carried out in this work, summarized in Fig. 1(a)-1(c), consist of two MPEFs with one window at two different positions along the taper (hereafter referred to as devices W1 and W2) and a two-window device (W1-2). Tapered fibers with N.A. = 0.22, core radius rcore = 25 µm, cladding radius rclad = 62.5 µm, core and cladding refractive index ncore = 1.464 and nclad = 1.447 (at λ = 473 nm) and taper half-angle ψ ~2.25° were obtained from OptogeniX (www.optogenix.com). A ~200 nm thick gold layer was thermally evaporated over the tapered region following the procedure described in [23]. Optical windows were milled on the taper surface to obtain light emission sites using the FEI Helios Nanolab 600i Dual Beam Focused Ion Beam (FIB) system with the methods and parameters previously described [22, 23]. Figure 1(d) and Fig. 1(e) show Scanning Electron Microscope (SEM) images of the optical windows milled in fibers W2 and W1, respectively. After optical characterization, fiber W1-2 was obtained from W1 by milling a second optical window at the same location and with the same geometrical properties of that milled on W2 (Fig. 1(f)). The resulting MPEF has two light emission sites ~700 µm apart, matching the distance between layers II/III and VI of the mouse primary motor cortex (Fig. 1(g)). In the following we will refer with H1 to the window nearest to the fiber tip and with H2 to the window farther from the tip.
Fig. 1.

(a)-(c): Schematic representation of the devices with one (a, b) and two (c) windows used for the experiments. (d), (e): Scanning electron microscope images showing in detail the optical windows milled on device W2 (d) and W1 (e). (f): Scanning electron microscope image of a typical two-window MPEF. (g): Schematic representation of a two-window MPEF implanted in the mouse primary motor cortex.
2.2 Light propagation model into the gold-coated taper
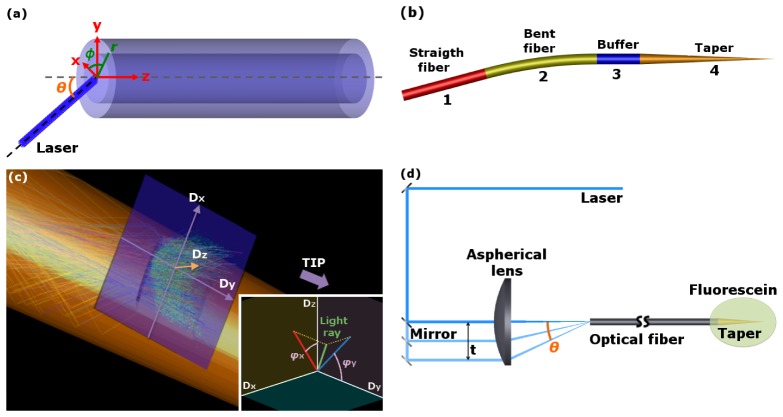
In a first instance, the fiber taper can be modeled as a lossless homogeneous cylindrical hollow metallic waveguide with circular cross section of radius a decreasing toward the tip. The axial and transversal propagation constants of a guided mode (βl,m and kt,l,m, respectively) strictly depend on a [24]
| (1) |
| (2) |
where ζl,m represents the m-th zero of the l-th order Bessel function of the first kind Jl(x) for TM modes or the m-th zero of the derivative of Jl(x) for TE modes, k0 and λ0 represent the free space wavenumber and wavelength, respectively, while n is the refractive index of the waveguide medium. For sections smaller than a critical radius (a<ac), kt,l,m>k0n and, from Eq. (2), βl,m is an imaginary number. Thus the mode is not able to propagate along the waveguide axis, but is subjected to an exponential decay [24, 25]. For two sections with different radii a(0) > a(1), as a direct consequence of Eq. (1) the transversal propagation constants of the l,m-th mode at these sections are related by the equation
| (3) |
For every single mode, kt,l,m increases as the taper diameter decreases, and each propagating mode will encounter its own critical section beyond which it undergoes exponential attenuation. Only the light confined in the lower order modes is able to reach the tip of the fiber, whereas higher order modes do not flow through the whole taper [25]. Hence, the metalized taper acts as a modal filter by virtue of its order selective cutoff properties.
2.3 Analytical model for light coupling inside the step-index waveguide section
The electromagnetic field guided by the waveguide in the presence of a known field profile at the input section was determined by exploiting the orthogonality of the modes with respect to an inner product [24, 26]. The intensity at which the l,m-th mode is excited was computed as [24, 26]
| (4) |
where Es,t(x,y) and ht,l,m(x,y) are, respectively, the source electric field and the l,m-th mode magnetic field in the plane orthogonal to the waveguide axis, both in correspondence of the input section of the waveguide. x, y and z refer to the reference system depicted in Fig. 2(a) and Σ represents the surface of the transversal section of the waveguide. In the particular case of a weakly guiding step-index optical fiber, with core radius rcore and refractive index of core and cladding ncore and nclad, respectively, the modal set is known as Linearly Polarized (LP) [26]. It is convenient to introduce the normalized transversal propagation constants in the core and in the cladding , and the fiber v parameter . For guided modes, both ul,m and wl,m are real-valued. The electric (et,l,m(x,y)) and magnetic (ht,l,m(x,y)) transversal field profiles for each LPl,m guided mode are [26, 27]
| (5) |
| (6) |
where , ζl,m represents the m-th zero of Jl(x), Kl(x) is the l-th order modified Bessel function of the second kind and η(r) is the characteristic impedance of the medium at distance r from the axis of the optical fiber.
Fig. 2.
(a): Definitions and coordinates system at the input face of the optical fiber. (b): Three-dimensional schematic layout of the ray tracing model in which the four blocks are indicated: a straight optical fiber (1), a bent optical fiber (2), the buffer region (3) and the tapered region (4). (c) Detail of the position of the detector recording the geometrical properties of the rays outcoupled by the windows. The inset shows the rays outcoupling angles φx and φy recorded by the detector. φx is the angle between Dz and the projection of the outcoupled ray propagation direction on the plane Dz-Dx. φy is the angle between Dy and the projection of the outcoupled ray propagation direction on the plane Dz-Dy. (d) Experimental setup used to select the coupling angle between the laser beam and the input facet of the optical fiber.
2.4 Ray tracing
For ray tracing simulations we used the software Zemax-OpticStudio. We modeled a 473 nm unpolarized laser source with a diverging bundle of rays with full-aperture angle Δθ = 0.9°, having uniform intensity profile and a 25 µm spot radius. A three-dimensional layout of the model is shown in Fig. 2(b). It consists of four blocks: (1) a straight piece of core-cladding fiber, (2) a bent fiber section, (3) a 0.5 mm long homogeneous dielectric cylinder of index neq (the average of ncore and nclad weighted by the occupied surface in a cross section of the fiber) with diameter 125 µm and (4) the tapered and metal-coated tip. Section (2) was implemented with a bend radius of 50 mm (above the recommended long term bend radius of 30 mm) and, without loss of generality, the overall length of the first two blocks was set at 55 mm in order to ensure good homogenization of the travelling rays at the opposite endface of block (1), to achieve good accuracy (less than 1% of rays terminated by geometrical errors and energy thresholds). The presence of section (3), hereafter referred to as buffer, is justified by the fabrication process of the taper: since the optical fiber is heated up, we suggest that the transition between the core-cladding and the homogeneous tapered portions of the waveguide is not abrupt. The taper was approximated by a cone-shaped volume with a half taper angle ψ = 2.25°, coated with a 200 nm thick gold layer of refractive index nc = 1.294 and extinction coefficient kc = 1.805 [28]. The same coating is on the buffer and both taper and buffer are immersed in a non-absorbing medium of refractive index nmedium (air or water). Surface and bulk scattering effects by imperfections, irregularities and external inclusions in the fiber were not modeled in the simulations. Provided that scattering parameters were correctly determined, unfeasibly long runtimes would result due to the increased number of ray segments and surface intersections. Furthermore, under the hypothesis of homogeneous media it is straightforward that the effects of external mechanical stresses were not accounted as well. The windows were modeled as four right-angled sidewalls and one convex bottom face following the local curvature of the conical volume. A square plane detector was placed in front of each window, as shown in Fig. 2(c), to record the angular properties of the rays outcoupled from the waveguide. The source was coupled with the optical fiber by a 1:1 imaging through a paraxial lens. The angle θ between the chief ray of the bundle and the optical axis of the fiber represents the launch angle of the beam. Each ray tracing session was run by launching 0.5M rays from each angle.
2.5 Emission properties characterization
The emission properties of MPEFs were experimentally characterized using the setup illustrated in Fig. 2(d). In order to tune θ, an aspherical lens (nominal focal length f = 100 mm at 780 nm, diameter d = 50 mm) and a sliding mirror were used: when the mirror is at the zero position, the laser beam (wavelength λ0 = 473 nm) propagates along the optical axis of the lens and is focused at the input facet of the fiber without being deflected (spot diameter FWHM at the fiber input 2ρ ~46 µm). As the mirror is translated along the beam propagation direction, light is focused at the input face of the fiber with an angle . The dependence of the values of the transversal wavevectors excited into the core-cladding section of the waveguide from the input-coupling angle was measured by collecting the optical Fourier transform of the plane at the output face of a piece of fiber (see optical path in Fig. 3(a)). Emitted power from the side windows was measured placing the fiber in front of a lightpower meter, with an input power of 15 mW. For MPEF W1-2 a razorblade was used as a shutter to detect only light intensity emitted via H1. Power outcoupled from H2 was retrieved from the difference between the powers read by the power meter with and without the razorblade in the detection path.
Fig. 3.
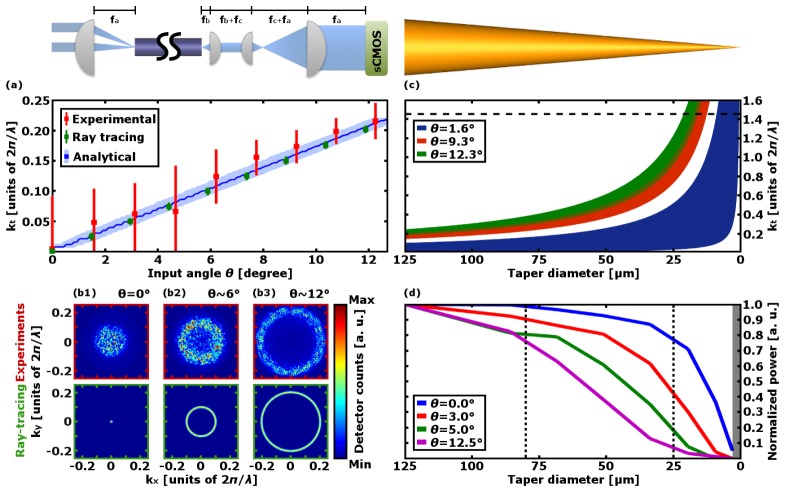
(a): Values of kt injected into the optical fiber as estimated by the analytical model (blue curves), the ray tracing model (green squares) and by experimental measurements (red squares). The dark blue curve represents the kt value of the mode excited with the highest power, the light blue area marks the subset of modes carrying at least 5% of the maximum excited power. Green and red bars indicate the kt value at which the detected intensity decays below the 50% with respect to the detected maximum. The upper inset displays the optical setup used to obtain the Fourier transform of the fiber output endface; nominal focal lengths are fa = 100.0 mm, fb = 7.5 mm, fc = 30.0 mm. (b): Fourier transform of the fiber output endface for three different values of θ both for experiments (upper row) and ray tracing simulations (lower row). (c) Evolution of kt values inside the taper for three different values of θ. Each shaded region was computed using both Eq. (3) and the extreme points of the corresponding bar in the experimental data shown in panel (a) as kt values for a taper diameter of 125 µm. The horizontal black line represents the cutoff limit. (d) Evolution of the power confined into the taper for four different values of θ. The two vertical black lines indicate the taper diameters where optical windows are placed. Taper diameters inside the gray area (i.e. below 3 µm) were excluded from the analysis.
3. Results
With the goal to demonstrate that the working principle behind MPEFs is based on the modal-dependent optical properties of the gold-coated fiber taper, this section is organized as follows. First, we define a method to inject different modal subsets with different transversal components of the wavevector (kt) in the core-cladding section of the waveguide, based on changing the angle θ at which light is injected into the fiber. kt values as a function θ were estimated by means of analytical calculations, ray tracing simulations and Fourier optics-based experiments. Then, the propagation length of injected modal subsets into the gold-coated taper are estimated, and with the support of the ray tracing model we assess the light power distribution along the taper for different θ. In paragraph 3.2 devices W1 and W2 are used to show that different modal subsets can be outcoupled by single optical windows realized at a specific section of taper, suggesting that the effect of the taper on wavevectors transversal component plays a predominant role. In section 3.3 MPEF W1-2 is then used to show that a two-window MPEF can selectively emit light from one or the other window based on the modal subset injected at the other end of the fiber.
3.1 Modal subsets injection
To control the subset of injected modes the light source was coupled into the fiber with an aspherical lens (focal length 100 mm) and a well defined angle θ (beam convergence Δθ ~0.9°) [26, 29]. Although a major selectivity on the launched modes can be obtained using an approach based on spatial light modulator [30], this comes at the price of an increased complexity in the optical setup. The dependence from θ of the power confined in each guided LPl,m mode was numerically determined using Eq. (4), Eq. (6) and the following Gaussian beam form:
| (7) |
where the approximation holds for θ << 1 rad. T(r,ϕ,θ) is the transmission coefficient for the electric field at the interface between air and fiber. The main results of this calculation are illustrated in Fig. 3(a). As θ increases, the transversal propagation constant of the mode excited with the highest power increases in a linear fashion (blue line), and the subset of kt,l,m values carrying at least 5% of the light power guided by the most powerful mode (light blue shadow) evolves accordingly. This was verified in the ray tracing model and experimentally by means of the setup schematized in the inset of Fig. 3(a). The resulting far field images are reported in Fig. 3(b1)-3(b3). kt values were then extracted and the obtained data reported by green and red squares in Fig. 3(a) for ray tracing and experiments, respectively. A comparison between the measured, the simulated and the numerical data confirm the actual selection on the modal subset propagating inside the waveguide and the good agreement between the two models and the experimental results. Experiments show larger sets of injected kt values with respect to numerical and simulation data, and the far field patterns show a transition from a disk shape to a ring: this is a phenomenon due to the mode mixing induced by imperfections and irregularities in the bulk of the fiber and at the core-cladding interface and surface scattering upon the input facet [31], which leads to a wider modal distribution for low injection angle with respect to high θ [32–35]. As mode mixing is more effective when light is coupled into the fiber with a high convergence angle [33], lowering this parameter by using a lens with a longer focal length to focus light at the input facet of the fiber or, ideally, a narrow collimated beam, would reduce mutual interference between modes, which reflects into a reduction in the thickness of the recorded experimental patterns (either disks or rings). We should say, however, that a lower limit exists: also if an ideal plane wave is coupled into the fiber at different input angles, modal mixing would result in wider sets of injected kt values for low order modes with respect to high order modes [32]. It is worth to highlight that while theoretical calculation and ray tracing simulations consider a perfectly straight piece of optical fiber for simplicity and in order to reduce computation time, experiments were performed using a gently curved optical fiber, with radius of curvature well above the value recommended by the manufacturer (30 mm).
With the goal to identify the position of the optical windows, the obtained experimental values of kt,l,m were then used to evaluate the trend of the transversal propagation constant inside the taper displayed in Fig. 3(c). The extreme points of the experimental bars reported in red in Fig. 3(a) were used as boundary for the shaded area at a taper diameter of 125 µm, and the trend was then computed using Eq. (3). The horizontal black line indicates the critical value above which modes become evanescent (hereafter referred to as cutoff value), whereas the colored curves represent three different modal subsets obtained for three different values of θ. The essential information provided by this graph is the diameter at which the cutoff occurs for the higher order modes, which increases as the injected kt,l,m values increase. In particular, for the highest value of θ the set of values of kt,l,m with a non-negligible amount of power overtake the cutoff at sections with diameters between ~18 µm and ~19 µm. As a consequence, an outcoupling site placed at a diameter smaller than 18 µm will not be irradiated by the guided radiation and will not be allowed to outcouple light for high θ. However, the gold coating introduces an additional attenuation neglected by this analytical model.
When the assumption of a perfect electrical conductive coating is dropped, i.e. the metal is considered as a dielectric medium with a complex refractive index ngold = nc + jkc, the field profiles of the modes are perturbed and the axial propagation constant becomes complex-valued (βl,m + jαl,m). This leads both to the presence of an attenuation term αl,m and to a slight variation of the values of βl,m and kt,l,m with respect to the case of a perfect electric conductor. For a>>ac, kt,l,m, αl,m and βl,m can be determined using the following relationships:
| (8) |
| (9) |
| (10) |
where ξl,m represents the m-th zero of Jl-1(x) and τ is related to nc and kc with a relation dependent on the nature of the considered mode (TM, TE or hybrid) [36]. Equation (9) highlights that αl,m increases with the order of the modes and is proportional to a−3. Despite the absence of a clear distinction between the propagation and the cutoff regime in a lossy waveguide [37], the increasing (decreasing) fashion of kt,l,m (βl,m) as a decreases still holds true until the ideal critical section is reached, and after that section the attenuation αl,m increases exponentially as the radius of the waveguide decreases [37]. To take into account this formalism and to evaluate the position of the optical windows in the particular case of gold coating, the dependence of the light power inside the taper from θ was investigated using a ray tracing model with no windows on the taper surface. The curves in Fig. 3(d) show the results of this analysis for four different values of θ, and reveal that for input angle larger than 5° the power available at taper sections with diameters smaller than 25 µm is less than the 20% of the power entering the fiber taper. Thus, an optical window placed beyond this point is significantly irradiated by light only when low values of θ are used to couple light into the waveguide (i.e. when low kt modes are injected into the fiber). In particular, for θ = 12.5° only the 5.4% of the power entering the tip reaches the taper section with a diameter of 25 µm. Taper sections with diameters below 3 µm were not investigated since, due to the high radius of curvature of the taper in these regions, the re-deposition effects during the FIB milling process make difficult to obtain windows with good quality surfaces. Moreover within this size domain diffraction effects are more pronounced and the ray tracing approach does not account for them.
3.2 Spatially selective modal outcoupling
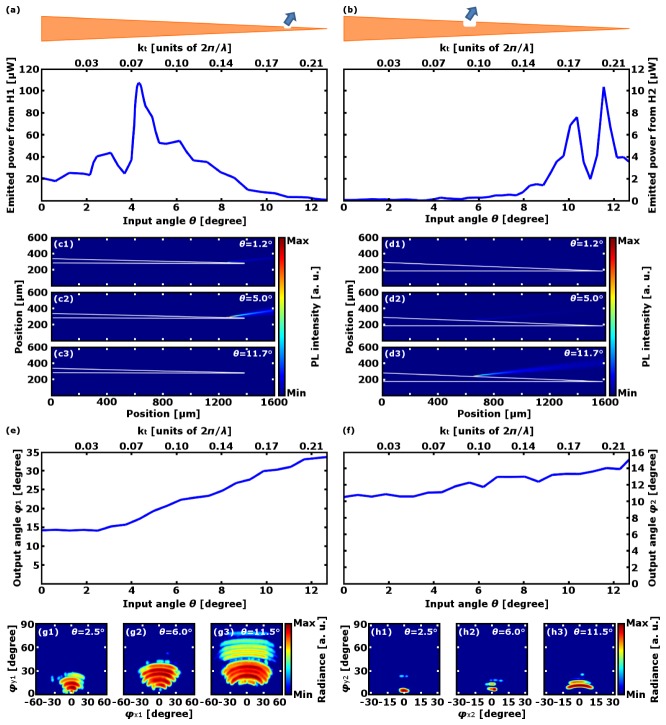
Two single window devices were realized in order to proof the ability of MPEFs to selectively outcouple a subset of propagating modes from windows placed at different positions along the taper. The output power from each device was measured for a set of values of θ in the interval [0°, 12.7°]. As shown in Fig. 4(a), if the window is realized at a taper diameter of 25 µm (device W1 in Fig. 1(a)) outcoupling is observed for about 1.2°<θ<8.6° with a maximum of ~107 µW at 4.3°. This lets us suggest that this type of devices can selectively outcouple in the surrounding medium defined modal subsets injected at the other end of the fiber, and in particular those with kt values between ~0.03 2π/λ0 and ~0.16 2π/λ0 (maximum outcoupling efficiency at 0.08 2π/λ0). When the window is moved 700 µm farther from the taper tip at a section with diameter 80 µm in order to match with the anatomical structure of the mouse motor cortex (device W2 in Fig. 1), and its dimensions are enlarged to 25×25×6 µm, light emission from the window can be activated for about 9.0°<θ<12.4° (Fig. 4(b)) with a maximum output of ~10 µW at 11.6°. This angles interval corresponds to a subset of kt values in the interval ~0.17 2π/λ0 < kt < ~0.23 2π/λ0. The need for a bigger and deeper window is related to the different way the power is coupled to higher order modes with respect to lower order modes. As the order of the most powerful mode increases, light power is spread among a higher number of modes and, as a consequence, the power confined in the emitted modal subset decreases. Realizing a wider window raises the area of the surface active in light emission and, therefore, the overall emitted power increases. Typical fluorescence images of the light emission obtained using an EPI-fluorescence microscope and a CCD camera while the tip was submerged into a fluorescent medium (see setup in Fig. 2(c)) are displayed in Fig. 4(c) and Fig. 4(d). From these images, the angular properties of the emitted light were evaluated. The trend of the outcoupling angles between the taper and the light beam emitted from H1 and H2, named φ1 and φ2 respectively, are reported in Fig. 4(e) and Fig. 4(f) as a function of θ. These results are an index of the transversal propagation properties of the light travelling inside the taper. The outcoupling angles from both H1 and H2 increase with θ, and the higher influence on the kt values of the smaller section at which H1 is realized is clearly visible, since the variation in φ1 (from ~14.2° to ~33.4°) is ~4 times greater than the variation in φ2 (from ~10.5° to ~15.5°). The radiance maps obtained from the ray tracing simulations reported in Fig. 4(g) and in Fig. 4(h), confirm the behavior of φ1 and φ2 as a function of θ. Indeed, the rays outcoupling angles with respect to the taper surface (φy values) show an overall increase as a function of θ. Additionally, the spread in the direction perpendicular to the taper surface (represented by the values of φx) increases with θ and is more pronounced for the window closest to the taper tip.
Fig. 4.
(a), (b): Power emitted from devices W1 (panel a) and W2 (panel b) as a function of θ for input power of 15 mW. (c), (d): Fluorescence images of the emission of devices W1 (panel c) and W2 (panels d) for three different values of θ, the taper being submerged in a fluorescein droplet. White lines show the taper profile. (e), (f): Outcoupling angle of the light emitted from device W1 (panel e) and W2 (panel f) as a function of θ. (g), (h): Normalized radiance maps of the light emitted from devices W1 (panels g) and W2 (panels h) obtained through the ray tracing model for three different values of θ. Definitions of φx and φy are reported in Fig. 2(c). For each map the colorbar represents a 6 decades logarithmic scale.
3.3 Two-window device
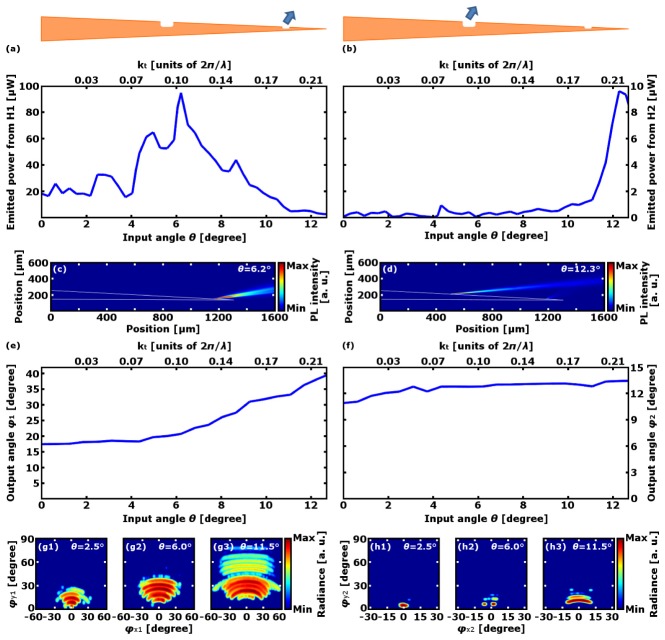
A two-window MPEF was obtained by milling H2 at the proper position on device W1, thus obtaining device W1-2. Experimental measurements of the output power were performed to ensure that the simultaneous presence of both windows preserves the ability to select the light emission point shown by injecting different modal subsets, and to exclude that mode mixing causes crosstalk of the two windows. Both the energetic and geometrical aspects of the output from the windows were evaluated. The powers output as a function of θ, displayed in Fig. 5(a) and Fig. 5(b) for H1 and H2, show that from ~4.0° to ~9.8° emission from H1 dominates over H2, whereas the situation is reversed from ~11.0° to ~12.4°. Therefore, H1 can emit light injected in the core-cladding section of the fiber with almost 0.08 2π/λ0<kt<0.18 2π/λ0, while H2 allows outcoupling for almost 0.20 2π/λ0<kt<0.23 2π/λ0, thus confirming the modal demultiplexing properties of this configuration. For the two windows, the output power maxima are, respectively, ~97 µW and ~10 µW. It is worth mentioning that the emission peak for H1 is reached for θ = 6.2°, while it was obtained for θ = 4.3° in device W1. We suggest that this difference is due to a slight redistribution of power among the modes, due to the perturbation on the waveguide symmetry with the introduction of H2. Micrographs of the light emission, a subset of which is reported in Fig. 5(c) and Fig. 5(d), were captured in order to evaluate the dependence of the outcoupling angle from θ shown in Fig. 5(e) and Fig. 5(f).
Fig. 5.
(a), (b): Power emitted from H1 (panel a) and H2 (panel b) as a function of θ for input power of 15 mW for device W1-2. (c), (d): Fluorescence images of the emission of devices W1-2 for θ = 6.2° (panel c) and for for θ = 12.3° (panel d) for three different values of θ, the taper being submerged in a fluorescein droplet. White lines show the taper profile. (e), (f): Outcoupling angle of the light emitted from H1 (panel e) and from H2 (panel f) as a function of θ. (g), (h): Normalized radiance maps of the light emitted from H1 (panels g) and from H2 (panels h) obtained through the ray tracing model for three different values of θ. Definitions of φx and φy are reported in Fig. 2(c). For each map the colorbar represents a 6 decades logarithmic scale.
The trend of an increasing output angle as θ increases is very similar to that observed with the single-window devices (φ1 varies from ~17.5° to ~39.9° while φ2 varies from ~10.9° to ~13.4°), with the exception of a small variation, which could be again ascribed to a slight modal-mixing induced by the presence of the second window. Furthermore, also the radiance maps obtained through ray tracing simulations (Fig. 5(g) and Fig. 5(h)) show only minor differences between one-window devices and W1-2 fiber, mostly located on the tails of the signals registered by the detectors, but the overall trend of φx and φy (i.e. increasing as a function of θ and of their proximity to the taper tip) is confirmed.
4. Discussion
Here we show that the modal-selective properties of metal-coated tapered fibers can be exploited to translate a mode diversity of light guided by the fiber to a spatial diversity on outcoupling sites distributed along the taper. Selective modal excitation at the fiber input is achieved by changing the input angle of a Gaussian beam, which results in the excitation of modal subsets with different ranges of kt values. Data reported in Fig. 3 show a difference between the modal-selection efficiency in the ideal condition (evaluated with ray tracing and analytical models) and in the experiments: due to mode mixing, a broader distribution of modes is bounded inside the fiber instead of a small set of kt, as already observed in other works [31–35]. When designing windows positions along the taper this is a very important point. Modal subsets injected at the different activation angles must be disjoint to allow for a straightforward operation of the device in the real experiment. In the two-window device presented here, for instance, H1 and H2 are activated at 4.0°<θ1<9.8° and 11.0°<θ2<12.4°, resulting in the two disjoint sets 0.08 2π/λ0<kt,1<0.18 2π/λ0 and 0.20 2π/λ0<kt,2<0.23 2π/λ0. Therefore, modal mixing represents a key factor to define the maximum number of stimulation points (hereafter referred to as N). The definition and the increment of N is of fundamental importance to extend the application of MPEFs to a plurality of brain regions, allowing to achieve the desired spatiotemporal resolution for the expected neural modulation scheme [4] and to develop closed-loop control systems [10]. By taking into account our optical setup and the optical parameters of our fibers, up to three windows can be controlled independently, as we have already shown in a previous work [22]. For optogenetic experiments requiring larger N, MPEFs should be realized by using optical fibers with higher numerical aperture, which sustain a higher number of guided modes and therefore a wider set of allowed kt values. It is also worth mentioning that during real operation and in free-moving animals experiments, strain and curves are an additional mode conversion source [38, 39]. However, it has already been demonstrated that for high radii of curvature the emission properties of two-window MPEFs do not change substantially in terms of emitted power, outcoupling angle, and light intensity profile [22]. This lets us suggest that bending redistributes power mainly among the subset of modes outcoupled from the activated window, and only a negligible fraction can leak into other modes. More severe mode mixing caused by sharp curves or twists of the optical fiber leads to crosstalk of windows and, as a consequence, to a less effective device.
Besides the optical properties of guided light, it is important to mention that when light outcouples into the brain its propagation is noticeably different with respect to free space conditions, due to tissue absorption and scattering of the medium. The main effects of brain inhomogeneity and absorbance are an exponential decay in light intensity along the main direction of propagation and the spreading of the beam [22, 40, 41], and this latter should be carefully considered when the distance between windows is designed.
5. Conclusions
In summary, the modal-selective outcoupling properties of nanopatterned tapered gold-coated optical fibers were experimentally demonstrated with the support of analytical and ray tracing models. By selecting the light injection angle at the device input, it is possible to inject a subset of the guided modes into the multimode optical fiber. The presented results suggest that the gold-coated fiber taper acts as a modal demultiplexer to allow for light emission at specific sites. Indeed, by virtue of the influence of the tapered region on the wavevector transversal component of the guided light, these modal subsets can be individually outcoupled from the optical windows realized at a defined position along the taper. The conjunction between electromagnetic theory, ray tracing simulations and modal-demultiplexing properties characterization, lets us suggest that these results can represent a straightforward guideline for engineering new multipoint emitting devices for optogenetic control of closely spaced brain regions.
Acknowledgments
The authors acknowledge Alberto Bramati for helpful discussions. This work was partially supported by PON project “ITEM”. The authors would like to acknowledge the Rotary Foundation and the Rotary International District 2120 for the support given to M. P. through the Global Grant GG1417647.
References and links
- 1.Deisseroth K., “Optogenetics,” Nat. Methods 8(1), 26–29 (2011). 10.1038/nmeth.f.324 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Zhang F., Aravanis A. M., Adamantidis A., de Lecea L., Deisseroth K., “Circuit-breakers: optical technologies for probing neural signals and systems,” Nat. Rev. Neurosci. 8(8), 577–581 (2007). 10.1038/nrn2192 [DOI] [PubMed] [Google Scholar]
- 3.Fenno L., Yizhar O., Deisseroth K., “The Development and Application of Optogenetics,” Annu. Rev. Neurosci. 34(1), 389–412 (2011). 10.1146/annurev-neuro-061010-113817 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Vaziri A., Emiliani V., “Reshaping the optical dimension in optogenetics,” Curr. Opin. Neurobiol. 22(1), 128–137 (2012). 10.1016/j.conb.2011.11.011 [DOI] [PubMed] [Google Scholar]
- 5.Bear M. F., Conners B. W., Paradiso M. A., Neuroscience. Exploring the Brain, 3rd ed. (Lippincott Williams and Wilkins, Philadelphia, 2007). [Google Scholar]
- 6.McAlinden N., Gu E., Dawson M. D., Sakata S., Mathieson K., “Optogenetic activation of neocortical neurons in vivo with a sapphire-based micro-scale LED probe,” Front. Neural Circuits 9, 25 (2015). 10.3389/fncir.2015.00025 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Tye K. M., Deisseroth K., “Optogenetic investigation of neural circuits underlying brain disease in animal models,” Nat. Rev. Neurosci. 13(4), 251–266 (2012). 10.1038/nrn3171 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Pisanello M., Pisanello F., Sileo L., De Vittorio M., “Photonic technologies for optogenetics,” in Transparent Optical Networks (ICTON), 2014 16th International Conference on, 2014), 1–4. 10.1109/ICTON.2014.6876293 [DOI] [Google Scholar]
- 9.Warden M. R., Cardin J. A., Deisseroth K., “Optical Neural Interfaces,” Annu. Rev. Biomed. Eng. 16(1), 103–129 (2014). 10.1146/annurev-bioeng-071813-104733 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Grosenick L., Marshel J. H., Deisseroth K., “Closed-Loop and Activity-Guided Optogenetic Control,” Neuron 86(1), 106–139 (2015). 10.1016/j.neuron.2015.03.034 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Dufour S., De Koninck Y., “Optrodes for combined optogenetics and electrophysiology in live animals,” Neurophotonics 2(3), 031205 (2015). 10.1117/1.NPh.2.3.031205 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Kim T. I., McCall J. G., Jung Y. H., Huang X., Siuda E. R., Li Y., Song J., Song Y. M., Pao H. A., Kim R.-H., Lu C., Lee S. D., Song I.-S., Shin G., Al-Hasani R., Kim S., Tan M. P., Huang Y., Omenetto F. G., Rogers J. A., Bruchas M. R., “Injectable, Cellular-Scale Optoelectronics with Applications for Wireless Optogenetics,” Science 340(6129), 211–216 (2013). 10.1126/science.1232437 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Goßler C., Bierbrauer C., Moser R., Kunzer M., Holc K., Pletschen W., Köhler K., Wagner J., Schwaerzle M., Ruther P., Paul O., Neef J., Keppeler D., Hoch G., Moser T., Schwarz U. T., “GaN-based micro-LED arrays on flexible substrates for optical cochlear implants,” J. Phys. D Appl. Phys. 47(20), 205401 (2014). 10.1088/0022-3727/47/20/205401 [DOI] [Google Scholar]
- 14.Stark E., Koos T., Buzsáki G., “Diode probes for spatiotemporal optical control of multiple neurons in freely moving animals,” J. Neurophysiol. 108(1), 349–363 (2012). 10.1152/jn.00153.2012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Zorzos A. N., Scholvin J., Boyden E. S., Fonstad C. G., “Three-dimensional multiwaveguide probe array for light delivery to distributed brain circuits,” Opt. Lett. 37(23), 4841–4843 (2012). 10.1364/OL.37.004841 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kwon K. Y., Lee H. M., Ghovanloo M., Weber A., Li W., “Design, fabrication, and packaging of an integrated, wirelessly-powered optrode array for optogenetics application,” Front. Syst. Neurosci. 9, 69 (2015). 10.3389/fnsys.2015.00069 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Schwaerzle M., Elmlinger P., Paul O., Ruther P., “Miniaturized 3x3 optical fiber array for optogenetics with integrated 460 nm light sources and flexible electrical interconnection,” in Micro Electro Mechanical Systems (MEMS), 2015 28th IEEE International Conference on, 2015), 162–165. [Google Scholar]
- 18.Hayashi Y., Tagawa Y., Yawata S., Nakanishi S., Funabiki K., “Spatio-temporal control of neural activity in vivo using fluorescence microendoscopy,” Eur. J. Neurosci. 36(6), 2722–2732 (2012). 10.1111/j.1460-9568.2012.08191.x [DOI] [PubMed] [Google Scholar]
- 19.Szabo V., Ventalon C., De Sars V., Bradley J., Emiliani V., “Spatially Selective Holographic Photoactivation and Functional Fluorescence Imaging in Freely Behaving Mice with a Fiberscope,” Neuron 84(6), 1157–1169 (2014). 10.1016/j.neuron.2014.11.005 [DOI] [PubMed] [Google Scholar]
- 20.Bovetti S., Fellin T., “Optical dissection of brain circuits with patterned illumination through the phase modulation of light,” J. Neurosci. Methods 241, 66–77 (2015). 10.1016/j.jneumeth.2014.12.002 [DOI] [PubMed] [Google Scholar]
- 21.Allegra Mascaro A. L., Silvestri L., Sacconi L., Pavone F. S., “Towards a comprehensive understanding of brain machinery by correlative microscopy,” J. Biomed. Opt. 20(6), 061105 (2015). 10.1117/1.JBO.20.6.061105 [DOI] [PubMed] [Google Scholar]
- 22.Pisanello F., Sileo L., Oldenburg I. A., Pisanello M., Martiradonna L., Assad J. A., Sabatini B. L., De Vittorio M., “Multipoint-emitting optical fibers for spatially addressable in vivo optogenetics,” Neuron 82(6), 1245–1254 (2014). 10.1016/j.neuron.2014.04.041 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Sileo L., Pisanello M., De Vittorio M., Pisanello F., “Fabrication of multipoint light emitting optical fibers for optogenetics,” Proc. SPIE 9305, 93052O (2015). 10.1117/12.2075819 [DOI] [Google Scholar]
- 24.Collin R. E., Foundations for Microwave Engineering, 2nd ed. (McGraw Hill, New York, 1992). [Google Scholar]
- 25.Novotny L., Hecht B., Principles of Nano-Optics (Cambridge University Press, Cambridge, 2012). [Google Scholar]
- 26.Snyder A. W., Love J. D., Optical Waveguide Theory (Chapman and Hall, London, 1983). [Google Scholar]
- 27.Snyder A. W., “Asymptotic Expressions for Eigenfunctions and Eigenvalues of a Dielectric or Optical Waveguide,” IEEE Trans. Microw. Theory Tech. 17(12), 1130–1138 (1969). 10.1109/TMTT.1969.1127112 [DOI] [Google Scholar]
- 28.Filmetrics, “Filmetrics refractive index database,” (http://www.filmetrics.com/refractive-index-database, 2015).
- 29.Khijwania S. K., Carter F. D., Foley J. T., Singh J. P., “Effect of launching condition on modal power characteristics of multi-mode step-index optical fiber: a theoretical and experimental investigation,” Fiber Integrated Opt. 29(1), 62–75 (2009). 10.1080/01468030903464501 [DOI] [Google Scholar]
- 30.Amphawan A., “Holographic mode-selective launch for bandwidth enhancement in multimode fiber,” Opt. Express 19(10), 9056–9065 (2011). 10.1364/OE.19.009056 [DOI] [PubMed] [Google Scholar]
- 31.Gloge D., “Optical power flow in multimode fibers,” Bell Syst. Tech. J. 51(8), 1767–1783 (1972). 10.1002/j.1538-7305.1972.tb02682.x [DOI] [Google Scholar]
- 32.Gambling W. A., Payne D. N., Matsumura H., “Mode conversion coefficients in optical fibers,” Appl. Opt. 14(7), 1538–1542 (1975). 10.1364/AO.14.001538 [DOI] [PubMed] [Google Scholar]
- 33.Rousseau M., Jeunhomme L., “Numerical solution of the coupled-power equation in step-index optical fibers,” IEEE Trans. Microw. Theory Tech. 25(7), 577–585 (1977). 10.1109/TMTT.1977.1129162 [DOI] [Google Scholar]
- 34.Jiang G., Shi R. F., Garito A. F., “Mode coupling and equilibrium mode distribution conditions in plastic optical fibers,” IEEE Photonics Technol. Lett. 9(8), 1128–1130 (1997). 10.1109/68.605524 [DOI] [Google Scholar]
- 35.Savović S., Djordjevich A., “Influence of numerical aperture on mode coupling in step-index plastic optical fibers,” Appl. Opt. 43(29), 5542–5546 (2004). 10.1364/AO.43.005542 [DOI] [PubMed] [Google Scholar]
- 36.Marcatili E. A. J., Schmeltzer R. A., “Hollow Metallic and Dielectric Waveguides for Long Distance Optical Transmission and Lasers,” Bell Syst. Tech. J. 43(4), 1783–1809 (1964). 10.1002/j.1538-7305.1964.tb04108.x [DOI] [Google Scholar]
- 37.Novotny L., Hafner C., “Light propagation in a cylindrical waveguide with a complex, metallic, dielectric function,” Phys. Rev. E 50(5), 4094–4106 (1994). 10.1103/PhysRevE.50.4094 [DOI] [PubMed] [Google Scholar]
- 38.Miyagi M., Yip G., “Mode conversion and radiation losses in a step-index optical fibre due to bending,” Opt. Quantum Electron. 9(1), 51–60 (1977). 10.1007/BF00624272 [DOI] [Google Scholar]
- 39.Gambling W. A., Matsumura H., Ragdale C. M., “Curvature and microbending losses in single-mode optical fibres,” Opt. Quantum Electron. 11(1), 43–59 (1979). 10.1007/BF00624057 [DOI] [Google Scholar]
- 40.Aravanis A. M., Wang L.-P., Zhang F., Meltzer L. A., Mogri M. Z., Schneider M. B., Deisseroth K., “An optical neural interface: in vivo control of rodent motor cortex with integrated fiberoptic and optogenetic technology,” J. Neural Eng. 4(3), S143–S156 (2007). 10.1088/1741-2560/4/3/S02 [DOI] [PubMed] [Google Scholar]
- 41.Yizhar O., Fenno L. E., Davidson T. J., Mogri M., Deisseroth K., “Optogenetics in Neural Systems,” Neuron 71(1), 9–34 (2011). 10.1016/j.neuron.2011.06.004 [DOI] [PubMed] [Google Scholar]