Application of full field optical studies for pulsatile flow in a carotid artery phantom

Abstract

A preliminary comparative measurement between particle imaging velocimetry (PIV) and laser speckle contrast analysis (LASCA) to study pulsatile flow using ventricular assist device in a patient-specific carotid artery phantom is reported. These full-field optical techniques have both been used to study flow and extract complementary parameters. We use the high spatial resolution of PIV to generate a full velocity map of the flow field and the high temporal resolution of LASCA to extract the detailed frequency spectrum of the fluid pulses. Using this combination of techniques a complete study of complex pulsatile flow in an intricate flow network can be studied.

1. Introduction

The measurement and monitoring of heart rate becomes imperative in any medical emergency or clinical situation. Active monitoring helps in cases of irregular pulse rate (arrhythmia), or offline studies of recorded data can be used as a diagnostic tool (heart rate variability). The technique of electrocardiography (ECG) is most commonly used. This method is expensive and not sufficiently non-contact due to electrodes which have to be attached. Several patients suffering from arrhythmia or eventual heart failure will be treated by Cardiac Resynchronization Therapy (CRT). The procedure involves implanting a pacemaker and a monitoring device to detect any possible irregularities. The implantation has shown to have a stabilizing effect on the hemodynamics and improves the left ventricular (LV) diastolic filling parameters [1]. However, the effect of CRT on diastolic function and diastolic filling are not well understood. To visualize the diastolic vortices, magnetic resonance phase contrast velocity mapping has been used but this method is not feasible in patients with a pacemaker implant. Recently, there have been some reports of Echo-PIV which use PIV in combination with LV contrast opacification. This is an ultrasound technique which overcomes some of the Doppler ultrasound limitation such as angle dependence. This method is based on detecting the contrast agent micro bubbles and helps in understanding, for instance, the left ventricular dysfunction, by giving a detailed hemodynamic study [2, 3]. Another technique for in-vivo analysis is transcranial Doppler sonography [4]. This method applies a low frequency transducer probe to monitor blood flow dynamics. The technique is non-invasive and has number of advantages for use in clinical evaluation. However, it needs an aqueous gel on the patient. The other drawback is the limited spatial resolution and limited range in patients with inadequate transtemporal acoustic window where it needs to be anatomically feasible. One of the limitations of ultrasound based techniques is the non-distinguishabililty of signals induced by slowly moving structures, like the blood vessel walls and the signals induced by slowly moving blood near the walls [5].

The study of pulsatile flow and heart pumping dynamics is also of critical importance for patients awaiting a cardiac-valve implantation, where accurate analysis needs to be done before the implantation. Heart pulsation creates a periodic variation of waves whose time analysis provides information over the heart valve dynamics. These studies help in diagnosing any variation in blood vessel stiffness caused by cardiac disease. Changes in the stiffness of arteries and veins creates a different range of speed of dilatation waves which eventually results in an irregular range of flow speed. The creation of plaque, is one of the causes to create flow instability. The plaques changes periodically with pulsatile flow and this is seen most obviously during the deceleration phase of systole. Under these unsteady conditions generated by pulsation, there will be a higher chance of platelet activation [6, 7]. This behavior is a characteristic of ailments like atherosclerosis,[8], which is the most common cause of death. These plaque formations on the inside of the artery and thickening of the vessel wall will result in narrowing lumen and stenosis [9, 10]. Different diagnostic approaches such as magnetic resonance imaging, duplex ultrasound or X-ray angiography have been developed to investigate this disease. These techniques are widely used, but due to fact of being either too expensive or invasive, there is still a demand for replacing these methods with more comfortable and less risky procedures.

Research has shown that a through and detailed study of influence of stenosis on hemodynamic parameters can play a major importance in diagnosis and early detection of atherosclerosis [11]. This has been a major motivation in conducting a thorough study with complementary optical diagnostic methods. In this paper, we are mapping flow dynamics using two optical techniques particle image velocimetry (PIV) and dynamic speckle. The common feature of these two methods is the ability to capture the whole field flow velocity measurement. Furthermore, both approaches are not-intrusive and can be made with no sample contact. In order to increase the understanding of flow variations at each cardiac pulse, different moments in the cardiac pulse cycle were analyzed for various regions in the carotid artery phantom.

2. Materials and experimental setup

In this section, an overview of different parts of the setup will be given. The main components of the system are the illumination source, the flow phantoms, the optical acquisition and analyzing systems for both techniques. In order to set the experiment based on biomedical flow characteristics, certain conditions of flow need to be addressed first.

2.1. Flow properties

To create a pulsatile flow, we have been using a Medos Ventricular Assist Device (VAD) including the driving unit and ventricular pump, connected to a flow setup which is compatible for different working fluids. This system creates a realistic flow profile of the human heart beat pulse waveform. A complete schematic of the flow loop is shown in Fig. 1. The system has the option of enabling a pulsatile or steady flow. To study a wide range of flow regimes, a bypass valve and mechanical control valves were installed. The system also has an air ventilation so that it can be easily filled and maintained in an air bubble free state. The electromagnetic flow meters (MAG-VIEW, model MVM-005-Q) were mounted in the system and used for real time monitoring of flow rate. In the VAD settings, we used a systolic pressure (Psys) of 270 mmHG and the diastolic pressure (Pdias) of −30 mmHG with a systolic time interval of 35 (%) with a ventricular pump of 60 ccm(ml) volume. The frequency of the cardiac pulsation is set for 40 beats per minute corresponding to 0.67Hz. There are two important parameters in pulsatile flow studies, which are the Reynolds number (Re) and the Womersley number (α). The Reynolds number describes the ratio of inertial forces to viscous forces in a flowing fluid and is defined as:

$$\mathit{Re}=\frac{v_{s}L}{\nu }$$ (1)

where the v_s is the time averaged velocity, L is the characteristic length (in present case this is the diameter of the cylinder or diameter at the inlet of the carotid artery), and ν is the kinematic viscosity of the fluid. Reynolds number is directly proportional to velocity and inversely proportional to viscosity. The measured values in different part of human circulatory system shows that the blood flow in majority of vessels follow a laminar behavior [12]. In general, the laminar flow has a regime of Re < 2000 where the pulsatile flow results in a lower Reynolds number compared to the steady flow [13]. The mean Reynolds number of 512 was estimated for our glycerol solution at fluid temp of 25°C.

Fig. 1.

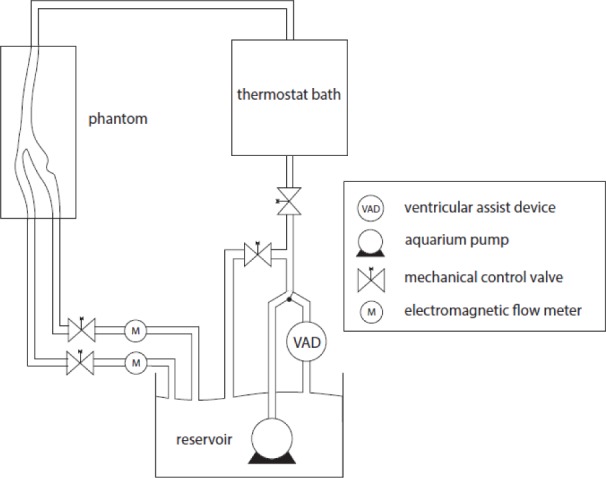
The schematic of the experimental flow loop.

The Womersley is a dimensionless number which relates the pulsation frequency to viscosity. It is often used in biofluid mechanics, and in general where there is a non-constant pressure gradient flow in the system, like in the case of heart pump flow. This value in healthy human beings can vary between 1 and 12.5 which is influenced by the physiological condition of the body [14]. The Womersley number is dependent on the pulsation frequency and physical properties of the vessel, and is defined as:

$$\alpha =R\sqrt{\frac{\omega }{\nu }}$$ (2)

where ω is the angular frequency given by the frequency of pulsation (f) as ω = 2πf and R is the pipe radius. In this measurement, the flow with a Womersley number of 4.5 has been studied. In these set of measurements, we have been trying to keep both the Reynolds and Womersley numbers in typical range that is found in the human carotid artery.

The outflow division between the Internal Carotid Artery (ICA) and the External Carotid Artery (ECA) has been defined as:

$$\gamma =\frac{Q_{ICA}}{Q_{ECA}}$$ (3)

The division of flow between the internal and external branches varies during the cardiac cycle. The flow has been regulated with the two additional valves, where the outflow division ratio of 50/50 between internal carotid artery and external carotid artery.

2.2. Fluid

In order to choose a fluid in our experiment, we need to consider its compatibility for both the PIV measurement, and to mimic some of the blood flow properties. The main requirements are that the solution should be transparent and have the same refractive index as the material used for phantom. The glycerol solution is commonly used to mimic blood flow, as it is easy to use, non-toxic and dissolves easily in water. The liquid we used is a mixture of water and glycerol so there is a refractive index match between the working liquid and the Polydimethylsiloxane (PDMS) phantom. To visualize the flow in an optically transparent platform, we need to use tracer particles. Choosing the right seeding particles is the most important parameters as the particles have to fit different requirements to be suitably detected using all the techniques while keeping the desired flow characteristics. In case of using water as fluid, the commonly used tracers particles are either hollow glass or polystyrene spheres with a diameter size of 2 to 20µm. The present measurements were done by adding tracer particles, hollow glass balls with an average diameter of 10 µm into the liquid. In case of PIV, these are the tracer particles. For speckle, the hollow glass particles are the main source of scattering the incoming laser light and creating the speckle patterns. If the flow is seeded sufficiently, a speckle pattern will be formed by the collective scattered light field from the seeding particles.

2.3. Phantoms

In general, the pulsatile flow can be characterized based on the two dimensionless numbers namely the Reynolds number and the Womersly number. However, the parameters going into the numbers change due to the change in geometry. Due to this constraint, we used two phantoms which were fabricated in house to do a complete analysis. In order to understand the flow properties, before doing the measurement directly on the main phantom, a set of measurements were done on a simple setup using a straight cylindrical phantom. Then the same parameters were used to study the flow in a carotid artery phantom.

2.3.1. Straight cylindrical phantom

To create a straight cylindrical tube, made of cured PDMS, a wax candle with outer diameter of 20 mm was used, as shown in the Fig. 2. We are using an aqueous glycerol solution with the same refractive index as our phantom housing (n = 1.413). This has been done for refractive index matching which can be clearly seen in the Fig. 2(b). This technique is commonly used in PIV and is also beneficial in the laser speckle technique to avoid any extra scattering due to sample structure.

Fig. 2.

Straight cylindrical flow phantom: a) in water and b) with index matched solution.

2.3.2. Carotid artery phantom

Another phantom which was used is the carotid artery phantom. The common carotid artery, which splits after bifurcation into the internal and external carotid artery, is the major artery connecting heart and head, whose role is to supply the brain with oxygenated blood. It is recognized in medical literature [15, 16] that the majority of the cardiovascular diseases occur in the coronary and carotid artery bifurcations. For example, one of the most common cause of stroke is a blockage (narrowing or stenosis) in the carotid arteries.

To create a carotid artery phantom, a 3D wax print of the artery of a patient was made. The geometry of the patient specific carotid artery was obtained using a Computed Tomography (CT) scanner images of a patient suffering from atherosclerosis, where all pathological conditions of blood vessels were automatically taken into account. This has been used as a mold for casting the PDMS liquid. The wax has been removed without applying any heat to avoid any diffused wall and results in a clear phantom. To have the phantom compatible for PIV measurements, we are using a aqueous glycerol solution with the same refractive index as our phantom housing (n = 1.413). The effect of refractive index matching can be clearly seen in the Fig. 3(b).

Fig. 3.

Flow phantom of patient based carotid artery: a) in water and b) with index matched solution.

2.4. Optical experimental setups

A general setup is shown in Fig. 4. This is the main setup which has been used in PIV experiment. The measurements were done with a double pulse Nd:YAG laser. The Nd:YAG laser output with a 1064 nm wavelength has been filtered for safety and only the laser light at the visible range of 532 nm is used for the experiment. To create a two-dimensional light sheet for illumination of the flow field, a cylindrical and spherical lens were applied to converge the laser beam into an actual sheet with a thickness of 1mm.

Fig. 4.

The experimental setup illuminated during PIV measurements.

For image acquisition and analysis, a standard PIV-package from La Vision including PIV-camera, frame-grabber and programmable-timing-unit (PTU) was used. The highly resolution and highly sensitive digital camera of LaVision is crucial for PIV applications. In order to have an accurate measurement of the velocity profile, a good synchronization between the event and recording of it is needed, so the pulsed laser is used in combination with a timing unit coupled to the camera. To prevent optical deformation of the laser sheet and images the laser and camera are both perpendicular to the phantom. For timing control, the capturing process and the analysis of the images the software package DaVis provided by LaVision was used.

For the laser speckle based measurements, the same arrangement was used except for the illumination source and camera. The continuous laser in this case is at 532 nm with 600 mW power and directly illuminates the sample. For our detection system, we used a variable frame rate high speed camera (Photron Fastcam SA3) with the pixel size of 17×17 µm and changeable aperture. Using the Fnumber of 32 and a magnification factor of 0.5 for the optical system we ensure a good average speckle size of 3–4 pixels.

3. Full field optical studies

3.1. Particle imaging velocimetry

At present, Particle Imaging Velocimetry (PIV) is a developed method and is considered as standard technique for non-intrusive measurements of velocity fields. It is an optical technique which is used for imaging the flow seeded with tracing particles. In comparison to Laser Doppler Velocimetry, PIV is considered to be less time consuming, being a whole field method and measuring instantaneous flow field. To monitor flow properties of the fluid, it is important that particles are chosen such that they do not influence the flow dynamics itself but rather follow it [17]. The technique is based on three possible strategies: a) two images can be captured after a short time, and by knowing the exact timing and applying a cross correlation on the successive images a vector field can be obtained, or b) using two bursts of light, only the possible displacement of tracers can be observed in single image and finally, c) is again based on one image being taken with short enough exposure time such that the movement of particle can be visualized. In this paper, we are using the first approach such that the cross correlation analysis of two consecutive images is made. That will result in a vector field where two velocity components can be measured using one camera. In this work, a time sequence of images was recorded with the camera by a time interval which is dependent on the flow conditions and can be set by the user accurately. The method used to estimate the average particle displacement and eventually velocity is based on statistical cross correlation in each corresponding regions between first and second frames [18]. The recorded images are divided into interrogation regions. The size of the regions is chosen such that there is almost a uniform motion and displacement of particles. Small fraction volume of particles is used as they should be homogeneously distributed and instead of influencing the flow, they should only follow the flow. In case of high particle density, it would be more difficult to follow individual tracers and might lead to wrong combination of the particles in two images, which lead to noise rather than displacement. The sample has been illuminated with a laser sheet with a thickness of around 1 mm for a pulse length of 7 ns. A set of images has been recorded as can be seen in Fig. 5 with the time interval of 750 ns between them. The pulse duration is short enough to avoid significant blurring due to motion in the images.

Fig. 5.

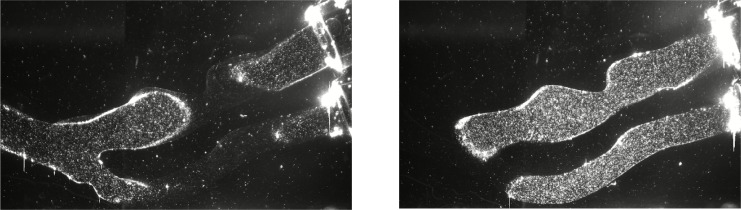
Two typical PIV images used for data analysis. The two characteristic cross-sections can be seen with tracer particles arise from two arms of the carotid artery phantom.

To achieve high contrast between the background and scattering particles, also to reduce the noise from background, certain measure are taken and data is processed for noise as explained below. In order to compute the flow vectors, the recorded images were further processed using the software package Davis 6.2. To improve the distinction between light reflected by the tracer particles and the background light, which results in wrong vectors, the average over all sets of two images was subtracted from each set of two images. After that a mask is applied to the images. The mask removes all the areas where the laser sheet does not cross the artery and this results in much cleaner images of the illuminated tracer particles. A series of these images has been further analyzed using the PIV algorithm. The main principle is based on a standard cross correlation between two images [19]. This program has the option of making multiple iterations with different interrogation sizes to result in an accurate measurement. The different interrogation areas from each image will be cross correlated and gives a final signal where its peaks indicate the displacement of each particle. For accurate PIV data analysis, the data should be captured such that on average particle displacements of about eight pixels that do not travel further than the interrogation window.

With a sufficient number of particle pairs and using a smaller pixel size for the chosen kernel, a more accurate displacement and ultimately a more accurate flow field can be extracted. It is important that the product of the velocity V of every particle and the time Δt between two subsequent images is smaller than the length of the interrogation area, i.e.:

$$\frac{\frac{s^{\prime }}{s}V\mathrm{\Delta }t}{d_{IA}}<0.25$$ (4)

where $\frac{s^{\prime }}{s}$ is the image magnification and d_IA is the side length of the interrogation area. The interrogation window was chosen to be eight by eight pixels with a 50% overlap resulting in a four by four pixel resolution. The camera scales used were 1 pixel per 7.559 · 10⁻⁵m resulting in a final resolution of 0.3mm by 0.3mm. To find the direction and amplitude of the velocity, the displacement of all the tracer particles is determined.

3.2. Laser speckle contrast analysis

Laser speckle contrast imaging is based on the analysis of laser speckle images. These images are created as a result of illuminating a diffusing sample with a coherent light source. The light scattered as many different wavelets with variable optical path lengths interferes and creates a grainy pattern called speckle. In the case of a static sample, this pattern is stationary but as soon as the scatterers in the sample start to move, these patterns have dynamic properties. The fluctuations in the speckle images are caused by displacement of the the diffusing sample or the particles causing the scattering. By studying these images dynamic scattering properties of the sample under investigation can be obtained. For the case of a strong diffuser a different speckle pattern is observed compared to a weak diffuser. Another similar technique is diffusion correlation spectroscopy [20]. This is an extension of single-scattering dynamic light scattering, which non-invasively measures local blood flow. Laser speckle imaging is based on the same physical principle, where the fluctuation of the propagated light in tissue due to dynamics of moving scatterers is monitored. In diffusion correlation spectroscopy, the inverse of correlation time is measured and related to the sample blood flow. A model has been proposed [21] to relate the laser speckle contrast to the speckle correlation time to provide a comparable measure.

We have done the laser speckle measurements with the same experimental setup as the PIV, that is in an optically transparent sample with the same density of moving scattering particles. These measurements have been done for both phantoms. A raw speckle image along the carotid artery is shown in Fig. 6.

Fig. 6.

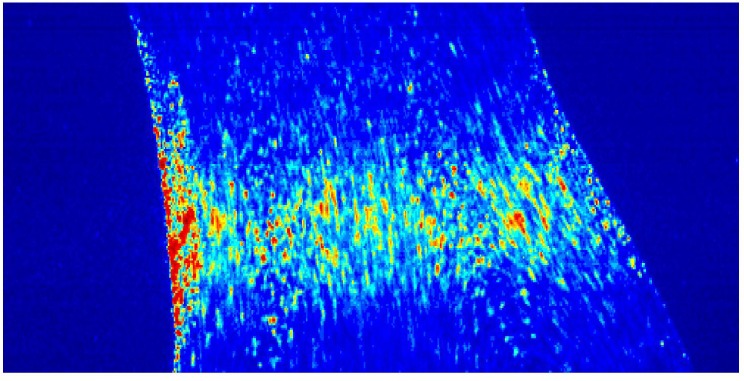
A typical laser speckle raw image along the carotid artery phantom.

One of the methodologies for analyzing the time fluctuation dynamics of speckle images, is based on the laser speckle contrast first introduced by Briers and Webster [22]. In this paper, the time integrated speckle images have been recorded using a single photograph with a specific exposure time. The speckles appear blurry when the integration time is longer than the speckle decorrelation time. This blurry effect is quantified by the contrast term (K) which is defined as the ratio of the standard deviation (σ) over the average (<I>), of the intensity fluctuations,

$$K=\frac{\sigma }{<I>}.$$ (5)

The calculated contrast has a lower value in case of a sample which has moving scatterers due to the fact that the standard deviation of the intensity is smaller while the average intensity remains constant. Different schemes of computing the speckle images from the raw data exists, such as temporal, spatial or a combination of these two. A more detailed description can be found in reference [23].

4. Results and discussion

4.1. PIV measurements

In the case of PIV measurements, the cross correlation for each interrogation window from the captured images, was repeated to yield a velocity vector map over the whole area. In this way, all the measured cross correlations of the individual image pairs for the chosen interrogation window were summed. Using this method, 80 instantaneous velocity vector fields were extracted and ensemble averaged to obtain the final velocity vector map at each time point. The result, Fig. 7, shows a better signal to noise ratio than if the velocity vector map was extracted using the instantaneous cross-correlations.

Fig. 7.

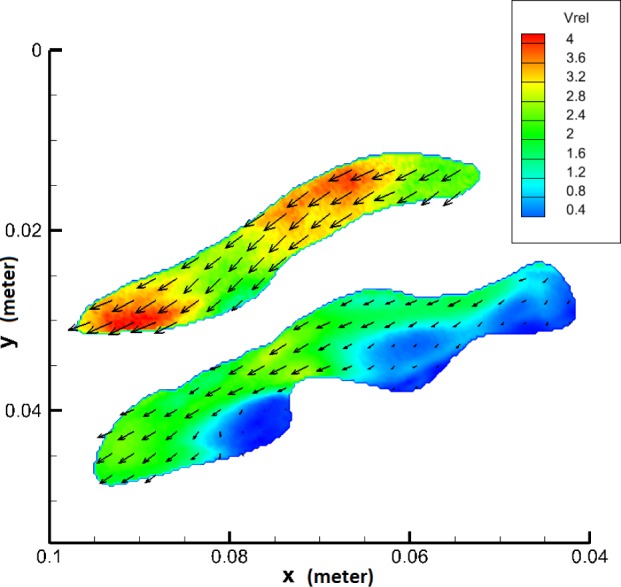
Final velocity map of the carotid artery phantom. Color indicates the velocity vectors amplitude. Vrel is the dimensionless velocity defined as ratio of velocity and mean inflow velocity.

In the case of the cylindrical phantom, due to its symmetrical geometry, measurements were done only in the middle plane. However, the geometry of the carotid artery phantom is more complex so the measurements were done in two orthogonal planes. To view the flow field from two orthogonal perspectives, two sets of configurations were measured. To cover the whole sample volume, initially the velocities in the XY plane were measured (V_x and V_y) and then by rotating the phantom over 90°, the velocities in XZ plane (V_x and V_z) were measured. For each data set, the velocity has been plotted as $V=\sqrt{V_x^2+V_y^2}$ and $V=\sqrt{V_x^2+V_z^2}$ respectively. The velocity profile through the entire phantom, is shown using 20 contour slices in Fig. 8. The left set of slices was made by using the XZ-planes while the right set of slices was made using the XY-planes.

Fig. 8.

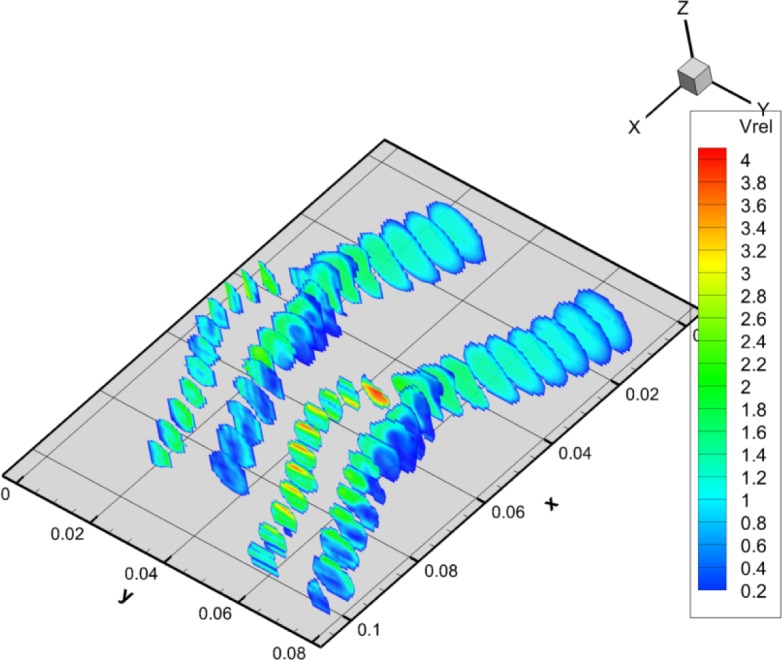
Contour profile through the carotid artery phantom. The length scale is in meter for both axes. The left set of slices was made by using the XZ-planes while the right set of slices was made using the XY-planes. Again Vrel is the dimensionless velocity.

4.2. Laser Speckle contrast analysis

For the case of the measurements done with the laser speckle contrast analysis, we have captured a time sequence of images keeping the flow parameters the same as for the PIV measurements. For each measurement 2700 images were recorded with an exposure time of 20 ms. The speckle contrast for each image from the time sequence was then calculated using a spatial window size of 7×7 camera pixels. The resulting contrast time series was then Fourier transformed to obtain the frequency spectrum of the speckle contrast which arises due to fluctuations caused by different processes, for the entire duration of each measurement. This gives an insight into all the frequencies that contribute to the flow pulse along with the modulation which is imposed on the flow due to the complexity of the structure into which the fluid is flowing.

4.3. Spectral analysis of pulse from PIV and LASCA

Spectral analysis was done for both PIV and LASCA data. In Fig. 9 we show for PIV, the estimation of velocities from the pulsatile flow in the cylindrical phantom. As explained before in the experimental setup, the flow has been generated by pulses from VAD. In order to plot the pulse, the laser and camera were triggered at the highest flow rate during the pulse. The flow rate profile was measured using the electromagnetic flow meters, and the the highest flow rate during the pulse was used as the triggering signal. In this way, 10 points in the cardiac cycle for the cylindrical phantom was measured. The average flow rate is measured as 2.85 liter/min with the max flow rate of 4 liter/min.

Fig. 9.

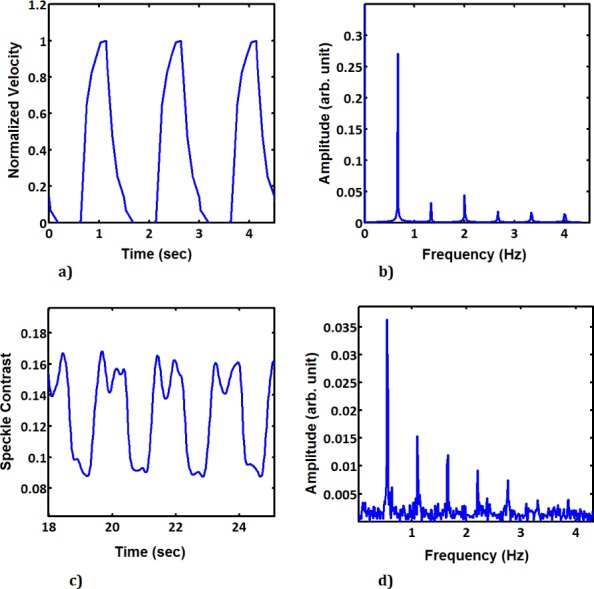
Time sequence of (a) PIV and (c) LASCA generated from images recorded during pulsatile flow in the cylindrical phantom. Frequency spectrum extracted from the time sequence for (b) PIV and (d) LASCA measurements.

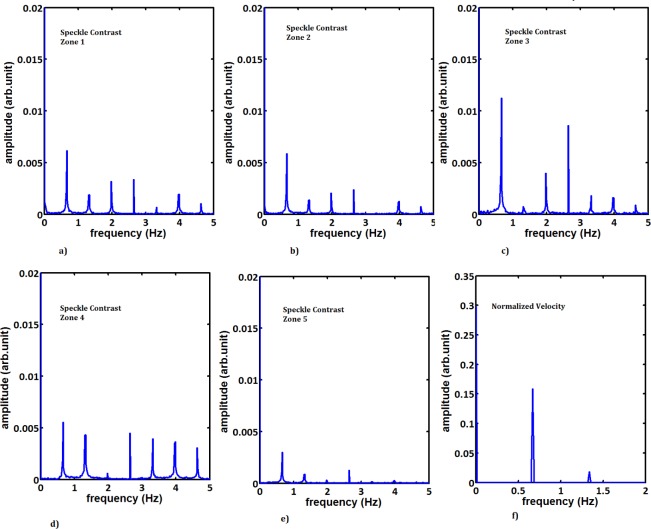
Time sequence signals for both PIV and LASCA was generated from images recorded during pulsatile flow in the cylindrical phantom. The frequency spectrum was extracted from the time sequence for both PIV and LASCA measurements by Fourier transforming the time sequences. After having established the feasibility of this technique in the simplified phantom, we conducted a similar study on the more complex carotid artery phantom. The same procedure has been done for the carotid artery phantom. Due to its complex geometry, the phantom of the carotid artery has been analyzed at five different locations of: bifurcation in common carotid artery (zone 1 and zone 2), internal carotid artery (zone 3), stenosis (zone 4) and external carotid artery (zone 5). The zones are shown in Fig. 10 with the squares. The time series for the measurements with PIV for zone 2 can be seen in Fig. 10(b) and for the LASCA measurements can be seen in Fig. 10(c), where we can see the difference between the two. For the LASCA measurements, regions of interest at these five locations were analyzed using the time sequence of speckle images as explained before. In all five zones we can see the complexity of the VAD pulses including the regions of back flow.

Fig. 10.

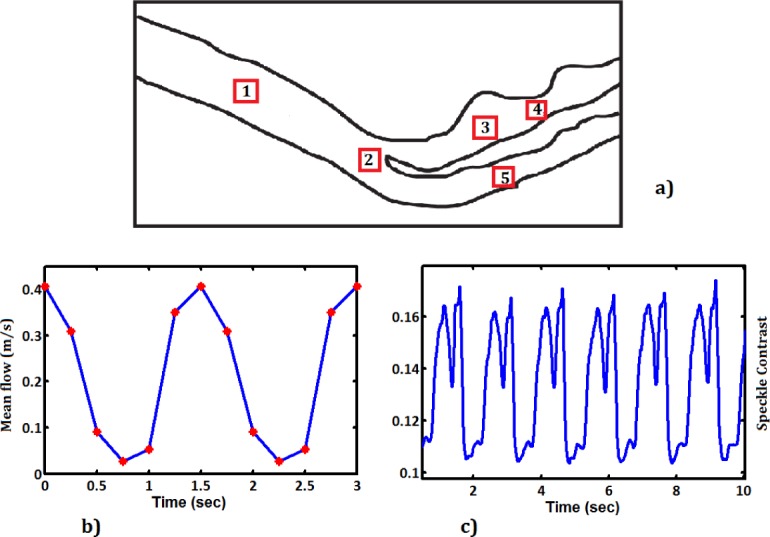
a) The selected zones for analysis from Carotid Aretry Phantom. b) Time sequence for PIV, c) Time sequence for LASCA, in zone 2.

The time sequence was then Fourier analyzed to get the frequency spectrum from both measurement techniques. We observe that in case of PIV the frequency spectrum of the time sequence measured from all five zones is the almost the same. This spectrum is shown in Fig. 11(f). The LASCA measurements contain more detail in the frequency spectrum and each zone gives a different spectrum. These spectra are shown in Fig. 11(a–e). The main difference is in the density of data being used to generate the frequency spectra. In case of PIV, the data is sparse along the pulse whereas in case of LASCA, the large number of captured images provides more detail in the time properties of the flow pulses. However, we observe that both techniques measure the main frequency of the pulsation of the flow, 0.67Hz, quite clearly.

Fig. 11.

a) – e) Spectral analysis of LASCA and f) PIV in five different zones along the carotid artery phantom.

5. Conclusion

In this paper, we report an initial comparative study of pulsatile flow in a carotid artery phantom using the full field techniques of PIV and LASCA. The measurements using two techniques were used to extract complementary properties of the pulses from the VAD device. We observe that PIV provides instantaneous velocity measurements with high accuracy. Using the technique of PIV in a different geometry, a complete 3D velocity map can be constructed. The LASCA measurements have a high temporal resolution and can study the frequency spectrum of the flow pulse much more accurately, without any direct imaging.

In spite of the significant progress made in studying flow using both methods, each technique has its own limitations. PIV is expensive and time consuming even though stereoscopic PIV is becoming increasingly popular. This technique provides a complete velocity map of flow throughout complex flow geometries which is very useful in studying the human circulatory network and diseases which arise there. The imaging needed for this technique, makes it quite difficult to capture with high resolution the temporal properties of the flow. That is not very efficient in case of studying dynamics in pulsatile flow. In comparison, LASCA requires relatively simple equipment, since no direct imaging is done. This is also a disadvantage for LASCA since no imaging information can be extracted from the LASCA data. The high temporal resolution of the data however makes LASCA quite efficient in studying the time evolution of the fluid pulses in various locations of a flow network. So the frequency spectrum measured using LASCA is quite rich and gives complete details of the pulse.

This makes the combination of techniques particularly attractive, since using both the disadvantage of the individual techniques can be overcome and a complete analysis of the dynamics of pulsatile flow can be done. PIV provides detailed quantitative information over flow structure and velocity profiles and LASCA gives an analysis of the flow pulse evolution. Combining the LASCA and PIV efficiently can provide a better use of current technologies to make a more efficient tool to study complex flow geometries having pulsatile flow like the human circulatory network. LASCA can provide a quick study of signal fluctuations over time with which transient phenomena can be recorded and observed. PIV can then be used for a detailed study of the cause of the phenomena. This is also very useful for studying geometries with flow instability.