Elucidating the temporal dynamics of optical birefringence changes in crustacean nerves

Abstract

Intrinsic optical properties, such as optical birefringence, may serve as a tool for minimally invasive neuroimaging methods with high spatiotemporal resolution to aid in the study of neuronal activation patterns. To facilitate imaging neuronal activity by sensing dynamic birefringence, temporal characteristics behind the signal must be better understood. We have developed a novel nerve chamber to investigate changes in birefringence at the stimulation site, and at distances ~4-28 mm from that site. Using crustacean nerves with either heterogeneous or homogeneous size distributions of axon diameters, we found that the gradual (slow) recovery of the crossed-polarized signal is not explained by the arrival times of action potentials in smaller axons. Through studying the effects of stimulating current and voltage pulses, we hypothesize that the recovery may be caused by a capacitive-like coupling between firing axons and adjacent tissue structures, and we report data consistent with this hypothesis. This study will aid in the utilization of action-potential-related changes in birefringence to study fast changes in neuronal network activity.

1. Introduction

The development of minimally invasive, high-resolution modalities for imaging neuronal activity, both for research and pre-clinical applications, is an ongoing endeavor that will allow for a greater understanding of neuronal network processes involved in complex functions, as well as neuropathies such as epilepsy, stroke and cortical spreading depressions associated with migraines [1–4]. Current methods for monitoring neuronal activity, while informative, have substantial limitations. Microelectrodes provide high temporal resolution, but at the expense of irreversible tissue damage and insufficient spatial resolution due to volume conduction effects and the limited number of electrodes [5]. Methods such as functional magnetic resonance imaging (fMRI), and autofluorescence of flavin adenine dinucleotide (FAD) and nicotinamide adenine dinucleotide phosphate (NADP-H), are limited in that they image metabolic activity indirectly associated with neural activity through the measurement of mitochondrial or hemodynamic responses, which present with a delay after neural impulses propagate [6,7]. Voltage sensitive dyes (VSDs) and calcium indicators can provide a fairly high spatial resolution, but are limited by the dyes’ temporal responsivities, and are cytotoxic and thus not suitable for clinical imaging [8,9].

Fast intrinsic optical signals (IOS), including changes in intensity, scattering and optical birefringence, have previously been explored as markers to measure neuronal activity directly in single neurons, nerves, and in vivo brain tissue, and can potentially be developed with high spatiotemporal resolution to study neural network activity with minimal invasiveness [10–13]. Scattering signals have been studied extensively, both in vivo and ex vivo; they have been attributed predominantly to cellular swelling and are small (signal-to-background = ~10⁻⁵) and challenging to record [10,12]. These signals are difficult to measure consistently with an acceptable signal-to-noise ratio (SNR) and are limited in spatial resolution in highly scattering tissue such as the cortex of the brain [11,14]

Changes in birefringence (or dynamic birefringence) provide an arguably cleaner method of measuring IOS as compared to scattering methods [12,15]. Nerves inherently exhibit a static (rest condition) birefringence that is associated with the structural anisotropies of axonal microtubules, membrane phospholipids and proteins, as well as surrounding tissues, which include Schwann cells and axon sheaths [15,16] The dynamic birefringence, or “crossed-polarized signal” (XPS), in neurons arises from activity in axons and occurs with a rapid momentary change, typically a decrease, in the birefringence when action potentials (APs) propagate along them [10].

The XPS (signal-to-background = ~10⁻⁴) is typically one order of magnitude larger than the scattering signal and has been detected successfully in single trials in large crustacean nerves [12]. While transmission geometry (between crossed linear polarizers) is typically used to detect the XPS, it has also been detected using a reflection geometry, demonstrating the possibility of using birefringence to track neuronal activity in cortical tissue in vivo [13]. Limited two-dimensional spatial resolution of AP activity has been obtained using a charge-coupled device (CCD) to image both the length and width of a section of the stimulated nerve, although only the peak of the signal could be reliably detected [17].

The physiological mechanisms underlying the cause of these changes in birefringence in neuronal tissue remain under discussion. One suggested mechanism is cellular swelling, which was found to occur rapidly with the onset of the XPS and to last 10-20 ms in both squid giant axons [18] and nerve bundles [19]. Cellular swelling was found to be highly correlated with the scattering signal, but not to the birefringence signal, which seemed to precede the scattering signal [12]. Furthermore, when the timing of the signals from VSDs and intrinsic birefringence were measured simultaneously, it was found that the birefringence signal was directly correlated with, and possibly even preceded, the VSD signal [20].

Other proposed mechanisms responsible for the XPS relate the dynamic electric field of propagating APs to membrane molecular and electron-cloud changes. In one proposition, the reorientation of dipoles (including membrane proteins and phospholipids) away from the radial axis may result in a decrease in birefringence of polarized light [21–23].

For single axons, the XPS was found to predominantly be isolated to areas near or through the membrane; and in nerve fibers, an appreciable contribution to static birefringence from Schwann cells and connective tissue was noted [15]. This complexity in optical signals caused by contributions from adjacent tissue structures presents a significant barrier to the full understanding of the underlying physiological origins of the XPS in higher-order neuronal structures. Additional information would lead to a more complete understanding of the causes of the XPS in nerves and brain tissues.

To this end, we carried out a direct comparison of the XPS in two different crustacean species with different axon size distributions (hence, different distributions of action-potential propagation velocities), and we designed a new nerve chamber (see Fig. 1(B)) with a longer viewing window than that in previous reports, which allows for an investigation of nerve XPS at the sites of electrical stimulation and recording (~24 mm from stimulation), as well as a range of distances of ~4-20 mm from the stimulus site. This chamber better facilitates direct observations of the XPS resulting from stimulation voltages and currents, as well as temporal comparisons as a function of distance, and between the electrical and optical recordings. Our results are consistent with others in demonstrating that the birefringence changes in nerves are closely associated with membrane potential, and also provide significant novel information that can contribute toward a fuller understanding of the basis of the XPS.

Fig. 1.

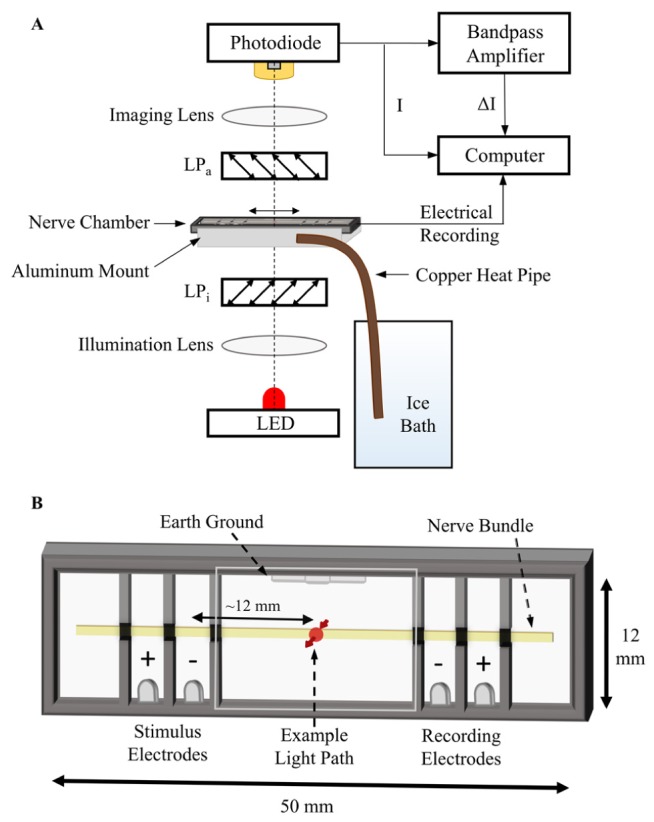
A) Diagram of the optical components and readout. B) An expanded depiction of the custom-built nerve chamber with quartz top and bottom in all wells. The chamber was divided into wells that are electrically isolated, except through the nerve. Blackened petroleum jelly was used to electrically insulate the areas around the nerve between each well. An example of the illumination area on the nerve in a typical experiment is shown, at ~12 mm from the positive stimulus well.

2. General experimental procedure and optical setup

A diagram of the optical system used is shown in Fig. 1(A). All optical elements were housed in 30 mm cage mounts (Thorlabs, Inc.). Illumination was provided by a 625-nm high-power LED (Thorlabs, Inc. M625L3) for minimizing noise due to source variability [24]. The LED was driven by an LED driver (Thorlabs, Inc. T-Cube) with variable output current control. Light from the LED was focused using a spherical plano-convex lens first onto the central plane of the nerve, and then reimaged using a second lens onto a 2.4 mm x 2.4 mm photodiode with pre-amplifier (Hamamatsu S8745-01). The incident light was polarized by a “wire-grid” linear polarizer (LP_i) (Moxtek PPL04C), and the light transmitted through the nerve was analyzed by another linear polarizer (LP_a) oriented 90° to LP_i. The pair of polarizers were placed with their optic axes at ± 45° relative to the length of the nerve, providing the maximum birefringence signal [15]. Before placing a specimen in the chamber, the measured extinction ratio (transmission ratio of perpendicular to parallel transmission axes) of the crossed polarizers was verified to be ≥1000, to ensure minimal effects of the crossed-polarizer efficiency on the comparison of data sets.

The nerve chamber (Fig. 1(B)) was fabricated from a thermally-conducting but electrically-insulating polymer (Cool Polymers, Inc.) and was cooled using a copper heat pipe of 4 mm diameter (water vapor medium: Enertron HP-HD04DI30000BA), with its distal end in an ice bath, thus maintaining the Ringer’s solution (fluid medium specific to the lobster nerve) at ~1-4° C to maintain the normal physiological temperature of the nerve. Petroleum jelly (mixed with painter’s charcoal to reduce light scattering) was used to surround the nerve in the openings between the wells to electrically isolate the wells. Two pairs of silver electrodes served to stimulate and record the AP propagation through the electrically conducting Ringer’s solution, and were located as indicated in Fig. 1(B). The central chamber electrode was grounded to reduce the effects of charge accumulation in the chamber. The top and bottom of the chamber were sealed with quartz slides, to contain the Ringer’s medium, such that optical measurement windows were available in all fluid sections (wells) of the chamber, as shown in Fig. 1(B). The top window reduced the effects of system vibrations on the fluid-air interface that can introduce optical noise. The chamber was positioned such that the illuminated area laid, typically, in the middle of the central well, ~12 mm from the positive stimulus well, but with that distance being adjusted for specific experiments.

The photodiode (PD) with preamplifier was operated using a custom, isolated power supply with a set of 9V batteries, and the output signal from the PD preamplifier was split into two lines, as shown in Fig. 1(A). The static birefringence, I_s, was measured as light transmitted through the crossed polarizers with no stimulation of APs, and was evaluated directly from one line of the PD’s unfiltered output, prior to administering a stimulus pulse. The dynamic birefringence signal, ΔI, was measured by feeding the second PD output line to a low-noise amplifier (A-M Systems, 3000) with a bandpass filter set for cutoffs of 0.l Hz (high-pass) and 1 kHz (low-pass) and amplified by a factor of 100. The high-pass portion of this filter removes the DC component, leaving only the AC component, which is the dynamic birefringence in this case. The electrical signal was measured from the recording electrodes, shown in Fig. 1(B), amplified by a factor of 1000 and filtered between 1 Hz and 10 kHz using another identical amplifier.

For a typical experiment, a walking leg nerve (WLN) from one of the four rostral-most walking legs of a lobster, Homarus americanus, was removed using the Furusawa pull-out method [25] and placed into the nerve chamber, which is shown in detail in Fig. 1(B). The nerve was immersed in Homarus Ringer’s solution, consisting of 523 mM NaCL, 52.7 mM MgCl₂, 13.3 mM KCl, 20.0 mM CaCl₂, 5.56 mM Glucose, and 5.0 mM HEPES [26].The lobster WLN has ~1000 axons whose diameters vary from ~0.1 to 100 μm in three groupings of small (0.1-5 μm), medium (20-30 μm) and giant (50-100 μm) [27,28]. The nerve was typically stimulated using a 1-ms, 1-mA (single-polarity) square current pulse from a linear stimulus isolator (WPI, Inc. A395R-C), initiated by a pulse generator (Berkeley Nucleonics, BNC 555) that was gated by a computer trigger. The stimulation parameters were chosen because of prior published results and by empirical trial-and-error to find the optimum range. The interference of electrical capacitance between the stimulation electrodes was tested by applying a stimulus with no nerve in the chamber, and the effects were found to be much lower than when a nerve is placed in the chamber.

The optical birefringence and electrical signals were collected using a 16-bit, 1 MS/s analog-to-digital converter (National Instruments, PXI-6120). System control and data analysis were performed using Matlab®. The XPS, expressed as the relative dynamic birefringence ΔI/I_s, was calculated by dividing the dynamic birefringence signal for each stimulus period by a 50-ms pre-stimulus mean of the static birefringence signal, after adjusting for the gain of 100 from the amplifier. Unless otherwise specified, ΔI/I_s was calculated by first averaging the traces generated by 100 consecutive stimuli, and then applying a computational bandpass filter between 0.1 Hz and 1000 Hz to the averaged traces, which will not remove relevant signal information, since an AP spike lasts around 1-2 ms.

3. Specific experimental procedures and results

3.1 The XPS as a function of distance in the lobster walking leg nerve

The novel nerve chamber facilitated the study of the birefringence signal in the lobster walking leg nerve (WLN) at the negative and positive stimulation wells (see Fig. 1(B)) and at various distances from the stimulus site. The lobster WLN is composed of ~1000 axons of variable diameter, which give rise to a compound crossed-polarized signal (XPS) that changes in shape as a function of distance from the stimulus. Each nerve has a unique distribution of axons, and while the corresponding XPS as a function of distance varies, the general temporal pattern is consistent across nerves.

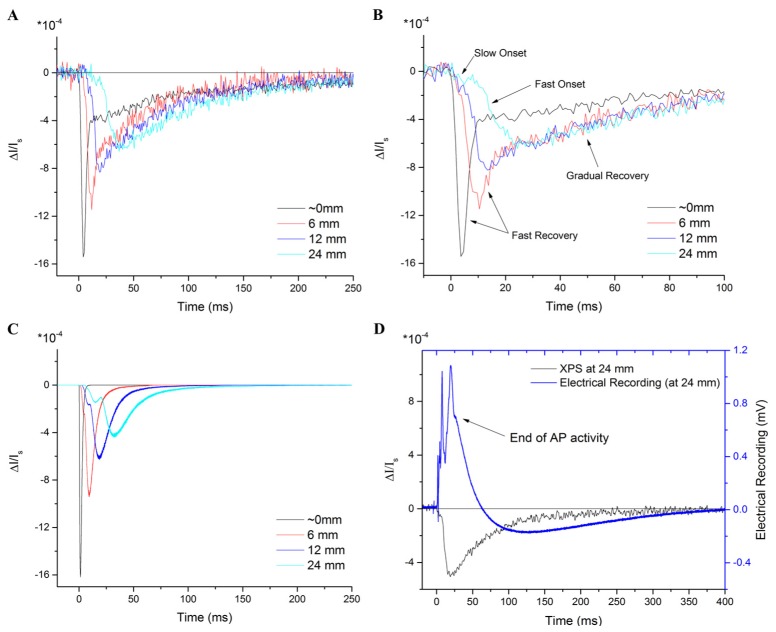
Figures 2(A) and 2(B) show the XPS data as a function of distance from the point of stimulus for a WLN (plotted for distances of 6 mm, 12 mm and 24 mm). Figure 2(B) presents the same data as Fig. 2(A), but adjusted in time to account for delays in the onset and to facilitate an analysis of the relative temporal shape of the signal. As can be seen, the peak of the XPS is incrementally delayed as a function of distance from the stimulus point, and its magnitude decreases while the peak width increases. We found that the delays in the peaks are consistent with Carter et al. [12]. Here, we extend the measurements to a 24-mm range and demonstrate a much clearer picture of the spreading XPS peak as a function of distance. By carefully translating the nerve chamber without changing the optics, we were also able to facilitate an accurate comparison of the XPS amplitude as a function of distance, showing a decrease and broadening of the peak, as well as the recovery of the signal to baseline at each distance. The peak of the XPS at the stimulus wells is larger than the typical signals presented here and by others when measuring signal due to action potentials at a distance from the electrodes, and is due to the larger effect of a direct perturbation by the applied electric field on the biophysical structures responsible for the birefringence signal.

Fig. 2.

A) Crossed-polarizer signal (XPS) for the lobster walking leg nerve (WLN) from a 1-ms, 1-mA stimulus pulse, measured at the negative stimulus electrode (origin of APs) as well as at 6 mm, 12 mm and 24 mm from the site of stimulation. The XPS peak decreases in magnitude and widens in time as a function of distance. Four phases are noted: a slow onset, a fast onset, a fast recovery of the peak, and a gradual recovery to baseline. The gradual recovery takes ~300-400 ms to return fully to baseline (not shown). B) The same data is temporally shifted to match the start of the onset of the XPSs to compare the onset and recovery times. The gradual recovery is similar for any distance from the stimulus, but is different at the stimulus site. C) Computational model of the compound XPS for the WLN as a function of distance. Both onset phases and the fast recovery phase can be reproduced, but the gradual recovery cannot. D) The electrical recording matches the peak width and recovery time of the XPS measured at the electrical recording site (~24 mm from the site of stimulation). AP activity is detected until the start of the gradual recovery of the XPS.

We found that the XPS of the WLN presents with four distinct phases, as identified in Fig. 2(B); 1) a slower initial onset, 2) a faster second-stage of the onset, 3) a fast initial recovery of the peak, followed by 4) a gradual recovery to baseline. The four phases are not all evident at the stimulation site, most likely due to direct interference from the stimulus pulse. The slow and fast onset phases are present in the traces at all distances from the stimulus site. After a distance of ~12 mm, the fast recovery in the trace begins to merge with the gradual recovery. The gradual recovery appears to be approximately the same at any distance from the stimulus site; however, at the stimulus site, the gradual recovery begins at a smaller magnitude.

To study whether the distribution of action potential (AP) velocities for the size-range of axons is sufficient to explain all phases of the XPS, a model that depicts the spreading AP birefringence signal as a function of distance from the stimulus point in the lobster WLN was generated in Matlab®. This simulated compound XPS was calculated as the sum of the individual axons comprising it. The shape of each axon’s XPS was designed to match the shape of the optical response measured by Cohen et al. [15], by using a 5th order chi-squared distribution with a variable time window (Τ_w) for the XPS, and assigning the amplitude of the peak to be on the order of 10⁻⁶. The relative velocities of axon APs was calculated as the ratio of the square root of the axon diameters; which holds true for unmyelinated axons (ignoring, for simplicity, membrane resistance, which varies randomly between adjacent axons) [29,30]. The empirically-determined maximum velocity of ~5 mm/ms (from the initial rise of the electrical recording) was assigned to the largest axons (~100 μm). The relative contributions of the XPS (rXPS) as a function of axonal diameter was treated as an adjustable parameter, since it has been reported that smaller neuronal processes may have a higher relative XPS [12]. The simulated compound birefringence signal is a sum of the individual contributing axon XPSs, each of which can be represented by Eq. (1).

$$XP{S}_{axon}=rXPS\cdot T_w\cdot \left(5\left[\frac{mm}{ms}\right]\sqrt{\frac{d\left[\mu m\right]}{100\mu m}}\right)$$ (1)

This model assumes an axon size distribution in three groups as described, in particular, by De Lorenzo et al. [28]. For simplicity, axon diameters across the nerve were assigned using three normal probability distribution functions Φ, defined around a mean μ and standard deviation σ as per Eq. (2),

$$\Psi =k\Phi \left(d,\mu ,\sigma \right)\left\{\begin{array}{cccc}k=0.5\mu m,& \mu =1.2\mu m,& \sigma =5\mu m,& 0.1\mu m<d<5\mu m\\ k=0.25\mu m,& \mu =26.7\mu m,& \sigma =8\mu m,& 20\mu m<d<30\mu m\\ k=0.25\mu m,& \mu =67\mu m,& \sigma =10\mu m,& 50\mu m<d<100\mu m\end{array}\right\}$$ (2)

where Ψ is a probability density function for the axon distribution, k is a scaling factor based on the percentage of total axons falling into that size range, and d is the axon diameter. Ψ is evaluated for the total number of axons in the nerve (typically ~1000). σ is not described previously, and therefore was approximated to smooth the output compound signal. Equation (2) is an idealization of three size groups and is used to provide the distribution of values for d and rXPS and for the loop that calculates XPS_Axon. All calculated XPS_Axon waveforms are summed to construct the simulated compound XPS waveform.

As shown in Fig. 2(C), the model can reliably reproduce the slow and fast phases of the onset, as well as the initial fast recovery, present in the XPS traces. We found that the smaller overall number and larger range of diameters of the giant and medium axons was sufficient to reproduce the distinct onset phases of the XPS at approximately the correct times. No adjustment of the relative XPS as a function of axon diameter was necessary to reproduce the data for those phases. The gradual recovery phase, however, could not be reproduced, regardless of the size of the temporal window for the constituent axons. If the physiological parameters such as AP velocity, axon diameter distribution and number of axons are artificially adjusted outside the normal ranges, then the gradual recovery can be reproduced, but the peak then becomes too wide and the onset phases are merged (not shown). In short, the gradual recovery phase cannot be explained on the basis of a range of AP propagation speeds.

Finally, we compared the electrical recording of the nerve to the XPS measured at the same location (~24 mm from the stimulus site) and found that they correspond in shape and recovery time, as shown in Fig. 2(D). The gradual recovery of the XPS continues, without a change in sign, during the period when the electrical signal has reversed polarity.

3.2 Comparison of heterogeneous lobster walking leg nerve and the homogeneous horseshoe crab lateral optic nerve

A comparison of the XPS of a complex nerve, such as the lobster WLN, with a relatively simple nerve (with narrow axon size-distribution) has not been shown before, and is instructive because it can yield new information regarding the contribution of axon heterogeneity to the XPS time-course. The lateral optic nerve (LON) of the horseshoe crab, Limulus polyphemus, extends through the optic tract, where >1500 eccentric axons may be present, with diameters varying within a narrow range (~10-20 μm), and without other axon types [31,32]. The LONs were excised from a living crab, after which the crab was sacrificed. Each LON was placed in the nerve chamber and sustained by a Limulus Ringer’s solution consisting of 430 mM NaCl, 9.56 mM KCl, 9.52 mM CaCl2∙2H2O, 9.97 mM MgCl2∙6H2O, 21.05 mM MgSO4∙7H2O, 50 mM TES, 50 mM HEPES, 10 ml/l Penstrep (Penicillin-Streptomycin 10,000 units/ml) [33]. The LON nerves were stimulated at 350 µA, with a 1-ms pulse.

As shown in Fig. 3(A), at 12 mm from the stimulus site, the XPS of the horseshoe crab LON (with a small variance in axon sizes) shows an even faster onset and a significantly faster initial recovery than that of the WLN, with its broader size distribution. Interestingly, the gradual recovery phase happens from above baseline rather than below baseline, as for the WLN. This temporal shape of the XPS for the LON was found to be relatively independent of the distance from the stimulation site. The electrical recording corresponding to this LON XPS is shown in Fig. 3(B) (overlaid with the XPS), which shows that the APs in the LON last for a duration of <10 ms, even though the electrical recording is taken at a distance 24 mm from the stimulus. This AP activity matches the width of the peak of the XPS. The gradual phase of the recovery occurs after the APs are no longer present.

Fig. 3.

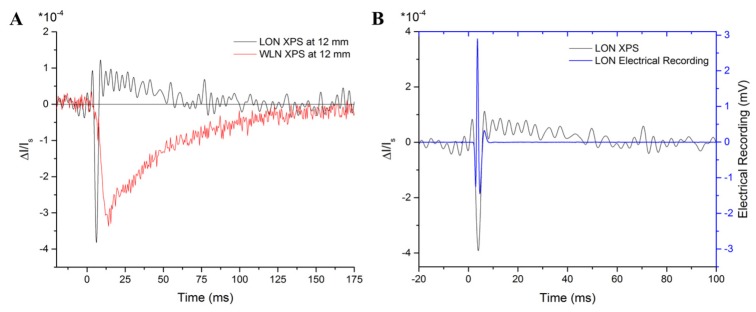
A) Horseshoe crab lateral optic nerve (LON) XPS measured at a distance ~12 mm from the stimulus site, overlaid with the lobster WLN XPS at the same location. The signal spreads with propagation distance for the heterogeneous WLN, but the same is not true for the homogeneous LON. The gradual recovery phase happens from above baseline for the LON and below baseline for the WLN. B) The corresponding electrical recording for the LON is time-adjusted and plotted over the peak of the XPS from Fig. 3(A) to show that this narrow optical peak can be explained by the concurrent arrivals of APs. The filter was set to remove frequencies below 300 Hz, allowing only for the detection of APs. As for the WLN, the gradual recovery of the XPS for the LON cannot be explained by the presence of APs.

3.3 ‘Dynamic’ birefringence in ‘dead’ nerves with standard stimulation

Once extracted, lobster walking leg nerves (WLNs) generally remain viable for up to ~2 hours, after which they will no longer generate action potentials in response to stimuli. Nonetheless, the applied electric field in the stimulus wells can force local changes in ion distributions and in the polarization of the nerve fiber structures in that location (hyperpolarizing or depolarizing), thereby inducing dynamic changes in birefringence, independent of action potentials. Standard 1-ms, 1-mA, and stronger 1-ms, 10-mA pulses, were applied to a live nerve, and to the same nerve after it no longer generated APs (>2 hours after extraction), and the XPS was recorded at the windows of either the positive or negative stimulus electrode (see Fig. 1(B)). This provided new information on the optical effects of an externally-applied electric field on the nerve tissue structures, without the confounding perturbations of generated action potentials or the use of exogenous substances.

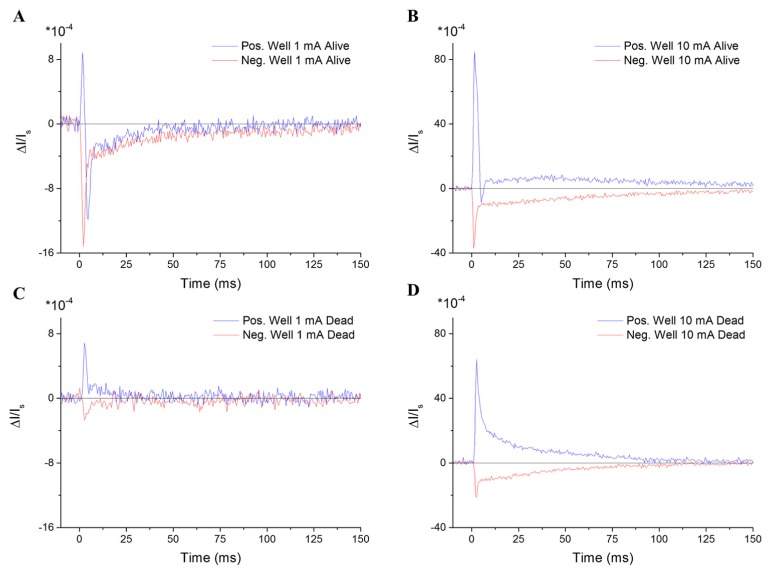
When standard stimulus pulse currents of 1 mA and a 10 mA (and 1 ms width) were applied to a nerve in both live and ‘dead’ conditions, and the XPS was measured in the positive and negative stimulus wells, the birefringence was found to follow the applied field, both in polarity and magnitude (Fig. 4). The positive-well XPS for a 1 mA stimulus in a live nerve (Fig. 4(A)) demonstrated a short increase in birefringence attributed to the stimulus itself, followed by a standard XPS time-course associated with the firing of APs (similar to that shown in Fig. 2(A)). For the 10-mA stimulus, again in the positive polarity well, both live and dead nerves exhibited a gradual recovery from above baseline (Figs. 4(B) and 4(D)). The gradual recovery time-course was extended by greater than a factor of 2 for the 10-mA stimulus compared to the 1-mA stimulus. The shape of the XPS in the negative-stimulus well was similar regardless of the stimulus amplitude or whether the nerve was alive or dead.

Fig. 4.

A) The XPS in the positive and negative stimulus wells with a 1-ms, 1-mA stimulus pulse in a live nerve shows an immediate peak correlated with the stimulus pulse followed by a standard shape associated with normal AP activity. B) A 10-mA stimulus pulse in a live nerve causes the XPS to recover from above baseline instead of below. C) The dead nerve XPS for a 1-mA stimulus is much smaller than for the live nerve, but is still present. D) For a 10-mA stimulus on a dead nerve, the XPS onset is an order of magnitude larger than for a 1-mA stimulus, and the gradual recovery is significantly longer (>2x).

3.4 Birefringence signal and the amplitude of externally applied electric field

To investigate the effect of applied fields on both the amplitude and temporal response of the nerve, square voltage pulses, 128 ms wide, were applied to the nerve with voltage amplitudes of 100 mV, 200 mV, 400 mV, 750 mV, 1 V, 2V and 5V. The voltage was generated by the DAQ card (National Instruments) and passed through an analog output channel. The XPS of the nerve was measured at the positive stimulus electrode well. The time constants of 63% of the rise and fall times for the resulting dynamic birefringence signals were calculated. The electrical resistance of the nerve (and thus the current applied) was measured during stimulation by recording the voltage across a 10 Ω resistor in series with the nerve.

The XPS closely followed both a positive and a negative applied voltage, with a small delay, as shown in Fig. 5(A). Rising and falling time constants of 14 ms and 19 ms were found for the positive stimulus XPS. These are significantly longer than the values reported by Cohen et al. [34] for individual squid giant axons (~68 μs). The WLN XPS was found to be approximately linear with applied voltages in the range −2 V to + 2 V (Fig. 5(B)), consistent with a linear electro-optic effect, or Pockels effect. This is in contrast to data reported for individual squid giant axons [34], which demonstrated a Kerr-like effect, or quadratic electro-optic effect, when measured at the membrane. The stimulation currents corresponding to this voltage range were 0.1 mA to 5 mA (not shown), depending on the applied voltage amplitude and varying with the impedance of each particular nerve. Beyond approximately the range of −2 V to + 2 V, the applied-field effect saturates for both polarities.

Fig. 5.

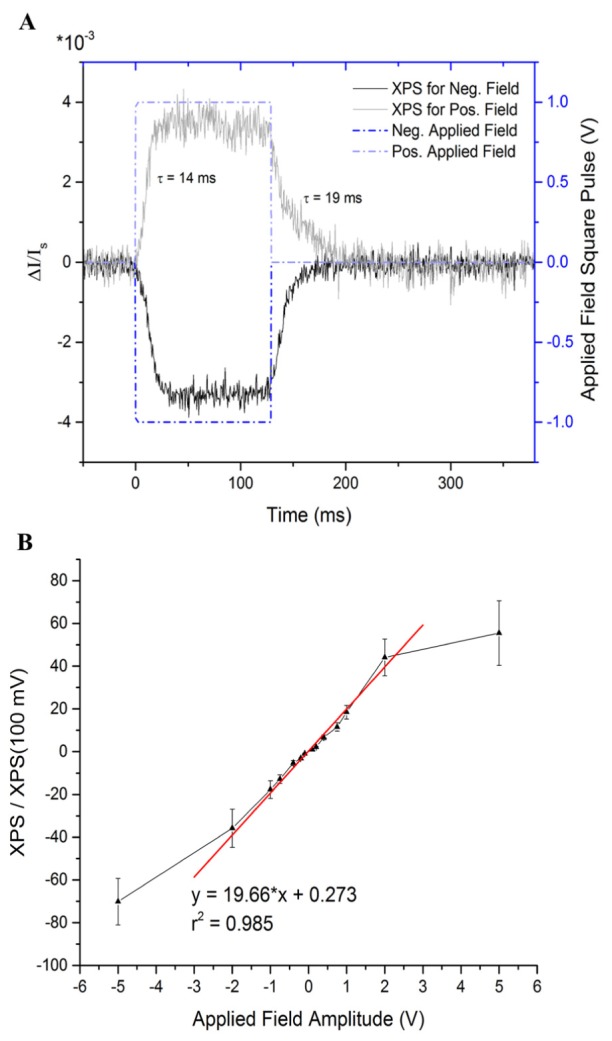
A) Example of a stimulus used in the experiment. 1V and −1V, 128-ms square voltage pulses were applied to nerve, and the XPS and stimulus voltage traces are shown together. The birefringence signal closely follows the applied electric field, with time constants of 14 ms rising and 19 ms falling. B) The XPS demonstrates a positive, linear relationship (shown here with a linear fit) to the amplitude of an applied voltage stimulus in the range −2 V to 2 V (data is normalized to the XPS at 100 mV for each nerve, n = 5). The signal saturates beyond that range, possibly related to limitations in the availability of the physiological structures causing changes in birefringence.

4. Discussion

The results of these experiments further characterize the dynamic birefringence signal associated with both action potential activity and applied electric fields in complex, heterogeneous nerves, and also with nerves having narrow axon size distributions, while providing new information regarding the temporal characteristics of the spreading and gradual recovery of the crossed-polarized signal. The new chamber design facilitates a comparison of the crossed-polarized signal (XPS) as a function of distance, over a more complete range of distances, including at both the stimulus application and electrical recording sites, allowing for an analysis of the direct effects of applied current and voltage pulses on the nerve. The data suggest that the gradual recovery of the XPS cannot be explained only by the spread of arrival times of individual axonal action potentials (APs). Further, the temporal dynamics of axon swelling are also incompatible with the slow recovery [18,19]. We hypothesize that a direct electric-field-induced change in polarizability due to capacitive-like charging and discharging from traveling APs in adjacent tissues is responsible for this portion of the XPS.

Previous researchers have hypothesized that the shape of the XPS (fast onset and slow recovery) in heterogeneous nerves such as the lobster walking leg nerve (WLN) is due in large part to the range of AP propagation velocities for the wide range of axonal diameters (and thus a wide range of arrival times) [12,15,17,19]. They did not, moreover, report distinct phases in the XPS, possibly due to a lack of detector sensitivity or noise from electronics. Our nerve chamber and detection electronics enabled a more comprehensive investigation of XPS as a function of distance from the stimulation site with higher sensitivity. We found, in both the computational model and experimental measurements, that the (initial) slow onset, the (second phase) fast onset, and the (initial) fast recovery, are consistent with the velocity-distribution hypothesis, but that the distribution of AP velocities for the constituent axons cannot explain the long tail of the gradual recovery phase. The gradual recovery phase is similar (lasting 100s of ms), regardless of distance of the measurement point from the stimulus site.

One possible explanation for the gradual recovery is a slow release of ions/charges that are stored at nearby tissue structures in response to a perturbation by the fluctuating electric field of the adjacent traveling APs. The electric fields of these stored charges would act to increase, or decrease, the optical polarizability (hence refractive index) of the nerve tissue. This would be consistent with, but alternative to the hypothesis previously proposed that considers the change in birefringence to be caused by a reorientation of sodium channels and other membrane-bound protein channels [21,22] or membrane phospholipid dipoles [21]. The fact that the nerve electrical recording (shown in Fig. 2(D)) exhibits a gradual recovery with temporal duration similar to that of the XPS (despite the relative polarity change) may be significant and is consistent with our hypothesis. Additionally, the electrical recording indicates that the vast majority of APs have subsided by the time the gradual recovery phase begins.

The computational model was able to reproduce both onset phases, as well as the initial fast recovery phase, demonstrating results similar to observations by Carter et al. [12], indicating that these phases of the XPS are consistent with the arrival times of the medium and giant axon groups of the WLN. The other size group is composed of small axons (~0.1-5 μm) [28], which spread out in time more significantly due to the large relative range of diameters within that size group. The model serves as additional evidence that indeed the observed gradual recovery is not related to AP activity. No adjustment of any of the parameters, neither those treated as variables nor the physiologically defined values, could fully reproduce the empirical XPS traces. Adding a gradual capacitive decay to the overall waveform produced by the model would be the simplest way to reproduce the empirical gradual recovery phase.

The homogeneous nature of the axon size-distribution in the horseshoe crab lateral optic nerve (LON) leads to the simultaneous arrival of APs at any distance from the stimulus, and this corresponds with the peak of the XPS (Figs. 3(A) and 3(B)), but not the gradual recovery, which is opposite in polarity to that of the lobster WLN. This gradual recovery occurring from above baseline (rather than below) in the LON was unexpected, but is consistent with an accumulation of charges that induces a hyperpolarizing effect of axonal membranes, increasing the electric field at 45° to the polarization angle of incident light (thus increasing the XPS). The significantly different temporal response of the LON compared to the WLN provides evidence that the complexity, both of the distribution of axons and of the tissue structures, in the WLN governs the temporal shape of the XPS.

Studies involving ‘dead’ nerves are not commonly performed, since they do not directly pertain to neuronal activity. In this study, the use of AP-inactive (as verified by an absence of activity in the electrical recording) but structurally sound nerves (as verified by both a similar static birefringence to that in the live nerve and through microscopic inspection) informs on the effects of electric field fluctuations in the entire tissue. APs originate in the negative stimulus well (evident by the earlier arrival time of the peak), which is consistent with a depolarization of the axonal membranes, causing a decrease in birefringence. The XPS for a ‘stimulated’ dead nerve is qualitatively similar in shape to that of a live nerve (in Fig. 4). The primary difference is that, in live nerves, generated APs cause a reversal of polarity of the XPS at the positive stimulus well, and also shift the gradual recovery downward compared to dead nerves. Furthermore, AP activity (in the live nerve) in the WLN always is accompanied by a decrease in birefringence. The application of a 10-mA stimulus pulse in a live nerve produced an upward shift in the section of the XPS trace associated with APs, followed by a gradual recovery from above baseline. This is consistent with a superposition in the XPS of both the arriving APs, and a capacitive charging that can induce a hyperpolarizing effect of axonal membranes, thus increasing the effective birefringence (the XPS). A more obvious capacitive-like discharging effect in both stimulus wells is evident in the XPS traces for the dead nerve in response to both the 1-mA and 10-mA stimuli (Figs. 4(C) and 4(D)). This provides evidence that not only is there a polarity dependence in the XPS, but that the tissue exhibits a charging and discharging phenomenon induced by a stimulus field, whose magnitude directly corresponds to the magnitude of the XPS.

Finally, the experiment for data in Fig. 5 for our fluid-coupled nerve stimulation, resembles an experiment presented by Cohen et al. [34], obtained by voltage-clamping individual squid giant axons. This demonstrates that hyperpolarization and depolarization were accompanied reliably by direct electric-field-induced changes in birefringence in the membrane. In our experiments, the whole WLN nerves (bundles of axons with a complex organization of surrounding tissues) were ‘clamped’ to specific voltages over a ~2 – 4 mm distance, and we found that the time constants for the whole nerve tissue are significantly slower (>2 orders of magnitude difference) than those observed in individual squid giant axons. The increased delay in whole nerves is likely caused by the influence of inter-axonal effects and non-axonal tissue structures. Furthermore, as shown in Fig. 5(B), the nerves exhibit a linear electro-optic effect. Given that Cohen et al. [34] demonstrated that individual axons exhibit a quadratic Kerr effect at the membrane, this indicates that other tissue structures and mechanisms may be involved in the response of whole nerves to fluctuating electric fields, possibly, in part, related to a bulk tissue capacitance [35,36]. The XPS associated with these fluctuations, from both applied fields and APs, is consistent with a coupling effect of adjacent axons, similar to ephaptic coupling [37,38]. Non-synaptic, or ephaptic, transmission between adjacent axons may be responsible for smoothing the peaks of XPS traces, which otherwise might be expected to have sharper features due to large gaps between the size-groups of the lobster WLN axon distribution. Furthermore, tissue capacitance and dielectric property changes are known to occur and have been associated with phenomena such as cortical spreading depression in migraines [39]. These observations imply that the gradual recovery from changes in birefringence associated with AP activity may occur in axon-adjacent tissue structures and are associated with a bulk tissue capacitance.

Our data collectively serves as a strong indication that there is a capacitive-charging-like effect directly inducing a gradual recovery of the XPS to baseline, and also causing a smoothing of the XPS trace. Determining specifically which physiological structures may be behind these changes in birefringence involving the peak of the XPS and the gradual recovery is outside the scope of this study. Future proposed endeavors include a more detailed investigation of the hypothesized capacitive-like charging and discharging effect in these tissues; the use of a fast frame-rate linear photodiode array to obtain live tracking of these intrinsic AP-induced changes in birefringence; and investigation of the birefringence signal in 2D neuronal structures, such as thin crab ganglia or mouse brain slices. Such studies can help pave the way toward utilizing changes in birefringence as an effective tool for imaging fast neuronal network activity in more complex neuronal systems.