Estimation of particle size variations for laser speckle rheology of materials

Abstract

Laser speckle rheology (LSR) is an optical technique for assessing the viscoelastic properties of materials with several industrial, biological, and medical applications. In LSR, the viscoelastic modulus, G^* (ω), of a material is quantified by analyzing the temporal fluctuations of speckle patterns. However, the size of scattering particles within the material also influences the rate of speckle fluctuations, independent of sample mechanical properties, and complicates the accurate estimation of G^* (ω). Here, we demonstrate that the average particle size may be retrieved from the azimuth-angle dependence of time-averaged speckle intensities, permitting the accurate quantification of the viscoelastic moduli of materials with unknown particle size distribution using LSR.

Laser speckle rheology (LSR) is a powerful optical tool for evaluating the viscoelastic properties of materials with many applications in polymer engineering, food sciences, and biomedical imaging [1–7]. The viscoelastic behavior of a material is usually described by the viscoelastic modulus, G^*(ω), and is often measured by a mechanical rheometer, in which a specimen is sheared between two parallel plates in an oscillatory manner, and the ratio of the exerted stress to the resulting strain is calculated.

Prior studies have demonstrated that LSR evaluates G^*(ω) in an optical, noncontact manner, using small sample volumes [1–6, 8]. In LSR, the sample is illuminated by a laser, and a high-speed camera is used to capture the temporally fluctuating speckle patterns, induced by Brownian movements of scattering particles. In compliant materials, unrestricted Brownian excursions provoke rapidly fluctuating speckle patterns, whereas in rigid substrates, restrained particle displacements elicit limited speckle modulation [1–6]. Cross-correlation analysis of speckle frames yields the speckle intensity auto-correlation curve, g₂(t), from which the mean-square displacement (MSD) of particles, 〈Δr²(t)〉, is deduced [4–6]. The generalized Stokes–Einstein relation (GSER) is then used to extract the G^*(ω) [4–6, 8]:

$$G^{\ast }\left(\omega \right)=\frac{K_{B}T}{\pi a\langle \Delta r^2(1∕\omega )\rangle \Gamma (1+\alpha (1∕\omega ))}.$$ (1)

Here, K_B is the Boltzman constant, T is the temperature (in Kelvins), a is the average sphere-equivalent radius of scattering particles, α is the log–log slope of MSD at t = 1/ω, and Γ is the gamma function [8]. Accurate quantification of G^*(ω) from g₂(t) curve is complicated since speckle fluctuations are not only modulated by the viscoelastic compliance, but also by optical properties and scattering particle size distribution of the medium. We have previously isolated the contribution of optical properties, by showing that the g₂(t) curve is related to both particles’ MSD and optical absorption and reduced scattering coefficients of the medium, μ_a and ${\mu }_s^{\prime }$ [4,5]. We have also shown that temporal averaging of speckle frames yields the diffuse reflectance profile (DRP) of the sample from which μ_a and ${\mu }_s^{\prime }$ are derived. Given these coefficients, MSD is seamlessly deduced from g₂(t) [4,6].

Beside optical properties, size of scattering particles also modifies speckle fluctuations, confounding the accurate estimation of G^*(ω). Equation (1) clarifies that for a medium of given G^*(ω), MSD depends on scattering particle size. For smaller particles, MSD grows faster and accelerates speckle decorrelation. Thus, to derive G^*(ω) from MSD, scattering particle size has to be estimated. Optical techniques such as dynamic light scattering (DLS) and angle-resolved low-coherence interferometry (a/LCI) have been used for particle sizing applications [9, 10]. Yet, limitation of DLS to dilute samples and complexity of a/LCI hardware restricts their integration into the LSR system to characterize turbid materials.

Here, we investigate a straightforward approach for evaluating the average radii of scattering particles, a, that may be conveniently integrated in the LSR system. Our approach builds on prior work [11] by further exploiting Monte–Carlo ray tracing (MCRT) simulations to describe the theoretical basis of particle sizing and identify the limitations. In particular, we show that the parallel-polarized DRP, derived from time-averaged speckle frames, exhibits certain azimuth angle dependence, related to both average scattering size, a, and refractive index mismatch, n_i. Further, we deduce that changes in DRP shape, due to varying a and n_i, may inform particle size estimation for accurate calculation of G^*(ω) in LSR.

First, we exploited a polarized MCRT algorithm [12] to verify the feasibility of estimating the scattering particle size and simulated the back-scattered polarized DRP pattern. The MCRT code incorporated the LSR system configuration, namely linearly polarized focused illumination (690 nm), finite slab sample geometry, and back-reflected (180°) collection through a linear polarizer. According to Mie theory, light scattering at each wavelength is governed by the scattering particle radius, a, and the ratio of refractive indices of background, n₁, and scattering particles, n₂, n_i n₂/n₁. MCRT simulations enabled us to independently inspect the influence of both a and n_i on the polarized DRP pattern. In these simulations, we considered spherical mono-disperse particles of a:0.1–3 μm and 3 refractive index pairs of (n₁ = 1.36, n₂ = 1.4, n_i = 1.03), (n₁ = 1.34, n₂ = 1.5, n_i = 1.1), and (n₁ = 1.34, n₂ = 1.59, n_i = 1.2), that covered the range pertinent to biomaterials and hydrogels of interest [13]. Mie theory was used to calculate μ_a, ${\mu }_s^{\prime }$, and the Mueller matrix elements, S11, S12, S33, and S34 [12]. Scattering concentration was adjusted such that ${\mu }_s^{\prime }$ = 1.1 mm ⁻¹. Optical properties were input to the MCRT code. One million photons, representing a normally incident focused beam, were launched. The beam was linearly polarized with Stokes vector S₀ = [1 1 0 0]. Upon photon scattering, Stokes vector, S, was updated via multiplication by Mueller matrix. For photons returning to the imaging plane, the intensity of light retaining the initial polarization was calculated as scalar product of S and S₀. The DRP pattern was calculated by spatial binning.

Next, we verified the accuracy of MCRT simulations experimentally, using standard polystyrene microsphere suspensions (n₁ = 1.34, n₂ = 1.59, n_i = 1.2) with radii: 0.1–3 μm (PolySciences Inc., Pennsylvania). The polybead suspensions were diluted such that ${\mu }_s^{\prime }$ = 1.1 mm⁻¹. One hundred μl of each sample was loaded in an imaging chamber (Grace Bio-Labs Inc., Oregon) for LSR evaluation. Briefly, in the LSR setup, light from a polarized laser (690 nm) was collimated and focused via a lens to a 50 μm spot on the sample. The back-scattered speckle patterns were acquired via a beam-splitter and a polarizer (parallel polarization) and detected by a high-speed CMOS camera (Basler Ace 2000-340 km, Germany), for 0.67 s at 753 frames per second (fps). DRP was obtained by temporally averaging the speckle frames.

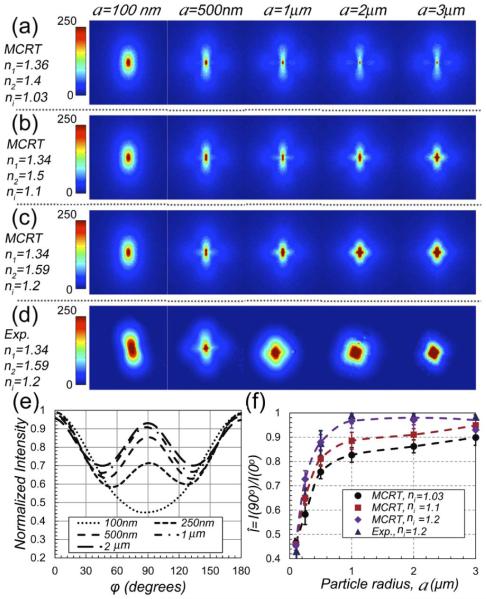
Figures 1(a)–1(c) display the MCRT-simulated DRP patterns for a:0.1–3 μm and n_i:1.03, 1.1, and 1.2. For comparison, for one of the n_i values (n_i = 1.2), Fig. 1(d) depicts the experimentally evaluated DRP patterns scattered from polystyrene suspensions. The visually perceived qualitative agreement between MCRT-simulated and experimentally measured patterns for a = 0.1–3 μm and n_i = 1.2 [Figs. 1(c) and 1(d)], establishes the validity of MCRT method. Both simulation and experimental results in Figs. 1(a)–1(d) reveal that by increasing the scattering particle size, DRP evolves from a bi-lobular pattern to a clover-like shape [11]. Beside, simulation results of Figs. 1(a)–1(c) demonstrate that increasing n_i accelerates this trend. Evolution of DRP by increasing a and n_i is likely due to transition between isotropic Rayleigh scattering to forwardly-directed Mie scattering [11]. To quantify the changes in DRP patterns of Fig. 1(c), in Fig. 1(e) the normalized intensity values (to maximum) versus azimuth angle, φ, for a:0.1–3 μm, and n_i = 1.2 are plotted. From Fig. 1(e), it appears that the ratio of DRP intensity at φ = 90° and φ = 0°, i.e., $\widehat{I}$ = I(90°)/I(0°), best describes the alteration of DRP pattern from bilobular to clover shaped. Thus, $\widehat{I}$ is a quantitative representation of DRP shape and is deemed to be the most sensitive metric that evolves with scattering particle size. Figure 1(f) shows the changes in $\widehat{I}$ versus a, derived from Figs. 1(a)–1(d). The purple diamonds and navy triangles, representing MCRT simulations and experimental results for a:0.1–3 μm and n_i 1.2, match closely and quantitatively establish the accuracy of the MCRT approach. For any n_i, $\widehat{I}$ grows monotonically as a increases from 100 nm to 2 μm, and saturates afterward. Yet, for a given a, $\widehat{I}$ varies by 12%, when n_i raises from 1.03 to 1.2. Thus, to deduce a from $\widehat{I}$, the variability of n_i has to be considered. To this end, we obtained 3 calibration curves for n_i = 1.03, 1.1, and 1.2 [black, red, and purple dashed lines in Fig. 1(f)] by cubic interpolation of discrete $\widehat{I}$ versus a points. These calibration curves sampled the typical small, medium, and large n_i values of specimens tested below and other biomaterials.

Fig. 1.

(a)–(c) MCRT simulated parallel-polarized DRP for a: 0.1–3 μm and n_i of 1.03, 1.1, and 1.2. Polarization direction is along vertical axis. Color bar represents the normalized intensity. (d) Experimental results for a:0.1–3 μm and n_i 1.2 [compare with MCRT results of (c)]. Color bars represent the pixel intensity. (e) Normalized intensity versus φ for varying particle radii and n_i = 1.2 obtained from MCRT. (f) $\widehat{I}$ versus a, obtained from MCRT and experimental results. Error bars display standard deviation. Cubic interpolation between discrete $\widehat{I}$ versus a (black, red, and purple dashed lines) serve as calibration curves for each n_i.

Next, we investigated the utility of this approach in evaluating the viscoelastic moduli of poly-disperse materials using LSR. To this end, we tested three common materials, namely: medicated soap (Steris Corp., Ohio), silicone conditioner (Procter and Gamble, Ohio), and mayonnaise (Kraft Foods, Illinois), which were scattering samples with unknown particle size distributions. The samples were loaded in imaging chambers, and speckle frames were acquired at 753 fps for 5 s. Figures 2(a)–2(d) display the corresponding DRP patterns, along with the intensity versus φ. As expected, the experimental plots of Fig. 2(d) are not identical to MCRT-generated plots in Fig. 1(e), due to differences in optical properties (n_i and ${\mu }_s^{\prime }$) and poly-dispersity, and the attributes of experimental factors like camera gain and exposure time. Despite poly-dispersity effects, the calibration curves of Fig. 1(f) can be used to estimate the average particle size, as discussed later. From Fig. 2(d), $\widehat{I}$ is equal to 0.4, 0.42, and 0.77, for soap, conditioner, and mayonnaise, respectively. In these materials, styrene, silica, and fat particles elicit n_i of 1.59/1.33 = 1.2 (soap), 1.46/1.33 = 1.1 (conditioner), and 1.46/1.33 = 1.1 (mayonnaise). Based on $\widehat{I}$ and n_i values and from the calibration curves of Fig. 1(f), we deduce the average a values of soap, conditioner, and mayonnaise to be ~0.1, 0.1, and 0.45 μm, respectively. These numbers agree with published particle size values [14–16]. The g₂(t) curves, displayed in Fig. 2(e), reveal that speckle fluctuations are most rapid in soap and the slowest in conditioner. Radial analysis of DRP [4,5] suggest that for soap, conditioner, and mayonnaise μ_a ~ 0 and ${\mu }_s^{\prime }$ ~ 1, 5, and 14 mm⁻¹, respectively. Knowing μ_a and ${\mu }_s^{\prime }$, we were able to deduce the MSD from g₂(t) curves [4,5]. The inset of Fig. 2(e) illustrates the large and growing MSD of soap particles versus time, which is a characteristic of viscous liquids. In contrast, the magnitude and slope of MSD are much lower in mayonnaise and conditioner, representing less compliant viscoelastic materials. The MSD curves partially elucidate the mechanical behavior of specimens. Still, particle size information is required to evaluate the absolute G^*(ω). Figure 2(f) displays the G^*(ω), evaluated by LSR via substituting the MSD and a, in Eq. (1). G^*(ω) curves obtained from mechanical rheometry are also shown. LSR measurements correspond closely with rheometry results for all samples. At high frequencies, mechanical rheometer results are degraded, as increased inertia inhibits proper shearing of the specimen and the raw phase, i.e., inverse tangent of viscous to elastic moduli ratio, is over-estimated. This is more evident in mayonnaise, for which the raw phase increases drastically at ω > 1 Hz [17]. Conversely, minute deviations between LSR and rheology at very low frequencies are likely caused by speckle blurring due to limited bit-depth and insufficient frame rate of the camera. Thus, the correlation between LSR and mechanical rheometry is best at intermediate frequencies. These results further corroborate the accuracy of DRP-based particle sizing approach in poly-disperse materials.

Fig. 2.

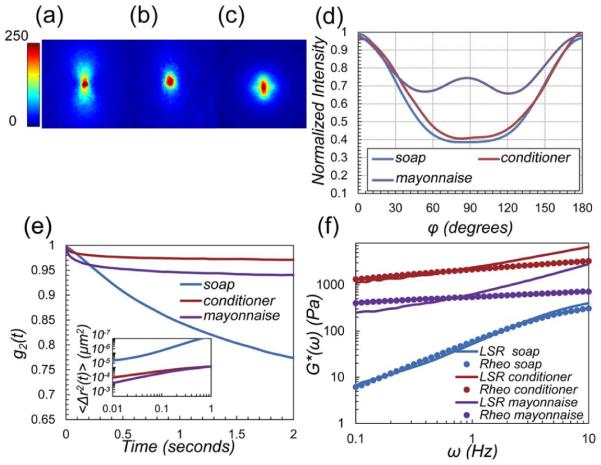
(a)–(c) Experimentally evaluated parallel-polarized DRP for soap, conditioner, and mayonnaise, respectively. Polarization direction is along vertical axis. Color bar represents pixel intensity. (d) Normalized intensity versus φ, derived from DRP images. $\widehat{I}$ values are 0.4, 0.42, and 0.77, respectively. Given the n_i values, scattering particle radii are 0.1, 0.1, and 0.45 μm. (e) g₂ (t) curves for soap, conditioner, and mayonnaise. Inset: MSD. (f) G^*(ω) obtained from LSR (lines) and mechanical rheometry (circles) agree well especially at intermediate frequencies.

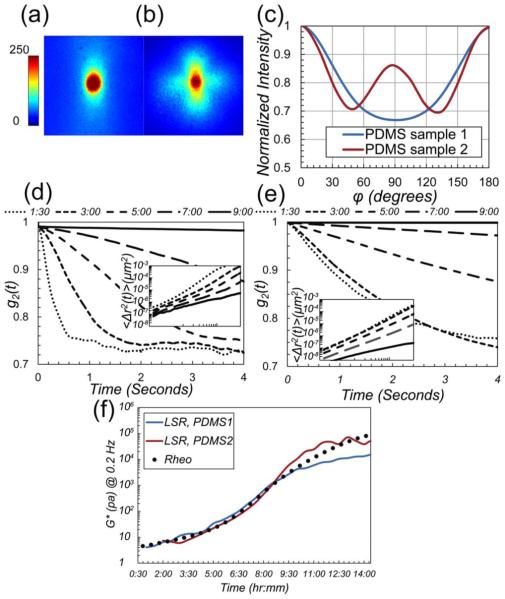
Last, we tested the sensitivity, dynamic range, and limitations of the proposed approach for LSR measurements in curing polydimethylsiloxane (PDMS) gels. PDMS1 and PDMS2 samples were prepared by mixing the base and curing agent (Sylgard 184, Dow Corning, Belgium) in 1:10 ratios. Silica (PolySciences, Inc.) and Borosilicate beads (Thermo Scientific Inc., MA) of two distinct sizes were added to precursor mixtures (w/v ~ 10%, and 4%) to induce light scattering. Samples were poured in spectroscopic cuvettes for LSR measurements. Speckle movies were acquired every 30 min for 24 h at 753 fps for 5 s. The remainders of samples were loaded in a mechanical rheometer, and frequency sweep test was conducted in tandem with LSR, every 30 min for 24 h. Gels fully cured in 48 h at room temperature. Figures 3(a) and 3(b) display the DRP images of PDMS samples. Using prior approaches, ${\mu }_s^{\prime }$ = 0.9 mm⁻¹ and 1.4 mm⁻¹ for PDMS1 and PDMS2 were calculated from the DRPs [4,6]. Figure 3(c) depicts the normalized intensity versus φ, obtained from DRP images of Figs. 3(a) and 3(b). From these curves, we calculated the $\widehat{I}$ of 0.67 for PDMS1 and 0.87 for PDMS2. Given n_i of 1.46/1.41 = 1.03 and 1.56/1.41 = 1.1, the black and red calibration curves of Fig. 1(f) return the radii of a₁ ~ 0.25 μm and a₂ ~ 0.75 μm for silica and borosilicate beads, respectively, which closely agree with manufacturer specifications (a₁ ~ 0.25 μm, a₂ ~ 1±0.25 μm). The time-lapse g₂(t) curves in Figs. 3(d) and 3(e) demonstrate the rate of speckle fluctuation during PDMS curing at different times. Using the ${\mu }_s^{\prime }$ values, we deduced the MSD from g₂(t) curves [Figs. 3(d) and 3(e), inset]. The time-lapse G^* measurements evaluated at ω = 0.2 Hz by LSR (lines) and rheometer (circles) are plotted in Fig. 3(f).

Fig. 3.

(a) and (b) Experimentally evaluated parallel-polarized DRP for PDMS1 and PDMS2 samples. Polarization direction is along vertical axis. Color bar represents pixel intensity. DRP patterns are significantly different due to distinct a and n_i values. (c) Normalized intensity versus φ, derived from DRP. $\widehat{I}$ values are 0.67 and 0.87, respectively, corresponding to a₁ ~ 0.25 μm and a₂ ~ 0.75 μm (from calibration curves of Fig. 1(f)). (d) and (e) The g₂ (t) curves for PDMS1 and PDMS2 are distinct due to differences in particle size, despite identical G^* values. (inset: MSD). (f) G^* at 0.2 Hz measured using LSR (lines) and mechanical rheometry (circles) show a close correspondence during PDMS curing over 14 h.

LSR measurements agree well with mechanical rheology results and accurately track small increments of G^*, (~few Pa), as PDMS transforms from a viscose liquid to an elastic solid with G^* ~ 10 kPa. Beyond the gel point, the viscosity of PDMS converges to infinity, and an elastic solid is formed with frozen and nonergodic speckle dynamics [18]. Consequently, LSR sensitivity to changes in G^* is diminished, and effects of CMOS sensor noise confound the measurements. Thus, LSR measurements deviate from rheology results at later phases of curing. However, our prior studies indicate that in biphasic biological tissue, speckle patterns remain fully fluctuating and ergodic up to G^* ~ 600 kPa, and LSR attains a dynamic range over 7 decades of moduli [3]. These results demonstrate that the DRP-based particle sizing incorporated in LSR system enables accurate evaluation of the viscoelastic moduli with high sensitivity across a wide range of moduli. Results of Fig. 1 display MCRT simulated and experimental DRPs of mono-disperse particles. For poly-disperse materials of Fig. 2, the measured DRP is a weighted-average of DRP patterns scattered from particles of identical sizes. Thus, calibration curves of Fig. 1(f) may still be used to extract the average particle size. Beside, DRP-based particle sizing is applicable to all turbid specimens. Variations of $\widehat{I}$ scale the DRP radially, without changing the angular dependence. Yet, this approach is mainly applicable in biomaterials, where n_i is small. For inorganic materials of larger n_i a distinct set of calibration curves is required.

In conclusion, we have investigated a straightforward particle-sizing scheme, based on azimuth-angle dependence of DRP, which may be conveniently integrated into the LSR system. The information on particle dimensions is necessary to accurately quantify G^*(ω) of materials using LSR.