Abstract
The question of what makes a good melody has interested composers, music theorists, and psychologists alike. Many of the observed principles of good “melodic continuation” involve melodic contour – the pattern of rising and falling pitch within a sequence. Previous work has shown that contour perception can extend beyond pitch to other auditory dimensions, such as brightness and loudness. Here, we show with two experiments that the generalization of contour perception to non-traditional dimensions also extends to melodic expectations. In the first experiment, subjective ratings for three-tone sequences that vary in brightness or loudness conformed to the same general contour-based expectations as pitch sequences. In the second experiment, we modified the sequence of melody presentation such that melodies with the same beginning were blocked together. This change produced substantively different results, but the patterns of ratings remained similar across the three auditory dimensions. Taken together, these results suggest that 1) certain well-known principles of melodic expectation (such as the expectation for a reversal following a skip) are dependent on long-term context, and 2) these expectations are not unique to the dimension of pitch and may instead reflect more general principles of perceptual organization.
Keywords: pitch, timbre, loudness, melody, expectation
What makes a good melody? Although the question may be most pressing for composers or songwriters wishing to write the next major hit, it has also been considered from several other perspectives. Cognitive psychologists have noted that when listeners are presented with a sequence of notes, they rapidly form expectations about how the melodic sequence will continue, based either on prior exposure to that melody, or on more general acquired or innate principles (Carlsen, 1981; Cuddy & Lunney, 1995; Huron, 2006). Music theorists have also studied the quality of “good continuation” in melodies, and have developed guidelines for writing perceptually independent melodic lines, referred to as the rules of voice leading (Schenker, 1935).
Studies of melodic expectation have identified two basic categories of expectations, one involving perceived musical key or tonality, and one involving contour – the pattern of directions (up or down) of the intervals in a melody (Narmour, 1990). Although it is necessary to take the influence of tonality into account to provide a complete description of melodic expectation, many of the well-established principles relate only to melodic contour. Novel melodies are more easily distinguished from melodies with different contours than from melodies with similar contours (Dowling, 1978). Indeed, the preservation of melodic contour alone is enough to allow for the memorization of unfamiliar melodies and the recognition of familiar melodies (Dowling & Fujitani, 1971).
Preference and expectation for melodies are distinct concepts (expected melodies may not be preferred), but are closely related, as expected continuations are more likely to be preferred than unexpected continuations. Melodic preferences, particularly those related to tonality, are likely to be culturally specific and so may depend on exposure to certain forms of music and melodies (Kessler, Hansen, & Shepard, 1984; Thompson, Balkwill, & Vernescu, 2000). Other preferences and expectations, particularly those related to melodic contour, may reflect more general perceptual principles related to the formation of auditory streams, and may not be specific to melodies or even music (Bregman, 1994; Huron, 2001; Schellenberg, Adachi, Purdy, & McKinnon, 2002). One way to test whether melodic contour expectations are domain specific, or whether they reflect more general perceptual principles, is to generate contours in dimensions other than pitch. Although the concept of melodic contour has traditionally been applied only to melodies consisting of a sequence of tones that vary in pitch, contours can be perceived, remembered, and even used for recognition of familiar melodies in dimensions other than pitch (McDermott, Lehr, & Oxenham, 2008).
Pitch is a perceptual auditory dimension primarily related to a sound’s overall periodicity or fundamental frequency (F0). The auditory dimension of brightness is an aspect of timbre related to the center of mass of a sound’s spectral envelope (sounds with more energy in the high-frequency range of the spectrum are perceived as being brighter). Loudness is primarily related to a sound’s intensity. Among these dimensions of sound, pitch is unique in that it can be classified according to both pitch height (a linear scale) and pitch chroma (a circular scale that repeats with every doubling of F0). Furthermore, perceived relationships between pitches form tonal hierarchies: Western listeners, especially those with musical training, judge notes belonging to an established musical scale as better “completions” following that scale (Krumhansl & Shepard, 1979). In the dimensions of brightness and loudness, there are no analogies to pitch chroma or tonal hierarchy, only to pitch height. To the extent that melodic expectations are influenced by tonality, they should not be replicable in other auditory dimensions. However, the aspects of expectation influenced by a melody’s contour, which relates only to the linear scale of pitch height, may generalize to domains other than pitch.
In this study we asked whether the same expectations that have been discovered for melodic contours in pitch also apply to contours in brightness and loudness. In two experiments, we presented our participants with 3-tone “melodies” that varied in pitch, brightness, or loudness, and we asked them to judge how well the final note of the melody completed the sequence. Against these results, we tested three well-established rules of melodic continuation, derived from music theory and from cognitive studies based on pitch variations. If expectations for melodic contour extend beyond the pitch dimension, then we would expect listeners’ judgments to conform to the predictions of these rules, not only for pitch sequences, but also for sequences based on brightness and loudness. On the other hand, if such expectations are specific to pitch, as expected if melodic contour expectations were learned just from exposure to music, then the rules should only successfully predict the results from pitch-based melodies.
Experiment 1: Melodic expectancy across pitch, brightness and loudness
Method
Stimuli
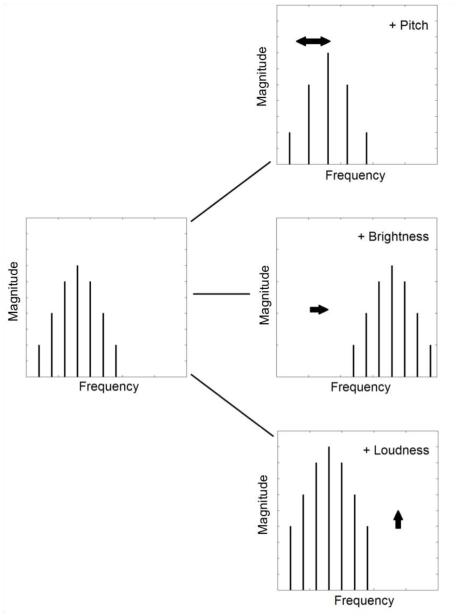
Harmonic complex tones were shaped with spectral envelopes determined by applying a Gaussian weighting function to the amplitudes of the individual harmonics. The standard deviation of the Gaussian was set to 25% of its center frequency. All the tones were gated on and off with 20-ms raised-cosine ramps. The tones were generated within MATLAB (The Mathworks, Natick, MA) and were played out from a 24-bit L22 soundcard (LynxStudio, Costa Mesa, CA) to both ears through HD580 headphones (Sennheiser USA, Old Lyme, CT), at a sampling rate of 48 kHz. Pitch variations were achieved by varying the F0 of the tones; brightness variations were achieved by varying the center frequency of the Gaussian weighting function; and loudness variations were achieved by varying the overall sound level of the tones. Fig. 1 demonstrates the difference between changes in pitch, brightness, and loudness.
Figure 1.
Simplified representations of a complex tone (left), increasing in pitch (top right), brightness (middle right), or loudness (bottom right).
The first step in designing the stimuli was to create broadly equivalent “scales” in the three dimensions of pitch, brightness, and loudness. This was achieved by using scale step sizes of 1 semitone (~6%) for F0, 2 semitones for the center frequency of the Gaussian weighting function, and 2 dB for the overall sound pressure level. The step sizes were selected to be approximately equally salient, based on previously reported interval-discrimination thresholds for pitch, timbre, and loudness (McDermott, Keebler, Micheyl, & Oxenham, 2010). It is important to note here that by “scale” we do not mean a musical key or any other kind of tonal hierarchy. Those elements of pitch melodies cannot be meaningfully translated into brightness or loudness melodies, since there is no analog to pitch chroma in those dimensions. “Scale” here simply means a set of ranked, evenly spaced steps from which values for pitch, brightness, and loudness are chosen.
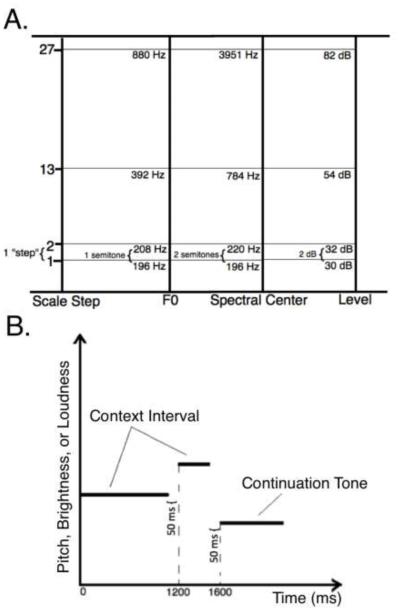
The scale for each dimension spanned 27 steps (Fig. 2A). In pitch, the F0s ranged from G3 (196 Hz) to A5 (880 Hz) in 1-semitone steps (an equal-temperament tuning including the A440 pitch standard). In brightness, the center frequency of the Gaussian function ranged from 196 Hz to 3951 Hz, in 2-semitone steps. In loudness, the overall level ranged from 30 to 82 dB SPL, in 2-dB steps. The range of these scales was determined by various constraints. First, the minimum and maximum loudness values were chosen to be easily audible and not uncomfortable, respectively. This level range, combined with the step-size of 2 dB, allowed for 27 scale steps. The same number of steps was then used for all three dimensions. The F0 range was selected to span a range that was within that normally used in Western music for melodies. The range of center frequencies for the Gaussian function was selected to begin at the lowest F0, with the highest frequency selected to be 27 steps away, based on a spectral step size of 2 semitones.
Figure 2.
(A) Visual representation of the scales used for F0 (for pitch melodies), spectral center (for brightness melodies), and level (for loudness melodies). Each scale contains 27 steps; the values of the 1st, 2nd, 13th, and 27th steps are given as examples. (B) Schematic diagram of an example melody, where horizontal lines represent individual tones in the melody.
Changes in one auditory dimension can interfere with the perception of others (e.g., Borchert, Micheyl, & Oxenham, 2011; Melara & Marks, 1990), so when the stimuli varied along a single dimension, the other two dimensions were held constant. The constant values for the three dimensions were 196 Hz for F0, 800 Hz for spectral center frequency, and 60 dB SPL for sound level. The constant values for spectral center and sound level were selected for their intermediate position in the overall range of values used, while the constant value for F0 was selected to prevent cases where F0 exceeded the spectral center frequency.
Once the scales were established, we adapted a paradigm that was used in an earlier study for generating pitch melodies (Cuddy & Lunney, 1995) to create melodies in the pitch, brightness, or loudness dimension. Melodies consisted of three notes each. The first two notes comprised the context interval. The third note is referred to as the “continuation tone” (Fig. 2B). The same eight context intervals originally used by Cuddy and Lunney (1995) were used. In Western music, these intervals in pitch are referred to as the ascending and descending forms of the major second, minor third, major sixth, and minor seventh. These intervals correspond to the following number of steps respectively: ±2, ±3, ±9, and ±10 steps. For each context interval, every continuation tone from 12 steps below to 12 steps above the second tone (25 intervals total) was tested for a total of 200 trials (8 context intervals by 25 continuation intervals). In every melody, the value of the second note was selected from a set of three equally probable values, corresponding to the three centermost values in the pitch, loudness, or brightness range. In pitch, for example, the second note of every melody was randomly sampled from the set of G4 (392.0 Hz), G#4/Ab4 (415.3 Hz), and A4 (440 Hz). The values of the first and third notes were then determined based on the value of the second note and the necessary interval sizes and directions for each trial. To allow for continuation tones 12 steps above or below the second note, 27 different values were defined, and the second note was either the 13th, 14th, or 15th of these 27 values.
The three notes were presented with the temporal relationships shown in Fig. 2B. The duration of each note (including onset and offset ramps) was 1150, 350, and 750 ms, respectively. Including the 50-ms silence after each note, the stimulus onset asynchronies were 1200, 400, and 800 ms, which was designed to create a sense of 4/4 meter, with the first and last notes falling on the first beat of the measure (Cuddy & Lunney, 1995). This temporal pattern accents the final note of the melody, which has been shown to heighten performance on perceptual tasks such as pitch change detection for the accented note (Monahan, Kendall, & Carterette, 1987).
Procedure
Eighteen listeners, 5 male and 13 female, were recruited from the Twin Cities campus of the University of Minnesota. Listeners ranged in age from 18 to 31 (M = 20.8, SD = 3.0). The average amount of musical training was 6.5 years (SD = 4.8; range 0 to 13 years). The five participants who reported the lowest amount of musical training (either 0 or 1 years) and the four participants who reported the highest amount of musical training (either 12 or 13 years) were taken as an approximation of the lower and upper quartiles, respectively, of participants ranked by musical experience. All listeners had normal audiometric hearing thresholds (defined as not exceeding 20 dB HL for octave frequencies between 250 and 8000 Hz).
Listeners gave subjective continuation ratings for 200 three-tone sequences each in pitch, brightness and loudness (600 total). After each sequence, the listener was asked to rate how well the third tone met expectations on a Likert scale (Likert, 1932) from −3 (“Very Poorly”) to 3 (“Very Well”). Listeners were encouraged to use the full range of possible integer ratings from −3 to 3.
Experiment 1 deviated from the paradigm established by Cuddy and Lunney (1995) in two ways. Firstly, the previous study presented the 200 possible melodies in blocks based on context interval size, such that all melodies beginning with the 9-steps-ascending context interval were heard in immediate succession. To avoid possible long-term context effects associated with presenting the same stimulus repeatedly, we randomized the presentation of the 8 different context intervals from trial to trial, just as the presentation of the 25 different continuation tones was randomized from trial to trial. Secondly, Cuddy and Lunney (1995) set the second note of their melodies as equal to C4 or F#4, alternating every other trial. With our selected step size in loudness (2 dB), the range required to follow this convention exactly would have been impossible to attain without presenting sounds that were either uncomfortably loud or inaudibly soft. For this reason, we used the convention described above, where the 2nd note was randomly sampled from the 13th, 14th, and 15th values of the 27-step scales.
The 200 trials in each condition were presented in a different random order for each participant and dimension. The presentation order for the dimensions was determined using a Latin square design, in which one third of the participants completed the tasks in the order pitch-brightness-loudness, one third in the order loudness-pitch-brightness, and one third in the order brightness-loudness-pitch.
Predictors
Certain contour-based principles of melodic continuation have been well established and supported by previous studies of melodic continuation in pitch (Larson, 2004; Schellenberg et al., 2002; Schellenberg, 1997; Temperley, 2008). We identified three principles that had received the most empirical support from these earlier studies: Proximity, Inertia, and Post-skip Reversal.
The first predictor, Proximity, refers to the difference, in terms of scale steps, between the second and third notes, where positive values indicate that the third note was higher than the second. Previous research on pitch-based melodic expectancy has found that small absolute values of Proximity are more expected than large ones (Cuddy & Lunney, 1995; Schellenberg et al., 2002; Temperley, 2008). Natural sound sources tend to stay within a limited pitch range, so large and rapid variations in pitch can be interpreted as the presence of multiple sound sources, which runs counter to the aim of creating the sense of a coherent melody (Bregman, 1994; Huron, 2001).
The second predictor, Inertia, corresponds to an expectation for pitch-based melodies to continue in the same direction after a small step (Larson, 2004). This principle can be interpreted as reflecting the Gestalt principle of good continuation (Balch, 1981), as applied to individual musical voices: once a direction has been established, a continuation of the established direction is expected.
The third predictor, Post-skip Reversal, reflects the tendency for a melody to move in the opposite direction following a large leap. This principle may reflect the tendency of melodies with good continuation, or auditory stimuli perceived as individual sound sources, to limit themselves to a restricted range of notes throughout the melody, and so to regress to the mean of that range after a leap (Temperley, 2008; von Hippel & Huron, 2000).
Among the contour-based predictors, we selected Proximity because it is one of the most broadly supported by evidence (Cuddy & Lunney, 1995; Schellenberg et al., 2002; Temperley, 2008). Post-skip Reversal is also well supported, though there is the question of whether it merely represents regression to the mean (von Hippel & Huron, 2000). There is less evidence for Inertia, with some studies, including our model study, finding no support for it (Cuddy & Lunney, 1995; Schellenberg, 1997). However, we included it in our analysis firstly because there is other evidence that supports it (Larson, 2004), and secondly because along with its symmetrical counterpart, Post-skip Reversal, it provides a general picture for which contours are expected for both small and large context intervals.
These are far from the only principles of melodic continuation that are supported by evidence, and there were alternative predictor variables we could have selected. However, many of these are disqualified from the present study because they are based on tonality, and as such there is no way to evaluate them in the dimensions of brightness and loudness. For example, one well-supported predictive principle favors continuation tones that are the tonic (primary) note of a musical key containing the previous two notes (Cuddy & Lunney, 1995). But this predictor could not be applied to brightness or loudness sequences, as musical keys cannot be formed in those dimensions. Tonality-based principles of melodic expectation, however well supported they may be, are not the concern of the present study, which seeks to compare contour-based expectations across pitch, brightness and loudness sequences.
In part, our expectations were that lower absolute values of Proximity would lead to higher ratings, and that both Post-skip Reversal and Inertia would be generally supported by our data, but our primary hypothesis was that listeners’ expectations would be similar for contours in loudness and brightness to expectations for contours in pitch. Thus, the exact choice of predictors was less critical than the comparison of responses across the three auditory dimensions.
To evaluate the strength of these principles against our data, we coded each melody heard by listeners with a value indicating the degree to which that melody fulfilled each principle. Proximity was coded as the absolute difference, in steps, between the second and third notes in a melody. For example, if the second and third notes were the same, Proximity was 0, and if the third note was 12 steps down from the second note, Proximity was −12. Inertia was coded as True when a small interval (2 or 3 steps) was followed by a continuation in the same direction, False when a small interval was followed by a continuation in the opposite direction, and Neutral for any large context interval (9 or 10 steps). Post-skip Reversal was coded as True when a large interval (9 or 10 steps) was followed by a continuation in the opposite direction, False when a large interval was followed by a continuation in the same direction, and Neutral for any small context interval (2 or 3 steps). For both of these predictors, we expected true values to produce higher ratings than false values.
This produced three predictor variables, which we later compared against listener ratings. Bayesian ordinal-regression (Congdon, 2006) and repeated-measures analyses of variance (ANOVAs) were used to evaluate the significance of the contribution of each predictor in the three auditory dimensions.
Results
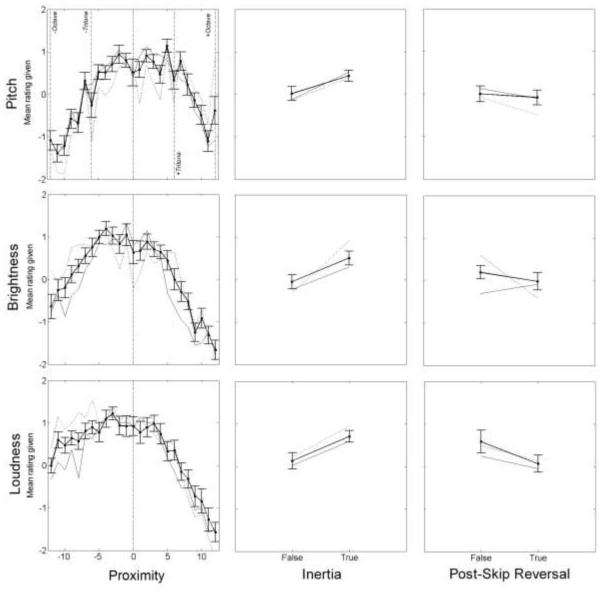
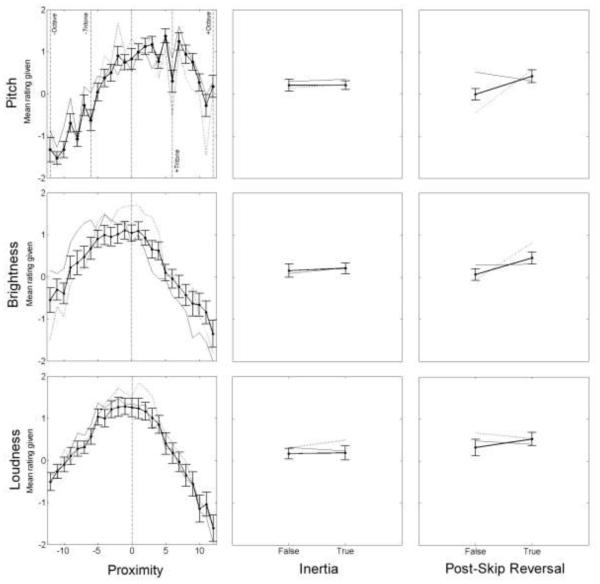
Figure 3 shows the means and between-subject standard errors of the ratings from all participants (thick solid line, n = 18), as well as means for the upper quartile (dotted line, n = 4) and lower quartile (thin solid line, n = 5) of participants ranked by musical experience. Ratings are plotted as a function of each predictor: Proximity, Inertia, and Post-skip Reversal.
Figure 3.
From Experiment 1, listener ratings of continuation for three-tone sequences in pitch (top), brightness (center), and loudness (bottom). Columns correspond to the three predictors (Proximity, Inertia, and Post-skip Reversal). Vertical dashed lines mark important values of the Proximity predictor. Mean ratings from all subjects are plotted in black with error bars +/− one standard error (between subjects). Dotted lines show mean ratings from the 4 subjects with 12 or more years of musical training. Thin solid lines show mean ratings from the 5 subjects with 1 or fewer years of musical training.
As expected based on earlier studies of the perception of pitch-based melodies (Schellenberg et al., 2002; Schellenberg, 1997), ratings in the pitch dimension were highest for small absolute values of Proximity, and decreased as the size of the interval between the second and third notes increased. Our new results show that the same general pattern also holds for both brightness and loudness (Fig. 3, left column). These rating data were fitted using an ordinal-regression model with asymmetric Gaussian functions (Kato, Omachi, & Aso, 2002) of the predictor (Proximity). Based on 95% credible intervals (Bayesian confidence intervals, CI), the mean (μ) of the fitted Gaussians did not differ significantly from zero for any of the three dimensions: pitch: μ = 0.88, CI = [−0.79; 2.70]; brightness: μ = −1.62, CI = [−3.45; 0.28]; loudness μ = 1.59, CI = [−0.50; 3.84]. For loudness, the difference between the upper and lower slopes of the fitted asymmetric Gaussians (Δ) was significantly larger than zero, Δ = 0.62, CI = [0.34; 0.92], reflecting lower ratings with an increasingly loud final tone; for pitch and brightness, no significant asymmetry was observed, Δ = −0.05, CI = [−0.28; 0.18] and Δ = 0.09, CI = [−0.17; 0.39], respectively.
Although the shape of responses as a function of Proximity was very similar across the three auditory dimensions, some “fine structure” was observed in the pitch ratings that did not appear to be present in the other dimensions. For instance, dips were observed at 6 semitones, corresponding to a musical interval of an augmented fourth. This fine structure was clearer in the most musically trained listeners (dotted lines) and was not apparent in the ratings of the least musically trained listeners (thin solid lines).
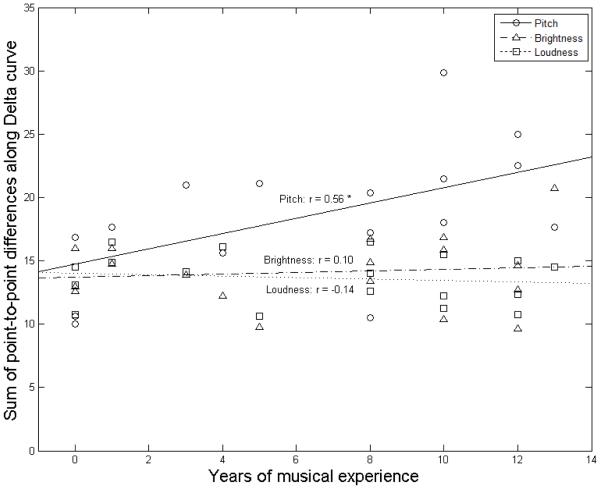
In order to quantify the degree of non-monotonic fine structure or “jaggedness” in ratings along the Proximity predictor, we summed the point-to-point absolute differences in ratings along this curve for each subject in each dimension. The results are plotted in Figure 4, as a function of the number of years of musical training experienced by each subject. A one-way repeated-measures ANCOVA considering dimension (within subjects) and years of musical experience (between subjects) showed a significant main effect of dimension, F(2,32) = 11.359, p < 0.001, η2 = 0.415, a significant main effect of musical experience, F(1,16) = 9.288, p = .008, η2 = 0.367, and a significant interaction between musical experience and dimension, F(2,32) = 3.377, p = .047, η2 = 0.174.
Figure 4.
Summed absolute point-to-point differences in ratings along the Proximity curve as a function of years of musical experience. Least-squares lines are plotted for all three dimensions along with correlation coefficients (r). The asterisk (*) indicates a significant correlation at p < 0.05.
The results from Experiment 1 lend support to the expectation for fulfillment of Inertia, i.e., a melody continuing in the same direction after a small step. A two-way repeated-measures ANOVA considering dimension (pitch, brightness, or loudness) and fulfillment of Inertia (true or false; only small context intervals considered) showed a significant main effect of Inertia fulfillment, F(1,17) = 6.23, p = 0.023, η2 = 0.268, but no significant main effect of dimension, F(2,34) = 2.28, p = 0.117, η2 = 0.119, and no significant interaction, F(2,34) = 0.664, p = 0.521, η2 = 0.038.
No evidence was found for a preference for Post-skip Reversal, i.e., a reversal in melodic direction after a large step: ratings either remained flat or decreased somewhat between negative and positive values of the predictor in all three auditory dimensions. A two-way repeated-measures ANOVA considering dimension (pitch, brightness, or loudness) and fulfillment of Post-skip Reversal (true or false, only large context intervals considered) showed no significant main effect of Post-skip Reversal fulfillment, F(1,17) = 1.24, p = 0.282, η2 = 0.068. The main effect of dimension was significant, F(2,34) = 4.9, p = 0.014, η2 = 0.224, presumably reflecting the fact that ratings for large implicative intervals were generally more positive in the loudness dimension. However, there was no significant interaction, F(2,34) = 1.82, p = 0.172, η2 = 0.098, suggesting that the effect of Post-skip Reversal fulfillment was similar across the three auditory dimensions.
Discussion
Overall, the ratings were very similar across the three auditory dimensions, with the predictors providing similar accounts of the data. In terms of coarsely-grained expectations for broad contour, no special status for pitch was found. However, on a more fine-grained level, there were some notable non-monotonicities observed in the pitch ratings in the most musically trained listeners that were absent in the brightness and loudness ratings.
The higher ratings at Proximity values of 7 and 12 semitones in either direction correspond to musical intervals of a perfect fifth and octave, respectively, which are considered in Western musical traditions to be the most consonant intervals, whereas the lower ratings at Proximity values of 1, 6, and 11 semitones, correspond to musical intervals of a minor second, augmented fourth, and major seventh, which are considered to be among the most dissonant (McDermott, Lehr, & Oxenham, 2010; Plomp & Levelt, 1965). The fact that preference for tonal consonance is stronger in musically trained listeners is consistent with many earlier findings (Krumhansl & Shepard, 1979; McDermott, Lehr, et al., 2010), and is consistent with the prevailing view that these preferences may be learned through training and exposure (Szpunar, Schellenberg, & Pliner, 2004; Thompson et al., 2000). On the other hand, the observed interaction between musical experience and “jaggedness” of ratings along the Proximity predictor may simply reflect increased sensitivity to pitch changes in musically trained listeners, in the absence of increased sensitivity to brightness and loudness changes. This is an empirical question that could be resolved with future research.
The absolute interval size (Proximity) was a strongly supported predictor, with smaller absolute values predicting higher ratings. In this respect our results are consistent with converging evidence for contour-based principles of melodic expectancy from two experimental paradigms: subjective ratings of continuation (Cuddy & Lunney, 1995; Schellenberg et al., 2002; Schellenberg, 1996; Schmuckler, 1989) and production, by singing or playing, of the note considered most likely to follow a melodic context (Carlsen, 1981; Schellenberg et al., 2002).
The results of Experiment 1 also lend support to the principle of Inertia, with fulfillment of this principle linked to higher ratings across melodies in all three stimulus dimensions. This is consistent with some previous support for this principle (Larson, 2004), but inconsistent with other studies that found no evidence for it (Cuddy & Lunney, 1995; Schellenberg, 1997).
Post-skip Reversal was not supported in any dimension, which seems contrary to both our expectations and the existing evidence. However, Post-skip Reversal may in fact be an emergent property, reflecting the restricted range of most melodies (von Hippel & Huron, 2000). Indeed, explicit prescriptions for small intervals between notes and for narrow overall ranges, taken together, produce an expectation for a small step in the opposite direction following a large leap, or a regression towards the mean (Temperley, 2008; von Hippel & Huron, 2000).
The explanation of Post-skip Reversal in terms of regression towards the mean may account for why it was not a strong predictor in Experiment 1. In the present study, individual trials occurred in quick succession and it is likely that listeners retained some memory of recent trials, making it plausible that subjects were basing judgments in part relative to the overall range of stimuli presented in the experiment. The second note in our paradigm was always taken from the middle of range of possible notes in the scale (the 13th, 14th, or 15th member of the 27-step scale). Therefore, a large context interval called for the first note, not the second note, to fall at an extreme end of the range. The first note in a large context interval was especially likely to sound “extreme” in Experiment 1 because the context interval changed from trial to trial, so it is likely that context intervals in the immediately preceding trials were small, or went in the opposite direction, or both. In this way, Experiment 1 effectively dissociated Post-skip Reversal from a regression towards the mean, and the results may imply that, once dissociated, Post-skip Reversal may not play an important role in predicting expectations. However, this conclusion may only be valid for short melodies such as we used in our experiments, reflecting a general expectation for continuation in any short sequence. It remains possible that longer melodies may still produce expectations for Post-skip Reversal, even when the skip does not end on a value far from the mean of recently heard notes.
The question remains why we did not find Post-skip Reversal to be a significant predictor, whereas Cuddy and Lunney (1995) did, while using a very similar paradigm. One important difference may be our randomized presentation of context intervals, compared with their blocked presentation method, which resulted in the same context interval being presented 25 times in a row. The other difference was that they alternated the second note of this context interval between C4 and F#4 on every trial, whereas in Experiment 1 the second note was randomly selected from a set of three intermediate values.
Eliminating both of these paradigmatic differences and replicating the experiment of Cuddy and Lunney as exactly as possible may produce similar results to theirs in the pitch dimension. Presenting the same context interval 25 times in a row shifts the overall mean of recently heard tones towards the mean of that context interval, which could cause listeners to expect regression towards that mean in the form of Post-skip Reversal, “filling in” the context interval. This is only true if the same absolute pitches are used on every trial, but that condition is almost fulfilled by alternating between C4 and F#4. It seems plausible that listeners could form templates based on alternating trials and that some form of “build up” could occur. Experiment 2 was designed to test this possibility by replicating the design of Cuddy and Lunney (1995) as closely as possible, and by extending their paradigm to the dimensions of brightness and loudness.
Experiment 2: Longer-term context effects on melodic expectation in three auditory dimensions
Rationale
The results from Experiment 1 supported our initial hypothesis that contour-based melodic expectation generalizes to auditory dimensions other than pitch. One aspect of the data, however, was not consistent with an earlier study of melodic expectation. In contrast to the results of Cuddy and Lunney (1995), we found no significant effect of Post-skip Reversal in any dimension, whereas they had found an effect using pitch contours. We ascribed this difference to their use of stimuli that were blocked by context interval. The current experiment had two main aims. The first aim was to attempt to replicate the findings of Cuddy and Lunney (1995) by using stimuli that were blocked by context interval. The second aim was to compare the responses in this altered paradigm across the three auditory dimensions tested in Experiment 1. If changes in the stimulus presentation method led to similar changes in all three dimensions, the results would further support our main hypothesis that contour-based melodic expectations generalize beyond the dimension of pitch.
Method
Stimuli
Harmonic complex tones were generated in the same way as Experiment 1. The “scales” created in Experiment 1 were adjusted slightly to increase the number of available steps from 27 to 33. In pitch, F0s ranged from C3 (131 Hz) to F#5 (741 Hz) in 1-semitone steps, with the 2nd note of every melody alternating between C4 (262 Hz) and F#4 (370.5 Hz). In brightness, the center frequency of the Gaussian function ranged from 131 Hz to 4192 Hz, in 2-semitone steps, with the 2nd note alternating between 524-Hz and 1048-Hz centroids. In loudness, the step size had to be decreased to 1.5 dB (down from 2 dB in Experiment 1), to allow for 33 levels ranging from 30 to 79.5 dB, with the 2nd note alternately 48 or 57 dB. As in Experiment 1, when the stimuli varied along a single dimension, the others were held constant. The constant values for the three dimensions were 131 Hz for F0, 800 Hz for spectral center frequency, and 50 dB SPL for sound level.
The same 8 context intervals (±2, ±3, ±9, and ±10 steps) and 25 continuation tones (12 steps below to 12 steps above the second tone) were tested, and the 1200ms-400ms-800ms pattern in stimulus onset asynchronies was also retained.
Procedure
Eighteen new listeners, 3 male and 15 female, were recruited from the Twin Cities campus of the University of Minnesota, ranging in age from 18 to 39 (M = 23.8, SD = 5.1). This group of participants reported an average of 6.2 years of musical training (SD = 7.2; range 0 to 20 years). The five participants who reported no musical training and the five participants who reported the highest amount of musical training (at least 8 years) were taken as an approximation of the lower and upper quartiles, respectively, of participants ranked by musical experience. Once again, all listeners had normal audiometric hearing thresholds (defined as not exceeding 20 dB HL for octave frequencies between 250 and 8000 Hz).
Listeners heard and rated melodies in the same way as Experiment 1, with two important exceptions. First, as noted above, the 2nd note of the melody alternated from trial to trial between the 13th and 19th notes of the 33-step scale. Second, the melodies were blocked by context interval, such that melodies beginning with the same context interval were all presented in immediate succession instead of being randomized from trial to trial. The presentation order for the dimensions was again counterbalanced with a Latin Square design.
Results
Figure 5 shows the means and between-subject standard errors of the ratings from all participants in Experiment 2 (thick solid line, n = 18), as well as means for the upper quartile (dotted line, n = 5) and lower quartile (thin solid line, n = 5) of participants ranked by musical experience. Ratings are plotted as a function of each predictor: Proximity, Inertia, and Post-skip Reversal.
Figure 5.
From Experiment 2, listener ratings of continuation for three-tone sequences in pitch (top), brightness (center), and loudness (bottom). Columns correspond to the three predictors (Proximity, Inertia, and Post-skip Reversal). Vertical dashed lines mark important values of the Proximity predictor. Mean ratings from all subjects are plotted in black with error bars +/− one standard error (between subjects). Dotted lines show mean ratings from the 5 subjects with 8 or more years of musical training. Thin solid lines show mean ratings from the 5 subjects with 0 years of musical training.
The pattern of results along the proximity predictor was broadly similar to the pattern found in Experiment 1. Once again, small absolute values of Proximity produced higher ratings in all three dimensions (Fig. 5, left column). We applied the ordinal-regression model introduced in Experiment 1, with asymmetric Gaussian functions of Proximity fitted to the data. The 95% Bayesian confidence intervals (CI) identified by this analysis found no evidence that the mean (μ) of the fitted Gaussians differed from zero for any of the three dimensions: pitch: μ = 0.95, CI = [−3.27 4.31]; brightness: μ = −0.98 , CI = [−3.22 1.33]; loudness μ = 1.98, CI = [−0.27 4.38]. The difference between the upper and lower slopes (Δ) of the fitted Gaussians was significantly larger than zero only in the loudness dimension, Δ = 0.36, CI = [0.18; 0.55], again reflecting lower ratings with an increasingly loud final tone; this asymmetry was not significant in pitch, Δ = −0.13, CI = [−0.41 0.11], or brightness, Δ = −0.03, CI = [−0.13; 0.22]. Also similarly to Experiment 1, there appears to be more fine-grained non-monotonicity in the ratings for pitch than in the other two dimensions, with characteristic dips at the tritones, and this effect appears more pronounced among the most musically trained listeners.
The results from Experiment 2 provided no support for the expectation for fulfillment of Inertia, i.e., a melody continuing in the same direction after a small step. A two-way repeated-measures ANOVA considering dimension (pitch, brightness, or loudness) and fulfillment of Inertia (true or false; only small context intervals considered) found neither a significant main effect of fulfillment, F(1,17) = 0.048, p = 0.829, nor a main effect of dimension, F(2,34) = 0.063, p = 0.939, and no interaction, F(2,34) = 0.070, p = 0.932.
In contrast, the results provided significant support for Post-skip Reversal, i.e., a reversal in melodic direction after a large step. A two-way repeated-measures ANOVA considering dimension (pitch, brightness, or loudness) and fulfillment of Post-skip Reversal (true or false, only large context intervals considered) showed a significant main effect of fulfillment, F(1,17) = 5.38, p = 0.033, η2 = 0.241, but no significant main effect of dimension, F(2,34) = 1.819, p = 0.178, and no significant interaction, F(2,34) = 0.649, p = 0.529.
Discussion
As predicted, we successfully replicated Cuddy and Lunney’s (1995) results in pitch by more precisely matching their paradigm in presentation order and absolute pitch selection. Experiment 1 found no support for Post-Skip Reversal, when context intervals were presented in random order from trial to trial, but in Experiment 2, when the melodies were blocked by context interval, the ratings lent support to the principle. More importantly, this substantive change in the pattern of results was observed in all three dimensions.
Taken together, the results from our two experiments, along with those of previous studies (Cuddy & Lunney, 1995; Schellenberg et al., 2002), suggest that some properties of melodic expectation, such as Post-skip Reversal and Inertia may be critically dependent on the presentation method. It could be argued that the randomized presentation method of Experiment 1 is more valid than the blocked method of Experiment 2, and that Post-skip Reversal in particular may simply reflect a more general principle of tendency towards the mean (Temperley, 2008; von Hippel & Huron, 2000). However, the question of whether certain predictors are valid is tangential to the main finding of the present study: regardless of the predictors and the methods used, the results from pitch, brightness, and loudness remain similar. This outcome further supports the hypothesis that contour-based expectations for melodic continuation generalize beyond the auditory dimension of pitch.
General Discussion
The purpose of our study was to test whether certain broadly supported principles and features of contour-based expectations for melodic continuation are specific to pitch, or whether they generalize to other auditory dimensions. We found substantial agreement between the ratings for sequences in all three auditory dimensions and established that the predictors that were successful in predicting expectations in pitch were similarly successful in the dimensions of brightness and loudness.
Composers such as Arnold Schoenberg and Anton Webern have composed melodic contours in timbre by switching melodies rapidly from instrument to instrument, a technique called Klangfarbenmelodie (Schoenberg, 1911). The present study found that listener expectations for musical contour can be fulfilled or violated not only by changes in pitch, but also by changes in timbre or loudness. This finding provides empirical evidence for the validity of composing melodic contours in dimensions other than pitch.
Melodic expectancies are stimulus-stimulus expectancies, where one stimulus type implies another stimulus type. This specific kind of expectancy is an essential part of learning (Bolles, 1972). More broadly, expectancies, as a general cognitive phenomenon, play a large part in determining behavior (Kirsch, 1985). Expectancies are often studied specifically through perception of musical melodies in pitch, as a controlled and limited context from which more general conclusions concerning expectancies can be drawn (Dowling, 1990; Schellenberg et al., 2002). Although it explores only auditory perception, the present study provides some evidence for the previously unsupported assumption that patterns of expectation for melodies can be generalized beyond the context of musical melodies defined by changes in pitch.
Overall, the results suggest that the principles of good melodic continuation, described in many earlier studies of both experimental psychology and music theory, are not specific to melodies, as traditionally defined by pitch movement. Instead they may reflect general principles that extend to many auditory dimensions. Specifically, the principles involving interval size (Proximity) and trajectory (Inertia) may be viewed as expressions of basic principles of auditory perceptual organization: sequential sounds that vary by only a small amount in any given dimension, and continue within a limited trajectory, are more likely to form a single “auditory stream.” Thus, as suggested by Huron (2001), expectations for melodic continuation and voice leading may reflect principles that encourage perceptual binding. Our results extend and generalize this conclusion to perceptual dimensions other than pitch, and suggest that rules of melodic continuation have not emerged from exposure to specific music or pitch-based melodies, but may instead reflect fundamental principles of perceptual organization that transcend the specific dimension of pitch.
Acknowledgements
This work was supported by NIH grant R01 DC005216 and a grant from the University of Minnesota Undergraduate Research Opportunities Program (UROP).
References
- Balch W. The role of symmetry in the good continuation ratings of two-part tonal melodies. Perception & Psychophysics. 1981;29(I):47–55. doi: 10.3758/bf03198839. [DOI] [PubMed] [Google Scholar]
- Bolles RC. Reinforcement, expectancy, and learning. Psychological Review. 1972;79(5):394–409. doi:10.1037/h0033120. [Google Scholar]
- Borchert EMO, Micheyl C, Oxenham AJ. Perceptual grouping affects pitch judgments across time and frequency. Journal of Experimental Psychology. Human Perception and Performance. 2011;37(1):257–69. doi: 10.1037/a0020670. doi:10.1037/a0020670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bregman A. Auditory Scene Analysis: The Perceptual Organization of Sound. MIT Press; Cambridge, MA: 1994. [Google Scholar]
- Carlsen JC. Some factors which influence melodic expectancy. Psychomusicology: Music, Mind & Brain. 1981;1:12–29. [Google Scholar]
- Congdon P. Bayesian Statistical Modelling. Wiley; Chichester, England: 2006. [Google Scholar]
- Cuddy LL, Lunney CA. Expectancies generated by melodic intervals. Perception & Psychophysics. 1995;57(4):451–462. doi: 10.3758/bf03213071. [DOI] [PubMed] [Google Scholar]
- Dowling WJ. Scale and contour: Two components of a theory of memory for melodies. Psychological Review. 1978;85(4):341–354. [Google Scholar]
- Dowling WJ. Expectancy and attention in melody perception. Psychomusicology: Music, Mind & Brain. 1990;9(2):148–160. [Google Scholar]
- Dowling WJ, Fujitani DS. Contour, interval, and pitch recognition in memory for melodies. The Journal of the Acoustical Society of America. 1971;49(2):524–531. doi: 10.1121/1.1912382. [DOI] [PubMed] [Google Scholar]
- Huron D. Tone and voice: A derivation of the rules of voice-leading from perceptual principles. Music Perception. 2001;19(1):1–64. [Google Scholar]
- Huron D. Sweet anticipation: Music and the psychology of expectation. MIT Press; Cambridge, MA: 2006. [Google Scholar]
- Kato T, Omachi S, Aso H. Asymmetric Gaussian and its application to pattern recognition. Proceedings of the Joint IAPR International Workshops SSPR 2002 and SPR 2002. 2002:404–413. [Google Scholar]
- Kessler E, Hansen C, Shepard R. Tonal schemata in the perception of music in Bali and in the West. Music Perception. 1984;2(2):131–165. [Google Scholar]
- Kirsch I. Response expectancy as a determinant of experience and behavior. American Psychologist. 1985:1189–1202. [Google Scholar]
- Krumhansl CL, Shepard RN. Quantification of the hierarchy of tonal functions within a diatonic context. Journal of Experimental Psychology: Human Perception and Performance. 1979;5(4):579–94. doi: 10.1037//0096-1523.5.4.579. [DOI] [PubMed] [Google Scholar]
- Larson S. Musical forces and melodic expectations: Comparing computer models and experimental results. Music Perception. 2004;21(4):457–499. [Google Scholar]
- Likert R. A technique for the measurement of attitudes. Archives of Psychology. 1932;22:5–55. [Google Scholar]
- McDermott JH, Keebler MV, Micheyl C, Oxenham AJ. Musical intervals and relative pitch: frequency resolution, not interval resolution, is special. The Journal of the Acoustical Society of America. 2010;128(4):1943–51. doi: 10.1121/1.3478785. doi:10.1121/1.3478785. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McDermott JH, Lehr AJ, Oxenham AJ. Is relative pitch specific to pitch? Psychological Science. 2008;19(12):1263–71. doi: 10.1111/j.1467-9280.2008.02235.x. doi:10.1111/j.1467-9280.2008.02235.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McDermott JH, Lehr AJ, Oxenham AJ. Individual differences reveal the basis of consonance. Current Biology. 2010;20(11):1035–1041. doi: 10.1016/j.cub.2010.04.019. doi:10.1016/j.cub.2010.04.019.Individual. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Melara RD, Marks LE. Interaction among auditory dimensions: Timbre, pitch, and loudness. Perception & Psychophysics. 1990;48(2):169–178. doi: 10.3758/bf03207084. [DOI] [PubMed] [Google Scholar]
- Monahan CB, Kendall R. a, Carterette EC. The effect of melodic and temporal contour on recognition memory for pitch change. Perception & Psychophysics. 1987;41(6):576–600. doi: 10.3758/bf03210491. [DOI] [PubMed] [Google Scholar]
- Narmour E. The analysis and cognition of basic melodic structures: The implication-realization model. University of Chicago Press; Chicago: 1990. [Google Scholar]
- Plomp R, Levelt WJ. Tonal consonance and critical bandwidth. The Journal of the Acoustical Society of America. 1965;38(4):548–60. doi: 10.1121/1.1909741. [DOI] [PubMed] [Google Scholar]
- Schellenberg EG. Expectancy in melody: Tests of the implication-realization model. Cognition. 1996;58(1):75–125. doi: 10.1016/0010-0277(95)00665-6. [DOI] [PubMed] [Google Scholar]
- Schellenberg EG. Simplifying the Implication-Realization model of Melodic Expectancy. Music Perception. 1997;14(3):295–318. [Google Scholar]
- Schellenberg EG, Adachi M, Purdy KT, McKinnon MC. Expectancy in melody: Tests of children and adults. Journal of Experimental Psychology: General. 2002;131(4):511–537. doi:10.1037//0096-3445.131.4.511. [PubMed] [Google Scholar]
- Schenker H. In: New musical theories and fantasies. Rothgeb J, editor. Schirmer Books; New York: 1935. [Google Scholar]
- Schmuckler M. Expectation in music: Investigation of melodic and harmonic processes. Music Perception. 1989;7:109–150. [Google Scholar]
- Schoenberg A. Harmonielehre. Verlagseigentum der Universal-Edition; Leipzig and Vienna: 1911. [Google Scholar]
- Szpunar KK, Schellenberg EG, Pliner P. Liking and memory for musical stimuli as a function of exposure. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2004;30(2):370–81. doi: 10.1037/0278-7393.30.2.370. doi:10.1037/0278-7393.30.2.370. [DOI] [PubMed] [Google Scholar]
- Temperley D. A probabilistic model of melody perception. Cognitive Science. 2008;32(2):418–44. doi: 10.1080/03640210701864089. doi:10.1080/03640210701864089. [DOI] [PubMed] [Google Scholar]
- Thompson WF, Balkwill LL, Vernescu R. Expectancies generated by recent exposure to melodic sequences. Memory & Cognition. 2000;28(4):547–55. doi: 10.3758/bf03201245. [DOI] [PubMed] [Google Scholar]
- Von Hippel P, Huron D. Why Do Skips Precede Reversals? The Effect of Tessitura on Melodic Structure. Music Perception. 2000;18(1):59–85. [Google Scholar]