A Numerical Study of Water Loss Rate Distributions in MDCT-based Human Airway Models

Abstract

Both three-dimensional (3D) and one-dimensional (1D) computational fluid dynamics (CFD) methods are applied to study regional water loss in three multi-detector row computed-tomography (MDCT)-based human airway models at the minute ventilations of 6, 15 and 30 L/min. The overall water losses predicted by both 3D and 1D models in the entire respiratory tract agree with available experimental measurements. However, 3D and 1D models reveal different regional water loss rate distributions due to the 3D secondary flows formed at bifurcations. The secondary flows cause local skewed temperature and humidity distributions on inspiration acting to elevate the local water loss rate; and the secondary flow at the carina tends to distribute more cold air to the lower lobes. As a result, the 3D model predicts that the water loss rate first increases with increasing airway generation, and then decreases as the air approaches saturation, while the 1D model predicts a monotonic decrease of water loss rate with increasing airway generation. Moreover, the 3D (or 1D) model predicts relatively higher water loss rates in lower (or upper) lobes. The regional water loss rate can be related to the non-dimensional wall shear stress (τ^*) by the non-dimensional mass transfer coefficient (h₀^*) as h₀^* = 1.15 τ^*0.272, R = 0.842.

INTRODUCTION

The major cause of water loss from the airway surface liquid (ASL) that lines the respiratory airways is evaporation into the inspired air. Although some water is recovered via condensation during expiration, there is a net water loss, the rate of which depends on the inhaled air temperature, humidity and minute ventilation. Dehydration of the ASL can cause dysfunction of the mucociliary transport system. This dysfunction is apparent in cystic fibrosis.² Dehydration of the ASL is also implicated in exercise-induced bronchoconstriction.²⁷ Although the total lung water loss is well established,^6,9,10,19 the water loss rate at the bronchial segment level is not well studied. Thus, an evaluation of subject-specific regional water loss is of interest to determine whether there may be geometry-based regional vulnerability to dehydration. Such an investigation requires evaluating the roles of key variables on the dehydration of the airways, including airway diameter, regional ventilation, minute ventilation, and the inhalation conditions. By coupling a model of airway surface water loss to an epithelial cell model for airway surface liquid regulation,¹³ such a composite model may provide new insights between airway fluid dynamics and regional cellular functions.

Most recent studies of 3D temperature and humidity in the respiratory tract have focused on an understanding of dynamic growth and deposition of hygroscopic aerosols/droplets.^7,12 Only a few previous studies have focused specifically on the airway water loss distribution with respiration. In experimental studies, inhaled and exhaled air humidities at the mouth or nose are measured and the overall water loss under various breathing conditions are calculated.^6,9,19 In numerical simulations, the temperature and humidity in the airways are computed, the instantaneous evaporative fluxes are estimated by Fick’s Law,^6,8,25 and then the amounts of water loss are estimated by integrating the evaporative fluxes over time. The key to numerical estimation of evaporative flux is to accurately capture the local water vapor concentration gradients, however previous studies evaluating airway surface water loss have largely been based on one-dimensional (1D)^6,25 or two-dimensional (2D)⁸ models which have several limitations. First, they make simplifying assumptions to reduce a complex 3D flow to 1D or 2D systems. One such assumption is axisymmetric air velocity, temperature, and humidity profiles in the airway radial direction, whereas previous studies have shown non-axisymmetric distributions especially near bifurcations.²⁸ Second, 1D and 2D geometric models lack many 3D geometric features, such as variation in cross-sectional area along an airway, curvature, and non-circular cross-sectional profiles. Moreover, most previous studies^6,8 have been limited to Weibel’s symmetric airway model,²⁶ and do not account for inter-subject variability.

To understand water loss in the ASL at the segmental level, we have previously developed and validated both 1D and 3D thermo-fluid computational fluid dynamics (CFD) models with realistic wall boundary conditions for temperature and humidity, and have applied these models to characterize temperature and humidity distributions in human airways.²⁸ The objectives of the present study are three-fold. First, both 1D and 3D models are applied to study the characteristics of regional water loss and water loss rate in response to our previously studied humidity and temperature distribution patterns in the human airways. We expand these investigations to the study of secondary flow effects, which only exist in 3D. As 1D models are more commonly used than 3D, the comparison of 1D and 3D results helps better understand the limitations in accuracy and validity of the 1D models. Second, the inter-subject variability of water loss due to subject-specific airway structure and regional ventilation is examined. Third, a correlation between local shear stress and a convective mass transfer coefficient is established to better understand ASL homeostasis.

MATERIALS AND METHODS

Volumetric multi-detector-row computed tomography (MDCT) lung images from three human subjects, acquired under separate studies (NIH grants HL064368 & EB005823) with the University of Iowa IRB and radiation safety committee approval, were used in this study. The three subjects were the same subjects used in a previous computational study.²⁸ All subjects were normal non-smokers: subject A was a 32 year-old male with BMI of 21.6; subject B was a 20 year-old male with BMI of 22.33; subject C was a 32 year-old female with BMI of 26.63. Imaging was acquired with the subjects placed in the supine body posture and coached to breath-hold near total lung capacity. Scanning was performed using a Siemens Sensation 64-slice MDCT scanner (Forchheim, Germany; scan parameters: 120 kV, 75–100 mAs, 0.75–0.13 mm slice thickness, 0.5–0.6 mm slice spacing, 1.00–1.25 pitch, and B35 reconstruction kernel).

The 3D CT-based airway models are reconstructed from segmentations of the MDCT images and consist of the upper (viz. extra-thoracic) airways and the central airways that resolve the surfaces of up to six or seven airway generations.²⁸ For example, the 3D CT-based upper (or central) airways for subject A corresponds to the portion of the 3D CT-based airway model above (or below) the horizontal line marked with “Top of trachea” in Fig. 1(a). The 1D CT-based central airway models are composed of the skeletons and segmental diameters of the corresponding 3D CT-based central airways models. At the most distal CT-resolved segments, the 1D airway model is supplemented using a volume-filling (VF) algorithm²² which generates an anatomically-consistent subject-specific 1D VF airway tree that extends to the terminal bronchioles. Figure 1 displays the 3D CT-based airway models overlaying with their corresponding 1D CT-based central airway tree and 1D VF tree. Hereafter, the ‘1D tree’ means the conducting airway tree that consists of the 1D CT-based central airway tree and the VF airway tree, and the ‘3D CT-based model’ consists of the upper and central airways unless “upper” or “central” is used.

FIGURE 1.

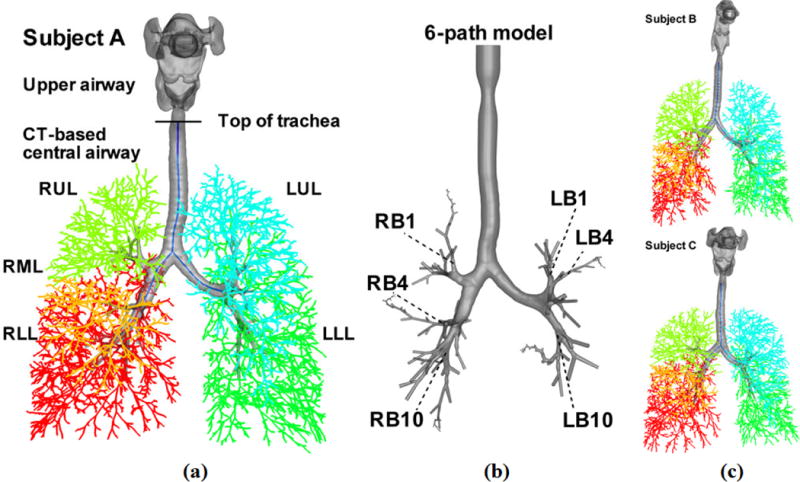
3D and 1D airway geometrical models of subject A in (a), and subject B and subject C in (c). LUL, left upper lobe (blue); LLL, left lower lobes (green); RUL, right upper lobe (light green); RML, right middle lobe (orange); RLL, right lower lobe (red). The CT-based models consist of the upper airways (above the top of trachea) and CT-based central airways (below the top of trachea). (b) The 3D 6 path model of subject A, which consists of the vocal cords, the CT-based central airways and, beyond CT resolution, 6 paths of cylindrical VF airways extending up to the 22^nd generation. These 6 paths go through the RB1, RB4, RB10, LB1, LB4, and LB10 segmental bronchi as marked, respectively.⁴

In addition to the above airway models, a ‘six path’ 3D model was created for subject A (hereafter referred to as the ‘6-path model’) as shown in Fig. 1(b), for assessment of water loss beyond the 3D CT-based airway. The 6-path model consists of the vocal cords above the trachea, the 3D CT-based central airways and – beyond CT resolution – 6 paths of 3D peripheral airways that extend up to the 22^nd generation.¹⁸ The six paths comprise the airway segments in the 1D VF tree that go through the LB1, LB4, LB10, RB1, RB4 and RB10 segmental bronchi, respectively. These segments are modeled as 3D cylinders using the diameters, orientations and lengths in the 1D VF tree as discussed by Lin et al.^13,15 The six paths used here are the same paths selected by the Severe Asthma Research Program (SARP), to study alterations of airway tree structure in asthmatic patients.⁴ The mesh of the 6-path model consists of 9.88 million tetrahedral elements with a non-dimensional distance of the first grid point from the wall of y+ = 4.8 in the trachea at 15 L/min. This mesh is comparable to that of the CT-based model for subject A with 9.76 million tetrahedral elements and y+ = 4.4 in the trachea at 15 L/min. For a mesh sensitivity test, please refer to the on-line supplementary material and Wu et al.²⁸.

The 3D thermo-fluid CFD approach solves the incompressible Navier-Stokes equations along with the transport equations for temperature and water vapor concentration using a large-eddy simulation technique.^13,14,28 The 1D model only solves the 1D transport equations for temperature and water vapor concentration, using the 1D flow rate distribution derived from image registration,²⁹ and the velocity radial profile given by Eq.(2).²⁸ At the airway wall, a heat conduction equation is solved, and energy balance is enforced at the interface between the airway lumen and the ASL for both 1D and 3D models.

After solving 3D temperature and water-vapor-concentration transport equations, the evaporative flux J_evap (μm/s) at the airway wall is calculated by Fick’s law using

$$J_{\mathit{evap}}=\frac{1}{\rho }(D+D_T)\frac{\partial C}{\partial r}{|}_{R^{-}},$$ (1)

where C denotes the water vapor concentration. ρ = 1.0e03 kg m⁻³ is the density of water in the ASL, D (2.7e-05 m² s⁻¹) and, $D_T\left(=\frac{v_T}{\mathit{St}}\right),$ are the molecular and turbulent diffusivities, respectively, of water vapor in air. St is the turbulent Schmidt number of water vapor in air (assumed to be equal to turbulent Prandtl number taken as 0.9¹¹) and v_T is Vreman’s subgrid-scale eddy viscosity,²⁴ which reduces to zero for laminar flow. D_T is set to zero for the 1D model and the effect of turbulence is lumped into θ in Eq. (2). In this case the assumed radial profiles of velocity, temperature and water vapor concentration take the form of:

$$\phi (r)={\phi }_R+({\phi }_0-{\phi }_R)(1-{(\frac{r}{R})}^{\theta })$$ (2)

where φ represents velocity, temperature, or water vapor concentration. φ₀ is the value at the center of the circular lumen, and φ_R is the value at the interface of airway lumen and wall. θ is assumed to depend on the Reynolds number.^21,28 Substitution of equation (2) with φ=C into equation (1) yields, $J_{\mathit{evap}}=\frac{1}{\rho }D\frac{\theta (C_R-C_0)}{D_a/2},$ where D_a is the local equivalent diameter computed as $D_a={(4A_L/\pi )}^{1/2}$ with A_L=local cross-sectional area. To improve the 1D solver prediction on the evaporative flux, instead of using θ = Re/50 as in Wu et al.,²⁸ θ is reformulated as described in the following two steps.

First, a mass flux balance equation is enforced at the interface between the airway lumen and the ASL, where the mass flux convected away from the airway wall equals the mass flux diffused from the ASL to the airway lumen:

$$\frac{1}{\rho }{h}_0(\overline{C_R}-\overline{C_m})=\frac{1}{\rho }\overline{(D+D_T)\frac{\partial C}{\partial r}{|}_{R^{-}}}$$ (3)

where h₀ is the mass transfer coefficient, $\overline{C_R}$ is the local water vapor concentration at the interface of ASL and lumen. $\overline{C_m}$ is the lumen water vapor concentration weight-averaged by the local mass flow rate, viz. $\overline{C_m}=\frac{1}{\dot{m}}{\displaystyle \int \rho uC}·d{A}_L,$ where ṁ is the mass flow rate, and u and C are the velocity and the water vapor concentration, respectively, expressed by Eq. (2). The overhead bar denotes the averaged value over a distance of D_a along a segment. R⁻ denotes the gradient at the lumen side of the interface. Equations (2) and (3) give Sh = 2(θ+1), where Sh is the Sherwood number (plesae refer to the supplementary material for detailed derivation).

Second, Sh was found to be correlated with $\mathit{Re}\frac{D_a}{D_t}$ in Wu et al.²⁸, where Re is the branch Reynolds number, and D_t is the equivalent diameter of the trachea. By fitting Sh computed from 3D CFD data in the airways of the three subjects under investigation at three minute ventilations at both peak inspiration and peak expiration using the method of least squares, one obtains:

$$\mathit{Sh}=3.521{(\mathit{Re}\frac{D_a}{D_t})}^{0.281},R=0.856$$ (4)

Thus, for $\mathit{Re}\frac{D_a}{D_t}>6.68,$ which corresponds to transitional and turbulent flows,

$$\theta =1.7605{(\mathit{Re}\frac{D_a}{D_t})}^{0.281}-1,$$ (5)

whereas for $\mathit{Re}\frac{D_a}{D_t}\le 6.68,$ θ = 2,²¹ which is derived from the parabolic velocity profile in fully developed laminar pipe flow.

All cases (listed in Table 1) use the room air condition of 27.6 °C and 34.7% RH as in the experimental study of McFadden et al.¹⁶ A sinusoidal waveform is used, with the periods and tidal volumes of 5 s and 0.5 L, 2 s and 0.5 L, 2 s and 1 L, for the simulations of 6, 15, and 30 L/min, respectively.²⁸ The image-registration-based subject-specific flow boundary condition²⁹ is adopted to obtain lobar ventilation distributions as shown in Table 2. For each case, the 1D model (as in Wu et al.²⁸) was first solved for 200 breaths to allow the temperature and humidity to reach quasi-steady state. The 1D solutions were then provided to the 3D models (including the three CT-based models and one 6-path model) to initialize the conditions at the 3D airway wall, and to act as boundary conditions at the most distal 3D airway openings during expiration. For the 1D cases, the temperature and humidity inlet conditions at the top of the trachea were taken from the corresponding 3D cases (see Table 1) at the top of the trachea (see Fig. 1). For more details, please refer to the supplementary material and Wu et al.²⁸

Table 1.

Case information: Three 3D CT-based airway geometric models are utilized to evaluate inter-subject differences. Their corresponding 1D airway trees are used to evaluate the difference between 3D and 1D models. The 3D and 1D CFD simulations employ subject-specific lobar ventilation, and consider three different minute ventilations (listed in Table 1). The 3D and 1D models are those that are primarily used to address the three objectives of this study. The 3D models extend only as far as the CT image resolution allows. To determine whether the characteristics of water loss rate in the 3D peripheral airways (beyond CT resolution) is consistent with the findings for the 3D CT-based central airway, a 6-path model was designed (including CT-based large airways plus smaller ‘generated’ airways). To test the impact of different assumptions for flow distribution, the lobar ventilation was altered from subject-specific (the control case) to uniform distribution (the experimental case) in a 3D and a 1D model. These are the final cases listed in the table.

Subject	Geometric Model	Boundary Condition	CFD Model	Minute Ventilation
Major cases
A	CT-based	Subject-specific lobar ventilation	3D	6, 15 and 30 L/min
B	CT-based	Subject-specific lobar ventilation	3D	6, 15 and 30 L/min
C	CT-based	Subject-specific lobar ventilation	3D	6, 15 and 30 L/min
A	1D tree	Subject-specific lobar ventilation	1D	6, 15 and 30 L/min
B	1D tree	Subject-specific lobar ventilation	1D	6, 15 and 30 L/min
C	1D tree	Subject-specific lobar ventilation	1D	6, 15 and 30 L/min
Test cases
A	6-path	Subject-specific ventilation	3D	15 L/min
A	CT-based	Uniform lobar ventilation	3D	15 L/min
A	1D tree	Uniform lobar ventilation	1D	15 L/min

Table 2.

Percent distributions of subject-specific and uniform lobar ventilations: Because the flow distribution to RML is the smallest, the percent distribution to RML for the experimental case (with uniform lobar ventilation) is set essentially to the value for its control counterpart (with subject-specific lobar ventilation).

Subject	LUL	LLL	RUL	RML	RLL
Subject-specific lobar ventilation
A	0.148	0.348	0.126	0.059	0.319
B	0.208	0.279	0.186	0.063	0.264
C	0.185	0.281	0.123	0.056	0.355
Uniform lobar ventilation
A	0.235	0.235	0.235	0.060	0.235

^*LUL, left upper lobe; LLL, left lower lobes; RUL, right upper lobe; RML, right middle lobe; RLL, right lower lobe.

RESULTS

Water loss validation

Water loss is defined as the volume of water lost due to evaporation over a minute over a region. In order to compare with existing measurement data of the overall water loss in the entire respiratory tract, column (e) (or (f)) in Table 3 shows the overall water loss estimated by the sum of the water loss in the 3D upper airways, the 3D (or 1D) CT-based central airways and the 1D VF airways. Please refer to the supplementary material for the unit conventions used for various quantities discussed here. The average overall water losses are 0.156, 0.359, and 0.662 mL/min at respective 6, 15, and 30 L/min based on the 3D CT-based central airways, while they are 0.157, 0.369, and 0.675 mL/min based on the 1D CT-based central airways. The differences are less than 3%. The upper airways are responsible for about 77, 73, and 67 % of the overall water loss at (respectively) 6, 15, and 30 L/min, agreeing with the reported 71% and 59 % of water loss in the upper airways for breathing from nose and mouth, respectively.¹⁰ The VF airways are responsible for about 3, 10, and 18 % of the overall water loss at 6, 15, and 30 L/min, respectively. The increased percentage in the VF airways is because increased ventilation draws a greater proportion of unsaturated inspiratory air deeper into the lung.

Table 3.

The overall water loss (mL/min) of the three subjects with three minute ventilations

Minute Ventilation	Subject	(a) 1D CT-based central airways	(b) 3D CT-based central airways	(c) 3D upper airways	(d) 1D VF airways	(e) Total water loss based on (a)+(c)+(d)	(f) Total water loss based on (b)+(c)+(d)	[(e)–(f)]/(e): 1D vs. 3D CT-based models (%)
6 L/min	A	3.38E-02	3.86E-02	1.19E-01	3.31E-03	1.56E-01	1.61E-01	−2.98%
	B	2.76E-02	2.02E-02	1.25E-01	4.98E-03	1.58E-01	1.50E-01	4.93%
	C	3.85E-02	3.68E-02	1.15E-01	4.88E-03	1.58E-01	1.57E-01	1.09%
	Avg.	3.33E-02	3.19E-02	1.20E-01	4.39E-03	1.57E-01	1.56E-01	1.01%
15 L/min	A	7.69E-02	7.22E-02	2.68E-01	3.12E-02	3.76E-01	3.71E-01	1.27%
	B	5.85E-02	4.13E-02	2.65E-01	3.53E-02	3.59E-01	3.42E-01	5.04%
	C	7.82E-02	7.02E-02	2.54E-01	3.85E-02	3.71E-01	3.63E-01	2.21%
	Avg.	7.12E-02	6.12E-02	2.62E-01	3.50E-02	3.69E-01	3.59E-01	2.84%
30 L/min	A	1.24E-01	1.15E-01	4.64E-01	1.12E-01	7.00E-01	6.91E-01	1.30%
	B	9.60E-02	7.42E-02	4.35E-01	1.16E-01	6.47E-01	6.25E-01	3.49%
	C	1.19E-01	1.11E-01	4.34E-01	1.26E-01	6.79E-01	6.71E-01	1.19%
	Avg.	1.13E-01	1.00E-01	4.44E-01	1.18E-01	6.75E-01	6.62E-01	1.99%

Time history of evaporative flux

The time histories of the 1D and 3D overall evaporative fluxes from the ASL within the CT-based central airways are shown in Fig. 2 for three breathing cycles, where positive (or negative) flux is taken as evaporation (or condensation). During inspiration (or expiration), the lumen humidity is lower (or higher) than the values at the interface between airway lumen and ASL. The humidity gradient between the lumen and the interface drives the water vapor to evaporate (or condense) from (or to) the ASL. However, the overall condensation during expiration is only 32% of the overall evaporation during inspiration, indicating that the ASL experiences a net water loss during breathing. Overall, both 1D and 3D transient evaporative fluxes agree well.

FIGURE 2.

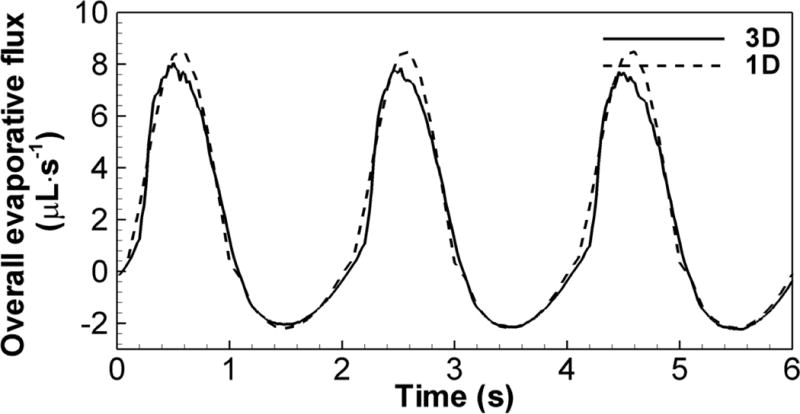
The time histories of 1D and 3D overall evaporative fluxes in CT-based central airways of subject C over a period of three cycles at 15 L/min.

Water loss rate distribution

The water loss rate is defined as the net loss of water by evaporation during respiration per area per min and has the unit of μL·cm⁻² min⁻¹. The water loss rate is considered so that water loss from epithelial cells per unit area at any specific region of interest can be quantified. Figure 3 shows the contours of the 3D water loss rate in the central airways. The general trends in the three subjects show good consistency. Specifically, the water loss rate is elevated at the bifurcation and then decreases along its inner wall. The water loss rate at the outer wall of the bifurcation is usually the lowest. There may exist some regions with negative water loss rate, meaning that there is more water condensation than evaporation from the surface, for example, at the outer wall of carina where swirls and recirculations are usually formed. The upper lobes experience less water loss than the lower lobes. In the case of 6 L/min, the water loss rate becomes quite small in the small distal branches, whereas in the cases of 15 L/min and 30 L/min more unsaturated air penetrates deeper into the small airways and the water loss rate remains high even at the small distal branches. In contrast, Figs. 4 (a), (b) and (c) show that the distribution of 1D water loss rate regardless of ventilation exhibits a generally monotonic feature that does not sensitively capture local variations. As the 1D distributions for the three subjects exhibit similar features, only subject A is shown. Figures 4 (b), (d) and (e) compare the distributions of water loss rate predicted by the 1D model, the 3D CT-based model and the 3D 6-path model of subject A at 15 L/min, respectively. The two 3D models yield almost the same distribution of water loss rate. The 6-path model also shows that the water loss rate drops to zero quickly after passing the 3D CT-based central airways. While the current study is focused on the intra-thoracic airways, for the sake of completeness, Fig. 4 (f) shows the water loss rate distributions in the upper airways obtained from the 3D CT-based airway model of subject A. The results show that the water loss rate tends to be higher near the constricted and/or curved regions where high flow-induced shear stress may occur as shown in locations marked as (i)–(iii). Moreover, it increases with increasing ventilation (not shown).

FIGURE 3.

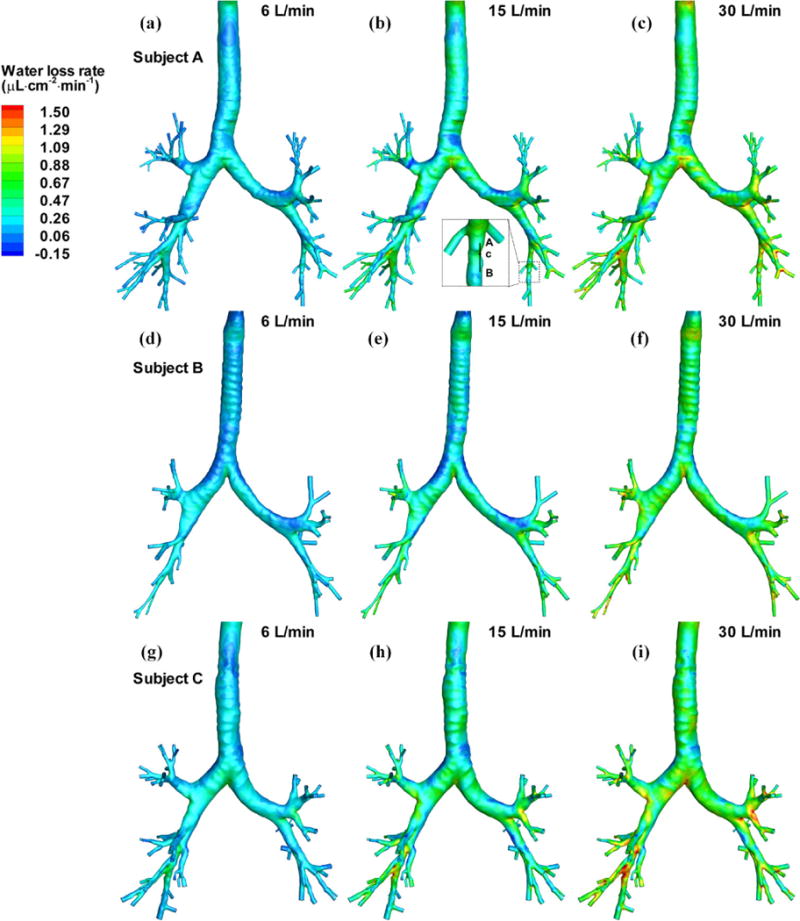
Distributions of the water loss rates of three subjects at three minute ventilations. The data along line AB in the insert of (b) are extracted for further analysis in Fig. 8.

FIGURE 4.

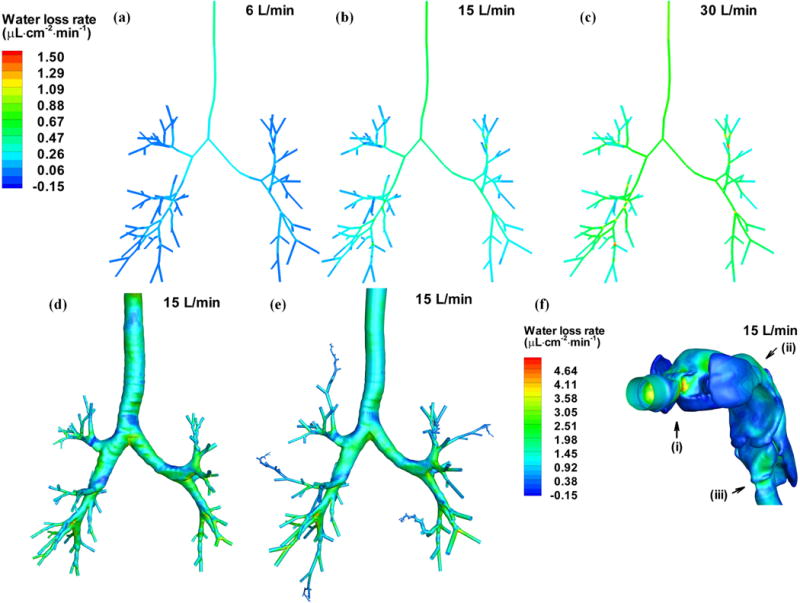
Distributions of the water loss rate of subject A in the 1D CT-based central airways at: (a) 6 L/min, (b) 15 L/min and (c) 30 L/min. (b), (d) and (e) compare the distributions of the water loss rate of subject A predicted by the (b) the 1D model, (d) the CT-based model and (e) the 6-path model, respectively. (f) Distribution of water rate in the upper airway of subject A at 15 L/min. (i), (ii) and (iii) mark the locations of high water loss rate.

To further quantify the above observations, the water loss rate is presented by lobe as well as by generation for both 1D and 3D data. Figure 5 shows the average water loss rate by lobe with (Lobe 0, LUL, LLL, RUL, RML, RLL, Overall)=(trachea + primary bronchi, left upper lobe, left lower lobe, right upper lobe, right middle lobe, right lower lobe, CT-based central airways). The results show that the water loss rate increases almost proportionally to increasing flow rate. Both models predict an increase of about 0.02 μL·cm^−2·min⁻¹ in the average water loss rate in the CT-based airways per liter increase in minute ventilation. However, the trends predicted by both models are quite different. The 1D water loss rate is the highest in Lobe 0, whereas the 3D water loss rate is the highest in the lower lobes. Furthermore, the differences between upper lobes and lower lobes are much greater in 3D than in 1D.

FIGURE 5.

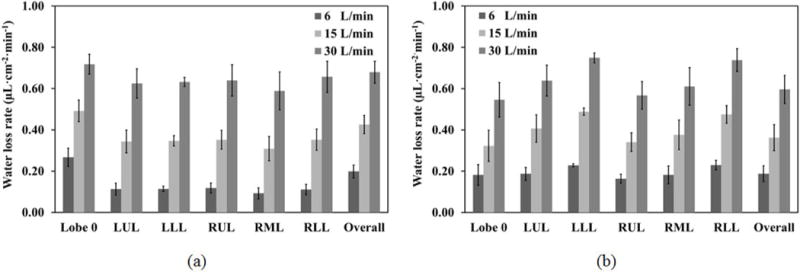
The average water loss rates (μL·cm^−2· min⁻¹) of the trachea and primary bronchi (Lobe 0), five lobes, and the CT-based airways (Overall) at three minute ventilations based on: (a) the 1D models and (b) the 3D CT-based models, of threes subjects.

To further investigate the differences between lobar water loss rates predicted by 1D and 3D models, we performed the 3D experimental case using subject A at 15 L/min, but with a uniform ventilation distribution in the upper and lower lobes as shown in Table 2. The 1D and 3D lobar distributions of the normalized water loss rate (=lobar water loss rate / average water loss rate in five lobes; it is used for fair comparisons between 1D and 3D, minimizing the absolute value differences for clarity.) in Figs. 6 (a) and (b) for the control and experimental cases resemble those of the lobar ventilation in the inserts on the upper left corner. However, when comparing the ratios of the water loss rates in the upper lobes to those of the lower lobes in 1D and 3D, the 3D results always have lower ratios than those of 1D regardless of ventilation distribution. For example, in the control case, the ratio of LUL to LLL water loss rate and the ratio of RUL to RLL water loss rate in 1D are 0.85 and 1.01, respectively, while they are 0.80 and 0.66 in 3D. In the experimental case, the ratio of LUL to LLL water loss rate and the ratio of RUL to RLL water loss rate in 1D are 1.16 and 1.61, respectively, while they are 0.97 and 1.01 in 3D. That is, regardless of the ventilation distribution, the 1D model tends to accommodate higher percentage of cold dry air in the upper lobes than the 3D model. The underlying reasons will be explained in the Discussion section.

FIGURE 6.

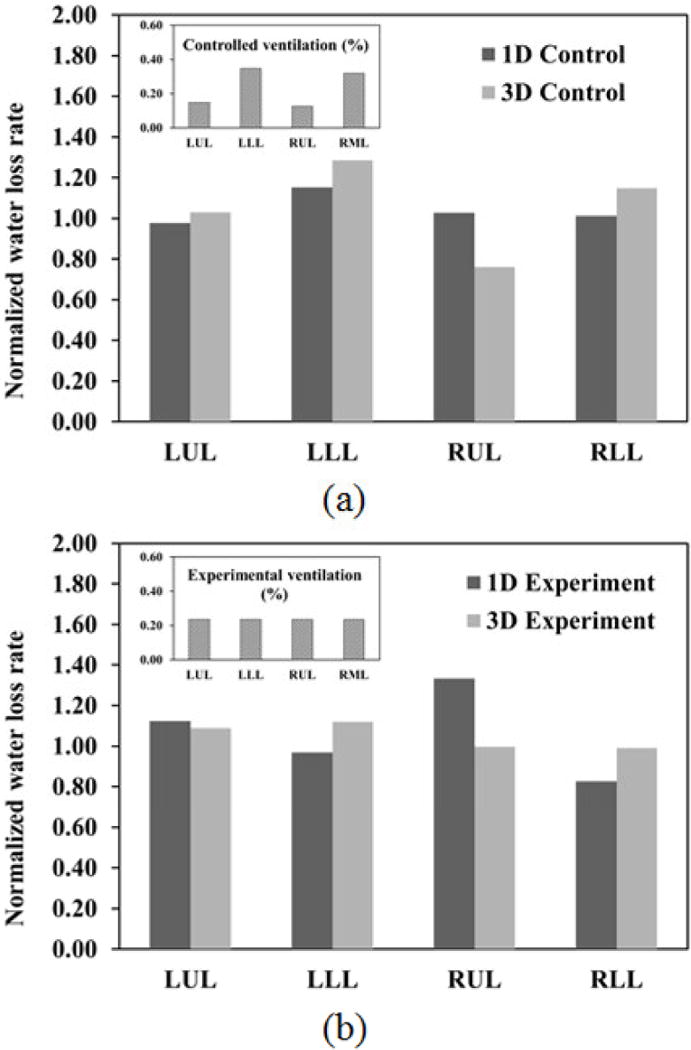
Comparison of the normalized lobar water loss rates by the average water loss rate in five lobes predicted by 1D and 3D CT-based models: (a) the control (original) cases with subject-specific lobar ventilation and (b) the experimental cases with uniform lobar ventilation for subject A at 15 L/min. The percent distributions of lobar ventilation for the control and experimental cases are shown in the inserts on the upper left corner.

Figure 7 (a) shows that both 1D and 3D models predict a decrease of the water loss with increasing generation number except from the 2^nd to 3^rd generation. Comparing with the water loss in the entire 1D tree, Fig. 7 (b) reveals that the peak water loss after the 0^th generation (trachea) roughly occurs between the 4^th and 6^th generations and then decreases monotonically. To eliminate the effect of the total surface area of the airway wall, the water loss rates by generation in the 1D and 3D CT-based central airway models are displayed in Fig. 7 (c), where both models predict completely different trends. That is, the 3D model predicts an increase of the water loss rate with increasing generation, while the 1D model predicts the highest water loss rate in the trachea and a monotonic decrease with generation. Figure 7 (d) compares the water loss rates in the entire 1D tree, the 3D 6-path model, and the 3D CT-based model of subject A and the average values of three CT-based models. The 6-path model predicts almost the same trend with the CT-based model in the first 5 generations. The water loss rates from the 6^th to 9^th generation predicted by the two 3D models still exhibit the similar trend, but are quantitatively different because the 6-path model has more branches than the CT-based model in these generations. The 6-path data starts to decrease at the 8^th generation and reduces to zero at about the 14^th generation. In contrast, the 1D data shows a monotonic decrease beginning from the trachea. Hence, the 3D-predicted water loss rate first increases and then decreases. The enhanced water loss rate in 3D may be caused by the secondary flows formed at bifurcations that are prohibited in 1D, as will be discussed later.

FIGURE 7.

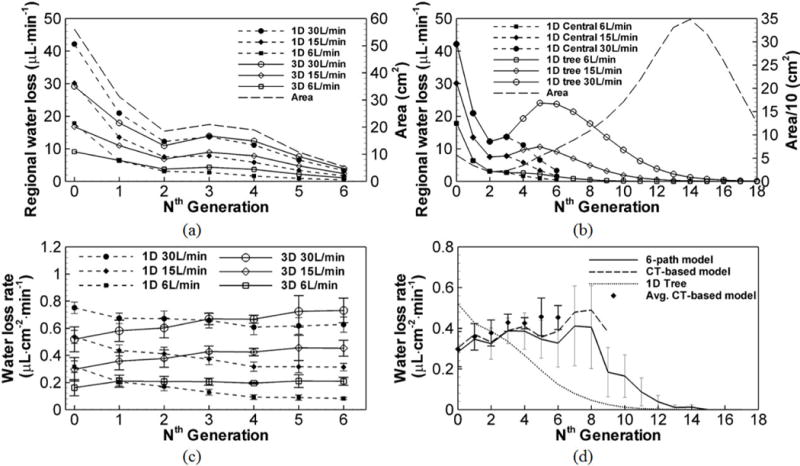
(a) The average water loss at the n^th generation of 1D and 3D CT-based central airways at the three minute ventilations. The surface area in each generation of the CT-based airway model is also plotted. (b) The average water loss at the n^th generation of the entire 1D tree comparing to that of the 1D CT-based central airway model (see “1D central” in the legend). The surface area in each generation of the 1D tree is plotted. (c) The average water loss rate of all three subjects at the n^th generation of 1D and 3D in the CT-based central airways at the three minute ventilations. (d) The water loss rates of subject A predicted by the 6-path model, the CT-based model and the 1D tree model, comparing to the average water loss rate of the three CT-based models at the n^th generation. The error bars of both 1D and 3D data in (c) and 3D CT-based model data in (d) show the standard deviation of the three subjects in a given generation. The error bars of the 6-path model data in (d) show the standard deviation of the water loss rates of the airway branches in a given generation.

Shear stress vs. evaporative flux

As both wall shear stress and evaporation are important factors in regulating ASL,^20,25 the relationship of these two quantities is examined. Theoretically, shear stress is related to evaporative flux because local velocity gradients affect local gradients of temperature and water vapor concentration. As shown in Figs. 3–5 and Fig. 7, with increasing flow rate the water loss rate increases almost proportionally. Figures 8 (a) and (b) show that the distribution of overall evaporation along line AB in an airway segment residing in the LLL of subject A in Fig. 3 (b) is similar to the distribution of average shear stress during inspiration, having a correlation coefficient of 0.967. Furthermore, the distribution of overall condensation is similar to the average shear stress during expiration, having a correlation coefficient of 0.978. In contrast, the 1D predicted values at the same location exhibit almost constant values mainly because of missing local geometric features. Figure 8 (c) shows that the time histories of evaporative flux and shear stress at a sample point c along line AB follow the imposed sinusoidal breathing waveform. Thus, the results in Figs. 8 (a), (b) and (c) suggest that local shear stress is strongly correlated with local evaporative flux in both time and space. Figure 8 (d) further shows that dimensionless wall shear stress ${\tau }^{\ast }=\frac{\tau }{\frac{v^2{\rho }_a}{{D_a}^2}}={(\frac{u^{\ast }{D}_a}{v})}^2={({\mathit{Re}}^{\ast })}^2,$ where ${\mathit{Re}}^{\ast }=\frac{u^{\ast }{D}_a}{v}$ with $u^{\ast }=\sqrt{\frac{\tau }{{\rho }_a}}$ and dimensionless mass transfer coefficient h₀^* = h₀D_a/D can be correlated as h₀^* = 1.15 τ^*0.272 (R = 0.842), where v = 1.65e − 05 m² s⁻¹ is the kinematic viscosity of moist air, and ρ_a=1.12 kg m⁻³ is the density of moist air.¹⁷ More than half of the data points, especially at low minute ventilation, have their dimensionless shear stresses varying within the range of [0, 50] ×1000. In this range, h₀^* increases rapidly with τ^*. The remaining data points in the range of [50, 300] ×1000 exhibit a moderate increase of h₀^* with τ^*.

FIGURE 8.

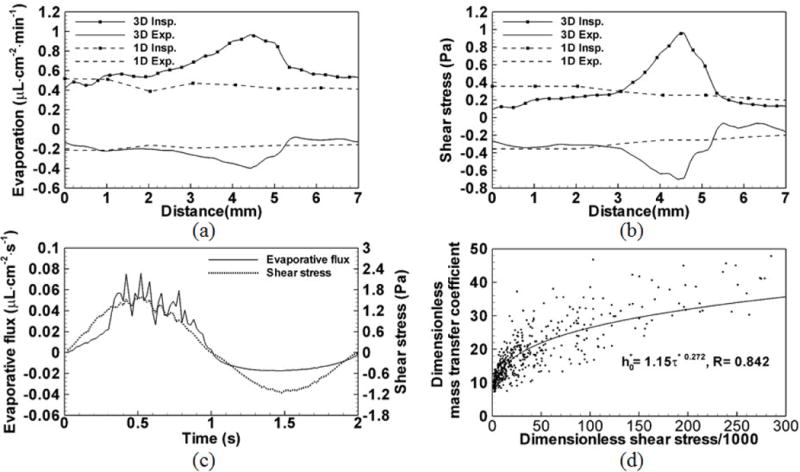
(a) Distributions of the overall evaporation during inspiration and the overall condensation during expiration along line AB in the insert of Fig. 3 (b). The 1D evaporation and condensation at the same location are also plotted. (b) Distributions of the average shear stress during inspiration and the average shear stress during expiration along line AB. The 1D shear stresses during inspiration and expiration are also plotted. (c) Time histories of shear stress and evaporative flux at point c in the insert of Fig. 3(b). Their distributions resemble the imposed sinusoidal wave-form. (d) The correlation between non-dimensional local mass transfer coefficient (h₀^*) and non-dimensional local shear stress (τ^*). Data points are extracted from the three subjects at peak inspiration and peak expiration of the three minute ventilation.

DISCUSSION

Water loss distribution

Both 1D and 3D overall water losses in the entire respiratory tract are in good agreement with existing in vivo measurements. Specifically, Freund et al.⁹ reported that the respiratory water losses under room air conditions of RH = 65%; T_I = 25 °C are about 0.167 mL/min for resting conditions, 0.5 mL/min for light to moderate exercise conditions, and 1 mL/min for moderate to heavy exercise conditions. Tabka et al.¹⁹ reported an overall water loss of 0.275±0.049 mL/min after 5 min at rest breathing wet warm air (RH = 31%; T_I = 30 °C), and of 0.592±0.093 mL/min after 5 min of exercise in slightly heated ambient air (RH = 18%; T_I = 28 °C). In comparison, with the condition of RH = 34.7%; T_I = 27.6 °C in McFadden et al.¹⁶, the current 3D CFD model predicted 0.156, 0.359 and 0.662 mL/min at respective 6, 15, and 30 L/min, and the 1D model predicted 0.157, 0.369, and 0.675 mL/min. 6 L/min is comparable to a resting minute ventilation, and 30 L/min is comparable to moderate exercise. To further validate the water loss predictions, additional benchmark cases with conditions in Tabka et al.¹⁹ (RH = 31%; T_I = 30 °C) and in Freund et al.⁹ (RH = 65%; T_I = 25 °C) were simulated. It is noted that these studies only indicated that the data were measured at resting conditions, but did not report actual minute ventilation values. The CT-based model of subject C was considered because the water loss of this subject is close to the average value of the three subjects (see Table 3). The reported range of ventilation at rest varies from 6 L/min to 10 L/min,^1,3 thus we performed simulations at 6 L/min and 10 L/min. The predicated water-loss values of 0.150 (at 6L/min) to 0.244 mL/min (at 10 L/min) are comparable to Tabak et al’s. measurements of 0.275±0.049 mL/min when using the condition of Tabak et al. and the predicted values of 0.123 (at 6L/min) to 0.195 mL/min (at 10 L/min) are comparable with the 0.167 mL/min observed by Freund et al. when using the Freund et al. conditions. From these results, it appears that minute ventilation and inspired humidity are more important factors than inspired temperature in affecting water loss. With the same inlet conditions, the water loss is nearly proportional to minute ventilation. Additionally, with the same minute ventilation, Freund et al.’s inspired condition of 25 °C and 65% RH (absolute humidity (AH) = 0.015 kg·m⁻³) comparing to Tabka et al.’s inspired condition of 30 °C and 31% RH (AH = 0.009 kg·m⁻³), the predicted water loss is lower in the Freund et al.’s case. This is because Freund et al.’s inspired absolute humidity is higher despite the lower inspired temperature. Therefore, both 3D and 1D models give reasonable predictions of the overall water loss.

The overall water loss is a function of both airway wall surface area and local water loss rate. Figure 7 (a) shows the distributions of both 1D and 3D water losses in the CT-based central airway tree by generation. The 1D model predicted higher water loss in the trachea, but slightly lower water loss in the 2^nd and higher generations at 6 L/min (or from the 3^rd generation at 30 L/min). Nonetheless, the 1D and 3D predicted water losses exhibit some similar trends, correlating to the surface area by generation. For example, Fig. 7 (b) shows that the 1D water loss follows the change of surface area through the 4^th generation (or the 6^th generation depending on minute ventilation). After the 4^th (or 6^th) generation, as air is close to its saturation point, the water loss rate decreases at a faster rate than the increase of surface area. This results in a decrease of water loss. Water loss drops to zero when the isothermic saturation boundaries (ISB) are reached. The ISBs vary with the paths and flow rates as demonstrated previously by Wu et al.²⁸ For peak inspiration at 15 L/min, saturation is reached at the 8^th to 9^th generation in the upper lobes and the 9^th to 12^th generations in the lower lobes as predicted by the 1D model. This is consistent with Fig. 7 (d). The water loss rates predicted by the 1D model drops to zero by around the 11^th generation for all paths.

1D and 3D comparisons

Unlike the 3D model, the radial profiles of air velocity, temperature and humidity in the 1D model are assumed axisymmetric and their gradients are determined by the parameter θ in Eq. (2) such that with the same T₀ and T_R, a greater θ leads to a higher evaporative flux. Even though the correlations in Eq. (4) and the parameterization of θ in Eq. (5) used by the 1D model are derived empirically by fitting to the 3D CFD data, the 1D model is still not sensitive enough to capture local heat and mass transfer processes in the human airways that depend on local gradients of air velocity, temperature and humidity. This is first evident in the trachea, where the rate of water loss in the 1D model is far higher than for the 3D model. Because the 3D model captures complex flow structures, the gradient of humidity near the walls depends on actual physical processes. For example, the laryngeal jet might increase the evaporative water loss locally if the jet core impinges on the tracheal wall, while the recirculation would decrease the evaporative water loss. However, as θ in the 1D model is determined by Re and airway diameter (which are largest in the trachea), θ tends to over-predict the water loss rate in the trachea. The 3D non-axisymmetric distributions of temperatures and water vapor concentrations at bifurcations also have significant influence on water loss rate, as reflected when studied by lobes and by generations.

Water loss rate by lobes

The use of subject-specific geometry and ventilation distribution is the primary cause of lobar difference in the water loss rates as shown in Fig. 5. However, if comparing the LUL and LLL or RUL and RLL, two other reasons should be accounted for. First, the upper lobes are more proximal to the trachea compared with other lobes and therefore when air enters the upper lobes, it has traveled less distance than it has traveled when it enters the lower lobes. As a result, the temperature and humidity of air entering the upper lobes are usually lower, causing the upper lobes to be prone to losing more water. Second, the secondary flow formed at the carina on inspiration tends to distribute more cold air to the lower lobes. Hence the lower lobes are prone to greater water loss. For the 1D model, without secondary flow, the shortened path to the upper lobes contributes to the water loss rate difference. For the 3D model, with both of the above effects contributing, the second effect dominates, thus explaining the 1D vs. 3D model differences in the lobar water loss rate. These tendencies can be seen clearly with the comparison between the control case and experimental case in Fig. 6. With the uniform lobar ventilation, the 1D model’s upper lobes have considerably higher water loss rates compared with the lower lobes, while in the 3D model, the secondary flow distributes cold air to the lower lobes, preventing significant increases in water loss rates in the upper lobes as those in 1D. In conclusion, the lower lobes tend to have higher water loss rates not only because of the higher ventilation to the lower lobes, but because of the secondary flow at the carina serving to asymmetrically distribute more cold air to the lower lobes as predicted only by the 3D model.

Water loss rate by generation

By eliminating the effect of surface area, Fig. 7 (c) shows that the trends of 1D and 3D water loss rates are quite different. The elevated water loss rate in 3D CT-based airways as illustrated in Fig. 3 can be attributed to convection-dominated secondary flows at bifurcations. As shown in a previous study²⁸, after reaching the bifurcations the air in the center of the lumen is skewed toward the inner wall of the bifurcation, forming secondary flows. The central air is cooler, skewing the radial temperature profile. This skewed profile creates a higher gradient of water vapor concentration along the inner wall and elevates the water loss rate in the vicinity of the bifurcation as illustrated in Fig. 3, contributing to an increase of the water loss rate as shown in Fig. 7 (c). However, as air approaches saturation, the water loss rate gradually decreases to zero as shown in Fig. 7 (d).

As previously described, the 3D splitting mechanism at the bifurcation only exists on inspiration. As a result, the 1D and 3D differences of water loss rate distribution by generation are only reflected in the overall evaporative flux distribution but not the overall condensation flux distribution. During inspiration the average 1D overall evaporative flux decreases with increasing generation, while the 3D evaporative flux increases with generation and then decreases. This resembles the trends of the 1D and 3D water loss rates in Fig. 7 (c). However, during expiration the average 1D and 3D overall condensation fluxes by generation exhibit similar trends; that is, both decrease almost linearly with generation at 6 L/min, both remain almost constant with generation at 15 L/min, and both increase almost linearly at 30 L/min.

Inter-subject variability

Because water loss rate is proportional to the gradient of water vapor concentration at the airway wall, it depends on a) the local humidity difference between the airway lumen and the ASL; and b) the local velocity gradient, which depends on local airway structure (e.g. diameter) and regional ventilation. However, as factor (a) contributes little to the inter-subject variability,²⁸ the variability in water loss rate between subjects, as reflected in the error bars in Fig. 5, mainly comes from subject-specific airway diameter and regional ventilation. Comparing the regional water loss rates (by every generation in every lobe) for the three subjects with both 1D and 3D models, the maximum differences could vary from 5% to 52% of the average water loss rate in the three subjects. In addition, the presence of airway narrowing/constriction may increase inter-subject variability of water loss rate. Thus, regional water loss rate in diseases lungs is expected to exhibit greater inter-subject⁵ and intra-subject²³ variations.

Shear stress vs. water loss rate

Previous studies suggest that shear stress acting on airway wall epithelial cells helps the ASL to stay hydrated,²⁰ while severe water loss may contribute to mucociliary dysfunction. Thus, investigations into the correlation of shear stress and evaporative flux will help to provide subject specific patterns of ASL homeostasis¹³. The outcomes will likely depend upon two counter effects: stress-related biological (epithelial) effects will stimulate water secretion while thermodynamic effects will stimulate water loss.

The correlation between local mass transfer coefficient and local shear stress was proposed to estimate local evaporative flux. Mathematically, an increase of shear stress correlates with an increase of the mass transfer coefficient h₀. Thus, with $J_{\mathit{evap}}=\frac{1}{\rho }{h}_0(\overline{C_R}-\overline{C_m})$ shear stress correlates with the evaporative flux. With minimum information such as temperature, airway diameter and flow rate, the level of local water loss can be estimated. More importantly, physiologically, the correlation between shear stress and the mass transfer coefficient reveals the inter-relationship between the evaporative flux and shear stress and correlates them everywhere inside the airway. As both evaporative flux and shear stress serve to affect cellular functions, understanding their inter-relationship helps to study their impact on biologic function.

When correlating evaporative flux and shear stress, we found that there are two ranges. In the first range (most data samples from 6 L/min are inside this region), the shear stress is relatively small, and the mass transfer coefficient increases with shear stress rapidly. That is evaporative flux and possibly water loss rate tend to increase fast with the increase of velocity gradient. However, the second range (most data samples from 30 L/min or at constrictions are inside this region) shows that extremely high velocity gradients will cause extremely high shear stresses but not mass transfer coefficients. In this case, the evaporative flux might be only moderately elevated. Interestingly, the ATP release increases rapidly with shear stress from [0, 0.06] Pa.²⁰ This is inside the region where mass transfer coefficient also increases rapidly with the shear stress, as the first range is roughly corresponding to the [0, 0.1] Pa without nondimensionalization.

Potential application and limitation

For epithelial cells, an increase of shear stress can also trigger ATP release resulting in fluid secretion.²⁰ This may compensate for the velocity gradient-induced water loss. However, the question remains as to whether or not the fluid secretion is sufficient to result in evaporative water loss when undergoing state changes such as rest to exercise or from relaxed to constricted airway smooth muscle. Such state changes would be expected to place the system within different range of the shear stress – mass transfer coefficient relationship. Such questions can be answered with the coupling of epithelial cell models and thermo-fluid CFD described here. That is, via the prediction of evaporation coupled with cellular secretion to predict the ASL depth,^13,25 hence evaluating the dehydration of ASL directly. This may also provide insightful information to better understand the pathophysiology of diseases such as cystic fibrosis.

The prediction of regional water loss rate could potentially be applied to asthmatic lungs with severe airway constriction. As regional ventilation distribution and airway diameter are statistically different between normal and asthma patients,⁵ the water loss rate distribution for the two groups might be statistically different. Quantitative analysis could be carried out to assess the effect of morphologic changes on airway dehydration in asthma patients. Airway constriction may induce elevated water loss, causing vulnerability to dehydration. This could increase sensitivity to exercise-induced bronchoconstriction in a subset of asthma patients.²⁷

A limitation of the work presented here lies in the fact that the correlation of shear stress with mass transfer coefficients only emphasizes the effect of velocity gradients; regions near bifurcations may deviate from the correlations established here due to elevated mass transfer induced by secondary flow. Another limitation of this study is that the airway geometrical models are assumed rigid during simulation. The CFD studies with deformable airway were reported in Yin et al.³⁰. Its effect on water loss rate is yet to be investigated.