Fluid displacement during droplet formation at microfluidic flow-focusing junction

Abstract

Microdroplets and microcapsules have been widely produced using microfluidic flow-focusing junction for biomedical and chemical applications. However, the multiphase microfluidic flow at the flow-focusing junction has not been well investigated. In this study, the displacement of two (core and shell) aqueous fluids that disperse into droplets altogether in a carrier oil emulsion was investigated both numerically and experimentally. It was found that extensive displacement of the two aqueous fluids within the droplet during its formation could occur as a result of the shear effect of the carrier fluid and the capillary effect of interfacial tension. We further identified that the two mechanisms of fluid displacement can be evaluated by two dimensionless parameters. The quantitative relationship between the degree of fluid displacement and these two dimensionless parameters was determined experimentally. Finally, we demonstrated that the degree of fluid displacement could be controlled to generate hydrogel microparticles of different morphologies using planar or nonplanar flow-focusing junctions. These findings should provide useful guidance to the microfluidic production of microscale droplets or capsules for various biomedical and chemical applications.

1. Introduction

Droplet-based microfluidics has been widely used to encapsulate a variety of cells for 3D culture,^1,2 cell-based therapy,^3,4 drug delivery,^5–7 and tissue engineering^8–10 applications, to study chemical kinetics^11,12 and protein crystallization,¹³ and to synthesize organic molecules,¹⁴ nanoparticles,^15,16 and microparticles^17–20. One of the key research subjects of droplet microfluidics is the fluid mixing including displacement (i.e., movement of fluids away from their original or ideal positions) within droplets, which has been mainly investigated during droplet transportation in straight or serpentine channels^21–23. It was found that effective mixing in straight microchannel can be achieved only when one dispersed fluid is located in the back or front end of the droplets (relative to the moving direction) as the internal recirculation is symmetrical to the central streamline in the microchannel.^24,25 In contrast, fast fluid redistribution is evident in serpentine microchannel due to the baker’s transformation.^11,23 Moreover, the mixing in droplets during their transportation in a microchannel is highly dependent on the initial distribution of the dispersed fluid within the droplets established during their formation.²⁵ However, only few studies have explored the fluid displacement during droplet formation. For example, the displacement of dispersed fluid during droplet growth in T-junction microfluidics was studied using μPIV or inorganic dyes^25,26 and the circular flow velocity was found to reach a maximum after a quarter of the total time of droplet formation.²⁷ A static recirculating zone was also observed in the liquid meniscus before it squeezes into a jet in the so-called liquid cone-jet mode in a microcapillary device.²⁸ However, no such study has been reported for the mixing in a flow-focusing junction (FFJ) although it has been widely used to generate droplets. Furthermore, an in-depth mechanistic understanding of fluid displacement within the droplets during their formation in FFJ is still missing.

Here we numerically and experimentally investigated the fluid displacement during droplet formation in both planar and nonplanar FFJs. By combining two independent level set functions with the Navier-Stokes equations, the numerical simulation identified two mechanisms that drive fluid displacement within droplets during their formation: the shear effect of carrier fluid and the capillary effect of interfacial tension between dispersed and carrier fluids. These two mechanisms can be represented by two dimensionless parameters, ζ and λ, respectively. Experimental results confirmed that the fluid displacement can lead to the formation of a non-intuitive O-shaped distribution of shell fluid, and the degree of fluid displacement I_in/I_out can be scaled as I_in/I_out = log₁₀(ζ^0.55/λ^0.82). Finally, we demonstrated that the degree of fluid displacement could be controlled to produce hydrogel microparticles with different morphologies using planar or nonplanar FFJs.

2. Numerical simulation

In general, microfluidic flow is governed by the laws of mass and momentum conservation. If the fluids are regarded incompressible with constant density ρ (which is fairly satisfied for the fluids in this study), the mass conservation can be described by the following equation:^29–31

$$\nabla ·\stackrel{\rightharpoonup }{u}=0$$ (1)

where u⃑ is velocity vector. For incompressible Newtonian fluid, the momentum conservation is governed by the following Navier-Stokes equation:^29–31

$$\rho \frac{\partial \overrightarrow{u}}{\partial t}+\rho (\overrightarrow{u}·\nabla )\overrightarrow{u}=\nabla ·[-p\mathit{I}+\mu (\nabla \overrightarrow{u}+{(\nabla \overrightarrow{u})}^T)]+\stackrel{\rightharpoonup }{f_b}$$ (2)

where p is hydrostatic pressure, μ is dynamic viscosity, $\stackrel{\rightharpoonup }{f_b}$ is volumetric body force. In multiphase microfluidics, only the interfacial tension force is usually considered for $\stackrel{\rightharpoonup }{f_b}$ because the effect of gravity is negligible. The body force due to interfacial tension can be calculated as follows:³²

$$\stackrel{\rightharpoonup }{f_b}=\nabla ·(\gamma (\mathit{I}-(\overrightarrow{n}{\overrightarrow{n}}^T))\delta )$$ (3)

where n⃗ is the unit outward normal vector of the interface, n⃗ = ∇∅₁/|∇∅₁|, ∅₁ is level set function, γ is interfacial tension between the carrier and dispersed phases, δ = 6|∇∅₁||∅₁(1 − ∅₁)| is Dirac delta function. The level set function ∅₁ can be calculated as follows:^33–36

$$\frac{\partial {\varnothing }_1}{\partial t}+\overrightarrow{u}·\nabla {\varnothing }_1={\gamma }_{ls}\nabla ·({\epsilon }_{ls}\nabla {\varnothing }_1-{\varnothing }_1(1-{\varnothing }_1)\frac{\nabla {\varnothing }_1}{\mid \nabla {\varnothing }_1\mid })$$ (4)

where the values of 0 and 1 for ∅₁ represent carrier oil (subscript c) and dispersed aqueous phase (including both core (subscript core) and shell (subscript shell) fluids, subscript d), respectively. The re-initialization parameter γ_ls is for controlling numerical stabilization of the level set method and the parameter ε_ls controls the interface thickness although they do not affect the final converged solution much. Another level set function ∅₁ is required to distinguish the core fluid from the aqueous shell phase as follows:^33–36

$$\frac{\partial {\varnothing }_2}{\partial t}+\overrightarrow{u}·\nabla {\varnothing }_2={\gamma }_{ls}\nabla ·({\epsilon }_{ls}\nabla {\varnothing }_2-{\varnothing }_2(1-{\varnothing }_2)\frac{\nabla {\varnothing }_2}{\mid \nabla {\varnothing }_2\mid })$$ (5)

where a value of 1 for ∅₁ indicates core fluid while a value of 0 for ∅₁ indicates the other two fluids. As a result, the values of 0, 1, and 2 of the summation (∅₁ + ∅₂) of the two level set functions are the carrier, shell, and core fluids, respectively. Furthermore, the fluid properties Ψ, such as density and viscosity, can be formulated as Ψ = Ψ_c + ∅₁ (Ψ_shell − Ψ_c) + ∅₂ (Ψ_core − Ψ_shell).

The equations (1) – (5) were solved using the commercial software COMSOL Multiphysics (Version 4.3) using the finite element method. The types of discretization for the velocity components, pressure field, and level set functions (∅₁ and ∅₂) are quadratic, linear, and quadratic, respectively. Both the streamline and crosswind diffusions were applied for the Navier-Stokes and level set equations for consistent stabilization with a tuning parameter C_k = 0.5. Backward differentiation was used to discretize time with a maximum order of 2 to further stabilize the numerical computation.

The inlet boundary conditions were specified with normal velocities or equivalent flow rates (q). The outlet was assumed as far field condition with zero pressure and zero viscous stress. The symmetry boundary condition was imposed for the symmetrical axis (if any), for which u⃑. $\stackrel{\rightharpoonup }{u}·\stackrel{\rightharpoonup }{n_a}=0,\partial K/\partial \stackrel{\rightharpoonup }{n_a}=0$, where $\stackrel{\rightharpoonup }{n_a}$ is the normal vector to the symmetrical axis and K represents all the dependent variables (including u⃑, p, ∅₁ and ∅₂ here). Because the fluid-fluid interface may move along the solid walls, they should be considered as wetted walls with the slip length β being equal to the local grid element size. A frictional force f_fr = −μu⃑/β was added onto the near-wall fluid so that the extrapolated tangential velocity component could be decreased to 0 at the distance of β outside the wall. For this time-dependent problem, the initial condition was assumed to be non-flow and non-pressurized fluids with known distribution of the level set functions ∅₁ and ∅₂.

The computational mesh was a free triangular grid. The maximum element size was set to be 15 μm and the maximum element growth rate was 1.1. The total number of elements in the computational domain was 8917, which could provide grid-independent computational results. The re-initialization parameter γ_ls was set as the maximum magnitude of the inlet velocities. The ε_ls was set as the average size of the maximum and minimum elements.

3. Experimental methods

3.1. Device fabrication

The planar (one layer of photosensitive epoxy) and non-planar (multiple layers of photosensitive epoxy) microfluidic devices were fabricated by standard soft lithography techniques.³⁷ Briefly, the first layer of photosensitive epoxy (SU-8 2025, MicroChem) was spun onto a 4-inch silicon wafer. The wafer was baked on a hot plate to solidify the SU-8. Next, it was exposed to ultra violet (UV) light through the shadow mask of the first layer design and baked on the hot plate again. Similarly, the second and third layers of microchannels were successively imposed onto the wafer, and these layers were aligned on an EVG620 mask aligner. Because the thicknesses of these layers are different, the spinning speeds of SU-8, the pre- and post-exposure baking times and temperatures, and the exposure time of UV light were adjusted according to the data sheet for SU-8 2000 (MicroChem). After patterning the features of microchannels, the wafer was developed with SU-8 developer (MicroChem) for 10 min, rinsed with isopropyl alcohol, and dried with nitrogen gas. Thereafter, polydimethylsiloxane (PDMS, Dow Corning) pre-polymer and its crosslinking agent (mass ration = 10:1) were fully mixed and poured onto the patterned wafer to make PDMS slabs (baked at 72 °C for 3 hours). After peeling the slabs off the wafer, they were aligned under a microscope to obtain the non-planar microfluidic devices (note: aligning is unnecessary for planar devices). Finally, the devices were baked in an oven at 72 °C for at least 72 hours to make the channel surfaces hydrophobic before use.

3.2. Fluid preparation

Three different fluids were used in the microfluidics. The core and shell fluids are aqueous solutions of carboxylmethyl cellulose (Sigma) of various concentrations and viscosities (2 – 797 mPa s). In addition, 1% (w/v) fluorescein isothiocyanate-dextran (500 kDa, Sigma) was dissolved in the shell fluid as the fluorophore. The carrier fluid was mineral oil with Span 80. The latter is a surfactant that was used for adjusting the viscosity (30 – 49 mPa s) of mineral oil and interfacial tension coefficient (3.0 – 60 mN m⁻¹) between the aqueous solutions and oil. For the production of hydrogel particles, the shell fluid was a 2% (w/v) solution of sodium alginate in deionized water and the carrier oil emulsion was prepared as detailed elsewhere.³⁷

3.3 Experimental setup

All the fluids were introduced into the microfluidic device using syringe pumps (Harvard Apparatus). To track the distribution of dispersed fluids within droplets, we took time-lapse fluorescence (rather than bright field) images of the shell fluid. This is because the refraction indices of the fluids and the materials of microchannel walls have to match for the bright field or phase images to accurately capture the flow within droplets near the liquid-liquid interface and near the channel walls, which would alter the properties of the fluids.^25,38 The fluorescence time-lapse images were taken by a Zeiss AxioCam HSm fast-speed CCD camera equipped on a Zeiss Axio Observer.Z1 microscope under a 2.5X objective. The image size was set as 462 × 346 pixels and the exposure time was 2 ms, resulting in imaging frequency of ~64 Hz. On the other hand, static images of hydrogel particles were taken using a Zeiss AxioCam MR3 CCD camera under phase contrast field of a 10X objective. The corresponding resolution was 1388 × 1040 pixels.

3.4. Measurement of viscosity

The viscosity of fluids was measured using an AR1000N rheometer (TA instruments) in the oscillation mode. The oscillation frequency was set to be 1 Hz and the shear stress varied from 0.1 to 10 Pa. Cone-shaped plate (2°) with a diameter of 40 mm was utilized and the gap between the bottom and top plates was 52 μm. During experiments, 600 μl of the sample fluid was loaded onto the bottom plate before descending the top plate. A total of 30 points were measured during each run and three independent runs were performed for each fluid. The average value of the three independent runs was taken as the measured viscosity of each fluid. All experiments were conducted at room temperature.

3.5. Measurement of interfacial tension

The interfacial tension coefficients between carrier and dispersed fluids were measured with a pendent droplet tensiometer (Rame-Hart). During the measurement, a total of 30 ml of aqueous fluid (dispersed fluid) was loaded in a transparent chamber and a droplet of carrier fluid was dispersed at the tip of a J-shaped needle (22 gauge) so that the droplet can be stabilized upside down. Photos of the pendent droplet were taken and the interfacial tension coefficient was calculated using the software (DROP image Advanced) built in the instrument. The interfacial tension coefficient of each pair of fluids was measured independently for at least three times and their average was used in this study.

3.6. Data analysis

The fluorescence intensity of the microdroplets and the size of the hydrogel particles were measured with ImageJ. The regression analysis for the degree of fluid displacement was performed using Matlab (version R2012a).

4. Results and discussion

4.1. Mechanisms of fluid displacement during droplet formation

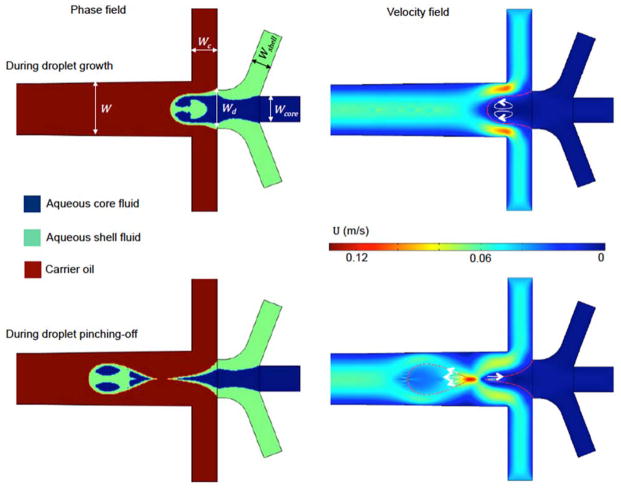
As shown in Fig. 1, numerical simulation revealed two mechanisms of fluid displacement during droplet formation. During the droplet growth stage, the dispersed fluids still attach to the inlets and the carrier fluid flows over the pendent droplet, which induces shear stress and two counter-rotating vortices (arrows in the velocity field) within the growing droplets. During droplet pinch-off stage, one of two the aqueous tails recoils back to the inlet from the pinching point with the capillary velocity of σ/μ_d.³⁹ The other aqueous tail recoils forward in the droplet that has pinched off. According to the numerical settings, σ/μ_d = 0.15 m s⁻¹, which is close to the velocity magnitude (0.133 m s⁻¹) observed at the pinching point. The recoiling could cause redistribution of the dispersed fluids in both the droplet that has pinched off and the next droplet to form. Of note, as the pinched-off droplet moves downstream in the same direction as the recoiling velocity, it causes less fluid displacement within the pinched-off droplet than the pendent one.⁴⁰ The counter-rotating vortices and the capillary recoil can disturb the aqueous core and shell fluid flows in the droplets, which could displace them away from their desired and ideal positions (i.e., the shell fluid should locate in the peripheral while the core fluid should be in the inner area of the droplets). This phenomenon was referred as fluid displacement in this study. However, these two driving forces of fluid displacement would be balanced by viscous damping effect of the dispersed fluids while the inertia effect within the droplets is negligible considering that the Reynolds Number (Re = ρ_du_dW/μ_d, where W is the channel width taken as the characteristic length) is ~0.01. As a result, it is anticipated that two dimensionless parameters could be used to characterize the relative impacts of these two driving forces for fluid displacement.

Fig. 1.

Numerical simulation of droplet formation at a planar flow-focusing junction for a typical flow condition. The arrows on the images of velocity field represent velocity vectors in the dispersed phase. Numerical settings: σ = 30 mN m⁻¹, μ_core = μ_shell = 200 mPa s, μ_c = 30 mPa s, q_core = q_shell = 0.4 ml hr⁻¹, and q_c = 10 ml hr⁻¹. Geometries: W = 400 μm, W_d = 300 μm, W_c = 200 μm, W_shell = 150 μm, and W_core = 200 μm.

4.2. Experimental observation of fluid displacement and verification of numerical simulation

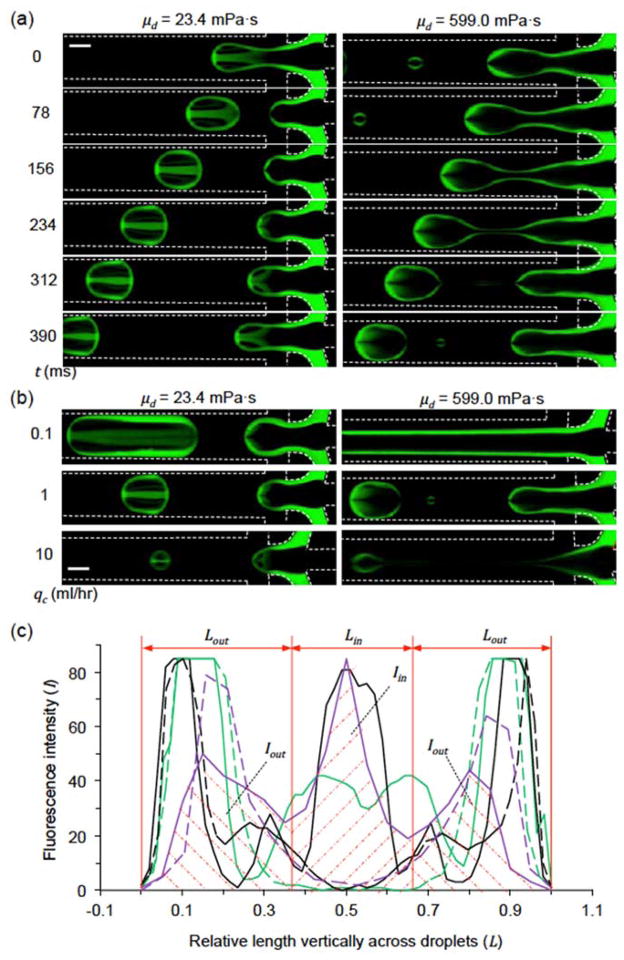
Experiments were performed to validate the fluid displacement during droplet formation observed by numerical simulation. A planar FFJ with the same design as that for numerical simulation was fabricated with depth H = 200 μm. Firstly, the presence of fluorescein isothiocyanate-dextran was proven not to affect the droplet size, morphology, internal distribution, and contact angle to the channel walls as demonstrated by the complementary images shown in Fig. S1. Because the hydrodynamic radius of fluorescein isothiocyanate-dextran is 24.3 nm,⁴¹ its diffusion coefficient in the dispersed fluids is small (D_f ≤ 3.9 × 10⁻¹³ m² s⁻¹) at room temperature according to the Stokes-Einstein equation. Therefore, the overall diffusion distance ( $\sqrt{2D_{f}t}$, where t is the total time for generating each droplet that is no more than 0.62 s in this study) of the fluorophore should be less than 0.7 μm, which is much shorter than the droplet size (> 200 μm) in this study. In addition, no fluorescence trail behind the moving droplet was observable on the fluorescence image of the droplet (Fig. 2(a) and 2(b)). The distribution and concentration of the shell fluid within the droplets were evaluated by the fluorescence intensity (I). The amount of shell fluid displaced into the central region was calculated as I_in = ∫ I d L_in and the remaining shell fluid in the peripheral region, where I_out = ∫ I d L_out is the normalized length vertically across the droplets as shown in Fig. 2(c). Therefore, I_in and I_out are the shaded area under the intensity curve (with the solid purple one as an example) over the distance of L_in in the center and L_out in the periphery of a droplet, respectively.

Fig. 2.

Fluid displacement during droplet formation in a planar flow-focusing junction. (a) Time-lapse fluorescence images during droplet formation with two different viscosities (μ_d = 23.4 or 599.0 mPa s) of the dispersed fluids. The carrier oil flow rate q_c = 1 ml hr⁻¹. (b) Fluorescence images of droplet formation with various carrier oil flow rates (q_c). (c) The fluorescence intensity (I) vertically across the newly pinched droplets in (b). Also shown are I_in and I_out as the shaded area under the intensity curve (using the solid purple one as an example) over the distance of L_in in the center and L_out in the periphery of a droplet, respectively. Solid line: μ_d = 23.4 mPa s, dashed line: μ_d = 599 mPa s; green: q_c = 0.1 ml hr⁻¹, black: q_c = 1 ml hr⁻¹, purple: q_c = 10 ml/hr. The heights of droplets are normalized to unit. For all the studies, q_core = 166.7 μl hr⁻¹ and q_shell = 33.3 μl hr⁻¹. Scale bars: 200 μm.

The spatiotemporal evolution of droplet formation at the planar FFJ is shown in Fig. 2(a). When the dispersed fluids are not very viscous (μ_d = 23.4 mPa s), a non-intuitive O-shaped distribution of the shell fluid was observed in the resultant droplet (similar to that in the pinched-off droplet predicted by numerical simulation, Fig. 1). This is probably due to the two mixing mechanisms revealed by the numerical simulation. Of note, mixing during traveling in straight channel (from 156 to 390 ms) is minimal because the shell fluid is not concentrated in either end (front or back) of the droplet.²³ Furthermore, when the flow rate of carrier fluid (q_c) varies (the droplet size changes accordingly), the distribution and intensity of shell fluid in the resultant droplet also changes (Fig. 2(b)). According to Fig. 2(c)), more shell fluid is displaced to the central region at a higher q_c. However, if the viscosity of dispersed fluid is high (μ_d = 599 mPa s), the shell fluid will stay at the peripheral of the droplets with an O-shaped distribution. This is probably due to the viscous damping effect on the momentum of fluid displacement.

Moreover, we compared our numerical simulations and experimental observations. As shown in Fig. S2, these two approaches demonstrate the same trend of the droplet morphology or the degree of fluid displacement. The O-shaped distribution of the shell fluid forms with the use of dispersed fluids of low viscosity (23.4 mPa s, Fig. S2(a)) while the distribution changes to O-shape when dispersed fluids of high viscosity are used (599 mPa s, Fig. S2(b)). In addition, O-shaped distribution or reduced degree of fluid displacement was observable in large droplets generated with the low-viscosity dispersed fluids (Fig. S2(c)).

4.3. Quantitative analysis of the degree of fluid displacement

The ratio I_in/I_out (Fig. 2(c)) was used to evaluate the degree of fluid displacement within the droplets. According to the definition of I_in and I_out, a higher value of I_in/I_out suggests more shell fluid is displaced to the inner region. As shown in Fig. 1, shear stress applied on the pendent droplet by the continuous carrier oil could induce vortices and fluid displacement during droplet formation, which however, could be balanced (with damping) by the viscous effect of the dispersed fluids. Of note, the potential Kelvin-Helmholtz instability caused by shear effect is nullified as the Re is far less than one in this microfluidics.⁴² Therefore, a shear stress ratio ζ can be used to represent the shear effect on the fluid displacement within a droplet as follows:

$$\zeta =\frac{\mathit{carrie}\mathit{fluid}\mathit{shear}}{\mathit{dispersed}\mathit{fluid}\mathit{damp}}·\frac{\mathit{shear}\mathit{time}}{\mathit{droplet}\mathit{formation}\mathit{time}}=\frac{q_c{\mu }_c}{q_d{\mu }_d}·1=\frac{q_c{\mu }_c}{q_d{\mu }_d}$$ (6)

where the value of 1 is a result of the equality of the time for shearing and droplet formation.

On the other hand, the recoiling of the dispersed tail during and after droplet pinch-off is caused by interfacial tension between dispersed and carrier fluids. This deformation and the resultant displacement of dispersed fluids are also balanced (with damping) by viscous effect although the duration may not span over the whole droplet formation period. As a result, the capillary effect on fluid displacement can be evaluated by a parameter λ as follows:

$$\frac{1}{\lambda }=\frac{\mathit{capillary}\mathit{recoil}}{\mathit{dispersed}\mathit{fluid}\mathit{damp}}·\frac{\mathit{recoil}\mathit{time}}{\mathit{droplet}\mathit{formation}\mathit{time}}=\frac{\sigma }{u_d{\mu }_d}·\left(\frac{W}{\sigma /{\mu }_d}·\frac{1}{V/q_d}\right)=\frac{\sigma }{u_d{\mu }_d}·\left(\frac{W}{\sigma /{\mu }_d}·\frac{u_{d}HW}{V}\right)=\frac{{HW}^2}{V}$$ (7)

where V is droplet volume and q_d is flow rate of dispersed fluids. The capillary number Ca = σ/(u_dμ_d) defines the ratio of capillary recoil to viscous damping in the dispersed fluids, W/(σ/μ_d) represents capillary recoil time, and V/q_d is droplet formation time. Equation (7) indicates that the capillary effect on fluid displacement during droplet formation can be estimated by the dimensionless droplet size λ = V/(HW²), and the fluid displacement in smaller droplets (i.e., smaller V) is more affected by the capillary effect. If the droplet volume is calculated as V = HA (A is droplet area in top-view) in this planar device of shallow depth, λ = A/W².

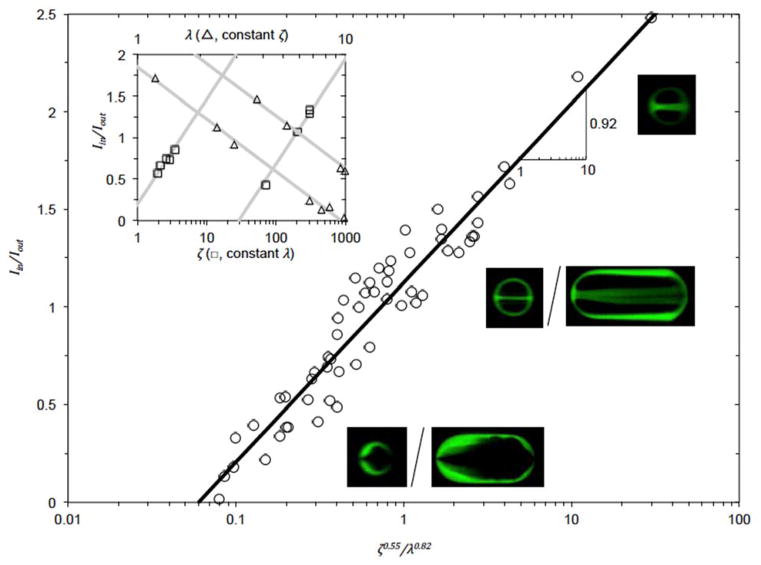
As shown in the upper left inset of Fig. 3, for constant λ, the slope between I_in/I_out and log₁₀(ζ) is 0.55. While for constant ζ, the slope between I_in/I_out and log₁₀(λ) is −0.82. As a result, the combined effect of these two mechanisms gives rise to the following relationship:

$$I_{in}/I_{\mathit{out}}=0.55{log}_{10}(\zeta )-0.82{log}_{10}(\lambda )-{log}_{10}({\zeta }^{0.55}/{\lambda }^{0.82})$$ (8)

Fig. 3.

Experimental data showing the dependence of I_in/I_out on the two dimensionless parameters: shear stress ratio ζ and relative droplet size λ. The slope of the least square fitting line (black line) between I_in/I_out and log₁₀(ζ^0.55/λ^0.82) is 0.92. The ratio of q_shell/q_core = 0.2 for all experiments. Upper left inset: I_in/I_out ~ 0.55 log₁₀(ζ) for constant λ, I_in/I_out ~ −0.82 log₁₀(λ) for constant ζ. Insets of fluorescence images: microdroplets generated with various combinations of ζ and λ.

The slope of the least square fitting line between I_in/I_out and log₁₀(ζ^0.55/λ^0.82) is 0.92, which is close to 1. The fitting goodness R² = 0.92. The insets of fluorescence micrographs show microdroplets of different I_in/I_out (i.e., different morphologies) for various combinations of ζ and λ.

Of note, the parameter λ for calculating the interfacial capillary effect on fluid displacement does not contain interfacial tension σ, which is due to the cancelation of fast capillary velocity with short recoil time or slow capillary velocity with long recoil time as indicated in the derivation of equation (7). As a result, the capillary effect on fluid displacement can be reflected by the dimensionless droplet size. As shown in Fig. S3, when the ζ and λ are the same, the degrees of fluid displacements in the final droplets are also the same even though the capillary number or interfacial tension is very different. These data further support the validity of using the two dimensionless parameters to estimate the degree of fluid displacement during droplet formation at the microfluidic FFJ.

4.4. Control of the fluid displacement in planar FFJ

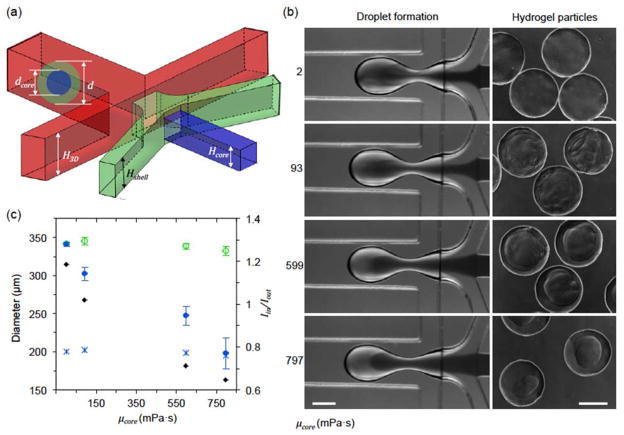
To generate hydrogel particles with various morphologies based on the control of the degree of the fluid displacement, we replaced the shell fluid with sodium alginate solution (μ_shell = 23.1 mPa s), which can be crosslinked into hydrogel by Ca²⁺ and visualized under phase microscopy. The CaCl₂-mineral oil emulsion³⁷ was used as carrier fluid for crosslinking. The droplets were collected in petri dish immediately after their formation to eliminate any potential mixing during further traveling in microchannel. Due to the short contact time with the CaCl₂-mineral oil emulsion, the sodium alginate was barely gelled⁴³, which allowed them to become sphere as a result of interfacial tension after exiting the microchannel and the partially gelled droplets were then further fully crosslinked in CaCl₂ solution (1.1%, w/v). The total viscous damping of dispersed fluids can be evaluated as q_dμ_d = q_coreμ_core + q_shellμ_shell, which gives rise to the equivalent viscosity μ_d = (q_coreμ_core + q_shellμ_shell)/q_d = (q_coreμ_core + q_shellμ_shell)/(q_core + q_shell). As a result, the degree of fluid displacement I_in/I_out can be calculated by equation (8). Figure 4(a) shows that if the core fluid is not very viscous (μ_core = 23.4 mPa s, I_in/I_out = 1.10), O-shaped distribution of calcium alginate hydrogel can be generated. If the viscosity of the core fluid is high (μ_core = 599 mPa s), the fluid displacement momentum could be dampened by higher viscous effect (ζ decreases, I_in/I_out = 0.48) and O-shaped configuration of alginate-shell is obtained as shown in Fig. 4(b). On the other hand, if the droplet size (λ) increases to reduce the capillary effect, O-shaped alginate shell can also be created even with a low-viscosity core fluid (μ_core = 23.4 mPa s, I_in/I_out = 0.27) as shown in Fig. 4(c). These results are consistent with the numerical predictions and on-chip experimental observations shwon in Fig. S(2).

Fig. 4.

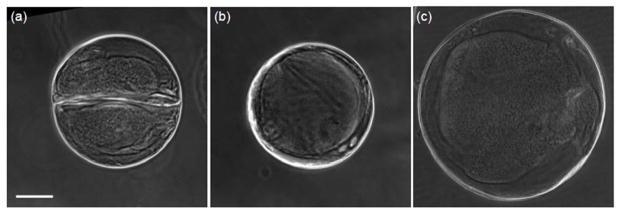
Displacement of shell fluid in hydrogel microparticle on planar flow-focusing junction. (a) O-shaped distribution of the shell fluid when μ_core = 23.4 mPa s for generating microparticles with a diameter of ~350 μm. I_in/I_out = 1.10. (b) O-shaped distribution when μ_core = 599 mPa s for generating microparticles with diameter of ~350 μm. I_in/I_out = 0.48. (c) O-shaped distribution when μ_core = 23.4 mPa s for generating microparticles with a diameter of ~515 μm. I_in/I_out = 0.27. Scale bar: 100 μm.

4.5. Control of the fluid displacement in nonplanar FFJ

This fluid displacement during droplet formation can also elucidate the generation of core-shell structured microcapsules in nonplanar FFJ. A nonplanar FFJ with the same top-view design as the planar FFJ is shown in Fig. 5(a). The carrier, shell, and core fluids are CaCl₂-mineral oil emulsion, aqueous sodium alginate solution, and aqueous carboxymethyl cellulose solution (with Amaranth dye) of various viscosities, respectively. The diffusion coefficient of the Amaranth dye (D_a) is 1.87 × 10⁻¹⁰ m² s⁻¹ in water,⁴⁴ giving rise to a Peclet Number (Pe = Wu_d/D_a) of 1.65 × 10³. This high Pe indicates that the transport of the dye in the core fluid is dominated by advection rather than diffusion. As shown in Fig. 5(b) and 5(c), the less viscous core fluid (μ_core ≤ 599 mPa s and I_in/I_out ≥ 0.71) mixes with the shell fluid during droplet formation before the shell fluid gelled into hydrogel. This leads to the formation of microcapsules either without an evident core-shell configuration (μ_core ≤ 2 mPa s and I_in/I_out ≥ 1.18) or with a core size bigger than the theoretical one (asterisks in Fig. 5(c), obtained by assuming no mixing (d_core /d = (q_core /(q_core + q_shell))^1/3). Furthermore, the core fluid could stay together in the inner region if μ_core = 797 mPa s (I_in/I_out = 0.65) or higher, leading to the formation of microcapsules with a core size close to the theoretical value. Although I_in/I_out = 0.65 is not very low for planar FFJ, the mixing is relatively less for nonplanar FFJ. This is probably due to the vertical flow components in the central area that dissipate the fluid displacement momentum.⁴⁵

Fig. 5.

Fluid displacement and mixing during the generation of microcapsules using nonplanar flow-focusing junction. (a) A schematic showing the nonplanar flow-focusing junction used. H_3D = 400 μm, H_shell = 300 μm, and H_core = 200 μm. (b) Micrographs of droplets at the flow-focusing junction and the final microcapsules formed with various μ_core. Flow rates: q_core = 50 μl hr⁻¹, q_shell = 200 μl hr⁻¹, and q_c = 6 ml hr⁻¹. Scale bars: 200 μm. (c) predicted I_in/I_out using equation (8) and measured microcapsule sizes. Symbols: ◆, I_in/I_out; , shell (outer) diameter d; , core diameter d_core, and , theoretical core diameter assuming no fluid displacement or mixing.

5. Conclusions

In summary, our study shows that strong fluid displacement could occur during droplet formation at both the planar and nonplanar FFJ. The fluid displacement is caused by the shear stress of carrier fluid and capillary effect of interfacial tension during droplet formation. The impact of these two mechanisms on fluid displacement can be evaluated by two dimensionless parameters ζ and λ, which represent the shear force ratio between carrier and dispersed fluids, and the dimensionless droplet size, respectively. The quantitative relationship between the degree of fluid displacement represented by I_in/I_out and these two dimensionless parameters is experimentally determined to be I_in/I_out = log₁₀(ζ^0.55/λ^0.82). This fluid displacement during droplet formation could be controlled by varying ζ and λ to generate hydrogel particles of various morphologies and dimensions.