Full factorial design for optimization, development and validation of HPLC method to determine valsartan in nanoparticles

Abstract

High performance liquid chromatographic method was optimized, developed and validated as per the ICH guidelines. In this study the 20 mM ammonium formate and acetonitrile in the 57:43 ratio were used as mobile phase for the analysis of valsartan. Full factorial design was used to optimize the effect of variable factors. The responses were peak area, tailing factor and number of theoretical plates. The quadratic effect of flow rate and wavelength individually as well as in interaction were most significant (p < 0.0001 and p < 0.0086, respectively) on peak area; the quadratic effect of pH of buffer was also most significant effect (p < 0.0001) on tailing factor (5%) whereas the quadratic effect of flow rate and wavelength individually was significant (p = 0.0006 and p = 0.0265, respectively) on the number of theoretical plates. The high-performance liquid chromatographic separation was performed at the flow rate 1.0 min/mL, UV detector wavelength 250 nm and pH of the buffer 3.0 as optimized parameters using design of experiments. The retention time values of valsartan were found to be 10.177 min. Percent recovery in terms of accuracy for the prepared valsartan nanoparticles was found in the range of 98.57–100.27%.

1. Introduction

Nowadays cardiovascular disorders are the main cause of deaths not only in developing countries, but all over the world. Cardiovascular disorders are associated with coronary heart disease, hypertension, ischemic heart disease, cerebrovascular disease, rheumatic heart disease, heart failure, high cholesterol levels, etc. As per the trends of deaths in developing countries due to this disorder around 1.5 billion deaths have been projected by 2015 (Grundy et al., 2004; Kearney et al., 2005; Gonzalez et al., 2009; Solanki et al., 2014). Hypertension is a key factor underlying cardiovascular disorder. Numerous antihypertensive drugs are available for the management of hypertension. Angiotensin II receptor (subtype AT1) blockers are the mainly used drugs for the management of hypertension. Valsartan is an example of angiotensin II receptor antagonist (Grundy et al., 2004), but its main problem is its low bioavailability (10–30%) which is because of its low aqueous solubility. This drug comes under BCS class II means it has low solubility and high permeability. To improve the solubility of this drug investigator has prepared the nanoparticles of drug. For the analysis of drug in nano-formulations the investigator has developed a new HPLC method.

HPLC method suitability is based upon the validation part. As per ICH guidelines, specificity, linearity, accuracy, precision, limits of detection (LOD) and limit of quantitation (LOQ) are the main parts of a new method validation (Ye et al., 2000; ICH Harmonized Tripartite Guideline and Methodology Q2 (R1), 2005).

The method for the analysis of drug in the nanoformulation should be enough robust, sensitive and precise; hence, in this method design of experiment has been applied to study the effect of factors individually and in combination also. Design of experiment (DOE) is based upon the principles of experimental design, mathematical equations or models and outcomes of the factors. This research article focuses on the optimization, development and validation of a new analytical method with DOE.

In this work, an analytical HPLC method has been optimized, developed and validated with DOE for the determination of valsartan in nano-formulations.

2. Experimental

2.1. Instrumentation

HPLC system consisted of a Shimadzu Corporation, Kyoto, Japan, LC-2010CHT model connected to PDA (Photodiode array, model no. SPD-M20A PDA with 220–230 V, Shimadzu Corporation, Kyoto, Japan) and dual wavelength UV detector, column oven and auto sampler (Shimadzu Corporation, Kyoto, Japan) was used in this study. Chromatograms were recorded by a computer and treated with the aid of LC solution 5.57 release.

A HyperClone (Phenomenex®) C₁₈ column (250 mm × 4.6 mm id, 5 μm, BDS 130 Å) was used to perform the separation, with a C₁₈ Phenomenex®, 4 × 3.0 mm id, security guard column.

The mobile phase was filtered through the Millipore glass filter (Millipore filter cellulose nitrate grided with 0.22 μ size and 47 mm diameter) assembly attached with vacuum pump. The mobile phase was sonicated with Ultrasonic Cleaner – 15L (Equitron – Medica Instrument Mfg. Co., Mumbai, India). The pH of mobile phase or buffer was measured with Eutech Instruments pH 510 using a glass electrode Van London Co., USA.

High pure water (18.2 MΩ cm resistivity, Milli-Q) was produced with a Direct-Q® 3 water purification system, Millipore Corporation (Billerica, MA, USA).

2.2. Chemical and solvents

Valsartan was obtained from Lupin Ltd. (Goa, India) as a gift sample. Ammonium formate was purchased from Sisco research Laboratories Pvt. Ltd. (Mumbai, India). Formic acid was purchased from RFCL Limited (New Delhi, India). Acetonitrile HPLC Grade was purchased from Finar Limited (Ahmadabad, India). Methanol HPLC Grade was purchased from Labort Fine Chem Pvt. Ltd. (Surat, India). High pure water (18.2 MΩ cm resistivity, Milli-Q) was produced with a Direct-Q® 3 water purification system, Millipore Corporation (Billerica, MA, USA).

2.3. Preparation of buffer for mobile phase

Ammonium formate buffer was prepared for mobile phase. The 20 mM ammonium formate buffer solution was prepared by dissolving pre-calculated amount of ammonium formate in 1000 mL Milli Q water and the pH 3.0 was adjusted with formic acid. The formic acid is also used as a solvent which helps to improve the peak characteristics (Grumbach et al., 2004; Yang et al., 2010; Solanki et al., 2014). Then the prepared buffer was passed through 0.22 μ filter.

2.4. Preparation of mobile phase

Mobile phase was used in the combination of buffer:acetonitrile ratio 57:43. The ammonium formate was used for the preparation of mobile phase, because it is volatile in nature and does not get precipitated in column and HPLC system (Dolan, 2014). Hence, the chances of development of high back pressure are less. The mobile phase was passed through the filter with 0.22 μ pore size and was sonicated for 15 min before pumping into HPLC system for degassing.

2.5. Optimization and development of HPLC method

In the present study, C₁₈ silica packed HPLC column was used for better separation. A HyperClone (Phenomenex®) C₁₈ column (250 mm × 4.6 mm id, 5 μm, BDS 130 Å) was used to perform the separation, with a C₁₈ Phenomenex®, 4 × 3.0 mm id, security guard column. In order to avoid column’s high internal pressure, acetonitrile was used as an organic solvent, because of its low viscosity.

The flow rate, pH of buffer solution and wavelength play an important role in HPLC method. Hence, in the present study, these three factors were optimized based on DOE.

Valsartan is a weak acidic drug and has approximately 4.9 pKa value (Cagigal et al., 2001). Three different pH of ammonium formate such as 2.8, 3.0 and 3.2 were studied and optimized with DOE. This pH was used in the study for best retention of acidic drug in a reversed-phase system. For best retention, the pH of buffer or the mobile phase should be approx. two pH units below its pKa value (Dolan, 2014). In this pH the drug will be totally unionized (more hydrophobic) which helps for better retention in a reversed-phase system. The mobile phase was selected in 57:43 ratio of buffer:acetonitrile. The 20 μl injection volume was used in the study. The UV detector was used for detection of drug in the samples. As like pH, three different wavelengths such as 248, 250 and 252 nm were studied and one wavelength was selected based on DOE. Similarly, the effect of flow rate (i.e. 0.8, 1.0 and 1.2 mL/min) was studied and based on DOE, the final flow rate was selected.

Most of the formulation studies involve only one variant at a time by keeping others as constant. With the help of full factorial design investigators can study the effect of all the factors by varied simultaneously. The factorial design helps to study the effects caused by independent factors and interactions between those self-governing factors (Bozkir and Saka, 2005). In the present work, three independent factors were used such as flow rate (A), wavelength (B) and pH of buffer (C). Three factorial levels were used in the study and were coded as −1, 0 and +1 for low, medium and high, respectively (Singh et al., 1995, 2008; Nagarwal et al., 2009; Yahiaoui and Aissani-Benissad, 2010). Totally 27 experimental runs were suggested by the software for analyzing the interaction of each level on formulation characters and the peak area (R₁), tailing factor (5%) (R₂) and number of theoretical plate USP (NTP) (R₃) were considered as response factors (dependent factors). Tables 1 and 2 show the factors chosen and different factor level settings. The significance of independent factors was determined using Fisher’s statistical test for Analysis of the Variance (ANOVA) model that was estimated.

Table 1.

Planned 3³ full factorial designs for robustness study.

Independent factors	Levels
−1	0	+1
Flow rate (mL/min)	0.8	1.0	1.2
Wavelength (nm)	248	250	252
pH of buffer	2.8	3.0	3.2

Table 2.

3³ Full factorial designs for robustness study.

Run	Independent variables
Flow rate (mL/min)	Wavelength (nm)	pH of buffer
Run 1	0.8	248	2.8
Run 2	1.0	248	2.8
Run 3	1.2	248	2.8
Run 4	0.8	250	2.8
Run 5	1.0	250	2.8
Run 6	1.2	250	2.8
Run 7	0.8	252	2.8
Run 8	1.0	252	2.8
Run 9	1.2	252	2.8
Run 10	0.8	248	3.0
Run 11	1.0	248	3.0
Run 12	1.2	248	3.0
Run 13	0.8	250	3.0
Run 14	1.0	250	3.0
Run 15	1.2	250	3.0
Run 16	0.8	252	3.0
Run 17	1.0	252	3.0
Run 18	1.2	252	3.0
Run 19	0.8	248	3.2
Run 20	1.0	248	3.2
Run 21	1.2	248	3.2
Run 22	0.8	250	3.2
Run 23	1.0	250	3.2
Run 24	1.2	250	3.2
Run 25	0.8	252	3.2
Run 26	1.0	252	3.2
Run 27	1.2	252	3.2

The polynomial equation for the experimental design with three factors is given below:

$$R={\beta }_0+{\beta }_{1}A+{\beta }_{2}B+{\beta }_{3}C+{\beta }_2\mathit{AB}+{\beta }_2\mathit{AC}+{\beta }_2\mathit{BC}+{\beta }_2{A}^2+{\beta }_2{B}^2+{\beta }_2{C}^2\text{.}$$

where R is the response, β is the regression coefficients and A, B and C represent flow rate, wavelength and pH of buffer, respectively.

2.6. Validation of HPLC method

The developed and optimized method was validated as per the ICH Q2 (R₁) guidelines for following parameters such as linearity, accuracy, precision, limit of detection (LOD) and limit of quantitation (LOQ) (Solanki et al., 2014; ICH Harmonized Tripartite Guideline and Methodology Q2 (R1), 2005).

2.6.1. System suitability

For system suitability determination 6 μg/mL of valsartan was used as stock solution. Six replicate injections of this standard solution were analyzed with HPLC. From these replicate injections, the acceptance criteria for peak area, tailing factor (5%), tailing factor (10%) and number of theoretical plate were studied.

2.6.2. Linearity

The standard calibration curve was prepared with different concentrations from 0.1 to 12 μg/mL. Three replicate injections of each concentration were analyzed for this study. The linear regression and correlation coefficient were found out from the graph between peak area and concentration.

2.6.3. Precision

The precision is a study which is based upon the intra-day precision and inter-day precision. Precision of the developed method was evaluated by performing repeatability (six times of each concentration) of three distinct concentrations two times in a day (i.e. morning and evening) whereas the intermediate precision study was performed by repeating three distinct concentrations on two different days. Intra-day and inter-day precision was performed by using three unusual concentrations such as 1, 6 and 12 μg/mL. The peak area was measured and percent relative standard deviation (% RSD) was calculated (Rajput and Sonanis, 2011).

2.6.4. Accuracy

The accuracy of developed method was studied by determining recovery values. The term accuracy means the value which is near to the value of reference. For the determination of accuracy, the standard drug in the range of 75%, 100% and 125% of the sample’s concentration (2 μg/mL) was mixed with sample solution, which produces the final concentration 3, 4 and 5 μg/mL. The same process has been performed in triplicate. The percent recovery (Sagirli et al., 2007) of the added standard drug to the assay samples was calculated with the following formula:

$$\text{Percent recovery}=[(C_c-C_f)/C_s]\times 100$$

where C_c is the concentration of analyte present in the combination of standard and test; C_f is the concentration of analyte in nano-formulation and C_s is the concentration of standard analyte used in the combination.

2.6.5. Limit of detection and limit of quantitation

The sigma method was used for the limit of detection (LOD) (Awotwe-Otoo et al., 2012). This method is based upon the slope and least standard deviation obtained from the response. The formula for the calculation of LOD used was LOD = 3.3σ/SP, where σ is the minutest standard deviation value in response and SP is the slope of the calibration curve. Similarly, the limit of quantitation (LOQ) was also calculated from the response of valsartan. The formula for the calculation of LOQ used was LOQ = 10σ/SP, where σ is the least standard deviation value in response and SP is the slope of the response.

3. Results and discussion

3.1. Development and optimization of HPLC method

In this study, the 27 runs were performed, and results were obtained for peak area, tailing factor (5%) and number of theoretical plates. The perturbation plots were created using Design Expert® version 9.0.3.1 software to estimate the effect of factors on peak area, tailing factor and number of theoretical plates.

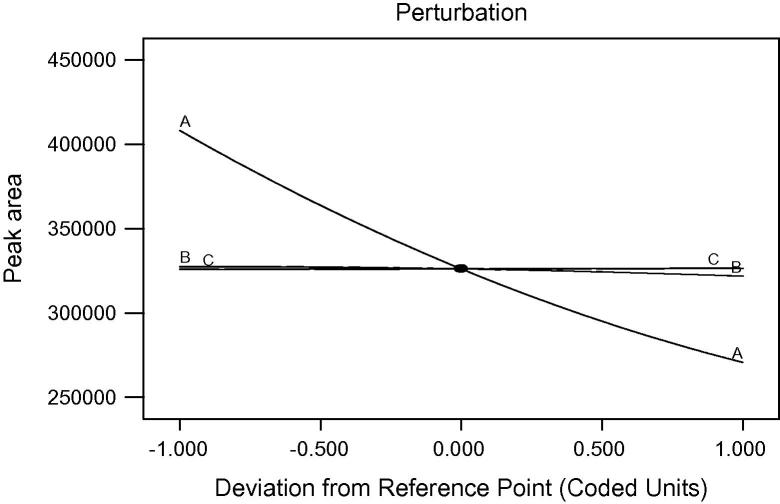
Perturbation plots bear the effect of self-governing factors on the dependent factors. Fig. 1 is related to the effect of independent factors on peak area. It shows that there is no effect of wavelength (B) and pH of buffer (C) on peak area, but the flow rate (A) shows an incredible effect on peak area as the increase in the flow rate decreases the peak area.

Figure 1.

Effect of flow rate (A), wavelength (B) and pH of buffer (C) on peak area (R₁).

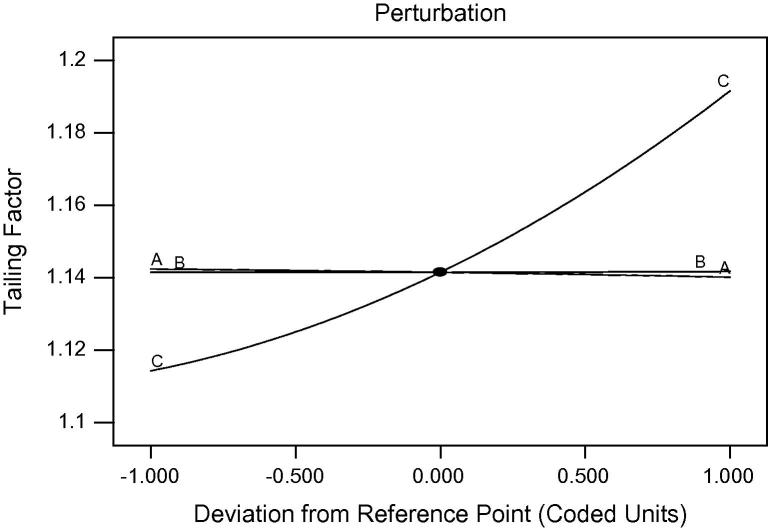
Fig. 2 gives the information about the effect of independent factors on tailing factor (5%). This figure shows that there is no effect of flow rate and wavelength on tailing factor, but pH of buffer plays an important role on the same as when the pH increases, the tailing factor also increases.

Figure 2.

Effect of flow rate (A), wavelength (B) and pH of buffer (C) on tailing factor (R₂).

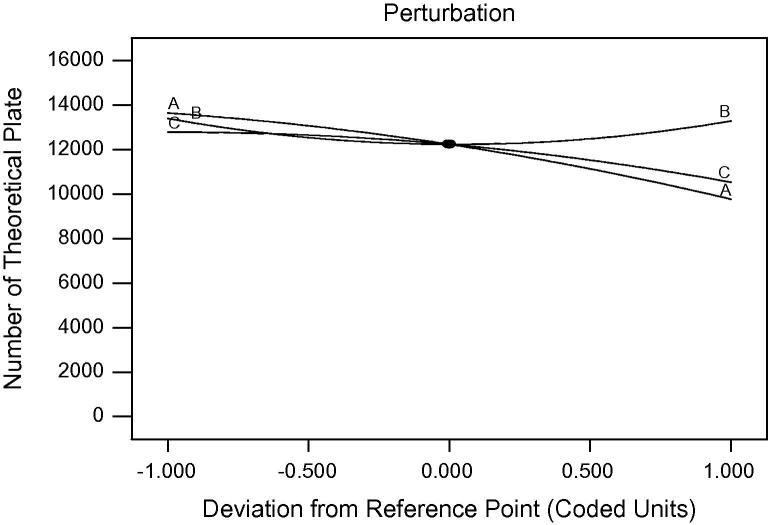
Fig. 3 informs the effect of independent factors on the number of theoretical plate. Figure shows that as the flow rate and buffer pH increase the number of theoretical plate decreases, whereas with the increase in the wavelength, there is a slight increase in the number of theoretical plate.

Figure 3.

Effect of flow rate (A), wavelength (B) and pH of buffer (C) on number of theoretical plates (R₃).

Similarly, the peak area, tailing factor (5%) and number of theoretical plates of each injection were entered in Design Expert® version 9.0.3.1 software and analyzed using the ANOVA with its significance method. For an experimental design with three variable factors, the suitable model fitting to the data was the quadratic model. The polynomial equations for the response factors are given below:

Peak area (R₁) = +(3.261E + 005) − 68744.94A − 2848.56B + 325.83C − 91.58AB − 1326.42AC − 269.92BC + 13321.83A² + 1468.33B² + 27.17C².

Tailing factor (R₂) = +1.14 − (1.111E−003)A + (1.111E−004)B + 0.039C + (2.500E−004)AB − (2.917E−003)AC − (1.167E−003)BC − (2.222E−004)A² + (1.111E−004)B² + 0.011C².

Number of theoretical plate (R₃) = +12240.15 − 1937.06A − 57.33B − 1124.67C + 52.75AB − 748.33AC + 3.33BC − 528.94A² + 1108.89B² − 578.11C².

where R₁, R₂ and R₃ are the response factors i.e. peak area, tailing factor and number of theoretical plate, respectively. The A, B and C are the flow rate, wavelength and pH of buffer, respectively.

The quadratic effect of flow rate and wavelength separately as well as in interaction was most significant (p < 0.0001 and p < 0.0086, respectively) on peak area; the quadratic effect of pH of buffer was also most significant effect (p < 0.0001) on tailing factor (5%) whereas the quadratic effect of flow rate and wavelength individually was significant (with p = 0.0006 and p = 0.0265, respectively) on the number of theoretical plates.

3.2. Validation of optimized factors

The results of optimized independent variable such as flow rate, wavelength and pH of buffer were validated by comparing the predicted results and observed results. The difference between the predicted and the observed results was found within ±11% as shown in Table 3. The formula used to calculate the percent residual value is

$$\text{Percent residual}=\frac{\text{Predicted results}-\text{Observed results}}{\text{Predicted results}}\times 100$$

Table 3.

Validation of optimized factors.

Response	Predicted results	Observed results	Residual values (%)
Peak area	326,124	360,930	−10.673
Tailing factor (5%)	1.1452	1.103	+3.685
Number of theoretical plate	12240.1	13,219	−7.997

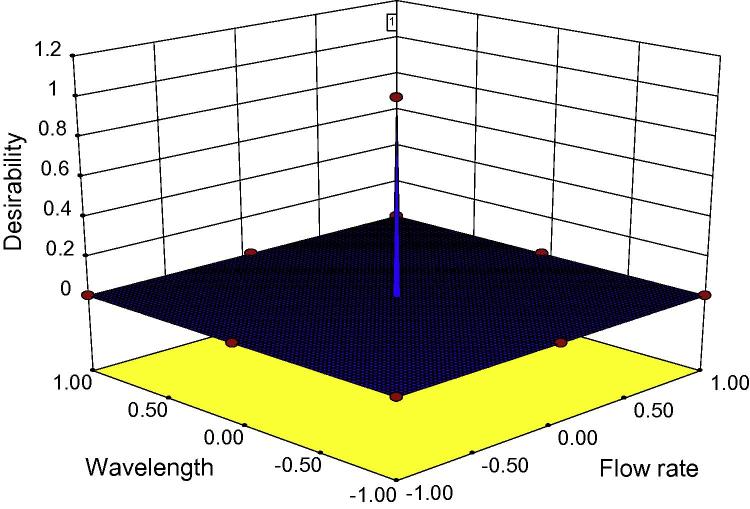
The desirability of the optimized factor is shown in Fig. 4. The desirability values usually exist in the range of 0–1. If the value is near to zero means the solution of the method is not strong whereas the value toward 1 side means the solution or method is very strong. The found desirability value was maximum (i.e. 1) which indicates the method is highly strong.

Figure 4.

The 3D surface response plot of desirability for optimization of factors.

3.3. Method validation

3.3.1. Selectivity

The study has been performed as per the ICH Q2 (R₁) guidelines (ICH Harmonized Tripartite Guideline and Methodology Q2 (R1), 2005). The chromatogram of blank and 6 μg/mL concentration of valsartan is shown in Fig. 5. The retention time of the drug was found to be 10.177 min.

Figure 5.

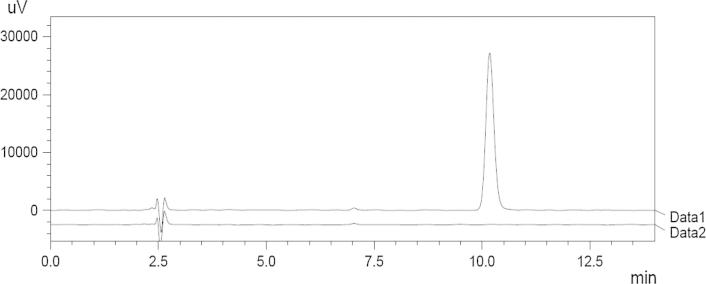
Chromatogram of blank (Data 2) and valsartan (Data 1).

3.3.2. System suitability

System suitability was expressed by percent relative standard deviations of peak area, tailing factor (5%), tailing factor (10%) and number of theoretical plate. System suitability was carried out by performing six replicates of 6 μg/mL. The% RSD of peak area, tailing factor (5%), tailing factor (10%) and number of theoretical plate results is reported in Table 4. The % RSD value of peak area, tailing factor (10%) and number of theoretical plate was found to be less than 0.5% and % RSD value of tailing factor (5%) was found to be <1%.

Table 4.

System suitability test using 6 μg/mL.

S no.	Parameters	Results
Mean	SD	% RSD
1	Peak area	363052.300	1245.4620	0.343
2	Tailing factor (5%)	1.114	0.0067	0.606
3	Tailing factor (10%)	1.092	0.0039	0.361
4	Number of theoretical plate	13153.500	49.6659	0.378

3.3.3. Linearity

The standard calibration curve over the valsartan concentration range 0.1–12 μg/mL shows r² = 0.9976 which is an acceptable value for correlation coefficients. The linear regression from the above gives concentration range that was found to be y = 54061x + 10210.

3.3.4. Precision

Precision of new developed method was evaluated by intra-day and inter-day precision and was expressed by percent relative standard deviations of peak area. Intra-day and inter-day precision was carried out by performing six replicates of 1, 6 and 12 μg/mL. The % RSD of peak area of intra-day and inter-day precision results is reported in Table 5. The % RSD value of intra-day precision (all three concentrations) was found to be less than 1% and % RSD value of inter-day precision (all three concentrations) was found to be <2%.

Table 5.

Intra-day and inter-day precision of valsartan.

S no.	Conc. (μg/mL)	Intra-day precision			Inter-day precision
Mean area	SD	% RSD	Mean area	SD	% RSD
1	1.0	60148.08	512.65	0.85	59316.92	809.18	1.36
2	6.0	360614.70	3150.57	0.87	357362.60	2292.19	0.64
3	12.0	637475.00	4276.53	0.67	636835.40	5108.63	0.80

3.3.5. Accuracy

The accuracy study has been performed by the addition of standard drug in samples at three different concentration levels such as 75%, 100% and 125%. The percent recovery at these three different concentration levels was found in the range of 98.57–100.27%. This study suggests a suitable method for the routine experimental analysis of drug in the formulations.

3.3.6. Limit of detection and limit of quantitation

The limit of detection and limit of quantitation were determined by the sigma method. The limits of detection and limit of quantitation were found to be 14.833 ng/mL and 44.95 ng/mL, respectively.

4. Conclusion

The method was successfully developed and optimized through DOE, and data were analyzed using Design Expert® version 9.0.3.1 software. The significant effect of independent factors was analyzed using ANOVA, and the effect was also reported in the form of perturbation plots. The design of experiments provides efficient tools for the optimization of variable factors for HPLC method development. Further the method was validated and as per the results, the present method is novel, simple, accurate, precise, economic and robust for the analysis of valsartan in nanoformulations.