Estimating and interpreting latent variable interactions: A tutorial for applying the latent moderated structural equations method

Abstract

Latent variables are common in psychological research. Research questions involving the interaction of two variables are likewise quite common. Methods for estimating and interpreting interactions between latent variables within a structural equation modeling framework have recently become available. The latent moderated structural equations (LMS) method is one that is built into Mplus software. The potential utility of this method is limited by the fact that the models do not produce traditional model fit indices, standardized coefficients, or effect sizes for the latent interaction, which renders model fitting and interpretation of the latent variable interaction difficult. This article compiles state-of-the-science techniques for assessing LMS model fit, obtaining standardized coefficients, and determining the size of the latent interaction effect in order to create a tutorial for new users of LMS models. The recommended sequence of model estimation and interpretation is demonstrated via a substantive example and a Monte Carlo simulation. Finally, extensions of this method are discussed, such as estimating quadratic effects of latent factors and interactions between latent slope and intercept factors, which hold significant potential for testing and advancing developmental theories.

Many exciting and cutting-edge lines of developmental science research center on interactions between key variables: gene by environment interactions, interactions among comorbid psychiatric conditions, and interactions among ecological components (e.g. home, school, neighborhood). Further, many variables of central interest to psychologists, such as IQ, mental health, and academic achievement, are commonly measured by latent variables. Straightforward methods for estimating interactions between latent variables are therefore necessary to enable advancements in areas of psychological research where theory predicts such interactions. Several methods for estimating and interpreting interactions between latent variables are available (e.g. Kenny & Judd, 1984; Klein & Moosbrugger, 2000; Little, Bovaird, & Widaman, 2006; Marsh et al., 2007). Of the available methods, the latent moderated structural equations (LMS; Klein & Moosbrugger, 2000) has two notable advantages: statistical efficiency (requiring estimation of only one parameter) and availability in commercial desktop software, Mplus (Muthén & Muthén, 1998–2012). However, the utility of the LMS method has traditionally been limited for several reasons: 1) traditional model fit indices used in structural equation modeling are not available for LMS models, 2) Mplus does not generate standardized coefficients for these models, and 3) Mplus does not produce the percentage of variance explained by the latent interaction, or any other indicator of the size of a latent interaction effect. The limitations of LMS make it difficult to interpret the interaction effect using only the standard output and therefore limit the utility of the method for the average researcher.

The current article compiles state-of-the-science techniques for assessing LMS model fit, obtaining standardized coefficients, and determining the size of the latent interaction effect in order to create a tutorial for new users of LMS models. The method is first demonstrated via a substantive example: the main effects and interactive effect of two sets of mental health symptoms, depressive symptoms and conduct problems, on alcohol use in a national adolescent sample. A Monte Carlo simulation is then conducted to explore how this approach to model estimation behaves with data drawn from both normal and skewed distributions and how the likelihood ratio test and R² behave.

Methods

This section presents a two-step estimation procedure for estimating latent moderated structural equations (Klein & Moosbrugger, 2000) using the XWITH command in Mplus software (Muthén & Muthén, 1998–2012). Guidelines for assessing model fit, calculating a standardized beta coefficient, determining the effect size of the interaction effect, and interpreting the interaction, are then presented. In subsequent sections, these strategies are demonstrated in both an empirical example and a Monte Carlo simulation study.

Data preparation

There are no LMS-specific data preparation steps that must be completed before estimating the models. It is not necessary to center the indicator variables used to form the latent variables. The XWITH procedure assumes normally distributed variables, and extreme skewness of indicator variables can lead to convergence problems and biased parameter estimates (Cham, West, Ma, & Aiken, 2012; Klein & Moosbrugger, 2000). The Monte Carlo simulation below illustrates the effect of skewed indicator variables on estimates of the latent interaction effect.

Model estimation

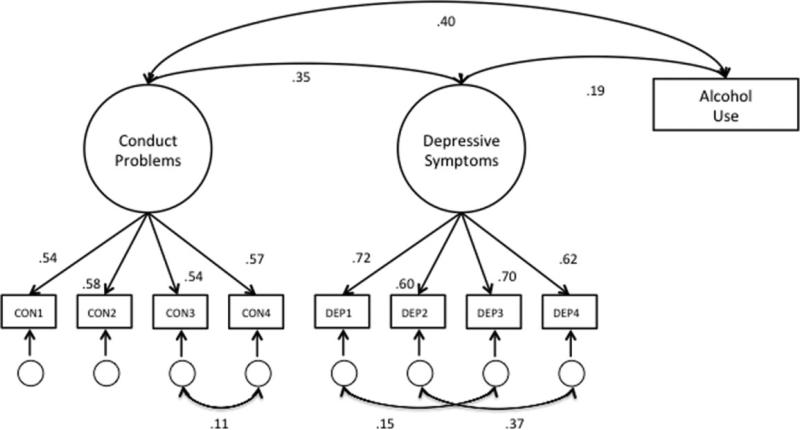
The researcher will generally estimate a measurement model and ensure its fit prior to estimating structural models (see Figure 1). CFI and TLI values greater than .95 and RMSEA values below .08 generally constitute good fit (Brown & Cucdeck, 1992, 1993; Little, 2013), though there remains some disagreement about ideal indices of model fit (Little, 2013). The latent interaction term is estimated in a subsequent step and is not included in the measurement model. The latent interaction term does not have a mean, variance, or a covariance with other parameters and therefore should not affect the fit of the measurement model (Muthén, 2012). Correlations between factors and between items on the same construct can be specified according to the investigator's hypotheses, as with a standard structural equation model.

Figure 1.

Measurement model, Study 1.

Note. X²(22) = 527.4, RMSEA = .013 (95% CI = .012 - .014), CFI = .994, TLI = .991. N = 143,173. All estimates are standardized.

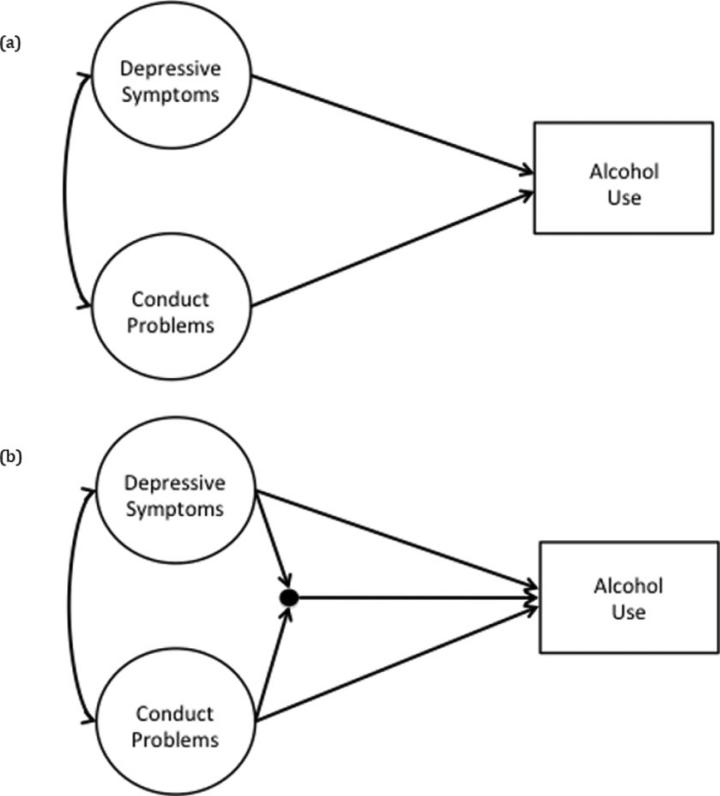
After ensuring the fit of the measurement model, structural models are estimated in two steps (Klein & Moosbrugger, 2000; Muthén, 2012). The first step is to estimate the structural model without the latent interaction term. This model will henceforth be referred to as Model 0 (Figure 2a). Model 0 will supply model fit indices (see below). The second step is to estimate the structural model with the latent interaction. This model will henceforth be referred to as Model 1 (Figure 2b). The output of Model 1 will provide the final regression coefficients and indicate whether the latent interaction is significant. If significant, the interaction can be interpreted by graphing as in standard regression models (Aiken & West, 1991). When graphing, regression coefficients for main effects and the latent interaction should be obtained from Model 1. If using standardized coefficients, one should use a graphing technique designed for standardized coefficients (Dawson, 2014).

Figure 2.

Structural models, without and with latent variable interaction.

Note. a) Model 0: Main effects of depressive symptoms and conduct problems predicting substance use. b) Model 1: Model including the latent variable interaction of depressive symptoms × conduct problems, depicted as a filled circle per Mplus standard notation.

Assessing model fit

Model fit indices generally used to interpret the fit of structural equation models, such as CFI, TLI, RMSEA, and χ², have not been developed for LMS models. Alternatively, a two-step method for assessing the overall fit of each LMS model can be used (Klein & Moosbrugger, 2000; Muthén, 2012). First, CFI, TLI, RMSEA, and χ² values are obtained from Model 0. Second, using a log-likelihood ratio test, the relative fit of Model 0 (null model, where the interaction is not estimated and therefore assumed to be zero) and Model 1 (alternative model, where the interaction is estimated) is compared. The log-likelihood ratio test is used to determine whether the more parsimonious Model 0 (i.e., model that does not estimate the interaction effect) represents a significant loss in fit relative to the more complex Model 1 (Satorra, 2000; Satorra & Bentler, 2010). If Model 0 fits well and, per the log-likelihood ratio test, Model 0 represents a significant loss in fit relative to Model 1, then the researcher can conclude that Model 1 is also a well-fitted model. If the log-likelihood ratio test is not significant, one can only conclude that Model 0 does not result in a significant loss of fit relative to Model 1. There is no way to assess whether the fit of Model 1 is equal to or worse than that of Model 0.

The test statistic for a log-likelihood ratio test, often denoted as D, is calculated using the following equation:

$$D=-2[\left(\text{log-likelihood for Model 0}\right)-\left(\text{log-likelihood for Model 1}\right)]$$

The values of D are approximately distributed as χ². The degrees of freedom (df) to determine the significance of D is calculated by subtracting the number of free parameters in Model 0 from the number of free parameters in Model 1. For example, in the case of modeling one latent interaction, there would be one additional parameter estimated in Model 1, so the difference in free parameters = 1, and the D statistic calculated using the loglikelihoods from Model 0 and Model 1 can be compared to a χ² distribution using df = 1. In Mplus output, the log-likelihood values needed to perform this calculation are labeled “H0 Value.” A recent simulation study indicates that the optimal difference test statistic for comparing LMS models is this raw, uncorrected difference between these two log-likelihood values (Gerhard et al., in press). The simulation study indicates that this uncorrected difference test, originally proposed by Klein & Moosbrugger (2000), performs better than the robust difference test (Satorra & Bentler, 2001) or the “strictly positive” difference value (Satorra & Bentler, 2010), which have been applied in past studies using LMS models.

Standardized coefficients

Psychologists often prefer to present standardized rather than unstandardized regression coefficients in their publications. Standardized regression coefficients are not provided by Mplus for LMS models. However, standardized beta coefficients can be obtained by standardizing the data prior to analysis (e.g. Klein & Moosbrugger, 2000). Standardization is accomplished in Mplus prior to model estimation using the “standardize” command, as demonstrated in the Mplus code in the Appendix.

Variance explained by latent interaction and total variance explained

For the dependent variable Y in Model 0, the structural model without an interaction, the $R_Y^2$ may be obtained from the Mplus STANDARDIZED output, or it can be calculated by hand. Coefficients for two “main” (first order) effects, β_X1 and β_X2, variances of each latent variable, ${\sigma }_{X1}^2$ and ${\sigma }_{X2}^2$, a covariance between the latent variables, ${\sigma }_{X1X2}^2$, and a residual variance for the response, ${\sigma }_{Yres}^2$, are all given in the Mplus output. These coefficients can be used estimate R² for the dependent variable with no interaction term:

$$R_{Y0}^2=\frac{{\beta }_{YX1}^2{\sigma }_{X1}^2+{\beta }_{YX2}^2{\sigma }_{X2}^2+2{\beta }_{YX1}{\beta }_{YX2}}{{\beta }_{YX1}^2{\sigma }_{X1}^2+{\beta }_{YX2}^2{\sigma }_{X2}^2+2{\beta }_{YX1}{\beta }_{YX2}+{\sigma }_{Yres}^2}$$

For the dependent variable Y in Model 1, the structural model with an interaction, estimates exist of the same parameters as before, plus a coefficient for the interaction, β_X1X2, given in the Mplus output. The LMS estimator of the interaction is constructed to have no covariance with the first order effects when data are normally distributed (Klein & Moosbrugger, 2000), which enables estimation of R² for the dependent variable using only these given values:

$$R_{Y1}^2=\frac{{\beta }_{YX1}^2{\sigma }_{X1}^2+{\beta }_{YX2}^2{\sigma }_{X2}^2+2{\beta }_{YX1}{\beta }_{YX2}+{\beta }_{X1X2}^2\left({\sigma }_{X1}^2{\sigma }_{X2}^2+{\left({\sigma }_{X1X2}^2\right)}^2\right)}{{\beta }_{YX1}^2{\sigma }_{X1}^2+{\beta }_{YX2}^2{\sigma }_{X2}^2+2{\beta }_{YX1}{\beta }_{YX2}+{\beta }_{X1X2}^2\left({\sigma }_{X1}^2{\sigma }_{X2}^2+{\left({\sigma }_{X1X2}^2\right)}^2\right)+{\sigma }_{Yres}^2}$$

Finally, $\Delta R_Y^2=R_{Y1}^2-R_{Y0}^2$, the difference between these two R² values, yields the portion of R² attributable to the interaction term.

Study 1: Empirical example

In this section, the previously presented strategies are demonstrated through a simple empirical example to motivate the use of the method. Here, two latent variables, conduct problems and depressive symptoms, and their interaction, are predictors of an observed, continuous outcome, alcohol use in the past month. Depressive symptoms and conduct problems are two of the most commonly co-occurring types of mental health symptoms in adolescence (e.g. Kovacs, Paulauskas, Gatsonis, & Richards, 1988; Wolff & Ollendick, 2006), yet there is limited research on their interaction as a predictor of substance use.

Study 1 methods

Data were self-reported survey measures completed by 8th-, 10th-, and 12th-grade girls who participated in national, cross-sectional Monitoring the Future surveys conducted from 1991 to 2009 (N = 143,173). Racial and ethnic composition of the sample reflected those of the US population: 63.6% White, 13.3% Black, 10.9% Hispanic, 11.6% other race/ethnicity. For additional information regarding the Monitoring the Future study, see Johnston, O'Malley, Bachman, and Schulenberg (2013). Monitoring the Future data are accessible via the Interuniversity Consortium for Political and Social Research (ICPSR; http://www.icpsr.umich.edu). Descriptive statistics for the current sample are presented in Table 1.

Table 1.

Descriptive statistics and 95% confidence intervals for observed variables, Study 1.

	1	2	3	4	5	6	7	8
1. dep1	1.838 (1.827–1.848)	.440 (.437–.443)	.577 (.575–.579)	.446 (.443–.449)	.144 (.141–.147)	.123 (.120–.126)	.149 (.146–.152)	.157 (.154–.160)
2. dep2	.697 (.693–.701)	1.367 (1.360–1.375)	.414 (.411–.417)	.608 (.606–.610)	.091 (.088–.094)	.096 (.093–.099)	.119 (.116–.122)	.137 (.134–.140)
3. dep3	.979 (.973–.984)	.606 (.602–.609)	1.572 (1.563–1.580)	.436 (.433–.439)	.134 (.131–.137)	.131 (.128–.134)	.137 (.134–140)	.152 (.149–.155)
4. dep4	.616 (.612–.619)	.724 (.720–.728)	.557 (.554–.560)	1.043 (1.037–1.048)	.124 (.121–.127)	.128 (.125–.131)	.127 (.124–.130)	.157 (.154–.160)
5. con1	.107 (.106–.108)	.058 (.058–.058)	.091 (.091–.092)	.069 (.069–.069)	.296 (.294–.298)	.338 (.335–.341)	.280 (.277–.283)	.314 (.311–.317)
6. con2	.094 (.093–.095)	.063 (.063–.063)	.093 (.092–.094)	.074 (.074–.074)	.100 (.099–.101)	.314 (.312–.315)	.307 (.304–.310)	.342 (.339–.345)
7. con3	.182 (.181–.183)	.125 (.124–.126)	.154 (.153–.155)	.116 (.115–.117)	.135 (.134–.136)	.152 (.151–.153)	.791 (.786–.795)	.385 (.382–.388)
8. con4	.143 (.142–.144)	.108 (.107–.109)	.128 (.127–.129)	.108 (.107–.109)	.113 (.112–.114)	.127 (.126–.128)	.228 (.227–.229)	.445 (.443–.447)
M	2.282 (2.271–2.293)	1.959 (1.949–1.968)	1.978 (1.968–1.988)	1.638 (1.630–1.646)	1.144 (1.139–1.148)	1.123 (1.118–1.127)	1.397 (1.392–1.402)	1.205 (1.200–1.210)
SD	1.356 (1.351–1.359)	1.169 (1.166–1.172)	1.254 (1.250–1.257)	1.021 (1.018–1.024)	.544 (.542–.545)	.561 (.579–.584)	.889 (.886–.892)	.667 (.666–.669)

Note. N = 143,173. Correlations appear above the diagonal, variances appear on the diagonal, and covariances appear below the diagonal. Intervals represent 95% confidence interval of each estimate. Conduct problems variables (Con1–Con4) were measured on a scale of 1 = “Never” to 5 = “5+ times in the past 12 months”. Depressive symptoms variables (Dep1–Dep4) were measured on a scale of 1 = “Disagree” to 5 = “Agree”.

The conduct problems latent variable was created using four items. Each item began with the stem, “In the past 12 months, how often have you:” The four items were: “taken something not belonging to you worth over $50?”, “damaged school property on purpose?”, “gotten into a serious fight in school or at work?”, “hurt someone badly enough to need bandages or a doctor?” Items were measured on a scale of 1 = “Never” to 5 = “5+ times in the past 12 months.”

The depressive symptoms latent variable was created using 4 items. Participants were asked, “How much do you agree or disagree with each of the following statements?” on a scale of 1 = “Disagree” to 5 = “Agree.” The four items were: “Life often seems meaningless,” “The future often seems hopeless,” “It feels good to be alive,” and “I enjoy life as much as anyone.” The latter two items were reverse-coded.

Alcohol use was measured via a single standard item, “On how many occasions have you drank alcohol, more than just a few sips, in the past 30 days?” on a scale of 1 = “0” to 7 = “40+”.

All analyses were performed via structural equation modeling using Mplus version 7.1 (Muthén & Muthén, 1998–2010). LMS models were estimated with the XWITH command, using full information maximum likelihood with robust standard errors. Latent variables were scaled by fixing the loading of the first item to 1.0, per Mplus defaults. Previous research has noted that the method of scaling the latent variables can have substantive impacts on the Wald significance test (Gonzalez & Griffin, 2001). Our analyses use the likelihood ratio test to determine significance of the latent variable interaction. We tested whether method of scaling affected the Wald and likelihood ratio test in the LMS procedure in our simulations, and found no effect on either test. Models were estimated according to the sequence described above. The Mplus code is contained in the Appendix.

Study 1 results

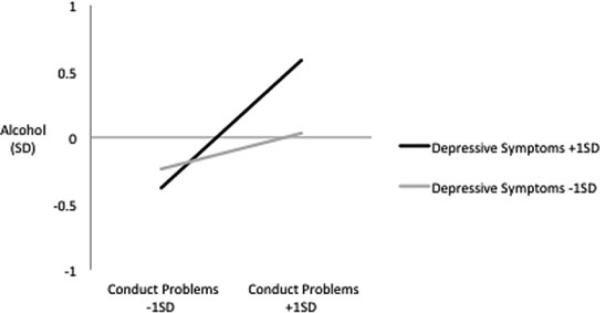
First, the fit of the measurement model was assessed (Figure 1). Next, Model 0 (Figure 2a) was estimated. Model 0 fit the data well: X²(22) = 527.4, RMSEA = .013 (95% CI = .012–.014), CFI = .994, TLI = .990. In this case, the relatively large X² value is likely attributable to the large N, as X² is known to be sensitive to sample size. Both conduct problems and depressive symptoms significantly predicted alcohol use (B = .39, p < .001, 95% CI = .26–.52, and B = .05, p < .001, 95% CI = .045–.055, respectively). The model explained 16.6% of variance in alcohol use. Model 1 (Figure 2b) was then estimated. The relative fit of Model 1 versus Model 0 was determined via a log-likelihood ratio test comparing the log-likelihood values of Model 0 and Model 1, yielding a log-likelihood difference value of D = 19.3. Based on the number of free parameters of Model 0 (32) and Model 1 (33), the difference in free parameters = 1, which represents the df value we should use for the log-likelihood ratio test. Using a chi-square distribution, this log-likelihood ratio test proved significant (p < .001), indicating that the null model (Model 0; the model without the interaction effect) represents a significant loss in fit relative to the alternative model (Model 1; the model with the interaction effect). The conduct problems × depressive symptoms interaction effect was significant (β = 0.62, SE = 0.21, p < .01, 95% CI = .21–.83). Plotting the interaction to aid in interpretation revealed that the relation between conduct problems and alcohol use becomes more positive as depressive symptoms increase (Figure 3).

Figure 3.

Interaction of depressive symptoms and conduct problems predicting past month alcohol use, Study 1, N = 143,173.

In order to interpret the size of the interaction effect, the method described above was used to calculate R² for Model 1, which yielded a value of R² = .20, or 20% of the variance in past month alcohol use explained. In Model 0, the model without the interaction, R² = .166. Subtracting R² of Model 0 from R² of Model 1 yielded R² value for the interaction of .034 or an additional 3.4% of variance in alcohol use explained by the interaction of conduct problems and depressive symptoms.

Study 2: Monte Carlo simulation

To further understand our estimates of the interaction parameter, the likelihood ratio testing the significance of the interaction, power to detect a significant latent variable interaction, and the change in R² due to the interaction, we conducted a series of Monte Carlo simulations. Parameter estimates obtained in Study 1, including variances and covariances between latent terms, as well as intercept and regression parameters and residual variances for observed terms, were the basis for our simulated data.

Study 2 methods

Data were generated in R software. Data generation code for R is contained in the Appendix. The simulations were performed using 1,000 data sets with N = 500 observations each. Data for the latent variables in each model were drawn from two distributions: a multivariate normal distribution and a multivariate chi-squared distribution. Indicator variables for the two independent latent variables and the dependent variable were then constructed with independent normal residual variances or with independent chi-square distributed residual variances chosen to represent the effect of skewed variables on estimating latent interactions. Two sets of parameters were used to generate data: the parameters estimated in Study 1, Model 1, and the same parameters from Model 0, which excluded the interaction term. In all there were four populations of data: two multivariate normally-distributed, two chi-square distributed, with one of each distribution containing a significant latent interaction and one containing no significant interaction.

Study 2 results

To calculate a likelihood ratio to test the significance of the interaction effect, we ran two models in Mplus for each of the data sets in our four populations of data: one model with the interaction term freely estimated, akin to Model 1 in Study 1, and one model with no interaction term estimated, akin to Model 0 in Study 1. Otherwise, the same set of parameters was freely estimated in each model. For each multivariate normal population, this yielded 1000 likelihood ratios. For the chi-square distributed populations, estimation problems limited the number of fewer successful models to compare due to the failure of some models to converge.

Measurement model

Our estimation model consisted of two parts, a measurement model and a structural model. Table 2 contains the data generation parameters as entered into the simulation and as reproduced by the models in the four data distributions: multivariate normal with no interaction present (MVN), multivariate normal with an interaction present (MVNI), Chi-Square with no interaction present (ChiSq), and Chi-Square with an interaction present (ChiSqI). The parameters included in Table 2 demonstrate that the simulation model accurately reproduced the measurement model parameters as they were specified. This then allows for estimation of the structural model with confidence that underlying measurement structure is properly represented in the simulated datasets.

Table 2.

Recovery of data generation parameters, Study 2

		Mean Parameter (Mean Standard Error)
	Data generation	Multivariate Normal, No Interaction in Data		Multivariate Normal, Interaction in Data		Chi Square Distribution, No Interaction in Data		Chi Square Distribution, Interaction in Data
CONDUCT BY
CON1	1.000	1		1		1		1
CON2	1.086	1.097	(0.146)	1.096	(0.145)	1.095	(0.148)	1.021	(0.130)
CON3	1.624	1.638	(0.225)	1.637	(0.223)	1.636	(0.227)	1.531	(0.203)
CON4	1.262	1.273	(0.172)	1.273	(0.171)	1.278	(0.174)	1.19	(0.154)
DEPRESS BY
DEP1	1.000	1		1		1		1
DEP2	0.747	0.750	(0.071)	0.749	(0.071)	0.751	(0.071)	0.729	(0.070)
DEP3	0.888	0.894	(0.080)	0.893	(0.080)	0.887	(0.079)	0.862	(0.077)
DEP4	0.675	0.678	(0.063)	0.678	(0.063)	0.680	(0.063)	0.658	(0.062)
Intercepts
CON1	1.146	1.146	(0.024)	1.146	(0.024)	1.147	(0.024)	1.142	(0.024)
CON2	1.122	1.122	(0.025)	1.122	(0.025)	1.124	(0.025)	1.120	(0.024)
CON3	1.393	1.393	(0.039)	1.393	(0.039)	1.395	(0.039)	1.391	(0.039)
CON4	1.203	1.203	(0.029)	1.203	(0.029)	1.204	(0.029)	1.201	(0.029)
DEP1	2.286	2.286	(0.061)	2.286	(0.061)	2.288	(0.061)	2.283	(0.061)
DEP2	1.956	1.956	(0.052)	1.956	(0.052)	1.957	(0.052)	1.955	(0.052)
DEP3	1.983	1.982	(0.056)	1.982	(0.056)	1.984	(0.056)	1.978	(0.055)
DEP4	1.636	1.637	(0.046)	1.637	(0.046)	1.637	(0.046)	1.636	(0.045)
ALC	1.554	1.557	(0.045)	1.559	(0.049)	1.554	(0.045)	1.397	(0.045)
Variances
CONDUCT	0.085	0.085	(0.017)	0.086	(0.017)	0.086	(0.017)	0.090	(0.015)
DEPRESS	0.907	0.903	(0.119)	0.903	(0.119)	0.914	(0.119)	0.894	(0.111)
Residuals
CON1	0.207	0.206	(0.017)	0.206	(0.017)	0.207	(0.017)	0.211	(0.016)
CON2	0.203	0.202	(0.017)	0.202	(0.017)	0.204	(0.017)	0.211	(0.017)
CON3	0.553	0.551	(0.044)	0.550	(0.044)	0.551	(0.044)	0.574	(0.044)
CON4	0.298	0.296	(0.025)	0.296	(0.025)	0.295	(0.025)	0.310	(0.024)
DEP1	0.945	0.939	(0.088)	0.939	(0.088)	0.941	(0.088)	1.011	(0.089)
DEP2	0.860	0.854	(0.067)	0.854	(0.067)	0.857	(0.067)	0.896	(0.069)
DEP3	0.865	0.862	(0.076)	0.863	(0.076)	0.863	(0.075)	0.912	(0.076)
DEP4	0.631	0.628	(0.051)	0.628	(0.051)	0.626	(0.051)	0.661	(0.052)
ALC	0.871	0.861	(0.058)	0.859	(0.060)	0.861	(0.058)	0.603	(0.052)

Note. Tabled values represent mean values of parameter estimates from the correct model for each population and their corresponding standard error. For data populations not containing interactions, estimates are derived from Model 0, the model in which an interaction is not estimated. For data populations containing interactions, estimates are derived from Model I, the model in which an interaction is estimated.

Structural model

Table 3 contains the structural parameters estimated in the simulation. For multivariate normal data with no interaction in the generation model, a likelihood ratio comparing Model 0 to Model 1 to test the significance of the latent interaction using α = 0:05 yielded a false positive in 6.1% of the data sets, close to the 5% false positive rate expected.

Table 3.

Simulation results, normally distributed and skewed data

		Multivariate Normal, No Interaction in Data		Multivariate Normal, Interaction in Data		Chi Square Distribution, No Interaction in Data		Chi Square Distribution, Interaction in Data
	Data generation	Mean Parameter (Mean Standard Error)
Path coefficients
Conduct Problems	1.074	1.083	(0.230)	1.083	(0.233)	1.089	(0.233)	1.019	(0.227)
Depressive Symptoms	0.109	0.112	(0.059)	0.112	(0.060)	0.104	(0.059)	0.088	(0.059)
Conduct Problems × Depressive Symptoms	0.000
Conduct Problems × Depressive Symptoms	0.620			0.619	(0.218)			1.736	(0.223)
Factor covariances
Conduct Problems with Depressive Symptoms	0.093	0.092	(0.020)	0.093	(0.020)	0.093	(0.021)	0.113	(0.020)
		Mean R2 (Standard Deviation of R2)
R2
Alcohol		0.136	(0.036)	0.166	(0.041)	0.137	(0.042)	0.426	(0.324)
Δ R2 of the interaction	0 or 0.03	0.004	(0.006)	0.034	(0.023)	0.014	(0.151)	0.193	(0.332)
		Mean Likelihood Ratio (Standard Deviation of Likelihood Ratio)
Likelihood Ratio		1.033	(1.476)	10.402	(6.65)	7.226	(22.329)	64.994	(56.603)
Proportion significant		0.061		0.841		0.349		0.987

Note. Path coefficients, factor covariances, and R2 represent mean values of parameter estimates from the correct model for each population and their corresponding standard error. For data populations not containing interactions, estimates are derived from Model 0, the model in which an interaction is not estimated. For data populations containing interactions, estimates are derived from Model 1, the model in which an interaction is estimated. Likelihood ratios and proportion of likelihood ratios significant are derived by estimating both Model 0 and Model 1 for each data population and comparing the likelihood ratio of the two models.

In multivariate normal data with an interaction in the data generation model, the same likelihood ratio test gave a significant result at α = 0:05 in 84.1% of our data sets. In other words, the multivariate normal data exhibited 84% power to detect the significant interaction effect known to be present in the data.

In multivariate chi-square distributed population with no interaction generated, models failed to converge in 2% of data sets, and negative likelihood ratios were produced in another 2.3% of data sets. In the remaining data sets, a 34.9% false positive rate was observed, in line with previous studies’ estimates (e.g. Cham et al., 2012).

Finally, in multivariate chi-square distributed data that includes an interaction in the generation model, the interaction was detected in 98.7% of data sets in which the model converged. In other words, power to detect the significant interaction that was indeed present was over 98% in those models that converged. However, the model failed to converge in 13.4% of these data sets, and produced a negative likelihood ratio in 0.01% of these data sets.

Effect of skewed data

One notable result of this simulation was the high rate of false positives results regarding the significance of the latent interaction in the chi-square distributed data. In chi-square distributed data in which no interaction was present, LMS falsely detected a significant interaction in 34.9% of datasets, with an average size of B = .40. In chi-square distributed data in which the interaction was present, and the expected value was B = .62, the average size of the interaction was overestimated almost threefold, at B = 1.74. By definition, the skew of a chi-square distribution is sqrt(8/k) where k represents degrees of freedom. We used a chi-square distribution with df = 1 in our study, therefore the skew of the simulated distribution was equal to 2.83. We are not able to describe effects of other values of skew given that we simulated only the chi-square distribution with 1 degree of freedom, but we expect that the degree of bias in the LMS estimates increases with increasing skew in a chi square distribution.

Given our results, and similar published findings exploring the effects of skewness on LMS estimates (e.g. Cham et al., 2012), it appears that latent variable interactions cannot be reliably estimated in skewed data using the LMS procedure.

Discussion

Although studies exploring interactions are ubiquitous in both psychological and developmental science, to date few studies have explored interactions between latent variables due, in good part, to the inaccessibility and complexity of available methods. This article demonstrates the LMS method of estimation and interpretation of latent variable interactions, and outlines a series of steps to use in order to streamline its application. The challenges of estimating latent variable interactions via the LMS method—including lack of fit indices, standardized estimates, and percentage of variance explained by the latent interaction—are reviewed, and strategies for overcoming these limitations are offered. The strategies presented are applicable to any psychological research question involving interactions of latent variables, including interactions between a latent and an observed variable as well as interactions between latent variables.

Benefits of latent variable interactions

The LMS method's wide applicability is important given the practical advantages of testing interactions via a latent variable framework. For example, unlike more conventional approaches to testing interactions (i.e., ordinary least squares regression), latent variable approaches, such as LMS, produce estimates of interactions that are unattenuated by measurement error, which serves to increase a study's power and reduce the likelihood of biased estimates (Buse-meyer & Jones, 1983; Little et al., 2006). LMS is also relatively simple to implement, requiring adding just one additional command to an existing syntax file, plus some additional calculations after estimating the model if one wishes to standardize the estimates as described in this article. Finally, the LMS method's third advantage is its efficiency, requiring estimating only one additional parameter in order to estimate the latent variable interaction.

Applicability to developmental research

Recent methodological advances such as the ability to estimate and easily interpret the results of latent variable interactions now permit important advances in developmental science, two of which we highlight here: (a) testing the quadratic effects of latent variables, and (b) estimating interactions between intercepts and growth factors. While many of the constructs developmental scientists are interested in are latent constructs (e.g., personality, mental health, self-esteem, intelligence) and therefore are best measured via a latent approach, nonlinear effects involving latent variables, such as quadratic effects of a latent variable, are often difficult to model and examine (Kenny & Judd, 1984; MacCallum & Austin, 2000; Tomarken & Waller, 2005). This creates a significant limitation, particularly given that quadratic relations are common among psychological constructs central to developmental science (Klein & Muthén, 2007; Marsh, Wen, & Hau, 2006; Ping, 1996). In addition to estimating interaction effects between two different variables, the LMS procedure can be used to create an interaction variable that is the square of a latent variable, enabling the researcher to test the quadratic effect of a given latent variable on an outcome (Muthén & Muthén, 1998–2010).

An increasingly common technique in longitudinal developmental research is latent growth modeling (LGM; McArdle, 2012). LGM and related techniques are used to analyse developmental trajectories. LGM typically involves estimating relations between an intercept and growth factor of an independent variable (e.g. depressive symptoms) and an outcome (e.g. alcohol use). Such latent growth models amount to a main effects model (i.e., they test the main effects of the intercept and growth factor), but they neglect the possibility of an interaction between the intercept and growth factor. LMS can be used to estimate interactions between intercept and growth factors within latent growth models. For example, does the effect of increases in depressive symptoms (i.e., growth) on alcohol use depend on one's starting point (i.e., intercept) in depressive symptoms? One could plausibly imagine that a moderate increase in depressive symptoms could differentially affect alcohol use among those who started with no symptoms versus those whose symptoms were already somewhat elevated. Though largely unaddressed within the developmental literature, identifying the circumstances under which intercept and slope interact with one another to impact adjustment is crucial to our understanding of healthy development.

Conclusion

Latent variables are a central feature of many empirical models of behavioral development. Using the straightforward series of steps outlined here, researchers can estimate interactions between latent variables in order to test the predictions of many psychological theories. The ability to model interactions and other nonlinearities in latent variables opens up an important new horizon of possibilities for modeling the complex relations that many of our theories predict to exist among psychological constructs. Important theoretical advances will no doubt result from the rigorous and increasingly widespread application of these methods.

Appendix

Mplus code for empirical model

Model 1

TITLE: Model 1, no interaction

DATA: FILE IS ‘filename’;

type is individual;

VARIABLE:

NAMES ARE CON1 CON2 CON3 CON4 DEP1 DEP2 DEP3 DEP4 ALC30;

USEVARIABLES ARE CON1 CON2 CON3 CON4 DEP1 DEP2 DEP3 DEP4 ALC30;

ANALYSIS:

ESTIMATOR IS MLR;

DEFINE: standardize ext1 ext2 ext3 ext4 int1 int2 int3 int4 alc30;

MODEL:

con by CON1 CON2 CON3 CON4;

dep by DEP1 DEP2 DEP3 DEP4;

! correlations

DEP1 with DEP3;

DEP2 with DEP4;

CON3 with CON4;

! paths

alc30 on dep;

alc30 on con;

! variances

dep;

con;

OUTPUT: SAMPSTAT TECH1 TECH 4 residual standardized;

Model 2

TITLE: Model 2, with interaction

DATA: FILE IS ‘filename’;

type is individual;

VARIABLE:

NAMES ARE CON1 CON2 CON3 CON4 DEP1 DEP2 DEP3 DEP4 ALC30;

USEVARIABLES ARE CON1 CON2 CON3 CON4 DEP1 DEP2 DEP3 DEP4 ALC30;

ANALYSIS:

ESTIMATOR IS MLR;

ALGORITHM = integration;

TYPE= random;

DEFINE: standardize ext1 ext2 ext3 ext4 int1 int2 int3 int4 alc30;

MODEL:

con by CON1 CON2 CON3 CON4;

dep by DEP1 DEP2 DEP3 DEP4;

depXcon | dep XWITH con;

! correlations

DEP1 with DEP3;

DEP2 with DEP4;

CON3 with CON4;

! paths

alc30 on dep;

alc30 on con;

alc30 on depXcon;

! variances

dep;

con;

OUTPUT: SAMPSTAT TECH1;

Simulation data generation code in R (multivariate normal, with an interaction)

nobs <- 500 # Observations per data set

nsim <- 1000 # Number of data sets for (i in 1: nsim) {

# generate twof“latent” variables, with required variances

# and covariance

L1 <- rnorm(nobs)

L2 <- rnorm(nobs)

L.matrix <- cbind(L1, L2)%*% chol(matrix(c(0.085,0.093,0.093,0.907), ncol = 2))

# extract latent variables into easy to use form

conduct <- L.matrix[,1]

depress <- L.matrix[,2]

# generate response from latent variables

alcohol <- 1.074*conduct + 0.109*depress+

0.624*conduct*depress + rnorm(nobs, mean=.554, sd=sqrt (0.871))

# generate measurement variables for latent variables

con1 <- 1*conduct + rnorm(nobs, mean=1.146, sd=sqrt (0.207))

con2 <- 1.086*conduct + rnorm(nobs, mean=1.122, sd=sqrt (0.203))

con3 <- 1.624*conduct + rnorm(nobs, mean=1.393, sd=sqrt (0.553))

con4 <- 1.262*conduct + rnorm(nobs, mean=1.203, sd=sqrt (0.298))

dep1 <- 1*depress + rnorm(nobs, mean=2.286, sd=sqrt (0.945))

dep2 <- 0.747*depress + rnorm(nobs, mean=1.956, sd=sqrt (0.860))

dep3 <- 0.888*depress + rnorm(nobs, mean=1.983, sd=sqrt (0.865))

dep4 <- 0.675*depress + rnorm(nobs, mean=1.636, sd=sqrt (0.631))

# package the observed variables as a matrix

obs.matrix <- cbind(con1, con2, con3, con4, dep1, dep2, dep3, dep4, alcohol)

print(i) # to give the user live feedback

# create one data set write.table(obs.matrix, file paste(“z:/mplus/mvni/mvni”, i,”.dat”, sep=““), row.names = FALSE, col.names = FALSE) }

# create a list of the data sets, for Mplus input write.table(paste(“mvni”, 1: nsim, “.dat”, sep=““), file “z:/mplus/mvni/mvnilist.dat”, row.names = FALSE, col.names=FALSE, quote=FALSE)

Mplus simulation study

title: MVN R data

Data without interaction, interaction analyzed;

data:

type montecarlo;

file=“z:\mplus\mvn\mvnlist.dat”;

! Data generated in “MVN data sim by eqs.inp”

variable: names = con1 con2 con3 con4 dep1 dep2 dep3 dep4

alcohol;

! Observed: con1 thru dep4, alcohol

! Latent: conduct depress

! Latent interaction: conxdep

model: conduct by con1@1 con2*1.086 con3*1.624 con4*1.262;

conduct*0.085;

[con1*1.146 con2*1.122 con3*1.393 con4*1.203];

con1*0.207 con2*0.203 con3*0.553 con4*0.298;

depress by dep1@1 dep2*0.747 dep3*0.888 dep4*0.675;

depress*0.907; [dep1*2.286 dep2*1.956 dep3*1.983 dep4*1.636];

dep1*0.945 dep2*0.860 dep3*0.865 dep4*0.631;

conduct with depress*0.093;

conxdep | conduct xwith depress;

alcohol on conduct*1.074 depress*0.109 conxdep*0;

[alcohol*1.554];

alcohol*0.871;

analysis: estimator ml;

type = random;

algorithm = integration;

output: tech4;

savedata: results = “z:\mplus\mvn\mvnparm0.dat”;