Distribution of the Height of Local Maxima of Gaussian Random Fields

Abstract

Let {f(t) : t ∈ T} be a smooth Gaussian random field over a parameter space T, where T may be a subset of Euclidean space or, more generally, a Riemannian manifold. We provide a general formula for the distribution of the height of a local maximum $\mathbb{P}\{f\left(t_0\right)>u\mid t_0$ is a local maximum of f(t)} when f is non-stationary. Moreover, we establish asymptotic approximations for the overshoot distribution of a local maximum $\mathbb{P}\{f\left(t_0\right)>u+v\mid t_0$ is a local maximum of f(t) and f(t₀) > v} as v → ∞. Assuming further that f is isotropic, we apply techniques from random matrix theory related to the Gaussian orthogonal ensemble to compute such conditional probabilities explicitly when T is Euclidean or a sphere of arbitrary dimension. Such calculations are motivated by the statistical problem of detecting peaks in the presence of smooth Gaussian noise.

1 Introduction

In certain statistical applications such as peak detection problems [cf. Schwartzman et al. (2011) and Cheng and Schwartzman (2014)], we are interested in the tail distribution of the height of a local maximum of a Gaussian random field. This is defined as the probability that the height of the local maximum exceeds a fixed threshold at that point, conditioned on the event that the point is a local maximum of the field. Roughly speaking, such conditional probability can be stated as

$$\mathbb{P}\{f\left(t_0\right)>u\mid t_0\text{is a local maximum of}f\left(t\right)\},$$ (1.1)

where {f(t) : t ∈ T} is a smooth Gaussian random field parameterized on an N-dimensional set $T\subset {\mathbb{R}}^N$ whose interior is non-empty, $t_0\in \mathring{T}$ (the interior of T) and $u\in \mathbb{R}$. In peak detection problems, this distribution is useful in assessing the significance of local maxima as candidate peaks. In addition, such distribution has been of interest for describing fluctuations of the cosmic background in astronomy [cf. Bardeen et al. (1985) and Larson and Wandelt (2004)] and describing the height of sea waves in oceanography [cf. Longuet-Higgins (1952, 1980), Lindgren (1982) and Sobey (1992)].

As written, the conditioning event in (1.1) has zero probability. To make the conditional probability well-defined mathematically, we follow the original approach of Cramer and Leadbetter (1967) for smooth stationary Gaussian process in one dimension, and adopt instead the definition

$$F_{t_0}\left(u\right)≔\underset{\epsilon \to 0}{\lim }\mathbb{P}\{f\left(t_0\right)>u\mid \exists \text{a local maximum of}f\left(t\right)\text{in}{U}_{t_0}\left(\epsilon \right)\},$$ (1.2)

if the limit on the right hand side exists, where $U_{t_0}\left(\epsilon \right)=t_0\oplus {(-\epsilon ∕2,\epsilon ∕2)}^N$ is the N-dimensional open cube of side ε centered at t₀. We call (1.2) the distribution of the height of a local maximum of the random field.

Because this distribution is conditional on a point process, which is the set of local maxima of f, it falls under the general category of Palm distributions [cf. Adler et al. (2012) and Schneider and Weil (2008)]. Evaluating this distribution analytically has been known to be a difficult problem for decades. The only known results go back to Cramer and Leadbetter (1967) who provided an explicit expression for one-dimensional stationary Gaussian processes, and Belyaev (1967, 1972) and Lindgren (1972) who gave an implicit expression for stationary Gaussian fields over Euclidean space.

As a first contribution, in this paper we provide general formulae for (1.2) for non-stationary Gaussian fields and T being a subset of Euclidean space or a Riemannian manifold of arbitrary dimension. As opposed to the well-studied global supremum of the field, these formulae only depend on local properties of the field. Thus, in principle, stationarity and ergodicity are not required, nor is knowledge of the global geometry or topology of the set in which the random field is defined. The caveat is that our formulae involve the expected number of local maxima (albeit within a small neighborhood of t₀), so actual computation becomes hard for most Gaussian fields except, as described below, for isotropic cases.

We also investigate the overshoot distribution of a local maximum, which can be roughly stated as

$$\mathbb{P}\{f\left(t_0\right)>u+v\mid t_0\text{is a local maximum of}f\left(t_0\right)>v\},$$ (1.3)

where u > 0 and $v\in \mathbb{R}$. The motivation for this distribution in peak detection is that, since local maxima representing candidate peaks are called significant if they are sufficiently high, it is enough to consider peaks that are already higher than a pre-threshold v. As before, since the conditioning event in (1.3) has zero probability, we adopt instead the formal definition

$${\stackrel{‒}{F}}_{t_0}(u,v)≔\underset{\epsilon \to 0}{\lim }\mathbb{P}\{f\left(t_0\right)>u+v\mid \exists \text{a local maximum of}f\left(t\right)\text{in}{U}_{t_0}\left(\epsilon \right)\text{and}f\left(t_0\right)>v\},$$ (1.4)

if the limit on the right hand side exists. It turns out that, when the pre-threshold v is high, a simple asymptotic approximation to (1.4) can be found because in that case, the expected number of local maxima can be approximated by a simple expression similar to the expected Euler characteristic of the excursion set above level v [cf. Adler and Taylor (2007)].

The appeal of the overshoot distribution had already been realized by Belyaev (1967, 1972), Nosko (1969, 1970a, 1970b) and Adler (1981), who showed that, in stationary case, it is asymptotically equivalent to an exponential distribution. In this paper we give a much tighter approximation to the overshoot distribution which, again, depends only on local properties of the field and thus, in principle, does not require stationarity nor ergodicity. However, stationarity does enable obtaining an explicit closed-form approximation such that the error is super-exponentially small. In addition, the limiting distribution has the appealing property that it does not depend on the correlation function of the field, so these parameters need not be estimated in statistical applications.

As a third contribution, we extend the Euclidean results mentioned above for both (1.2) and (1.4) to Gaussian fields over Riemannian manifolds. The extension is not difficult once it is realized that, because all calculations are local, it is essentially enough to change the local geometry of Euclidean space by the local geometry of the manifold and most arguments in the proofs can be easily changed accordingly.

As a fourth contribution, we obtain exact (non-asymptotic) closed-form expressions for isotropic fields, both on Euclidean space and the N-dimensional sphere. This is achieved by means of an interesting recent technique employed in Euclidean space by Fyodorov (2004), Azaïs and Wschebor (2008) and Auffinger (2011) involving random matrix theory. The method is based on the realization that the (conditional) distribution of the Hessian ∇²f of an isotropic Gaussian field f is closely related to that of a Gaussian Orthogonal Ensemble (GOE) random matrix. Hence, the known distribution of the eigenvalues of a GOE is used to compute explicitly the expected number of local maxima required in our general formulae described above. As an example, we show the detailed calculation for isotropic Gaussian fields on ${\mathbb{R}}^2$. Furthermore, by extending the GOE technique to the N-dimensional sphere, we are able to provide explicit closed-form expressions on that domain as well, showing the two-dimensional sphere as a specific example.

The paper is organized as follows. In Section 2, we provide general formulae for both the distribution and the overshoot distribution of the height of local maxima for smooth Gaussian fields on Euclidean space. The explicit formulae for isotropic Gaussian fields are then obtained by techniques from random matrix theory. Based on the Euclidean case, the results are then generalized to Gaussian fields over Riemannian manifolds in Section 3, where we also study isotropic Gaussian fields on the sphere. Lastly, Section 4 contains the proofs of main theorems as well as some auxiliary results.

2 Smooth Gaussian Random Fields on Euclidean Space

2.1 Height Distribution and Overshoot Distribution of Local Maxima

Let {f(t) : t ∈ T} be a real-valued, C² Gaussian random field parameterized on an N-dimensional set $T\subset {\mathbb{R}}^N$ whose interior is non-empty. Let

$$\begin{array}{cc}\hfill f_i\left(t\right)=& \frac{\partial f\left(t\right)}{\partial t_i},\nabla f\left(t\right)={(f_1\left(t\right),\dots ,f_N\left(t\right))}^T,\Lambda \left(t\right)=\mathrm{Cov}(\nabla f\left(t\right)),\hfill \\ \hfill f_{ij}\left(t\right)=& \frac{{\partial }^{2}f\left(t\right)}{\partial t_i{t}_j},{\nabla }^{2}f\left(t\right)={\left(f_{ij}\left(t\right)\right)}_{i\le i,j\le N},\hfill \end{array}$$

and denote by index(∇²f(t)) the number of negative eigenvalues of ∇²f(t). We will make use of the following conditions.

(C1). f ∈ C²(T) almost surely and its second derivatives satisfy the mean-square Hölder condition: for any t₀ ∈ T, there exist positive constants L, η and δ such that

$$\mathbb{E}{(f_{ij}\left(t\right)-f_{ij}\left(s\right))}^2\le L^2{\Vert t-s\Vert }^{2\eta },\forall t,s\in U_{t_0}\left(\delta \right),i,j=1,\dots ,N.$$

(C2). For every pair (t, s) ∈ T² with t ≠ s, the Gaussian random vector

$$(f\left(t\right).\nu \nabla f\left(t\right),f_{ij}\left(t\right),f\left(s\right),\nabla f\left(s\right),f_{ij}\left(s\right),1\le i\le j\le N)$$

is non-degenerate.

Note that (C1) holds when f ∈ C³(T) and T is closed and bounded.

The following theorem, whose proof is given in Section 4, provides the formula for F_t0(u) defined in (1.2) for smooth Gaussian fields over ${\mathbb{R}}^N$.

Theorem 2.1 Let {f(t) : t ∈ T} be a Gaussian random field satisfying (C1) and (C2). Then for each $t_0\in \mathring{T}$ and $u\in \mathbb{R}$,

$$F_{t_0}\left(u\right)=\frac{\mathbb{E}\{\mid \det {\nabla }^{2}f\left(t_0\right)\mid 1_{\{f\left(t_0\right)>u\}}{1}_{\{\text{index}\left({\nabla }^{2}f\left(t_0\right)\right)=N\}}\mid \nabla f\left(t_0\right)=0\}}{\mathbb{E}\{\mid \det {\nabla }^{2}f\left(t_0\right)\mid 1_{\{\text{index}\left({\nabla }^{2}f\left(t_0\right)\right)=N\}}\mid \nabla f\left(t_0\right)=0\}}.$$ (2.1)

The implicit formula in (2.1) generalizes the results for stationary Gaussian fields in Cramér and Leadbetter (1967, p. 243), Belyaev (1967, 1972) and Lindgren (1972) in the sense that stationarity is no longer required.

Note that the conditional expectations in (2.1) are hard to compute, since they involve the indicator functions on the eigenvalues of a random matrix. However, in Section 2.2 and Section 3.2 below, we show that (2.1) can be computed explicitly for isotropic Gaussian fields.

The following result shows the exact formula for the overshoot distribution defined in (1.4).

Theorem 2.2 Let {f(t) : t ∈ T} be a Gaussian random field satisfying (C1) and (C2). Then for each $t_0\in \mathring{T},v\in \mathbb{R}$, and u > 0,

$${\stackrel{‒}{F}}_{t_0}(u,v)=\frac{\mathbb{E}\{\mid \det {\nabla }^{2}f\left(t_0\right)\mid 1_{\{f\left(t_0\right)>u,v\}}{1}_{\{\text{index}\left({\nabla }^{2}f\left(t_0\right)\right)=N\}}\mid \nabla f\left(t_0\right)=0\}}{\mathbb{E}\{\mid \det {\nabla }^{2}f\left(t_0\right)\mid 1_{\{f\left(t_0\right)>v\}}{1}_{\{\text{index}\left({\nabla }^{2}f\left(t_0\right)\right)=N\}}\mid \nabla f\left(t_0\right)=0\}}.$$

Proof The result follows from similar arguments for proving Theorem 2.1.

The advantage of overshoot distribution is that we can explore the asymptotics as the pre-threshold v gets large. Theorem 2.3 below, whose proof is given in Section 4, provides an asymptotic approximation to the overshoot distribution of a smooth Gaussian field over ${\mathbb{R}}^N$. This approximation is based on the fact that as the exceeding level tends to infinity, the expected number of local maxima can be approximated by a simpler form which is similar to the expected Euler characteristic of the excursion set.

Theorem 2.3 Let {f(t) : t ∈ T} be a centered, unit-variance Gaussian random field satisfying (C1) and (C2). Then for each $t_0\in \mathring{T}$ and each fixed u > 0, there exists α > 0 such that as v → ∞,

$${\stackrel{‒}{F}}_{t_0}(u,v)=\frac{{\int }_{u+v}^{\infty }\varphi \left(x\right)\mathbb{E}\{\det {\nabla }^{2}f\left(t_0\right)\mid f\left(t_0\right)=x,\nabla f\left(t_0\right)=0\}dx}{{\int }_v^{\infty }\varphi \left(x\right)\mathbb{E}\{\det {\nabla }^{2}f\left(t_0\right)\mid f\left(t_0\right)=x,\nabla f\left(t_0\right)=0\}dx}(1+o\left(e^{-\alpha v^2}\right)).$$ (2.2)

Here and in the sequel, ϕ(x) denotes the standard Gaussian density.

Note that the expectation in (2.2) is computable since the indicator function does not exist anymore. However, for non-stationary Gaussian random fields over ${\mathbb{R}}^N$ with N ≥ 2, the general expression of the expectation in (2.2) would be complicated. Fortunately, as a polynomial in x, the coefficient of the highest order of the expectation above is relatively simple, see Lemma 4.2 below. This gives the following approximation to the overshoot distribution for general smooth Gaussian fields over ${\mathbb{R}}^N$.

Corollary 2.4 Let the assumptions in Theorem 2.3 hold. Then for each $t_0\in \mathring{T}$ and each fixed u > 0, as v → ∞,

$${\stackrel{‒}{F}}_{t_0}(u,v)=\frac{{(u+v)}^{N-1}{e}^{-{(u+v)}^2∕2}}{v^{N-1}{e}^{-v^2∕2}}(1+O\left(v^{-2}\right)).$$ (2.3)

Proof The result follows immediately from Theorem 2.3 and Lemma 4.2 below.

It can be seen that the result in Corollary 2.4 reduces to the exponential asymptotic distribution given by Belyaev (1967, 1972), Nosko (1969, 1970a, 1970b) and Adler (1981), but the result here gives the approximation error and does not require stationarity. Compared with (2.2), (2.3) provides a less accurate approximation, since the error is only O(v^–2), but it provides a simple explicit form.

Next we show some cases where the approximation in (2.2) becomes relatively simple and with the same degree of accuracy, i.e., the error is super-exponentially small.

Corollary 2.5 Let the assumptions in Theorem 2.3 hold. Suppose further the dimension N = 1 or the field f is stationary, then for each $t_0\in \mathring{T}$ and each fixed u > 0, there exists α > 0 such that as v → ∞,

$${\stackrel{‒}{F}}_{t_0}(u,v)=\frac{H_{N-1}(u+v)e^{-{(u+v)}^2∕2}}{H_{N-1}\left(v\right)e^{-v^2}∕2}(1+o\left(e^{-\alpha v^2}\right)),$$ (2.4)

where H_N–1(x) is the Hermite polynomial of order N – 1.

Proof (i) Suppose first N = 1. Since Var(f(t)) ≡ 1, $\mathbb{E}\left\{f\left(t\right)f^{\prime }\left(t\right)\right\}\equiv 0$ and $\mathbb{E}\left\{f^{″}\left(t\right)f\left(t\right)\right\}=-\mathrm{Var}\left(f^{\prime }\left(t\right)\right)=-\Lambda \left(t\right)$. It follows that

$$\mathbb{E}\{\det {\nabla }^{2}f\left(t\right)\mid f\left(t\right)=x,\nabla f\left(t\right)=0\}=\mathbb{E}\{f^{″}\left(t\right)\mid f\left(t\right)=x,f^{\prime }\left(t\right)=0\}=(\mathbb{E}\left\{f^{″}\left(t\right)f\chi \left(t\right)\right\},\mathbb{E}\left\{f^{″}\left(t\right)f^{\prime }\left(t\right)\right\})\left(\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \frac{1}{\mathrm{Var}\left(f^{\prime }\left(t\right)\right)}\hfill \end{array}\right)\left(\begin{array}{c}\hfill x\hfill \\ \hfill 0\hfill \end{array}\right)=-\Lambda \left(t\right)x.$$

Plugging this into (2.2) yields the desired result.

(ii) If f is stationary, it can be shown that [cf. Lemma 11.7.1 in Adler and Taylor (2007)],

$$\mathbb{E}\{\det {\nabla }^{2}f\left(t_0\right)\mid f\left(t_0\right)=x,\nabla f\left(t_0\right)=0\}={(-1)}^N\det \left(\Lambda \left(t_0\right)\right)H_N\left(x\right).$$

Then (2.4) follows from Theorem 2.3 and the following formula for Hermite polynomials

$${\int }_v^{\infty }{H}_N\left(x\right)e^{-x^2∕2}dx=H_{N-1}\left(v\right)e^{-v^2∕2}.$$

An interesting property of the results obtained about the overshoot distribution is that the asymptotic approximations in Corollaries 2.4 and 2.5 do not depend on the location t₀, even in the case where stationarity is not assumed. In addition, they do not require any knowledge of spectral moments of f except for zero mean and constant variance. In this sense, the distributions are convenient for use in statistics because the correlation function of the field need not be estimated.

2.2 Isotropic Gaussian Random Fields on Euclidean Space

We show here the explicit formulae for both the height distribution and the overshoot distribution of local maxima for isotropic Gaussian random fields. To our knowledge, this article is the first attempt to obtain these distributions explicitly for N ≥ 2. The main tools are techniques from random matrix theory developed in Fyodorov (2004), Azaïs and Wschebor (2008) and Auffinger (2011).

Let {f(t) : t ∈ T} be a real-valued, C², centered, unit-variance isotropic Gaussian field parameterized on an N-dimensional set $T\subset {\mathbb{R}}^N$. Due to isotropy, we can write the covariance function of the field as $\mathbb{E}\left\{f\left(t\right)f\left(s\right)\right\}=\rho \left({\Vert t-s\Vert }^2\right)$ for an appropriate function $\rho (\cdot ):[0,\infty )\to \mathbb{R}$, and denote

$${\rho }^{\prime }={\rho }^{\prime }\left(0\right),{\rho }^{″}={\rho }^{″}\left(0\right),\kappa =-{\rho }^{\prime }∕\sqrt{{\rho }^{″}}.$$ (2.5)

By isotropy again, the covariance of (f(t), ∇f(t), ∇²f(t)) only depends on ρ′ and ρ″, see Lemma 4.3 below. In particular, by Lemma 4.3, we see that Var(f_i(t)) = –2ρ′ and Var(f_ii(t)) = 12ρ″ for any i ∈ {1, . . . , N}, which implies ρ′ < 0 and ρ″ > 0 and hence κ > 0. We need the following condition for further discussions.

(C3). κ ≤ 1 (or equivalently ρ″ – ρ′² ≥ 0).

Example 2.6 Here are some examples of covariance functions with corresponding ρ satisfying (C3).

• (i)Powered exponential: ρ(r) = e^–cr, where c > 0. Then ρ′ = –c, ρ″ = c² and κ = 1.
• (ii)Cauchy: ρ(r) = (1 + r/c)^–β, where c > 0 and β > 0. Then ρ′ = –β/c, ρ″ = β(β + 1)/c² and $\kappa =\sqrt{\beta ∕(\beta +1)}$.

Remark 2.7 By Azaïs and Wschebor (2010), (C3) holds when ρ(∥t – s∥²), t, $s\in {\mathbb{R}}^N$, is a positive definite function for every dimension N ≥ 1. The cases in Example 2.6 are of this kind.

We shall use (2.1) to compute the distribution of the height of a local maximum. As mentioned before, the conditional distribution on the right hand side of (2.1) is extremely hard to compute. In Section 4 below, we build connection between such distribution and certain GOE matrix to make the computation available.

Recall that an N × N random matrix M_N is said to have the Gaussian Orthogonal Ensemble (GOE) distribution if it is symmetric, with centered Gaussian entries M_ij satisfying Var(M_ii) = 1, Var(M_ij) = 1/2 if i < j and the random variables {M_ij, 1 ≤ i ≤ j ≤ N} are independent. Moreover, the explicit formula for the distribution Q_N of the eigenvalues λ_i of M_N is given by [cf. Auffinger (2011)]

$$Q_N\left(d\lambda \right)=\frac{1}{c_N}\prod _{i=1}^N{e}^{-\frac{1}{2}{\lambda }_i^{2}d{\lambda }_i}\prod _{1\le i\le N}\mid {\lambda }_i-{\lambda }_j\mid 1_{\{{\lambda }_1\le \cdots \le {\lambda }_N\}},$$ (2.6)

where the normalization constant c_N can be computed from Selberg's integral

$$c_N=\frac{1}{N!}{\left(2\sqrt{2}\right)}^N\prod _{i=1}^N\Gamma \left(1+\frac{i}{2}\right).$$ (2.7)

We use notation ${\mathbb{R}}_{GOE}^N$ to represent the expectation under density Q_N(dλ), i.e., for a measurable function g,

$${\mathbb{E}}_{GOE}^N\left[g({\lambda }_1,\dots ,{\lambda }_N)\right]={\int }_{{\lambda }_1\le \dots \le {\lambda }_N}g({\lambda }_1,\dots ,{\lambda }_N)Q_N\left(d\lambda \right).$$

Theorem 2.8 Let {f(t) : t ∈ T} be a centered, unit-variance, isotropic Gaussian random field satisfying (C1), (C2) and (C3). Then for each $t_0\in \mathring{T}$ and $u\in \mathbb{R}$,

$$F_{t_0}\left(u\right)=\{\begin{array}{cc}\frac{{(1-{\kappa }^2)}^{-1∕2}{\int }_u^{\infty }\varphi \left(x\right){\mathbb{E}}_{GOE}^{N+1}\left\{\exp [{\lambda }_{N+1}^2∕2-{({\lambda }_{N+1}-\kappa x∕\sqrt{2})}^2∕(1-{\kappa }^2)]\right\}dx}{{\mathbb{E}}_{GOE}^{N+1}\left\{\exp [-{\lambda }_{N+1}^2∕2]\right\}}\hfill & if\kappa \in (0,1),\hfill \\ \frac{{\int }_u^{\infty }\varphi \left(x\right){\mathbb{E}}_{GOE}^N\left\{{\left(\prod _{i=1}^N\mid {\lambda }_1-x∕\sqrt{2}\mid \right)}_{\{{\lambda }_N<x∕\sqrt{2}\}}\right\}dx}{\sqrt{2∕\pi }\Gamma \left(\frac{N+1}{2}\right){\mathbb{E}}_{GOE}^{N+1}\left\{\exp [-{\lambda }_{N+1}^2∕2]\right\}}\hfill & if\kappa =1,\hfill \end{array}\phantom{\}}$$

where κ is defined in (2.5).

Proof Since f is centered and has unit variance, the numerator in (2.1) can be written as

$${\int }_u^{\infty }\varphi \left(x\right)\mathbb{E}\{\mid \det {\nabla }^{2}f\left(t_0\right)\mid 1_{\{\text{index}\left({\nabla }^{2}f\left(t_0\right)\right)=N\}}\mid f\left(t_0\right)=x,\nabla f\left(t_0\right)=0\}dx.$$

Applying Theorem 2.1 and Lemmas 4.6 and 4.7 below gives the desired result.

Remark 2.9 The formula in Theorem 2.8 shows that for an isotropic Gaussian field over ${\mathbb{R}}^N$, F_t0(u) only depends on κ. Therefore, we may write F_t0(u) as F_t0(u, κ). As a consequence of Lemma 4.4, F_t0(u, κ) is continuous in κ, hence the formula for the case of κ = 1 (i.e. ρ″ – ρ′² = 0) can also be derived by taking the limit lim_κ↑1 F_t0(u, κ).

Next we show an example on computing F_t0(u) explicitly for N = 2. The calculation for N = 1 and N > 2 is similar and thus omitted here. In particular, the formula for N = 1 derived in such method can be verified to be the same as in Cramer and Leadbetter (1967).

Example 2.10 Let N = 2. Applying Proposition 4.8 below with a = 1 and b = 0 gives

$${\mathbb{E}}_{GOE}^{N+1}\left\{\exp \left[-\frac{{\lambda }_{N+1}^2}{2}\right]\right\}=\frac{\sqrt{6}}{6}.$$ (2.8)

Applying Proposition 4.8 again with a = 1/(1 – κ²) and $b=\kappa x∕\sqrt{2}$, one has

$${\mathbb{E}}_{GOE}^{N+1}\left\{\exp \left[\frac{{\lambda }_{N+!}^2}{2}-\frac{{({\lambda }_{N+1}-\kappa x∕\sqrt{2})}^2}{1-{\kappa }^2}\right]\right\}=\frac{\sqrt{1-{\kappa }^2}}{\pi \sqrt{2}}\left\{\pi {\kappa }^2(x^2-1)\Phi \left(\frac{\kappa x}{\sqrt{2-{\kappa }^2}}\right)+\frac{\kappa x\sqrt{2-{\kappa }^2}\sqrt{\pi }}{\sqrt{2}}{e}^{-\frac{{\kappa }^2{x}^2}{2(2-{\kappa }^2)}}+\frac{2\pi }{\sqrt{3-{\kappa }^2}}{e}^{-\frac{{\kappa }^2{x}^2}{2(3-{\kappa }^2)}}\Phi \left(\frac{\kappa x}{\sqrt{(3-{\kappa }^2)(2-{\kappa }^2)}}\right)\right\},$$ (2.9)

where $\Phi \left(x\right)={\left(2\pi \right)}^{-1∕2}{\int }_{-\infty }^x{e}^{-\frac{t^2}{2}}$ is the c.d.f. of standard Normal random variable. Let h(x) be the density function of the distribution of the height of a local maximum, i.e. $h\left(x\right)=-F_{t_0}^{\prime }\left(x\right)$. By Theorem 2.8, (2.8) and (2.9),

$$h\left(x\right)=\sqrt{3}{\kappa }^2(x^2-1)\varphi \left(x\right)\Phi \left(\frac{\kappa x}{\sqrt{2-{\kappa }^2}}\right)+\frac{\kappa x\sqrt{3(2-{\kappa }^2)}}{2\pi }{e}^{-\frac{x^2}{2-{\kappa }^2}}+\frac{\sqrt{6}}{\sqrt{\pi (3-{\kappa }^2)}}{e}^{-\frac{3x^2}{2(3-{\kappa }^2)}}\Phi \left(\frac{\kappa x}{\sqrt{(3-{\kappa }^2)}(2-{\kappa }^2)}\right),$$ (2.10)

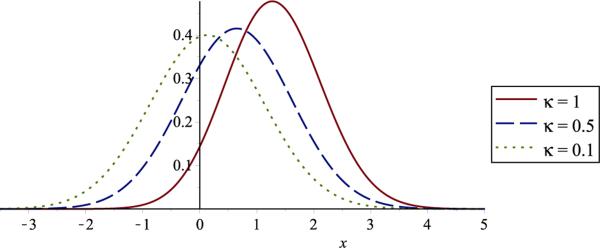
and hence $F_{t_0}\left(u\right)={\int }_u^{\infty }h\left(x\right)dx$. Figure 1 shows several examples. Shown in solid red is the extreme case of (C3), κ = 1, which simplifies to

$$h\left(x\right)=\sqrt{3}(x^2-1)\varphi \left(x\right)\Phi \left(x\right)+\frac{\sqrt{3}}{2\pi }x{e}^{-x^2}+\frac{\sqrt{3}}{\sqrt{\pi }}{e}^{-\frac{3x^2}{4}}\Phi \left(\frac{x}{\sqrt{2}}\right).$$

As an interesting phenomenon, it can be seen from both (2.10) and Figure 1 that h(x) → ϕ(x) if κ → 0.

Figure 1.

Density function h(x) of the distribution F_t0 for isotropic Gaussian fields on ${\mathbb{R}}^2$.

Theorem 2.11 Let {f(t) : t ∈ T} be a centered, unit-variance, isotropic Gaussian random field satisfying (C1), (C2) and (C3). Then for each $t_0\in \mathring{T},v\in \mathbb{R}$, and u > 0,

$${\stackrel{‒}{F}}_{t_0}(u,v)=\{\begin{array}{cc}\frac{{\int }_{u+v}^{\infty }\varphi \left(x\right){\mathbb{E}}_{GOE}^{N+1}\left\{\exp [{\lambda }_{N+1}^2∕2-{({\lambda }_{N+!}-\kappa x∕\sqrt{2})}^2∕(1-{\kappa }^2)]\right\}dx}{{\int }_v^{\infty }\varphi \left(x\right){\mathbb{E}}_{GOE}^{N+1}\left\{\exp [{\lambda }_{N+1}^2∕2-{({\lambda }_{N+1}-\lambda x∕\sqrt{2})}^2∕(1-{\kappa }^2)]\right\}dx}\hfill & if\kappa \in (0,1),\hfill \\ \frac{{\int }_{u+v}^{\infty }\varphi \left(x\right){\mathbb{E}}_{GOE}^N\left\{{\left(\prod _{i=1}^N\mid {\lambda }_i-x∕\sqrt{2}\mid \right)}_{\{{\lambda }_N<x∕\sqrt{2}\}}\right\}dx}{{\int }_v^{\infty }\varphi \left(x\right){\mathbb{E}}_{GOE}^N\left\{{\left(\prod _{i=1}^N\mid {\lambda }_i-x∕\sqrt{2}\mid \right)}_{\{{\lambda }_N<x∕\sqrt{2}\}}\right\}dx}\hfill & if\kappa =1,\hfill \end{array}\phantom{\}}$$ (2.11)

where κ is defined in (2.5).

Proof The result follows immediately by applying Theorem 2.2 and Lemma 4.7 below.

Note that the expectations in (2.11) can be computed similarly to (2.9) for any N ≥ 1, thus Theorem 2.11 provides an explicit formula for the overshoot distribution of isotropic Gaussian fields. On the other hand, since isotropy implies stationarity, the approximation to overshoot distribution for large v is simply given by Corollary 2.5.

3 Smooth Gaussian Random Fields on Manifolds

3.1 Height Distribution and Overshoot Distribution of Local Maxima

Let (M, g) be an N-dimensional Riemannian manifold and let f be a smooth function on M. Then the gradient of f, denoted by ∇f, is the unique continuous vector field on M such that g(∇f, X) = X f for every vector field X. The Hessian of f, denoted by ∇²f, is the double differential form defined by ∇²f(X, Y) = XY f – ∇_XY f, where X and Y are vector fields, ∇_X is the Levi-Civitá connection of (M, g). To make the notations consistent with the Euclidean case, we fix an orthonormal frame {E_i}_1≤i≤N, and let

$$\begin{array}{cc}\hfill \nabla f=& (f_1,\dots ,f_N)=(E_{1}f,\dots ,E_{N}f),\hfill \\ \hfill {\nabla }^{2}f=& {\left(f_{ij}\right)}_{1\le i,j\le N}={\left({\nabla }^{2}f(E_i,E_j)\right)}_{1\le i,j\le N}.\hfill \end{array}$$ (3.1)

Note that if t is a critical point, i.e. ∇f(t) = 0, then ∇²f(E_i, E_j)(t) = E_iE_jf(t), which is similar to the Euclidean case.

Let B_t0(ε) = {t ∈ M : d(t, t₀) ≤ ε} be the geodesic ball of radius ε centered at $t_0\in \mathring{M}$, where d is the distance function induced by the Riemannian metric g. We also define F_t0(u) as in (1.2) and F̄_t0(u, v) as in (1.4) with U_t0(ε) replaced by B_t0(ε), respectively.

We will make use of the following conditions.

(C1′). f ∈ C²(M) almost surely and its second derivatives satisfy the mean-square Hölder condition: for any t₀ ∈ M, there exist positive constants L, η and δ such that

$$\mathbb{E}{(f_{ij}\left(t\right)-f_{ij}\left(s\right))}^2\le L^{2}d{(t,s)}^{2\eta },\forall t,s\in B_{t_0}\left(\delta \right),i,j=1,\dots ,N.$$

(C2′). For every pair (t, s) ∈ M² with t ≠ s, the Gaussian random vector

$$(f\left(t\right),\nabla f\left(t\right),f_{ij}\left(t\right),f\left(s\right),\nabla f\left(s\right),f_{ij}\left(s\right),1\le i\le j\le N)$$

is non-degenerate.

Note that (C1′) holds when f ∈ C³(M).

Theorem 3.1 below, whose proof is given in Section 4, is a generalization of Theorems 2.1, 2.2, 2.3 and Corollary 2.4. It provides formulae for both the height distribution and the overshoot distribution of local maxima for smooth Gaussian fields over Riemannian manifolds. Note that the formal expressions are exactly the same as in Euclidean case, but now the field is defined on a manifold.

Theorem 3.1 Let (M, g) be an oriented N-dimensional C³ Riemannian manifold with a C¹ Riemannian metric g. Let f be a Gaussian random field on M such that (C1′) and (C2′) are fulfilled. Then for each $t_0\in \mathring{M}$, u, $v\in \mathbb{R}$ and w > 0,

$$\begin{array}{cc}\hfill F_{t_0}\left(u\right)=& \frac{\mathbb{E}\{\mid \det {\nabla }^{2}f\left(t_0\right)\mid 1_{\{f\left(t_0\right)>u\}}{1}_{\{\text{index}\left({\nabla }^{2}f\left(t_0\right)\right)=N\}}\mid \nabla f\left(t_0\right)=0\}}{\mathbb{E}\zeta \{\mid \det {\nabla }^{2}f\left(t_0\right)\mid 1_{\{\text{index}\left({\nabla }^{2}f\left(t_0\right)\right)=N\}}\mid \nabla f\left(t_0\right)=0\}},\hfill \\ \hfill {\stackrel{‒}{F}}_{t_0}(w,v)=& \frac{\mathbb{E}\{\mid \det {\nabla }^{2}f\left(t_0\right)\mid 1_{\{f\left(t_0\right)>w+v\}}{1}_{\{\text{index}\left({\nabla }^{2}f\left(t_0\right)\right)=N\}}\mid \nabla f\left(t_0\right)=0\}}{\mathbb{E}\{\mid \det {\nabla }^{2}f\left(t_0\right)\mid 1_{\{f\left(t_0\right)>v\}}{2}_{(\text{index}\left({\nabla }^{2}f\left(t_0\right)\right)=N\}}\mid \nabla f\left(t_0\right)=0\}}.\hfill \end{array}$$ (3.2)

If we assume further that f is centered and has unit variance, then for each fixed w > 0, there exists α > 0 such that as v → ∞,

$$\begin{array}{cc}\hfill {\stackrel{‒}{F}}_{t_0}(w,v)=& \frac{{\int }_{w+v}^{\infty }\varphi \left(x\right)\mathbb{E}\{\det {\nabla }^{2}f\left(t_0\right)\mid f\left(t_0\right)=x,\nabla f\left(t_0\right)=0\}}{{\int }_v^{\infty }\varphi \left(x\right)\mathbb{E}\{\det {\nabla }^{2}f\left(t_0\right)\mid f\left(t_0\right)=x,\nabla f\left(t_0\right)=0\}dx}(1+o\left(e^{-\alpha v^2}\right))\hfill \\ \hfill =& \frac{{(w+v)}^{N-1}{e}^{-{(w+v)}^2∕2}}{v^{N-1}{e}^{-v^2∕2}}(1+O\left(v^{-2}\right)).\hfill \end{array}$$ (3.3)

It is quite remarkable that the second approximation in (3.3) does not depend on the curvature of the manifold nor the covariance function of the field, which need not have any stationary properties other than zero mean and constant variance.

3.2 Isotropic Gaussian Random Fields on the Sphere

Similarly to the Euclidean case, we explore the explicit formulae for both the height distribution and the overshoot distribution of local maxima for isotropic Gaussian random fields on a particular manifold, sphere.

Consider an isotropic Gaussian random field $\{f\left(t\right):t\in {\mathbb{S}}^N\}$, where ${\mathbb{S}}^N\subset {\mathbb{R}}^{N+1}$ is the N-dimensional unit sphere. For the purpose of simplifying the arguments, we will focus here on the case N ≥ 2. The special case of the circle, N = 1, requires separate treatment but extending our results to that case is straightforward.

The following theorem by Schoenberg (1942) characterizes the covariance function of an isotropic Gaussian field on sphere [see also Gneiting (2013)].

Theorem 3.2 A continuous function $C(\cdot ,\cdot ):{\mathbb{S}}^N\times {\mathbb{S}}^N\to \mathbb{R}$ is the covariance of an isotropic Gaussian field on ${\mathbb{S}}^N$, N ≥ 2, if and only if it has the form

$$C(t,s)=\sum _{n=0}^{\infty }{a}_n{P}_n^{\lambda }\left(\langle t,s\rangle \right),t,s\in {\mathbb{S}}^N,$$

where λ = (N – 1)/2, $a_n\ge 0$, ${\sum }_{n=0}^{\infty }{a}_{n}Pn\lambda \left(1\right)<\infty$, and $P_n^{\lambda }$ are ultraspherical polynomials defined by the expansion

$${(1-2rx+r^2)}^{-\lambda }=\sum _{n=0}^{\infty }{r}^n{P}_n^{\lambda }\left(x\right),x\in [-1,1].$$

Remark 3.3 (i). Note that [cf. Szegö (1975, p. 80)]

$$P_n^{\lambda }\left(1\right)=\left(\begin{array}{c}\hfill n+2\lambda -1\hfill \\ \hfill n\hfill \end{array}\right)$$ (3.4)

and λ = (N – 1)/2, therefore, ${\sum }_{n=0}^{\infty }{a}_n{P}_n^{\lambda }\left(1\right)<\infty$ is equivalent to ${\sum }_{n=0}^{\infty }{n}^{N-2}{a}_n<\infty$.

(ii). When N = 2, λ = 1/2 and $P_n^{\lambda }$ become Legendre polynomials. For more results on isotropic Gaussian fields on ${\mathbb{S}}^2$, see a recent monograph by Marinucci and Peccati (2011).

(iii). Theorem 3.2 still holds for the case N = 1 if we set [cf. Schoenberg (1942)] $P_n^0\left(\langle t,s\rangle \right)=\cos \left(n\arccos \langle t,s\rangle \right)=T_n\left(\langle t,s\rangle \right)$, where T_n are Chebyshev polynomials of the first kind defined by the expansion

$$\frac{1-rx}{1-2rx+r^2}=\sum _{n=0}^{\infty }{r}^n{T}_n\left(x\right),x\in [-1,1].$$

The arguments in the rest of this section can be easily modified accordingly.

The following statement (C1″) is a smoothness condition for Gaussian fields on sphere. Lemma 3.4 below shows that (C1″) implies the pervious smoothness condition (C1′).

(C1″). The covariance C(·, ·) of $\{f\left(t\right):t\in {\mathbb{S}}^N\}$, N ≥ 2, satisfies

$$C(t,s)=\sum _{n=0}^{\infty }{a}_n{P}_n^{\lambda }\left(\langle t,s\rangle \right),t,s\in {\mathbb{S}}^N,$$

where $\lambda =(N-1)∕2,a_n\ge 0$, ${\sum }_{n=1}^{\infty }{n}^{N+8}{a}_n<\infty$, and $P_n^{\lambda }$ are ultraspherical polynomials.

Lemma 3.4 [Cheng and Xiao (2014)]. Let f be an isotropic Gaussian field on ${\mathbb{S}}^N$ such that (C1″) is fulfilled. Then the covariance $C(\cdot ,\cdot )\in C^5({\mathbb{S}}^N\times {\mathbb{S}}^N)$ and hence (C1′) holds for f.

For a unit-variance isotropic Gaussian field f on ${\mathbb{S}}^N$ satisfying (C1″), we define

$$\begin{array}{cc}\hfill C^{\prime }=& \sum _{n=1}^{\infty }{a}_n\left(\frac{d}{dx}{P_n^{\lambda }\left(x\right)\mid }_{x=1}\right)=(N-1)\sum _{n=1}^{\infty }{a}_n{P}_{n-1}^{\lambda +1}\left(1\right),\hfill \\ \hfill C^{″}=& \sum _{n=2}^{\infty }{a}_n\left(\frac{d^2}{d{x}^2}{P_n^{\lambda }\left(x\right)\mid }_{x=1}\right)=(N-1)(N+1)\sum _{n=2}^{\infty }{a}_n{P}_{n-2}^{\lambda +2}\left(1\right).\hfill \end{array}$$ (3.5)

Due to isotropy, the covariance of (f(t), ∇f(t), ∇²f(t)) only depends on C′ and C″, see Lemma 4.10 below. In particular, by Lemma 4.10 again, Var(f_i(t)) = C′ and Var(f_ii(t)) = C′ + 3C″ for any i ∈ {1, . . . , N}. We need the following condition on C′ and C″ for further discussions.

(C3′). C″ + C′ – C′² ≥ 0.

Remark 3.5 Note that (C3′) holds when C(·, ·) is a covariance function (i.e. positive definite function) for every dimension N ≥ 2 (or equivalently for every N ≥ 1). In fact, by Schoenberg (1942), if C(·, ·) is a covariance function on ${\mathbb{S}}^N$ for every N ≥ 2, then it is necessary of the form

$$C(t,s)=\sum _{n=0}^{\infty }{b}_n{\langle t,s\rangle }^n,t,s\in {\mathbb{S}}^N,$$

where b_n ≥ 0. Unit-variance of the field implies ${\sum }_{n=0}^{\infty }{b}_n=1$. Now consider the random variable X that assigns probability b_n to the integer n. Then $C^{\prime }={\sum }_{n=1}^{\infty }n{b}_n=\mathbb{E}X$, $C^{″}={\sum }_{n=2}^{\infty }n(n-1)b_n=\mathbb{E}X(X-1)$ and C″ + C′ – C′² = Var(X) ≥ 0, hence (C3′) holds.

Theorem 3.6 Let $\{f\left(t\right):t\in {\mathbb{S}}^N\}$, N ≥ 2, be a centered, unit-variance, isotropic Gaussian field satisfying (C1″), (C2′) and (C3′). Then for each $t_0\in {\mathbb{S}}^N$ and $u\in \mathbb{R}$,

$$F_{t_0}\left(u\right)=\{\begin{array}{cc}\frac{{\left(\frac{C^{″}+C^{\prime }}{C^{″}+C^{\prime }-C^{\prime 2}}\right)}^{1∕2}{\int }_u^{\infty }\varphi \left(x\right){\mathbb{E}}_{GOE}^{N+1}\left\{\exp \left[\frac{{\lambda }_{N+1}^2}{2}-\frac{C^{″}{\left({\lambda }_{N+1}-\frac{C^{\prime }x}{\sqrt{2C^{″}}}\right)}^2}{C^{″}+C^{\prime }-C^{\prime 2}}\right]\right\}dx}{{\mathbb{E}}_{GOE}^{N+1}\left\{\exp [\frac{1}{2}{\lambda }_{N+1}^2-\frac{C^{″}}{C^{″}+C^{\prime }}{\lambda }_{N+1}^2]\right\}}\hfill & if{C}^{″}+C^{\prime }-C^{\prime 2}>0,\hfill \\ \frac{{\int }_u^{\infty }\varphi \left(x\right){\mathbb{E}}_{GOE}^N\left\{{\left(\prod _{i=1}^N\mid {\lambda }_i-\frac{C^{\prime }x}{\sqrt{2C^{″}}}\mid \right)}_{\{{\lambda }_N<\frac{C^{\prime }x}{\sqrt{2C^{″}}}\}}\right\}dx}{{\left(\frac{2C^{″}}{\partial (C^{″}+C^{\prime })}\right)}^{1∕2}\Gamma \left(\frac{N+1}{2}\right){\mathbb{E}}_{GOE}^{N+1}\left\{\exp \left[\frac{1}{2}{\lambda }_{N+1}^2-\frac{C^{″}}{C^{″}+C^{\prime }}{\lambda }_{N+1}^2\right]\right\}}\hfill & if{C}^{″}+C^{\prime }-C^{\prime 2}=0,\hfill \end{array}\phantom{\}}$$

where C′ and C″ are defined in (3.5).

Proof The result follows from applying Theorem 3.1 and Lemmas 4.12 and 4.13 below.

Remark 3.7 The formula in Theorem 3.6 shows that for isotropic Gaussian fields over ${\mathbb{S}}^N$, F_t0(u) depends on both C′ and C″. Therefore, we may write F_t0(u) as F_t0(u, C′, C″). As a consequence of Lemma 4.11, F_t0(u, C′, C″) is continuous in C′ and C″, hence the formula for the case of C″ + C′ – C′² = 0 can also be derived by taking the limit lim_{C″+C′–C′²↓0} F_t0(u, C′, C″).

Example 3.8 Let N = 2. Applying Proposition 4.8 with $a=\frac{C^{″}}{C^{″}+C^{\prime }}$ and b = 0 gives

$${\mathbb{E}}_{GOE}^{N+1}\left\{\exp \left[\frac{1}{2}{\lambda }_{N+1}^2-\frac{C^{″}}{C^{″}+C^{\prime }}{\lambda }_{N+1}^2\right]\right\}=\frac{\sqrt{2}}{2}\left\{\frac{C^{\prime }}{2C^{″}}{\left(\frac{C^{″}+C^{\prime }}{C^{″}}\right)}^{1∕2}+{\left(\frac{C^{″}+C^{\prime }}{3C^{″}\times +C^{\prime }}\right)}^{1∕2}\right\}.$$ (3.6)

Applying Proposition 4.8 again with $a=\frac{C^{″}}{C^{″}+C^{\prime }-C^{\prime 2}}$ and $b=\frac{C^{\prime }x}{\sqrt{2C^{″}}}$, one has

$$\begin{gathered} {\mathbb{E}}_{GOE}^{N+1}\left\{\exp \left[\frac{{\lambda }_{N+1}^2}{2}-\frac{C^{″}{\left({\lambda }_{N+1}-\frac{C^{\prime }x}{\sqrt{2C^{″}}}\right)}^2}{C^{″}+C^{\prime }-C^{\prime 2}}\right]\right\}=\frac{1}{\pi \sqrt{2}}{\left(\frac{C^{″}+C^{\prime }-C^{\prime 2}}{C^{″}}\right)}^{1∕2} \\ \left\{\frac{C^{\prime 2}(x^2-1)+C^{\prime }}{C^{″}}\pi \Phi \left(\frac{C^{\prime }x}{\sqrt{2C^{″}+C^{\prime }-C^{\prime 2}}}\right)+\frac{x{C}^{\prime }\sqrt{2C^{″}+C^{\prime }-C^{\prime 2}}}{C^{″}\sqrt{2}}{\sqrt{\pi e}}^{-\frac{C^{\prime 2}{x}^2}{2(2C^{″}+C^{\prime }-C^{\prime 2})}} \\ +\frac{2\pi \sqrt{C^{″}}}{\sqrt{3C^{″}+C^{\prime }-C^{\prime 2}}}{e}^{-\frac{C^{\prime 2}{x}^2}{2(3C^{″}+C^{\prime }-C^{\prime 2})}}\Phi \left(\frac{x{C}^{\prime }\sqrt{C^{″}}}{\sqrt{(2C^{″}+C^{\prime }-C^{\prime 2})(3C^{″}+C^{\prime }-C^{\prime 2})}}\right)\right\}. \end{gathered}$$ (3.7)

Let h(x) be the density function of the distribution of the height of a local maximum, i.e. $h\left(x\right)=-F_{t_0}^{\prime }\left(x\right)$. By Theorem 3.6, together with (3.6) and (3.7), we obtain

$$\begin{gathered} h\left(x\right)={\left(\frac{C^{\prime }}{2C^{″}}+{\left(\frac{C^{″}}{3C^{″}+C^{\prime }}\right)}^{1∕2}\right)}^{-1}\left\{\frac{C^{\prime 2}(x^2-1)+C^{\prime }}{C^{″}}\varphi \left(x\right)\Phi \left(\frac{C^{\prime }x}{\sqrt{2C^{″}+C^{\prime }-C^{\prime 2}}}\right) \\ +\frac{x{C}^{\prime }\sqrt{2C^{″}+C^{\prime }-C^{\prime 2}}}{2\pi C^{″}}{e}^{-\frac{(2C^{″}+C^{\prime })x^2}{2(2C^{″}+C^{\prime }-C^{\prime 2})}} \\ +\frac{\sqrt{2C^{″}}}{\sqrt{\pi }\sqrt{3C^{″}+C^{\prime }-C^{\prime 2}}}{e}^{-\frac{(3C^{″}+C^{\prime })x^2}{2(3C^{″}+C^{\prime }-C^{\prime 2})}}\Phi \left(\frac{x{C}^{\prime }\sqrt{C^{″}}}{\sqrt{(2C^{″}+C^{\prime }-C^{\prime 2})(3C^{″}+C^{\prime }-C^{\prime 2})}}\right)\right\}, \end{gathered}$$ (3.8)

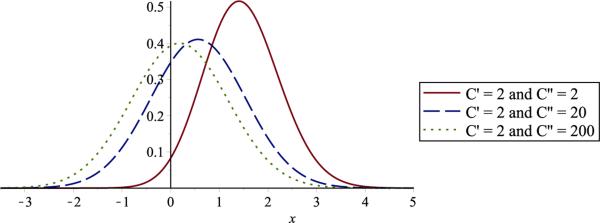
and hence $F_{t_0}\left(u\right)-{\int }_u^{\infty }h\left(x\right)dx$. Figure 2 shows several examples. The extreme case of (C3′), C″ + C′ – C′² = 0, is obtained when C(t, s) = 〈t, s〉ⁿ, n ≥ 2. Shown in solid red is the case n = 2, which simplifies to

$$h\left(x\right)=(2x^2-1)\varphi \left(x\right)\Phi \left(\sqrt{2}x\right)+\frac{x\sqrt{2}}{2\pi }{e}^{-\frac{3x^2}{2}}+\frac{1}{\sqrt{\pi }}{e}^{-x^2}\Phi \left(x\right).$$

It can be seen from both (3.8) and Figure 2 that h(x) → ϕ(x) if max(C′, C′²)/C″ → 0.

Figure 2.

Density function h(x) of the distribution F_t0 for isotropic Gaussian fields on ${\mathbb{S}}^2$.

Theorem 3.9 Let $\{f\left(t\right):t\in {\mathbb{S}}^N\}$, N ≥ 2, be a centered, unit-variance, isotropic Gaussian field satisfying (C1″), (C2′) and (C3′). Then for each $t_0\in {\mathbb{S}}^N$ and u, v > 0,

$${\stackrel{‒}{F}}_{t_0}(u,v)=\{\begin{array}{cc}\frac{{\int }_{u+v}^{\infty }\varphi \left(x\right){\mathbb{E}}_{GOE}^{N+1}\left\{\exp \left[\frac{{\lambda }_{N+1}^2}{2}-\frac{C^{″}{\left({\lambda }_{N+1}-\frac{C^{\prime }x}{\sqrt{2C^{″}}}\right)}^2}{C^{″}+C^{\prime }-C^{\prime 2}}\right]\right\}dx}{{\int }_v^{\infty }\varphi \left(x\right){\mathbb{E}}_{GOE}^{N+1}\left\{\exp \left[\frac{{\lambda }_{N+1}^2}{2}-\frac{C^{″}{\left({\lambda }_{N+1}-\frac{C^{\prime }x}{\sqrt{2C^{\prime }}}\right)}^2}{C^{″}+C^{\prime }-C^{\prime 2}}\right]\right\}dx}\hfill & if{C}^{″}+C^{\prime }-C^{\prime 2}>0,\hfill \\ \frac{{\int }_u^{\infty }\varphi \left(x\right){\mathbb{E}}_{GOE}^N\left\{{\left(\prod _{i=1}^N\mid {\lambda }_i-\frac{C^{\prime }x}{\sqrt{2C^{″}}}\mid \right)}_{\{{\lambda }_N<\frac{C^{\prime }x}{C^{2C^{″}}}\}}\right\}dx}{{\left(\frac{2C^{″}}{\pi (C^{″}+C^{\prime })}\right)}^{1∕2}\Gamma \left(\frac{N+1}{2}\right){\mathbb{E}}_{GOE}^{N+1}\left\{\exp [\frac{1}{2}{\lambda }_{N+1}^2-\frac{C^{″}}{C^{″}+C^{\prime }}{\lambda }_{N+1}^2]\right\}}\hfill & if{C}^{″}+C^{\prime }-C^{\prime 2}=0,\hfill \end{array}\phantom{\}}$$

where C′ and C″ are defined in (3.5).

Proof The result follows immediately by applying Theorem 3.1 and Lemma 4.13.

Because the exact expression in Theorem 3.9 may be complicated for large N, we now derive a tight approximation to it, which is analogous to Corollary 2.5 for the Euclidean case.

Let $\chi \left(A_u(f,{\mathbb{S}}^N)\right)$ be the Euler characteristic of the excursion set $A_u(f,{\mathbb{S}}^N)=\{t\in {\mathbb{S}}^N:f\left(t\right)>u\}$. Let ${\omega }_j=\mathrm{Vol}\left({\mathbb{S}}^j\right)$, the spherical area of the j-dimensional unit sphere ${\mathbb{S}}^j$, i.e., ${\omega }_j=2{\pi }^{(j+1)∕2}∕\Gamma \sigma \left(\frac{j+1}{2}\right)$. The lemma below provides the formula for the expected Euler characteristic of the excursion set.

Lemma 3.10 [Cheng and Xiao (2014)]. Let $\{f\left(t\right):t\in {\mathbb{S}}^N\}$, N ≥ 2, be a centered, unit-variance, isotropic Gaussian field satisfying (C1″) and (C2′). Then

$$\mathbb{E}\left\{\chi \left(A_u(f,{\mathbb{S}}^N)\right)\right\}=\sum _{j=0}^N{\left(C^{\prime }\right)}^{j∕2}{\mathcal{L}}_j\left({\mathbb{S}}^N\right){\rho }_j\left(u\right),$$

where C′ is defined in (3.5), ρ₀(u) = 1–Φ(u), ρ_j(u) = (2π)^–(j+1)/2H_j–1(u)e^–u2/2 with Hermite polynomials H_j−1 for j ≥ 1 and, for j = 0, . . . , N,

$${\mathcal{L}}_j\left({\mathbb{S}}^N\right)=\{\begin{array}{cc}2\left(\begin{array}{c}\hfill N\hfill \\ \hfill j\hfill \end{array}\right)\frac{{\omega }_N}{{\omega }_{N-j}}\hfill & ifN-jiseven\hfill \\ 0\hfill & otherwise\hfill \end{array}\phantom{\}}$$ (3.9)

are the Lipschitz-Killing curvatures of ${\mathbb{S}}^N$.

Theorem 3.11 Let $\{f\left(t\right)\mid t\in {\mathbb{S}}^N\}$, N ≥ 2, be a centered, unit-variance, isotropic Gaussian field satisfying (C1″) and (C2′). Then for each $t_0\in {\mathbb{S}}^N$ and each fixed u > 0, there exists α > 0 such that as v → ∞,

$${\stackrel{‒}{F}}_{t_0}(u,v)=\frac{\sum _{j=0}^N{\left(C^{\prime }\right)}^{j∕2}{\mathcal{L}}_j\left({\mathbb{S}}^N\right){\rho }_j(u+v)}{\sum _{j=0}^N{\left(C^{\prime }\right)}^{j∕2}{\mathcal{L}}_j\left({\mathbb{S}}^N\right)0{\rho }_j\left(v\right)}(1+o\left(e^{-\alpha v^2}\right)),$$ (3.10)

where C′ is defined in (3.5), ρ_j(u) and ${\mathcal{L}}_j\left({\mathbb{S}}^N\right)$ are as in Lemma 3.10.

Remark 3.12 Note that (3.10) depends on the covariance function only through its first derivative C′. In comparison with Corollary 2.5 for the Euclidean case, there we only have the highest order term of the expected Euler characteristic expansion because we do not consider the boundaries of T. On the sphere, we need all terms in the expansion since sphere has no boundary.

Proof By Theorem 3.1,

$${\stackrel{‒}{F}}_{t_0}(u,v)=\frac{{\int }_{u+v}^{\infty }\varphi \left(x\right)\mathbb{E}\{\det \nabla {\zeta }^{2}f\left(t_0\right)\mid f\left(t_0\right)=x,\nabla f\left(t_0\right)=0\}dx}{{\int }_v^{\infty }\varphi \left(x\right)\mathbb{E}\{\det {\nabla }^{2}f\left(t_0\right)\mid f\left(t_0\right)=x,\nabla f\left(t_0\right)=0\}dx}(1+o\left(e^{-\alpha v^2}\right))$$

Since f is isotropic, integrating the numerator and denominator above over ${\mathbb{S}}^N$, we obtain

$$\begin{array}{cc}\hfill {\stackrel{‒}{F}}_{t_0}(u,v)=& \frac{{\int }_{{\mathbb{S}}^N}{\int }_{u+v}^{\infty }\varphi \left(x\right)\mathbb{E}\{\det {\nabla }^{2}f\left(t\right)\mid f\left(t\right)=x,\nabla f\left(t\right)=0\}dxdt}{{\int }_{{\mathbb{S}}^N}{\int }_v^{\infty }\varphi \left(x\right)\mathbb{E}\{\det {\nabla }^{2}f\left(t\right)\mid f\left(t\right)=x,\nabla f\left(t\right)=0\}dxdt}(1+o\left(e^{-\alpha v^2}\right))\hfill \\ \hfill =& \frac{\mathbb{E}\left\{\chi \left(A_{u+v}(f,{\mathbb{S}}^N)\right)\right\}}{\mathbb{E}\left\{\chi \left(A_v(f,{\mathbb{S}}^N)\right)\right\}}(1+o\left(e^{-\alpha v^2}\right)),\hfill \end{array}$$

where the last line comes from applying the Kac-Rice Metatheorem to the Euler characteristic of the excursion set, see Adler and Taylor (2007, pp. 315-316). The result then follows from Lemma 3.10.

4 Proofs and Auxiliary Results

4.1 Proofs for Section 2

For u > 0, let μ(t₀, ε), μ_N(t₀, ε), ${\mu }_N^u(t_0,\epsilon )$ and ${\mu }_N^{u-}(t_0,\epsilon )$ be the number of critical points, the number of local maxima, the number of local maxima above u and the number of local maxima below u in U_t0(ε) respectively. More precisely,

$$\begin{array}{cc}\hfill \mu (t_0,\epsilon )=& \#\{t\in U_{t_0}\left(\epsilon \right):\nabla f\left(t\right)=0\},\hfill \\ \hfill {\mu }_N(t_0,\epsilon )=& \#\{t\in U_{t_0}\left(\epsilon \right):\nabla f\left(t\right)=0,\text{index}\left({\nabla }^{2}f\left(t\right)\right)=N\},\hfill \\ \hfill {\mu }_N^u(t_0,\epsilon )=& \#\{t\in U_{t_0}\left(\epsilon \right):f\left(t\right)>u,\nabla f\left(t\right)=0,\text{index}\left({\nabla }^{2}f\left(t\right)\right)=N\},\hfill \\ \hfill {\mu }_N^{u-}(t_0,\epsilon )=& \#\{t\in U_{t_0}\left(\epsilon \right):f\left(t\right)>u,\nabla f\left(t\right)=0,\text{index}\left({\nabla }^{2}f\left(t\right)\right)=N\},\hfill \end{array}$$ (4.1)

where index(∇²f(t)) is the number of negative eigenvalues of ∇²f(t).

In order to prove Theorem 2.1, we need the following lemma which shows that, for the number of critical points over the cube of lengh ε, its factorial moment decays faster than the expectation as ε tends to 0. Our proof is based on similar arguments in the proof of Lemma 3 in Piterbarg (1996).

Lemma 4.1 Let {f(t) : t ∈ T} be a Gaussian random field satisfying (C1) and (C2). Then for each fixed $t_0\in \mathring{T}$, as ε → 0,

$$\mathbb{E}\left\{\mu (t_0,\epsilon )(\mu (t_0,\epsilon )-1)\right\}=o\left({\epsilon }^N\right).$$

Proof By the Kac-Rice formula for factorial moments [cf. Theorem 11.5.1 in Adler and Taylor (2007)],

$$\mathbb{E}\left\{\mu (t_0,\epsilon )(\mu (t_0,\epsilon )-1)\right\}={\int }_{U_{t_0}\left(\epsilon \right)}{\int }_{U_{t_0}\left(\epsilon \right)}{E}_1(t,s)p_{\nabla f\left(t\right),\nabla f\left(s\right)}(0,0)dtds,$$ (4.2)

where

$$E_1(t,s)=\mathbb{E}\{\mid \det {\nabla }^{2}f\left(t\right)\Vert \det {\nabla }^{2}f\left(s\right)\Vert \nabla f\left(t\right)=\nabla f\left(s\right)=0\}.$$

By Taylor's expansion,

$$\nabla f\left(s\right)\nabla f\left(t\right)+{\nabla }^{2}f\left(t\right){(s-t)}^T+{\nabla s-t\nabla }^{1+\eta }{\mathbf{Z}}_{t,s},$$ (4.3)

where ${\mathrm{Z}}_{t,s}={(Z_{t,s}^1,\dots ,Z_{t,s}^N)}^T$ is a Gaussian vector field, with properties to be specified. In particular, by condition (C1), for ε small enough,

$$\underset{t,s\in U_{t_0}\left(\epsilon \right),t\ne s}{\sup }\mathbb{E}{\Vert {\mathbf{Z}}_{t,s}\Vert }^2\le C_1,$$

where C₁ is some positive constant. Therefore, we can write

$$E_1(t,s)=\mathbb{E}\{\mid \det {\nabla }^{2}f\left(t\right)\Vert \det {\nabla }^{2}f\left(s\right)\Vert \nabla f\left(t\right)=0,{\nabla }^{2}f\left(t\right){(s-t)}^T=-{\Vert s-t\Vert }^{1+\beta }{\mathbf{Z}}_{t,s}\}.$$

Note that the determinant of the matrix ∇²f(t) is equal to the determinant of the matrix

$$\left(\begin{array}{cccc}\hfill 1\hfill & \hfill -(s_1-t_1)\hfill & \hfill \cdots \hfill & \hfill -(s_N-t_N)\hfill \\ \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill ⋮\hfill & \hfill \hfill & \hfill {\nabla }^{2}f\left(t\right)\hfill & \hfill \hfill \\ \hfill 0\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\right).$$

For any i = 2, . . . , N + 1, multiply the ith column of this matrix by (s_i – t_i)/∥s_i – t_i∥², take the sum of all such columns and add the result to the first column, obtaining the matrix

$$\left(\begin{array}{cccc}\hfill 0\hfill & \hfill -(s_1-t_1)\hfill & \hfill \cdots \hfill & \hfill -(s_N-t_N)\hfill \\ \hfill -{\Vert s-t\Vert }^{-1+\eta }{Z}_{t,s}^1\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill ⋮\hfill & \hfill \hfill & \hfill {\nabla }^{2}f\left(t\right)\hfill & \hfill \hfill \\ \hfill -{\Vert s-t\Vert }^{-1+\eta }{Z}_{t,s}^N\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\right).$$

whose determinant is still equal to the determinant of ∇²f(t). Let r = max_1≤i≤N |s_i – t_i|,

$$A_{t,s}=\left(\begin{array}{cccc}\hfill 0\hfill & \hfill -(s_1-t_1)∕r\hfill & \hfill \cdots \hfill & \hfill -(s_N-t_N)∕r\hfill \\ \hfill Z_{t,s}^1\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ \hfill ⋮\hfill & \hfill \hfill & \hfill {\nabla }^{2}f\left(t\right)\hfill & \hfill \hfill \\ \hfill Z_{t,s}^N\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \end{array}\right).$$

Using properties of a determinant, it follows that

$$\mid \det {\nabla }^{2}f\left(t\right)\mid =r{\Vert s-t\Vert }^{-1+\eta }\mid \det A_{t,s}\mid \le {\Vert s-t\Vert }^{\eta }\mid \det A_{t,s}\mid .$$

Let e_t,s = (s – t)^T/∥s – t∥, then we obtain

$$E_1(t,s)\le {\Vert s-t\Vert }^{\eta }{E}_2(t,s),$$ (4.4)

where

$$\begin{array}{cc}\hfill E_2(t,s)=& \mathbb{E}\{\mid \det A_{t,s}\Vert \det {\nabla }^{2}f\left(s\right)\Vert \nabla f\left(t\right)=0,{\nabla }^{2}f\left(t\right){(s-t)}^T=-{\Vert s-t\Vert }^{1+\eta }{\mathbf{Z}}_{t,s}\}\hfill \\ \hfill =& \mathbb{E}\{\mid \det A_{t,s}\Vert \det {\nabla }^{2}f\left(s\right)\Vert \nabla f\left(t\right)=0,{\nabla }^{2}f\left(t\right)e_{t,s}+{\Vert s-t\Vert }^{\eta }{\mathbf{Z}}_{t,s}=0\}.\hfill \end{array}$$

By (C1) and (C2), there exists C₂ > 0 such that

$$\underset{t,s\in U_{t_0}\left(\epsilon \right),t\ne s}{\sup }{E}_2(t,s)\le C_2.$$

By (4.2) and (4.4),

$$\mathbb{E}\left\{\mu (t_0,\epsilon )(\mu (t_0,\epsilon )-1)\right\}\le C_2{\int }_{U_{t_0}\left(\epsilon \right)}{\int }_{U_{t_0}\left(\epsilon \right)}{\Vert s-t\Vert }^{\eta }{p}_{\nabla f\left(t\right),\nabla f\left(s\right)}(0,0)dtds.$$

It is obvious that

$$p_{\nabla f\left(t\right),\nabla f\left(s\right)}(0,0)\le \frac{1}{{\left(2\pi \right)}^N\sqrt{\mathrm{detCov}(\nabla f\left(t\right),\nabla f\left(s\right))}}.$$

Applying Taylor's expansion (4.3), we obtain that as ∥s – t∥ → 0,

$$\begin{array}{cc}\hfill \mathrm{detCov}(\nabla f\left(t\right),\nabla f\left(s\right))=& \mathrm{detCov}(\nabla f\left(t\right),\nabla f\left(t\right)+{\nabla }^{2}f\left(t\right){(s-t)}^T+{\Vert s-t\Vert }^{1+\eta }{\mathbf{Z}}_{t,s})\hfill \\ \hfill =& \mathrm{detCov}(\nabla f\left(t\right),{\nabla }^{2}f\left(t\right){(s-t)}^T+{\Vert s-t\Vert }^{1+\eta }{\mathbf{Z}}_{t,s})\hfill \\ \hfill =& {\Vert s-t\Vert }^{2N}\mathrm{detCov}(\nabla f\left(t\right),{\nabla }^{2}f\left(t\right)e_{t,s}+{\Vert s-t\Vert }^{\eta }{\mathbf{Z}}_{t,s})\hfill \\ \hfill =& {\Vert s-t\Vert }^{2N}\mathrm{detCov}(\nabla f\left(t\right),{\nabla }^{2}f\left(t\right)e_{t,s})(1+o\left(1\right)),\hfill \end{array}$$

where the last determinant is bounded away from zero uniformly in t and s due to the regularity condition (C2). Therefore, there exists C₃ > 0 such that

$$\mathbb{E}\left\{\mu (t_0,\epsilon )(\mu (t_0,\epsilon )-1)\right\}\le C_3{\int }_{U_{t_0}\left(\epsilon \right)}{\int }_{U_{t_0}\left(\epsilon \right)}\frac{1}{{\Vert t-s\Vert }^{N-\eta }}dtds,$$

where C₃ η and are some positive constants. Recall the elementary inequality

$$\frac{x_1+\cdots +x_N}{N}\ge {(x_1\cdots x_N)}^{1∕N},\forall x_1,\dots ,x_N>0.$$

It follows that

$$\begin{array}{cc}\hfill \mathbb{E}\left(\mu (t_0,\epsilon )(\mu (t_0,\epsilon )-1)\right\}\le & C_3{N}^{eta-N}{\int }_{U_{t_0}\left(\epsilon \right)}{\int }_{U_{t_0}\left(\epsilon \right)}\prod _{i=1}^N{\mid t_i-s_i\mid }^{\frac{\eta }{N}-1}dtds\hfill \\ \hfill =& C_3{N}^{\eta -N}{\left({\int }_{-\epsilon ∕2}^{\epsilon ∕2}{\int }_{-\epsilon ∕2}^{\epsilon ∕2}{\mid x-y\mid }^{\frac{\eta }{N}-2}dxdy\right)}^N\hfill \\ \hfill =& C_3{N}^{\eta }{\left(\frac{2N}{\eta (\eta +N)}\right)}^N{\epsilon }^{N+\eta }=o\left({\epsilon }^N\right).\hfill \end{array}$$

Proof of Theorem 2.1 By the definition in (1.2),

$$F_{t_0}\left(u\right)=\underset{\epsilon \to 0}{\lim }\frac{\mathbb{P}\{f\left(t_0\right)>u,{\mu }_N(t_0,\epsilon )\ge 1\}}{\mathbb{P}\{{\mu }_N(t_0,\epsilon )\ge 1\}}.$$ (4.5)

Let $p_i=\mathbb{P}\{{\mu }_N(t_0,\epsilon )=i\}$, then $\mathbb{P}\{{\mu }_N(t_0,\epsilon )\ge 1\}={\sum }_{i=1}^{\infty }{p}_i$ and $\mathbb{E}\left\{{\mu }_N(t_0,\epsilon )\right\}={\sum }_{i=1}^{\infty }i{p}_i$, it follows that

$$\begin{array}{cc}\hfill \mathbb{E}\left\{{\mu }_N(t_0,\epsilon )\right\}-\mathbb{P}\{{\mu }_N(t_0,\epsilon )\ge 1\}=& \sum _{i=2}^{\infty }(i-1)p_i\hfill \\ \hfill \le & \sum _{i=2}^{\infty }\frac{i(i-1)}{2}{p}_i=\frac{1}{2}\mathbb{E}\left\{{\mu }_N(t_0,\epsilon )({\mu }_N(t_0,\epsilon )-1)\right\}.\hfill \end{array}$$

Therefore, by Lemma 4.1, as ε → 0,

$$\mathbb{P}\{{\mu }_N(t_0,\epsilon )\ge 1\}=\mathbb{E}\left\{{\mu }_N(t_0,\epsilon )\right\}+o\left({\epsilon }^N\right).$$ (4.6)

Similarly,

$$\mathbb{P}\{{\mu }_N^u(t_0,\epsilon )\ge 1\}=\mathbb{E}\left\{{\mu }_N^u(t_0,\epsilon )\right\}+o\left({\epsilon }^N\right).$$ (4.7)

Next we show that

$$\mid \mathbb{P}\{f\left(t_0\right)\ge u,{>}_N(t_0,\epsilon )\ge 1\}-\mathbb{P}\{{\mu }_N^u(t_0,\epsilon )\ge 1\}\mid =o\left({\epsilon }^N\right).$$ (4.8)

Roughly speaking, the probability that there exists a local maximum and the field exceeds u at t₀ is approximately the same as the probability that there is at least one local maximum exceeding u. This is because in the limit, the local maximum occurs at t₀ and is greater than u. We show the rigorous proof below.

Note that for any evens A, B, C such that C ⊂ B,

$$\mid \mathbb{P}\left(AB\right)-\mathbb{P}\left(C\right)\mid \le \mathbb{P}\left(AB{C}^c\right)\mathbb{P}\left(A^{c}C\right).$$

By this inequality, to prove (4.8), it suffices to show

$$\mathbb{P}\{f\left(t_0\right)>u,{\mu }_N(t_0,\epsilon )\ge 1,{\mu }_N^u(t_0,\epsilon )=0\}+\mathbb{P}\{f\left(t_0\right)\le u,{\mu }_N^u(t_0,\epsilon )\ge 1\}=o\left({\epsilon }^N\right),$$

where the first probability above is the probability that the field exceeds u at t₀ but all local maxima are below u, while the second one is the probability that the field does not exceed u at t₀ but all local maxima exceed u.

Recall the definition of ${\mu }_N^{u-}(t_0,\epsilon )$ in (4.1), we have

$$\begin{array}{cc}\hfill \mathbb{P}\{f\left(t_0\right)>u,{\mu }_N(t_0,\epsilon )\ge 1,{\mu }_N^u(t_0,\epsilon )=0\}\le & \mathbb{P}\{f\left(t_0\right)>u,{\mu }_N^{u-}(t_0,\epsilon )\ge 1\}\hfill \\ \hfill =& \mathbb{E}\left\{{\mu }_N^{u-}(t_0,\epsilon )1_{\{f\left(t_0\right)>u\}}\right\}+o\left({\epsilon }^N\right),\hfill \end{array}$$ (4.9)

where the second line follows from similar argument for showing (4.6). By the Kac-Rice metatheorem,

$$\mathbb{E}\left\{{\mu }_N^{u-}(t_0,\epsilon )1_{\{f\left(t_0\right)>u\}}\right\}={\int }_u^{\infty }\mathbb{E}\{{\mu }_N^{u-}(t_0,\epsilon )\mid f\left(t_0\right)=x\}{p}_{f\left(t_0\right)}\left(x\right)dx={\int }_u^{\infty }{p}_{f\left(t_0\right)}\left(x\right)dx{\int }_{U_{t_0}\left(\epsilon \right)}{p}_{\nabla f\left(t\right)}(0\mid f\left(t_0\right)=x)\times \mathbb{E}\{\mid \det {\nabla }^{2}f\left(t\right)\mid 1_{\{\text{index}\left({\nabla }^{2}f\left(t\right)\right)=N\}}{1}_{\{f\left(t\right)\le u\}}\mid \nabla f\left(t\right)=0,f\left(t_0\right)=x\}dt.$$ (4.10)

By (C1) and (C2), for small ε > 0,

$$\underset{t\in U_{t_0}\left(\epsilon \right)}{\sup }{p}_{\nabla f\left(t\right)}(0\mid f\left(t_0\right)=x)\le \underset{t\in U_{t_0}\left(\epsilon \right)}{\sup }\frac{1}{{\left(2\pi \right)}^{N∕2}{\left(\mathrm{detCov}(\nabla f\left(t\right)\mid f\left(t_0\right))\right)}^{1∕2}}\le C$$

for some positive constant C. On the other hand, by continuity, conditioning on f(t₀) = x > u, ${\sup }_{t\in U_{t_0}\left(\epsilon \right)}{1}_{\{f\left(t\right)\le u\}}$ tends to 0 a.s. as ε → 0. Therefore, for each x > u, by the dominated convergence theorem (we may choose ${\sup }_{t\in U_{t_0}\left({\epsilon }_0\right)}\mid \det {\nabla }^{2}f\left(t\right)\mid$ as the dominating function for some ε₀ > 0), as ε → 0,

$$\underset{t\in U_{t_0}\left(\epsilon \right)}{\sup }\mathbb{E}\{\mid \det {\nabla }^{2}f\left(t\right)\mid 1_{\{\text{index}\left({\nabla }^{2}f\left(t\right)\right)=N\}}{1}_{\{f\left(t\right)\le u\}}\mid \nabla f\left(t\right)=0,f\left(t_0\right)=x\}\to 0.$$

Plugging these facts into (4.10) and applying the dominated convergence theorem, we obtain that as ε → 0,

$$\frac{1}{{\epsilon }^N}\mathbb{E}\left\{{\mu }_N^{u-}(t_0,\epsilon )1_{\{f\left(t_0\right)>u\}}\right\}\le \frac{C}{{\epsilon }^N}{\int }_u^{\infty }\underset{t\in U_{t_0}\left(\epsilon \right)}{\sup }\mathbb{E}\{\mid \det {\nabla }^{2}f\left(t\right)\mid 1_{\{\text{index}\left({\nabla }^{2}f\left(t\right)\right)=N\}}{1}_{\{f\left(t\right)\le u\}}\mid \nabla f\left(t\right)=0,f\left(t_0\right)=x\}\times p_{f\left(t_0\right)}\left(x\right)dx{\int }_{U_{t_0}\left(\epsilon \right)}dt\to 0,$$

which implies $\mathbb{E}\left\{{\mu }_N^{u-}(t_0,\epsilon )1_{\{f\left(t_0\right)>u\}}\right\}=o\left({\epsilon }^N\right)$. By (4.9),

$$\mathbb{P}\{f\left(t_0\right)>u,{\mu }_N(t_0,\epsilon )\ge 1,{\mu }_N^u(t_0,\epsilon )=0\}=o\left({\epsilon }^N\right).$$

Similar arguments yield

$$\mathbb{P}\{f\left(t_0\right)\le u,{\mu }_N^u(t_0,\epsilon )\ge 1\}=o\left({\epsilon }^N\right).$$

Hence (4.8) holds and therefore,

$$F_{t_0}\left(u\right)=\underset{\epsilon \to 0}{\lim }\frac{\mathbb{P}\{f\left(t_0\right)>u,{\mu }_N(t_0,\epsilon )\ge 1\}}{\mathbb{P}\{{\mu }_N(t_0,\epsilon )\ge 1\}}=\underset{\epsilon \to 0}{\lim }\frac{\mathbb{P}\{{\mu }_N^u(t_0,\epsilon )\ge 1\}+o\left({\epsilon }^N\right)}{\mathbb{P}\{{\mu }_N(t_0,\epsilon )\ge 1\}}=\underset{\epsilon \to 0}{\lim }\frac{\mathbb{E}\left\{{\mu }_N^u(t_0,\epsilon )\right\}+o\left({\epsilon }^N\right)}{\mathbb{E}\left\{{\mu }_N(t_0,\epsilon )\right\}+o\left({\epsilon }^N\right)},$$ (4.11)

where the last equality is due to (4.6) and (4.7). By the Kac-Rice metatheorem and Lebesgue's continuity theorem,

$$\underset{\epsilon \to 0}{\lim }\frac{1}{N}\mathbb{E}\left\{{\mu }_N^u(t_0,\epsilon )\right\}=\underset{\epsilon \to 0}{\lim }\frac{1}{{\epsilon }^N}{\int }_{U_{t_0}\left(\epsilon \right)}\mathbb{E}\{\mid \det {\nabla }^{2}f\left(t\right)\mid 1_{\{f\left(t\right)>u\}}{1}_{\{\text{index}\left({\nabla }^{2}f\left(t\right)\right)=N\}}\mid \nabla ft)0\}{p}_{\nabla f\left(t\right)}\left(0\right)dt=\mathbb{E}\{\mid \det {\nabla }^{2}f\left(t_0\right)\mid 1_{\{f\left(t_0\right)>u\}}{1}_{\{\text{index}\left({\nabla }^{2}f\left(t_0\right)\right)=N\}}\mid \nabla f\left(t_0\right)=0\}{p}_{\nabla f\left(t_0\right)}\left(0\right),$$

and similarly,

$$\underset{\epsilon \to 0}{\lim }\frac{1}{{\epsilon }^N}\mathbb{E}\left\{{\mu }_N(t_0,\epsilon )\right\}=\mathbb{E}\{\mid \det {\nabla }^{2}f\left(t_0\right)\mid 1_{\{\text{index}\left({\nabla }^{2}f\left(t_0\right)\right)=N\}}\mid \nabla f\left(t_0\right)=0\}{p}_{\nabla f\left(t_0\right)}\left(0\right).$$

Plugging these into (4.11) yields (2.1).

Proof of Theorem 2.3 By Theorem 2.2,

$${\stackrel{‒}{F}}_{t_0}(u,v)=\frac{{\int }_{u+v}^{\infty }\varphi \left(x\right)\mathbb{E}\{\mid \det {\nabla }^{2}f\left(t_0\right)\mid 1_{\{\text{index}\left({\nabla }^{2}f\left(t_0\right)\right)=N\}}\mid f\left(t_0\right)=x,\nabla f\left(t_0\right)=0\}dx}{{\int }_v^{\infty }\varphi \left(x\right)\mathbb{E}\{\mid \det {\nabla }^{2}f\left(t_0\right)\mid 1_{\{\text{index}\left({\nabla }^{2}f\left(t_0\right)\right)=N\}}\mid f\left(t_0\right)=x,\nabla f\left(t_0\right)=0\}dx}.$$ (4.12)

We shall estimate the conditional expectations above. Note that f has unit-variance, taking derivatives gives

$$\mathbb{E}\left\{f\left(t_0\right){\nabla }^{2}f\left(t_0\right)\right\}=-\mathrm{Cov}(\nabla f\left(t_0\right))=-\Lambda \left(t_0\right).$$

Since Λ(t₀) is positive definite, there exists a unique positive definite matrix Q_t0 such that Q_t0Λ(t₀)Q_t0 = I_N (Q_t0 is also called the square root of (Λ(t₀)), where I_N is the N × N unit matrix. Hence

$$\mathbb{E}\left\{f\left(t_0\right)\left(Q_{t_0}{\nabla }^{2}f\left(t_0\right)Q_{t_0}\right)\right\}=-Q_{t_0}\Lambda \left(t_0\right)Q_{t_0}=-I_N.$$

By the conditional formula for Gaussian random variables,

$$\mathbb{E}\{Q_{t_0}{\nabla }^{2}f\left(t_0\right)Q_{t_0}\mid f\left(t_0\right)=x,\nabla f\left(t_0\right)=0\}=-x{I}_N.$$

Make change of variable

$$W\left(t_0\right)=Q_{t_0}{\nabla }^{2}f\left(t_0\right)Q_{t_0}+x{I}_N,$$

where W(t₀) = (W_ij(t₀))_1≤i,j≤N. Then (W(t₀)|f(t₀) = x, ∇f(t₀) = 0) is a Gaussian matrix whose mean is 0 and covariance is the same as that of (Q_t0 ∇²f(t₀)Q_t0|f(t₀) = x, ∇f(t₀) = 0). Denote the density of Gaussian vector ((W_ij(t₀))_{1≤i≤j≤N}|f(t₀) = x, ∇f(t₀) = 0) by h_t0(w), $w={\left(w_{ij}\right)}_{1\le i\le j\le N}\in {\mathbb{R}}^{N(N+1)∕2}$, then

$$\mathbb{E}\{\det \left(Q_{t_0}{\nabla }^{2}f\left(t_0\right)Q_{t_0}\right)1_{\{\text{index}\left({\nabla }^{2}f\left(t_0\right)\right)=N\}}\mid f\left(t_0\right)=x,\nabla f\left(t_0\right)=0\}=\mathbb{E}\{\det \left(Q_{t_0}{\nabla }^{2}f\left(t_0\right)Q_{t_0}\right)1_{\{\text{index}\left(Q_{t_0}{Q}_{t_0}\right)=N\}}\mid f\left(t_0\right)=x,\nabla f\left(t_0\right)=0\}={\int }_{w:\text{index}(\left(w_{ij}\right)-x{I}_N)=N}\det \left(\left(w_{ij}\right)-x{I}_N\right)h_{t_0}\left(w\right)dw,$$ (4.13)

where (w_ij) is the abbreviation of matrix (w_ij)_1≤i,j≤k. Note that there exists a constant c > 0 such that

$$\mathrm{index}(\left(w_{ij}\right)-x{I}_N)=N,\forall \Vert \left(w_{ij}\right)\Vert ≔{\left(\sum _{i,j=1}^N{w}_{ij}^2\right)}^{1∕2}<\frac{x}{c}.$$

Thus we can write (4.13) as

$${\int }_{{\mathbb{R}}^{N(N+1)∕2}}\det \left(\left(w_{ij}\right)-x{I}_N\right)h_{t_0}\left(w\right)dw-{\int }_{w:\text{index}\left(w_{ij}\right)-x{I}_N)<N}\det \left(\left(w_{ij}\right)-x{I}_N\right)h_{t_0}\left(w\right)dw=\mathbb{E}\{\det (Q_{t_0}{\nabla }^{2}f\left(t_0\right)\mid f\left(t_0\right)=x,\nabla f\left(t_0\right)=0\}+Z(t,x),$$ (4.14)

where Z(t, x) is the second integral in the first line of (4.14) and it satisfies

$$\mid Z(t,x)\mid \le {\int }_{\Vert \left(w_{ij}\right)\Vert \ge \frac{x}{c}}\mid \det \left(\left(w_{ij}\right)-x{I}_N\right)\mid h_{t_0}\left(w\right)dw.$$ (4.15)

By the non-degenerate condition (C2), there exists a constant α′ > 0 such that as ∥(w_ij)∥ → ∞, $h_{t_0}\left(w\right)=o\left(e^{-{\alpha }^{\prime }}{\Vert \left(w_{ij}\right)\Vert }^2\right)$. On the other hand, the determinant inside the integral in (4.15) is a polynomial in w_ij and x, and it does not affect the exponentially decay, hence as x → ∞, |Z(t, x)| = o(e^–αx2) for some constant α > 0. Combine this with (4.13) and (4.14), and note that

$$\det {\nabla }^{2}f\left(t_0\right)=\det \left(Q_{t_0}^{-1}{Q}_{t_0}{\nabla }^{2}f\left(t_0\right)Q_{t_0}{Q}_{t_0}^{-1}\right)=\det \left(\Lambda \left(t_0\right)\right)\sigma \det \left(Q_{t_0}{\nabla }^{2}f\left(t_0\right)Q_{t_0}\right),$$

we obtain that, as x → ∞,

$$\begin{array}{c}\mathbb{E}\{\mid \det {\nabla }^{2}f\left(t_0\right)\mid 1_{\{\text{index}\left({\nabla }^{2}f\left(t_0\right)\right)=N\}}\mid f\left(t_0\right)=x,\nabla f\left(t_0\right)=0\}\hfill \\ ={(-1)}^N\det \left(\Lambda \left(t_0\right)\right)\mathbb{E}\{\det \left(Q_{t_0}{\nabla }^{2}f\left(t_0\right)Q_{t_0}\right)1_{\{\text{index}\left({\nabla }^{2}f\left(t_0\right)\right)=N\}}\mid f\left(t_0\right)=x,\nabla f\left(t_0\right)=0\}\hfill \\ ={(-1)}^N\det \left(\Lambda \left(t_0\right)\right)\mathbb{E}\{\det \left(Q_{t_0}{\nabla }^{2}f\left(t_0\right)Q_{t_0}\right)\mid f\left(t_0\right)=x,\nabla f\left(t_0\right)=0\}+o\left(e^{-\alpha x^2}\right)\hfill \\ ={(-1)}^N\mathbb{E}\{\det {\nabla }^{2}f\left(t_0\right)\mid f\left(t_0\right)=x,\nabla f\left(t_0\right)=0\}+o\left(e^{-\alpha x^2}\right)\hfill \end{array}$$

Plugging this into (4.12) yields (2.2).

Lemma 4.2 Under the assumptions in Theorem 2.3, as x → ∞,

$$\mathbb{E}\{\det {\nabla }^{2}f\left(t\right)\mid f\left(t\right)=x,\nabla f\left(t\right)=0\}={(-1)}^N\det \left(\Lambda \left(t\right)\right)x^N(1+O\left(x^{-2}\right)).$$ (4.16)

Proof Let Q_t be the N × N positive definite matrix such that Q_tΛ(t)Q_t = I_N. Then we can write ${\nabla }^{2}f\left(t\right)=Q_t^{-1}{Q}_t{\nabla }^{2}f\left(t\right)Q_t{Q}_t^{-1}$ and therefore,

$$\mathbb{E}\{\det {\nabla }^{2}f\left(t\right)\mid f\left(t\right)=x,\nabla f\left(t\right)=0\}=\det \left(\Lambda \left(t\right)\right)\mathbb{E}\{\det \left(Q_t{\nabla }^{2}f\left(t\right)Q_t\right)\mid f\left(t\right)=x,\nabla f\left(t\right)=0\}.$$ (4.17)

Since f(t) and ∇f(t) are independent,

$$\mathbb{E}\{Q_t{\nabla }^{2}f\left(t\right)Q_t\mid f\left(t\right)=x,\nabla f\left(t\right)=0\}=-x{I}_N.$$

It follows that

$$\mathbb{E}\{Q_t{\nabla }^{2}f\left(t\right)Q_t\mid f\left(t\right)=x,\nabla f\left(t\right)=0\}=\mathbb{E}\left\{\det (\tilde{\Delta }\left(t\right)-x{I}_N)\right\},$$ (4.18)

where $\tilde{\Delta }\left(t\right)={\left({\tilde{\Delta }}_{ij}\left(t\right)\right)}_{1\le i,j\le N}$ is an N × N Gaussian random matrix such that $\mathbb{E}\left\{\tilde{\Delta }\left(t\right)\right\}=0$ and its covariance matrix is independent of x. By the Laplace expansion of the determinant,

$$\det (\tilde{\Delta }\left(t\right)-x{I}_N)={(-1)}^N[x^N-S_1\left(\tilde{\Delta }\left(t\right)\right)x^{N-1}+S_2\left(\tilde{\Delta }\left(t\right)\right)x^{N-2}+\cdots +{(-1)}^N{S}_N\left(\tilde{\Delta }\left(t\right)\right)],$$

where $S_i\left(\tilde{\Delta }\left(t\right)\right)$ is the sum of the $\left(\begin{array}{c}\hfill N\hfill \\ \hfill i\hfill \end{array}\right)$ principle minors of order i in $\tilde{\Delta }\left(t\right)$. Taking the expectation above and noting that $\mathbb{E}\left\{S_1\left(\tilde{\Delta }\left(t\right)\right)\right\}=0$ since $\mathbb{E}\left\{\tilde{\Delta }\left(t\right)\right\}=0$, we obtain that as x → ∞,

$$\mathbb{E}\left\{\det (\tilde{\Delta }\left(t\right)-x{I}_N)\right\}={(-1)}^N{x}^N(1+O\left(x^{-2}\right)).$$

Combining this with (4.17) and (4.18) yields (4.16).

Lemma 4.3 [Azaïs and Wschebor (2008), Lemma 2]. Let {f(t) : t ∈ T} be a centered, unit-variance, isotropic Gaussian random field satisfying (C1) and (C2). Then for each t ∈ T and i, j, k, l ∈ {1, . . . , N},

$$\mathbb{E}\left\{f_i\left(t\right)f\left(t\right)\right\}=\mathbb{E}\left\{f_i\left(t\right)f_{jk}\left(t\right)\right\}=0,\mathbb{E}\left\{f_i\left(t\right)f_j\left(t\right)\right\}=\mathbb{E}\left\{f_{ij}\left(t\right)f\left(t\right)\right\}=-2{\rho }^{\prime }{\delta }_{ij},\mathbb{E}\left\{f_{ij}\left(t\right)f_{kl}\left(t\right)\right\}=4{\rho }^{″}({\delta }_{ij}{\delta }_{kl}+{\delta }_{ik}{\delta }_{jl}+{\delta }_{il}{\delta }_{jk}),$$ (4.19)

where δ_ij is the Kronecker delta and ρ′ and ρ″ are defined in (2.5).

Lemma 4.4 Under the assumptions in Lemma 4.3, the distribution of ∇²f(t) is the same as that of $\sqrt{8{\rho }^{″}}{M}_N+2\sqrt{{\rho }^{″}}\xi I_N$, where M_N is a GOE random matrix, ξ is a standard Gaussian variable independent of M_N and I_N is the N × N identity matrix. Assume further that (C3) holds, then the conditional distribution of (∇²f(t)|f(t) = x) is the same as the distribution of $\sqrt{8{\rho }^{″}}{M}_N+[2{\rho }^{\prime }x+2\sqrt{{\rho }^{″}-{\rho }^{\prime 2}}\xi ]I_N$.

Proof The first result is a direct consequence of Lemma 4.3. For the second one, applying (4.19) and the well-known conditional formula for Gaussian variables, we see that (∇²f(t)|f(t) = x) can be written as Δ + 2ρ′xI_N, where Δ = (Δ_ij)_1≤i,j≤N is a symmetric N × N matrix with centered Gaussian entries such that

$$\mathbb{E}\left\{{\Delta }_{ij}{\Delta }_{kl}\right\}=4{\rho }^{″}({\delta }_{ik}{\delta }_{jl}+{\delta }_{il}{\delta }_{jk})+4({\rho }^{″}-{\rho }^{\prime 2}){\delta }_{ij}{\delta }_{kl}.$$

Therefore, Δ has the same distributionm as the random matrix $\sqrt{8{\rho }^{″}}{M}_N+2\sqrt{{\rho }^{″}-{\rho }^{\prime 2}}\xi I_N$, completing the proof.

Lemma 4.5 below is a revised version of Lemma 3.2.3 in Auffinger (2011). The proof is omitted here since it is similar to that of the reference above.

Lemma 4.5 Let M_N be an N × N GOE matrix and X be an independent Gaussian random variable with mean m and variance σ². Then,

$$\mathbb{E}\left\{\mid \det (M_N-X{I}_N)\mid 1_{\{\text{index}(M_N-X{I}_N)=N\}}\right\}=\frac{\Gamma \left(\frac{N+1}{2}\right)}{\sqrt{\pi }\sigma }{\mathbb{E}}_{GOE}^{N+1}\left\{\exp \left[\frac{{\lambda }_{N+1}^2}{2}-\frac{{({\lambda }_{N+1}-m)}^2}{2{\sigma }^2}\right]\right\},$$ (4.20)

where ${\mathbb{E}}_{GOE}^{N+1}$ is the expectation under the probability distribution Q_N+1(dλ) as in (2.6) with N replaced by N + 1.

Lemma 4.6 Let {f(t) : t ∈ T} be a centered, unit-variance, isotropic Gaussian random field satisfying (C1) and (C2). Then for each t ∈ T,

$$\mathbb{E}\{\mid \det {\nabla }^{2}f\left(t\right)\mid 1_{\{\text{index}\left({\nabla }^{2}f\left(t\right)\right)=N\}}\mid \nabla f\left(t\right)=0\}={\left(\frac{2}{\pi }\right)}^{1∕2}\Gamma \left(\frac{N+1}{2}\right){\left(8{\rho }^{″}\right)}^{N∕2}{\mathbb{E}}_{GOE}^{N+1}\left\{\exp \left[-\frac{{\lambda }_{N+1}^2}{2}\right]\right\}.$$

Proof Since ∇²f(t) and ∇f(t) are independent for each fixed t, by Lemma 4.4,

$$\begin{array}{cc}\hfill \mathbb{E}\{\mid \det {\nabla }^{2}f\left(t\right)\mid 1_{\{\text{index}\left({\nabla }^{2}f\left(t\right)\right)=N\}}\mid \nabla f\left(t_0\right)=0\}=& \mathbb{E}\left\{\mid \det {\nabla }^{2}f\left(t\right)\mid 1_{\{\text{index}\left({\nabla }^{2}f\left(t\right)\right)=N\}}\right\}\hfill \\ \hfill =& \mathbb{E}\left\{\mid \det (\sqrt{8{\rho }^{″}}{M}_N+2\sqrt{{\rho }^{″}}\xi I_N)\mid 1_{\{\text{index}(\sqrt{8{\rho }^{″}}{M}_N+2\sqrt{{\rho }^{″}}\xi I_N)=N\}}\right\}\hfill \\ \hfill =& {\left(8{\rho }^{″}\right)}^{N∕2}\mathbb{E}\left\{\mid \det (M_N-X{I}_N)\mid 1_{\{\text{index}(M_N-X{I}_N)=N\}}\right\},\hfill \end{array}$$

where X is an independent centered Gaussian variable with variance 1/2. Applying Lemma 4.5 with m = 0 and $\sigma =1∕\sqrt{2}$, we obtain the desired result.

Lemma 4.7 Let {f(t) : t ∈ T} be a centered, unit-variance, isotropic Gaussian random field satisfying (C1), (C2) and (C3). Then for ach t ∈ T and $x\in \mathbb{R}$,

$$\mathbb{E}\{\mid \det {\nabla }^{2}f\left(t\right)\mid 1_{\{\text{index}\left({\nabla }^{2}f\left(t\right)\right)=N\}}\mid f\left(t\right)=x,\nabla f\left(t\right)=0\}=\{\begin{array}{cc}{\left(\frac{2}{\pi }\right)}^{1∕2}\Gamma \left(\frac{N+1}{2}\right){\left(8{\rho }^{″}\right)}^{N∕2}{\left(\frac{{\rho }^{″}}{{\rho }^{″}-{\rho }^{\prime 2}}\right)}^{1∕2}\times {\mathbb{E}}_{GOE}^{N+1}\left\{\exp \left[\frac{{\lambda }_{N+1}^2}{2}-\frac{{\rho }^{″}{({\lambda }_{N+1}+\frac{{\rho }^{\prime }x}{\sqrt{2{\rho }^{″}}})}^2}{{\rho }^{″}-{\rho }^{\prime 2}}\right]\right\}\hfill & if{\rho }^{″}-{\rho }^{\prime 2}>0,\hfill \\ {\left(8{\rho }^{″}\right)}^{N∕2}{\mathbb{E}}_{GOE}^N\left\{\left(\prod _{i=1}^N\mid {\lambda }_i-\frac{x}{\sqrt{2}}\mid \right)1_{\{{\lambda }_N<\frac{x}{\sqrt{2}}\}}\right\}\hfill & if{\rho }^{″}-{\rho }^{\prime 2}=0.\hfill \end{array}\phantom{\}}$$

Proof Since ∇f(t) is independent of both f(t) and ∇²f(t) for each fixed t, by Lemma 4.4,

$$\begin{array}{c}\mathbb{E}\{\mid \det {\nabla }^{2}f\left(t\right)\mid 1_{\{\text{index}\left({\nabla }^{2}f\left(t\right)\right)=N\}}\mid f\left(t\right)=x,\nabla f\left(t\right)=0\}\hfill \\ =\mathbb{E}\{\mid \det {\nabla }^{2}f\left(t\right)\mid 1_{\{\text{index}\left({\nabla }^{2}f\left(t\right)\right)=N\}}\mid f\left(t\right)=x\}\hfill \\ =\mathbb{E}\{\mid \det (\sqrt{8{\rho }^{″}}{M}_N+[2{\rho }^{\prime }x+2\sqrt{{\rho }^{″}-{\rho }^{\prime 2}}\xi ]I_N)\mid \times 1_{\{\text{index}(\sqrt{8{\rho }^{\prime }}{M}_N+[2{\rho }^{\prime }x+2\sqrt{{\rho }^{″}-{\rho }^{\prime 2}}\xi ]I_N)=N\}}\}.\hfill \end{array}$$ (4.21)

When ρ″ – ρ′² > 0, then (4.21) can be written as

$${\left(8{\rho }^{″}\right)}^{N∕2}\mathbb{E}\left\{\mid \det (M_N-X{I}_N)\mid 1_{\{\text{index}(M_N-X{I}_N)=N\}}\right\},$$

where X is an independent Gaussian variable with mean $m=-\frac{{\rho }^{\prime }x}{\sqrt{2{\rho }^{″}}}$ and variance ${\sigma }^2=\frac{{\rho }^{″}-{\rho }^{\prime 2}}{2{\rho }^{″}}$. Applying Lemma 4.5 yields the formula for the case ρ″ – ρ′² > 0.

When ρ″ – ρ′² = 0, i.e. ${\rho }^{\prime }=-\sqrt{{\rho }^{″}}$, then (4.21) becomes

$${\left(8{\rho }^{″}\right)}^{N∕2}\mathbb{E}\left\{\mid \det (M_N-\frac{x}{\sqrt{2}}{I}_N)\mid 1_{\{\text{index}(M_N-\frac{x}{\sqrt{2}}{I}_N)=N\}}\right\}={\left(8{\rho }^{″}\right)}^{N∕2}{\mathbb{E}}_{GOE}^N\left\{\left(\prod _{i=1}^N\mid {\lambda }_i-\frac{x}{\sqrt{2}}\mid \right)1_{\{{\lambda }_N<\frac{x}{\sqrt{2}}\}}\right\}.$$

We finish the proof.

The following result can be derived from elementary calculations by applying the GOE density (2.6), the details are omitted here.

Proposition 4.8 Let N = 2. Then for positive constants a and b,

$${\mathbb{E}}_{GOE}^{N+1}\left\{\exp \left[\frac{1}{2}{\lambda }_{N+1}^2-a{({\lambda }_{N+1}-b)}^2\right]\right\}=\frac{1}{\sqrt{2}\pi }\left\{(\frac{1}{a}+2b^2-1)\frac{\pi }{\sqrt{a}}\Phi \left(\frac{b\sqrt{2a}}{\sqrt{a+1}}\right)+\frac{b\sqrt{a+1}\sqrt{\pi }}{a}3e^{-\frac{a{b}^2}{a+1}}+\frac{2\pi }{\sqrt{2a+1}}{e}^{-\frac{a{b}^2}{2a+1}}\Phi \left(\frac{\sqrt{2}ab}{\sqrt{(2a+1)(a+1)}}\right)\right\}.$$

4.2 Proofs for Section 3

Define μ(t₀, ε), μ_N(t₀, ε), ${\mu }_N^u(t_0,\epsilon )$ and ${\mu }_N^{u-}(t_0,\epsilon )$ as in (4.1) with U_t0(ε) replaced by B_t0(ε) respectively. The following lemma, which will be used for proving Theorem 3.1, is an analogue of Lemma 4.1.

Lemma 4.9 Let (M, g) be an oriented N-dimensional C³ Riemannian manifold with a C¹ Riemannian metric g. Let f be a Gaussian random field on M such that (C1′) and (C2′) are fulfilled. Then for any $t_0\in \mathring{M}$, as ε → 0,

$$\mathbb{E}\left\{\mu (t_0,\epsilon )(\mu (t_0,\epsilon )-1)\right\}=o\left({\epsilon }^N\right).$$

Proof Let (U_α, φ_α)_α∈I be an atlas on M and let ε be small enough such that φ_α(B_t0(ε)) ⊂ φ_α(U_α) for some α ∈ I. Set

$$f^{\alpha }=f\circ {\phi }_{\alpha }^{-1}:{\phi }_{\alpha }\left(U_{\alpha }\right)\subset {\mathbb{R}}^N\to \mathbb{R}.$$

Then it follows immediately from the di eomorphism of φ_α and the definition of μ that

$$\mu (t_0,\epsilon )=\mu (f,U_{\alpha };t_0,\epsilon )\equiv \mu (f^{\alpha },{\phi }_{\alpha }\left(U_{\alpha }\right);{\phi }_{\alpha }\left(t_0\right),\epsilon ).$$

Note that (C1′) and (C2′) imply that f^α satisfies (C1) and (C2). Applying Lemma 4.1 gives

$$\mathbb{E}\left\{\mu (f^{\alpha },{\phi }_{\alpha }\left(U_{\alpha }\right);{\phi }_{\alpha }\left(t_0\right),\epsilon )[\mu (f^{\alpha },{\phi }_{\alpha }\left(U_{\alpha }\right);{\phi }_{\alpha }\left(t_0\right),\epsilon )-1]\right\}=o\left(\mathrm{Vol}\left({\phi }_{\alpha }\left(B_{t_0}\left(\epsilon \right)\right)\right)\right)=o\left({\epsilon }^N\right).$$

This verifies the desired result.

Proof of Theorem 3.1 Following the proof in Theorem 2.1, together with Lemma 4.9 and the argument by charts in its proof, we obtain

$$F_{t_0}\left(u\right)=\underset{\epsilon \to 0}{\lim }\frac{\mathbb{P}\{f\left(t_0\right)>u,{\mu }_N(t_0,\epsilon )\ge 1\}}{\mathbb{P}\{{\mu }_N(t_0,\epsilon )\ge 1\}}=\underset{\epsilon \to 0}{\lim }\frac{\mathbb{P}\{{\mu }_N^u(t_0,\epsilon )\ge 1\}+o\left({\epsilon }^N\right)}{\mathbb{P}\{{\mu }_N(t_0,\epsilon )\ge 1\}}=\underset{\epsilon \to 0}{\lim }\frac{\mathbb{E}\left\{{\mu }_N^u(T_0,\epsilon )\right\}+o\left({\epsilon }^N\right)}{\mathbb{E}\left\{{\mu }_N(T_0,\epsilon )\right\}+o\left({\epsilon }^N\right)}.$$ (4.22)

By the Kac-Rice metatheorem for random fields on manifolds [cf. Theorem 12.1.1 in Adler and Taylor (2007)] and Lebesgue's continuity theorem,

$$\underset{\epsilon \to 0}{\lim }\frac{\mathbb{E}\left\{{\mu }_N^u(t{\zeta }_0,\epsilon )\right\}}{\mathrm{Vol}\left(B_{t_0}\left(\epsilon \right)\right)}=\underset{\epsilon \to 0}{\lim }\frac{1}{\mathrm{Vol}\left(B_{t_0}\left(\epsilon \right)\right)}{\int }_{B_{t_0}\left(\epsilon \right)}\mathbb{E}\{\mid \det {\nabla }^{2}f\left(t\right)\mid 1_{\{f\left(t\right)>u\}}{1}_{\{\text{index}\left({\nabla }^{2}f\left(t\right)\right)=N\}}\mid \nabla f\left(t\right)=0\}\times p_{\nabla f\left(t\right)}\left(0\right){\mathrm{Vol}}_g=\mathbb{E}\{\mid \det {\nabla }^{2}f\left(t_0\right)\mid 1_{\{f\left(t_0\right)>u\}}{1}_{\{\text{index}\left({\nabla }^{2}f\left(t_0\right)\right)=N\}}\mid \nabla f\left(t_0\right)=0\}{p}_{\nabla f\left(t_0\right)}\left(0\right),$$

where Vol_g is the volume element on M induced by the Riemannian metric g. Similarly,

$$\underset{\epsilon \to 0}{\lim }\frac{\mathbb{E}\left\{{\mu }_N(t_0,\epsilon )\right\}}{\mathrm{Vol}\left(B_{t_0}\left(\epsilon \right)\right)}=\mathbb{E}\{\mid \det {\nabla }^{2}f\left(t_0\right)\mid 1_{\{\text{index}\left({\nabla }^{2}f\left(t_0\right)\right)=N\}}\mid \nabla f\left(t_0\right)=0\}{p}_{\nabla f\left(t_0\right)}\left(0\right).$$

Plugging these facts into (4.22) yields the first line of (3.2). The second line of (3.2) follows similarly.

Applying Theorem 2.3 and Corollary 2.4, together with the argument by charts, we obtain (3.3).

Lemma 4.10 below is on the properties of the covariance of (f(t), ∇f(t), ∇²f(t)), where the gradient ∇f(t) and Hessian ∇²f(t) are defined as in (3.1) under some orthonormal frame {E_i}_1≤i≤N on ${\mathbb{S}}^N$. Since it can be proved similarly to Lemma 3.2.2 or Lemma 4.4.2 in Auffinger (2011), the detailed proof is omitted here.

Lemma 4.10 Let f be a centered, unit-variance, isotropic Gaussian field on ${\mathbb{S}}^N$, N ≥ 2, satisfying (C1″) and (C2′). Then

$$\mathbb{E}\left\{f_i\left(t\right)f\left(t\right)\right\}=\mathbb{E}\left\{f_i\left(t\right)f_{jk}\left(t\right)\right\}=0,\mathbb{E}\left\{f_i\left(t\right)f_j\left(t\right)\right\}=-\mathbb{E}\left\{f_{ij}\left(t\right)f\left(t\right)\right\}=C^{\prime }{\delta }_{ij},\mathbb{E}\left\{f_{ij}\left(t\right)f_{kl}\left(t\right)\right\}=C^{″}({\delta }_{ik}{\delta }_{jl}+{\delta }_{il}{\delta }_{jk})+(C^{\prime }+C^{\prime }){\delta }_{ij}{\delta }_{kl},$$ (4.23)

where C′ and C″ are defined in (3.5).

Lemma 4.11 Under the assumptions in Lemma 4.10, the distribution of ∇²f(t) is the same as that of $\sqrt{2C^{″}}{M}_N+\sqrt{C^{″}+C^{\prime }}\xi I_N$, where M_N is a GOE matrix and ξ is a standard Gaussian variable independent of M_N. Assume further that (C3′) holds, then the conditional distribution of (∇²f(t)|f(t) = x) is the same as the distribution of $\sqrt{2C^{″}}{M}_N+[\sqrt{C^{″}+C^{\prime }-C^{\prime 2}}\xi -C^{\prime }x]I_N$.

Proof The first result is an immediate consequence of Lemma 4.10. For the second one, applying (4.23) and the well-known conditional formula for Gaussian random variables, we see that (∇²f(t)|f(t) = x) can be written as Δ – C′xI_N, where Δ = (Δ_ij)_1≤i,j≤N is a symmetric N × N matrix with centered Gaussian entries such that

$$\mathbb{E}\left\{{\Delta }_{ij}{\Delta }_{kl}\right\}=C^{″}\left({\delta }_{ik}{\delta }_{jk}\right)+(C^{″}+C^{\prime }-C^{\prime 2}){\delta }_{ij}{\delta }_{kl}.$$

Therefore, Δ has the same distribution as the random matrix $\sqrt{2C^{″}}{M}_N+\sqrt{C^{″}+C^{\prime }-C^{\prime 2}}\xi I_N$, completing the proof.

By similar arguments for proving Lemmas 4.6 and 4.7, and applying Lemma 4.11 instead of Lemma 4.4, we obtain the following two lemmas.

Lemma 4.12 Let $\{f\left(t\right):t\in {\mathbb{S}}^N\}$ be a centered, unit-variance, isotropic Gaussian field satisfying (C1″) and (C2′). Then for each $t\in {\mathbb{S}}^N$,

$$\mathbb{E}\{\mid \det {\nabla }^{2}f\left(t\right)\mid 1_{\{\text{index}\left({\nabla }^{2}f\left(t\right)\right)=N\}}\mid \nabla f\left(t\right)=0\}={\left(\frac{2C^{″}}{\pi (C^{″}+C^{\prime })}\right)}^{1∕2}\Gamma \left(\frac{N+1}{2}\right){\left(2C^{″}\right)}^{N∕2}{\mathbb{E}}_{GOE}^{N+1}\left\{\exp \left[\frac{1}{2}{\lambda }_{N+1}^2-\frac{C^{″}}{C^{″}+C^{\prime }}{\lambda }_{N+1}^2\right]\right\}.$$

Lemma 4.13 Let $\{f\left(t\right):t\in {\mathbb{S}}^N\}$ be a centered, unit-variance, isotropic Gaussian field satisfying (C1″), (C2′) and (C3′). Then for each $t\in {\mathbb{S}}^N$ and $x\in \mathbb{R}$,

$$\mathbb{E}\{\mid \det {\nabla }^{2}f\left(t\right)\mid 1_{\{\text{index}\left({\nu }^{2}f\left(t\right)\right)=N\}}\mid f\left(t\right)=x,\nabla f\left(t\right)=0\}=\{\begin{array}{cc}{\left(\frac{2C^{″}}{\pi (C^{″}+C^{\prime }-C^{\prime 2})}\right)}^{1∕2}\Gamma \left(\frac{N+1}{2}\right){\left(2C^{″}\right)}^{N∕2}\times {\mathbb{E}}_{GOE}^{N+1}\left\{\exp \left[\frac{{\lambda }_{N+1}^2}{2}-\frac{C^{″}{({\lambda }_{N+1}-\frac{C^{\prime }x}{\sqrt{2C^{″}}})}^2}{C^{″}+C^{\prime }-C^{\prime 2}}\right]\right\}\hfill & if{C}^{″}+C^{\prime }-C^{\prime 2}>0.\hfill \\ {\left(2C^{″}\right)}^{N∕2}{\mathbb{E}}_{GOE}^N\left\{\left(\prod _{i=1}^N\mid {\lambda }_i-\frac{C^{\prime }x}{\sqrt{2C{\zeta }^{″}}}\mid \right)1_{\{{\lambda }_N<\frac{C^{\prime }x}{\sqrt{2C^{″}}}\}}\right\}\hfill & if{C}^{″}+C^{\prime }-C^{\prime 2}=0.\hfill \end{array}\phantom{\}}$$