Accurate structure, thermodynamics and spectroscopy of medium-sized radicals by hybrid Coupled Cluster/Density Functional Theory approaches: the case of phenyl radical

Abstract

The CCSD(T) model coupled with extrapolation to the complete basis-set limit and additive approaches represents the “golden standard” for the structural and spectroscopic characterization of building blocks of biomolecules and nanosystems. However, when open-shell systems are considered, additional problems related to both specific computational difficulties and the need of obtaining spin-dependent properties appear. In this contribution, we present a comprehensive study of the molecular structure and spectroscopic (IR, Raman, EPR) properties of the phenyl radical with the aim of validating an accurate computational protocol able to deal with conjugated open-shell species. We succeeded in obtaining reliable and accurate results, thus confirming and, partly, extending the available experimental data. The main issue to be pointed out is the need of going beyond the CCSD(T) level by including a full treatment of triple excitations in order to fulfil the accuracy requirements. On the other hand, the reliability of density functional theory in properly treating open-shell systems has been further confirmed.

I. INTRODUCTION

Integration between in vitro and in silico spectroscopy is providing a wealth of new interesting results in several fields of fundamental and applied research.^1-6 However, accurate computational models are often available only for small isolated molecules and require a careful use by specialists.^7-13 Extension of such models to large systems is by no means trivial and the problems become worse when one aims at developing robust, user-friendly codes to be used by non-specialists. The development of such “virtual ab initio spectrometers” for a wide range of wavelengths has been one of our major research goals in the last years.¹⁴

Since vibrational spectra depend on the molecular composition and bond topology, the large amount of information they hold allows a detailed characterization of molecular systems in terms of chemical linkage, conformation, polarization and charge transfer, as modulated by electronic, thermodynamic, and environmental effects. For these reasons, vibrational spectroscopies (IR, Raman, etc.) are among the most powerful techniques for characterizing the structure and dynamical behavior of molecules over a wide range of dimensions and lifetimes.^3,8,15,16 However, proper assignment of spectra relies more and more on quantum-mechanical (QM) computations for both interpretative and predictive aspects. In the frame of a virtual spectrometer, moving from the current practice of extracting numerical data from experiment to be compared with QM results to a vis-à-vis comparison of experimental and simulated spectra would strongly reduce any arbitrariness and allow a proper account of the information connected to the position and intensity of all transitions, thus defining the overall spectra line-shape.¹⁷ In the case of open-shell systems, EPR spectroscopy provides an invaluable support in view of the difficulty of identifying vibrational spectral features of the interesting transient species within complex spectra also containing signals originating from several other species.¹⁸

A possible route to obtain accurate results, even for relatively large molecular systems (few dozens of atoms), is provided by hybrid QM/QM’ models, which combine accurate structures, equilibrium properties and, possibly, harmonic force fields with anharmonic contributions and vibrational effects from cheap yet reliable electronic structure approaches (e.g., rooted into the Density Functional Theory (DFT)).^19-25 In this respect, we can mention the high accuracy of hybrid Coupled Cluster (CC)/DFT anharmonic frequencies,¹⁹ or hyperfine couplings terms.²⁶ Within CC/DFT approaches, significant improvements are provided by proper inclusion of core-correlation and basis-set effects. As concerns the extrapolation to the complete basis set (CBS) limit, we have recently shown that for large closed-shell systems, the evaluation of the corresponding contribution at the second-order Møller-Plesset perturbation theory (MP2) level for structures and harmonic force fields is effective once coupled with CC calculations in order to account for higher-order electron correlation effects.^27-29 Unfortunately, this route cannot be followed for open-shell species whenever spin contamination in the reference Hartree-Fock (HF) wave-function is large. From one side, by definition, restricted open-shell (RO) MP2 approaches do not take spin polarization into account, and from the other side, unrestricted approaches require to go beyond MP2 level and include higher-order terms to reduce sufficiently spin-contamination.³⁰ Under such circumstances, only two routes remain open, based on multi-reference and “pure” CC approaches, respectively. Note that this remark applies not only to energies and properties, but also to structures and harmonic force fields. In this frame, CC/DFT approaches still represent the only cost-effective alternative to CC computations, as DFT essentially retains the same level of accuracy for closed- and open-shell systems.^19,25 For light atom-bearing molecules, the most challenging situation is represented by σ-radicals in which the molecular orbital formally containing the unpaired electron is localized in the molecular plane (or the average molecular plane). We have recently investigated this problem for small prototypical systems (H₂CX,²⁶ vinyl¹⁸) obtaining results in remarkable agreement with experiment by means of an integrated CC/DFT approach and using purposely-tailored basis sets for magnetic properties. Here, we extend our analysis to a larger member of the same family, the phenyl radical, C₆H₅ (X²A₁), which is an important species in organic chemistry and combustion processes.

C₆H₅ is believed to be a precursor in the synthesis of polyaromatic hydrocarbons (PAHs),³¹ which are of great interest to chemists, spectroscopists, and astrophysicists, as significant chemical compounds detected in the interstellar space.³² As a matter of fact, the accepted mechanism for the formation of PAHs begins with ions and molecules containing two or three carbon atoms and involves C₆H₅ as the first aromatic transient intermediate encountered along the overall reaction path.³³ From another point of view, the cleavage of one C-H bond in benzene, D₀(C₆H₅–H) = 469 ± 3 kJ mol⁻¹, produces an H atom and this C_2v radical, whose formation enthalpy at 0 K is known³⁴ to be Δ_fH₀ = 352.9±2.5 kJ mol⁻¹ (the Active Thermochemical Tables³⁵ provides a more accurate value of 351.44(59) kJ mol⁻¹). With respect to its spectroscopic investigation, we mention that the rotational spectrum has been recorded,³⁶ thus providing accurate rotational constants, which in turn can be used to assess the accuracy of computed equilibrium structures. Although the infrared and Raman spectra of C₆H₅ and of several deuterated isotopologues have been studied by different research groups,^37-39 the assignment of some bands still remains controversial. The same applies to the EPR spectrum; while the g-tensor and the hydrogen hyperfine constants have been available for long time,⁴⁰ nothing is known about ¹³C couplings.

The present study complements the recent investigation of the phenyl radical carried out with our virtual spectrometer, reporting the simulation of the UV-vis spectrum,¹⁷ which allowed some re-assignments and interpretation of experimental results.⁴¹ On these grounds, we have undertaken a systematic study of the molecular structure, thermochemistry, as well as vibrational and EPR spectra of the C₆H₅ radical aiming at obtaining results within the so-called spectroscopic accuracy. To this purpose, we resorted to an integrated approach based on the CC ansatz, together with extrapolation to CBS limit and account of core correlation, and DFT evaluation of anharmonic contributions and vibrational effects, along with the recently introduced general VPT2 approach to compute vibrational averages and transition moments.⁴²

II. METHODOLOGY

A. Coupled-cluster calculations

The coupled-cluster (CC) level of theory employing the CC singles and doubles (CCSD) approximation augmented by a perturbative treatment of triple excitations (CCSD(T))⁴³ has been mainly used in the present work in conjunction with the correlation-consistent, (aug)-cc-p(C)VnZ (n=T,Q), basis sets.^44-46 All CC calculations have been performed with an unrestricted Hartree-Fock (UHF) reference determinant. The second-order Møller-Plesset perturbation theory (MP2)⁴⁷ has also been considered with a restricted open-shell Hartree-Fock (ROHF) reference wave function.^48,49 MP2 and CCSD(T) computations have been carried out with the quantum-chemical CFour program package.⁵⁰

1. Best-estimated molecular structure

In the molecular structure determination, the basis-set effects as well as core-correlation contributions have been accounted for simultaneously at an energy-gradient level.^51,52 The extrapolation to the complete basis set (CBS) limit has been performed as described in Ref.⁵¹. The CBS gradient is given by

$$\frac{{\mathit{dE}}_{\mathrm{CBS}}}{\mathit{dx}}=\frac{{\mathit{dE}}^{\infty }(\mathrm{HF}-\mathrm{SCF})}{\mathit{dx}}+\frac{d\Delta E^{\infty }\left(\mathrm{CCSD}\right(\mathrm{T}\left)\right)}{\mathit{dx}},$$ (1)

where dE^∞(HF-SCF)/dx and dΔE^∞(CCSD(T))/dx are the energy gradients corresponding to the exp(−Cn) extrapolation scheme for the HF-SCF energy⁵³ and to the n⁻³ extrapolation formula for the CCSD(T) correlation contribution,⁵⁴ respectively. In the expression given above, n=T, Q and 5 have been chosen for the HF-SCF extrapolation, and n=T and Q have been used for CCSD(T). To monitor the convergence to the CBS limit, geometry optimizations at the CCSD(T) level in conjunction with the cc-pVnZ (n=T,Q) basis sets have also been performed.

Core-correlation (CV) effects have been included by adding the corresponding correction, dΔE_CV/dx, to Eq. (1):

$$\frac{{\mathit{dE}}_{\mathrm{CBS}+\mathrm{CV}}}{\mathit{dx}}=\frac{{\mathit{dE}}^{\infty }(\mathrm{HF}-\mathrm{SCF})}{\mathit{dx}}+\frac{d\Delta E^{\infty }\left(\mathrm{CCSD}\right(\mathrm{T}\left)\right)}{\mathit{dx}}+\frac{d\Delta E_{\mathrm{CV}}}{\mathit{dx}},$$ (2)

The core-correlation energy correction, ΔE_CV, is obtained as difference of all-electron and frozen-core CCSD(T) calculations using the core-valence cc-pCVTZ basis set.

Finally, the effects of diffuse functions has been considered at the MP2 level. More precisely, the corresponding corrections have been obtained as the following differences in the geometrical parameters:

$$\Delta r\left(\text{aug}\right)\simeq r\left(\text{MP2/augVTZ}\right)-r\left(\text{MP2/VTZ}\right),$$ (3)

where MP2/augVTZ and MP2/VTZ are the geometry optimized at the MP2 level employing the aug-cc-pVTZ and cc-pVTZ basis sets, respectively. While there is no theoretical justification for the inclusion of diffuse function effects once extrapolation to the CBS limit is performed, the latter correction is introduced to recover on an empirical basis the limitations affecting extrapolation procedures carried out with small- to medium-sized basis sets.

The overall best estimated geometry, accounting for extrapolation to the CBS limit, core-correlation corrections and effects of diffuse functions, is denoted as CBS+CV+aug.

2. Thermochemistry and molecular properties

For the determination of the formation enthalpy, a composite scheme^55-58 has been employed to evaluate the energy of all atomic and molecular species considered. The total energies have been obtained by the following formula:

$$E_{\text{tot}}=E_{\mathrm{HF}-\mathrm{SCF}}^{\infty }+\Delta E_{\mathrm{CCSD}\left(\mathrm{T}\right)}^{\infty }+\Delta E_{\mathrm{CV}},$$ (4)

where the best-estimated equilibrium geometry (CBS+CV+aug) has been used for the phenyl radical. Its zero-point vibrational energy (ZPVE) has been evaluated from the anharmonic frequencies obtained within the hybrid approach introduced in the following section, while the various contributions of Eq. (4) have been obtained with the same basis sets as for the molecular structure determination. For the carbon atom, the impact of spin-orbit (SO) coupling has also been taken into account by including the experimental SO correction (lowest spin-orbit level relative to the j-averaged energy).⁵⁹

As it will be clear from the results’ discussion, the chosen level of theory turns out to be insufficient for reaching the so-called chemical accuracy (1 kcal/mol = 4.2 kJ/mol). Therefore, the contribution due to the full treatment of triples excitation has also been considered by performing full CC singles, doubles and triples (CCSDT)^60-62 single-point energy calculations at the best-estimated equilibrium structure in conjunction with a double-zeta quality basis set. As this correction is also important for hyperfine coupling constant, the EPR-II basis^63-65 set has been chosen. Since an UHF reference function has been used, CCSDT calculations have been performed with the MRCC package⁶⁶ by Kállay interfaced to CFour.^50,67

As the atomization reaction has been considered and the experimental data available is at 0 K, the following expression has been used to compute the heat of formation of the phenyl radical, Δ_fH⁰:

$${\Delta }_f{\mathrm{H}}^0={\Delta }_r{\mathrm{H}}^0+\sum _{\mathit{atoms}}{\Delta }_f{\mathrm{H}}_a^0,$$ (5)

with the heats of formation of atoms taken from thermodynamic tables^34,35 and the reaction enthalpy given by

$${\Delta }_r{\mathrm{H}}^0=E_{{\mathrm{C}}_6{\mathrm{H}}_5}-\sum _{\mathit{atoms}}E+E_{\mathrm{ZPVE}}\left({\mathrm{C}}_6{\mathrm{H}}_5\right).$$ (6)

The heat of formation at 298 K can be derived by adding the corresponding temperature correction:

$${\Delta }_r{\mathrm{H}}^{298}={\Delta }_f{\mathrm{H}}^0+\delta {\mathrm{H}}^{298-0}\left({\mathrm{C}}_6{\mathrm{H}}_5\right)-\sum _{\mathit{atoms}}\delta {\mathrm{H}}^{298-0},$$ (7)

where the enthalpy corrections for temperature, δH^298–0, can be obtained from thermodynamic tables.³⁵

3. Hyperfine couplings

To evaluate the isotropic and anisotropic hyperfine coupling constants (hfcc), the spin density at the nucleus and the dipole-dipole coupling terms are the quantities required, respectively. All hyperfine contributions can be therefore evaluated as expectation values of the corresponding one-electron operators.^68-70 The corresponding calculations have been carried out at the CCSD(T) level of theory, at the best-estimated equilibrium structure (CBS+CV+aug). According to Ref.²⁶ and as it will be clear from the discussion section, the contribution due to the full treatment of triples is expected to be large and mandatory for a quantitative agreement with experiment. In fact, for open-shell systems formal single excitations involving spin flipping can be quite important and their correlation requires the explicit treatment of triple excitations. Therefore, the corresponding correction has been obtained as the difference between CCSDT and CCSD(T) results, with the same basis set. Due to the high computational cost, a double-zeta quality basis set has been employed; in particular, a purposely-tailored for magnetic properties, the EPR-II basis set,^63-65 has been chosen. The choice of the basis set is a delicate issue for obtaining quantitative predictions of the isotropic hfcc’s. On one hand, in order to correctly describe the spin density at a nucleus, core correlation and very tight s primitives are needed,^26,71 on the other hand, to take into account the influence of neighbouring atoms, diffuse functions on surrounding atoms are required.⁷¹ In fact, isotropic hyperfine couplings at one atom are determined by one-center contributions (which require tight s-functions), but also by the tails of wave functions on neighboring atoms (whose description requires diffuse functions). For these reasons, the aug-cc-pCVTZ basis sets have been chosen for carbons, while hydrogen atoms require additional tight s functions. We therefore employed the aug-cc-pVQZ set augmented by three even-tempered uncontracted functions (with exponents: 413.2, 2066, 10330; see Ref.²⁶), denoted by the extension et3 (i.e., aug-cc-pVQZ-et3). In the following, the overall basis set will be shortly named ET3. In Ref.²⁶, the effectiveness of the latter basis set has been demonstrated. The purposely-tailored EPR-II⁷² and EPR-III⁷³ basis sets^63-65 for magnetic properties have also been considered. C₆H₅ being a semi-rigid system, vibrational corrections have been obtained by means of perturbation theory using Density Functional Theory, as explained later in the text.

B. Evaluation of anharmonic contributions

Among the various theoretical approaches dealing with the nuclear vibrations (see e.g. Ref.⁷⁴ and references therein), second-order vibrational perturbation theory (VPT2)^75-78 is particularly appealing to treat medium-to-large systems. Within VPT2 models, a general framework to compute frequencies, intensities of fundamental transitions, overtones and combination bands, as well as vibrationally averaged properties (e.g., ESR parameters) and thermodynamic parameters has been devised in our group.^25,42,79-81

1. Vibrational frequencies and zero-point vibrational energy

The VPT2 approach,^75,76,78-86 when applied to a fourth-order normal mode representation of the anharmonic force field, provides a cost-effective route to compute accurate vibrational properties, at least for semi-rigid systems. However, its efficient application to large molecular systems requires to overcome the problem of possible singularities, known as resonances, plaguing the simplest VPT2 model. To obtain coherent spectroscopic results, we resort to the so-called generalized second-order perturbation theory (GVPT2) model. Within the latter, the resonant terms of type I (ω_i ≈ 2ω_j) and type II (ω_i ≈ ω_j + ω_k), the so-called Fermi-resonances, are identified by means of semi-empirical criteria, generally based on Martin’s test.⁸⁷ The model that simply removes the terms defined as resonant from the VPT2 treatment is denoted as deperturbed VPT2 (DVPT2), while in GVPT2 the removed terms are reconsidered in the second step through a proper reduced-dimensionality variational approach. Moreover, for the calculation of thermodynamic properties, the resonance-free expression of the ZPVE proposed by Schuurman et al.⁸⁸ has been used.

The quality of vibrational frequencies computed at the GVPT2 level,^76,78 as implemented in the GAUSSIAN package,^25,79,80 has already been well documented (see for example Refs.^19,25,89).

2. IR and Raman intensities

A general formulation proposed by some of the present authors⁴² has been derived for any property that is function of either the normal coordinates or their associated momenta, and that can be expressed in a polynomial expansion truncated to the third order. In this work, in order to simulate IR and Raman spectra, we consider the molar absorption coefficient $ϵ\left({\stackrel{‒}{\nu }}_0\right)$ and Raman scattering at 90° for any polarization of an incident light with perpendicular polarization $\partial \sigma \left({\stackrel{‒}{\nu }}_0\right)∕\partial \Omega$.⁴²

Similarly to vibrational frequencies, the equations for transition moments might be plagued by singularities, which lead to excessive contributions from anharmonic terms. In addition to the Fermi resonances described above, 1-1 resonances (ω_i ≈ ω_j) can also be present. The protocol used to avoid unphysical contributions in the anharmonic corrections is similar to that used for energies, which means that the terms identified as resonant through ad hoc tests are removed (DVPT2). Contrary to energy calculations (within the GVPT2 model), there is no subsequent variational treatment of the resonant terms. In practice, the Martin test⁸⁷ is adopted to find Fermi resonances. For 1-1 resonances, the test described in Ref.⁴² is used here.

The quality of IR and, in particular, Raman intensities computed at the DVPT2 level still needs to be thoroughly tested, but the current general implementation has already provided several encouraging results.^14,29,42

3. Vibrational averaging of molecular properties

Vibrational effects on the properties considered (generically denoted P) have been accounted for by performing a vibrational averaging⁹⁰ of the molecular properties themselves by means of second-order perturbation theory and using anharmonic vibrational nuclear wavefunctions.^42,79,80 The geometrical dependence of a molecular property is included within the model by expanding it in a Taylor series around the equilibrium structure. In this framework, the averaged property, as function of the normal coordinates, is expressed as the sum of the purely electronic property and a temperature-dependent anharmonic-vibrational correction given by:^42,90

$$\Delta P=-\frac{\hslash }{4}\sum _i\frac{1}{{\omega }_i^2}{\left(\frac{\partial P}{\partial Q_i}\right)}_0\sum _j\frac{K_{\mathit{ijj}}}{{\omega }_j}\text{coth}\frac{\hslash {\omega }_j}{2k_{\mathrm{B}}T}+\frac{\hslash }{4}\sum _i\frac{1}{{\omega }_i}{\left(\frac{{\partial }^{2}P}{\partial Q_i^2}\right)}_0\text{coth}\frac{\hslash {\omega }_i}{2k_{\mathrm{B}}T}$$ (8)

Equation (8) shows that vibrational corrections depend explicitly on the temperature T and require the first and diagonal second derivatives of the molecular property P with respect to the mass-weighted normal modes evaluated at the equilibrium geometry of the molecule, the harmonic frequencies ω_i, and the cubic semi-diagonal force constants K_ijj. Note that a rotational term can also be included in equation (8) in order to take into account centrifugal-distortion effects.⁹¹

C. DFT and hybrid approaches

1. DFT calculations

The Density Functional Theory has been employed to compute molecular structure, magnetic properties as well as harmonic and anharmonic force fields. Within the DFT approach, the standard B3LYP functional⁹² has been used in conjunction with the double-ζ SNSD⁹³ basis set, developed for spectroscopic studies of medium-to-large closed- and open-shell molecular systems. This basis set has been constructed from the polarized double-ζ N07D basis set⁹⁴ by consistently including diffuse s functions on all atoms, and one set of diffuse polarized functions (d on heavy atoms and p on hydrogens). This basis set allows cost-effective prediction of a broad range of spectroscopic properties¹⁴, including electron-spin resonance (ESR), vibrational (IR, Raman, VCD) and electronic (absorption, emission, ECD) spectra.

For a complete account on the computational requirements for anharmonic force field determination, we refer the reader to Refs.^42,79,80. Here, we only note that in all cases equilibrium structures have been optimized using tight convergence criteria (maximum forces and displacements lower than 1.5 × 10⁻⁵ a.u/Bohr and 6 × 10⁻⁵ Å, respectively), while the semi-diagonal quartic force field have been obtained by numerical differentiation of the analytical second derivatives (with the standard 0.01 Å step).

All DFT computations have been performed employing a locally modified version of the Gaussian suite of programs for quantum chemistry.⁹⁵

2. Hybrid CC/DFT models

To further improve the description of the anharmonic force field, hybrid CCSD(T)/DFT approaches (shortly denoted CC/DFT) have been used, assuming that the differences between anharmonic frequencies computed at the CCSD(T) and DFT levels are only due to the harmonic terms. To this purpose, the harmonic force field has been computed at the CCSD(T)/cc-pVTZ level (within the frozen-core approximation) using analytic second derivatives.^96,97

Recently, hybrid CCSD(T)/DFT schemes, already validated for small closed- and open-shell systems,^19-24 have proved to provide accurate results for relatively large closed-shell systems,^28,98 also including the evaluation of accurate ZPVE corrections.²⁵ In the present study, the CC/DFT approach has been applied for the first time to an aromatic open-shell system. Within the CC/DFT model, two slightly different approaches have been adopted for frequencies and IR intensities, respectively. The hybrid CCSD(T)/DFT anharmonic force field has been obtained in a normal-coordinate representation by adding the cubic and semi-diagonal quartic force constants computed at the DFT level to the CCSD(T)/cc-pVTZ harmonic frequencies within the VPT2 expressions. Since the DFT and CCSD(T) normal modes are very similar (as expected in most cases), DFT cubic and quartic force constants have been used without any transformation. The hybrid CCSD(T)/DFT anharmonic force field has then been used to compute anharmonic frequencies and zero-point vibrational energies. With respect to intensities, anharmonic hybrid CCSD(T)/DFT IR intensities have been obtained by means of an a posteriori scheme, again assuming that the differences between the two levels of theory can only be ascribed to the harmonic part. Therefore, hybrid intensities have been derived by adding the DFT anharmonic corrections, $\Delta I_{\mathit{DFT}}^{\mathit{anh}}$, to the CCSD(T)/VTZ harmonic intensities:

$$I_{\mathit{CC}∕\mathit{DFT}}^{\text{anh}}=I^{\text{harm}}\left(\mathrm{CC}\right)+\Delta I_{\mathit{DFT}}^{\text{anh}}.$$ (9)

III. RESULTS AND DISCUSSION

A. Molecular Structure and thermochemistry

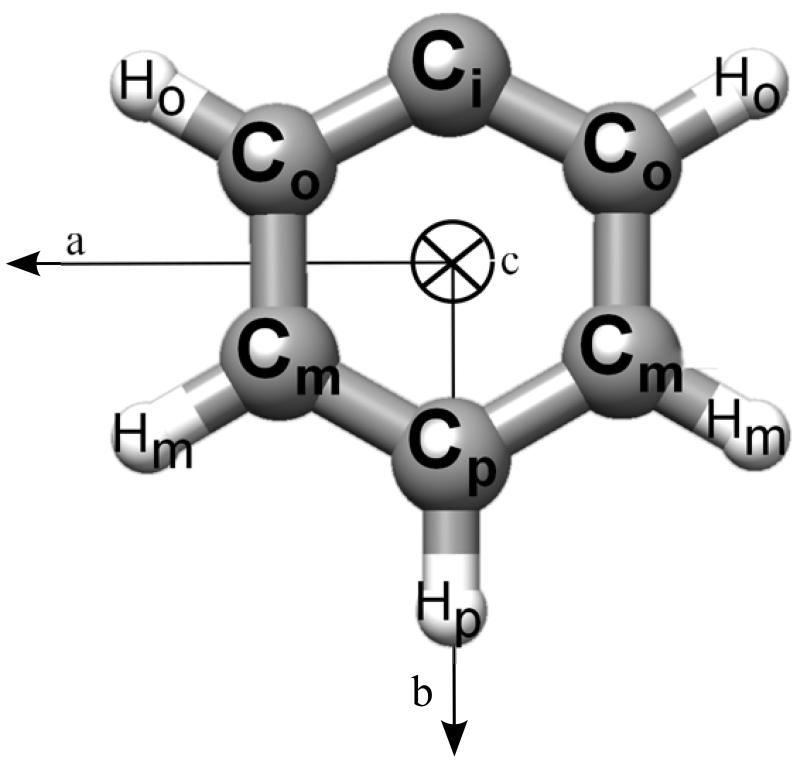
The phenyl radical is a planar asymmetric rotor with C_2υ symmetry (²A₁ electronic ground state) and a calculated electric dipole moment of 0.85 D (our best-estimated equilibrium value 0.87 D – see Table I – is here corrected for vibrational effects – −0.02 D – at the B3LYP/SNSD level) along the principal inertial b axis (see Figure 1).

TABLE I.

Structural parameters of the phenyl radical obtained at different levels of theory.^a Distances in Å, angles in degrees, rotational constants in MHz, and dipole moment in debye.

	B3LYP/SNSD	CC/VTZ	CC/VQZ	CC/CBS	CC/CBS+CV	CBS+CV+aug	Semi-exp.b
CiCo	1.3761	1.3766	1.3737	1.3715	1.3691	1.3693	1.37347(60)
CoCm	1.4041	1.4002	1.3980	1.3963	1.3940	1.3947	1.39366(60)
CmCp	1.3969	1.3942	1.3917	1.3901	1.3877	1.3882	1.39616(13)
HoCo	1.0867	1.0824	1.0819	1.0815	1.0803	1.0811
HmCm	1.0871	1.0837	1.0831	1.0827	1.0815	1.0822
HpCp	1.0860	1.0827	1.0820	1.0816	1.0804	1.0812
CoCiCo	125.98	125.67	125.67	125.67	125.70	125.78
CiCoCm	116.52	116.61	116.61	116.62	116.60	116.56
CoCmCp	120.14	120.24	120.27	120.28	120.28	120.29
HoCoCi	122.46	122.29	122.34	122.37	122.39	122.44
HmCmCo	119.66	119.64	119.60	119.57	119.57	119.56
HpCpCm	119.65	119.69	119.71	119.74	119.73	119.74
	C6H5
Ae	6280.50	6300.54	6319.77	6333.81	6355.45	6351.79	6320.66
Be	5601.80	5622.10	5643.82	5659.32	5677.82	5672.41	5636.81
Ce	2960.89	2971.01	2981.35	2988.80	2998.78	2996.45	2979.59
	C6D5
Ae	5452.45	5471.07	5487.58	5499.67	5518.02	5514.59	5486.99
Be	4638.11	4656.33	4673.16	4685.00	4700.02	4695.32	4668.73
Ce	2506.21	2515.46	2523.86	2529.88	2538.14	2536.04	2522.45
μ	0.864	0.847	0.859	0.869	0.870	0.873

^aCC means the CCSD(T) level of theory and VnZ means the cc-pVnZ (n=T,Q) basis set. CBS, CV, and ‘aug’ are defined in the text.

^bSemi-experimental equilibrium C–C distances as obtained from a least-square fit to the experimental ground-state rotational constants (Ref.³⁶) corrected for vibrational corrections at the B3LYP/SNSD level. See text. The corresponding equilibrium rotational constants are also reported.

FIG. 1.

Molecular structure of the phenyl radical: atom labeling and rotational axes.

The optimized geometries, as obtained at the CCSD(T) level employing different basis sets, are summarized in Table I together with the extrapolated structure (CBS), and those including the core-correlation corrections (CBS+CV) as well as effects of diffuse functions (CBS+CV+aug). From these results, it is first observed that the valence correlation limit is not reached at the CCSD(T)/cc-pVQZ level, as changes as large as 0.002-0.003 Å for the C–C bond lengths are observed when going to the CBS limit. Core-valence corrections are known to be important for improving the molecular structure accuracy,^52,99,100 and they are actually as large as 0.002 and 0.001 Å for C–C and C–H distances, respectively. Effects of diffuse functions are small (the corresponding corrections being smaller than 0.001 Å) and in the opposite direction with respect to extrapolation to CBS and core correlation (i.e., they enlarge the bond distances). In fact, extrapolation to the CBS limit using small- to medium-sized basis sets usually tends to overestimate the basis-set truncation errors which can be, at least partially compensated, by inclusion of diffuse functions. On the basis of our experience,^27,101,102 this procedure works rather well. As concerns angles, they seem to be already well converged at the CCSD(T)/cc-pVQZ level and for them core-correlation as well as diffuse-function effects seem to be small. According to the literature on this topic (see, for example, Refs.^10,51,52 and references therein), the uncertainties affecting the CBS+CV+aug structure are expected to be on the order of 0.001-0.002 Å for bond distances and about 0.05-0.1 degrees for angles, but as it will be clear from the following discussion, more conservative estimates for errors on bond lengths are 0.003-0.004 Å.

Since to the best of our knowledge there is no experimental structure available to compare with, the only way to check the accuracy of our best-estimated geometry is to compare the corresponding equilibrium rotational constants with the semi-experimental ones, as obtained from the experimental ground-state rotational constants³⁶ corrected for the computed vibrational corrections¹⁰ (with the latter calculated at the B3LYP/SNSD level). From such a comparison, we note that our best estimated equilibrium rotational constants seem to be overestimated by about 25-35 MHz (~5-7%). According to our experience,^27,101,102 discrepancies of only a few MHz were expected instead (~0.1-1% in relative terms). Therefore, our best estimated structure seems to be affected by a systematic deficiency, which cannot be entirely ascribed to the potential overestimation of the basis-set truncation errors due to the procedure employed. In fact, already at the CCSD(T)/cc-pVQZ level inclusion of the core-correlation corrections leads to a large overestimation for the computed equilibrium rotational constants. While the coupled-cluster T₁ diagnostic¹⁰³ (0.039) indicates that non-dynamical correlation effects should not be relevant, a multi-reference character might be the reason for such deficiency. By resorting only to single-reference coupled-cluster methods, high-order excitations in the cluster expansion would be required to at least partially recover the multi-reference character. In particular, quadruple excitations are known to be effective (see for example, Ref.¹⁰⁴). Unfortunately, CCSDTQ calculations for the system under consideration are computationally very expensive, and their account, even with a double-zeta basis set, in the frame of a composite scheme requires an effort beyond the scope of the present work. From the available literature,⁵² we note that the corrections due to full treatment of quadruples are important especially for bond distances and positive (i.e., they lengthen bonds), ranging in size usually from 0.001 to 0.003 Å. Larger corrections are expected when a multi-reference character is present.¹⁰⁴ By increasing the C–C and C–H bonds by 0.0035 and 0.0007 Å, respectively, while keeping the angles unchanged, equilibrium rotational constants in good agreement with the corresponding semi-experimental ones are obtained. Another route for investigating the accuracy of our best-estimated structural parameters is offered by the semi-experimental approach for deriving equilibrium geometry, which is based on experimental ground-state rotational constants for different isotopic species and the corresponding computed vibrational corrections.^105,106 That is to say, the semi-experimental equilibrium rotational constants mentioned above for different isotopic species are used in a fitting procedure for deriving equilibrium geometry (for a detailed description of this approach, the reader is referred to Refs.^10,105,106 and references therein). Unfortunately, in the present case experimental rotational constants are available only for two isotopic species (namely, C₆H₅ and C₆D₅), which means that we have at our disposal only four rotational constants.¹⁰⁷ Therefore, only a partial semi-experimental equilibrium structure might be derived and its determination is hampered by the fact that, while we are mainly interested in the C–C bonds, the available isotopic substitution is at the hydrogen atoms. By performing the required least-square fit with all angles and the C–H distances fixed at the best-estimated values, the three C–C distances have been determined and reported in Table I. We note that the CiCo distance is about 0.004 Å longer than the corresponding best-estimated value, thus supporting the conclusions drawn above. On the other hand, the CoCm and CmCp bond lengths are about 0.001 Å shorter and ~0.008 Å longer than the corresponding best-estimated values, respectively. While we consider the semi-experimental CiCo distance reliable, the other two C–C bond lengths are strongly correlated and thus should be treated with caution. Inclusion of data for species involving isotopic substitution at carbons would very likely solve the problem.

In Table I, the equilibrium structure and the corresponding rotational constants at the B3LYP/SNSD level are also collected. We note a qualitative agreement with CCSD(T) results, with the DFT distances being slightly overestimated. According to the discussion above, the overestimation is evaluated to be on the order of 0.005 Å.

For the sake of completeness, the spectroscopic constants, namely, the ground-state rotational constants derived from the equilibrium structures at the B3LYP and CCSD(T) levels of theory augmented by the DFT vibrational corrections as well as the B3LYP and CCSD(T) quartic centrifugal-distortion constants are compared in Table II with the available experimental data.³⁶ From the comparison with experiment, the good predictive capabilities of DFT in the field of rotational spectroscopy can be pointed out.

TABLE II.

Spectroscopic constants^a computed at the CCSD(T)/cc-pVTZ and B3LYP/SNSD levels, compared to the experimental results. All values in MHz.

Constant	C6H5			C6D5
	B3LYP/SNSD	CCSD(T)/VTZ	Exp.b	B3LYP/SNSD	CCSD(T)/VTZ	Exp.b
A0	6240.8	6260.8	6279.8 (3)	5418.3	5437.0	5453.8 (4)
B0	5563.6	5583.9	5599.9 (2)	4608.7	4626.9	4640.8 (3)
C0	2940.3	2950.5	2959.4 (6)	2489.8	2499.1	2506.8 (9)
103 DJ	1.348	1.348	1.419 (4)	0.847	0.847	0.878 (5)
103 DK	0.732	0.744	1.09 (6)	0.420	0.431	0.654 (8)
103 DJK	−1.971	−1.985	−2.39 (1)	−1.195	−1.203	−1.46 (1)
103 dJ	0.124	0.120	-	0.098	0.096	-
103 dK	1.151	1.136	-	0.563	0.548	-
ϵ cc			4.78 (2)			4.22 (2)

^aGround-state rotational constants from the equilibrium values (either CCSD(T) or B3LYP) augmented by DFT anharmonic vibrational contributions. Quartic-centrifugal distortion constants at the corresponding level of theory.

^bExperimental data from Ref.³⁶.

The enthalpy of formation at 0 K, Δ_fH⁰, has been obtained following the procedure described in section II A. At the CBS+CV level, the reaction energy, Δ_rH⁰, including the ZPVE contribution for the phenyl radical and the SO correction for C turns out to be −5009.04 kJ/mol. According to Eq. 5, by adding to this value the enthalpies of formation of six C and five H atoms at 0 K, Δ_fH⁰ is obtained to be 341.89 kJ/mol, which should be compared with the experimental values of 352.9(2.5) kJ/mol¹⁰⁸ and 351.44(59) kJ/mol.³⁵ We note that our best-estimated value deviates from experiment by about 10-11 kJ/mol. As for the molecular structure determination, we can ascribe this discrepancy to the missing contribution of higher-order excitations in the coupled-cluster treatment, while diagonal Born-Oppenheimer corrections (DBOC) are expected to contribute in a negligible manner. In order to shed some light on the observed disagreement, the accurate results available for benzene have been analyzed.¹⁰⁹ It is noted that the largest contribution is due to the full treatment of triple excitations (11.2 kJ/mol), which is partially reduced by the perturbative treatment of quadruples (i.e., negative correction); relativistic effects also turn out to be non-negligible, the corresponding contribution being 4.2 kJ/mol, while DBOC contributes for less than 1 kJ/mol. On the whole, a correction of about 8 kJ/mol is obtained and it is reasonable to expect a similar value also for the phenyl radical that would lead to a reasonable agreement between theory and experiment. In view of the discussion above, we decided to carry out CCSDT calculation in conjunction with a double-zeta quality basis set, as explained in the methodology section. The correction due to the full treatment of triple excitations turns out to be +4.41 kJ/mol, thus leading to a total computed value of 346.20 kJ/mol. In order to check whether scalar relativistic effects^55,110,111 play a role also for the phenyl radical, the corresponding corrections to energy including the perturbative corrections due to the mass-velocity and the one- and two-electron Darwin terms have been obtained at the CCSD(T)/aug-cc-pCVTZ level. These lead to a contribution of +4.13 kJ/mol, which is very similar to what obtained for benzene at the same level of theory.¹⁰⁹ A final best-estimated heat of formation of 350.33 kJ/mol has thus been obtained, with the final value showing a good agreement with experiment and the initial discrepancy essentially canceled out. Even if the obtained theoretical value is expected to be affected by an uncertainty mainly due to the missing contribution of quadruples (which can be estimated in a negative correction of about 2-3 kJ/mol), we can anyway claim that it fulfills well the chemical accuracy requirements (the latter being about 4 kJ/mol). Finally, we note that the effect of geometry is small; in fact, the difference in Δ_rH⁰ due to the use of an empirically corrected geometry (i.e., obtained by enlarging the C–C best-estimated values by 0.0035 Å) instead of the best-estimated one is only ~0.5 kJ/mol.

B. Electron Spin Resonance Parameters

The experimental⁴⁰ and calculated (B3LYP/SNSD) g-tensor components are listed in Table III. We recall that the g-tensor axes of a radical with C_2υ symmetry are expected to be aligned with the molecular inertial axes¹¹² (see Figure 1) and that the accuracy of experimental data is expected to be approximately 1 × 10⁻³.¹¹³ Since the difference between experimental and computed tensor components range between 1 × 10⁻⁴ and 4 × 10⁻⁴, we can conclude that the B3LYP/SNSD results are remarkably accurate and well within experimental error bars. We furthermore note that vibrational effects are entirely negligible, the differences between the equilibrium and vibrationally averaged values at 298 K being smaller than 100 ppm. These results are particularly encouraging since CC calculations of the electronic g-tensor are at the moment available only at the CCSD and CCSDT levels.¹¹⁴ The former level of theory is expected to provide an accuracy of about 10-15%, i.e., an accuracy similar to what can be obtained at the DFT level, but at a significantly higher computational cost. The CCSDT model provides improved results, but only in conjunction with basis sets of at least triple-zeta quality including diffuse functions, thus leading to unaffordable calculations for the system under investigation.

TABLE III.

Electronic g-tensor components of the phenyl radical.

Component	Equilibrium	Vibr. averaged 298K	Experiment
gaa	2.0015	2.0015	2.0014
gbb	2.0021	2.0021	2.0023
gcc	2.0030	2.0030	2.0034
〈g〉	2.0022	2.0022	2.0024

Table IV summarizes the results for the isotropic hyperfine coupling constants computed at the CCSD(T) and B3LYP levels of theory, as described in the methodology section. By comparing the CCSD(T) results obtained with different basis sets and corrected for vibrational corrections at the DFT level with the available experimental data (i.e., the isotropic hfcc’s for hydrogens), we note a rather disappointing poor agreement, with systematic deviations of the order of 2-3 G. First of all, in order to point out whether such disagreement might be, at least partially, ascribed to the inaccuracy of the molecular structure employed (see section III A), an empirically corrected geometry (as for thermochemistry) has also been considered in the calculation of the isotropic hfcc’s. From the corresponding results we note that the effects of the molecular structure is rather limited, i.e., well smaller than 1%. Only for the hydrogens in ortho at the radical center the isotropic hfcc varies by about 3%, which is anyway far less than the observed discrepancy. As demonstrated in Ref.²⁶ and as explained in the computational section, the contribution to full treatment of triple excitations might be large, especially when hydrogens are connected to carbon atoms involved in π bonds, while quadruple excitations are expected to contribute little. The importance of full triples is further confirmed by the present investigation. Indeed, the corresponding corrections for hydrogens are a little bit larger than 2 G (in absolute values) and go in the right direction. As a consequence, their inclusion leads to a very good agreement with experiment. The last comment concerns the performance of the EPR-II and EPR-III basis sets that, at a strongly reduced computational cost, provide results in line with those obtained with the aug-cc-pVQZ-et3 set.

TABLE IV.

Isotropic hyperfine coupling constants (A_iso) of the phenyl radical (in Gauss).

	Cipso	Cortho	Cmeta	Cpara	Hortho	Hmeta	Hpara
B3LYP/SNSD	140.09	4.47	16.66	−2.70	17.56	5.58	2.11
B3LYP/SNSD - vib. corr. 0 K	+0.04	−0.36	+0.39	−0.28	+0.71	+0.25	+0.29
B3LYP/SNSD - vib. corr. 298 K	−0.02	−0.36	+0.38	−0.28	+0.70	+0.24	+0.28
CCSD(T)/EPR-II	131.95	6.79	12.47	2.01	14.74	8.03	−0.74
CCSD(T)/EPR-III	125.14	8.56	10.93	3.23	14.12	8.69	−1.33
CCSD(T)/ET3a	123.55	8.49	10.85	3.09	14.40	8.87	−1.37
CCSDT/EPR-II - correction	+3.09	−4.00	+4.14	−4.13	+2.15	−2.31	+2.25
Best estimateb	126.64	4.49	14.99	−1.04	16.55	6.56	0.88
Best estimate + vib. corr.c	126.62	4.13	15.37	−1.32	17.25	6.80	1.16
Experiment					17.4(1)	5.9(1)	1.9(1)

^aET3 means aug-cc-pCVTZ on C and aug-cc-pVQZ-et3 con H. See text.

^bCCSD(T)/ET3 results incorporating the correction due to full treatment of triples at the CCSDT/EPR-II level.

^cBest-estimated results incorporating the DFT vibrational correction at 298 K.

Table IV also reports the ¹³C isotropic hyperfine coupling constants computed at different levels of theory. We once again note that the full treatment of triple excitations plays a significant role and that the results obtained with the cost-effective EPR-III basis set are in remarkable agreement with those obtained employing the large ET3 set. As for hydrogens, the CC results are in good agreement with their DFT counterparts only once the correction due to full treatment of triples is included. In detail, the agreement is good or fairly good for C^ortho and C^para, while for C^ipso a discrepancy of more than 10 Gauss is observed, which anyway corresponds to about 10% in relative terms. Unfortunately, experimental values are not available to compare with.

The calculated and experimental ¹H anisotropic hyperfine coupling constants are collected in Table V. Due to symmetry, H^para (i.e., the hydrogen in para at the radical center) has vanishing off-diagonal tensor components, whereas H^ortho and H^meta (i.e., hydrogen atoms in ortho and meta at the radical center) show a non negligible coupling between components along the two principal axes lying in the molecular plane (a and b, see Figure 1), thus removing the spatial equivalence between the ortho and the meta pairs, and in principle leading to five magnetically non-equivalent protons. Since the fitting of the tensor components in the analysis of the experimental EPR spectrum is not without ambiguities,¹¹⁵ the agreement between theory and experiment can be considered more than satisfactory. From Table V, it is also apparent that both basis-set extension and inclusion of full treatment of triple excitations in the coupled-cluster ansatz provide non-negligible contributions, which are anyway expected to be smaller than the experimental error bars. As a consequence, the cost-effective EPR-II basis set can be used for reliable predictions and interpretative purposes.

TABLE V.

Anisotropic hyperfine coupling tensor (A_dip) for hydrogens in the phenyl radical (in Gauss).

	Hortho
	aa	bb	cc	ab
B3LYP/SNSD	−4.46	2.02	2.44	±1.03
B3LYP/SNSD - vib. corr. 0 K	−4.25	1.90	2.35	±1.01
B3LYP/SNSD - vib. corr. 298 K	−4.24	1.90	2.34	±1.00
CCSD(T)/EPR-II	−4.46	2.09	2.38	±0.77
CCSD(T)/EPR-III	−4.74	2.31	2.43	±0.55
CCSD(T)/ET3a	−4.81	2.41	2.40	±0.51
CCSDT/EPR-II - correction	+0.29	−0.20	−0.09	±0.04
Best estimate	−4.52	2.21	2.31	±0.55
Best estimate + vib. corr.	−4.30	2.09	2.21	±0.53
Experiment	−4.6	2.1	2.5	±0.84

	Hmeta
	aa	bb	cc	ab
B3LYP/SNSD	−0.26	−0.81	1.08	±1.01
B3LYP/SNSD - vib. corr. 0 K	−0.23	−0.81	1.04	±0.99
B3LYP/SNSD - vib. corr. 298 K	−0.22	−0.81	1.03	±0.98
CCSD(T)/EPR-II	−0.30	−0.72	1.02	±0.75
CCSD(T)/EPR-III	−0.30	−0.78	1.07	±0.62
CCSD(T)/ET3a	−0.35	−0.76	1.11	±0.59
CCSDT/EPR-II - correction	−0.02	−0.06	+0.08	±0.04
Best estimate	−0.37	−0.82	1.19	±0.63
Best estimate + vib. corr.	−0.33	−0.82	1.14	±0.60
Experiment	−0.4	−0.5	0.9	±0.25

	Hpara
	aa	bb	cc
B3LYP/SNSD	0.46	−0.58	0.12
B3LYP/SNSD - vib. corr. 0 K	0.46	−0.58	0.12
B3LYP/SNSD - vib. corr. 298 K	0.46	−0.58	0.12
CCSD(T)/EPR-II	0.46	−1.04	0.58
CCSD(T)/EPR-III	0.61	−1.19	0.58
CCSD(T)/ET3a	0.64	−1.21	0.57
CCSDT/EPR-II - correction	−0.04	+0.05	−0.07
Best estimate	0.60	−1.16	0.49
Best estimate + vib. corr.	0.60	−1.16	0.49
Experiment	0.6	−0.7	0.1

C. IR and Raman spectra

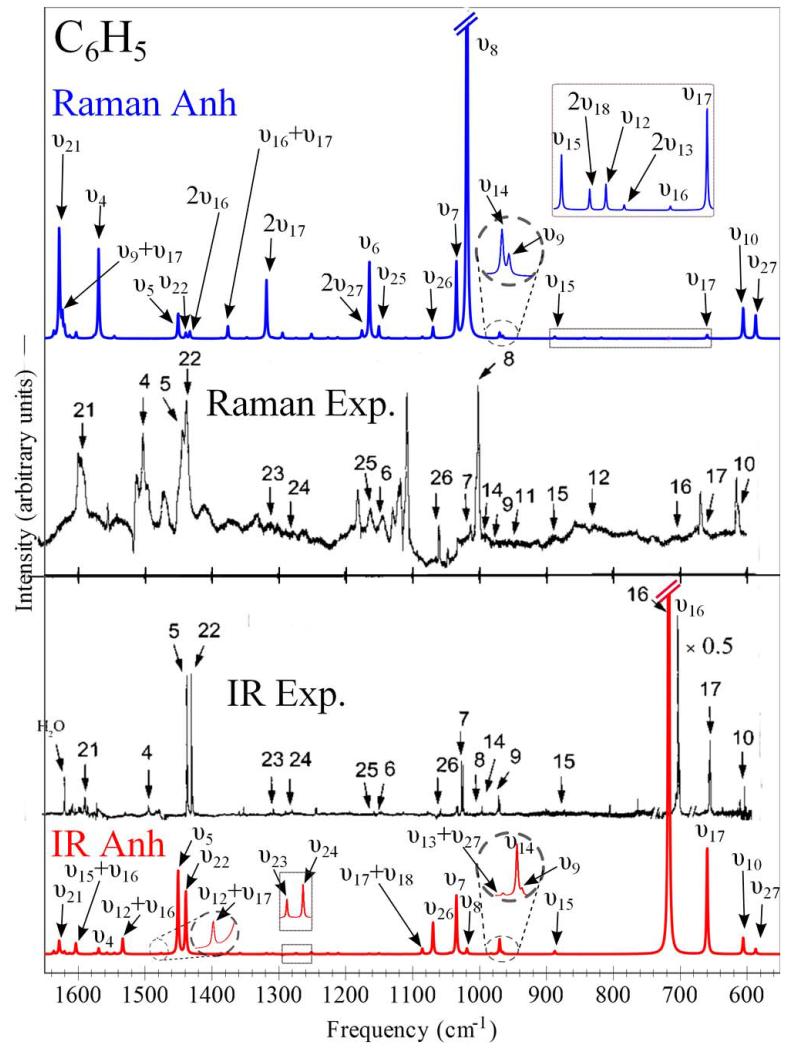
The 27 fundamentals of the phenyl radical can be directly correlated to the 30 fundamentals of the parent C₆H₆ molecule, and have (like those of C₆D₅, p-C₆H₄D, and p-C₆HD₄ isotopologues) symmetries: Γ_vib(C_2υ) = 10a₁ ⊕ 3a₂ ⊕ 5b₁ ⊕ 9b₂. Two different notations can be used for their assignment: υ, which corresponds to the phenyl radical normal modes numbered in the spectroscopic order, and ν, which is related to the Wilson notation,¹¹⁶ proposed for numbering the aromatic ring modes (first and last columns, respectively, in Tables VI and VII.) All the 24 IR-active fundamentals of the main isotopologue were identified in a careful experimental study of the matrix-isolated radical.³⁷ In the same study, several bands were also assigned to 5 deuterated isotopologues, while Raman spectra have been measured only for fully hydrogenated species containing both ¹²C and ¹³C.³⁸ Before proceeding with the discussion of the computational results, a thorough analysis of the experimental data and, in particular, of how matrix effects affect the frequency values with respect to the gas phase is required. Comprehensive studies of free radicals and ions in Ne and Ar matrices^117,118 suggest that the frequency shift with respect to gas-phase data is smaller than 1% and usually to red. Analogous conclusions were drawn by Friderichsen and coworkers³⁷ for all vibrational frequencies of C₆H₅, including the C–H stretchings, and are further confirmed by a remarkable agreement between Ar-matrix and high-resolution gas-phase data for the υ₁₉ mode.^39,119

TABLE VI.

Harmonic and anharmonic vibrational frequencies (in cm⁻¹) and IR intensities (in km/mol) of C₆H₅.

Mode	Symmetry	B3LYP/SNSD				CCSD(T)/VTZ		CC/DFT		Exp.a		Assignmentb
		ω	I harm	Δ ν	Δ Ianh	ω	I harm	ν	I anh	ν	I
1	A1	3191	8.4	−132	8.50	3209	5.6	3077	14.1	3086	3.1	υ 2
2	A1	3179	3.9	−132	−3.38	3198	6.7	3066	3.3	3072	0.2	υ 20a
3	A1	3159	0.8	−137	0.75	3174	0.4	3037	1.2	3037	0.2	υ 7b
4	A1	1572	1.3	−41	−0.21	1611	0.8	1569	0.6	1581(1497c)	2.2	υ 8a
5	A1	1468	7.2	−31	0.21	1482	8.8	1451	9.0	1441	8.7	υ 19a
6	A1	1172	0.1	−15	−0.01	1179	0.1	1165	0.1	1154	0.1	υ CH scissor
7	A1	1047	8.4	−21	−1.23	1055	7.5	1035	6.3	1027	7.9	υ 18a
8	A1	1015	0.4	−15	0.30	1034	0.3	1019	0.6	997	0.2	υ 1
9	A1	982	1.0	−13	0.56	983	0.9	970	1.5	976	1.6	υ 12
10	A1	614	1.6	−5	0.36	611	1.4	606	1.8	605	1.4	υ 6b
11	A2	968	0.0	−26	0.0	981	0.0	954	0.0	945d	/	υ 17a
12	A2	814	0.0	−20	0.0	838	0.0	818	0.0	816d	/	υ 10a
13	A2	400	0.0	−9	0.0	404	0.0	395	0.0	/	/	υ 16a
14	B1	995	0.1	−27	0.07	992	0.1	965	0.2	972	0.1	υ 17b
15	B1	893	0.5	−22	−0.11	910	0.4	888	0.3	874	0.9	υ 10b
16	B1	720	78.1	−15	−4.89	733	81.3	717	76.4	706	55.9	υ 11
17	B1	668	20.1	−14	−0.95	674	12.6	660	11.7	657	1.1	υ 4
18	B1	424	6.2	−8	0.16	430	5.4	422	5.6	416	3.4	υ 16b
19	B2	3182	17.1	−153	11.00	3202	13.6	3049	24.6	3071	10.6	υ 20b
20	B2	3166	4.5	−134	−1.25	3182	5.8	3048	4.5	3060	0.1	υ 7a
21	B2	1630	1.7	−34	−0.57	1663	2.0	1628	1.4	1624(1593c)	0.1	υ 8b
22	B2	1460	4.7	−28	0.25	1467	6.4	1439	6.7	1432	6.3	υ 3
23	B2	1334	0.3	−17	−0.11	1312	0.0	1294	0.2e	1321	0.3	υ 14
24	B2	1302	0.1	−24	0.03	1275	0.2	1251	0.2	1283	3.6	υ 9b
25	B2	1171	0.1	−12	0.01	1163	0.1	1151	0.1	1159	0.1	υ 15
26	B2	1069	3.8	−8	−0.17	1077	3.5	1070	3.3	1063	1.1	υ 18b
27	B2	594	0.6	−6	−0.04	593	0.6	587	0.6	587	0.2	υ 6a

^aExperimental data from Ref.³⁷

^bAssignment based on the Wilson notation¹¹⁶ proposed for the numbering of aromatic ring modes.

^cReassigned in Raman spectrum³⁸.

^dObserved only in the Raman spectrum³⁸.

^eAnharmonic IR intensity computed at the B3LYP/SNSD level.

TABLE VII.

Harmonic and anharmonic vibrational frequencies (in cm⁻¹) and IR intensities (in km/mol) of C₆D₅.

Mode	Symmetry	B3LYP/SNSD				CCSD(T)/VTZ		CC/DFT		Expa		Assignmentb
		ω	I harm	Δ ν	Δ Ianh	ω	I harm	ν	I anh	ν	I
1	A1	2367	4.2	−85	1.15	2381	3.5	2296	4.7	2292	0.2	υ 2
2	A1	2352	2.1	−81	0.00	2366	3.2	2285	3.2	2290	0.4	υ 20a
3	A1	2330	0.4	−82	−0.15	2339	0.2	2257	0.1	2282	0.7	υ 7b
4	A1	1532	2.6	−40	−0.22	1573	1.7	1533	1.5	1494	0.1	υ 8a
5	A1	1335	0.5	−20	−0.10	1349	1.2	1329	1.1	1314	1.3	υ 19a
6	A1	859	0.0	−11	0.02	864	0.1	853	0.1	851	0.2	υ CH scissor
7	A1	812	7.2	−12	−0.05	817	6.8	805	6.7	803	3.4	υ 18a
8	A1	978	0.3	−16	−0.04	994	0.3	978	0.3	/	/	υ 1
9	A1	952	0.1	−11	0.00	954	0.1	943	0.1	/	/	υ 12
10	A1	590	1.6	−4	0.27	587	1.4	583	1.7	590	0.9	υ 6b
11	A2	793	0.0	−16	0.00	797	0.0	781	0.0	/	/	υ 17a
12	A2	634	0.0	−13	0.00	652	0.0	639	0.0	/	/	υ 10a
13	A2	346	0.0	−7	0.00	352	0.0	345	0.0	/	/	υ 16a
14	B1	830	0.0	−18	0.01	806	0.0	788	0.0	/	/	υ 17b
15	B1	724	0.2	−14	−0.05	733	0.3	719	0.3	/	/	υ 10b
16	B1	598	3.3	−12	0.06	613	2.7	601	2.8	/	/	υ 11
17	B1	527	43.2	−9	−2.11	538	42.0	529	39.9	517	/	υ 4
18	B1	380	9.3	−7	0.06	386	8.2	379	8.3	382	/	υ 16b
19	B2	2355	10.7	−94	2.94	2371	9.4	2277	12.3	2271	1	υ 20b
20	B2	2336	1.3	−81	−0.38	2348	2.0	2267	1.6	2264	0.5	υ 7a
21	B2	1602	1.0	−36	−0.21	1633	1.2	1597	1.0	1561c	0.1	υ 8b
22	B2	1358	0.5	−27	0.22	1342	2.0	1315	2.2	1312	0.5	υ 3
23	B2	1285	0.5	−28	0.10	1246	0.1	1218	0.2	1297d	0.8	υ 14
24	B2	1021	0.2	−17	−0.03	1022	0.2	1005	0.2	/	/	υ 9b
25	B2	849	0.3	−11	−0.11	852	0.4	841	0.3	/	/	υ 15
26	B2	813	2.9	−10	0.08	815	2.7	805	2.8	806	1.9	υ 18b
27	B2	569	0.6	−6	−0.02	568	0.7	562	0.7	547	/	υ 6a

^aExperimental data from Ref.³⁷

^bAssignment based on the Wilson notation¹¹⁶ proposed for the numbering of aromatic ring modes.

^cPossible tentative assignment to υ₁₁ + υ₁₄ combination transition at 1567 cm⁻¹ (see text for the details).

^dPossible tentative assignment to 2υ₁₂ overtone at 1279 cm⁻¹ or υ₁₅, + υ₁₇ combination transition at 1246 cm⁻¹ (see text for the details).

In Table VI, it is noted that the fundamental transition frequencies computed by means of the hybrid CC/DFT approach generally deviate by less than 1% from experiment, showing a Mean Absolute Error (MAE) of about 10 cm⁻¹ and maximum discrepancies of 30 cm⁻¹. The only surprisingly large discrepancy is observed for υ₄ (computed at 1569 cm⁻¹), assigned to 1581 cm⁻¹ based on the IR spectra of Ref.³⁷, and reassigned to 1497 cm⁻¹ in the integrated IR and Raman experiment of Ref.³⁸. This outlier has been excluded from the statistics and will be discussed later in the text by means of the comparison of the simulated and experimental spectra reported in Figure 2. In addition to υ₄, the most notable exceptions from the overall good agreement are υ₈ (2%, 22 cm⁻¹), υ₂₃ (3%, 26 cm⁻¹) and υ₂₄ (2.5%, 32 cm⁻¹). The first band corresponds to a ring breathing motion (ν₁), is very weak and, in some cases, obscured by a close lying precursor band (997 cm⁻¹ vs. 999 cm⁻¹), thus leading to an apparent high intensity. In support of our prediction, it should be noted that both the observed intensity and spectral shifts for deuterated isotopologues agree with our computations. The band at 1321 cm⁻¹ (υ₂₃) corresponds to a Kekulé mode (ν₁₄). Here, the discrepancy between DFT and CCSD(T) harmonic frequencies (22 cm⁻¹) might suggest some inaccuracy of the DFT anharmonic contribution¹²⁰, possibly due to different compositions of the reference normal modes. The same remark applies to the last outlier, namely, the band observed at 1283 cm⁻¹ (υ₂₄) and assigned to an out-of-phase combination of the two Co-Cm stretchings coupled to the corresponding Cm-Co-Ho and Co-Cm-Hm bendings (ν_9b).

FIG. 2.

Anharmonic theoretical IR and Raman spectra of C₆H₅ in the 550-1650 cm⁻¹ energy range, compared to their experimental counterparts detected in Ar Low-Temperature Matrix³⁸

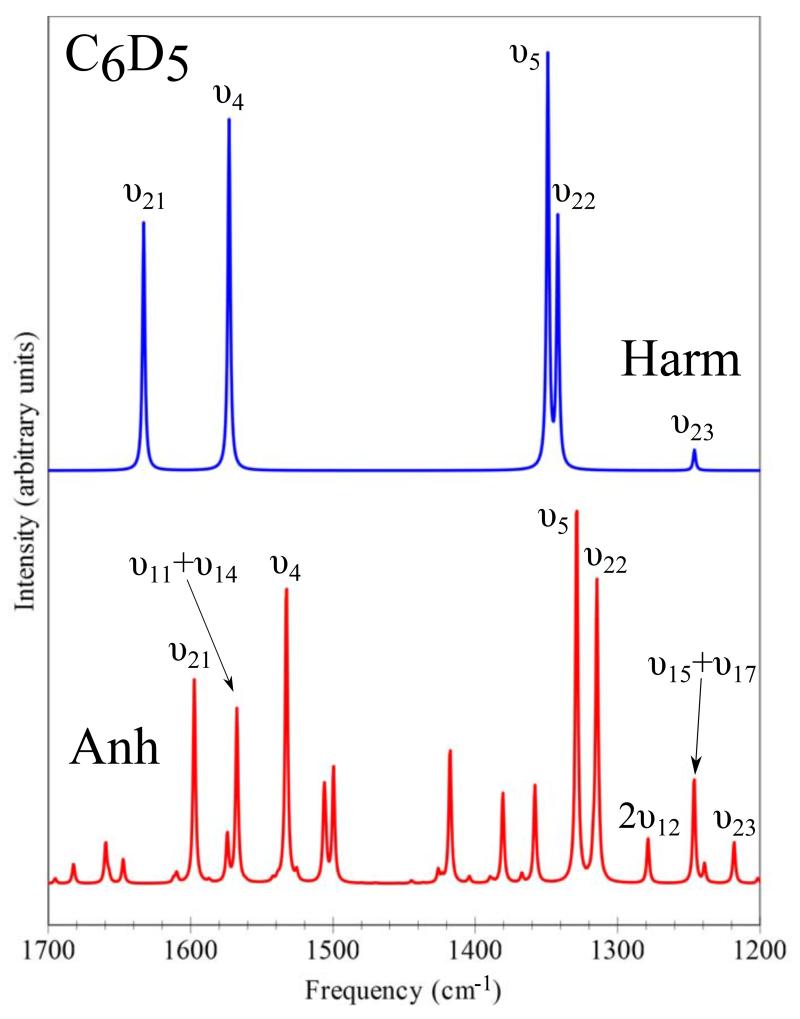
For C₆D₅, a remarkably good agreement between anharmonic CC/DFT frequencies and experiment is generally observed. In this case, significant outliers are represented by υ₃(2% error), υ₄ (2% error), υ₂₁ (4% error), and especially υ₂₃ (6% error) (see Table VII). It is worth noting that for υ₄, υ₂₁ and υ₂₃, replacement of the CC harmonic contributions by their DFT counterparts leads to anharmonic frequencies (1491, 1566, and 1257 cm⁻¹, respectively) significantly closer to experiment. The error on υ₂₁ (ν_8b) is particularly puzzling in view of the very good agreement between CC/DFT and experimental values for the corresponding band of C₆H₅ (1628 vs. 1624 cm⁻¹) and the significantly underestimated value computed by DFT (1593 cm⁻¹). For υ₂₃ (ν₁₄), an analogous situation is observed for both C₆H₅ and C₆D₅, with DFT showing a better agreement with experiment, but with especially large discrepancy for C₆D₅. However, an alternative explanation can be provided by tentative assignments of experimentally observed transitions to overtone or combination bands. Indeed, our computations show that the υ₁₁+υ₁₄ combination frequency (at 1567 cm⁻¹) has an intensity comparable to that of υ₂₁, while the 2υ₁₂ overtone (at 1279 cm⁻¹) as well as the υ₁₅+υ₁₇ combination band (at 1246 cm⁻¹) present higher intensities than the υ₂₃ fundamental frequency. Such explanation seems to be plausible in view of the low intensity of these problematic transitions (below 1 km/mol) and of the fact that experimental assignments have been performed by comparing the recorded spectra with computed fundamental harmonic frequencies. In fact, Figure 3 clearly shows the more complex pattern of the anharmonic spectrum with respect to the harmonic one, with several transitions of similar intensity lying in the 1200-1700 cm⁻¹ frequency range. The last outlier of C₆H₅ (i.e., υ₈) has not been observed in C₆D₅. Finally, we note that CC and DFT results are similar for υ₃ (ν_7b) in both C₆H₅ and C₆D₅ and this finding, together with the good agreement with experiment for υ₃ of C₆H₅, suggests some care in accepting the experimental assignment.

FIG. 3.

Harmonic and anharmonic theoretical IR spectra of C₆D₅ in the 1200-1700 cm⁻¹ energy range.

The situation is more involved for IR intensities, but a conservative estimate by Friderichsen and coworkers³⁷ suggests that the uncertainty is roughly 15%. In any case, a direct comparison of absolute values appears quite useless (except, perhaps, for estimating the role of anharmonic contributions) and a more significant analysis should be based on direct comparison of computed and experimental spectra. In Figure 2, the IR and Raman spectra of C₆H₅ clearly show that intensity patterns are well reproduced not only for the fundamental transitions but also for the weak spectral features due to overtones and combination bands. It is worth noting that anharmonic effects are mandatory in order to simulate non-fundamental transitions for which the harmonic approximation yields null intensity. It can be observed that in some cases these bands show intensity comparable to those of the close-lying fundamentals, as for example, it happens in the case of the Raman and IR spectra in the 1150-1450 cm⁻¹ and 1500-1650 cm⁻¹ frequency ranges, respectively. For the latter spectral range, two bands, namely, υ₄ and υ₂₁, have been recently reassigned in combined IR and Raman experiment.³⁸ For υ₄ (ν_8a), this reassignment leads to an exceptionally large discrepancy between the computed frequency, 1569 cm⁻¹, and the new experimental value, 1497 cm⁻¹, while a definitely better agreement is obtained when comparing to the previously proposed value of 1581 cm⁻¹, based on the IR measurements of Ref.³⁷. Furthermore, simulated IR spectra show non-negligible features due to the combination bands, υ₁₂ + υ₁₇ and υ₁₂ + υ₁₆, at 1477 cm⁻¹ and 1535 cm⁻¹, respectively, while the υ₄ fundamental, intense in simulated Raman spectrum, can be hidden by a transition assigned to the C₆H₅NO precursor. Concerning particularly difficult analyzes of experimental spectra of free radicals, it has already been shown (e.g., for the F₂NO²⁰ or vinyl^18,121,122 radicals) that accurate computational studies can lead to correction of the vibrational frequencies assignment. Actually, for the vinyl radical the discrepancies observed between the computed and experimental gas-phase infrared spectrum¹²³ led to an experimental re-investigation,¹²⁴ which in turn confirmed the theoretical predictions. In this frame, it is suggested that the 1400-1600 cm⁻¹ spectral zone of C₆H₅, where bands due to precursor and water impurities are clearly present as well as the assignment of υ₂₃ of C₆D₅ should be re-investigated with the help of fully anharmonic IR and/or Raman simulated spectra, also accounting for the species possibly present in the experimental mixture and, in case, including a few sets of isotopically substituted precursors. This would allow a more direct comparison with experimental outcomes and increase the accuracy and reliability of reported experimental results.

IV. CONCLUSIONS

This work reports a joint CC/DFT investigation, which couples highly accurate coupled-cluster approaches, also including extrapolation to the CBS limit and core-correlation effects, with DFT calculations of the anharmonic contributions to molecular structure and spectroscopic (IR, Raman, EPR) parameters. Despite the computational and theoretical challenges provided by open-shell systems, we succeeded in obtaining reliable and accurate results, with the key point being the full treatment of triple excitations in the cluster expansion. Concerning the molecular structure, a best-estimated equilibrium geometry has been obtained, which turned out to be less accurate than usual. Its accuracy has been investigated in terms of rotational constants and a partial semi-experimental equilibrium structure, with the latter based on the availability of the rotational constants of C₆H₅ and C₆D₅ and of the corresponding DFT vibrational corrections. In such determination, the C–H distances and angles were kept fixed at the theoretically best-estimated values; the results are encouraging and call for the experimental observation of other isotopic species by means of rotational spectroscopy. With respect to the spectroscopic parameters, it is worth mentioning the accurate isotropic hyperfine coupling constants obtained thanks to the use of purposely tailored basis sets and the corresponding CCSDT contributions. Furthermore, anharmonic DFT corrections to both frequencies and intensities allowed us to critically analyze the IR and Raman spectra with an unprecedented accuracy.

In summary, the results presented in this work hold the promise of reliable and yet computationally feasible calculations for medium-sized open-shell systems by means of integrated CC and DFT approaches, where highly accurate CC values for the structural parameters, energetics, and harmonic frequencies are complemented by anharmonic corrections obtained at the DFT level. Characterizations of other free radicals of biological interest are currently in progress in our laboratories.