General Approach to First-Order Error Prediction in Rigid Point Registration

Abstract

A general approach to the first-order analysis of error in rigid point registration is presented that accommodates fiducial localization error (FLE) that may be inhomogeneous (varying from point to point) and anisotropic (varying with direction) and also accommodates arbitrary weighting that may also be inhomogeneous and anisotropic. Covariances are derived for target registration error (TRE) and for weighted fiducial registration error (FRE) in terms of covariances of FLE, culminating in a simple implementation that encompasses all combinations of weightings and anisotropy. Furthermore, it is shown that for ideal weighting, in which the weighting matrix for each fiducial equals the inverse of the square root of the cross covariance of its two-space FLE, fluctuations of FRE and TRE are mutually independent. These results are validated by comparison with previously published expressions and by simulation. Furthermore, simulations for randomly generated fiducial positions and FLEs are presented that show that correlation is negligible correlation coefficient < 0.1 in the exact case for both ideal and uniform weighting (i.e., no weighting), the latter of which is employed in commercial surgical guidance systems. From these results we conclude that for these weighting schemes, while valid expressions exist relating the covariance of FRE to the covariance of TRE, there are no measures of the goodness of fit of the fiducials for a given registration that give to first order any information about the fluctuation of TRE from its expected value and none that give useful information in the exact case. Therefore, as estimators of registration accuracy, such measures should be approached with extreme caution both by the purveyors of guidance systems and by the practitioners who use them.

I. Introduction

In 2009, a new method of first-order analysis of the point-registration problem was introduced [2]. The method was developed to facilitate the statistical analysis of a phenomenon that had been observed years earlier, first by Steinmeier using phantoms [3] and more recently by Woerdeman in vivo [4]. These investigators attempted to establish for several fiducial-based, surgical navigation systems, a correlation between the displayed estimates of accuracy and the true accuracy. Steinmeier found no correlation, and Woerdeman observed a negligible correlation coefficient of only 0.08. Thus, lower than normal estimated accuracies were not accompanied by lower than normal true accuracies, nor were there correlations for higher than normal values. The navigational systems’ estimates of accuracy are based on the goodness of fit of the fiducial points after registration, and the surprising result that these estimates seem to be unrelated to truth, suggests that there is an underlying problem with this method of error prediction. The 2009 work [2] investigated this problem for a special case in which expected error in fiducial localization is isotropic and identical for all fiducials, and it proved to first order that fluctuations in registration accuracy are statistically independent of the fluctuations of any estimate of that accuracy based on the goodness of fit. In the present work, we extend this analysis to the general case. We show that, when ideal weighting is used for each fiducial, this independence is maintained, and we show by simulations that, without weighting, the correlation between them is on the order of that low value observed by Woerdeman. In addition, we provide new expressions for error statistics that are more general than those previously provided. We begin in Section II by providing background on, and precise definitions of, error in these navigation systems. In Section III we present our new approach and derive independence and the new statistical expressions. In Sections IV and V we compare our results to previously published results and to results from computer simulations. In Sections VI and VII we discuss our theory and its results and present our conclusions.

II. Background

Fiducial-based navigation has become a ubiquitous adjunct to surgery when rigid anatomy—bone or soft tissue constrained by bone—is involved. The major commercial guidance systems—the StealthStation Surgical Navigation System (Medtronic, Inc., Minneapolis, MN) and the VectorVision System (BrainLAB AG, Feldkirchen, Germany), each provide it as an option in addition to surface-based navigation, and both options incorporate rigid point registration in their algorithms to determine the position of the surgeon’s tracked probe or tracked instrument. The registration approach analyzed in the following sections is employed by both of these systems. Fiducials, often called “markers,” are provided that typically adhere to the skin, but the selection of anatomical “fiducials” are supported by these systems as well. Both fiducial and surface registration approaches are often called “frameless” stereotaxy, in reference to the cumbersome stereotactic frame that they are designed to replace. These frameless approaches are offered by virtually every surgical center as an adjunct to neurosurgery, spine surgery, and orthopedic surgery, and they are provided as well by radiation oncology centers as an adjunct to radiosurgery.

Because fiducials by their nature are discrete objects, they provide positional information only at isolated regions of the anatomy. Information about the position or movement of anatomy outside these regions can be inferred only if all these regions move as a single rigid object. As a result, fiducial-based navigation systems employ only rigid transformations during the registration process. To the extent that the anatomy is non-rigid, rigid transformations are inappropriate, but for surgical resections involving bone, such as a vertebra or a femur, or tissue and bone that move as a single rigid object, such as the head, rigidity is a reasonable assumption. Failure of the anatomy to remain rigid will cause systems’ predictions of fiducial-registration accuracy, such as those studied by Steinmeier and Woerdeman, to fail, but nonrigidity is not the source of failure that we present here. Indeed Steinmeier’s experiments involved only rigid phantoms. Instead we confine our attention to those applications in which rigidity is a valid assumption.

For rigid anatomy, the image-guidance problem is reduced to the determination of the rigid transformation that the anatomy has undergone between image acquisition and intervention. That transformation can be estimated via fiducials that are attached to the anatomy before imaging and remain in place through the registration procedure. The position of each fiducial is localized in both image space and physical space, and then a transformation from image space to physical space is usually chosen such that it minimizes the fiducial registration error (FRE), where, in the simplest method, which is employed by commercial systems, FRE is the root-mean-square of distances between corresponding fiducials after the registration, i.e., the distance between the localized position of each fiducial as transformed from image space to physical space and the position of that corresponding fiducial localized in physical space. In the general case, the displacement between the transformed image point and the physical point is multiplied by a “weighting” matrix, which may be different for each fiducial, and FRE is the root-mean-square of the lengths of the resulting vectors. The weighting matrix is used in cases when some information about the nature of fiducials localization procedure is available. The simplest method described above is equivalent to uniform weighting, and it is employed by commercial systems in the absence of such information. Because of fiducial localization error (FLE), the registration is invariably flawed to some degree, and FRE is a readily available measure of registration error that serves as the most commonly used indicator of the goodness of fit of the of the corresponding points.

Sibson in 1979 investigated the statistical relation between FRE and FLE for the case of isotropic FLE and provided an expression that can be used to relate their expected root-mean-square values as follows [5]:

$$\langle {\text{FRE}}^2\rangle =\left(1-\frac{2}{N}\right)\langle {\text{FLE}}^2\rangle$$ (1)

where 〈·〉 means “expected value of.” Expressions for FRE for each individual fiducial have also been derived [10]. FRE is an easily measured quantity, but it is not as important as target registration error, TRE, which is the displacement from its true position of a registered point not used as a fiducial¹. The target error TRE(r) at a point r of interest to the surgeon is the true measure of registration error. In 1998 and 2001, the statistical relation between TRE and FLE was investigated for isotropic FLE and expressions were provided relating their expected root-mean-square values [6], [7]

$$\langle {\mid \mathbf{TRE}(r)\mid }^2\rangle =\frac{1}{N}\left(1+\frac{1}{3}\sum _{k=1}^3\frac{d_k^2}{f_k^2}\right)\langle {\text{FLE}}^2\rangle$$ (2)

where d_k is the distance of x from principal axis k of the fiducial configuration, $f_k^2$ is the mean of the squared distances of the fiducials from that axis. Equation (1) can be used to estimate the distribution of FLE from measurements of FRE for many cases. With this estimate available, (2) can then be exploited to predict TRE based on the fiducial configuration when fiducials are used (a) on a patient, (b) on a coordinate reference frame attached to a patient, and (c) on a surgical probe [8]. Equation (2) is not appropriate for FLE that is anisotropic, which means that it varies with direction, inhomogeneous, which means that it is different for different points. For anisotropic and inhomogeneous FLE, more complex expressions than that of (2) have recently been derived by Wiles [9], [23] and Moghari [11].

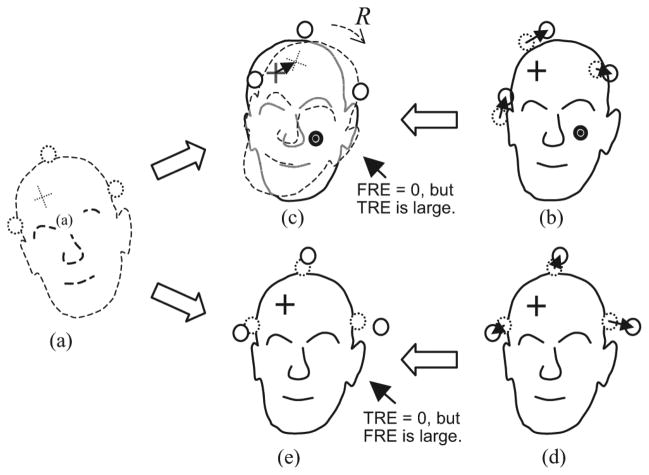
Since both 〈FRE²〉 and 〈|TRE(r)|²〉 are proportional to 〈FRE²〉, it might be expected that for a given registration, if FRE is small, then |TRE(r)| will be small and when one is large the other will be large. While it may seem intuitive to expect the size of TRE to be correlated with that of FRE, it is easy to construct counter-examples, as is shown by Fig. 1. That figure shows two examples. For one of them FRE is zero while |TRE(r)| is large, and for the other |TRE(r)| is zero while FRE is large. The key difference is that in the first example the set of FLEs are equivalent to a rigid transformation, while in the second example, they are not. Fig. 1(a) shows image space, while (b) and (d) show physical space. The localizations are assumed to be perfect in image space. The “rigid” set of localization errors occur in (b), while the errors in (d) cannot be represented exactly or even approximately by any rigid transformation.

Fig. 1.

FRE and TRE for two example registrations (a) Image space showing patient (dashed outline), three fiducials (dotted circles), and an anatomical target (dotted cross). For simplicity localization errors are zero (b) Physical space showing a set of fiducial localization errors. Arrows show the displacements from true positions (dotted outlines) to localized positions (solid outlines). The same anatomical target is shown (solid cross). This set of localization errors can be duplicated exactly by a rigid transformation that comprises a clockwise rotation R about the “bull’s eye” that is located just to the right of the nose (c) Point registration has been applied to the image to register the localized positions in (a) with those in (b) The transformation is incorrect by the same rotational error R (dashed arrow) about the bull’s eye, but it achieves an FRE of zero. TRE (arrow) is large, however, because R is large (d) Physical space showing a second set of fiducial localization errors. This set of localization errors can be duplicated by expansion from the target point but cannot be approximated by any rigid transformation (e) Point registration has been applied to the image in (a), and the resulting rigid transformation is perfect. Since the transformation is perfect, TRE is zero, but since no rigid transformation can approximate the localization errors, the fiducial fit is poor, as can be seen from the relatively large size of the individual FREs (distance between circles with dotted and solid outlines, so the root-mean square FRE is large.

Fig. 1 shows schematically that, despite the fact that 〈FRE²〉 and 〈|TRE(r)|²〉 are related functionally through (1) and (2), TRE is not necessarily related to FRE for specific registration instances. Thus, the fact that their means are related does not imply that their variations around those means are related. It is easy to construct such examples, but no example or set of examples can answer the question, “Are the fluctuations² of FRE and TRE about their means correlated?” In the next sections we will show that, for the case of small FLE, when either of the two most common weighting schemes is employed, the answer to this question is, “No.”

We begin by proving this answer mathematically to first order in localization error for the case of so-called “ideal weighting”. That proof requires a statistical analysis of a linear model of the problem of rigid point registration. Recently a new approach [2] for such an analysis was developed for the special case of isotropic, homogeneous FLE with uniform weighting (i.e., un-weighted). In the next section, we extend that approach to the general case of anisotropic, inhomogeneous FLE with arbitrary weighting, and we use the approach both to investigate the dependence of FRE and TRE and to provide unified formulas for their respective covariances that are more general than any previous expressions.

III. Derivations

Our derivations are based on a linearization of the rigid, point registration problem. We begin with a statement of the registration problem, followed by the linearization of the problem for small FLE.

A. Registration Problem

The fundamental problem of rigid, fiducial registration is to find the rotation matrix R and translation vector t that minimize the expression

$${\text{FRE}}^2=\sum _{i=1}^N{\mid W_i(R(x_i+\mathrm{\Delta }{x}_i)+t-(y_i+\mathrm{\Delta }{y}_i))\mid }^2$$ (3)

where FRE is the weighted fiducial registration error x_i,y_i, are 3×1 vectors representing corresponding points in two spaces, where at least three of the x_i are not collinear, Δx_i and Δy_i represent localization errors in the two spaces, W_i is a 3×3 non-singular weighting matrix, which may be a function of R (see the discussion of “ideal weighting” at the beginning of Section III-G). Clearly the solution, R, t, obtained by minimizing FRE² in (3) is unchanged if all the W_i are multiplied by the same factor w, while FRE² itself is multiplied by w². Thus, size of FRE as defined by (3) is somewhat arbitrary. For example, the general form for the uniform weighting scheme employed by commercial systems is W_i = wI, where I is the 3×3 identity matrix, and for this weighting FRE equals times the root-means square of the distance between fiducials after registration. We can remove this arbitrary factor of w from FRE by stipulating that the W_i be normalized such that ${\sum }_1^N{\mid W_i\mid }^2={\sum }_1^N\text{trace}(W_i^t{W}_i)=3$. With this stipulation, uniform weighting requires that W_i = N^−1/2I, and FRE recaptures its meaning as the unweighted root-mean square of the fiducial fitting errors and satisfies (1).

The rotation matrix is restricted to be orthogonal, which means that R^tR = I. The points, y_i, arise from the application of the true, but unknown, rigid transformation, R⁽⁰⁾, t⁽⁰⁾, to the x, as follows:

$$y_i=R^{(0)}{x}_i+t^{(0)}.$$ (4)

R⁽⁰⁾, t⁽⁰⁾ is the transformation that is sought by the minimization of FRE in (3), but because of fiducial localization error, the transformation that minimizes FRE, namely R, t, will differ from the true transformation R⁽⁰⁾, t⁽⁰⁾. We model the Δx_i and Δy_i as random, independent vectors of fiducial localization error, with each of their three components being normally distributed with zero means and covariances ${\mathrm{\sum }}_i^{(1)}$ and ${\mathrm{\sum }}_i^{(2)}$, respectively. Thus, the localization errors in the two spaces may be anisotropic and inhomogeneous. While these statistics are known, it is assumed that no other information about the errors themselves is available. If any relationships among the specific errors for a given set of localizations or if any components of any of the errors were known, that information could be employed in the registration process, and the derivations and proofs below would need to be modified. It is helpful to rewrite (3) as

$${\text{FRE}}^2=\sum _{i=1}^N{\mid W_i({Rx}_i+t-y_i-\mathrm{\Delta }{\xi }_i)\mid }^2$$ (5)

where Δξ_i = Δy_i−RΔx_i, is the “two-space” localization error vector for point-pair i, and its elements are normally distributed with zero means and covariances $R{\mathrm{\sum }}_i^{(1)}{R}^t+{\mathrm{\sum }}_i^{(2)}$. We define ${\mathrm{\sum }}_i=R{\mathrm{\sum }}_i^{(1)}{R}^t+{\mathrm{\sum }}_i^{(2)}$ to be the “two-space” covariance of FLE. Once the rotation and translation that minimize FRE² have been found, they can be used to determine the vector TRE of target registration error at any point r that is not used as a fiducial point

$$\mathbf{TRE}(r)=Rr+t-\left(R^{(0)}r+t^{(0)}\right).$$ (6)

B. Linearization

Sibson showed how derivations of error statistics for this problem could be made tractable by (a) assuming that FLE is small, (b) approximating to first-order in FLE, (c) moving the origin of the coordinate system to the centroid of the x_i, (d) reorienting the coordinate system along the principal axes of the x_i, and (e) separating the rotational and translational problems [5]. He used this approach to investigate FRE; we and others have used it to investigate TRE [6], [7], [9], [11] and FRE [10], [19]. For our present investigation, we have developed a new approach. We employ (a) and (b), but we omit (c), (d), and (e). Thus, we solve to first order in FLE, but we retain the laboratory coordinate system, and we solve for both the rotation and the translation simultaneously. Solving the first-order problem allows us to cast the problem as a simple, unconstrained set of 3N linear algebraic equations in six unknowns of the form: Cq = e, where C is a 3N×6 matrix, e is a 3N×1 vector, and q is a 6×1 vector whose elements are Δθ₁, Δθ₂, Δθ₃, Δt₁, Δt₂, Δt₃, where Δθ_k, is an angle of rotation (in radians) about axis k, and Δt_k, is a translation along that axis.

We begin by defining $x_i^{(0)}=R^{(0)}{x}_i$, and Δt = t − t⁽⁰⁾, which allows us to transform the vector whose squared length appears in the summation in (3) as follows:

$$\begin{array}{l}R(x_i+\mathrm{\Delta }{x}_i)+t-(y_i+\mathrm{\Delta }{y}_i)=R\left(R^{{(0)}^t}{R}^{(0)}\right)(x_i+\mathrm{\Delta }{x}_i)+t-R^{(0)}{x}_i-t^{(0)}-\mathrm{\Delta }{y}_i\\ =\left({RR}^{{(0)}^t}-I\right)R^{(0)}{x}_i+\mathrm{\Delta }t-\left(\mathrm{\Delta }y-R^{(0)}\mathrm{\Delta }{x}_i\right)+\left({RR}^{{(0)}^t}-I\right)R^{(0)}\mathrm{\Delta }{x}_i\\ =\mathrm{\Delta }{Rx}_i^{(0)}+\mathrm{\Delta }t-\mathrm{\Delta }{\xi }_i^{(0)}+\mathrm{\Delta }{RR}^{(0)}\mathrm{\Delta }{x}_i\end{array}$$ (7)

where we have used (4) and have defined

$$\mathrm{\Delta }R={RR}^{{(0)}^t}-I$$ (8)

and

$$\mathrm{\Delta }{\xi }_i^{(0)}=\left(\mathrm{\Delta }{y}_i-R^{(0)}\mathrm{\Delta }{x}_i\right).$$ (9)

Using (7) in (3) gives us

$${\text{FRE}}^2=\sum _{i=1}^N{\left|W_i\left(\mathrm{\Delta }{Rx}_i^{(0)}+\mathrm{\Delta }t-\mathrm{\Delta }{\xi }_i^{(0)}+\mathrm{\Delta }{RR}^{(0)}\mathrm{\Delta }{x}_i\right)\right|}^2.$$ (10)

From assumption (a), we know that the components of $\mathrm{\Delta }{\xi }_i^{(0)}$ and Δx_i, will be small. If they were all zero, then (10) tells us that we could achieve a perfect minimum of zero for (3) by setting ΔR and Δt to zero. For finite but small $\mathrm{\Delta }{\xi }_i^{(0)}$ and Δx_i, we see from this same equation that, when FRE is minimized, the elements of both ΔR and Δt will be of first order in $\mathrm{\Delta }{\xi }_i^{(0)}$ and Δx_i. We note that the elements of ΔR^tΔR can be expected to be small relative to those of ΔR and that the elements of ΔRR⁽⁰⁾Δx_i will be small relative to those of $\mathrm{\Delta }{\xi }_i^{(0)}$, because they are all of second degree in the elements of $\mathrm{\Delta }{\xi }_i^{(0)}$ and Δx_i, which themselves can be expected to be small. Following Sibson, we now make the assumption that the $\mathrm{\Delta }{\xi }_i^{(0)}$ and Δx_i are small enough to render the elements of ΔR^tΔR negligible in comparison to the elements of ΔR and the elements of ΔRR⁽⁰⁾Δx_i negligible in comparison to the elements of $\mathrm{\Delta }{\xi }_i^{(0)}$. We note that

$$\begin{array}{l}\mathrm{\Delta }{R}^t\mathrm{\Delta }R={\left({RR}^{{(0)}^t}-I\right)}^t\left({RR}^{{(0)}^t}-I\right)\\ =I-R^{(0)}{R}^t-{RR}^{{(0)}^t}+I\\ =-(\mathrm{\Delta }{R}^t+\mathrm{\Delta }R)\end{array}$$ (11)

where we have used the orthogonality of rotation matrices to go from the first line to the second. From (11), we see that, if the elements of ΔR^tΔR are indeed negligible in comparison to the elements of ΔR, then ΔR^t + ΔR ≈ 0, which means that ΔR is antisymmetric, i.e., ΔR^t= −ΔR. Thus, the nonlinear restriction R^tR = I is replaced by a linear one.

This relaxed constraint is essential to the original approach of Sibson on the statistics of FRE [5], the approaches of the subsequent work on the statistics of TRE [6], [7], [9], and our current approach. However, we show in simulations below that our results hold to an excellent approximation even without linearization. The difference being that for the linearized equations we can prove that they hold for all configurations, all ${\mathrm{\sum }}_i^{(1)}$ and all ${\mathrm{\sum }}_i^{(2)}$, whereas for the nonlinear version, we can show agreement only for those cases that are simulated. Using our definitions of ΔR and Δt in (6) gives

$$\begin{array}{l}\mathbf{TRE}(r)=\left({RR}^{{(0)}^t}-I\right)R^{(0)}r+t-t^{(0)}\\ =\mathrm{\Delta }{RR}^{(0)}+\mathrm{\Delta }t\end{array}$$ (12)

where we have defined r⁽⁰⁾ = R⁽⁰⁾r (similarly to our definition above of $x_i^{(0)}$). We note finally, that, to first order ${\mathrm{\sum }}_i=R^{(0)}{\mathrm{\sum }}_i^{(1)}{R}^{{(0)}^t}+{\mathrm{\sum }}_i^{(2)}$.

C. Some Useful Results From Linear Algebra

The minimization of (10), subject to ΔR^t= −ΔR with ΔRR⁽⁰⁾Δx_i ignored in comparison to $\mathrm{\Delta }{\xi }_i^{(0)}$ is equivalent to finding the least-squares solution to the following over-determined set of 3N linear equations in the six unknowns, Δθ₁, Δθ₂, Δθ₃, Δt₁, Δt₂, Δt₃

$${\left(W_i\mathrm{\Delta }{Rx}_i^{(0)}\right)}_j+{(W_i\mathrm{\Delta }t)}_j={\left(W_i\mathrm{\Delta }{\xi }_i^{(0)}\right)}_j,i=1,2,\dots N,j=1,2,3,$$ (13)

where

$$\mathrm{\Delta }R=\left[\begin{array}{ccc}0& -\mathrm{\Delta }{\theta }_3& \mathrm{\Delta }{\theta }_2\\ \mathrm{\Delta }{\theta }_3& 0& -\mathrm{\Delta }{\theta }_1\\ -\mathrm{\Delta }{\theta }_2& \mathrm{\Delta }{\theta }_1& 0\end{array}\right]$$ (14)

and the subscript j enumerates the components of the three-dimensional vectors.

The meaning of ΔR can be understood by adding I to both sides of its definition in (8) and multiplying on the right by R⁽⁰⁾. The result, (I+ΔR)R⁽⁰⁾ = R shows that the rotation matrix that we seek by minimizing (3) is the equivalent to the true rotation followed by a “rotation” I+ΔR. Thus, I+ΔR approximates the rotation away from the truth caused by fiducial localization error. If localization error were zero, then ΔR would also equal zero. Our assumption that localization error is merely small results in the approximation, ΔR^t = −ΔR. The displacement Δr of a point r caused by that small rotation is Δr = (I+ΔR)r − r = ΔRr, which, because ΔR^t is equal to −ΔR, can be written in the form of the familiar cross product for small rotations, Δr = ΔRr = Δθ × r, where Δθ = (Δθ₁, Δθ₂, Δθ₃). This cross product produces the exact expression for Δr in the limit of small rotation angle $\mid \mathrm{\Delta }\theta \mid ={(\mathrm{\Delta }{\theta }_1^2+\mathrm{\Delta }{\theta }_2^2+\mathrm{\Delta }{\theta }_3^2)}^{1/2}$. Equation (14) can also be derived by representing the exact rotation I+ΔR in terms of Euler angles, expanding each sine and each cosine in that representation via a Taylor’s series in the angles Δθ₁, Δθ₂, and Δθ₃, and dropping all but zeroth- and first-order terms from those expansions. The first-order terms all equal one and give rise to the identity I; the first-order terms produce the expression given for ΔR in (14).

We now define the 3N×6 matrix C

$$C=\left[\begin{array}{cc}{W}_1{X}_1^{(0)}& W_1\\ W_2{X}_2^{(0)}& W_2\\ \dots & \dots \\ W_N{X}_N^{(0)}& W_N\end{array}\right]$$ (15)

where

$$X_i^{(0)}=\left[\begin{array}{ccc}0& x_{i3}^{(0)}& -x_{i2}^{(0)}\\ -x_{i3}^{(0)}& 0& x_{i1}^{(0)}\\ x_{i2}^{(0)}& -x_{i1}^{(0)}& 0\end{array}\right]$$ (16)

and $x_{ik}^{(0)}=\text{the}k\text{th}\text{component}\text{of}{x}_i^{(0)}$. By defining the 3N×1 vector e as follows:

$$e_{3(i-1)+j}={\left(W_i\mathrm{\Delta }{\xi }_i^{(0)}\right)}_j,i=1,\dots ,N,j=1,2,3$$ (17)

and using our definition of C, we can transform (13) into

$$Cq=e.$$ (18)

With (18), we have transformed the problem into a generic linear-algebra problem, and we need to establish some properties of the least-squares solution to that problem. We begin by considering the singular-value decomposition [15] of C

$$C=U\mathrm{\Lambda }{V}^t$$ (19)

where U is a 3N×3N orthogonal matrix, Λ is a 3N×6 diagonal matrix whose diagonal elements Λ_ii are the singular values of C, and V is a 6×6 orthogonal matrix³. We will require that the six singular values Λ_ii of C all be nonzero. This requirement is equivalent to the requirement that the columns of C be independent. We can prove that they are independent via proof by contradiction. Thus, we assume instead that the columns C of are linearly dependent, which means that for some set of six constants, a₁, a₂, …, a₆, ${\sum }_{i=1}^6{a}_i{C}_i=0$, where each C_i is a column of C. Because each column is of length 3N, this constraint is equivalent to 3N equations, which have the form

$$\begin{array}{c}{x}_{i2}^{(0)}{a}_3-x_{i3}^{(0)}{a}_2=a_4\\ x_{i3}^{(0)}{a}_1-x_{i1}^{(0)}{a}_3=a_5\\ x_{i1}^{(0)}{a}_2-x_{i2}^{(0)}{a}_1=a_6\end{array}\}\text{for}i=1,2,\dots ,N.$$ (20)

These 3N equations are in turn equivalent to the N vector equations $x_i^{(0)}\times a_{1,2,3}=a_{4,5,6}$, where a_α,β,γ is the 3×1 column vector whose elements are a_α, a_β, a_γ. In order for all N of these cross products to be equal to the same constant vector N, all points $x_i^{(0)}$ must be collinear. We note from Section III-A above that at least three of the points x_i must not be collinear and that rotating and translating these points to produce the points $x_i^{(0)}$ does not change the linearity of the points. Thus, our assumption that the columns of C are dependent has led to a contradiction. Therefore, the columns of C are in fact independent, and therefore the singular values of C are all nonzero.

The least-squares solution of (18) is given as follows [15],

$$q_{min}=C^{+}e$$ (21)

where

$$C^{+}=V{\mathrm{\Lambda }}^{+}{U}^t$$ (22)

and Λ⁺ is a 6×3N diagonal matrix for which ${\mathrm{\Lambda }}_{ii}^{+}={\mathrm{\Lambda }}_{ii}^{-1}$. We note that ${\mathrm{\Lambda }}_{ii}^{+}$ are well defined because, as we have shown above, the ${\mathrm{\Lambda }}_{ii}^{+}$ are nonzero. The elements of the 3N×1 vector

$$f_{min}=e-C{q}_{min}$$ (23)

are the residual errors in the solution and can be rewritten as follows:

$$f_{min}=\left(I-{\text{CC}}^{+}\right)e$$ (24)

where is the 3N×3N identity matrix. Using (19) and (22) in (24), we have

$$\begin{array}{l}{f}_{min}=(I-{\text{CC}}^{+})e\\ =(I-U\mathrm{\Lambda }{\mathrm{\Lambda }}^{+}{U}^t)e\\ =U(I-\mathrm{\Lambda }{\mathrm{\Lambda }}^{+})U^{t}e.\end{array}$$ (25)

For i, j = 1, …, 3N, we have ${(\mathrm{\Lambda }{\mathrm{\Lambda }}^{+})}_{ij}={\sum }_{k=1}^6{\mathrm{\Lambda }}_{ik}{\mathrm{\Lambda }}_{kj}^{+}={\sum }_{k=1}^6{\mathrm{\Lambda }}_{ik}{\mathrm{\Lambda }}_{kj}^{-1}$, from which we find that the first six diagonal elements of ΛΛ⁺ are equal to 1 and the last 3N − 6 are equal to 0. Furthermore, we see that the first six diagonal elements of I − ΛΛ⁺ are equal to 0 and the last 3N − 6 are equal to 1. Using these diagonal elements of I − ΛΛ⁺ in the last line of (25), and defining

$$\stackrel{\sim }{e}=U^{t}e$$ (26)

we find that

$${(f_{min})}_k=\sum _{j=1}^6{U}_{kj}·0·{\stackrel{\sim }{e}}_j+\sum _{j=7}^{3N}{U}_{kj}·1·{\stackrel{\sim }{e}}_j=\sum _{j=7}^{3N}{U}_{kj}{\stackrel{\sim }{e}}_j.$$ (27)

Thus we see that each element of f_min is a function of only the last 3N − 6 elements of ẽ.

D. FRE in Terms of ẽ

We now return to the registration problem. We note that the elements of f_min in (27) are the components of the individual fiducial registration error vectors, FRE_i, of those points. Thus, (f_min)_3(i−1)+j = FRE_ij for i = 1, …, N, j = 1, 2, 3. Therefore, each component of FRE_i for each fiducial point is a function of only the last 3N − 6 elements of ẽ.

E. TRE in Terms of ẽ

Our expression for TRE(r) in (12) can be transformed into a simple matrix-times-vector multiplication

$$\delta =Dq$$ (28)

by defining δ_j = TRE(r)_j, j = 1, 2, 3 and defining the 3×6 matrix

$$D=\left[\begin{array}{cccccc}0& r_3^{(0)}& -r_2^{(0)}& 1& 0& 0\\ -r_3^{(0)}& 0& r_1^{(0)}& 0& 1& 0\\ r_2^{(0)}& -r_1^{(0)}& 0& 0& 0& 1\end{array}\right]$$ (29)

where $r_k^{(0)}=\text{the}k\text{th}\text{component}\text{of}{r}^{(0)}$. In (28), we use the least-squares solution of (18), as given by (21), and the decomposition of as given by (22), to get

$${\delta }_{min}={Dq}_{min}=D{C}^{+}e=DV{\mathrm{\Lambda }}^{+}{U}^{t}e=DV{\mathrm{\Lambda }}^{+}\stackrel{\sim }{e}.$$ (30)

Thus,

$${({\delta }_{min})}_k=\sum _{j=1}^6\sum _{l=1}^{3N}{(DV)}_{kj}{\mathrm{\Lambda }}_{jl}^{+}{\stackrel{\sim }{e}}_l=\sum _{j=1}^6{(DV)}_{kj}{\mathrm{\Lambda }}_{jj}^{-1}{\stackrel{\sim }{e}}_j$$ (31)

where, in the second step, we have used the explicit form of Λ⁺ given just after (22). From (31) we see that each component of TRE(r) is a function of only the first 6 elements of ẽ.

F. General Formulation for the Covariances of FRE and TRE

Equation (31) can be employed to derive a general expression for Σ_FRE, the covariance of FRE, and Σ_FRE, the covariance of TRE. First, we define two 3N×3N block-diagonal matrices: a covariance matrix Σ for the entire set of FLEs and a weighting matrix W for the entire set of fiducial points. Each matrix is nonzero only within 3×3 blocks on the diagonal. Specifically, Σ_{3(i−1)+j,3(i−1)+j′} = (Σ_i)_jj′ and W_{3(i−1)+j,3(i−1)+j′} = (W_i)_jj′, for i = 1 … N, j = 1, 2, 3, j′ = 1, 2, 3, and all other elements of each matrix equal zero. With these definitions it can be seen from the definition e of given by (17) that

$$\langle {ee}^t\rangle =W\mathrm{\sum }{W}^t.$$ (32)

Our expression for Σ_FRE can be gotten by noting that ${({\mathrm{\sum }}_{\text{FRE}})}_{kl}=\langle {(f_{min})}_k{(f_{min}^t)}_l\rangle$ and then using (27), followed by (26) and (32), to get

$$\begin{array}{l}{({\mathrm{\sum }}_{\text{FRE}})}_{kl}=\sum _{j,j^{\prime }=7}^{3N}{U}_{kj}{U}_{l{j}^{\prime }}\langle {\stackrel{\sim }{e}}_j{\stackrel{\sim }{e}}_{j^{\prime }}\rangle \\ =\sum _{j,j^{\prime }=7}^{3N}{U}_{kj}{U}_{l{j}^{\prime }}{(U^{t}W\mathrm{\sum }{W}^{t}U)}_{j{j}^{\prime }}.\end{array}$$ (33)

The summation over three diagonal elements corresponding to the same marker provides an expression for an individual weighted FRE of that marker

$$\begin{array}{l}\langle {\text{FRE}}_i^2\rangle =\sum _{k=3i-2}^{3i}\sum _{j,j^{\prime }=7}^{3N}{U}_{kj}{U}_{k{j}^{\prime }}\langle {\stackrel{\sim }{e}}_j{\stackrel{\sim }{e}}_{j^{\prime }}\rangle \\ =\sum _{k=3i-2}^{3i}\sum _{j,j^{\prime }=7}^{3N}{U}_{kj}{U}_{k{j}^{\prime }}{(U^{t}W\mathrm{\sum }{W}^{t}U)}_{j{j}^{\prime }}.\end{array}$$ (34)

The trace of Σ_FRE provides a general expression for 〈FRE²〉

$$\begin{array}{l}\langle {\text{FRE}}^2\rangle =\sum _{k=1}^{3N}{({\mathrm{\sum }}_{\text{FRE}})}_{kk}\\ =\sum _{k=1}^{3N}\sum _{j,j^{\prime }=7}^{3N}{U}_{kj}{U}_{k{j}^{\prime }}{(U^{t}W\mathrm{\sum }{W}^{t}U)}_{j{j}^{\prime }}\\ =\sum _{j=7}^{3N}{(U^{t}W\mathrm{\sum }{W}^{t}U)}_{jj}.\end{array}$$ (35)

The expressions in (33) through (35) give statistics for the weighted FRE. Statistics for unweighted FRE (but with weighting used in the registration step), which we designate by using lower case, fre, are given by replacing U_jk and U_kj′ by (W⁻¹U)_kj and (W⁻¹U)_kj′ in each of these equations, resulting in

$${({\mathrm{\sum }}_{\text{fre}})}_{kl}=\sum _{j,j^{\prime }=7}^{3N}{(W^{-1}U)}_{kj}{(W^{-1}U)}_{l{j}^{\prime }}{(U^{t}W\mathrm{\sum }{W}^{t}U)}_{j{j}^{\prime }}$$ (36)

$$\langle {\text{fre}}_i^2\rangle =\sum _{k=3i-2}^{3i}\sum _{j,j^{\prime }=7}^{3N}{(W^{-1}U)}_{kj}{(W^{-1}U)}_{k{j}^{\prime }}{(U^{t}W\mathrm{\sum }{W}^{t}U)}_{j{j}^{\prime }}$$ (37)

and

$$\langle {\text{fre}}^2\rangle =\sum _{j,j^{\prime }=7}^{3N}{(U^t{W}^{-2}U)}_{j{j}^{\prime }}{(U^{t}W\mathrm{\sum }{W}^{t}U)}_{j{j}^{\prime }}.$$ (38)

For isotropic weighting, i.e., W_i = w_iI, it can with some manipulation be seen that $\langle {\text{FRE}}_i^2\rangle =w_i\langle {\text{fre}}_i^2\rangle$.

Our expression for Σ_TRE can be gotten by remembering that in TRE(r)_j = δ_j (31). Therefore,

$$\begin{array}{l}{({\mathrm{\sum }}_{\text{TRE}})}_{kl}=\langle {({\delta }_{min})}_k{({\delta }_{min})}_l\rangle \\ =\sum _{j,j^{\prime }=1}^6{(DV)}_{kj}{(DV)}_{l{j}^{\prime }}\frac{\langle {\stackrel{\sim }{e}}_j{\stackrel{\sim }{e}}_{j^{\prime }}\rangle }{{\mathrm{\Lambda }}_{jj}{\mathrm{\Lambda }}_{j^{\prime }{j}^{\prime }}}.\end{array}$$ (39)

By applying (26) and (32) to 〈ẽ_jẽ_j′〉, we achieve the following result:

$${({\mathrm{\sum }}_{\text{TRE}})}_{kl}=\sum _{j,j^{\prime }=1}^6{(DV)}_{kj}{(DV)}_{l{j}^{\prime }}\frac{{(U^{t}W\mathrm{\sum }{W}^{t}U)}_{j{j}^{\prime }}}{{\mathrm{\Lambda }}_{jj}{\mathrm{\Lambda }}_{j^{\prime }{j}^{\prime }}}.$$ (40)

The trace of Σ_TRE provides a general expression for 〈TRE²〉

$$\begin{array}{l}\langle {\text{TRE}}^2\rangle =\sum _{k=1}^3{({\mathrm{\sum }}_{\text{TRE}})}_{kk}\\ =\sum _{k=1}^3\sum _{j,j^{\prime }=1}^6{(DV)}_{kj}{(DV)}_{k{j}^{\prime }}\times \frac{{(U^{t}W\mathrm{\sum }{W}^{t}U)}_{j{j}^{\prime }}}{{\mathrm{\Lambda }}_{jj}{\mathrm{\Lambda }}_{j^{\prime }{j}^{\prime }}}.\end{array}$$ (41)

It should be noted that (33) through (41) are completely general. Thus they are appropriate both for general fiducial localization error (i.e., possibly inhomogeneous and possibly anisotropic) and for general weighting (i.e., possibly not ideal). We have included in Fig. 4 in the Appendix an implementation of (33), (35), (40), and (41) written in Matlab (MathWorks, Inc., Natick, MA). This function is likewise completely general. While these equations have all been derived specifically for three-dimensional space, they all hold for the 2-D case as well with only minor changes to accommodate the reduced dimensionality. The details are given in Appendix C of the Appendix.

Fig. 4.

Computer code to implement the derived formulas. The code is a function written in Matlab (The Mathworks, Natick, MA). Its input and output parameters are described in comments (lines beginning with a percent sign) and in the text.

G. Statistical Independence of FRE and TRE for Ideal Weighting

In Fig. 1, we show examples for which FRE is zero and TRE is nonzero. It can easily be seen from (5) that the number of such examples is infinite. Indeed, whenever there exists a rigid transformation R, t for which Rx_i + t = y_i + Δξ_i for all i, then FRE is zero, but unless all the Δξ_i are zero, TRE will be nonzero. The simplest example is for the localization errors in a given space to be equivalent to a global translation, i.e., all the Δx_i are equal to the same nonzero vector v_x, and all the Δy_i are equal to some other nonzero vector v_y ≠ v_x. As a result, each Δξ_i = v_y − v_x, the rigid transformation that minimizes FRE² is, R = R⁽⁰⁾, t = t⁽⁰⁾ + v_y − v_x, and TRE(r) = v_y − v_x ≠ 0. Substituting these values into (5) reveals that each of the terms in the summation is zero. Thus, each FRE_i = 0. There is likewise an infinity of examples in which TRE is zero and FRE is nonzero. These examples occur when no rigid transformation can reduce the effect of the localization errors, and the transformation that minimizes (5) is the identity. One such example is also shown in Fig. 1. These examples suggest that FRE may not be a good predictor of TRE, but they provide little insight into their statistical relationship. In this section we examine the statistical relationship between FRE and TRE for our model of independent, normally distributed localization errors when an important weighting scheme—“ideal weighting”—is employed, and we show that for this weighting scheme FRE and TRE are statistically independent.

Ideal weighting is important in the rigid point registration problem because it maximizes the probability that the resulting transformation is the true one. We derive ideal weighting in Appendix I-A of the Appendix and show that it has the form $W_i=w\times {\mathrm{\sum }}_i^{-1/2}=w\times {\left(R{\mathrm{\sum }}_i^{(1)}{R}^t+{\mathrm{\sum }}_i^{(2)}\right)}^{-1/2}$, where w is a constant, which for normalized weighting is equal to $3^{1/2}{\left({\mathrm{\sum }}_1^N\text{trace}\left({\mathrm{\sum }}_i^{-1}\right)\right)}^{-1/2}$. Ideal weighting is not new. It was introduced into point registration as early as 1998 by Ohta and Kanatani [16], and it was employed by West et al. in 2001 [17] and Moghari et al.. in 2009 [11], [19]. In both of these 2009 papers a first-order registration equation equivalent to (18) was derived for the special case in which ideal weighting is employed and ${\mathrm{\sum }}_i^1=0$⁴. As mentioned at the end of Section III-B, to first order R can be replaced by R⁽⁰⁾ in the expression for Σ_i. This approximation is adequate for our purposes, and with it we can see that the R dependence of ideal weighting does not affect the first-order character of (13). Using this weighting in (32) gives us

$$\langle {ee}^t\rangle =W\mathrm{\sum }{W}^t=w^2\times {\mathrm{\sum }}^{-1/2}\mathrm{\sum }{\mathrm{\sum }}^{-1/2}=w^{2}I.$$ (42)

Since 〈ee^t〉 is diagonal, the elements e_i are uncorrelated; since they are uncorrelated and also normally distributed, they are statistically independent [2], [18]. Because the diagonal elements equal w², the variance of each e_i is w². As shown in Appendix I-B, since U is orthogonal, the elements of ẽ are also independent and normally distributed with variance equal to w². In Section III-D, we found that each component of FRE_i for each fiducial point, which is also an element of f_min, is a function of only the last 3N − 6 elements of ẽ, while in Section III-E we found that each component of TRE(r), which is also a component of δ_min, is a function of only the first six elements of ẽ. Since the elements of ẽ are independent of each other, any functions of nonoverlapping subsets of them are independent each other as well. It is important to note that this conclusion depends crucially on the fact that all 3N of the elements of ẽ are mutually independent. That independence is a consequence of ideal weighting.

Therefore, for the case of ideal weighting, every component of FRE_i of every one of the N fiducial points is statistically independent of any component of the vector TRE(r) at any point r. Thus fluctuations in TRE(r) are, in our first-order approximation, independent of fluctuations of any and all functions of the goodness of fit! We note that the overall fiducial registration error, FRE, from (3), is given in the linearized problem by (10) and can be expressed in terms of f_min as $\text{FRE}={(f_{min}^t{f}_{min})}^{1/2}$ and that the length of the vector TRE(r) can be expressed in terms of δ_min as $\mathbf{TRE}(r)={({\delta }_{min}^t{\delta }_{min})}^{1/2}$. Since the elements of f_min are statistically independent of those of δ_min, any function of only f_min is statistically independent of any function of only δ_min. As primary examples, FRE is statistically independent of |TRE(r)|. Since they are independent, they are also uncorrelated. We let CC (FRE, TRE) be the correlation coefficient of FRE and |TRE(r)|

$$\text{CC}(\text{FRE},\text{TRE})=\frac{\langle (\text{FRE}-{\mu }_{\text{FRE}})(\text{TRE}-{\mu }_{\text{TRE}})\rangle }{({\sigma }_{\text{FRE}}{\sigma }_{\text{TRE}})}$$ (43)

where we have abbreviated |TRE(r)| as TRE, and are letting μ and σ denote means and standard deviations. It easy to see that, to first order in FLE, CC (FRE, TRE) = 0, meaning that there is to first order no correlation between FRE and TRE.

H. Two-Dimensional Space

The results of this section hold not only for 3-D space, but for 2-D space as well. The details are provided in Appendix I-C of the Appendix along with the 2-D forms of (33) through (41), but these equations can be transliterated to two dimensions merely by making the following changes to the summation limits:3N → 2N, 7 → 4, 3i → 2i, 3i − 2 → 2i − 1, and 6 → 3.

I. Comparison With Previously Published Derivations

We compare our formulations with five previous derivations. These derivations, which are spread among many publications with differing notations, are, unlike our general derivation, limited in every case to uniform weighting (i.e., no weighting) or to ideal weighting. In our validation section below, we compare our formulas with these other authors’ formulations on specific cases and find agreement in every case.

The first result is an expression for the probability density of FRE² when ideal weighting is employed. We note that ${\text{FRE}}^2=f_{min}^t{f}_{min}={\sum }_{k=1}^{3N}{(f_{min})}_k^2$, which by (27) equals ${\sum }_{j=7}^{3N}{\sum }_{l=7}^{3N}{\stackrel{\sim }{e}}_j{\stackrel{\sim }{e}}_l{\sum }_{k=1}^{3N}{U}_{kl}{U}_{kj}$, and since U is orthogonal, we have ${\text{FRE}}^2={\sum }_{j=7}^{3N}{\stackrel{\sim }{e}}_j^2$. As noted in Section III-G, when ideal weighting is employed, the ẽ_j become statistically independent and normally distributed with equal variances (= w²). Therefore, FRE² is chi-square distributed with 3N − 6 degrees-of-freedom. The probability density of such a function is well known [22]

$$p\left({\text{FRE}}^2\right)=\frac{{\text{FRE}}^{(3N-8)}{e}^{-\left({\text{FRE}}^2\right)/2}}{w^2{2}^{(3/2N-3)}\mathrm{\Gamma }\left(\frac{3}{2}N-3\right)}$$ (44)

where Γ denotes the Gamma function⁵. This probability density is identical to that derived by Sibson for the case of isotropic, homogeneous FLE with no weighting [5]. Here we have not only re-derived a thirty-year-old result but also shown that it applies to a more general case, namely inhomogeneous, anisotropic FLE with ideal weighting. It differs from the distribution for ideal weighting published recently by Moghari [19] for fre (instead of FRE). Also, for ideal weighting, since the ẽ_j are independent and normally distributed with variances equal to w², we have 〈FRE²〉 = (3N − 6)w², and for normalized weighting

$$\langle {\text{FRE}}^2\rangle =\frac{3(3N-6)}{{\displaystyle \sum _1^N}\text{trace}\left({\mathrm{\sum }}_i^{-1}\right)}.$$ (45)

For the special case of homogeneous FLE (45) reduces to $\langle {\text{FRE}}^2\rangle =3(3N-6)/{\sum }_k^3{\sigma }_k^2$, where ${\sigma }_k^2$ is the variance of FLE along one of its principal axes, and for the case of homogenous, isotropic FLE, which is the case originally treated by Sibson, it reduces exactly to (1).

The second result is an expression for 〈FRE²〉 for ideal weighting, first derived for the case of isotropic, homogeneous FLE in 1998 [6] and given above by (2) and derived for general FLE in 2009 [11]. With ideal weighting we find from (32) and (42) that (U^tWΣW^tU)_jj′ = δ_ij′ (i.e., the Kronecker delta). Using this result in (41) yields

$$\langle {\text{TRE}}^2\rangle =\sum _{k,j=1}^{3,6}\frac{{(DV)}_{kj}^2}{({\mathrm{\Lambda }}_{jj}^2)}.$$ (46)

Despite the considerable detail in our derivations of this result, its calculation is quite simple, requiring evaluation only of (16), (15), (19), (29), and (46) in that order.

The third result is an expression for 〈TRE²〉 when FLE is inhomogeneous and anisotropic but no weighting is employed, first derived in 2009 by Wiles first for the homogeneous case [9] and then for the general case [23]. Our expression for this case is gotten simply by removing W from the expression in (41) and noting that, in the construction of the block-diagonal covariance matrix Σ, the nonzero blocks Σ, are all equal.

The fourth result is the decomposition of TRE into three statistically independent orthogonal normally distributed components when FLE is homogeneous and isotropic and no weighting is employed, which was first accomplished in 2001 [7]. We begin by noting that, for this case, having no weighting is equivalent to employing ideal weighting with w = 1. We then have (U′WΣW′U)_jj′ = δ_ij′, as in the second result above. Using this result in (39), we find that ${({\mathrm{\sum }}_{\text{TRE}})}_{kl}={\sum }_{j=1}^6{(DV)}_{kj}{(DV)}_{l_j}/{\mathrm{\Lambda }}_{jj}^2$. Performing an eigen decomposition yields ${\mathrm{\sum }}_{\text{TRE}}=V_{\text{TRE}}{\mathrm{\Lambda }}^{(\text{TRE})}{V}_{\text{TRE}}^{\prime }$. Since Σ_TRE is symmetric, V_TRE is orthogonal. If we define $\eta =V_{\delta }^{\prime }{\delta }_{min}$, then, since V_TRE is orthogonal and the elements of ẽ are independent and normally distributed, the three components, η_k, are uncorrelated, normally distributed, orthogonal components of TRE with variances equal to η_k.

The fifth result is the set of expressions in (36) through (38) for the statistics of the unweighted individual fiducial registration error with ideal weighting used the registration step when FLE is homogeneous or isotropic. Analytical expressions for these two cases were first derived in 2009 [19]. They reduce in the homogeneous and isotropic case to expressions first derived in 2008 [10].

IV. Validation

Our theory has three major results, which can be summarized as follows: For arbitrary weighting and arbitrary FLE, (a) (33) gives the covariance of FRE, (b) (40) gives the covariance of TRE, (c) FRE and TRE are statistically independent. Our other results are derived from (a) and (b). We tested our results as follows (1) We compared (33), (37), (41) and (46) to previously published analytic expressions for special cases. (2) We compared (33) and (39) to true values obtained by means of simulations, and we measured their cross correlation and dependence. All calculations were performed using Matlab 2010b (Mathworks, Natick, MA) on a Dell Latitude D830 with an Intel Centrino Duocore 2.2 GHz CPU with 2 GB RAM.

A. Comparisons to True Values via Simulations

For each simulation experiment, the following was performed: Randomly select a set S(N) of N unperturbed fiducial positions x_i inside a 200 mm cube and one random target position r inside a 400 mm cube (the cubes share a common corner). Then repeat the following 15 times.

1. For each x_i, define a covariance FLE matrix ${\mathrm{\sum }}_i^{(1)}=V_i^{(1)}{\mathrm{\Lambda }}_i^{(1)}{\left(V_i^{(1)}\right)}^t$, where the columns of $V_i^{(1)}$ are the principal axes of FLE and the diagonal elements ${\left({\mathrm{\Lambda }}_i^{(1)}\right)}_{jj}={\left({\sigma }_i^{(1)}\right)}_j^2$the variances of the independent components of FLE.

2. Construct a random rotation R⁽⁰⁾ and a random translation t⁽⁰⁾ and apply them to the x_i to produce N corresponding unperturbed positions y_i [see (4)].

3. Generate a covariance FLE matrix ${\mathrm{\sum }}_i^{(2)}$ for each y_i in a similar manner to that used to define ${\mathrm{\sum }}_i^{(1)}$.

4. Generate a weighting matrix W_i for each point.

5. Repeat the following steps 10 000 times.

   1. Perturb each fiducial position in each space to produce x_i + Δx and y_i + Δy according to ${\mathrm{\sum }}_i^{(1)}$ and ${\mathrm{\sum }}_i^{(2)}$, respectively, with random, normally distributed, zero-mean components.

   2. Employ a registration algorithm to find R and t that minimize the exact registration formula of (3).

   3. Calculate TRE(r) and FRE.

6. Calculate CC(FRE, TRE) for the 10 000 registrations of Step 5.

7. Perform the chi-square test described in Appendix I-D of the Appendix to detect dependence between FRE and TRE for the 10 000 registrations of Step 5.

8. Compute rms(TRE) and rms(FRE) for the 10 000 registrations of Step 5.

9. Calculate rms(TRE) = 〈TRE²〉^1/2 and rms(FRE) = 〈FRE²〉^1/2 our formulas.

10. Calculate CC between rms(TRE) from Steps 8 and 9; calculate CC between rms(FRE) from Steps 8 and 9.

The registration algorithm employed to accomplish Step 5b, depends on the weighting being used. For uniform weighting, the method of singular-value decomposition was employed (e.g., [20, Algorithm 8.1]). For ideal weighting, the algorithm of [21] was employed, except that in Step 1 of that algorithm, $W_i=w\times {\left(R{\mathrm{\sum }}_i^{(1)}{R}^t+{\mathrm{\sum }}_i^{(2)}\right)}^{-1/2}=\langle {\text{fre}}_i^2\rangle$, as given in Section III-G. This amendment to the algorithm is necessary for ideal weighting when FLE is anisotropic and/or inhomogeneous.

We employed these simulation experiments to determine the accuracy of 1) our expressions for TRE and FRE and 2) our claims that TRE and FRE are statistically independent and hence uncorrelated. As pointed out in [2], a failure to detect dependence does not guarantee that correlation is zero. The more specific correlation test may succeed where the dependence test fails, so we apply separate tests for correlation and dependence—the t-test to detect correlation and the chi-square test based on contingency tables to detect dependence [22]. The latter test is described Appendix I-D of the Appendix. For all tests we chose p = 0.05 with Bonferroni correction applied where appropriate. These tests were also used in [2].

V. Results

A. Comparison to Previously Published Expressions

We compared (33), (37), (41), and (46) with previously published and validated analytic expressions for the first three cases and the fifth case in Section III-A. Regarding (33), as pointed out in Section III-A, the simplification of that equation produced by the assumption of isotropy and homogeneity for FLE yields (45), which agrees exactly with the formula for FRE² derived by Sibson that case. We compared the outputs of (41) to the formulas for V_i = 〈TRE²〉 published by Moghari [11] and Wiles [9] for a large set of inputs. Similarly we compared (37) to the formula for $V_i=\langle {\text{fre}}_i^2\rangle$ published by Moghari [19]. For each comparison, we repeated the following 1000 times: We generated sets S(N) of random fiducials and a random target and in the manner described above for the simulations, with N = 3, 4, 5,…, 10, 20, 30 and 40 fiducials. We generated a two-space covariance Σ_i in the same manner as that used in the simulations to generate ${\mathrm{\sum }}_i^{(1)}$, based on V_i and (σ_i)_j. We chose random orientations for each set of principle axes and chose random values of (σ_i)_j. We compared (46), with the formulation of Moghari, who provided an analytic formula for the case of isotropic, inhomogeneous FLE with ideal weighting [11], and we compared (41) with W set to the identity (i.e., no weighting) to the formula given by Wiles’s for the case of anisotropic, homogeneous FLE with no weighting [9]. We compared (37) to Moghari’s formula for the case of isotropic inhomogeneous FLE with ideal waiting [17]. In every case, our outputs agreed with those of these previously published formulas (maximum difference = 1.2 × 10⁻¹⁰). In summary, our new general formulas agree with existing formulas, each of which is limited to a special case.

B. Comparison With Simulations

The important new feature that our theory supports is arbitrary weighting for arbitrary FLE. The sets of possible weightings and FLEs are each infinite, but we focused on two types of weighting—ideal weighting and uniform weighting, which is equivalent to no weighting—and on two sizes of FLE—small, which we defined as rms(FLE) < 1 mm, and large. For the latter case we used rms(FLE) = 2, 3, 4, 5, 6, 7, 8, 9, 10, 20, 30, 40, 50, 60, and 70 mm. Our motivation for the small-versus-large-FLE dichotomy is to explore the limitations of our linear approximation, which is strictly correct only in the limit of small FLE. For small FLE, we tested with N = 3, 4, 5, 6, 7, 8, 9, 10, 20, 30, and 40 fiducials. For the large FLE values, we limited our testing to four fiducials in order to control the requisite simulation time, which for each value of N requires 24 h for 15 values of rms(FLE). For the case of no weighting, we investigated only the case of small FLE, because we found correlation without moving above 1 mm.

Utilizing the simulation scheme above, in every case, we found the values calculated in Steps (8) and (9) to be statistically equivalent (no significant difference via paired t-test at p < 0.05). The maximum absolute percentage differences were less than 1.5% for FLE in the range from 1 to 10 mm (n = 555) and were less than 4.1% for FLE in the range from 1 to 50 mm (n = 120). For Step 10, in which we calculated the CC between the values of rms(TRE) of Steps 8 and 9, and the CC between the values of rms(FRE) calculated in Steps 8 and 9, we found in both cases that CC was well above 99.9%. The minimal lower bound of 95% confidence was 99.99%. Thus, our formulas for both FRE and TRE agree with simulation and show only a slight degradation in accuracy even when FLE is far larger than any value that would be tolerated in surgical guidance (50 mm is equal to one-fourth of the side of the 200 mm cube within which the fiducials were randomly placed for this simulation).

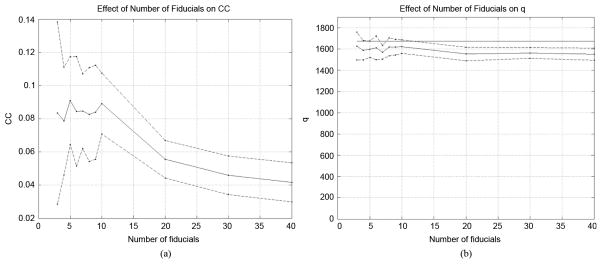
Figs. 2 and 3 summarize the results of our investigation into the correlation and dependence of FRE and TRE. As predicted by our theory, neither correlation nor dependence is detectable when ideal weighting is employed, and FLE is less than 1 mm [Fig. 2(a)]. For FLE > 20 mm, correlation is statistically significant but remains negligible (CC < 0.1) even for FLE = 70 mm [Fig. 2(b)]. For uniform weighting (i.e., no weighting) a very small correlation is observed, CC ≤ 0.1 that decreases with increasing N [Fig. 3(a)]. This correlation is statistically significant for all values of N, showing that, while FRE has some predictive power when higher order terms are included, that power is negligible. The dependence that this tiny correlation implies was undetectable for all but a very few cases. Detection is achieved when the chi-square statistic q (Appendix I-D of the Appendix) rises above a critical value shown by the horizontal line in Fig. 3(b). Such values were observed very rarely, as can be seen by the sub-critical means and, for N ≥ 20, the sub-critical values of mean + standard deviation.

Fig. 2.

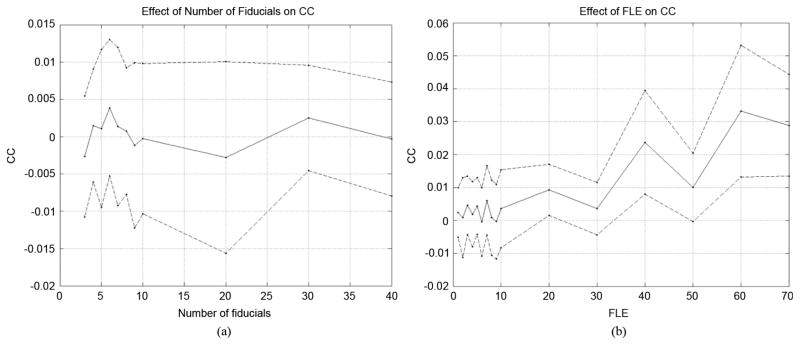
FRE-TRE correlation coefficient CC for ideal weighting (a) FLE < 1 mm with varying number of fiducials (b) Varying FLE with four fiducials. In each case, the solid line is the mean of 15 sets of 10,000 registrations for randomly selected fiducial and target positions (see text). The dashed lines are mean ± one standard deviation. Correlation is insignificant at p < 0.05 for all of (a) and for FLE < 10 mm in (b). Statistically significant but negligible (<0.1) correlation occurs for FLE ≥ 20 mm, showing that, while FRE has some predictive power when higher order terms are included, the power is negligible.

Fig. 3.

FRE-TRE statistics for FRE < 1 mm when uniform weighting (i.e., no weighting) is employed (a) Correlation coefficient CC versus number of fiducials. A statistically significant but negligible (<0.1), correlation is apparent that decreases with increasing number of fiducials (b) The chi-square statistic q for dependence versus number of fiducials. The dashed lines are mean ± one standard deviation. The horizontal solid line in (b) is the critical level above which values of q indicate dependence. The slight dependence implied by the small correlation in (a) is not detected by q, whose mean remains below the critical level.

Finally, we repeated our experiments with targets positions chosen to be equal to fiducial positions in order to determine whether some dependence between TRE and FRE might appear in the special case in which a target is close to a fiducial. No such correlation is possible according to our theoretical development, but we explored this case to eliminate the possibility that appreciable second-order dependence might appear. The results were the same as for the randomly chosen target positions—no detectable dependence and no significant correlation.

VI. Discussion

We have generalized a method of first-order analysis of the point-registration problem introduced in 2009 [2] so that it accommodates inhomogeneous and anisotropic FLE with arbitrary weighting. With this generalization we are able to provide first-order expressions for the covariance matrices of FRE and TRE—(33) and (40)—an expression for individual FRE—(34)—and expressions for 〈FRE²〉 and 〈TRE²〉—(35) and (41). As a result, we have unified the theory of first-order FRE and TRE statistics, which has heretofore been solved piecemeal only for special cases, each of which involved a separate formulation [6], [7], [9], [11], [19]. We have included in Appendix I-E of the Appendix an implementation of (33), (35), (40), and (41) in Matlab. With this implementation, we have reduced to 25 lines of Matlab not only all the many special cases of weightings and FLE anisotropies heretofore spread over many pages of many papers with different notations but also all other possible combinations of weightings, inhomogeneities, and anisotropies.

In addition, by means of our new method we are able to generalize the major result of [2]: namely, that, to first order, FRE and TRE are independent when FLE is homogeneous and isotropic. Our generalization reveals that, in addition, if ideal weighting is employed, FRE and TRE are independent to first order when FLE is inhomogeneous and/or anisotropic. Ideal weighting, which we define in Section III-G, is not a new concept. It was introduced to point registration by Ohta and Kanatani in 1998 [16] and used by West et al.. in 2001 [17] and by Moghari et al.. in 2009 [11], [19] as well, but the proof that it produces independence between FRE and TRE is new.

We note that this independence in no way detracts from the importance of (1) and (2), from the generalizations of these expressions provided in the excellent work by Wiles [9], [23], Balachandran [10], and Moghari [11], [19], and further generalizations given in (33) through (38), (40) and (41), each of which relates one expectation value to another. Equation (1) and Wiles’s generalization of that relationship [23] can be used to estimate the FLE covariance from measurements of FRE obtained from repeated registrations based on independent fiducial localizations. Based on this estimate, (2) or one of its generalizations can then be used to estimate an expectation value for TRE for a given fiducial configuration and target position. What we have shown is that the value of FRE observed for a given registration is unreliable as means to estimate the deviation of TRE from its expected value for that same registration.

We have compared our results to previously published formulas for FRE and TRE and to our own simulations to validate our new formulation. While there is an infinite variety of FLE patterns and weighting schemes available, we focused on inhomogeneous and anisotropic FLE with both ideal weighting and uniform weighting. We generated random fiducial and target positions and used both small FLE—rms(FLE) < 1 mm, and large FLE—up to 70 mm. We found excellent agreement in all cases. We also used simulations to evaluate correlation and dependence between FRE and TRE when the first-order approximation is not made. We found, in agreement with our theoretical results, that correlation and dependence approach zero for both weighting schemes as FLE approaches zero, for every case tested. We found for very large FLE that, while there is clearly a statistically significant correlation at higher order, that correlation is so small as to have negligible value as a predictor of TRE.

Our experiments on uniform weighting explain why neither Steinmeier nor Woerdeman, both of whom experimented with systems that apply this weighting scheme, were able to detect appreciable correlation between FRE and TRE, and it provides further support for the argument advanced in [2] that estimates of fluctuations of registration accuracy, i.e., TRE, based on the goodness of fit of the fiducials, e.g., FRE, are unreliable.

VII. Conclusion

By means of a new unified approach to the first-order analysis of the point registration problem, we are able to provide general expressions for the covariances of fiducial registration error and of target registration error. These two expressions and all the other expressions that we derived from them are appropriate for any set of fiducial localization error patterns, whether inhomogeneous or not and whether anisotropic or not. Furthermore, they are appropriate for any arbitrary set of weightings in the point registration problem, including ideal weighting and uniform weighting. Furthermore, this approach allows us to show that, for ideal weighting, FRE and TRE are to first order neither correlated nor dependent. We have verified these results by means of comparison to previous derivations and to simulations. Finally, by means of simulation we have shown that, for all cases examined, correlation between FRE and TRE is also negligible for uniform weighting even for the exact case. These results reinforce the message delivered in [2] that for ideal weighting and uniform weighting, the latter of which is used in commercial guidance systems, fluctuations of measures of the goodness of fit of the fiducials, e.g., fiducial registration error, have no statistical relationship, or at most a negligible relationship, to fluctuations of individual measures of registration accuracy, i.e., target registration error. Therefore, as estimators of registration accuracy, they are unreliable and should approach with extreme caution both by the purveyors of guidance systems and by the practitioners who use them.

Appendix

Derivation of Ideal Weighting

The standard approach to finding the rigid transformation by minimizing (3) is based on maximum likelihood. Maximum likelihood was introduced into the point registration problem by Ohta and Kanatani in 1998 [16] and used by West et al. in 2001 [17] and by Moghari in 2009 [11], [19]. It has also been invoked for intensity-based registration methods [23]. The goal in point registration is to find the transformation that is most likely to be correct given the measured positions of the fiducial points in the two spaces. That goal can be reached only if the matrices W_i in that equation provide “ideal” weighting. In this section we derive the ideal weighting matrices and show that they provide the maximum-likelihood solution. We begin with the given sets { $x_i^{\prime }$} and { $u_i^{\prime }$}, i = 1, …, N of measured vector positions in two spaces, where $x_i^{\prime }=x_i+\mathrm{\Delta }{x}_i$ and $y_i^{\prime }=y_i+\mathrm{\Delta }{y}_i$, x_i and y_i are the true but unknown positions of corresponding points in the respective spaces, and Δx_i and Δy_i are their unknown localization errors. We wish to find the most likely rigid transformation, but, as we do, we will also find the most likely true positions. Specifically, we wish to find the rotation matrix and translation vector R,t and the {x_i} and{y_i} that together maximize the conditional probability density $p(R,t,\{y_i\}\mid \{x_i^{\prime }\},\{y_i^{\prime }\})$. The set of true points {x_i} is missing from the variables in this density because they are completely determined by R,t, and the {y_i}, since by definition x_i = R^ty_i − R^tt.

Thus, we wish to maximize $p(R,t,\{y_i\}\mid \{x_i^{\prime }\},\{y_i^{\prime }\})$ with respect to R,t, and {y_i} for fixed { $x_i^{\prime }$} and { $y_i^{\prime }$}. From Bayes’ law, we have that

$$p(R,t,\{y_i\}\mid \{x_i^{\prime }\},\{y_i^{\prime }\})=p(\{x_i^{\prime }\},\{y_i^{\prime }\}\mid R,t,\{y_i\})\frac{p(R,t\{y_i\})}{p(\{x_i^{\prime }\},\{y_i^{\prime }\})}$$ (47)

and, absent prior knowledge of $p(\{x_i^{\prime }\},\{y_i^{\prime }\})$, we neglect its dependence on R,t, and {y_i}. Furthermore, $p(\{x_i^{\prime }\},\{y_i^{\prime }\})$ is fixed because both { $x_i^{\prime }$} and { $y_i^{\prime }$} are fixed. Therefore, we may achieve our goal by maximizing the conditional probability $p(\{x_i^{\prime }\},\{y_i^{\prime }\}\mid R,t,\{y_i\})$ with respect to R,t, and {y_i}.

We now assume that all localization errors are independent and that their components have zero mean and are normally distributed about their principal axes. With this assumption we have

$$p(\{x_i^{\prime }\},\{y_i^{\prime }\}\mid R,t,\{y_i\})=cexp\left(-\sum _{i=1}^N(\mathrm{\Delta }{x}_i^t{\mathrm{\sum }}_{xi}^{-1}\mathrm{\Delta }{x}_i+\mathrm{\Delta }{y}_i^t{\mathrm{\sum }}_{yi}^{-1}\mathrm{\Delta }{y}_i)\right)$$ (48)

where Σ_xi and Σ_yi are respectively the covariances of Δx_i and Δy_i. It can be seen from our definitions above and from minor manipulation that $\mathrm{\Delta }{x}_i^t{\mathrm{\sum }}_{xi}^{-1}\mathrm{\Delta }{x}_i$ equals ${({Rx}_i^{\prime }+t-y_i)}^t{S}_{xi}({Rx}_i^{\prime }+t-y_i)$, where $S_{xi}=R{\mathrm{\sum }}_{xi}^{-1}{R}^t$, and that $\mathrm{\Delta }{y}_i^t{\mathrm{\sum }}_{yi}^{-1}\mathrm{\Delta }{y}_i$ equals ${(y_i^{\prime }-y_i)}^t{S}_{yi}(y_i^{\prime }-y_i)$, where $S_{yi}={\mathrm{\sum }}_{yi}^{-1}$. After these substitutions, we have $p(R,t,\{x_i\},\{y_i\}\mid \{x_i^{\prime }\},\{y_i^{\prime }\})=cexp(-G(R,t,\{x_i^{\prime }\},\{y_i^{\prime }\},\{y_i\}))$, where

$$G(R,t,\{x_i^{\prime }\},\{y_i^{\prime }\},\{y_i\})=\sum _{i=1}^N{({Rx}_i^{\prime }+t-y_i)}^t\times R{\mathrm{\sum }}_{xi}^{-1}{R}^t({Rx}_i^{\prime }+t-y_i)+{(y_i^{\prime }-y_i)}^t{S}_{yi}(y_i^{\prime }-y_i).$$ (49)

Thus, in order to maximize the likelihood, we need to minimize $G(R,t,\{x_i^{\prime }\},\{y_i^{\prime }\},\{y_i\})$ with respect to R,t, and {y_i}. We minimize with respect to the {y_i} by taking the derivative of G with respect to each of the components of each of the and setting all 3N derivatives to zero. The result is

$$y_i={(S_{xi}+S_{yi})}^{-1}(S_{xi}({Rx}_i^{\prime }+t)+S_{yi}{y}_i^{\prime }).$$ (50)

We note that the expression for y_i given in (50), which is a weighted mean of the ith transformed measured point in x space and its corresponding measured point in y space, provides the best available approximation for the true positions needed in all the expressions for TRE and FRE statistics derived in the body of this paper. In the case of isotropic, homogeneous FLE, as, for example, in (2), this expression reduces to $y_i=(({Rx}_i^{\prime }+t)+y_i^{\prime })/2$, i.e., a simple unweighted average.

Finally, we substitute our expression for y_i into G to obtain (after considerable manipulation)

$$G(R,t,\{x_i^{\prime }\},\{y_i^{\prime }\},\{y_i\})=\sum _{i=1}^N{({Rx}_i^{\prime }+t-y_i^{\prime })}^t{W}_i^2({Rx}_i^{\prime }+t-y_i^{\prime })$$ (51)

where W_i = (RΣ_xiR^t + Σ_yi)^−1/2. In order to reach our goal, the remaining task is to find the transformation R,t that minimizes G. In this minimization process, we can use W_i = w(RΣ_xiR^t + Σ_yi)^−1/2, where w is any constant. For this reason we refer to W_i = w(RΣ_xiR^t + Σ_yi)^−1/2 as “ideal” weighting. The right side of (51) has the same form as the right side of (3), but the weighting is unspecified in (3), whereas the derivation above shows that only ideal weighting can achieve maximum likelihood.

Statistical Independence of the Elements of ẽ

In this appendix we show that, if the M elements of the vector e are statistically independent, normally distributed variables with zero mean, then, if the M×M matrix V is orthogonal, the following vector has these same three characteristics:

$${\stackrel{\sim }{e}}_i=\sum _{k=1}^M{V}_{ki}{e}_k.$$ (52)

1. If the mean of e is zero, then the mean of ẽ is zero.

   That the mean is zero is easily seen by computing the expectation value, which we denote by 〈.〉, of both sides of (52)

   $$\langle {\stackrel{\sim }{e}}_i\rangle =\langle \sum _{k=1}^M{V}_{ki}{e}_k\rangle =\sum _{k=1}^M{V}_{ki}\langle e_k\rangle =\sum _{k=1}^M{V}_{ki}·0=0.$$ (53)

2. If the elements of e are uncorrelated with equal variances and V is orthogonal, then the elements ẽ are uncorrelated.

   Because of (53), the correlation of ẽ_i and ẽ_j is equal to 〈(ẽ_i − 〈ẽ_i〉) (ẽ_j − 〈ẽ_j〉)〉

   $$\begin{array}{l}\langle ({\stackrel{\sim }{e}}_i-\langle {\stackrel{\sim }{e}}_i\rangle )({\stackrel{\sim }{e}}_j-\langle {\stackrel{\sim }{e}}_j\rangle )\rangle =\langle \sum _k^M{V}_{ki}(e_k-\langle e_k\rangle )\sum _l^M{V}_{lj}(e_l-\langle e_l\rangle )\rangle \\ =\sum _k^M\sum _l^M{V}_{ki}{V}_{lj}\langle (e_k-\langle e_k\rangle )(e_l-\langle e_l\rangle )\rangle \\ ={\sigma }^2\sum _k^M\sum _l^M{V}_{ki}{V}_{lj}{\delta }_{kl}\\ ={\sigma }^2\sum _k^M{V}_{ki}{V}_{kj}={\sigma }^2{\delta }_{ij}\end{array}$$ (54)

   where we used the fact that the elements of e are uncorrelated and equal in going from the first line of (54) to the second, defined ${\sigma }^2=\langle e_i^2\rangle$ to be the variance of an element of e, and used the orthogonality of V in the last step.

3. If the elements of e are independent and normally distributed with equal variances and V is orthogonal, then the elements of ẽ are independent and are normally distributed with the same variance.

   We note that, since the elements e_i are independent and normally distributed with variance σ², their joint probability density has the form

   $$\begin{array}{l}{p}_{1,2,\dots ,M}(e_1,e_2,\dots ,e_N)=\prod _{i=1}^M{\left(\sigma \sqrt{2\pi }\right)}^{-1}exp\left(\frac{-e_i^2}{(2{\sigma }^2)}\right)\\ ={\left(\sigma \sqrt{2\pi }\right)}^{-M}exp\left(\frac{-1}{2{\sigma }^2}\sum _{i=1}^M{e}_i^2\right)\end{array}$$ (55)
   where we have used the fact that the means of the e_i are zero⁶. Because each ẽ_i is a linear combination of the e_i, their joint density has the form (by generalizing the derivations in [18, p. 199–201 ] from two variables to M variables)

   $$q_{1,2,\dots ,M}({\stackrel{\sim }{e}}_1,{\stackrel{\sim }{e}}_2,\dots ,{\stackrel{\sim }{e}}_M)={\mid J\mid }^{-1}{p}_{1,2,\dots ,M}(z_1,z_2,\dots ,z_M)$$ (56)
   where J = det(V^t) and z = (V^t)⁻¹ẽ. Since V is orthogonal, |J| = 1 and (V^t)⁻¹ = V. Using these properties and (55) in (56) gives us that

   $$\begin{array}{l}{q}_{1,2,\dots ,M}({\stackrel{\sim }{e}}_1,{\stackrel{\sim }{e}}_2,\dots {\stackrel{\sim }{e}}_M)={\left(\sigma \sqrt{2\pi }\right)}^{-M}exp\left(-\sum _{i=1}^M\frac{{(V\stackrel{\sim }{e})}_i^2}{(2{\sigma }^2)}\right)\\ ={\left(\sigma \sqrt{2\pi }\right)}^{-M}exp\left(-\frac{{(V\stackrel{\sim }{e})}^{t}V\stackrel{\sim }{e}}{2{\sigma }^2}\right)\\ ={\left(\sigma \sqrt{2\pi }\right)}^{-M}exp\left(-\frac{{\stackrel{\sim }{e}}^t{V}^{t}V\stackrel{\sim }{e}}{2{\sigma }^2}\right)\\ ={\left(\sigma \sqrt{2\pi }\right)}^{-M}exp\left(-\frac{{\stackrel{\sim }{e}}^t\stackrel{\sim }{e}}{2{\sigma }^2}\right)\\ ={\left(\sigma \sqrt{2\pi }\right)}^{-M}exp\left(-\sum _{i=1}^M\frac{{\stackrel{\sim }{e}}_i^2}{2{\sigma }^2}\right)\end{array}$$ (57)

   where we have used the orthogonality of V in going from the second line of (57) to the third line. Equation (57) can be written as a product of functions of the individual ẽ_i as follows: $q_{1,2,\dots M}({\stackrel{\sim }{e}}_1,{\stackrel{\sim }{e}}_2,\dots ,{\stackrel{\sim }{e}}_M)={\displaystyle \prod _{i=1}^M}{q}_i({\stackrel{\sim }{e}}_i)$, where $q_i({\stackrel{\sim }{e}}_i)={\left(\sigma \sqrt{2\pi }\right)}^{-1}exp\left(-{\stackrel{\sim }{e}}_i^2/\left(2{\sigma }^2\right)\right)$, which is of normal form. Since the joint probability density of the ẽ_i is equal to the product of individual functions, the ẽ_i are mutually statistically independent. Since the individual functions are of normal form, they are normally distributed with variance σ².

Two-Dimensional Case

The formulas and the proof of independence are derived in Section III only for 3-D transformations, but they all carry over to the 2-D case as well. We highlight here the salient changes that result when the points and the transformations are 2-D. First, x_i, y_iΔx_i, Δy_i, Δξ_i, and $\mathrm{\Delta }{\xi }_i^{(0)}$ are 2×1. Second, W_i, R, R⁽⁰⁾, ${\mathrm{\sum }}_i^{(1)},{\mathrm{\sum }}_i^{(2)}$, Σ_i, I, and ΔR, are now 2×2 matrices, t, Δt, and

$$\mathrm{\Delta }R=\left[\begin{array}{cc}0& -\mathrm{\Delta }\theta \\ \mathrm{\Delta }\theta & 0\end{array}\right]$$ (58)

Third, C is a now a 2N×3 matrix, and q is a three-element vector whose elements are Δθ, Δt₁, Δt₂. Fourth,

$$X_i^{(0)}=\left[\begin{array}{c}-x_{i2}^{(0)}\\ x_{i1}^{(0)}\end{array}\right]$$ (59)

and

$$e_{2(i-1)+j}={\left(W_i\mathrm{\Delta }{\xi }_i^{(0)}\right)}_j,i=1,\dots ,N,j=1,2$$ (60)

Fifth, Λ is 2N×3, V is 3×3, Λ⁺ is 3×2N, and the proof that all singular values (there are now only three of them) are nonzero involves only the third of the three equations in (20). It is now the first three (instead of first six) diagonal elements of ΛΛ⁺ that are equal to 1, and the last 2N −3 (instead of the last 2N − 6) are equal to 0. As a result, each component of FRE_i for each fiducial point is a function of only the last 2N − 3 elements of ẽ_i, and each component of TRE(r) is a function of only the first three elements of ẽ. The proof that the 2N elements of ẽ are independent makes no reference to the dimension of the space (see Appendix I-B above). Therefore, FRE_i and TRE(r) are statistically independent for the 2-D case, just as they are for the 3-D case.

Sixth, the block-diagonal matrices have slightly different forms to accommodate the reduced spatial dimensionality: Σ_{2(i−1)+j,2(i−1)+j′} = (Σ_i)_jj′ and W_{2(i−1)+j,2(i−1)+j′} = (W_i)_jj′, for i = 1,…, N, j = 1, 2, j′ = 1,2 with all other elements equaling zero.

Seventh, (33) through (41) must be altered to accommodate the reduced dimensionality, as follows:

$$\begin{array}{l}{({\mathrm{\sum }}_{\text{FRE}})}_{kl}=\sum _{j,j^{\prime }=4}^{2N}{U}_{kj}{U}_{l{j}^{\prime }}\langle {\stackrel{\sim }{e}}_j{\stackrel{\sim }{e}}_{j^{\prime }}\rangle \\ =\sum _{j,j^{\prime }=4}^{2N}{U}_{kj}{U}_{l{j}^{\prime }}{(U^{t}W\mathrm{\sum }{W}^{t}U)}_{j{j}^{\prime }}\end{array}$$ (61)

$$\begin{array}{l}{\text{FRE}}_i^2=\sum _{k=2i-1}^{2i}{\left(\sum _{j,j^{\prime }=4}^{2N}{U}_{kj}{U}_{k{j}^{\prime }}\langle {\stackrel{\sim }{e}}_j{\stackrel{\sim }{e}}_{j^{\prime }}\rangle \right)}_{kk}\\ =\sum _{k=2i-1}^{2i}{\left(\sum _{j,j^{\prime }=4}^{2N}{U}_{kj}{U}_{k{j}^{\prime }}{(U^{t}W\mathrm{\sum }{W}^{t}U)}_{j{j}^{\prime }}\right)}_{kk}\end{array}$$ (62)

$$\begin{array}{l}\langle {\text{FRE}}^2\rangle =\sum _{k=1}^{2N}{({\mathrm{\sum }}_{\text{FRE}})}_{kk}\\ =\sum _{k=1}^{2N}\sum _{j,j^{\prime }=4}^{2N}{U}_{kj}{U}_{k{j}^{\prime }}{(U^{t}W\mathrm{\sum }{W}^{t}U)}_{j{j}^{\prime }}\\ =\sum _{j=4}^{2N}{(U^{t}W\mathrm{\sum }{W}^{t}U)}_{jj}\end{array}$$ (63)

$${({\mathrm{\sum }}_{\text{fre}})}_{kl}=\sum _{j,j^{\prime }=4}^{2N}{(W^{-1}U)}_{kj}{(W^{-1}U)}_{l{j}^{\prime }}{(U^{t}W\mathrm{\sum }{W}^{t}U)}_{j{j}^{\prime }}$$ (64)

$$\langle {\text{fre}}_i^2\rangle =\sum _{k=2i-1}^{2i}\sum _{j,j^{\prime }=4}^{2N}{(W^{-1}U)}_{kj}{(W^{-1}U)}_{k{j}^{\prime }}{(U^{t}W\mathrm{\sum }{W}^{t}U)}_{j{j}^{\prime }}$$ (65)

$$\langle {\text{fre}}^2\rangle =\sum _{j,j^{\prime }=4}^{2N}{(U^t{W}^{-2}U)}_{j{j}^{\prime }}{(U^{t}W\mathrm{\sum }{W}^{t}U)}_{j{j}^{\prime }}$$ (66)

$${({\mathrm{\sum }}_{\text{TRE}})}_{kl}=\langle {({\delta }_{min})}_k{({\delta }_{min})}_l\rangle =\sum _{j,j^{\prime }=1}^3{(DV)}_{kj}{(DV)}_{l{j}^{\prime }}\frac{\langle {\stackrel{\sim }{e}}_j{\stackrel{\sim }{e}}_{j^{\prime }}\rangle }{{\mathrm{\Lambda }}_{jj}{\mathrm{\Lambda }}_{j^{\prime }{j}^{\prime }}}$$ (67)

$${({\mathrm{\sum }}_{\text{TRE}})}_{kl}=\sum _{j,j^{\prime }=1}^3{(DV)}_{kj}{(DV)}_{l{j}^{\prime }}\frac{{(U^{t}W\mathrm{\sum }{W}^{t}U)}_{j{j}^{\prime }}}{{\mathrm{\Lambda }}_{jj}{\mathrm{\Lambda }}_{j^{\prime }j}}$$ (68)

$$\langle {\text{TRE}}^2\rangle =\sum _{k=1}^2{({\mathrm{\sum }}_{\text{TRE}})}_{kk}=\sum _{k=1}^2\sum _{j,j^{\prime }=1}^3{(DV)}_{kj}{(DV)}_{k{j}^{\prime }}\frac{{(U^{t}W\mathrm{\sum }{W}^{t}U)}_{j{j}^{\prime }}}{{\mathrm{\Lambda }}_{jj}{\mathrm{\Lambda }}_{j^{\prime }{j}^{\prime }}}.$$ (69)

Chi-Square Test for Dependence

To detect dependence, we employ the standard chi-square test based on the contingency tables [22]. Each element, C(i,j), i = 1,2, …, N_c, j = 1,2, …, N_c, of an N_c×N_c contingency table is a count of the number of registrations for which FRE_i ≤ FRE < FRE_i+1 and TRE_j ≤ TRE < TRE_j+1, where the thresholds, FRE_i and TRE_j can be chosen arbitrarily. The resulting table is then used to calculate the following test statistic: $q={\sum }_{i,j=1}^{N_C}{(C(i,j)-C_0(i,j))}^2/C_0(i,j)$, where C₀(i, j) is the count that is to be expected when FRE and TRE are independent, namely, C₀(i, j) = C₁(i)C₂(j)/M, where M is the total of all counts, $C_1(i)={\sum }_{j^{\prime }=1}^{N_C}C(i,j^{\prime })$, and $C_2(j)={\sum }_{i^{\prime }=1}^{N_C}C(i^{\prime },j)$. The variance in q over repeated experiments (i.e., with different random localization errors) can be reduced by choosing the thresholds FRE_i and TRE_j such that ${\sum }_{j^{\prime }=1}^{N_C}C(i_1,j^{\prime })\approx {\sum }_{j^{\prime }=1}^{N_C}C(i_2,j^{\prime })$ and ${\sum }_{i^{\prime }=1}^{N_C}C(i^{\prime },j_1)\approx {\sum }_{i^{\prime }=1}^{N_C}C(i^{\prime },j_2)$. If q is sufficiently large, then it can be concluded that FRE and TRE are dependent. A “sufficiently large” value is that of the chi-square distribution (i.e., cumulative distribution) ${\chi }_{\nu }^2(1-p_0)$⁷, where 1 − p₀ is the desired confidence in the truth of dependence. The number, v, of degrees of freedom for this problem equals (N_C −1)². Thus, a value of q that is larger than ${\chi }_{\nu }^2(1-p_0)$ indicates that dependence between FRE and TRE is detected at p ≤ p₀. Failure to detect q exceeding ${\chi }_{\nu }^2(1-p_0)$ suggests that our theory of independence can be extended from the linear approximation to the exact problem encountered in surgical guidance.

Computer Code to Implement the Derived Formulas

We provide in Fig. 4 a Matlab function to implement our new formulas for FRE and TRE. The values that it returns correspond to our equations as follows: (RMS_TRE)² = 〈TRE²〉 from (41), (RMS_FRE)² = 〈FRE²〉 from (35), Cov_TRE = Σ_TRE from (40), and Cov_FRE = Σ_FRE from (33). The inputs correspond to our definitions above as follows: $\mathrm{X}0(:,i)=x_i^{(0)}=R^{(0)}{x}_i$, W(:,:,i) = W_i, $\text{Cov}\_\text{FLE}(:,:,i)={\mathrm{\sum }}_i=R^{(0)}{\mathrm{\sum }}_i^{(1)}{R}^{{(0)}^t}+{\mathrm{\sum }}_i^{(2)}$, and r0 = r⁽⁰⁾ = R⁽⁰⁾r.

Like the formulas that it implements, this code is general. This relatively simple function handles the special cases of uniform weighting for homogeneous, isotropic FLE, first solved by Fitzpatrick et al. [6], uniform weighting for homogeneous, anisotropic FLE first solved by Wiles et al. [9], and ideal weighting for inhomogeneous, anisotropic FLE first solved by Moghari et al. [11], and it handles all other cases as well.