Statistical Learning is Related to Early Literacy-Related Skills

Abstract

It has been demonstrated that statistical learning, or the ability to use statistical information to learn the structure of one’s environment, plays a role in young children’s acquisition of linguistic knowledge. Although most research on statistical learning has focused on language acquisition processes, such as the segmentation of words from fluent speech and the learning of syntactic structure, some recent studies have explored the extent to which individual differences in statistical learning are related to literacy-relevant knowledge and skills. The present study extends on this literature by investigating the relations between two measures of statistical learning and multiple measures of skills that are critical to the development of literacy—oral language, vocabulary knowledge, and phonological processing—within a single model. Our sample included a total of 553 typically developing children from prekindergarten through second grade. Structural equation modeling revealed that statistical learning accounted for a unique portion of the variance in these literacy-related skills. Practical implications for instruction and assessment are discussed.

The acquisition of literacy skills is a key educational milestone for children in many cultures. Literacy skills are strong predictors of both future academic success (National Institute of Child Health and Human Development [NICHD], 2000) and broader life outcomes (Beck, McKeown, & Kucan, 2002). The outcomes associated with success (or failure) in learning to read underscore the importance of developing an understanding of the theoretical mechanisms involved in the acquisition of literacy skills. This requires an examination not only of the abilities most often thought to be directly involved in learning to read (e.g., phonological awareness; Wagner & Torgesen, 1987; Burgess & Lonigan, 1998) but also of the cognitive capacities that may contribute to the acquisition of these abilities. Whereas many studies have documented the role that individual variation in particular cognitive capacities—working memory (e.g., Just & Carpenter, 1992; MacDonald & Christiansen, 2002) and inhibitory skill (e.g., Khanna & Boland, 2010; Trueswell, Sekerina, Hill, & Logrip, 1999) as examples—play in reading (and language use more generally), the role of individual variation in other capacities that are known to play a role in language acquisition and use has received considerably less attention. One such capacity is the ability to use statistical information gleaned from the surrounding environment to learn about the structural properties of one’s environment. This capacity, called statistical learning, has been demonstrated to play a role in word segmentation, which is important for language acquisition (e.g., Saffran, Aslin, & Newport, 1996; Thiessen & Saffran, 2003), and has recently been suggested to be linked to literacy-related outcomes (e.g., Arciuli & Simpson, 2012). The goal of the present study was to build upon this literature by examining the relations between statistical learning and other abilities (e.g., oral language and phonological processing skills) known to be critical to the development of early literacy skills.

We live in an environment that contains multiple sources of statistical information. As a simple example, the likelihood of encountering rain, thunder, and lightening can be reasonably predicted by looking for the presence of dark clouds in the sky. The use of probabilistic information to learn about the structure of the environment—that is, the ability to engage in statistical learning—is an ability that has been observed in many species, including humans (e.g., Reber, 1996), using a wide range of tasks. For example, learning based on statistical regularities has been shown in studies of probability matching and the acquisition of artificial grammars (see Reber, 1996, for an extensive review), in studies involving the acquisition of both artificial (Conway, Bauernschmidt, Huang, & Pisoni, 2010; Gómez & Gerken, 1999; Saffran et al., 1996) and naturally occurring (e.g., Fine & Jaeger, 2013) linguistic stimuli, in visual search tasks (e.g., Jones & Kaschak, 2012), and in a range of additional tasks that have been used to study the implicit learning of rules (e.g., Kaufman et al., 2010). Indeed, statistical learning and implicit learning are two closely related skills, and in several instances, statistical learning has been conceptualized as a facet of implicit learning (see Perruchet & Pacton, 2006, for a discussion).

Statistical learning is an ability that develops very early, being detectable shortly after birth (Teinonen, Fellman, Näätänen, Alku, & Huotilainen, 2009). This ability has been linked to language acquisition in young children. Statistical learning plays a role in a variety of language-based processes (Arciuli & von Koss Torkildsen, 2012; Gómez & Gerken, 2000). Multiple studies have demonstrated that statistical learning affects children’s ability to segment words from a fluent stream of speech (i.e., word segmentation; Saffran et al., 1996), acquire new vocabulary (Yu, 2008), and process language (Misyak, Christiansen, & Tomblin, 2010a). Statistical learning has also been shown to impact the acquisition of orthographic and syntactic knowledge in young children (Arciuli, Monaghan, & Seva, 2010; Kidd, 2012; Rowland & Pine, 2000). Moreover, the effects of statistical learning on language processes are maintained throughout adulthood. In several instances, statistical learning has been shown to influence adults’ knowledge of orthographic information as well as their vocabulary knowledge (de Zubicaray, Arciuli, & McMahon, 2013; Finn & Hudson Kam, 2008) and language comprehension skills (Misyak & Christiansen, 2012; Misyak, Christiansen, & Tomblin, 2010b).

Thus, statistical learning appears to play a broad role in the development and continued application of language skills. This is not surprising, given the many sources of statistical regularities that are found in spoken and written language (e.g., Arciuli & Monaghan, 2009; Deacon, Conrad, & Pacton, 2008; Kidd, 2012; MacDondald, Pearlmutter, & Seidenberg, 1994; Pacton, Perruchet, Fayol, & Cleeremans, 2001). As one example, elements of syntactic structure are signaled by probabilistic information—speakers of English who encounter the word “the” know that there is a strong likelihood of a noun appearing in the next word or two (the car or the brown car), thus revealing something about the structure of noun phrases. Similarly, speakers of English who encounter a noun phrase at the beginning of a sentence know that there is a high likelihood of a verb coming directly thereafter (The brown car raced…), thus revealing something about phrase structure rules.

Statistical learning appears to play a role in a broad range of linguistic skills, and, as such, it is reasonable to expect that statistical learning should play a role in the acquisition of literacy skills. This expectation has not received much attention in the literature, but there is evidence that statistical learning is related to literacy skills. For instance, Arciuli and Simpson (2012) demonstrated that statistical learning ability (indexed by a non-linguistic visual learning task) was associated with reading ability, as indexed by the Wide Range Achievement Test, Fourth Edition (WRAT-4; Wilkinson & Robertson, 2006). This relation was found both in elementary-school-age children (between ages 6 and 12) and in adults, suggesting that statistical learning ability may be important both for initial stages of literacy development and for long-range literacy outcomes. Further, the statistical variability in grapheme-phoneme correspondences facilitates the acquisition of such knowledge in young children (Apfelbaum, Hazeltine, & McMurray, 2013).

Arciuli and Simpson (2012) and Apfelbaum et al. (2013) provided direct evidence that statistical learning plays a role in the acquisition of literacy skills in one’s native language (see Frost, Siegelman, Narkiss, & Afek, 2013, for evidence that statistical learning predicts literacy development in a second language). Their findings are complemented by the results of studies that provide an indirect look at the statistical learning-literacy development link. There is an extensive body of work suggesting that statistical learning plays a role in the development and performance of oral language skills, vocabulary knowledge, and phonological knowledge (Conway et al., 2010; Evans, Saffran, & Robe-Torres, 2009; Harm & Seidenberg, 2004; Misyak & Christiansen, 2011; Rowland & Pine, 2000; Yu, 2008), all of which are known to be related to the development of literacy. For instance, Evans et al., (2009) investigated statistical learning in elementary-aged children with and without specific language impairments. Both groups of children were required to listen to 21 min of an artificial language speech stream, and afterwards, they were prompted to select which syllable sound pair sounded most like those that they heard. Results indicated that typically developing children performed significantly better on the language task than children with specific language impairment; children with language impairments continued to perform at chance levels throughout the duration of the task. This suggests that children with specific language impairment may also have corresponding impairments regarding statistical learning, which would account for their markedly poorer performance on the language task (Evans et al., 2009). Moreover, the authors reported significant correlations between performance on the implicit learning task and performance on expressive and receptive measures of vocabulary knowledge for typically developing children (see also Stoodley, Ray, Jack, & Stein, 2008; Vicari et al., 2005 for evidence that implicit learning predicts literacy development).

The present study

Although the aforementioned studies suggest a link between statistical learning and literacy development, much remains to be learned about the details of these relations. The current study sought to address two specific issues. First, previous work in this area has examined the relations between statistical learning and single, broad measures of literacy outcomes (such as scores on the WRAT; Arciuli & Simpson, 2012). The present study was designed to allow a finer-grained examination of the role of statistical learning in literacy development by examining how statistical learning is related to three constructs that have been shown to be crucial to the development of early literacy skills—oral language skill, vocabulary knowledge, and phonological processing. As such, it was possible to assess the extent to which statistical learning underpins individual elements of literacy development.

The second goal of this work was to examine how different elements of statistical learning relate to oral language skills, vocabulary knowledge, and phonological processing. Thiessen, Kronstein and Hufnagle (2013) proposed that there are at least two distinct processes involved in statistical learning—integration and extraction. Extraction refers to the use of local contingencies to chunk the input into units. An example of this is the use of local contingencies, such as the probability of one syllable following another, to segment a fluent stream of speech into individual words (e.g., Saffran et al., 1996). Integration refers to the process of abstracting across these discrete units to learn about the distributional features of the information set. Therefore, one might use local contingencies to find words such as the and car in a speech stream (extraction) and then generalize over many of these discrete units to discover more abstract information about the speech stream, such as the phrase structure rules that underlie the generation of the speech (integration; see Thiessenetal., 2013, for an extensive discussion). As extraction and integration are likely to play different roles in the acquisition of language skills (e.g., extraction is more important to segmenting the speech stream into words; integration is more important to learning about syntactic structure), they may also play different roles in the development of individual components of literacy skill.

Measures of statistical learning

This study investigated the relations between elements of statistical learning (extraction and integration) and elements of developing literacy-related skills (oral language, vocabulary knowledge, and phonological processing) in preschool and early elementary age children (pre-k—second grade) using structural equation modeling (SEM) methods. We employed two measures of statistical learning.

The first measure was a word segmentation task that was used by Sell and Kaschak (2009). In this task, participants were exposed to an artificial language that consisted of four words (i.e., “nifopa”, “dibo”, “kuda”, and “lagoti”) that were arranged into a series of training sentences (see Table 1 for a list of the words and a few example training sentences). The sentences were produced by a trained speaker such that there were no obvious cues (e.g., stress patterns, changes in intonation) to the boundaries between words. This task was normed prior to its use in the current study (see Sell & Kaschak, 2009). Undergraduate university students were asked to listen to a sentence and then verbally indicate which syllable clusters they believed comprised a word. Only two out of the 69 responses were correct, which suggests an absence of word boundary cues within the speech stream. The only cue to word boundaries was the statistical regularities that existed between syllables. Further, previously reported analyses revealed no statistically significant differences among syllables with regard to pitch, amplitude, and duration (Sell & Kaschak, 2009).

Table 1.

Words and example training sentences for the word segmentation task

Words		Example training sentencesa,b
Nifopa	Kuda	monifopadibokudalagotifa
Dibo	Lagoti	molagotinifopakudadibo

^aSentences began with the syllable mo and ended with the syllable fa to prevent participants from using the onset and offset of sentences to find word boundaries

^bFollowing up on the example from the text, after the first example sentence there is a 100 % likelihood of fo following ni, of pa following fo, and of di following pa. Thus, the statistics do not provide a clue to word boundaries. After the second sentence, the likelihood of fo following ni and pa following fo is still 100 %, but now the likelihood of di or ku following pa is 50 %. This change in probability signals the presence of a word boundary.

In the training sentences ni was always followed by fo, and fo was always followed by pa. That is, there was a 100 % chance of one syllable following another within a word in this language. Word final syllables, such as pa, could be followed by any of a number of other syllables (i.e., the likelihood of any particular syllable following pa was < 100 %). This dip in probability of moving from one syllable to the next was a cue that one had encountered a boundary between words (e.g., Saffran et al., 1996). The question of interest was whether learners could use this cue to learn the words of the artificial language successfully. The word segmentation task served as our measure of the extraction process in statistical learning.

The second measure of statistical learning was the Simon task, which is a visual sequence-learning task. The Simon task is modeled on the Milton Bradley game Simon (Conway et al., 2010; Conway, Pisoni, Anaya, Karpicke, & Henning, 2011). Participants were presented with sequences of four colored squares (red, blue, green, likelihood of fo following ni, of pa following fo, and of di following pa. Thus, the statistics do not provide a clue to word boundaries. After the second sentence, the likelihood of fo following ni and pa following fo is still 100 %, but now the likelihood of di or ku following pa is 50 %. This change in probability signals the presence of a word boundary and yellow) on a computer screen. At the conclusion of each sequence, participants were asked to reproduce the sequence of colors in the correct order. Color sequences ranged from a minimum of two colors (e.g., red–blue) to a maximum of five colors (e.g., red–blue–red–green–yellow), and were based on a set of probabilistic rules. During the training phase of the Simon task, participants were presented with sequences based on these rules. Following the training phase, participants were provided with both rule-following and rule-violating color sequences. The difference in performance on the rule-following and rule-violating sequences provides the measure of statistical learning ability on this task.

Although the Simon task is a non-linguistic task (i.e., it is a visual learning task, just like the one used by Arciuli & Simpson, 2012), performance on this measure is related to language performance in both children and adults (Conway et al., 2010, 2011). Sensitivity to distributional features of the training set (i.e., abstraction across many training strings) is necessary to learn the rules that generate the test items. Thus, the Simon task taps into integration processes of statistical learning.

Oral language, vocabulary knowledge, and phonological processing

We also collected several measures of oral language abilities, vocabulary knowledge, and phonological processing. Oral language is simply spoken language and is comprised of several components, including semantic knowledge, syntactical knowledge, and morphological and phonological awareness (Richgels, 2004). The Simple View of Reading (Gough & Tunmer, 1986; Hoover & Gough, 1990) acknowledges the importance of oral language to reading via its inclusion within the linguistic comprehension portion of the theoretical model. The relation between oral language and literacy is well documented, and research shows that oral language provides a clear foundation for early literacy skills and is predictive of future reading ability (Kendeou, van den Broek, White, & Lynch, 2009; Scarborough, 2001).

Vocabulary knowledge is another critical component of early literacy because readingtextrequiresafairlyconstantprocessofdeterminingorinferringwordmeanings to achieve understanding; however, vocabulary knowledge is also considered a component skill of oral language if an individual is engaged with verbal language as opposed to print (NICHD, 2000). Vocabulary knowledge is an understanding of word meanings and can include knowledge of definitions, synonyms and antonyms, usage ability, and morphological awareness. Researchers have demonstrated that vocabulary knowledge is a strong and robust predictor of literacy skills (Anderson & Freebody, 1981; Beck & McKeown, 1991; Joshi, 2005) and have demonstrated that children with more limited vocabularies are at a higher risk of having comprehension difficulties and, thus, are more likely to face problems in their academic careers (Nash & Snowling, 2006). Children are learning up to 2,000–3,000 new words per year during the early elementary grades (Nagy & Anderson, 1984), making it highly likely that direct instruction is only accounting for a portion of this growth; additional cognitive processes, such as statistical learning, may help to explain these large gains in vocabulary (Stokes, 2010; see Landauer & Dumais, 1997, for suggestions of how statistical information might aid in vocabulary acquisition).

When engaging with written text, the recovery of phonological information (either through “inner speech” or reading aloud) is an important step in the comprehension process (e.g., Ashby, 2006; Ashby & Clifton, 2005). This auditory identification and processingofindividualwordsoundsintextorspokenlanguageisknownasphonological processing and has three components: phonological awareness, phonological recoding in lexical access, and short-term verbal memory (Wagner & Torgesen, 1987). Phonological processing has been shown to influence literacy skills (e.g., Wagner, Torgesen, & Rashotte, 1994; Wagner& Torgesen, 1987) and has been identified as being fundamental to early reading (Siegel, 1993; Stanovich, 1988).Further, research has uncovered positive correlations between vocabulary knowledge and phonological processing (Lonigan et al., 2009), highlighting the need to study these skills in conjunction.

Hypotheses

The aim of this study was to investigate the contribution of statistical learning to early literacy-related skills. Specifically, we sought to address two main questions: (a) Does statistical learning uniquely explain variance in oral language, vocabulary, and phonological processing skills; and if so, (b) Do the word segmentation and Simon tasks differentially predict performance across these early literacy skills? First, we expected to replicate the previous finding that statistical learning is related to early literacy related skills (e.g., Arciulietal., 2010; Evansetal., 2009). Second, with regard to question two, because distributional learning has been shown to be important for the acquisition of phonological knowledge (Kuhl, 2004; Werker, Yeung, & Yoshida, 2012), we believed it likely that the Simon task (i.e., the measure of integrative statistical learning processes) would explain unique variance in phonological processing. Given that distribution learning has also been shown to be important for acquiring lexical (e.g., Landauer & Dumais, 1997) and syntactic information (e.g., MacDonald & Christiansen, 2002; Kidd 2012), it is also possible that performance on the Simon would be predictive of oral language and vocabulary knowledge. Furthermore, we expected that the word segmentation task would predict performance on the oral language (as segmenting the speech stream into units is essential for oral language processing) and vocabulary tasks (as segmenting word units from the speech stream is necessary for acquiring words). It was less clear whether the word segmentation task would be related to phonological skills.

METHOD

Participants

Participants were 553 typically developing children¹ from pre-kindergarten to second grade who ranged in age from 4.3 to 10.5 years (M_age = 6.6 years; SD_age = 1.34 years) and who were involved in a larger study. They were recruited from public schools in five different counties within the Southeastern United States. Participants were identified as White (62 %), African American (21 %), Asian American (2 %), Native American (2 %), Multiracial (2 %), or Other (1 %), and 12 % were unidentified. The sample had an even gender distribution (50 % were male).

Materials and procedure

Test of language development—primary—morphological comprehension (TOLD-PMC), fourth edition

The TOLD-P-MC (Hammill & Newcomer, 2008) is an individually- and orally administered standardized oral language assessment that measures understanding, recognition, and use of morphological forms. Participants are required to distinguish between grammatically correct an incorrect sentences. This subtest contains 38 items, and participants are either scored as 1 (correct) or 0 (incorrect). If no response is given, the item is marked as incorrect. Raw scores are reported.

Test of language development—primary—picture vocabulary (TOLD-P-PV), fourth edition

The TOLD-P-PV (Hammill & Newcomer, 2008) is an individually- and orally-administered standardized oral language assessment that measures understanding of spoken English words. Participants respond to spoken stimuli by pointing to one of several presented pictures. This subtest contains 34 items, and participants are either scored as 1 (correct) or 0 (incorrect). If no response is given, the item is marked as incorrect. Raw scores are reported.

Test of language development—primary—relational vocabulary (TOLD-P-RV), fourth edition

The TOLD-P-RV (Hammill & Newcomer, 2008) is an individually- and orally-administered standardized oral language assessment that measures the ability to orally express the relations between two spoken words. Participants explain how two spoken words are alike. This subtest contains 34 items, and participants are either scored as 1 (correct) or 0 (incorrect). If no response is given, the item is marked as incorrect. Raw scores are reported.

Test of language development—primary—syntactic understanding (TOLD-P-SU), fourth edition

The TOLD-P-SU (Hammill & Newcomer, 2008) is an individually- and orally-administered standardized oral language assessment that measures the ability to comprehend sentences. This subtest contains 30 items, and participants are either scored as 1 (correct) or 0 (incorrect). If no response is given, the item is marked as incorrect. Raw scores are reported.

Expressive one-word picture vocabulary test (EOWPVT), fourth edition

The EOWPVT (Martin & Brownell, 2011a) is an individually administered standardized assessment that measures the ability to name objects, actions, and concepts using a single word. Participants are shown pictures and asked to provide a word that best represents the picture. The assessment contains up to 170 items. Raw scores are reported.

Receptive one-word picture vocabulary test (ROWPVT), fourth edition

The ROWPVT (Martin & Brownell, 2011b) is an individually administered standardized assessment that measures the ability to match a spoken word with a picture of an object, concept, or action. The assessment contains up to 170 items. Raw scores are reported.

Comprehensive test of phonological processing—elision (CTOPP-E)

The CTOPP-E (Wagner, Torgesen, Rashotte, & Pearson, 1999) is an individually administered standardized assessment that measures the ability to remove phonological segments from spoken words to create other words. The examiner instructs participants to remove the phoneme from a spoken word to produce a new word. This subtest contains 20 items, and participants are scored as either 1 (correct) or 0 (incorrect) for each response. If no response is given, the item is marked as incorrect. There is no basal for this subtest, and testing ceases after the child misses three consecutive items. If a child is unable to answer at least one of the practice items given prior to actual assessment, test administration ends and no score is given. Raw scores are reported.

Comprehensive test of phonological processing—blending words (CTOPP-BW)

The CTOPP-BW (Wagner et al., 1999) is an individually administered standardized assessment that measures the ability to synthesize sounds to create words. Participants are given the phonemes that make up a word and asked to say the word when it is blended together. For example, /k//a//t/. This subtest contains 20 items, and participants are scored as either 1 (correct) or 0 (incorrect) for each response. If no response is given, the item is marked as incorrect. There is no basal for this subtest, and testing ceases after the child misses three consecutive items. If a child is unable to answer at least one of the practice items given prior to actual assessment, test administration ends and no score is given. Raw scores are reported.

Comprehensive test of phonological processing—blending nonwords (CTOPP-BNW)

The CTOPP-BNW (Wagner et al., 1999) is an individually-administered standardized assessment that measures the ability to synthesize sounds to form nonwords. Similar to blending words but nonsense word phonemes are provided instead. This subtest contains 18 items, and participants are scored as either 1 (correct) or 0 (incorrect) for each response. If no response is given, the item is marked as incorrect. There is no basal for this subtest, and testing ceases after the child misses three consecutive items. If a child is unable to answer at least one of the practice items given prior to actual assessment, test administration ends and no score is given. Raw scores are reported.

Comprehensive test of phonological processing—memory for digits (CTOPP-MFD)

The CTOPP-MFD (Wagner et al., 1999) is an individually administered standardized assessment that measures the ability to repeat numbers accurately. Participants listened to strings of numbers and are instructed to repeat the numbers back in the order that they were given. This subtest contains 21 items, and participants are scored as either 1 (correct) or 0 (incorrect) for each response. If no response is given, the item is marked as incorrect. There is no basal for this subtest, and testing ceases after the child misses three consecutive items. If a child is unable to answer at least one of the practice items given prior to actual assessment, test administration ends and no score is given. Raw scores are reported.

Comprehensive test of phonological processing—nonword repetition (CTOPP-NWR)

The CTOPP-NWR (Wagner et al., 1999) is an individually administered standardized assessment that measures the ability to repeat nonwords accurately. Participants are asked to listen to nonsense words and instructed to repeat them back verbatim. This subtest contains 18 items, and participants are scored as either 1 (correct) or 0 (incorrect) for each response. If no response is given, the item is marked as incorrect. There is no basal for this subtest, and testing ceases after the child misses three consecutive items. If a child is unable to answer at least one of the practice items given prior to actual assessment, test administration ends and no score is given. Raw scores are reported.

Word segmentation task

The word segmentation task was a pre-recorded artificial language stream that was spoken by a trained speaker who produced a monotone auditory stream that contained no cues (such as pauses, stress patterns, and so on) that would clue participants into the location of word boundaries (see Sell & Kaschak, 2009, for an extensive discussion of this task). The only cues to word boundaries provided were in the form of transitional probabilities between syllables: within-word transitional probability was 1.0; between-word transitional probability was .25. Participants were presented with 12 training sentences prior to test administration (see Table 1 for examples). The total duration for the training session was approximately 1 min. During testing, participants were presented with four pairs of “words.” Each pair consisted of one word from the language (e.g., “nifopa”) and one non-word that contained parts of two or more words from the language (e.g., “fopadi”). Participants had to choose which of the two words was a word they heard in the training language. Scores could range between 0 and 100 % correct.

Simon task

The “Simon” task is an individual differences measure of implicit statistical learning (see Conway et al., 2010, 2011) that contained four colored squares (i.e., red, green, yellow, and blue) and required participants to replicate a generated color sequence (e.g., green-blue-yellow-green) using a touch screen computer. Color sequences ranged from a minimum string of two colors to maximum string of five, and participants were awarded one point for each correct response made during the test phase (e.g., a five-string sequence was worth five points if it was accurately repeated in its entirety). The training phase of the task involved the participant attempting to reproduce sequences that were generated using a probabilistic grammar. In the test phase of the task, participants were presented with sequences generated from the probabilistic grammar, and sequences that were generated from a different grammar (i.e., sequences that “followed the rules” and sequences that did not). The transition from the training phase to the test phase was seamless from the perspective of the participants. There was no break between phases, and participants continued attempting to replicate the strings that were presented to them throughout the task. Learning scores on the Simon task were calculated based on the participants’ performance in the test phase. For each participant, we calculated the number of points earned on “rule following” trials (e.g., correctly replicating strings of 5, 4, and 3 colors would result in a total of 12 points) and the number of points earned on the “rule violating” trials (e.g., correctly replicating strings of 4, 3, and 2 colors would result in a total of 9 points). The difference between these point totals (rule-following points minus rule-violating points) was the participant’s learning score (in our example, the learning score would be 12–9, or 3 points). Scores could range from 48 (getting all of the “correct” sequences right, and getting none of the “incorrect” sequences right) to -48 (getting all of the “incorrect” sequences right, and none of the “correct” sequences right).

Procedure

The study was approved by the Institutional Review Board prior to data collection. All parents of students who participated in the current study provided informed consent for their children’s participation, and all students provided assent prior to participation. In light of budget and time constraints, a missing-by-design assessment strategy was used for the cognitive measures. Trained testers administered all tasks individually during the Spring of 2011 and Fall of 2012.

RESULTS

Preliminary analyses

Using SPSS Statistics 19.0, the data were screened for potential outliers prior to SEM analyses. Outliers were identified using the median plus or minus two interquartile ranges (IQR) criterion.² Similar to the standard deviation, the IQR describes the spread of the data. The IQR is calculated by getting the difference between the 1st and 3rd quartiles (the 25th and 75th percentiles).³ Because these outliers were not particularly extreme (over two-thirds of all outliers were no more than three points outside of the IQR criteria), outliers were included in the analysis.⁴ Missing data was handled using multiple imputation in SPSS.

Descriptive statistics are presented in Table 2. Many of the oral language, vocabulary, and phonological processing assessments were significantly correlated in the low to moderate range. Only six of the assessments were correlated with the statistical learning tasks (CTOPP-BNW, r = −.10, p < .05; CTOPP-NWR, r = .10, p < .05; EOWPVT = .08, p < .05; and ROWPVT, r = .13, p < .01 for word segmentation and CTOPP-E, r = .09, p < .05; CTOPP-BNW r = .09, p < .05; and CTOPP = MFD, r = .09, p < .05 for the Simon task). The word segmentation task was significantly correlated with age (r = .09, p < .05) but the Simon task was not (r = −.01, p = .55) (see also Table 3 for zero-order correlations). Data were also checked for floor and ceiling effects.

Table 2.

Descriptive statistics and partial correlations for all tasks controlling for age (N = 553)

Task	1	2	3	4	5	6	7	8	9	10	11	12	13
1. Word Seg.	–
2. Simon Task	−.02	–
3. CTOPP-E	.03	.09*	–
4. CTOPP-BW	.06	−.02	.41***	–
5. CTOPP-BNW	−.10*	.09*	.46***	.59***	–
6. CTOPP-MFD	.01	.09*	.41***	.27***	.31***	–
7. CTOPP-NWR	.10*	−.02	.28**	.44***	.38***	.34***	–
8. EOWPVT	.08*	.05	.36***	.23***	.24**	.18***	.06	–
9. ROWPVT	.13**	.04	.47***	.45***	.28***	.36***	.28***	.41***	–
10 . TOLDP-MC	.05	.05	.46***	.35***	.32***	.44***	.33***	.35***	.55***	–
11. TOLDP-PV	.05	.05	.35***	.37***	.28***	.26***	.19***	.31***	.55***	.38***	–
12. TOLDP-RV	.07	.07	.49***	.4***	.35***	.36***	.33***	.21***	.51***	.51***	.46***	–
13. TOLDP-SU	.02	.02	.39***	.28***	.17***	.32***	.26***	.31***	.57***	.51***	.40***	.43***	–
Mean	.54	−1.69	10.01	10.50	10.76	9.29	7.97	96.74	100.60	9.01	10.23	8.05	10.08
SD	.27	12.62	2.82	2.50	2.29	2.66	2.62	17.50	15.55	2.82	2.78	2.93	2.85
Observed min	−.25	−44	1	2	5	1	0	54	54	2	2	1	1
Observed max	1.24	38	19	18	19	18	19	146	146	18	18	16	16

Word Seg. word segmentation task, CTOPP comprehensive test of phonological processing, E elision, BW blending words, BNW blending nonwords, MFD memory for digits, NWR nonword repetition, E/ROWPVT expressive/receptive one-word picture vocabulary task, TOLD-P test of language development—primary, MC morphological construction, PV picture vocabulary, RV relational vocabulary, SU syntactical understanding, SD standard deviation

^*p < .05;

^**p < .01;

^***p < .001

Table 3.

Zero-order correlations between statistical learning tasks and outcome measures (N = 553)

SL Task	CTOPP-E	CTOPP-BW	CTOPP-BNW	CTOPP-MFD	CTOPP-NWR	EOWPVT	ROWPVT	TOLDP-MC	TOLDP-PV	TOLDP-RV	TOLDP-SU
Word Seg.	.02	.07	−.20***	−.03	.13**	.08	.10*	−.00	−.01	.04	−.10*
Simon	.05	−.08	.11**	.06	−.07	.00	−.03	−.03	−.03	−.06	.17*

SL statistical learning, Word Seg. word segmentation task, CTOPP comprehensive test of phonological processing, E elision, BW blending words, BNW blending nonwords, MFD memory for digits, NWR nonword repetition, E/ROWPVT expressive/receptive one-word picture vocabulary task, TOLD-P test of language development—primary, MC morphological construction, PV picture vocabulary, RV relational vocabulary, SU syntactical understanding

^*p < .05;

^**p < .01;

^***p < .001

For the CTOPP-E, less than 4 % of children were unable to complete the subtest (i.e., scores below six). For the CTOPP-BW, -BNW, -MFD, and -NWR, these values were 1.3, .9, 6.5, and 14.1 %, respectively. There was an absence of ceiling effects (i.e., scores of 18 or more) on all subtests of the CTOPP. Less than 2 % of participants obtained scores above 18 across all subtests. Less than 7 % and less than 2.5 % of the sample scored more than two standard deviations below the mean on the EOWPVT and ROWPVT, respectively. Almost no ceiling effects were found for the EOWPVT and ROWPVT (i.e., scores above 150). For all subtests of the TOLD-P, scoring near the floor was defined as getting less than at least five items correct. Less than 7 % of children scored near the floor for the TOLD-P-MC. These values were 1.4, 13.7, and 4.0 % for the TOLD-P-PV, -RV, and -SU subtests, respectively. No ceiling effects were found for any of the TOLD-P subtests (i.e., scores above 34 for the TOLD-PMC, scores above 30 for the TOLD-P-PV and -RV, and scores above 27 for the TOLD-P-SU). For the word segmentation task, less than 7 % of participants attained scores that were less than .25 (i.e., they only answered 25 % of items correctly) and about 10 % of participants attained scores that were above .75. For the Simon task, floor and ceiling effects (i.e., scores below -24 or above 24) were also absent, as only 5 and 3 % of participants, respectively, scored at these more extreme ends.

Skewness and kurtosis values were all within an acceptable range of plus or minus one, indicating that all tasks had adequate variability. Zero-order correlations between the statistical learning tasks and the outcome measures are presented in Table 3. Although the data were nested (i.e., children nested within classrooms and schools), the intraclass correlation (ICC) values were near zero for each predictor (ICC values were all B.05 for all tasks), suggesting that the majority of task variance was at the student level. Therefore, we did not employ multilevel modeling.

Structural equation modeling of statistical learning and literacy skills

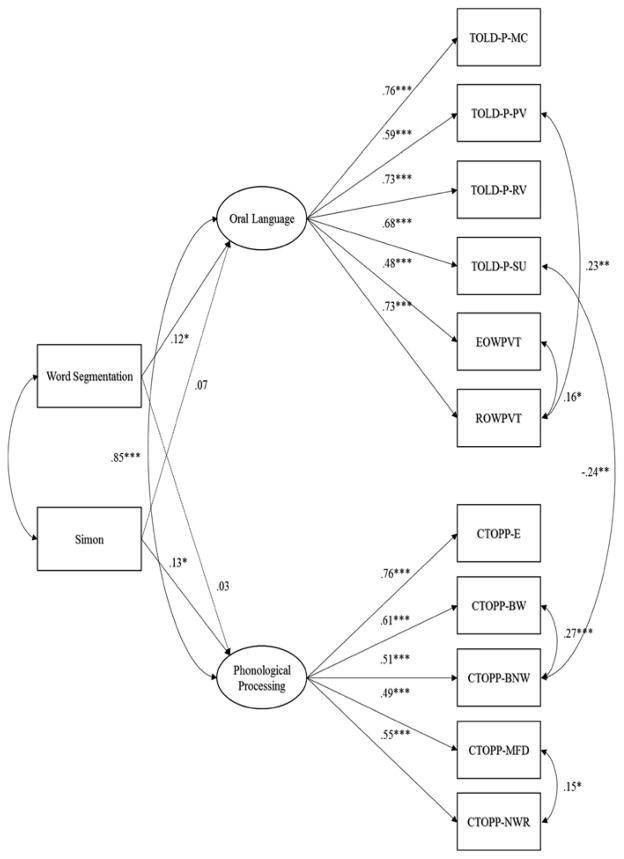
Structural equation modeling was carried out using Mplus Version 7.0 (Muthén & Muthén, 2013). The two measures of statistical learning (the word segmentation and Simon tasks) did not load onto a single latent variable. This is not entirely surprising, considering both that the measures were tapping different aspects of statistical learning and that previous work using different tasks have shown that measures of statistical learning may not be strongly correlated with each other (see Gebauer & Mackintosh, 2007). Thus, the word segmentation and Simon tasks were included as observed indicators within the SEM model. Preliminary confirmatory factor analysis suggested that a two-factor model (with a combined oral language/vocabulary factor, and a phonological processing factor) provided the best fit to the data,⁵ so we regressed our two latent variables on both measures of statistical learning (see Fig. 1). Additionally, in an effort to improve overall model fit, several assessments were allowed to correlate based on model modification indices (i.e., the blending words and blending nonwords subtests of the CTOPP; the memory for digits and nonword repetition subtests of the CTOPP; the EOWPVT and ROWPVT; and the ROWPVT and picture vocabulary subtest of the TOLD-P; the CTOPP blending nonwords and syntactic understanding subtest of the TOLD-P).

Fig. 1.

Unconstrained SEM model of oral language, vocabulary knowledge, phonological processing, and statistical learning. Note ***p < .001; **p < .01; *p < .05. Solid lines indicate significant pathways. Dashed lines indicate non-significant pathways. CTOPP-E comprehensive test of phonological processing–elision, BW blending words, BNW blending nonwords, MFD memory for digits, NWR nonword repetition, E/ROWPVT expressive/receptive one-word picture vocabulary task, TOLD-P test of language development—primary, MC morphological construction, PV picture vocabulary, RV relational vocabulary, SU syntactical understanding

The model provided an excellent fit to the data and had a significant chi-square probability, χ² (65) = 104.90, p < .01. The Comparative Fit Index (CFI) and Tucker-Lewis Index (TLI) values were .96 and .95, respectively. For the present model, RMSEA = .04; SRMR = .04. Results showed that statistical learning influenced oral language and phonological processing; however, the word segmentation and Simon tasks significantly explained different variance in these skills (see Fig. 1).

As the next step in our analysis, we examined several additional models to assess the extent to which the statistical learning tasks account for similar amounts of variance in the oral language/vocabulary and phonological processing factors. We accomplished this by imposing different equality constraints on the model shown in Fig. 1 as a means of testing whether each of the statistical learning tasks were, in fact, uniquely predicting performance in oral language and phonological processing: constraining paths from Simon and word segmentation tasks to the Oral Language factor to equality (Model A); constraining paths from Simon and word segmentation tasks to the Phonological Processing factor to equality (Model B); constraining paths from the Simon task to the Oral Language and Phonological Processing factors to equality (Model C); and constraining paths from word segmentation task to the Oral Language and Phonological Processing factors to equality (Model D). Model fit indices can be found in Table 4.

Table 4.

Comparison of model fit statistics for SEM models imposing various constraints

Indices	Model A	Model B	Model C	Model D
χ2	109.08	105.03	106.14	107.97
df	66	66	66	66
p	<.001	<.01	<.01	<.001
RMSEA	.04	.04	.04	.04
p	.85	.89	.88	.86
SRMR	.05	.04	.04	.04
CFI	.96	.96	.96	.96
TLI	.94	.95	.95	.94
AIC	17,064.85	17,060.80	17,061.91	17,063.74
BIC	17,238.33	17,234.29	17,235.40	17,237.22

Model A constrained paths from the Simon and word segmentation tasks to Oral Language factor to equality. Model B constraining paths from Simon and word segmentation tasks to Phonological Processing factor to equality. Model C constrained paths from the Simon task to Oral Language and Phonological Processing factors to equality. Model D constrained paths from the word segmentation task to Oral Language and Phonological Processing factors to equality χ² Chi square, df degrees of freedom, RMSEA root mean square error of approximation, SRMR standardized root mean square residual, CFI comparative fit index, TLI Tucker–Lewis index, AIC Akaike information criteria, BIC Bayesian Information Criteria

If model constraints led to a significant degradation in model fit (i.e., significant chi-square difference values between our original unconstrained model and the constrained model), this would indicate that the path estimates from the word segmentation and Simon tasks to oral language/vocabulary and phonological processing were not equivalent. Because the four constrained models were non-nested, the Akaike Information Criteria and Bayesian Information Criteria values were used for model comparisons. Of these four models, constraining paths from the word segmentation and Simon tasks to the Phonological Processing factor to equality (Model B) provided better fit than did Models A, C, and D (see Table 4). Model B provided an excellent fit to the data. This model had a significant chi-square probability χ²(66) = 105.03, p < .01.CFI and TLI values were .96 and .95, respectively. For the constrained model, RMSEA = .04; SRMR = .04. For Model B, all factor loadings and path estimates remained identical to the unconstrained model with the exception of the path from word segmentation to phonological processing, which was significant within the constrained model (.003, p < .05). Therefore, the Simon task significantly predicted variance in phonological processing, and the word segmentation task predicted variance in both oral language and phonological processing.

Chi square difference testing revealed no significant difference between our original unconstrained model and the constrained model (Model B; χ² difference = .13 with 1 degree of freedom), which indicated that the more parsimonious model—the constrained model—was the preferred model. Thus, additional model testing suggested that the word segmentation task significantly predicted performance on both the oral language/vocabulary knowledge and the phonological processing tasks, whereas the Simon task predicted performance only on the phonological processing tasks.

DISCUSSION

The purpose of this study was to assess the extent to which statistical learning abilities were related to early literacy components and to assess the degree to which different aspects of statistical learning were related to those literacy components. We had two research hypotheses and associated predictions. First, consistent with previous work showing a relation between statistical learning and oral language and vocabulary outcomes (e.g., Arciuli & Simpson, 2012; Conway et al., 2010, 2011; Evans et al., 2009), we expected that our statistical learning measures would be related to early literacy skills. This prediction was confirmed, as we found a small but reliable relation between our measures of statistical learning and our measures of literacy skills. Statistical learning, thus, appears to be related to three central components of early literacy—oral language skill, vocabulary knowledge, and phonological processing. This finding is also in line with previous investigations that suggest that poor implicit learning is related to literacy-based deficits (e.g., Lum, Ullman, & Conti-Ramsen, 2013; Stoodley et al., 2008; Vicari et al., 2005).

Regarding our second hypothesis, we predicted that the Simon task, which is an integrative statistical learning task, would be related to phonological processing, such as has been found by others (e.g., Kuhl, 2004). This prediction was confirmed. However, in contrast to past studies that suggested a contribution of learning of distributional information (as exemplified by the Simon task) to other aspects of language, such as lexicon (e.g., Landauer & Dumais, 1997) and syntax (e.g., MacDonald & Christiansen, 2002), the performance on the Simon task did not significantly predict performance on our measures of oral language/vocabulary.

Based on findings from previous studies (e.g., Evans et al., 2009), we expected that the word segmentation task, which is an extraction statistical learning task, would be related to oral language and vocabulary knowledge. This prediction was confirmed. Word segmentation is a key process for splitting the speech stream into units (e.g., Saffran et al., 1996), thus providing an important foundation for oral language skills and the development of vocabulary. Although we were unsure if the word segmentation task would also predict performance on the phonological processing task, the results indicated a slight but significant contribution of word segmentation to phonological processing. If one considers phonemes and syllables to be discrete units that need to be extracted from the speech stream, it may explain why the word segmentation task significantly predicted phonological processing. However, it should be noted that the contribution of the word segmentation task to variability in the acquisition of phonological knowledge was small. Thus, this finding should be approached cautiously.

Implications

Our results make at least two important contributions to understanding the relation between statistical learning and literacy. First, we replicated the finding of a relation between statistical learning and literacy and language skills (e.g., reading ability, vocabulary knowledge) with both a larger and more diverse sample of individuals, and a broader range of tasks, than had been used in previous studies (Arciuli & Simpson, 2012; Apfelbaum et al., 2013; Evans et al., 2009). In this regard, it is interesting to note that the relation observed in our study was somewhat weaker than that observed by Arciuli and Simpson (2012; see also Evans et al., 2009). Future work will be needed to determine whether this difference is due to the nature of the samples used in both studies, the nature of the tasks used, or some combination of both factors. A second key finding of our study is that the relation between statistical learning and literacy development is not monolithic—extraction and integration processes of statistical learning are differentially related to component literacy skills. This finding lends credence to Thiessen et al.’s (2013) claim that there are distinct processes involved in statistical learning.

The present findings have several practical implications for both educators and researchers. First, the fact that statistical learning is related to early literacy skills may have implications for the design of instructional materials as well as more targeted literacy interventions. For instance, Apfelbaum et al. (2013) demonstrated that the statistical structure of their training materials had implications for how well first graders were able to learn and generalize particular grapheme-to-phoneme relations, which is, in turn, predictive of reading comprehension skill (Ehri, 1998; Snowling, 1980). The generality of the relation between statistical learning and literacy development suggests the possibility that training in other domains of literacy skills (such as reading in a second language; Frost et al., 2013) may likewise benefit from a consideration of the probabilistic structure of the instructional materials that are provided. Additionally, our results have implications for the delivery of classroom-based instruction, as it has been argued that students’ knowledge accumulation is due to the interactivity of implicit (e.g., extracting regularities from text) and explicit instruction (Gombert, 2003), further suggesting that implicit instruction (i.e., statistical learning) is a potentially important component of academic success.

On a theoretical level, our findings provide initial support for Thiessen et al.’s (2013) claim that there are two components—extraction and integration—involved in statistical learning. Our findings extend this approach by demonstrating that extraction and integration may play different roles in the acquisition of literacy skills. Future work should be aimed at exploring the ways that these processes support children’s ability to learn to read. For example, it is possible that the extractive and integrative elements of statistical learning become more or less important at different phases of both the language and literacy acquisition processes. Both processes may be important during early stages of literacy acquisition, when individuals are relying more heavily on various sources of information to aid their understanding of written and spoken language. Extractive processes may become less important when literacy skills approach maturity and reading becomes more automatic (i.e., readers rely more on integrative processes as they learn to exploit their knowledge about broad patterns of language use to become more fluent comprehenders).

As researchers consider the role of extraction and integration processes in the acquisition of literacy skills, it will be necessary to determine whether extraction and integration are monolithic process categories (i.e., there is one “extraction” process, and one “integration” process), and whether the range of tasks used to measure these processes are all tapping into the same underlying skill or construct. To our knowledge, there are no published studies that explore the extent to which different statistical learning tasks assessing the same process (e.g., the Simon task and Serial Response Tasks both require integration processes) are in fact tapping into the same underlying abilities. A key future direction for studies of this sort will therefore be to develop our understanding of the psychometric properties of the various statistical learning tasks that have been used in the literature (see Erickson, Kaschak, Thiessen, & Berry, under review, for a discussion).

It is important to acknowledge several limitations of the current study. First, one qualification to our assertion that extraction and integration elements of statistical learning play different roles in the acquisition of literacy skills is that we used single tasks to represent each learning process. These tasks differed on several dimensions (e.g., the word segmentation task is “linguistic” and auditory, and the Simon task is “non-linguistic” and visual). Although it is not immediately obvious why such differences would produce the results that we observed, we acknowledge that it will be important to replicate our findings with a broader range of extraction and integration tasks in order to shore up the claim that these processes are differentially related to literacy acquisition. Based on the present study, it is difficult to tease apart whether the observed differences in variance accounted for by the two measures of statistical learning were due to the differing cognitive processes of extraction and integration or a result of differences related to task characteristics (e.g., modality; Conway & Christiansen, 2005, 2006). Second, because our data are correlational, we can only describe the relations between statistical learning and oral language/vocabulary knowledge and phonological processing. We are unable to make definitive causal statements about our findings to say that statistical learning caused the observed differences in these literacy skills. Third, because our study focused exclusively on younger children, we are unable to draw conclusions about the relations between these skills for children in the older grades (e.g., late-elementary and middle school), and it is certainly possible that relations between these skills may be subject to developmental influences and change over time. Finally, the nature of the present study does not shed light on whether statistical learning abilities are malleable for instruction and/or intervention. Thus, it is important to replicate this study including additional measures of statistical learning, other cognitive abilities (e.g., IQ), and different samples.

Although further investigation is required to determine whether statistical learning abilities are malleable and represent a viable target for intervention, our results suggest that statistical learning is a significant predictor of literacy-related outcomes for preschool and early elementary-aged children and that different statistical learning processes are uniquely predictive of oral language/vocabulary knowledge and phonological processing. At least in the earlier grades, statistical learning appears to be an influential component of academic success that deserves greater attention.