The Comparative Study of Metacognition: Sharper Paradigms, Safer Inferences

Abstract

Results that point to animals’ metacognitive capacity bear a heavy burden given the potential for competing behavioral descriptions. This article uses formal models to evaluate the force of these descriptions. One example is that many existing studies have directly rewarded so-called “uncertainty” responses. Modeling confirms that this practice is an interpretative danger because it supports associative processes and encourages simpler interpretations. Another example is that existing studies raise the concern that animals avoid difficult stimuli not because of uncertainty monitored but because of aversion given error-causing or reinforcement-lean stimuli. Modeling also justifies this concern and shows that this problem is not addressed by the common practice of comparing performance on Chosen and Forced trials. The models and related discussion have utility for metacognition researchers and theorists broadly because they specify the experimental operations that will best indicate a metacognitive capacity in humans or animals by eliminating alternative behavioral accounts.

Humans feel uncertain when they do not know or remember. They often respond appropriately to these feelings. These responses are the empirical phenomena that ground the literature on metacognition (Flavell, 1979; Koriat, 1993; Nelson, 1992; Schwartz, 1994). The idea in this literature is that a cognitive executive in mind monitors perception and memory, judging its progress and prospects. This happens, for example, when we realize the difficulty of a passage in a scientific article and make deliberate efforts to grasp its meaning. These monitoring functions are assessed in the laboratory by collecting metacognitive judgments (e.g., feelings of knowing, confidence ratings).

Researchers take humans’ metacognitive behavior to indicate important aspects of mind. They link metacognitive states to self-awareness (because uncertainty and doubt are so personal and subjective—Gallup, 1982) and to declarative consciousness (because humans so easily introspect and communicate these states—Koriat, 2007; Nelson, 1996). Metacognition is one of humans’ sophisticated cognitive capacities and it could be uniquely human (Metcalfe & Kober, 2005). This possibility makes it important to ask whether nonhuman animals (hereafter animals) have a similar capacity.

Accordingly, Smith and his colleagues inaugurated a new area of comparative inquiry by asking whether animals have a capacity for cognitive monitoring (Shields, Smith, & Washburn, 1997; Smith, Schull, et al., 1995; Smith, Shields, Allendoerfer, & Washburn, 1998; Smith, Shields, Schull, & Washburn, 1997). Active research continues in this area (Beran, Smith, Redford, & Washburn, 2006; Call & Carpenter, 2001; Foote & Crystal, 2007; Hampton, 2001; Inman & Shettleworth, 1999; Kornell, Son, & Terrace, 2007; Washburn, Smith, & Shields, 2006; see reviews in Smith, Shields, & Washburn, 2003; Smith & Washburn, 2005; Smith, 2007). In some of these studies, researchers presented a mix of easy and difficult trials. They gave animals (a dolphin, monkeys, pigeons, and rats) an additional response—beyond the primary discrimination responses—that let them decline to complete any trials they chose. Animals who accurately monitor cognition should recognize difficult trials as error-risking and decline those trials selectively. Some animals do so and produce data patterns in cognitive-monitoring tasks like those of humans. This additional response has come to be called the uncertainty response, and it is presently interpreted to show some species’ capacity for uncertainty monitoring and metacognition.

If this interpretation is correct, these experiments tap theoretically important cognitive capacities in animals. They raise intriguing issues about animal mind, awareness, and consciousness, though they do not resolve them. They could help cognitive scientists reflect on the phylogenetic roots of human metacognition. They could also sharpen theoretical questions about human metacognition (e.g., how explicit is human cognition if animals show a more implicit form of this capacity; how dependent is human metacognition on verbal-symbolic representations if animals show a nonverbal form of this capacity). Finally, these experiments could also help reveal the ontogenetic roots of human metacognition. The simple, nonverbal, perceptual tasks suitable for animals are more appropriate for young human children than are the complex, verbal, and introspective metacognitive assessments that young children normally fail (Acredolo & O’Connor, 1991; Brown et al., 1983).

However, this area of comparative research bears a heavy interpretative burden, for there is a long tradition in comparative psychology (e.g., Morgan, 1906) of explaining behavior at the lowest possible psychological level. Thus, even given performances by some animals that might indicate metacognition and uncertainty monitoring, one must consider carefully the alternative possibility that these performances might be explained using simpler, associative mechanisms.

The existing paradigms illustrate this tension between explanatory frameworks. They often combine a psychophysical discrimination (in which one presents a range of trial difficulties including difficult trials near participants’ perceptual thresholds) with an uncertainty response (with which participants can decline to complete trials). In Foote and Crystal (2007), the task was a duration discrimination in which Short or Long responses were correct for durations shorter or longer than 4 s. In Smith et al. (1997), the task was a density discrimination in which Sparse or Dense responses were correct for sparser or denser pixel boxes. In both tasks, difficulty was varied to map participants’ response patterns in the region surrounding the breakpoint of the discrimination where rats could hardly tell Short from Long or monkeys Sparse from Dense. In fact, rats and monkeys most often declined the difficult trials near this breakpoint. These tasks ground the simulations in the present article.

These paradigms illustrate some ongoing methodological concerns in the comparative metacognition literature. First, Foote and Crystal (2007) rewarded animal participants directly for their uncertainty responses. That is, rats were not only rewarded with food for every correct Short or Long response, but they also received a smaller food reward whenever they declined a trial. This is a common practice. Kornell et al. (2007) gave monkeys a reward for every uncertainty response because their animals were biased against making that response. Hampton (2001) gave monkeys food pellets for uncertainty responses compared to highly desired peanuts for correct responses. Suda-King (2007) gave orangutans one grape for uncertainty responses compared to two grapes for correct responses. Inman and Shettleworth (1999) gave pigeons small grain rewards for uncertainty responses compared to large grain rewards for correct responses. The potential problem with this approach is that it might grant the uncertainty response its own associative response strength independent of any uncertainty role it plays in a task. It might be used because of its reward properties. Thus, it is important to understand what role these reward properties play in existing comparative studies of animal metacognition, and in particular whether these properties could by themselves, absent any metacognitive assessment by the animal, produce the observed data patterns. One purpose of the present formal analyses is to evaluate this possibility. This evaluation is especially important given that many studies have used these food-rewarded uncertainty responses.

Smith et al. (1997) illustrated a second potential problem with uncertainty paradigms. Researchers generally make reinforcement transparent by giving feedback on every trial. Every consequence is experienced and can be associated to the stimulus-response pairing that produced the negative or positive outcome. In particular, monkeys in Smith et al. (1997) were often wrong when they made Sparse or Dense responses for threshold stimuli. Then they were denied rewards and received a timeout period. Perhaps, then, the threshold stimuli and Sparse and Dense responses in those stimulus contexts came to be aversive for the monkeys. Perhaps they were conditioned not to use those responses in those stimulus contexts. In contrast, when monkeys declined threshold stimuli, the outcome—a transition to the next trial—was in a sense more neutral. Perhaps, then, the monkeys were conditioned to use the uncertainty response in those stimulus contexts. If so, the function of the uncertainty response would have been to avoid aversive stimuli, not to express uncertainty about difficult trials. Aversion-avoidance and uncertainty monitoring are different psychological interpretations at different psychological levels. A second purpose of the present formal analyses is to evaluate the weight this associative interpretation should be given. We deliberately target our own paradigm in this case to make it clear that we include our own research in this article’s partially negative assessment.

The paradigm of Foote and Crystal (2007) also illustrates the common attempt to address the aversion-avoidance confound by intermixing trials in which the animal can choose to respond uncertain with trials in which the animal is forced to complete the trial. The rationale behind this approach is as follows. Animals may have privileged metacognitive knowledge about whether they will likely get a trial correct. If so, then when they choose to accept a trial (by not responding uncertain), they should show strong performance because they will accept the trials that have a good metacognitive feel. In contrast, Forced trials would include some felicitous trials the animal would have accepted and some trials the animal would have declined because they had a bad metacognitive feel. Thus, animals should show poorer performance on Forced trials than on Chosen trials. There is a current view that this Chosen-Forced advantage protects one from associative interpretations based in aversion, avoidance, and reinforcement history, and that it is a strong index for animal metacognition (see also Inman & Shettleworth, 1999; Hampton, 2001). On this point, Foote and Crystal (2007, p 553) suggested that “the observed difference in accuracy between choice and forced tests is not predicted by differential reinforcement associated with specific stimulus durations.” However, this suggestion does not seem to have been formally evaluated, and doing so is critical for the interpretation of several influential experiments. The third purpose of the present formal analyses is to make this evaluation.

We emphasize that all the experiments discussed in this article have strengths, that all of them met admirably the challenge of asking animals a difficult experimental question, and that all of them have combined, in a short time, to produce a sophisticated and intriguing research area. Nonetheless, regarding the research in this area, including our own, it seems constructive to outline residual concerns and evaluate alternative explanatory frameworks in this growing field. There may be practices that cannot be endorsed because they produce data patterns that are too threatened by confounding associative interpretations. But there may also be ways to sharpen the field’s paradigms so that they allow the strongest inference about a metacognitive capacity in nonhuman animals because they are safest from associative interpretations. In fact, this is the fourth purpose and overarching goal of the present article.

General Method

Our simulation methodology and modeling framework were described previously (Smith et al., 2003). They use standard perceptual and decisional processes that have been incorporated into many articles on animal perception (e.g., Stebbins, 1970). They provide a unifying description of performance by supporting cross-task and cross-species comparisons among data patterns. They let us illustrate important paradigms so that their behavioral and performance implications can be evaluated.

Our models are grounded in Signal Detection Theory (SDT – MacMillan & Creelman 1991). SDT assumes that performance in perceptual tasks is organized along an ordered series (a continuum) of psychological representations of changing impact or increasing strength. In a duration- or density-judgment task, for example, the continuum of subjective impressions would run from clearly short to clearly long or clearly sparse to clearly dense. In typical metacognition tasks, these continua would have a discrimination breakpoint in the middle. One primary discrimination response or the other would be correct for trials below or above this breakpoint.

Following SDT, we also assume that the objective stimulus presented on each trial is perceived with some degree of perceptual error. Thus, objective stimuli actually create, from trial to trial, subjective impressions scattered in a Gaussian distribution around the mean value established by the stimulus. An observer’s perceptual error can be summarized by the standard deviation of that normal distribution (i.e., how far are subjective impressions generally scattered from trial to trial around objective stimulus values).

We also assume that the observer establishes response regions by placing decision criteria along the continuum of subjective impressions. By the usual metacognitive interpretation of the referent experiments, one would assume that there are upper and lower criteria defining three response regions, the leftmost reserved for one primary discrimination response, the rightmost for the other discrimination response, and the middle region demarcating problematic subjective impressions that might be from either stimulus class and that should receive uncertainty responses.

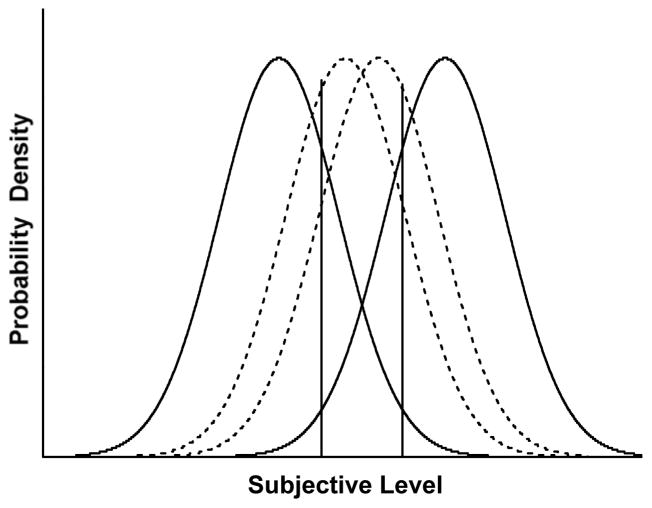
Figure 1 illustrates the formal situation. The Gaussian distributions show the ranges of subjective impressions engendered by four objective stimuli along a perceptual continuum. The outer distributions represent trials farther from the breakpoint of the discrimination that would often be answered correctly. The inner distributions represent difficult stimuli nearer the discrimination’s breakpoint. The overlap between these distributions shows that fairly often opposing trial types create identical psychological impressions. This causes errors and fosters uncertainty in the task—both kinds of trials can feel alike to the perceiver. The Uncertain response region between the two criterion lines would let the observer avoid many of these trials.

Figure 1.

A signal detection theory (SDT) portrayal of performance in a discrimination task with an uncertain response sometimes allowed. The horizontal axis indicates the subjective impression of the trial. The range of subjective impressions engendered by four objective trial levels is also shown (normal distributions). The observer would obey the two criterion lines, making one or the other primary discrimination response for impressions below the left criterion or above the right criterion. Subjective impressions in between would be declined.

The first two simulations illustrate our modeling framework and show how it recovers two influential results in the comparative metacognition literature.

Simulation 1: Illustrating the Short-Long Metacognition Paradigm

Method

Foote and Crystal’s (2007) Short-Long paradigm was grounded in a duration continuum that runs from 2 s (Short) to 8 s (Long), spanning 71 steps in which each logarithmic step defines a duration that is 2% longer than the last. Foote and Crystal used Levels 1, 11, 21, 31, 41, 51, 61, and 71 along this continuum, with Level 36 the discrimination breakpoint.

To illustrate a metacognitive performance in this task, we placed along the 71-step continuum a Short-Uncertainty criterion at Level 23 and an Uncertainty-Long criterion at Level 49. This produced a 26-Step uncertainty region, centered on the breakpoint (36) and adaptive for allowing the simulated observer to avoid the difficult trials near that breakpoint. We gave the simulated observer a perceptual error of 18, close to that observed by Foote and Crystal (2007). That is, we gave Figure 1’s normal distributions a standard deviation of 18. These choices were made pragmatically to provide a typical data pattern and an appropriate target for fitting by alternative formal frameworks.

Foote and Crystal (2007) followed the common practice to intermix Forced trials—in which observers must make a primary discrimination response (e.g., Short or Long)—and Chosen trials—in which they can either accept the discrimination trial (responding Short or Long) or decline it. In Simulation 1, we let our simulated observer be guided by the Short-Uncertainty and Uncertainty-Long criteria on Chosen trials, because all three responses were then available. On Forced trials, we made the simulated observer be guided by a Short-Long criterion, because in this case its only response options were Short or Long. This criterion was set at Level 36, the unbiased and optimal strategy.

We gave the simulated observer 10,000 Forced and 10,000 Chosen trials at each duration level (1–71). Objective durations were scattered into subjective impressions through the application of Gaussian perceptual error. On Forced trials, the observer responded Short or Long to impressions that were below or above the Short-Long criterion, and guessed for impressions at criterion. On Chosen trials, the observer made Short responses to impressions at or below the Short-Uncertainty criterion, Long responses to impressions at or above the Uncertainty-Long criterion, and Uncertain responses for impressions in between.

Results

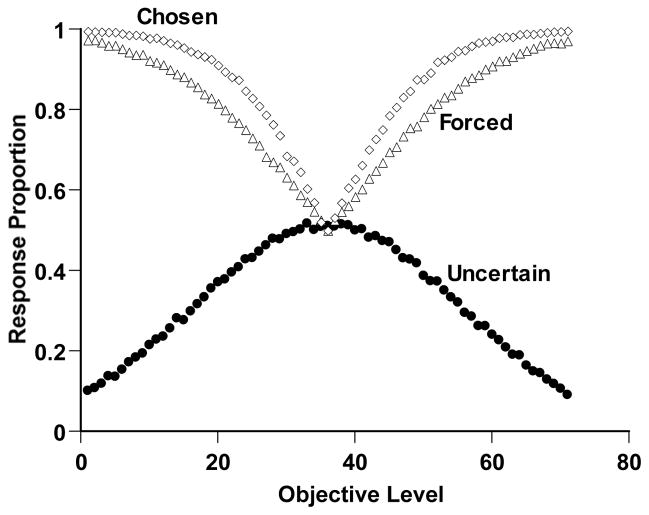
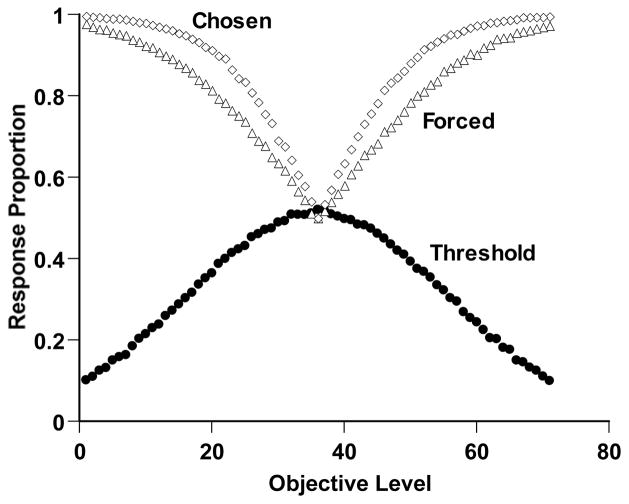
Figure 2 shows the performance of this simulated observer. The open diamonds and open triangles, respectively, show the proportion of correct responses on Chosen and Forced trials. For short- or long-duration trials, respectively, the observer was mostly able to respond Short or Long correctly. The greater difficulty of the middle region of the continuum is reflected in the decreasing performance levels there for both Chosen and Forced trials. The simulated observer responded adaptively to this difficulty by responding uncertain for more trials in this region (filled circles). Finally, the Chosen-Forced performance advantage—a crucial result in several studies—is also expressed by this simulation. Chosen trials were more often answered correctly. The metacognitive interpretation of this result is that the Chosen trials reflect performance on a population of trials that were mostly answered correctly because they were motivated by a positive metacognitive assessment. In short, Simulation 1 captures, using an established formal framework, the components of an influential metacognitive performance that animals have recently shown. It also provides a target phenomenon within the present article.

Figure 2.

Temporal-duration discrimination performance by a simulated observer in Simulation 1 that performed as illustrated in Figure 1. Details of the simulation are described in the text. The horizontal axis indicates the objective duration of the trial (Levels 1–35 Short; Levels 37–71 Long). The open diamonds and open triangles, respectively, show the proportion correct the observer achieved on the trials it chose to complete or was forced to complete. The filled circles show the proportional use of the uncertainty response for different trial levels.

As a reliability check, we reran the same configuration of the model (18-23-49-36) for 10,000 Chosen and Forced trials at 71 levels. Across the two runs of the simulation, we compared the 213 corresponding response proportions (i.e., proportions of Uncertain, Chosen correct, and Forced correct trials at 71 levels). We calculated the Sum of the Squared Deviations (SSD) and the Average Absolute Deviation (AAD) between the two data patterns. The SSD was 0.008. The AAD was 0.005, meaning that pairs of observations in the two runs differed by 0.5%. The two performances were essentially identical. Though this is not surprising, this analysis provides a benchmark of reproducibility that will be useful below.

Simulation 2: Illustrating the Sparse-Dense Metacognition Paradigm

Method

The Sparse-Dense paradigm uses a continuum of the pixel density within a box shown on a computer screen. The paradigm can be illustrated using a continuum spanning 41 steps, with Level 21 its breakpoint, and with each logarithmic step defining a density 1.8% greater than the last.

To illustrate a metacognitive performance in this task, we placed a Sparse-Uncertainty criterion at Level 16 and an Uncertainty-Dense criterion at Level 26. This produced a 10-Step uncertainty region, centered on the discrimination breakpoint (21) and adaptive for allowing the simulated observer to avoid the most difficult trials. We gave the simulated observer a perceptual error of 7, close to that observed by Smith et al. (1997). Once again these pragmatic choices produced a typical data pattern suitable for model fitting by alternative formal frameworks.

As in research on the Sparse-Dense task, all trials were Chosen in the sense that three responses were always available. We gave the simulated observer 10,000 trials at each objective density level from 1 to 41, except that trials at the breakpoint (Level 21) were not given. Each objective density was scattered into a subjective impression through the application of Gaussian perceptual error. The observer made Sparse responses to impressions at or below the Sparse-Uncertainty criterion, Dense responses to impressions at or above the Uncertainty-Dense criterion, and Uncertain responses for subjective impressions in between.

Results

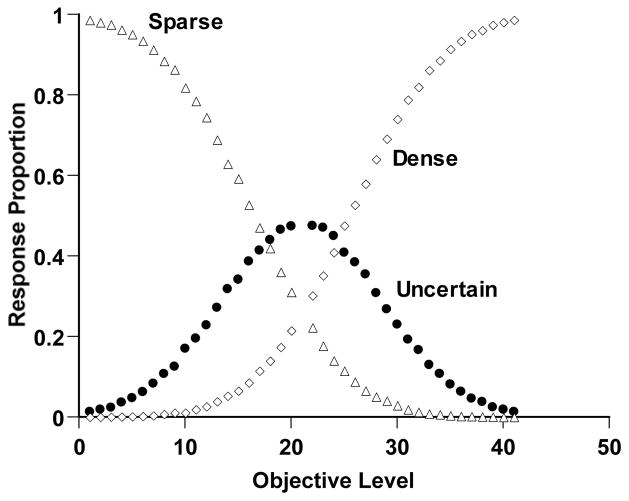
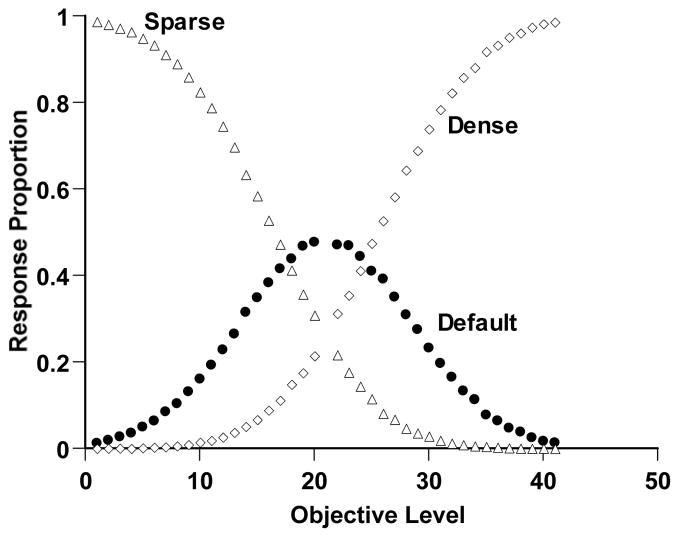
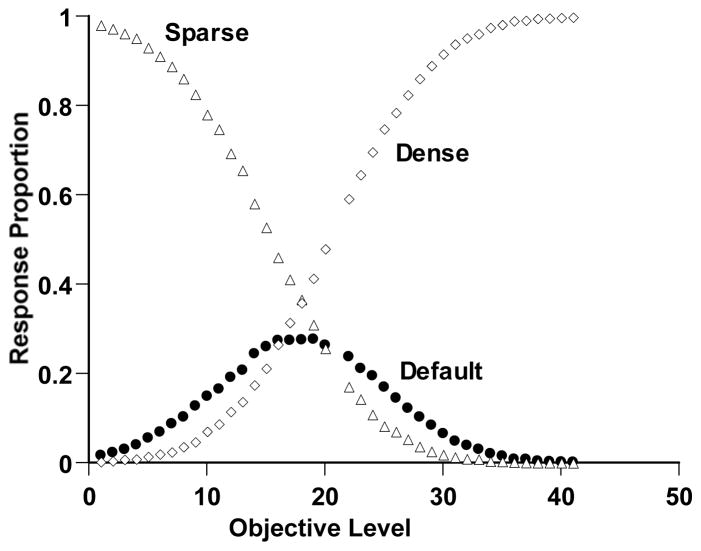
Figure 3 shows the performance of this simulated observer. The open triangles and diamonds show the proportion of Sparse and Dense responses, respectively. For clearly sparse or dense trials, the observer mostly responded Sparse or Dense correctly. The observer’s discriminative capacity waned moving toward the discrimination’s breakpoint. The simulated observer responded adaptively to this difficulty by responding uncertain for more trials in this region (filled circles). Thus, Simulation 2 reproduced the components of a second kind of metacognitive performance that animals have recently shown. It provides another target phenomenon within the present article.

Figure 3.

Sparse-Dense discrimination performance by a simulated observer in Simulation 2. Details of the simulation are described in the text. The horizontal axis indicates the objective density of the trial (Levels 1–20 Sparse, Levels 22–41 Dense). The open triangles and diamonds, respectively, show the proportion of Sparse and Dense responses. The filled circles show the proportional use of the uncertainty response for different trial levels.

As a reliability check, we reran the same configuration of the model (7-16-26) and compared the two data patterns. Across the 120 corresponding response proportions (i.e., Sparse, Dense, and Uncertain response proportions at 40 levels), we found an SSD of 0.002 and an AAD of 0.003, meaning that on average pairs of observations in the two runs differ by 0.3%. The two performances were essentially identical. Once again, this analysis provided a benchmark of reproducibility.

Simulations 1 and 2 used an SDT framework to illustrate some basic phenomena in the animal metacognition literature. We point out that the ability to recreate a phenomenon with continua and criteria does not imply or rule out that that phenomenon is associative or metacognitive. For example, human performances could be modeled in this way, even if those performances were explicit, conscious, meta-representational and metacognitive. In our view, interpreting the behavioral phenomena illustrated by these simulations depends on understanding the representations and processes that underlie the target performances by animals, not on the suitability of these phenomena for SDT modeling. Nonetheless, there are serious concerns about the nature of the underlying representations and processes, and we turn to these now.

Simulation 3: Rewarded Uncertainty Responses and Stimulus Generalization

The most common interpretation of positive findings in animal metacognition experiments is that the animals are incorporating into their response pattern both their perception of the stimulus and their self-judged level of confidence about knowing its correct answer. This interpretation has profound implications regarding the general character and cognitive level of animal minds.

However, we know that many studies have introduced an additional factor into the situation by directly rewarding uncertainty responses with food or with highly desired food tokens (Foote & Crystal, 2007; Hampton, 2001; Inman & Shettleworth, 1999; Kornell et al., 2007; Suda-King, 2007). This fact has created concern in the field (e.g., Smith et al., 2003, Section R4.2) because it raises the possibility that animals might be motivated by these rewards more than by uncertainty when they make “uncertainty” responses. But this concern has apparently never been evaluated systematically.

This was the purpose of Simulation 3. It incorporates two established associative- behaviorist principles and asks whether a system that operated by these associative rules would produce a metacognitive data pattern like that observed in the literature. Simulation 3 embodies a particularly strong test of this associative mechanism. It lets us evaluate whether one could—using only parameters based in simple associative principles—recover exactly the metacognitive performance already shown in Figure 2. The implications are serious if one can. Then one would know that associative and metacognitive interpretations are direct theoretical rivals—on par with each other when the uncertainty response is directly rewarded—with neither having explanatory precedence. Then one would have to consider letting theoretical parsimony and Morgan’s Canon recommend against the metacognitive interpretation.

Method

Simulation 3 was constructed using the 71-step duration continuum and the Short and Long discrimination regions already described. We incorporated SDT’s Gaussian formulation of perceptual error and we let simulated observers respond to their subjective impressions of stimuli. As before, we gave simulated observers a mix of Forced trials—in which they were forced to make a primary discrimination response (Short or Long)—and Chosen trials—in which they could either accept the discrimination trial (responding Short or Long) or decline it.

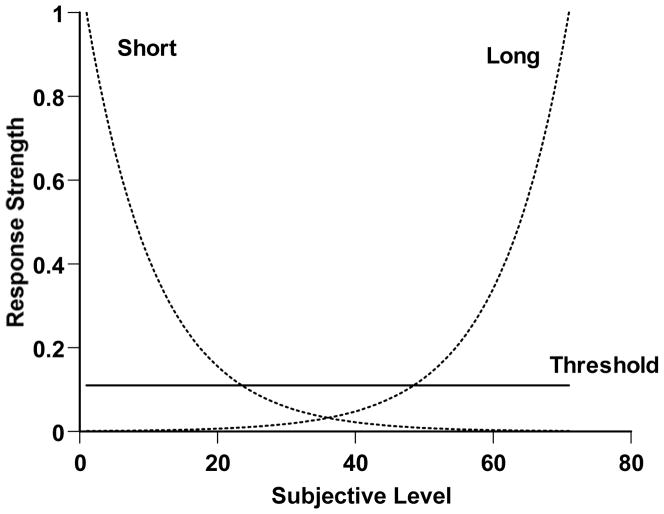
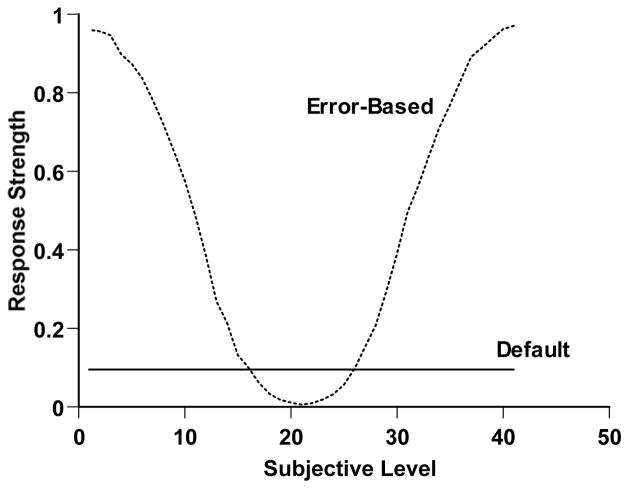
The response decisions in Simulation 3 were made differently, though. First, we addressed the direct reward for uncertainty responses. We assumed that this gave that response a constant attractiveness across the duration continuum (i.e., in every trial context), because the uncertainty response would bring the same reward in every case. This threshold attraction level is shown as the horizontal line in Figure 4. The level of the threshold was a free parameter in our modeling. As it was set higher, the simulated observer would tend to choose the uncertainty response more often.

Figure 4.

A stimulus-generalization/response-strength portrayal of performance in a temporal-duration discrimination with a third response sometimes allowed and directly rewarded. The horizontal axis indicates the subjective impression of the trial. The solid line instantiates the idea that the directly rewarded third response would have a constant response strength or attraction across the range of trial levels. The otted lines instantiate the idea that response strength for the Short and Long responses would wane exponentially going inward away from the task’s anchors (Level 1 and Level 71).

Second, we addressed the attractiveness of Short and Long responses in different stimulus contexts. We assumed that Level 1 and Level 71 stimulus durations anchored the discrimination. In many studies, these stimuli would lead off in training, would dominate the early stages of training, and would even dominate later testing, with intermediate values interspersed occasionally as probe trials. Level 1 and Level 71 stimuli would also be the clearest tokens of the duration categories and would receive the highest levels of correct Short and Long responses.

We assumed that there was an exponential-decay function from these anchor stimuli in to the middle regions of the continuum, so that generalization to the anchor stimuli faded rapidly at first, then more slowly. This shape for the generalization function incorporated extensive empirical and theoretical contributions by Shepard (Shepard, 1987, 1994) who showed that confusions between stimuli are an exponential-decay function of the psychological distance between them. The sensitivity parameter of the exponential-decay function, that governs the steepness of the decay, became a free parameter (sens) in our model. For any subjective impression of duration, we calculated the distance (dist) from the impression to each anchor in steps along the continuum, and took the quantity e^−sensXdist to be the response strength for making each response given that subjective impression.

Figure 4 shows these generalization functions proceeding inward from both perceptual anchors in the task. Simulated observers had progressively weaker Short or Long response tendencies as subjective impressions were farther from the anchors. Figure 4 shows the response strategy that simulated observers obeyed in Simulation 3. On Forced trials, they simply responded according to which generalization curve was higher at the point of their subjective perceptual impression—that is, in accord with the anchor their subjective impression was closer to. On Chosen trials, they responded according to the greatest response strength among all three responses, including the constantly attractive uncertainty response. For Level 1 and Level 71 stimuli generally, the organism would be attracted correctly to the Short or Long response, respectively. For Level 31 and 41 stimuli generally, the organism would make more uncertainty responses. In the discrimination’s difficult middle, the constant threshold response strength is higher than that of the generalization-based response strengths.

This modeling procedure, using distance, sensitivity, exponential decay, and threshold, was decided a priori, with no prior knowledge of what would occur, and with only the disciplined instantiation of Shepard’s generalization theory and the intuitive instantiation of the automatic rewards for uncertainty responses.

Procedures for fitting formal models

Simulation 3’s goal was to reproduce the outcome of Simulation 1. Accordingly, we sampled a range of threshold values and sensitivity values. For each configuration of the model in Simulation 3 (i.e., for each set of parameter values), we ran that simulated observer for 10,000 Forced and Chosen trials at 71 stimulus levels. We compared its 213 response proportions (i.e., proportions of Uncertain, Chosen correct, and Forced correct trials at 71 stimulus levels) to the corresponding values from Simulation 1. Across configurations of the model, we minimized the SSD between the two sets of performance values.

Results

Figure 5 shows the performance of the simulated observer that best recovered Figure 2’s data pattern. This best-fitting observer had sensitivity and threshold parameters of 0.098 and 0.110, respectively. Simulation 3, using only response strengths, reproduced Figure 2 exactly. The SSD between the corresponding values in Figures 2 and 5 was 0.006. The AAD per data point in the two graphs was 0.004—on average, pairs of observations in the two graphs differed by 0.4%. In short, the response-attraction model reproduced the metacognitive pattern shown in Figure 2 as well as did the second run of the metacognitive model offered as a reliability check above. When the uncertainty response was directly rewarded, simple stimulus-generalization and response-strength principles reproduced perfectly an apparently metacognitive performance.

Figure 5.

Temporal-duration discrimination performance by a simulated observer in Simulation 3 that performed as illustrated in Figure 4. Details of the simulation are described in the text. The horizontal axis indicates the objective duration of the trial (Levels 1–35 Short; Levels 37–71 Long). The open diamonds and open triangles, respectively, show the proportion correct the observer achieved when it used the most attractive response from among 3 options (Chosen trials) or 2 options (Forced trials). The filled circles show the proportion of trials on which the response strength for the third response was highest.

We redid this model-fitting process, paying careful attention to the logarithmic properties of the duration continuum. The stimulus-generalization model was still able to fit the metacognitive target with an SSD of 0.028 and an AAD of 0.009. The only difference in this case was that both graphs now showed the expected logarithmic compression toward the shorter-duration regions of the temporal-duration continuum.

We also tested the ability of the stimulus-generalization model to fit variations in the metacognitive data pattern. We reran Simulation 1 to produce 49 metacognitive data patterns for the model to fit. Across these 49 targets, we varied perceptual error from 9 to 27 in 3-step intervals, and we varied the width of the uncertainty region from 8 (criteria at Levels 32 and 40) to 44 (criteria of 14 and 58) in 6-step intervals. The stimulus generalization model fit the 49 metacognitive data patterns with an average SSD and AAD of 0.033 and 0.009, respectively, proving this model’s robustness in the face of varying perceptual errors and varying uncertainty-region widths.

Simulation 4: Reinforcement History and Stimulus Aversion-Avoidance

Another ongoing concern in the comparative metacognition area is that almost every study gives animals trial-by-trial feedback. When consequence and reinforcement are transparent in this way, the organism can track and tabulate in memory the outcomes that accompany different impression-outcome combinations. The lost rewards and time-outs served could make the animal averse or avoidant of making certain responses in certain stimulus contexts. In particular, the animal could be conditioned not to make primary discrimination responses for mid-level trials. In contrast, the uncertainty response would have the same neutral outcome on every trial and therefore for every subjective impression the animal might have. Viewed against the background of aversion and avoidance gradients, the uncertainty response, whether rewarded or not, could feel the safest and most felicitous in some trial contexts, and could become the default avoidance response. But then it would not be either a true uncertainty response or a report of subjective difficulty. This aversion-avoidance conditioning mechanism is the most often raised objection to metacognition findings in animals. But this concern, too, has apparently never been evaluated systematically.

This was the purpose of Simulation 4. Like Simulation 3, it incorporated well-established associative principles and asked whether a system that operated by these associative rules would produce the typical metacognitive data pattern. We also made Simulation 4 a strong test of this associative mechanism by asking whether one could—using only parameters based in associative principles—recover the metacognitive performance shown in Figure 3. If so, then again the explanatory field would be leveled between associative accounts and metacognitive accounts, and making the theoretical choice between these accounts would require further research.

Method

Simulation 4 was constructed using Simulation 2’s 41-step density continuum, its Sparse and Dense discrimination regions, and its Gaussian perceptual errors. The response decisions in Simulation 4 were made differently, though. We addressed the attraction to Sparse and Dense responses as follows. We assumed that organisms grew averse or avoidant of responding to stimuli in proportion to their error rate on those stimuli. We assumed that there was a decay function of response strength from the best-performed trials in toward the worst-performed trials in the middle regions of the continuum, so that response attractiveness faded rapidly at first with more errors, and then more slowly. The sensitivity parameter of the exponential-decay function, that governs the steepness of the decay, became a free parameter in our model.

To estimate perceived error rates in the task, we gave a simulated observer with a perceptual error of 7 10,000 trials at each of 40 objective density levels (Level 1–41 but not Level 21). These trials were all Forced trials, because the idea of this preliminary analysis was to build a picture of how the simulated observer would fare—in the currency of error rates—when it experienced any possible subjective impression of density. We stored this array of error rates by subjective impression, and this array was available to simulated observers in Simulation 4. Thus, we calculated the attractiveness of the best primary response to be the quantity e^−sensXerrs, where sens is the sensitivity parameter and errs the stored error rate for the subjective impression on a trial. Figure 6 shows this response-strength function as it wanes from both ends to the middle of the continuum where there are often-missed trials. Thus, simulated observers in Simulation 4 had progressively weaker response tendencies for the middle trial levels that constitute the most difficult trials.

Figure 6.

A reinforcement-history/aversion-avoidance portrayal of performance in a density discrimination with a third response allowed for managing response aversion and avoidance. The horizontal axis indicates the subjective impression of the trial. The solid line instantiates the idea that the third response could be the default option when aversion or avoidance weakens the tendency to respond Sparse or Dense. The dotted line instantiates the idea that response strength for the Sparse and Dense responses would wane exponentially going inward as the frequency of errors increased.

We assumed again that the third, default avoidance response had a slight constant attractiveness across the continuum in accordance with its neutral, constant consequence. This threshold attraction level is the horizontal line in Figure 6. The level of the threshold was a free parameter in our modeling, with higher values producing more uncertainty responses over a wider range of the continuum.

One can see in Figure 6 the response strategy that simulated observers obeyed in Simulation 4. They made a primary discrimination response if the reinforcement-based response strength was greater. (They responded Sparse or Dense in this case as their subjective impression was below or above 21.) They made the avoidance response if the default response strength was greater. For Level 1 and Level 41 stimuli generally, the organism would be attracted correctly to the Sparse or Dense response, respectively. For Level 18 and Level 24 stimuli generally, the organism would make more avoidance responses. In the middle range, the constant threshold response strength is higher than that of the reinforcement-based response strength.

Here, too, the modeling procedure was established and executed a priori, with no prior knowledge about its success, and with only the disciplined link between error rate and response aversion and the intuitive link between avoidance and a default response to manage it.

Results

The hill-climbing procedure already described eventually allowed Simulation 4 to find the parameters that recovered as nearly as possible the 120 proportions (3 responses by 40 stimulus levels) shown in Figure 3.

Figure 7 shows the performance of the best-fitting simulated observer. Its sensitivity and threshold parameters were 0.104 and 0.095, respectively. Simulation 4, using only response-avoidance processes, reproduced Figure 3 exactly. The SSD between the corresponding values in Figures 3 and 7 was 0.001. The AAD per data point in the two graphs was 0.002—on average, pairs of observations differed by 0.2%. When a simulated observer based response avoidance on reinforcement history, associative principles reproduced perfectly an apparently metacognitive performance.

Figure 7.

Density discrimination performance by a simulated observer in Simulation 4 that performed as illustrated in Figure 6. Details of the simulation are described in the text. The horizontal axis indicates the objective density of the trial (Levels 1–20 Sparse; Levels 22–41 Dense). The open triangles and diamonds, respectively, show the proportion of Sparse and Dense responses. The filled circles show the proportional use of the third, aversion-avoidance response.

The Chosen-Forced Performance Advantage

Next, we examine the common way of addressing this aversion-avoidance confound—that is, by intermixing trials in which the animal can choose to respond uncertain with trials in which the animal is forced to complete the trial. The rationale behind this approach is that in this case animals can use their privileged metacognitive knowledge to choose trials they will mainly get right and decline trials they will mainly get wrong. As a result, they should show a performance advantage on Chosen trials as compared to Forced trials (for which this selection of favored trials is not possible). The current view is that this Chosen-Forced advantage protects one from the aversion-avoidance confound and points strongly to animal metacognition (Foote & Crystal, 2007; Inman & Shettleworth, 1999; Hampton, 2001). Therefore, it is important to understand this effect clearly so that it can be interpreted judiciously in future research.

Any model of perception has to incorporate perceptual error. Stimuli are not perceived veridically, or even equivalently, from trial to trial. Perceptual error is a grounding assumption of SDT. Moreover, observers can only respond to their perceptions of stimuli; that is, according to the subjective impression the stimulus engenders in them. They have no way to filter the error to get back to the thing in itself.

These facts about perception let one see the Chosen-Forced advantage in a new and constrained light. The advantage emerges because animals have an adaptive way to use perceptual error asymmetrically, even though it occurs symmetrically. Consider again a duration continuum with Levels 1 to 71 and a discrimination breakpoint at Level 36. Given an objective Level 32 trial (a difficult Short trial), a strong short impression (if perceptual error acts downward) will be safe to respond to because the trial is Short, but a weak long impression (if perceptual error acts upward) will produce an error. Likewise, given an objective Level 40 trial (a difficult Long trial), a strong long impression (if perceptual error acts upward) will be safe to respond to, but a weak short impression (if perceptual error acts downward) will produce an error. The rule is that strong subjective impressions are likely to have come from objective stimuli on the same side of the continuum as the impression. Weak impressions may have come from objective stimuli on the other side of the discrimination breakpoint, so error is likely. Responding to strong short and long impressions is a good and safe thing to do. Responding to intermediate subjective impressions is not.

To illustrate this mechanism more systematically, suppose we give a simulated observer objective trials as follows: 500 Level 20s (easy Shorts), 500 Level 30s (difficult Shorts), 500 Level 42s (difficult Longs), and 500 Level 52s (easy Longs). Assume that the observer’s perceptual error is discrete and symmetrical. It misperceives trials with equal probability as 10 levels lower or higher. If this observer sets up response criteria at 31 and 41 on the subjective-impression continuum, it will accept and win all the Level 20 and Level 52 trials. It will accept and win all the 30s that produce Level 20 impressions, and all the Level 42s that produce Level 52 impressions. It will decline the Level 30s that produce Level 40 impressions, and the Level 42s that produce Level 32 impressions, and adaptively so because these trials would have produced errors.

The crucial point is that to use perceptual error asymmetrically like this, the animal does not have to track perceptual error or know its extent or direction. It can’t know this. But the level of the subjective impression alone is enough to decide the question. The subjective impression is correlated with the objective stimulus level. It is also correlated with the magnitude and direction of perceptual error. It is a good cue to use in deciding to accept or decline the trial. But it is a primary, first-order, direct, unmediated perceptual signal. It needs no judgment of confidence, no assessment of prospects, and no support from a metacognitive agency or a cognitive executive. Supporting this conclusion is that the Chosen-Forced advantage emerged in exactly the expected way even in the purely associative systems modeled in Simulations 3 and 4. The Chosen-Forced advantage must therefore be reconsidered carefully by the literature for what it says and does not say about animal metacognition.

Interim Discussion

We have raised three concerns about the comparative literature on metacognition. First, many influential articles have directly rewarded uncertainty responses. This practice is not recommended. It raises the concern—confirmed by Simulation 3—that simple response strengths could underlie uncertainty responses. It compromises the relevant studies because it introduces a plausible associative interpretation. Many studies are significantly compromised by this reward contingency.

Second, there is the problem that trial-by-trial feedback lays down a reinforcement history along a continuum that associative processes let behavior reflect. Animals may come to be averse to some stimuli, and avoid primary discrimination responses to them, using the third, aversion-avoidance response instead as a default or safety response. This also raises the concern—confirmed by Simulation 4—that associative phenomena underlie uncertainty responses. Thus, in many tasks—certainly some of our own studies—it is difficult to discern whether a meta-representational system or a response-avoidance system is used by the animal. This has been the concern raised by other formal-analytic and philosophical accounts of metacognition experiments (Staddon, Jeremie, & Cerutti, 2007; Proust, 2003).

Third, there is the problem of interpreting the Chosen-Forced advantage. This advantage does not always support the idea that animals have privileged metacognitive knowledge that differentiates auspicious and inauspicious trials deserving response or avoidance, respectively. To the contrary, these effects can sometimes be explained using only unsophisticated reactions to first-order perceptual representations. Several studies are compromised by this interpretative problem.

These concerns resonate with existing findings. For example, Smith and Schull (unpublished) found that rats did not recruit adaptive uncertainty responses for the difficult trials near their discrimination threshold. Uncertainty responses in that study were unrewarded. Foote and Crystal (2007) found that rats did use uncertainty responses adaptively for difficult trials. Uncertainty responses in that study were directly rewarded. One can interpret this difference in the light of Simulation 3, with direct rewards granting the uncertainty response its own positive response strength.

Likewise, Beran, Smith, Couchman, and Coutinho (2007) gave six capuchin monkeys two density-discrimination tasks. In one task, difficult stimuli could be avoided through an Uncertainty response. In the other task, the same stimuli could be rewarded through a Middle response. Capuchins used the Middle response but essentially did not use the Uncertainty response. This dissociation occurred even within individual animals and even from one session to another.

It is theoretically important that rats in Smith and Schull (unpublished) and capuchin monkeys in Beran et al. (2007) failed to make uncertainty responses when the associative support for these responses was removed. That animals lose a target behavior when denied an aspect of the situation marks that aspect of the situation (here, the associative support for uncertainty responses) as important to the behavior. But these results also underscore the concerns expressed in the present article.

Together, the three concerns ground a provisionally negative assessment of research in this area. They also raise important questions. How can the field best move beyond these problems? What should the next phase of research in this field look like?

Next Steps and Positive Approaches

Pure, unreinforced uncertainty responses

One negative feature of existing research is the direct rewards given for uncertainty responses. Though this has become common practice, it creates interpretative problems.

Accordingly, one critical next step is to find ways to train animals to use purer uncertainty responses that have a simpler, trial-decline functionality because they have no positive consequence except to remove a difficult trial and bring on the next one.

Illustrating this approach, Beran et al. (2006) placed monkeys into a numerosity-judgment task in which they judged whether arrays of dots had lesser or greater numerosity than a learned central value that was never presented and that changed daily. Of course trials nearest the central value were the most difficult for the animals. Monkeys were able to use the uncertainty response adaptively to decline these difficult trials, even though this response had no consequence except to end one trial and begin another.

It is recommended in light of the present article that researchers put more effort toward studying this kind of pure uncertainty response. We believe this is an essential step toward building stronger paradigms in this area because it insulates metacognitive data patterns from patent behavioral interpretations.

Dissociating uncertainty responses from aversion and avoidance

However, that essential step is not sufficient to demonstrate animal metacognition convincingly. We saw in Simulation 4 that the interaction of aversion-avoidance gradients (based in the animal’s perceived reinforcement history) with a neutral uncertainty response (never rewarded but also never punished) could also recreate typical data patterns in this area. Therefore, another constructive step would be to eliminate the animal’s perception of reinforcement, or its ability to track it, and in that way dissociate difficulty (and perhaps the mental state of uncertainty) from reinforcement-based response strengths.

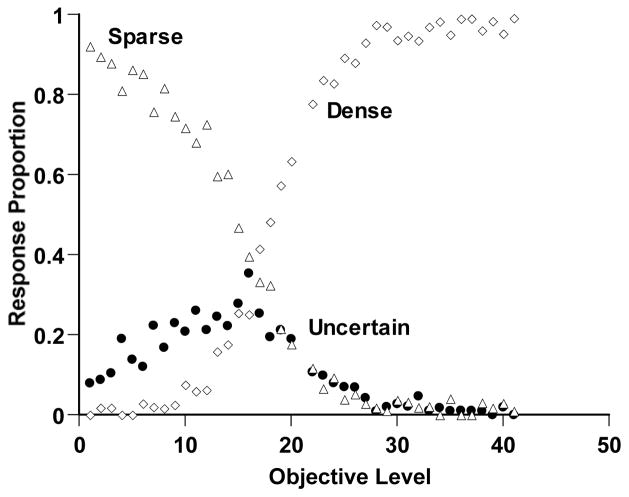
Smith et al. (2006) illustrated this approach by targeting the problem of trial-by-trial reinforcement and aversion reactions to poorly reinforced stimuli. They trained a monkey to perform blocks of trials, with all reinforcements deferred until the block’s end and moreover scrambled out of trial-by-trial order. They did this to prevent the association of consequences back to specific trials and to prevent the processes of conditioning. Then they transferred the animal to new discriminations in which it had never received trial-by-trial reinforcement and in which it could not have built up useable reinforcement histories along a continuum. Figure 8 shows the result from an animal who still made adaptive uncertainty responses in this situation.

Figure 8.

Sparse-Dense discrimination performance by a monkey in the experiment of Smith et al. (2006). The horizontal axis indicates the objective density of the trial (Levels 1–20 Sparse, Levels 22–41 Dense). The open triangles and diamonds, respectively, show the proportion of Sparse and Dense responses. The filled circles show the proportional use of the uncertainty response for different trial levels.

We subjected this result to the same formal scrutiny given other results above, by asking whether avoidance reactions given a stored reinforcement history could explain it. The details of this formal analysis are given in the Appendix. Figure 9 shows the best fit that the reinforced-based model could achieve. The fit was poor—the error of prediction per data point was 5% and this is large in almost all formal-analytic domains. From Levels 1 to 31, the theoretically important uncertainty response was mispredicted on average by 7% per stimulus level. Though some of this misfit resulted from fitting an animal’s real and variable performance, the principle reason for it is that the animal’s response curves, especially his uncertainty curve, were displaced to the left from the reinforcement structure of the task that was centered at Level 21. In fact, the animal responded Uncertain the same amount at Level 12 (when he was 92% correct when he tried the trial) and Level 20 (when he was only 22% correct when he tried the trial). This shows that his uncertainty responses were not based on reinforcement history. If he had somehow tracked the associative history of these latter trials, or tracked the frequent negative consequences of primary responses to these trials, he would have been strongly conditioned to avoid primary responses on these trials and he would have bailed out of far more of them. He did not.

Figure 9.

Density discrimination performance by a simulated observer that performed as illustrated in Figure 6. Details of the simulation are described in the text and Appendix. The horizontal axis indicates the objective density of the trial (Levels 1–20 Sparse; Levels 22–41 Dense). The open triangles and diamonds, respectively, show the proportion of Sparse and Dense responses. The filled circles show the proportional use of the third, aversion-avoidance response.

In some respects, this result from Smith et al. (2006) is powerful because it shows for the first time that uncertainty responses can be dissociated from reinforcement and associative mechanisms. Thus, we believe that this approach of deferred/rearranged reinforcement may play a constructive role in future studies of comparative metacognition. After all, humans in real test situations often perform blocks of trials (whole tests) and then receive only deferred, summary feedback (their grade!).

This approach may also contribute to other lines of comparative research. Behavioral researchers have commonly made the contingencies regarding reward and punishment for responses made in different stimulus contexts transparent to animals through direct and immediate feedback signals. But doing this is not mandatory. By removing immediate reinforcement from the situation, one may open a new window on animals’ choice and decision processes when these are dissociated from reinforcement.

However, in other respects, Smith et al.’s (2006) result has limitations. Only one monkey showed the crucial result. Moreover, in line with the formal-analytic perspective of this article, it is possible that the associative model could be amplified with additional parameters, perhaps assuming that the animal stored reinforcement history asymmetrically across the continuum, somehow encoding or remembering rewards on Dense trials better than rewards on Sparse trials. This could have moved his response curves to the left. One would have to justify carefully imputing this asymmetrical process to the animal, explaining why the animal would have developed an asymmetrical sense of reinforcement when 1) he demonstrably did not track the task’s reinforcement structure, and 2) he was associatively punished for the asymmetrical response strategy he selected (e. g., because he was below chance on several stimulus levels).

Readers will see that the result from Smith et al. (2006) juxtaposes two forms of explanatory parsimony. One might explain the performance in a gradient-based way, using a complex mathematical model that makes psychological assumptions that at present may not be justified. Or, one can explain the performance using a more sophisticated decisional process based in uncertainty that allows a simple performance model based on difficulty declined.

Immediate Transfer

The immediate transfer of the uncertainty response to new tasks may provide another kind of protection from associative interpretations, as transfer has often been judged to do in comparative studies. Regarding associative interpretations, it is not enough that the uncertainty response has a positive response strength. If this were the only force at work, the animal would escape a constant proportion of trials across the stimulus continuum. But this is not what animals do and this would be a nonoptimal strategy wasteful of many easy and rewarding trials. In addition, then, the animal must have constructed response-strength gradients for the primary responses, too, so that it can know the trials deserving avoidance. But given an untrained stimulus domain, animals cannot have built up stimulus- or reinforcement-based generalization gradients that could prompt avoidance responses.

Illustrating the task-transfer approach, Washburn et al. (2006) showed that rhesus monkeys could generalize their use of the uncertainty response even to the first trial of other tasks. Washburn et al. borrowed Harlow’s learning-set approach, giving animals a series of novel two-shape discrimination problems (6 consecutive trials with each problem). The monkeys could respond to a shape to try to win the trial directly, or they could respond Uncertain and receive a hint about the problem’s answer. Washburn et al. found that monkeys made more uncertainty responses on Trial 1 of a discrimination problem, when they could not know the answer. They made fewer uncertainty responses on Trials 2–6, when they could know and demonstrably did know the answer. In a sense, these monkeys demonstrated an uncertainty-based learning set that it is an interesting complement to the outcome-based learning set that Harlow demonstrated (Win-Stay; Lose-Shift). Harlow’s monkeys had to risk an error on Trial 1 to gain information about the problem. Washburn et al.’s monkeys had the uncertainty response as a safer route to that information. This result showing instantaneous transfer with no contingency training discourages associative interpretations and encourages uncertainty-based interpretations of the use of the uncertainty response.

However, task transfer does not necessarily confer protection against the associative mechanisms considered in this article. For example, Kornell et al. (2007) trained first the primary contingencies in the transfer task (allowing the construction of stimulus- and reinforcement-based gradients) and then the uncertainty-judgment phase was added. It is possible that the uncertainty response carried forward into the new task its constant response strength borne of being directly rewarded in that study. Then, escape from the difficult trials would be predicted based not on metacognition but on the interaction among established response gradients that was explored in the simulations in this article.

Abstract cognitive domains

The use of the uncertainty response in abstract cognitive domains can also provide protection against associative interpretations. Associative interpretations depend on stimulus-based gradients of similarity generalization or reinforcement history. Abstract and derived cognitive judgments lack this basis by definition. For example, some studies have asked whether animals and humans respond uncertain adaptively when a trace in memory is indeterminately or ambiguously active (Hampton, 2001; Kornell et al., 2007; Smith et al., 1998). Unlike in the perceptual tasks used by Smith et al. (1997) or Foote and Crystal (2007), in which there were stimuli possibly linked to aversion, avoidance, or particular reinforcement histories, in the three memory studies the discriminative cue was an internal and trial-specific representation of a remembered item. This result is less open to associative criticisms and could verge on a demonstration of metamemory in animals—depending on the cognitive sophistication one grants to the monitoring of memory trace strengths.

However, the memory studies did have limitations. All three provided trial-by-trial reinforcement. Hampton and Kornell et al. directly rewarded uncertainty responses. Hampton’s inference of metamemory depended critically on the Chosen-Forced advantage. Here one sees by turns all of the methodological approaches that have been evaluated negatively in this article. In addition, some might view trace strength as an unsophisticated discriminative cue that animals can use associatively much as they use perceptual stimuli.

In our view, these limitations do not invalidate the important principle embodied by these studies. Their goal is to make tasks more cognitive, sophisticated, elaborated, and symbolic, and in that way to distance performance and uncertainty responses from the traditional senses of stimulus control and associative responding. This principle is sound, though it may be that the trace-strength studies did not go far enough up the scale of sophistication to show a form of metamemory that will convince all readers. But this is a comment on the present waypoint, not the final destination. If the animal reported uncertainty about episodic, biographical, past memories that involved ‘time travel,’ these uncertainty responses would show metamemory in its full form.

We point out that the SDT model used in the present article would be equally well applied to performances that concern representations at all levels in the cognitive system, those involving conditioned stimuli, memory trace-strengths, levels of episodic memory retrieval, conscious feelings of knowing, and up to and including the explicit and declarative meta-representations that characterize full human metacognition. Therefore, it is an important point that the potential applicability of the decision model cannot help one assess a performance’s metacognitive status. Instead, one must query carefully the relevant processes, representations, and meta-representations to make that assessment, and one must particularly in animal studies eliminate the operation of the simpler, associative response bases. This process/representation focus is critical in pursuing metacognition comparatively and equitably.

Retrospective judgments

The use of retrospective judgments in uncertainty tasks may also have a constructive role to play in future studies. For example, Kornell et al. (2007) and Shields et al. (2005) let animals complete their response on trials, and then after that response asked them whether they would risk large or small timeouts for the chance of earning large or small rewards. In essence, these studies used a behavioral betting response or confidence judgment. This approach also makes associative interpretations difficult, because the instrumental or discriminative behavior on the trial has already occurred, and now the animal is being asked how it feels about the outcome landscape of that trial.

Unfortunately, both studies of retrospective confidence judgments fell short of the mark, creating a need for further research. (Note: our laboratory produced the second of these studies--there is direct self-criticism here, too.) In Kornell et al., the so-called high-risk and low-risk responses were qualitatively different in effect, and cannot be said to have formed a scale of confidence. Moreover, the low-risk option was in reality a no-risk option that brought the animal a guaranteed reward. In Shields et al., there were low-risk and high risk icons available for both sparse and dense trials separately. Therefore, animals could have used these icons to mean super sparse, sparse, dense, and super dense, which is not the same thing as rating one’s confidence of correctness.

More study of retrospective confidence judgments by animals is clearly warranted.

Conclusions

We have raised a variety of concerns about the comparative literature on metacognition, including that many influential articles have directly rewarded uncertainty responses and that many paradigms have provided trial-by-trial reinforcement in a way that could elicit uncertainty responses associatively. In these cases, it is difficult to discern whether a meta-representational system or a response-avoidance system is used by the animal. These concerns ground a provisionally negative assessment of a substantial portion of research in this area.

There are ways to begin to address the associative mechanisms that still shadow the target phenomena in this field, including the use of pure, unrewarded, uncertainty responses, immediate transfer to untrained stimulus domains, and dissociations that let one study animals’ monitoring and decision processes when the animals are denied the reinforcements that would let them construct stimulus-response associations. These are promising techniques that deserve more study. This study is just beginning as this area of research enters its second phase. These newer, positive approaches have by no means solved the problem of animal metacognition, and there is still generous room for new innovations that will bring the animal metacognition paradigms nearer to their human counterparts. There is promise, though, that this research area can move beyond the associative mechanisms described in this article, and there is preliminary evidence that some species may meet more stringent tests of their uncertainty systems.

In the end, though our assessment is partially negative, we emphasize that we view this area of research as a distinctive one within comparative cognition. It is distinctive for its ongoing efforts to ground itself in traditional behavioral approaches and careful behavioral analyses while seeking disciplined ways to transcend those traditions (e.g., by showing that stimulus and reinforcement gradients can be dissociated away from the phenomenon of uncertainty responding). This article is part of these ongoing efforts, and it is a positive sign that there are sufficient studies in this new field for this article to summarize, to characterize, and to try to strengthen. Our hope is that sharper paradigms will lead to safer inferences in this area, especially by distancing the findings and the conclusions from associative and behavioral explanatory frameworks. In this way, this field will best fulfill its potential to open new windows on animals’ minds. This potential is all the stronger because so many insightful scholars are working to advance this discipline.

Appendix

Figure 8’s data were fit using Simulation 4’s 41-step density continuum, Sparse and Dense discrimination regions, and Gaussian perceptual errors. We assumed again that observers were exponentially averse or avoidant of responding to subjective impressions in proportion to their error rate on them. The sensitivity parameter governing the exponential function again became a free parameter in our model.

Initially, we fit the data shown in Figure 8 using Simulation 2’s model to find out this animal’s basic operating characteristics. His perceptual error was estimated to be 7, much like that of other monkeys we have tested. The breakpoint of his discrimination was Level 16, even though the objective breakpoint of the discrimination was Level 21. His uncertainty region was estimated to be six levels wide (Levels 13 to 19).

Next, we gave a simulated observer with a perceptual error of 7 and a discrimination crossover of 16 10,000 trials at each of 40 objective density levels (Level 1–41 but not Level 21). This gave us a picture of the reinforcement history that this monkey would actually experience in this task (if, despite deferred feedback, he had been able to track it). We stored this array of error rates by subjective impression, and this array was available to simulated observers. Thus, as in Simulation 4, we calculated the attractiveness of the best primary response to be the quantity e^−sensXerrs, where sens is the sensitivity parameter and errs the stored error rate for the subjective impression on the trial. We also gave the uncertainty response a threshold attractiveness as the neutral default response for coping with response avoidance. This threshold value was also a free parameter in the model.

The hill-climbing procedure already described allowed us to find the parameters that recovered as nearly as possible the 120 observations (3 responses by 40 stimulus levels) shown in Figure 8. The best-fitting sensitivity and threshold values were 0.061 and 0.048, respectively.

However, the fit of the reinforcement-based model to the target pattern was poor. The SSD between the values in Figures 8 and 9 was 0.5648, 403 times as large as that found in Simulation 4. The corresponding AAD was 0.0514, 20 times as large as found in Simulation 4.